Survival Analysis

Clinical and epidemiologic studies describe how an outcome is affected by an exposure. Incidence rates describe the effect of the exposure on the outcome. Oftentimes clinical studies are designed so that the desired endpoint can be reached in a short enough period of time to ensure that all observations can be made with minimal dropout and an effect that is fairly constant over time.

Sometimes, however, the desired outcome cannot be observed in the short term. In the case of a failure rate, such as number of deaths, the investigator may want to follow a cohort of patients for a longer period of time in order to follow the number of deaths as a function of time. Specifically, the investigator could be looking to quantify the effect as a function of time.¹

Survival time is defined as the time until failure.² In clinical studies, the failure being investigated is often death. Survival analysis describes the methodologies used in biostatistics to quantify and describe survival time and to examine the magnitude of differences in survival time. This review will focus on these methodologies, particularly actuarial life-table analysis and the Kaplan-Meier product limit method.

The Dilemma of Survival Time

In an ideal situation, a study would be designed to cover a time interval that guarantees that an entire cohort of patients enter a reached at the same time and exit the study because they reached the outcome of interest (such as death) before the study period was completed. A group of elderly patients over the age of 85 on a specific drug could be selected as a cohort to be followed for 20 years to examine survival. In this case it is likely that most, if not all, patients will die before the study period is completed.

The ideal situation would also require that all patients enter the study at the same time. All subjects would begin the exposure at the same time. Patients would not leave the ideal study, resulting in zero loss to follow-up. All patients who began the study would stay in the study until the outcome of interest was achieved.

Such conditions are rarely possible. To follow a large group of patients until each one dies is often not practical. Frequently, patients have already begun their exposure prior to entering the study. Patients are sometimes recruited for entry after the study period has already started. Finally, subjects in the real world are lost to follow-up. These conditions require certain accommodations to be made in the study design and analysis. One approach would be to discard all of these observations and calculate simple proportions; however, this would result in a significant loss of statistical power. An alternative is to develop statistical strategies to account for and obtain information from the subjects with incomplete data; these strategies form the backbone of survival analysis.

When an observation that is entered into survival analysis is obtained either before the patient achieves the desired outcome or with incomplete data because the patient is lost to follow-up, the observation becomes known as a censored observation. Data which represent observations on patients who enter a study at different times and thus with varying degrees of exposure are said to be progressively censored. Survival analysis permits the investigator to make observations and comparisons even when censoring occurs.

Survival analysis needs to be distinguished from simpler measures of survival. Both person-years of observation and mortality rates, two frequently cited measures of survival, present challenges when used to analyze survival. For example, person-years are calculated based on the number of days each patient contributes to a study. However, the same number of additional person-years accrues from one patient contributing 10 years as by 10 patients contributing 1 year. For a mortality rate to describe survival accurately, it can only be calculated when the entire length of the study has passed. When using mortality rates to describe survival, the rate will be significantly lower at the beginning of the time period than at the end of the time period; thus mortality rates depend on when the data are analyzed.³ Survival analysis corrects for some of the shortcomings of these simpler survival measures. We will describe the two major methods used for survival analyses, life table (or actuarial) and the Kaplan-Meier method, and provide examples below.

Life-Table or Actuarial Analysis

First described in 1958 by Cutler and Ederer, life-table analysis provides a straightforward, easy-to-perform method of analyzing survival.⁴ Their method takes into account both patients who are lost to follow-up and who are censored because they are still alive at the completion of the study. Data are organized into tables and are grouped within intervals of fixed length.²

Table 1 shows the makeup of a life table. The first column of the table identifies the interval. Columns 2 and 3 indicated the number of patients alive at the beginning of the interval and the number who died during the interval. Columns 4 and 5 show the numbers lost to follow-up and the numbers withdrawn alive during the interval. Withdrawn alive indicates that the subject withdrew from the study prior to the close of the interval but was known to be alive at the time of withdrawal. Column 6 shows the effective number of patients who were exposed to the risk being studied.

Table 1.

Actuarial (Life-Table) Analysis

Interval	Number of Patients at the Beginning of the Interval	Number of Patients Who Died During the Interval	Number of Patients Lost to Follow-up During the Interval	Number of Patients Withdrawn Alive During the Interval	Number of Patients Exposed to Risk of Death	Conditional Probability of Death	Conditional Probability of Survival	Survival Rate
X	Nx	Dx	Lx	Wx	Ex=(Wx+Lx)/2	Qx=Dx/Ex	px=1-Dx/Ex	Px=p1×p2×···px
1	N1	D1	L1	W1	E1	Q1	p1	P1
2	N2	D2	L2	W2	E2	Q2	p2	P2

The number of patients is said to be effective because it takes into account those observations censored because the subjects were withdrawn alive or lost to follow-up.⁵ This brings up an important point about actuarial analysis: it assumes that patients who withdraw from the study do so randomly throughout the interval. As a result, it is thought that patients withdraw, on average, halfway through the interval and the denominator is reduced by half.³

The next columns are the conditional probabilities of death and survival. The probability of survival is known as the survival function and measures the proportion of those individuals who have not yet failed during the interval. Since the probability of surviving one interval is dependent on surviving previous intervals, the cumulative survival rate is based on multiplying the survival rates from all the previous survival intervals (ie, p₁ × p₂ × ... p_x).

Life-table analysis is also called actuarial analysis because it is based on methodologies frequently used in actuarial circles to calculate insurance rates based on mortality risks and subsequent benefit payments. In fact, most life tables are cross-sectional or current. This indicates that the individuals being studied at different intervals do not represent the same individuals. Rather, they represent different subjects who are alive at the same time but representing different time intervals. For example, an interval might represent a decade of life. The individuals of intervals 10–20 and 21–30 do not represent the same group of individuals followed for progressive decades. Instead, one cohort of individuals enters at age 10 and another at age 20 with both groups being studied simultaneously. This is in contrast to a longitudinal life table in which a group of individuals is followed over a long period of time. The same group passes from one interval to another.

Life-table analysis can also be presented graphically as a survival curve that plots time versus cumulative survival. Because the number of patients diminishes as time progresses, the standard deviation of the estimate of the proportion surviving increases. As a result, 95% confidence bands for each interval are often shown.³

Life-table analysis provides easy-to-understand and easily performed analysis of data obtained at predetermined intervals. It assumes that withdrawals occur randomly throughout the interval and, if the sample size is large, will occur, on average, halfway between each interval. It also assumes that the probability of survival at one interval, though conditional on surviving previous intervals, is independent of the probability of survival at the prior interval(s).

The first assumption is easily fulfilled when the intervals are short. As the length of the interval increases, however, this assumption becomes less likely. An investigator may be interested in studying patients who can enter a study at any point. The investigator may wish to orient the study around when a patient dies rather than when a predetermined interval is completed.³ The Kaplan-Meier product-limit method of survival analysis can be used in these cases.

The Kaplan-Meier Product-Limit Method

The survival function is defined as the number of subjects who have not yet failed (or died) divided by the number of subjects at the start of the study (subjects at risk). The goals of both the life-table and product-limit methods of survival analysis are to compute this survival function.

The Kaplan-Meier product-limit method uses exact survival times rather than intervals to analyze survival. Given that most survival curves are not normal and tend to be skewed to the right, the nonparametric nature of Kaplan-Meier analysis makes it more appealing to use for most clinical and epidemiologic studies.

As with the actuarial method, the product-limit method is also calculated in tabular form. Time becomes the reference point and divides the different points of calculation of the survival function, as in the actuarial method. With this method, rather than listing time in terms of predetermined intervals, we mark time in terms of the time of a failure or when censoring occurs. Therefore, the time between intervals varies based on when an event (failure) occurs or a subject is censored. Next, we delineate the numbers of patients at the beginning of each interval and the number of deaths by the completion of the interval. Finally, the new survival function is calculated as the product of the survival functions of the previous intervals.

As with life-table analysis, Kaplan-Meier analysis can be presented as a survival curve in addition to tabular form. As with survival curves for life-table analysis, time is plotted on the x-axis and the survival function is plotted on the y-axis. Standard errors can be calculated in a similar fashion as with life-table analysis.

Usually the goal of a study is not merely to assess the survival of one group of subjects. The investigator may want to compare the survival between two groups. For purposes of hypothesis testing, it is necessary to use a nonparametric method for statistical analyses as survival is rarely normally distributed with a right tail reflecting long survivors. The Wilcoxon rank sum test can be used to compare survival in groups where no censoring occurs. If the data do include censored observations, then the log-rank test or the Mantel-Haenszel chi-square statistic can be used to compare survival curves.

As with the other techniques, the log-rank method tests the null hypothesis that there is no difference in the survival time in the two groups being compared. The log-rank test involves comparing the observed and expected number of failures and setting up a chi-square statistic to test whether this difference is zero. The P value tests the likelihood that the difference from zero could be due to chance alone. The calculation is difficult and is usually performed with a computer program.

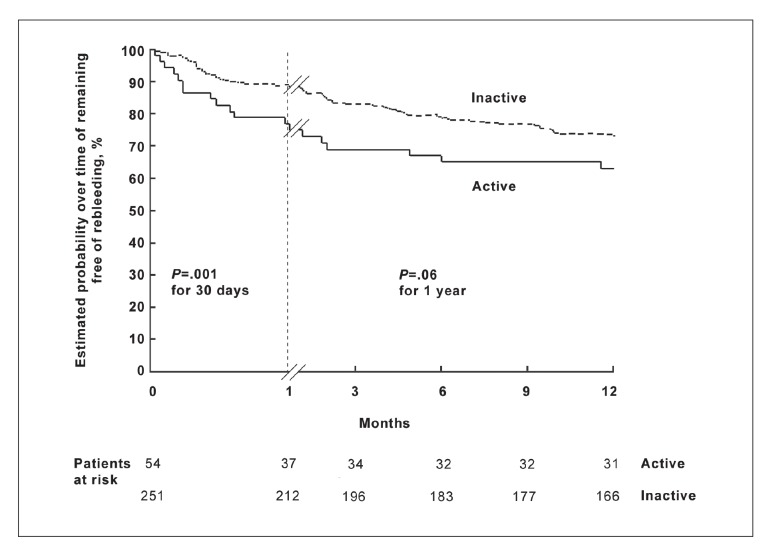
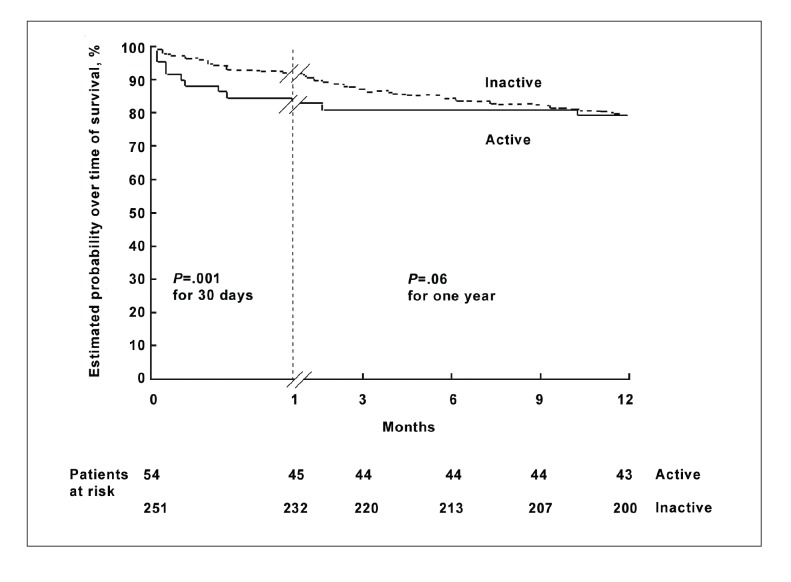
As an example, in a study of the prognosis of patients presenting with acutely bleeding esophageal varices at endoscopy, Lo and colleagues⁶ used Kaplan-Meier survival analysis to compute, and the log-rank test to compare, the survival function among groups of patients with both active and inactive bleeding at the time of endoscopy.⁶ As shown in Figures 1 and 2, the authors compared the groups in terms of two types of failures: the recurrence of variceal bleeding and death. In both analyses, the active bleeding groups appear to have higher failure rates than the inactive groups.

Figure 1.

Probability of rebleeding among patients with actively and inactively bleeding esophageal varices seen on initial endoscopy. The difference in risk of rebleeding was significant at 1 month but not at 1 year.

Reprinted with permission from Lo et al.⁶

Figure 2.

Survival among patients with actively and inactively bleeding esophageal varices on initial endoscopy after 1 month and 1 year. While the difference in survival was significant at 1 month, it was not significant at 1 year.

Reprinted with permission from Lo et al.⁶

The authors compared the groups at intervals of 30 days and 1 year. In the analysis of the risk of recurrent variceal bleeding, the active bleeding group had a significantly higher risk of failure than the inactive bleeding group after comparison using the log-rank test at 30 days (P=.01) but not at 1 year (P=.06). Similarly, the estimated mortality was significantly greater in the active bleeding group at 30 days (P=.03) but not at 1 year (P=.90). The authors concluded that rates of recurrent bleeding and mortality were significantly higher among patients with active bleeding on endoscopy at 1 month but similar after 1 year to those of patients with no active bleeding on endoscopy. In this case, survival analysis allowed the authors to compare bleeding episodes and deaths during predetermined intervals as a function of time, providing direct point-to-point comparisons in both the exposed (actively bleeding at time of endoscopy) and nonexposed groups. The survival function allowed comparisons of mortality via the log-rank test. In addition, comparisons of the two groups as simple proportions surviving would likely not be adequately powered to achieve statistical significance, a hurdle overcome by survival methodology.

Once the observed and expected numbers of deaths are tabulated, the investigator can further use this information to calculate a hazard ratio. As with an odds ratio, a hazard ratio describes the proportional increase in risk of failure in the exposed group. If one were comparing survival curves for patients who had and had not been exposed to a toxic substance, and found a hazard ratio of 3 for early death, it would indicate that the estimated risk of death in the group exposed to the toxic substance is three times that of the risk of death in the nonexposed group.

An example of the use of the hazard ratio can be found in a paper by Merion and associates⁷ on the survival benefit of liver transplantation in which they compared the likelihood of 1-year mortality for patients transplanted (ie, exposed) versus those remaining on the waiting list (not exposed) at any given Model for End-stage Liver Disease (MELD) score. The authors found that at a MELD score of 18–20 the hazard ratio was 0.62 (P<.001), indicating that the risk of death was 38% lower in patients transplanted than those who were not transplanted. In contrast, for patients with low MELD scores the risk of death at 1 year was higher in transplanted patients. For patients with MELD scores between 6 and 11, the hazard ratio was 3.64 (P<.001), indicating that patients receiving transplants with these MELD scores had a 3.64 times higher risk of death than those who were not transplanted. The authors concluded that liver transplant survival benefit at 1 year is greatest in those who have higher risks of pretransplant death and lower among those at the lowest risk of pretransplant death as assessed by MELD.

Summary

Both the actuarial and Kaplan-Meier methods allow for analysis of survival rates in incomplete, censored data. The actuarial method uses a simple technique for measuring survival based on data accrued during predetermined intervals while the Kaplan-Meier method, which is preferable for most clinical trials, calculates the survival function based on intervals measured with reference to death or censoring. In summary, techniques of survival analysis provide the investigator with tools to account for the problem of relatively short periods of follow-up and attrition and to account for the effect of time in analyses of survival and other clinical and epidemiologic questions.