Climate change is projected to have severe impacts on the frequency and intensity of peak electricity demand across the United States

Significance

The existing empirical literature on the impacts of climate change on the electricity sector has focused on changing electricity consumption patterns. In this paper, we show that incorporating impacts on the frequency and intensity of peak load consumption during hot days implies sizable required investments in peak generating capacity (or major advances in storage technology or the structure of electricity prices), which results in substantially larger impacts than those from just changes in overall consumption.

Abstract

It has been suggested that climate change impacts on the electric sector will account for the majority of global economic damages by the end of the current century and beyond [Rose S, et al. (2014) Understanding the Social Cost of Carbon: A Technical Assessment]. The empirical literature has shown significant increases in climate-driven impacts on overall consumption, yet has not focused on the cost implications of the increased intensity and frequency of extreme events driving peak demand, which is the highest load observed in a period. We use comprehensive, high-frequency data at the level of load balancing authorities to parameterize the relationship between average or peak electricity demand and temperature for a major economy. Using statistical models, we analyze multiyear data from 166 load balancing authorities in the United States. We couple the estimated temperature response functions for total daily consumption and daily peak load with 18 downscaled global climate models (GCMs) to simulate climate change-driven impacts on both outcomes. We show moderate and heterogeneous changes in consumption, with an average increase of 2.8% by end of century. The results of our peak load simulations, however, suggest significant increases in the intensity and frequency of peak events throughout the United States, assuming today’s technology and electricity market fundamentals. As the electricity grid is built to endure maximum load, our findings have significant implications for the construction of costly peak generating capacity, suggesting additional peak capacity costs of up to 180 billion dollars by the end of the century under business-as-usual.

Integrated Assessment Models (IAMs) used to estimate the US government’s social cost of carbon include large costs due to changes in electricity demand resulting from climate change (1–3). The Climate Framework for Uncertainty, Negotiation, and Distribution (FUND), for example, estimates the majority of the costs of climate change to result from the additional cost of cooling (4). However, FUND and the other IAMs rely on a highly simplified and outdated estimate of the relationship between rising temperatures and heating and cooling costs (5, 6). At the same time, future capital investments in electric generation capacity require accurate, region-specific forecasts of future electricity demand. Many aspects of these forecasts are well understood: electricity demand tends to rise with population, income, and the presence of energy-intensive industries (7). However, because electricity use by residential, commercial, industrial, and agricultural customers is strongly affected by ambient temperature, climate change-induced changes in temperature are likely to significantly affect future generation, transmission, and distribution requirements relative to a world with a stationary climate. As the electricity grid is designed for maximum load days, which tend to be the hottest days in many areas, the increasing intensity of extreme heat days will require additional investments in peak generation capacity, transmission, or storage.

Prior work has examined the relationship between electricity load, i.e., the quantity of electricity demanded, and temperature at the regional and local level. Estimates to date have focused primarily on aggregate consumption impacts, using state-level monthly averages of residential electricity load (8, 9), high-frequency data at the single-state or regional level (10–13), and residential billing data from electric utilities (14). The majority of this literature is based on California and the American South. The applicability of these state-level or regional results to a broader geographical area may be limited. Prior efforts to quantify peak impacts had to rely on structural models and highly aggregated consumption data (15). We estimate peak and consumption impacts of climate change for the United States as a whole using observed high-frequency data.

We contribute to this literature by considering capacity impacts, driven by variability in impacts across space and time. This analysis is made possible through the construction of a high-frequency dataset of electric load. We examine the temperature responsiveness of daily consumption and peak load across the United States, now the second largest producer and consumer of electricity in the world. In 2012, the United States alone composed approximately 20% of the world electricity market, producing greater quantities than all of Europe combined, and second only to China. In sum, our paper combines spatially disaggregated high-frequency data on regional electricity load and temperature across the United States with regional climate predictions, allowing us to simulate disaggregated changes in future electricity demand resulting from climate change based on observed instead of modeled behavior.

Specifically, we construct a dataset that combines fine-scaled electricity load data and comprehensive sectoral coverage with daily weather patterns. We use this dataset to estimate separate temperature response functions for 166 distinct load zones (for our definition of load zones, see SI Appendix, Compilation of Energy Consumption Data). We exploit the richness of our data to document nonlinearities in the response functions. We also introduce a method that allows us to forecast beyond the support of the temperature distributions we observe, focusing on the “tails” of the temperature distribution to properly estimate changes due to the increases in extreme temperature expected as a result of climate change.

Because electricity cannot currently be cost-effectively stored at scale, hour-to-hour variability in demand significantly impacts production costs. Because electricity planners in the United States often use reserve margins (capacity requirements above forecasted peak load) of 15 to 20%, the response of peak load to climate change will translate directly into increases in capital costs, even if the average generation impacts are not large. Noting that a significant share of the levelized cost of electricity generation is composed of capital costs (7), we again use the high frequency of our time series data to estimate separate response functions and predictions for both average and peak loads. In particular, we use multiple regression analysis that exploits interday variation. We find that peak load responds more strongly to increases in temperature, suggesting that required increases in generation (or storage) capacity investments may be significantly larger than previously thought.

Next, we combine these results with projections of future temperature change from a set of downscaled climate projections under two Representative Concentration Pathways (RCPs) to estimate the change in both average and peak loads due to climate change. We demonstrate how these predictions vary spatially, as a result of regional differences in both temperature response curves and climate projections. Overall, if the US had faced, over the past decade, the warmer climate that scientists predict for the future, our results show that much greater generation or storage capacity would have been needed. As such, even absent population and income changes, climate change will demand significant changes to the electric grid. We conclude by discussing scenarios under which technology, policy, or market changes would mitigate these effects.

Results

We estimate separate temperature response functions for average and peak loads for every load zone in the data. SI Appendix, Fig. S1 displays the load zones in our sample. For simplicity of display, we first visually show results for the two largest Independent System Operators (ISOs) in our data: the Electricity Reliability Council of Texas (ERCOT) and the PJM Interconnection. ERCOT covers Texas only and can be thought of as more representative of warmer regions. PJM covers parts of Delaware, Illinois, Indiana, Kentucky, Maryland, Michigan, New Jersey, North Carolina, Ohio, Pennsylvania, Tennessee, Virginia, West Virginia, and the District of Columbia, and it can be thought of as representative of colder regions.

Temperature Response Functions.

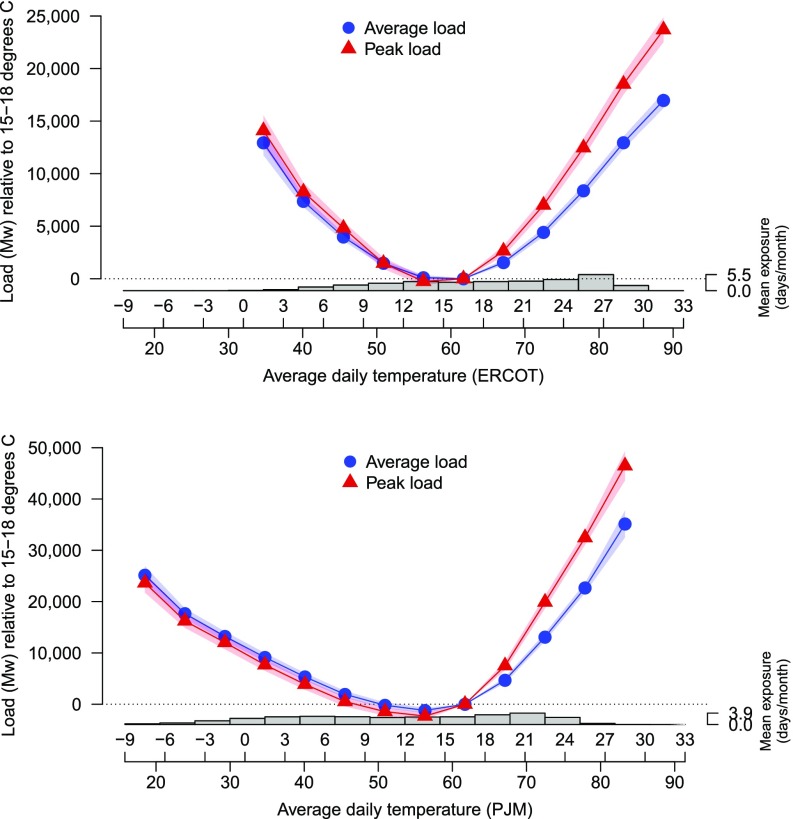
We estimate temperature response functions for daily average and peak loads. Fig. 1 documents response functions for ERCOT and PJM with minimal restrictions on the functional form that the responses take. Visual inspection of these lines suggests that imposing a linear model above roughly 21 °C may be an appropriate fit for higher temperatures, a hypothesis we will return to in order to conduct climate impact projections. The height of the blue lines at each temperature represents the differences in average load (in megawatt hours) for that temperature relative to the omitted category, a day with average daily temperature between 15 °C and 18 °C. The height of the red lines represents the same difference for peak load. We also plot a histogram of the temperature distribution for these ISOs on the same graph to show the support of the data used to identify these curves statistically. SI Appendix, Figs. S3 and S4 display the estimated response functions for all load zones in our data.

Fig. 1.

Daily electricity temperature response functions, average (total hourly load/24) (blue) and peak (max hourly load) (red). Each point estimate represents the effect of replacing a day with average temperature in the omitted category (15 °C to 18 °C) with a day of the relevant average temperature. Regressions use as controls: precipitation, day of week fixed effects, month of year fixed effects, and a sixth-order Chebychev polynomial in time. The 95th percentile confidence intervals are estimated using Newey–West standard errors. ERCOT (Top, relatively warm) and PJM (Bottom, relatively cold) are the two largest ISOs in the data. Histograms at the bottom of each panel display the average number of days per month in each temperature bin.

Temperature responses are predominantly driven by the extent to which an area heats or cools with electricity. ERCOT, which exclusively serves Texas, has nearly symmetric response functions for both average and peak loads across high and low temperatures. In contrast, we document an asymmetric temperature response curve for PJM, with higher average and peak loads resulting from cooling loads. This difference is consistent with different heating and cooling technologies across the two regions. Whereas half of Texas residences use electricity for space heating, only 12% of homes in the Northeast use electricity—far more use natural gas or fuel oil (16).

We also note the linear shape of the response function above 21°C for both average and peak loads. This finding supports our early supposition that imposing a linear function over 21°C is well justified as a method to obtain out-of-sample predictions for high temperatures. To confirm this, we also calculate the correlation between predicted values for a regression using bins above 21°C versus a regression imposing a linear response above 21°C. The average of this correlation coefficient across the zones is above 0.9 for both average and peak loads.

The difference in the shape of these regional response functions has particular implications for climate change. For nearly all regions, increases in the mean of the temperature distribution will increase average and peak loads at higher temperatures. However, this increase in average load in some areas (such as ERCOT) will be partly compensated by the reduction in the number of heating degree days. Other areas (such as PJM), which show relatively little load response to cooler temperatures, will not experience as substantial a compensating reduction in average loads due to the reduction of cool days.

Climate Simulations.

Combining results from our empirical model and future predictions of climate change, we estimate end-of-century percent changes in average load, daily peak load, the 95th/99th percentiles of load, and the counts of days over the current 95th/99th percentiles. For visual display, we aggregate the load zone results to five groups: ERCOT, ISO-New England (ISONE), New York ISO (NYISO), PJM, and all other load zones. The upper half of Table 1 shows the summary of results under the modest warming RCP4.5 scenario. In line with prior estimates for a subset of regions, we find that end-of-century results predict 2.8% increases (column 1) in average hourly load across all regions as a result of climate change. However, daily peak electricity demand rises 3.5% (column 2), indicating that effects on peak demand are more pronounced than effects on average demand.

Table 1.

Increases in peak demand dwarf increases in average demand by end of century

	%Δ average hourly load	%Δ peak daily load	%Δ 95th percentile daily peak load	%Δ frequency days w. peak load > current 95th percentile	%Δ frequency days w. peak load > current 99th percentile
Simulation type	Intensity	Intensity	Intensity	Frequency	Frequency
RCP 4.5
FERC	2.8	3.5	6.8	158	382
ERCOT	3.7	4.3	6.2	150	460
ISONE	1.6	2	7.1	103	260
NYISO	2.7	3.3	8.5	128	312
PJM	2.3	3.1	8	133	329
Total	2.8	3.5	7	152	374
RCP 8.5
FERC	8	9.7	17.2	407	1, 532
ERCOT	10.1	11.5	15.2	406	1, 634
ISONE	5	6	17.7	281	1, 024
NYISO	8	9.2	21.2	334	1, 230
PJM	7	8.9	20.5	354	1, 347
Total	7.9	9.6	17.6	395	1, 492

Column 1 is the projected percent change in hourly generation, column 2 is the projected percent change in daily peak load, column 3 is the projected percent change in the 95th percentile of daily peak load, and columns 4 and 5 are the projected percent change in the number of days with peak load greater than the present-day 95th and 99th percentiles, respectively. Each projection is based on the average projected change in temperature for 19 independent climate models. The five rows display results across five geographic regions of the United States.

Next, we examine the impact on the right tail of the daily peak load distribution. Although we have used the term “peak” to refer to daily peaks, capacity planning is based off longer-term horizons, e.g., annual peaks. To capture this impact, column 3 documents the average shift in the 95th percentile of daily peak load. This upward shift in the right tail is 7.2%, reflecting that the upper end of the distribution will “stretch” farther outward than the middle. Columns 4 and 5 estimate the percent change in the number of days with peak load greater than the current 95th and 99th percentiles, respectively. We project 153 and 389% increases for the 95th and 99th percentile, respectively. That is, levels of demand that are currently considered unusually high will become much more common, even absent changes in population or income.

The lower half of Table 1 simulates results for the higher-emissions scenario, RCP8.5. As under RCP4.5, percentage increases in peak load exceed percentage increases in average load. Because RCP8.5 reflects a higher emissions trajectory and, on average, more pronounced increases in temperature, we find larger percentage changes in all categories. Of particular note are increases of over 1,500% in the number of days over the current 99th percentile of electricity consumption. To put this number in perspective, this would indicate that, for ERCOT, 65 days a year would have the peak load of or in excess of the currently four highest load days.

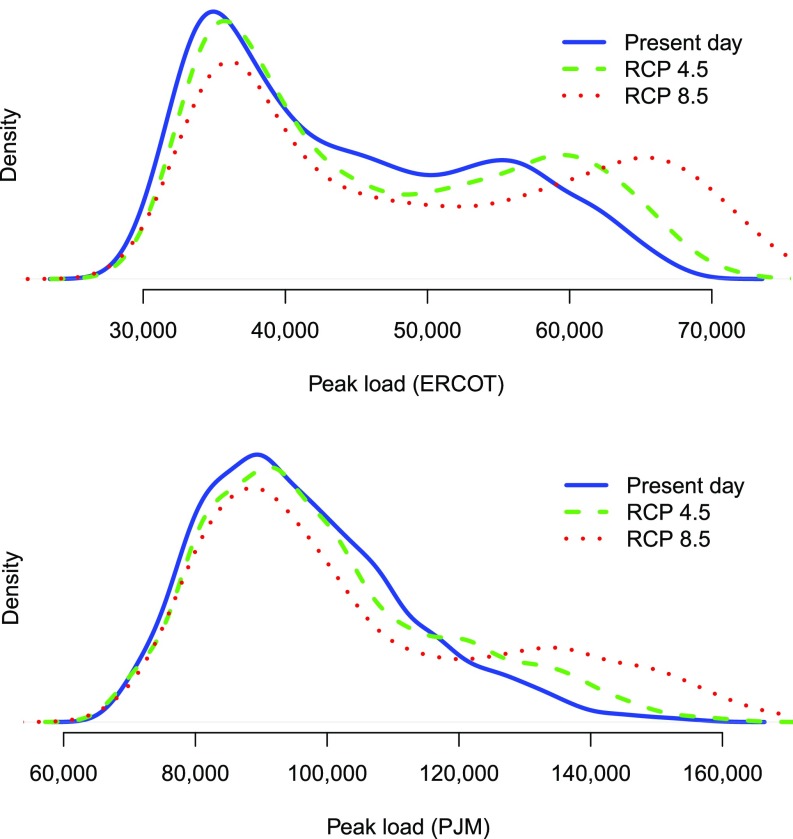
To better understand why peak load increases more than average load, we again focus on ERCOT and PJM as representative regions. Fig. 2 plots predicted end-of-century changes in peak electricity demand obtained by combining our empirical model with the ensemble of climate predictions. We plot three distributions. First, we plot (in blue) the distribution of peak load under present-day temperature distribution. This bimodal distribution in ERCOT shows two peaks in the peak demand distribution: one with relatively low use and one with relatively high use. On the same graph, we also plot predictions from the ensemble of climate models under RCP4.5 (green) and RCP8.5 (red). Note that the low-use mode does not shift substantially for either ERCOT or PJM; this is because the number of days with moderate heating needs decreases even as the number of days with moderate cooling needs increases. However, because most of the high-peak days are generated by warmer temperatures, the upward shift of the temperature distribution has a corresponding effect on the distribution of peak load days, driving the second mode higher under RCP4.5 and higher still under RCP8.5. PJM shows a similar but less pronounced effect, with a second mode beginning to emerge under the RCP8.5 scenario. These simulations are possible due to the high-frequency nature of our data.

Fig. 2.

Climate change shifts the distribution of peak electricity demand upwards. The distribution of daily peak load is bimodal and shifts to the right by end of century. Shown is a comparison of kernel density plots of the observed hourly peak of daily load (blue), predicted peak load under RCP4.5 (green), and predicted peak load under RCP8.5 (red), by end of century. Results are averaged across 20 independent climate models.

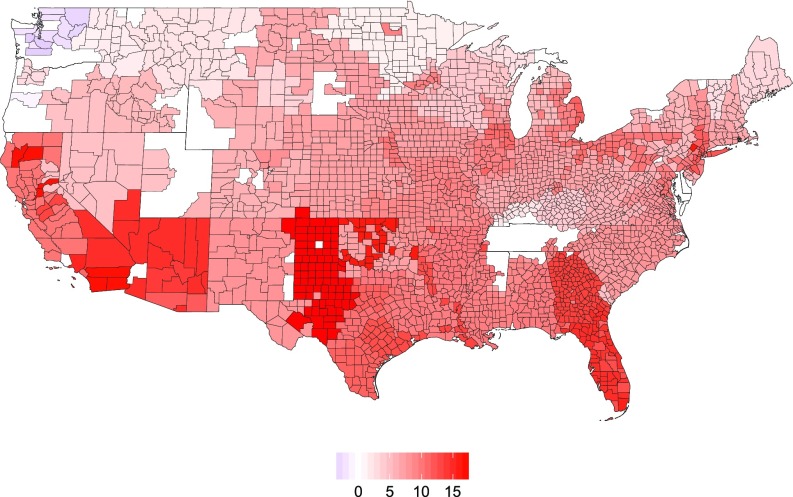
Fig. 3 documents by-county changes in the intensity of peak load under RCP8.5 (SI Appendix, Fig. S2 displays the results for RCP4.5). The southern United States experiences the greatest increases in load as a result of climate change, whereas the Northwest actually sees decreases in load. These regional differences are driven by heterogeneity in both the estimated temperature response curves and the shift in the temperature distribution predicted by the climate models. The differences in temperature response functions are due to, among other factors, the difference between areas with primarily electricity and natural gas heating, air conditioning penetration, and the proportion of load required for heating and cooling relative to that required for industrial processes.

Fig. 3.

Projected change in intensity of peak load (RCP8.5). The projected change in intensity of peak load under RCP8.5 varies geographically, with the largest increases in the South and West. Coloring reflects projected percentage increases in the daily peak load due to temperature rise by end of century.

These results are indicative of a need for regionally distinct strategies to adapt to climate change. Some areas, particularly in the southern United States, will experience substantial increases in the “peakiness” of electricity demand, whereas others, such as the Northwest, may actually see decreases in average and peak loads as a result of climate change. Some regions, such as the Northwest, currently have “winter peaks”: Most energy is consumed during the coldest hours of the year, because much of the heating load is borne by electricity. This regional heterogeneity in future peakiness will depend, of course, on appliance choices in the future. That is, regional differences are likely to persist in some form, although perhaps not in ways we can currently anticipate. In conclusion, these regional changes imply shifts in the need for new transmission and generation (or storage) capacity in particular.

Discussion

Overall, we find that peak load, at both the daily and annual levels, is impacted by climate change far more than is average load (consumption). Moreover, the impacts on peak load vary substantially across space, driven by differences in the distribution of heating and cooling degree days as well as differences in heating and cooling technologies. These results imply that the average generation impacts found to date in the literature could substantially underestimate the total cost in the electricity sector of climate change. In particular, adaptation could require additional expenses in terms of capacity or storage or transmission investments, not simply generation costs.

We find that, while average generation needs increase by 2.8% by end of century for RCP4.5, the upper tail of peak load increases by 7.2%. The upper tail of peak load increases by 18% in the RCP8.5 scenario. Installing an additional 7% of capacity in the United States at current prices would cost around 70 billion dollars, and increasing capacity by 18% would cost around 180 billion dollars. That is, the cost implications are nontrivial. These estimates show that the existing papers focusing solely on consumption level impacts ignore a large portion of the likely costs of climate change.

Calibrating the impact of temperature changes on capital costs remains an important area for future work. Our results imply that the ratio of peak load to average load will increase under climate change, implying that the mix of power plants on the grid will likely change. Simulations of the grid that incorporate these peak and average responses, as well as heterogeneity across space, will be valuable for grid planners as well as for integrated assessment modelers.

We caution that these results are meant to illustrate the change in electricity demand as a result of climate change in a business-as-usual setting, used in many modeling contexts (7). Importantly, the reduced-form model we estimate holds adaptation, economic growth, technology, and current infrastructure constant. Here we discuss the possible effects of alternative assumptions.

The direction of adaptation impacts are ambiguous. Although increasing temperatures may spur greater adoption of air conditioners (and therefore greater temperature impacts), they may also spur the development of more efficient air conditioning technologies. Greater economic growth would imply level changes in electricity demand as well as greater temperature responses, because heating and air conditioning use tends to increase with income (17, 18). Thus, economic growth would imply that our estimates are likely too small.

Changes in technology and infrastructure could mitigate the peak load effects we estimate, in the following ways. Electricity storage technologies currently face significant challenges related to cost and financing, although they are the focus of a sizable amount of research and development, and costs are declining (19, 20). Advances in batteries or the use of electric vehicles for storage would smooth and narrow the distributions displayed in Fig. 2. As such, although average generation would not be directly impacted, peaks would diminish.

The impact of increasing penetration of renewable technologies is ambiguous. Both wind and solar outputs are highly variable, with peaks in electricity demand more closely matching solar production than wind production (21). As such, increases in solar capacity could smooth some of peak demand. However, California’s experience has demonstrated that operational challenges can arise because solar production is not exactly coincident with peak demand (22).

Finally, widespread adoption of time-varying prices, such as real-time prices, could smooth the distribution of demand, with customers finding the optimal way to shift some of their demand from peak to off-peak hours. As of 2014, 4% of customers faced time-varying prices, and the count is growing (23). If those programs continue to grow, and if customers respond by shifting load, the impacts we estimate would be mitigated.

In conclusion, we can envision several changes to the electric grid that would mitigate the peak impacts we estimate. Our results point to the possibility of climate changing increasing the demand for storage technology, demand response programs, and alternative pricing schemes.

Data and Methods

Data.

Electricity data.

The electricity load data used in this paper come from the Federal Energy Regulatory Commission (FERC) Form 714—Annual Electric Balancing Authority Area and Planning Area Report (for short, FERC 714) and from individual ISO reports, where available.

Specifically, we gather hourly energy use from 2006–2014 for every balancing authority area and planning area. Because this time period covers the Great Recession, we verify that our results are not sensitive to dropping recessionary months (see SI Appendix). Our sample covers most of the balancing authorities in the FERC 714 data, although we exclude areas that overlap with data we obtain directly from the ISOs (see below). To link the FERC 714 data to the geographic areas they serve, we create a mapping from each respondent to county Federal Information Processing Series codes using data from Energy Information Agency Form 861 (see SI Appendix). Additionally, some ISOs provide load data independent of the FERC 714 system. Where available, we use ISO data instead of the FERC data to obtain more disaggregated estimates. In total, our data contain 166 distinct load zones. SI Appendix, Fig. S1 displays the sample area, with distinct colors for each zone. Coverage gaps indicate areas where load data are either missing or could not be linked to a geographic zone.

For expositional clarity, we use the generic phrase “load area” to refer to the balancing authorities, planning areas, and ISO zones in our data. We define average hourly load (in megawatt hours) as the total daily load divided by 24, and peak load as the maximum hourly load in a given calendar day. We obtain daily data on minimum temperature, maximum temperature, and precipitation from the Parameter-elevation Relationships on Independent Slopes Model (PRISM) Climate Group’s AN81d dataset. These data are created using observations from more than 10,000 weather stations, interpolated to 4 × 4 km grid cells using PRISM (24). This method accounts precisely for weather variation induced by topological features that may be inappropriately captured by more basic interpolation algorithms (25).

Climate data.

After estimating the temperature response functions for each load zone, we combine those response functions with regional predictions of temperature change to produce zone-specific projections of changes in both average and peak loads due to climate change.

To create region-specific predictions of end-of-century changes in electricity load due to climate change, we use a set of climate projections from the Coupled Model Intercomparison Project 5 (26) downscaled using the Multivariate Adaptive Constructed Analogs method (27). These projects combine output from disaggregated climate predictions with historical data on regional climate variations to predict changes in climate that vary by region.

Model.

Statistical model.

To estimate the response function of average and peak loads to weather, we estimate a set of time series models, one for each load zone. We rely on interday variation in total load or peak load as a function of daily weather to identify the regression coefficients used in our simulations. The estimating equation is given by

$$Loa{d}_t=\alpha +{\sum }_b{\beta }_b{T}_t^b+\gamma T_{t}1[T_t>21]+\delta P_t+f(t)+{\varphi }_{dow}+{\psi }_{mon}+{\epsilon }_t,$$ [1]

where $t$ is day of sample, $Loa{d}_t$ is either average or peak load for day t, $T_t^b$ is a dummy for daily average temperature falling within a given temperature bin b, $T_{t}1[T_t>21]$ is daily average temperature when greater than 21 °C, $P_t$ is total daily precipitation, $f(t)$ is a sixth-order Chebychev polynomial in day of sample, and ${\varphi }_{dow}$ and ${\psi }_{mon}$ are dummies for day of week and month of year. The coefficients of interest are $\beta$ and $\gamma$, representing the impact of temperature below and above 21 °C, respectively.

For the $\beta$ coefficients, we use 3 °C temperature bins to capture nonlinearities in the response function, omitting the 15 °C to 18 °C bin, which tends to be the minimum load in our data. This semiparametric function is commonly used in the literature to capture nonlinearities in the response (8, 28, 29). However, we depart from the literature by imposing a linear response above 21 °C. That is, the bins are used for temperatures below 21 °C, and a linear response is used thereafter. We impose this restriction to project responses for temperature predictions that lie above the historical support of our data. Otherwise, we would be unable to simulate electricity demand for temperatures not observed historically in our data. As noted above, the correlation between the predicted values for average and peak loads for all observations with temperature greater than 21 °C is above 0.9, supporting the assertion that the linear response function is appropriate in this setting.

The coefficients are identified under the assumption that changes in temperature are as good as random after controlling for seasonal variation and time trends. We include precipitation as a covariate to isolate the effect of temperature on electricity demand. In principle, one could also control for humidity. We assume that the correlation between humidity and temperature in our sample remains stable for the simulation horizon, implying that not controlling for humidity will not bias our results. Finally, the day of week dummy is included to increase precision, because load varies predictably by day of week. Standard errors are estimated using Newey–West standard errors that account for up to 15 days of serial correlation.

Climate simulation.

We predict end-of-century climate by taking the monthly average difference between model projections in 2000–2020 and 2086–2099 and adding that difference to a historical baseline of weather variation (25). This method gives us a simulated time series of data for each load zone, adjusted for changes in the mean of the temperature distribution but retaining representative daily variance in temperatures. We then apply the coefficients from our estimated model to predict future average and peak electricity demand under different climate change scenarios. To estimate percentage changes, we compare estimates of average and peak loads under a given climate change scenario and under a baseline scenario in which no warming occurs.