Significance
Reducing dimensionality often entails striking new physics, as, e.g., the Quantum Hall effect in 2D electron systems or the different recurrence probabilities of random walks in various dimensions. In addition, phase transitions in 2D and 3D differ significantly: Long before graphene came into focus, theories for melting of 2D crystals were developed and probed with colloidal monolayers. In 2D, the crystalline and fluid phase is separated by a so-called hexatic phase, unknown in 3D. Furthermore, 2D crystals exhibit instabilities on large length scales. Here, we show that those instabilities also exist in 2D amorphous solids, but do not melt them—a topic that emerged only recently, 50 y after the prediction in 2D crystals by D. Mermin and H. Wagner.
Keywords: Mermin–Wagner fluctuations, 2D ensembles, glass transition, phase transition, confined geometry
Abstract
In a recent commentary, J. M. Kosterlitz described how D. Thouless and he got motivated to investigate melting and suprafluidity in two dimensions [Kosterlitz JM (2016) J Phys Condens Matter 28:481001]. It was due to the lack of broken translational symmetry in two dimensions—doubting the existence of 2D crystals—and the first computer simulations foretelling 2D crystals (at least in tiny systems). The lack of broken symmetries proposed by D. Mermin and H. Wagner is caused by long wavelength density fluctuations. Those fluctuations do not only have structural impact, but additionally a dynamical one: They cause the Lindemann criterion to fail in 2D in the sense that the mean squared displacement of atoms is not limited. Comparing experimental data from 3D and 2D amorphous solids with 2D crystals, we disentangle Mermin–Wagner fluctuations from glassy structural relaxations. Furthermore, we demonstrate with computer simulations the logarithmic increase of displacements with system size: Periodicity is not a requirement for Mermin–Wagner fluctuations, which conserve the homogeneity of space on long scales.
For structural phase transitions, it is well known that the microscopic mechanisms breaking symmetry are not the same in two and in three dimensions. Whereas 3D systems typically show first-order transitions with phase equilibrium and latent heat, 2D crystals melt via two steps with an intermediate hexatic phase. Unlike in 3D, translational and orientational symmetry are not broken at the same temperature in 2D. The scenario is described within the Kosterlitz, Thouless, Halperin, Nelson, Young (KTHNY) theory (1–5), which was confirmed (e.g., in colloidal monolayers) (6, 7). However, for the glass transition, it is usually assumed that dimensionality does not play a role for the characteristics of the transition, and 2D and 3D systems are frequently used synonymously (8–12), whereas differences between the 2D and 3D glass transition are reported in ref. 13.
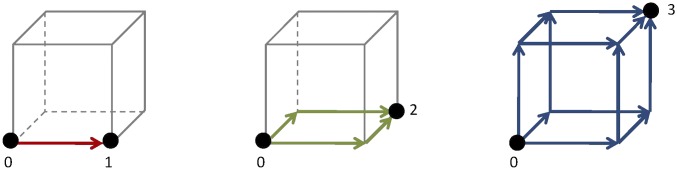
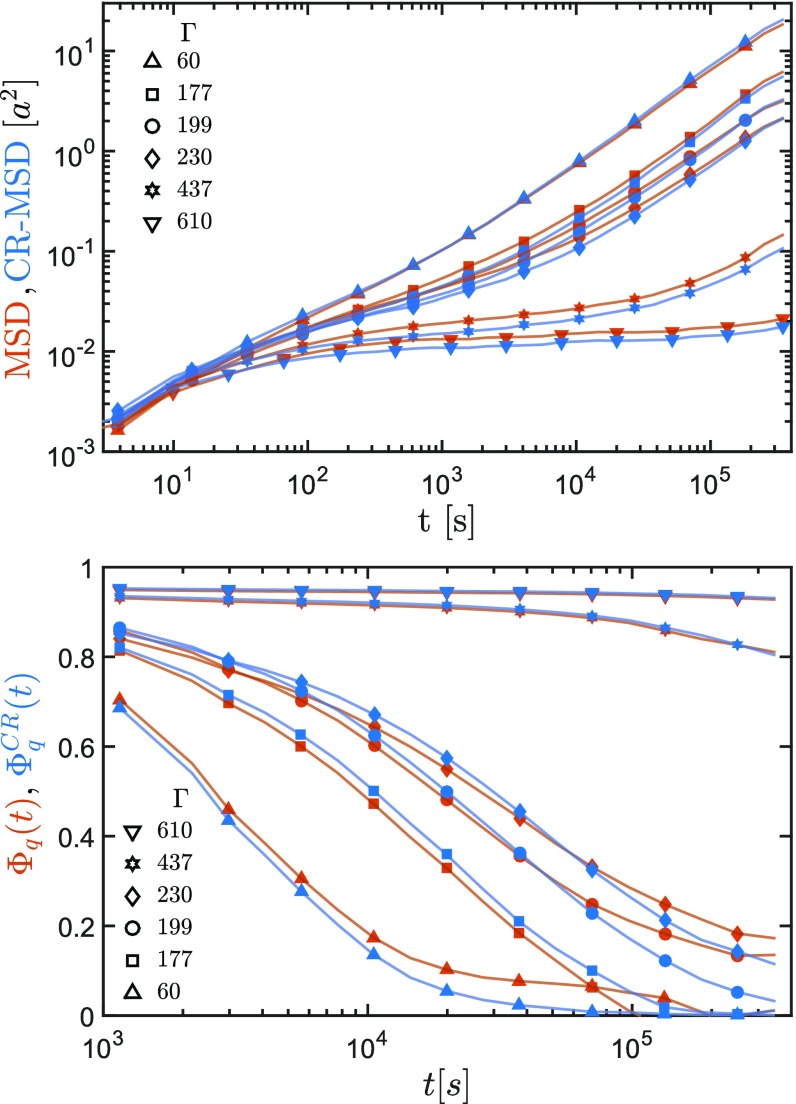
In the present work, we compare data from colloidal crystals and glasses and show that Mermin–Wagner fluctuations, well known from 2D crystals, are also present in amorphous solids (14, 15). Mermin–Wagner fluctuations are usually discussed in the framework of long-range order (magnetic or structural). However, in the context of 2D crystals, they have also had an impact on dynamic quantities like mean squared displacements (MSDs). Long before 2D melting scenarios were discussed, there was an intense debate as to whether crystals and perfect long-range order (including magnetic order) can exist in 1D or 2D at all (16–19). A beautiful heuristic argument was given by Peierls (17): Consider a 1D chain of particles with nearest neighbor interaction. The relative distance fluctuation between particle and particle at finite temperature may be . Similar is the fluctuation between particle and . The relative fluctuation between second nearest neighbors, namely, particle and , is then because they add up statistically independently. Thus, the amplitude of the fluctuations grows with if counts the number of particles in the chain. Periodicity cannot exist at large scales in 1D crystals. To cover 3D space, one has to investigate three linear independent directions. Within a cube, for instance, there are six ways to get along the space diagonal, say, from the lower left front corner to the upper right back corner (Fig. 1). It follows that in 3D, the fluctuations cannot add up independently, and the amplitude of the fluctuations stays finite being of the order of . In 2D, one can show that fluctuations add up logarithmically at finite temperatures. Translational correlation functions decay algebraically, whereas, and this is important to note, orientational order is not affected (14, 15, 17, 20, 21).
Fig. 1.
Counting the path to cover space in various dimensions. In 1D, fluctuations can add up independently on an axis along 0 to 1, whereas in 3D they have to be correlated along the six different ways from 0 to 3 and stay finite. In 2D, fluctuations add up logarithmically.
What is the impact of Mermin–Wagner fluctuations? They are long(est) wavelength density fluctuations, and, mapping locally a perfect mathematical 2D lattice with commensurable density and orientation, one finds the displacement of particles to diverge. It is shown analytically that this displacement from perfect lattice sites increases in two dimensions logarithmically with distance (15, 20). Having a closer look at the arguments given in ref. 17, one finds that periodicity is not a requirement for those fluctuations. They will also be present in other 2D (and 1D) systems like quasicrystals or amorphous structures, provided the fact that nearest-neighbor distances have low variance (unlike, e.g., in a gas). D. Cassi, F. Merkl, and H. Wagner (22–24) mapped the absence of spontaneously broken symmetries to the recurrence probability of random walks. In this work, it is proven that spontaneous magnetization on amorphous or fractal networks cannot occur in . The dualism with random walks shows that Mermin–Wagner fluctuations are time-dependent for nonzero temperatures. In 2D crystals, Mermin–Wagner fluctuations cause translational correlation functions to decay algebraically (3). With respect to dynamic measures, they cause the MSD to diverge and the standard Lindemann parameter to fail. The impact on the dynamics is independent of periodicity and should be found in quasicrystals and amorphous solids, too (25). By using local coordinates as introduced by Bedanov et al. and Lozovik and Farztdinov (26, 27), namely, subtracting the trajectories of the nearest neighbors, the so-called reduced or local MSD stays finite in a 2D crystal, but still diverges in the fluid. This defines a dynamic Lindemann criterion in 2D (28), which is a maximal threshold for the local displacements in a solid. In the language of glass theory, the nearest neighbors are given by the cage, and the “cage-relative MSD” (CR-MSD) was shown to have much more contrast [e.g., for dynamical heterogeneities in a 2D glass former compared with standard MSD (29, 30)].
We do not intend to enter the discussion about an “ideal” vs. “quasi-ideal” glass transition in the sense of infinite or just extremely large viscosities. Because infinite timescales are required to measure infinite viscosities, this is a purely academic discussion, and no experiment (or simulation) will prove this strictly. With respect to Mermin–Wagner fluctuations, we can state that it will depend on the way we measure: As in crystals, the viscosity will always be finite on arbitrary large length scales. On a local scale, Mermin–Wagner fluctuations do not change the cage-escape process, and thus the microscopic mechanism of 2D and 3D glass transitions are not necessarily different. Recent work by Vivek et al. using cage-relative intermediate scattering functions support this idea (31), and computer simulations by Shiba et al. independently found similar results (32).
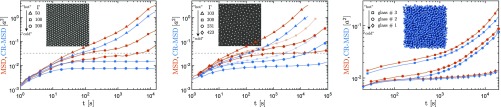
Fig. 2 shows MSDs, where the sum runs over all particles and the brackets additionally denote an average about starting times
| [1] |
and CR-MSDs
| [2] |
for crystals and amorphous solids at various temperatures. The second sum in Eq. 2 is the center of mass of the cage given by the nearest neighbors of particle determined by Voronoi–Tesselation. Fig. 2, Left shows the standard MSD as a function of time in red for a fluid system (red triangles) and two crystalline samples (red squares and circles). In a 2D crystal, the MSD is not confined. This indicates the failure of the Lindemann criterion in 2D. By using cage-relative coordinates (blue curves), the fluid data still diverge (blue triangles), but the CR-MSD from solid samples are confined (blue squares and triangles). The dashed line shows the critical value given by the dynamic Lindemann criterion (which is for the given system). Below this value, the system is a crystal (28, 33). Because grain boundaries, which emerge for finite cooling rates during preparation of the sample (34), might cause some plasticity, they are excluded in the analysis.∗ This is done by analyzing only particles that have a crystalline environment (six nearest neighbors) for the time of investigation. Fig. 2, Center shows the same analysis for a glass-forming system. The MSD of the fluid sample is labeled with red triangles; the transparent squares label a sample that is glassy but very close to the transition temperature; and the circles and diamonds represent amorphous solids (35, 36). Focusing on the CR-MSDs (blue curves), one finds that the amplitude of the local displacements is lower, but even for the deepest supercooled amorphous solid (blue diamond), there is an upturn for long times. Whereas for the CR-MSD (blue curves), long wavelength phonons are shortcut and thus invisible, the structural relaxation, which typically appears for glasses, is still visible. The so-called -process, which is usually attributed to particles escaping their cage given by nearest neighbors, is detectable in glass, but not in the crystal. Note that the upturn in MSD (red) appears earlier compared with the CR-MSD (blue) in the 2D glass. Fig. 2, Right shows a 3D glass that lacks per definition Mermin–Wagner fluctuations. The amplitude of the CR-MSD (blue) is only slightly smaller, compared with the standard MSD (red), and the upturn seem to happen simultaneously. Only structural relaxation is measured that is shifted beyond the accessible time window for the system deepest in the glass (diamonds). The corresponding Fig. 2, Insets show typical snapshots of the 2D systems (see experimental details below and in SI Text, whereas for the 3D system, a sketch is shown, reconstructed from structural data of the amorphous solid.
Fig. 2.
(Left) MSD of a defect free 2D crystal (red). The control parameter is an inverse temperature; increasing triggers solidification (melting is at ). On long times, the MSD diverges. Even a 2D crystal has fluid-like character due to Mermin–Wagner fluctuations, whereas, using local coordinates, the CR-MSD stays finite (blue). (Center) In a 2D glass, an additional -process causes the CR-MSD (blue) not to stay finite, and the amplitude of the global fluctuation given by the MSD (red) is significantly larger (the glass transition is at , this curve is therefore plotted transparent). Both 2D systems labeled with triangles are fluid. (Right) MSD (red) and CR-MSD (blue) for a 3D glass for various supercooling (details below). The difference in the amplitude is significantly smaller, and the upturn seem to appear simultaneously. Note that the ordinate is zoomed in in 3D compared with 2D. Glasses labeled with diamonds are deep in the glass phase, and the -process starts to appear only at the end of the accessible time window.
1. Colloidal Systems
This difference of global and local fluctuations in 2D is already a hallmark of Mermin–Wagner fluctuations, but before we focus in orientational and structural decay, the experimental realization of 2D and 3D systems and details about the simulations are briefly discussed. The 2D systems are well established, and we investigated crystallization, defects (37–40), and the glass transition (30, 35, 36) with this setup. They consist of colloidal monolayers where individual particles are sedimented by gravity to a flat a water/air interface in hanging-droplet geometry. The colloids are a few microns in size and perform Brownian motion within the plane. The control parameter of the system is , given by the ratio of potential energy of the particles (due to mutual dipolar interaction) and the kinetic energy due to thermal motion. It can be interpreted as an inverse temperature (or dimensionless pressure); thus, large values of refer to small temperatures and vice versa. The whole monolayer consists of a few hundred thousand particles, and a few thousand are monitored by standard video microscopy and digital image analysis. As shown in Fig. S1 and as explained in SI Text, 2% of pinned particles on a solid substrate is enough to suppress Mermin–Wagner fluctuations.
Fig. S1.
(Upper) MSD of a colloidal monolayer on a solid substrate. Accidentally, between 1 and 3% of particles were pinned to the substrate, which efficiently suppresses Mermin–Wagner fluctuations. The upper two curves are fluid; the circles indicate a system close to the glass transition, whereas the lower three curves are solid. Lower shows the density correlator (main text) for the same system (again, ).
The 3D colloidal systems consist of more than a billion particles, dissolved in an organic solvent with identical mass density; thus, particles do not sediment. The colloids are slightly charged and the interaction is given by Coulomb interaction screened by a small amount of counterions in the solvent (Yukawa potential). Additional details are given in Table S1 and SI Text. Monitoring is performed with confocal microscopy, providing 3D images with several thousand particles being tracked in the field of view. Finite size effects in 2D were additionally investigated with computer simulations, specifically Brownian dynamics simulation of hard disks (see below). To prevent crystallization, a binary mixture of different sizes of disks was used. The phase diagram was controlled by entropy (not temperature), and the control parameter in this systems was solely given by the (area) packing fraction of disks in the plane. The comparison of MSD and CR-MSD for the 2D simulation is given in Fig. S2, completely in line with Fig. 2 for 2D experimental glass data.
Table S1.
Parameters of the 3D glass
| Glass 1 | 21.5 | 0.183 | 500 |
| Glass 2 | 19.2 | 0.176 | 500 |
| Glass 3 | 19 | 0.166 | 500 |
Fig. S2.
The separation of MSD (red) and CR-MSD (blue) for the hard disk system shows Mermin–Wagner fluctuations. The triangles indicate a fluid system; the squares indicate a system with critical packing fraction; and the circles and diamonds show a solid sample. The data are the same as for the density correlator in Fig. 3, except for the fluid data.
Colloidal systems are so-called soft-matter systems: The interaction energy between particles is of the order (tenth of) eV, comparable to atomic or molecular systems. However, because length scales (distances between particles) are approximately to times larger, energy densities (and therefore elastic moduli) are smaller by to in 2D, and even to in 3D. Thus, soft matter has a rich variety of excited states at moderate temperatures, and thermally induced fluctuations are easily accessible. This offers the unique possibility to measure Mermin–Wagner fluctuations in the laboratory. For atomic systems, including Graphene, it has been argued that sheets of cosmologic size are necessary to detect any realistic amplitude of Mermin–Wagner fluctuations (41–43).
2. Structural and Orientational Decay in 2D and 3D
To measure the structural decay and to investigate the -process in glass, one frequently uses the intermediate scattering function , where is the Fourier transform of the density at time . The self-part of the intermediate scattering function ignores cross-correlations between different particles at and , but correlates the position of particle at with its position at in Fourier space, where the sum runs over all particles .
| [3] |
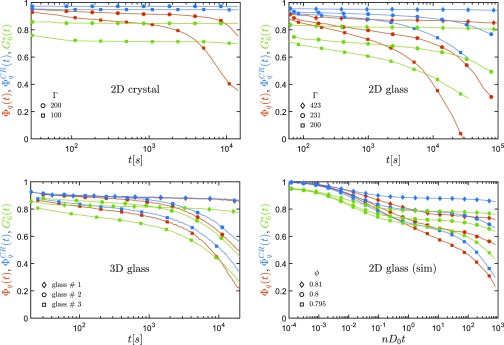
Eq. 3 is nothing but distribution of displacements in Fourier space . The wave vector is as usual chosen to be , the position where the structure factor has its first maximum. Angular brackets indicate the canonical ensemble average for simulations and an average about various starting times in experiments. In Fig. 3, is plotted as red curves for four different systems: Shown are the 2D crystal (Fig. 3, Upper Left) and 2D glass (Fig. 3, Upper Right) of dipolar particles as in Fig. 2, but omitting the fluid curves. After an initial decay due to thermal vibrations (which is hardly seen on the log-lin scale), the red curves enter a plateau, indicating the dynamic arrest. Only the stiffest glass (diamonds) is stable on the accessible timescale. Fig. 3, Lower Right shows data from simulations of a 2D hard disk system for comparison. The qualitative behavior is the same as for the 2D dipolar glass. Fig. 3, Lower Left shows the 3D glass, again with a typical two-step decay, except for the strongest glass (red diamonds), where the decay is hardly visible on the experimental accessible timescale.
Fig. 3.
Self-intermediate scattering function (red), cage-relative self-intermediate scattering (blue), and bond order correlation function (green) for various temperatures of a 2D crystal (Upper Left), a 2D glass (Right), and 3D glass (Lower Left). In the 2D crystal and do not decay, whereas decays due to Mermin–Wagner fluctuations. In the experimental and simulated 2D glass, and decay simultaneously due to structural relaxations within the -process, whereas decays earlier due to Mermin–Wagner fluctuations and the -process. In the 3D glass, only an -process occurs, and no separation in timescales is visible. The stiffest glasses (diamonds) do not decay within the accessible time window, but indicate the stability of our experiments.
In analogy to the CR-MSD, one can define a cage-relative intermediate scattering function given in blue in Fig. 3, where the displacement is reduced by the center of mass motion of the nearest neighbors (31). In 2D, the nearest neighbors are defined by Voronoi–Tessellation, whereas in 3D a cutoff value of is used to identify particles within the first shell representing the cage,
| [4] |
where the displacement of the cage of particle given by the neighbors reads .
We further introduce the bond order correlation function , which correlates the local director field in time. In the crystal, the director field is given by the bond direction to the nearest neighbors in sixfolded space:
| [5] |
and is the time-dependent angle of the bond direction between particle and and an arbitrary reference axis. For the 2D glass, only of the particles are sixfolded, are fivefolded and sevenfolded (together and similar distributed), whereas are fourfolded or eightfolded. Thus, for the 2D binary mixture, we sum up all relevant director fields,
| [6] |
still . For the 3D glass, the local director field of particle is given by based on the spherical harmonics for with polar and azimutal angle of the bond (44). The 3D correlation function reads
| [7] |
In Fig. 3, we now compare the cage-relative intermediate scattering function plotted in blue and the bond-order correlation function plotted in green. In the crystal, both correlation functions do not decay. As for the MSD, the Mermin–Wagner fluctuations are shortcut by using local coordinates. The orientational order does not decay because the modulus of rotational stiffness, (usually called Frank’s constant in analogy to liquid crystal theory) is infinite in a 2D crystal (4, 6), even if translational order decays and the MSD diverges. Long-range bend and splay are suppressed, while long range density fluctuations are allowed in 2D crystals (4, 45).
For the soft glasses (green and blue squares/circles in Fig. 3, Upper Right), both correlation function and decay, but not the stiffest one for (diamonds), where the standard was already stable within the given time window. Note that the timescales for orientational and cage-relative structural decay is the same for identical (comparing curves with green and blue squares for and green and blue circles for ). The separation in timescales compared with the standard structural decay (red) is clearly visible. The 2D simulations show the same behavior, which means that 2D glasses are affected by slow Mermin–Wagner fluctuations and structural relaxations. Fig. 3, Lower Left shows the 3D glass. The stiffest glass 1 (diamonds) is almost stable. In glass 2 (blue, red, and green circles) and glass 3 (blue, red, and green squares), all correlation functions decay on the same timescale due to structural relaxations, but without Mermin–Wagner fluctuations. We conclude that 2D crystals are affected by Mermin–Wagner fluctuations, and 2D glasses are affected by Mermin–Wagner fluctuations and -relaxation, whereas 3D glasses are only affected by -relaxation.
3. Finite Size Effects
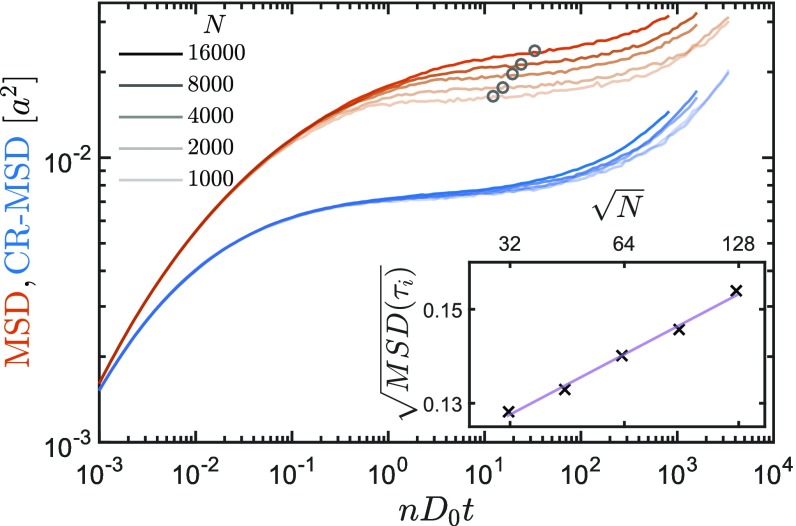
In Fig. 3, a separation of timescales between standard structural and orientational decay was shown for the 2D glasses. However, the -relaxation is strongly dependent on the supercooling, but only marginally affected by system size. Escaping the cage is a local mechanism. Note that all experimental systems are much larger than the examined fields of view. The amplitude of Mermin–Wagner fluctuations, conversely, depends on elasticity (which is a function of temperature), but more importantly, it depends logarithmically on system size (14, 15, 20). No predictions exist for the timescale of Mermin–Wagner fluctuations, but it is reasonable to assume that they also depend on system size. Accidentally, it might be the case that Mermin–Wagner fluctuations and -relaxation fall on top of each other. Therefore, we vary systematically the number of particles for the simulated hard disk system at fixed packing fraction between 1,000 and 16,000 disks. Fig. 4 shows a comparison of cage-relative and normal MSDs. All displacements measured in local coordinates collapse. The normal MSD, conversely, shows a strong finite size effect. The height of the plateau is extracted by taking the amplitudes of the displacement at the inflection point , indicated by open circles in Fig. 4, being determined by fitting a third-order polynomial in the region of interest. Note that the inflection point shifts to later times for larger systems, validating the assumption above.
Fig. 4.
MSD and CR-MSD of a hard disk system for various system sizes at for up to 16,000 particles. Although the CR-MSD (blue) does not show finite size effects in the plateau, the standard MSD (red) is strongly affected. Increasing opacity of the curves corresponds to increasing size. A total of independent simulations were performed for each curve (except for with runs). Inset shows the linear amplitude of the fluctuations vs. system size in log-lin scale. is given by the inflection point of the curves, marked as gray circles. The straight line is a linear fit of the log10(L) behavior and verifies Mermin–Wagner fluctuations in 2D amorphous solids.
Plotting the square root of the amplitude of the inflection point as a function of the logarithm of the linear system size gives a straight line. This is the logarithmic fingerprint of Mermin–Wagner fluctuations. A recent manuscript by H. Shiba et al. (32) independently reports the same logarithmic increase of long wavelength fluctuations in 2D of a simulated soft sphere glass, although to our knowledge they have not yet been directly measured in crystals.
4. Discussion
In ref. 13, E. Flenner and G. Szamel reported fundamental differences between glassy dynamics in two and three dimensions and detected strong finite size effects in 2D. The localization in a 2D glass (e.g., measured by the plateau of the intermediate scattering function or MSD) is not well pronounced and decays faster in large systems. Bond-order correlation functions (taking only sixfolded particles into account) decay later and show less size dependence. Additionally, particle trajectories show sudden jumps in 3D, but not in 2D, and dynamical heterogeneities are significantly pronounced in 3D. They conclude that vitrification in 2D and 3D is not the same, calling for a reexamination of the present glass transition paradigm in 2D. We perform this reexamination, taking Mermin–Wagner fluctuations into account. We cannot address differences between Newtonian and Brownian dynamics (13) in colloidal experiments, and thus they are not discussed in the present manuscript. All other differences observed in ref. 13 for 2D and 3D disappear in our system when using local coordinates (25). E. Flenner and G. Szamel investigated remarkably large systems to reduce finite size effects, but this even enhances Mermin–Wagner fluctuations: Those fluctuations affect translational degrees of freedom, but not orientational ones, and depend logarithmically on the system size. In ref. 29, we showed that non-Gaussian behavior of the self part of the van-Hove function (which measures the variance of displacements at a given time) in 2D systems is only visible in local, cage-relative coordinates. Equivalently, the dynamical heterogeneities show significantly more contrast in cage-relative coordinates. Mermin–Wagner fluctuations simply “smear out” local events like hopping and cage escape if particles are measured in a global coordinate frame (29).
In ref. 30, we assumed that the presence of collective motion might be due to long wavelength fluctuations. Now this is validated in direct comparison with 2D crystals. A recent manuscript by S. Vivek et al. (31) reports results of a soft sphere and a hard sphere glass in 2D compared with a 3D glass. Using similar correlation functions, their results are essentially the same, but the (almost) hard sphere glass showed less signature of Mermin–Wagner fluctuations. This can be explained by the work of Fröhlich and Pfister (20): They determined the following conditions for Mermin–Wagner fluctuations to appear: (i) The pair-potential of particles has to be integrable in the far field and (ii) analytically at the origin. The first condition rules out Coulomb interaction, because for this long-range potential, the second, third, and higher nearest-neighbors interaction is strong enough that particle displacements cannot add up statistically independently. The second condition questions hard sphere interaction. An easy argument in the limit of zero temperature might go as follows: When all particles are at contact and closed packed, no positional fluctuations can appear at all. At finite temperature, the Mermin–Wagner fluctuations are excited, as shown in Fig. 4, but the separation of timescales is less pronounced in Fig. 3 for the hard-disks simulation, consistent with the results of Vivek et al. (31). An alternative ansatz to investigate Mermin–Wagner fluctuations is reported by H. Shiba et al., showing analogue results in large-scale computer simulations. Shiba et al. analyzed bond-breakage correlations, four-point correlations (46), and intermediate scattering functions in 2D and in 3D. Being a local quantity, bond-breakage correlations do not differ in 2D and 3D; thus, the microscopic nature of the glass transition is similar. However, the density of vibrational states of a 2D system, computed from the velocity autocorrelation function, shows an infinite growth of acoustic vibrations, very similar to 2D crystals (32). Those beautiful results are completely in line with our arguments.
Connecting Mermin–Wagner fluctuations and glassy behavior in 2D points to another question that is yet not completely solved, namely, how (shear) solidity appears. Glass is a solid on intermediate timescales, but on infinite times it may flow. A 2D crystal is soft on infinite length scales (lacking globally broken symmetries) and a solid only at intermediate scales.
5. Conclusions
Comparing experimental and simulation data in 2D and 3D, we show that a 2D crystal is affected by Mermin–Wagner fluctuations in the long time limit; a 2D glass has Mermin–Wagner fluctuations as a “second channel of decay” beside the standard -process of structural relaxation, whereas a 3D glass only shows an -process. The existence of Mermin–Wagner fluctuations is not limited to low dimensional crystals; they also appear in 2D amorphous solids and certainly in 2D quasicrystals. The comparison of structural and orientational measures shows that Mermin–Wagner fluctuations can explain the differences in orientational relaxation times (not affected by long wavelength fluctuations) and translational relaxation times (affected by those fluctuations). Furthermore, Mermin–Wagner fluctuations exist on large scales, and the local effect (within the size of the cage) is only an affine translation. Thus, the cage-escape mechanism is not influenced by Mermin–Wagner fluctuations. We can conclude that the microscopic mechanism of the 2D and 3D glass transition is not necessarily different, whereas the transient localization measured by global variables is less pronounced in 2D compared with 3D, taking Mermin–Wagner fluctuations into account.
SI Text
The confinement of colloids to two dimensions is achieved by sedimentation to an interface, which in our case is the lower water/air surface in hanging droplet geometry. The volume is regulated actively with a microsyringe to get a flat interface. The fluid interface guarantees free diffusion of the colloids (without any pinning) within the horizontal monolayer, but the sedimentation height is about and negligible compared with the size of the colloids. The latter consist of polystyrene beads with diameter (species A) for the crystals and a mixture of species A and B (to avoid crystallization) for the glass samples. Species B has and the glassy mixture has a relative concentration of , where and are the number of particles of both species in the field of view. The colloidal beads are further doped with iron oxide nanoparticles, which results in a superparamagnetic behavior and a mass density of 1.7 kg/dm3. The whole monolayer consists of several hundred thousand particles, where particles are monitored by video microscopy in a subwindow in the glass sample and particles in a subwindow in the crystalline sample. The individual colloids are tracked with a spatial resolution of and with a time resolution of the order of a second. The system is kept at room temperature and exempt from density gradients due to a monthlong precise control of curvature and inclination of the interface.
Because of the superparamagnetic nature of the particles, the potential energy can be tuned by means of an external magnetic field applied perpendicular to the monolayer, which induces a repulsive dipole–dipole interaction between the particles. The ratio between potential energy and diffusive thermal energy ,
| [S1] |
acts as inverse temperature (or dimensionless pressure for fixed volume and particle number). is the 2D particle density with a mean particle distance (depending on the kind of sample). The magnetic susceptibility per bead is and for species A and B, respectively. For low , the system is fluid because the thermal motion dominates. Increasing induces crystallization at (39) or dynamic arrest and vitrification at (36). Digital image analysis gives the positions of the beads as a function of time. This provides the complete phase-space information of the colloidal ensembles at all relevant timescales on an “atomic” level. Our glasses are “well-aged”; we carefully checked that the -process is independent of waiting time. Additional details of the 2D setup are described elsewhere (47). Using the water/air interface is crucial: We performed additionally a whole set of measurements as function of on a solid substrate (object plate) where accidentally between 1 and 3% of particles were pinned. This pinning sufficiently suppresses Mermin–Wagner fluctuations and the differences between MSD and CR-MSD disappears, as shown in Fig. S1.
The 3D glass consists of monodisperse, charged polymethylmetacrylate (PMMA) particles of diameter, covered with poly-12-hydroxystearic acid to prevent aggregation, which are dissolved in a well-adjusted cyclohexylbromide (CHB) and decaline mixture. This mixture matches the mass density to prevent sedimentation and simultaneously the refractive index of solvent and colloid. Because of the latter, the ensemble is not turbid, and one can look deep into the sample (which consists of several billion particles). The particles are doped with rhodamine 6G, and by using standard confocal microscopy, the 3D trajectories of up to 6000 particles can be monitored and analyzed simultaneously in a field of view of approximately . Care has to be taken to use thoroughly cleaned solvents. CHB was passed through an activated alumina column to remove H2O, HBr, and any other polar molecules and ions (48). Dispersed in CHB, PMMA colloids acquire a moderate positive charge. This seems to originate from the adsorption of protons and bromide ions stemming from the decomposition of CHB (with protons being adsorbed more likely) (49). Together with the small abundance of ions in the solvent, one obtains a screened Coulomb interaction with the dimensionless Yukawa potential:
| [S2] |
where is the inverse screening length of the ions and is the Bjerrum length. This is the length where the interaction potential between two elementary charges in the medium with dielectric constant equals the thermal energy ( is the dielectric constant of the vacuum). System parameters are determined from fits of theoretically computed structure factors [using an approximate integral equation theory (50)] to the experimental data. The effective mean charge on the surface of the colloid is the same for all three presented systems. Thus, the phase diagram has two relevant parameters left that counteract: These are the packing fraction , which is given by the particle distance (and size), and the screening length , given by the density of counterions and any other ions. The charge polydispersity is dominated by the surface area polydispersity, thus being of the order of up to for a size polydispersity determined by electron microscopy to be . This effectively suppresses crystallization, which occurs not earlier than 1–2 wk after rejuvenation of the sample by shaking. Table S1 shows the parameters of three different glasses.
In the following, we will also compare experimental results with simulations. Those are made for a 2D binary mixture of hard disks undergoing Brownian motion by using an event-driven simulation algorithm (51, 52). The system contains particles, is made up of a 50:50 mixture with diameters , , and is equilibrated by Newtonian dynamics before data are collected. The packing fraction , giving the ratio of the area occupied by the disks to the area of the system, varies from to , hence in the vicinity of the glass transition point (53). For the simulations, the averaging (angular brackets) is done for typically runs as function of density and for finite size effects up to independent runs as function of system size. Fig. S2 shows the comparison of MSD and CR-MSD in similar manner as Fig. 2 for the experimental systems.
We observed Mermin–Wagner fluctuations in 2D crystal and 2D glass. This raises the question of which low-dimensional systems will show Mermin–Wagner fluctuations. Because well-defined neighbor distances with low variance as in glasses, quasicrystals, and crystals are required, we suggest hyperuniformity, originally formulated to characterize structures with isotropic photonic bandgaps (54, 55), to be a necessary requirement: in hyperuniform structures the number variance of atoms within a n-dimensional sphere of radius is proportional to the n − 1 dimensional surface of the sphere.
Acknowledgments
P.K. thanks Herbert Wagner for fruitful discussion. H.K. thanks M. K. Klein and A. Zumbusch for the synthesis of polymethylmetacrylate colloids. P.K. was supported by the Young Scholar Fund, University of Konstanz. S.F. was supported in part by German Research Foundation FOR 1394, Project P3.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
∗Because real 3D monocrystals incorporate vacancies and interstitials due to entropic reasons, the MSD can, strictly spoken, not be finite due to defect migration in 3D, too.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1612964114/-/DCSupplemental.
References
- 1.Kosterlitz JM, Thouless DJ. Long-range order and metastability in 2-dimensional solids and superfluids. J Phys C Solid State Phys. 1972;5:L124–L126. [Google Scholar]
- 2.Kosterlitz JM, Thouless DJ. Ordering, metastability and phase transitions in 2 dimensional systems. J Phys C Solid State Phys. 1973;6:1181–1203. doi: 10.1088/0953-8984/28/48/481001. [DOI] [PubMed] [Google Scholar]
- 3.Halperin BI, Nelson DR. Theory of 2-dimensional melting. Phys Rev Lett. 1978;41:121–124. [Google Scholar]
- 4.Nelson DR, Halperin BI. Dislocation-mediated melting in 2 dimensions. Phys Rev B. 1979;19:2457–2484. [Google Scholar]
- 5.Young AP. Melting and the vector Coulomb gas in 2 dimensions. Phys Rev B. 1979;19:1855–1866. [Google Scholar]
- 6.Keim P, Maret G, von Grünberg HH. Frank’s constant in the hexatic phase. Phys Rev E. 2007;75:031402. doi: 10.1103/PhysRevE.75.031402. [DOI] [PubMed] [Google Scholar]
- 7.Kosterlitz JM. Commentary on ‘ordering, metastability and phase transitions in two-dimensional systems’—the early basis of the successful Kosterlitz–Thouless theory. J Phys Condens Matter. 2016;28:481001. doi: 10.1088/0953-8984/28/48/481001. [DOI] [PubMed] [Google Scholar]
- 8.Doliwa B, Heuer A. Cooperativity and spatial correlations near the glass transition: Computer simulation results for hard spheres and disks. Phys Rev E. 2000;61:6898–6908. doi: 10.1103/physreve.61.6898. [DOI] [PubMed] [Google Scholar]
- 9.Harrowell P. Nonlinear physics: Glass transitions in plane view. Nat Phys. 2006;2:157–158. [Google Scholar]
- 10.Shintani H, Tanaka H. Frustration on the way to crystallization in glass. Nat Phys. 2006;2:200–206. [Google Scholar]
- 11.Berthier L, Biroli G. Theoretical perspective on the glass transition and amorphous materials. Rev Mod Phys. 2011;83:587–645. [Google Scholar]
- 12.Hunter GL, Weeks ER. The physics of the colloidal glass transition. Rep Prog Phys. 2012;75:066501. doi: 10.1088/0034-4885/75/6/066501. [DOI] [PubMed] [Google Scholar]
- 13.Flenner E, Szamel G. Fundamental differences between glassy dynamics in two and three dimensions. Nat Commun. 2015;6:7392. doi: 10.1038/ncomms8392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mermin ND, Wagner H. Absence of ferromagnetism or antiferromagnetism in one- or 2-dimensional isotropic heisenberg models. Phys Rev Lett. 1966;17:1133–1136. [Google Scholar]
- 15.Mermin ND. Crystalline order in 2 dimensions. Phys Rev. 1968;176:250–254. [Google Scholar]
- 16.Bloch F. Zur Theorie des Ferromagnetismus. Z Phys. 1930;61:206–219. [Google Scholar]
- 17.Peierls RE. Bemerkungen über Umwandlungstemperaturen. Helv Phys Acta. 1934;7:81–83. [Google Scholar]
- 18.Landau LD. Theory of phase transformations I. Phys Z Sowj. 1937;11:25–35. [Google Scholar]
- 19.Landau LD. Theory of phase transformations II. Phys Z Sowj. 1937;11:545–552. [Google Scholar]
- 20.Fröhlich J, Pfister C. On the absence of spontaneous symmetry-breaking and of crystalline ordering in two-dimensional systems. Comm Math Phys. 1981;81:277–298. [Google Scholar]
- 21.Dash JG. Helium films from two to three dimensions. Phys Rep. 1978;38:177–226. [Google Scholar]
- 22.Cassi D. Phase transitions and random walks on graphs: A generalization of the Mermin-Wagner theorem to disordered lattices, fractals, and other discrete structures. Phys Rev Lett. 1992;68:3631–3634. doi: 10.1103/PhysRevLett.68.3631. [DOI] [PubMed] [Google Scholar]
- 23.Merkl F, Wagner H. Recurrent random walks and the absence of continuous symmetry breaking on graphs. J Stat Phys. 1994;75:153–165. [Google Scholar]
- 24.Cassi D. Local vs average behavior on inhomogeneous structures: Recurrence on the average and a further extension of Mermin-Wagner theorem on graphs. Phys Rev Lett. 1996;76:2941–2944. doi: 10.1103/PhysRevLett.76.2941. [DOI] [PubMed] [Google Scholar]
- 25.Keim P. 2015. Mermin-Wagner fluctuations in 2D amorphous solids. arXiv:1510.05804v1.
- 26.Bedanov VM, Gadiyak GV, Lozovik YE. On a modified Lindemann-like criterion for 2D melting. Phys Lett A. 1985;109:289–291. [Google Scholar]
- 27.Lozovik YuE, Farztdinov VM. Oscillation spectra and phase diagram of two-dimensional electron crystal: “New” (3+4)-self-consistent approximation. Solid State Commun. 1985;54:725–728. [Google Scholar]
- 28.Zheng XH, Earnshaw JC. On the Lindemann criterion in 2D. Europhys Lett. 1998;41:635–640. [Google Scholar]
- 29.Mazoyer S, Ebert F, Maret G, Keim P. Dynamics of particles and cages in an experimental 2D glass former. Europhys Lett. 2009;88:66004. [Google Scholar]
- 30.Mazoyer S, Ebert F, Maret G, Keim P. Correlation between dynamical heterogeneities, structure and potential-energy distribution in a 2D amorphous solid. Eur Phys J E. 2011;34:11101. doi: 10.1140/epje/i2011-11101-1. [DOI] [PubMed] [Google Scholar]
- 31.Vivek S, Kelleher CP, Chaikin PM, Weeks ER. Long-wavelength fluctuations and the glass transition in two dimensions and three dimensions. Proc Natl Acad Sci USA. 2016 doi: 10.1073/pnas.1607226113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shiba H, Yamada Y, Kawasaki T, Kim K. Apparent dimensionality dependence of glassy dynamics—infinite growth of acoustic vibrations in two dimensions. Phys Rev Lett. 2016;117:245701. doi: 10.1103/PhysRevLett.117.245701. [DOI] [PubMed] [Google Scholar]
- 33.Zahn K, Maret G. Dynamic criteria for melting in two dimensions. Phys Rev Lett. 2000;85:3656–3659. doi: 10.1103/PhysRevLett.85.3656. [DOI] [PubMed] [Google Scholar]
- 34.Deutschländer S, Dillmann P, Maret G, Keim P. Kibble-Zurek mechanism in colloidal monolayers. Proc Natl Acad Sci USA. 2015;112:6925–6930. doi: 10.1073/pnas.1500763112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Klix CL, et al. Glass elasticity from particle trajectories. Phys Rev Lett. 2012;109:178301. doi: 10.1103/PhysRevLett.109.178301. [DOI] [PubMed] [Google Scholar]
- 36.Klix CL, Maret G, Keim P. Discontinuous shear modulus determines the glass transition temperature. Phys Rev X. 2015;5:041033. [Google Scholar]
- 37.Keim P, Maret G, Herz U, von Grünberg HH. Harmonic lattice behavior of two-dimensional colloidal crystals. Phys Rev Lett. 2004;92:215504. doi: 10.1103/PhysRevLett.92.215504. [DOI] [PubMed] [Google Scholar]
- 38.Gasser U, Eisenmann C, Maret G, Keim P. Melting of crystals in two dimensions. ChemPhysChem. 2010;11:963–970. doi: 10.1002/cphc.200900755. [DOI] [PubMed] [Google Scholar]
- 39.Deutschländer S, Puertas AM, Maret G, Keim P. Specific heat in two-dimensional melting. Phys Rev Lett. 2014;113 doi: 10.1103/PhysRevLett.113.127801. [DOI] [PubMed] [Google Scholar]
- 40.Lechner W, Polster D, Maret G, Dellago C, Keim P. Entropy and kinetics of point defects in two-dimensional dipolar crystals. Phys Rev E Stat Nonlin Soft Matter Phys. 2015;91:032304. doi: 10.1103/PhysRevE.91.032304. [DOI] [PubMed] [Google Scholar]
- 41.Abraham FF. Melting in two dimensions is first order: An isothermal-isobaric Monte Carlo study. Phys Rev Lett. 1980;44:463–466. [Google Scholar]
- 42.Abraham FF. The phases of two-dimensional matter, their transitions, and solid-state stability: A perspective via computer simulation of simple atomic systems. Phys Rep. 1981;80:340–374. [Google Scholar]
- 43.Thompson-Flagg RC, Moura MJB, Marder M. Rippling of graphene. Europhys Lett. 2009;85:46002. [Google Scholar]
- 44.Steinhardt PJ, Nelson DR, Ronchetti M. Bond-orientational order in liquids and glasses. Phys Rev B. 1983;28:784–805. [Google Scholar]
- 45.Eisenmann C, Gasser U, Keim P, Maret G, von Grünberg HH. Pair interaction of dislocations in two-dimensional crystals. Phys Rev Lett. 2005;95:185502. doi: 10.1103/PhysRevLett.95.185502. [DOI] [PubMed] [Google Scholar]
- 46.Shiba H, Kawasaki T, Onuki A. Relationship between bond-breakage correlations and four-point correlations in heterogeneous glassy dynamics: Configuration changes and vibration modes. Phys Rev E. 2012;86:041504. doi: 10.1103/PhysRevE.86.041504. [DOI] [PubMed] [Google Scholar]
- 47.Ebert F, Dillmann P, Maret G, Keim P. The experimental realization of a two-dimensional colloidal model system. Rev Sci Inst. 2009;80:083902. doi: 10.1063/1.3188948. [DOI] [PubMed] [Google Scholar]
- 48.Pangborn AB, Giardello MA, Grubbs RH, Rosen RK, Timmers FJ. Safe and convenient procedure for solvent purification. Organometallics. 1996;15:1518–1520. [Google Scholar]
- 49.van der Linden MN, El Masri D, Dijkstra M, van Blaaderen A. Expansion of charged colloids after centrifugation: Formation and crystallisation of long-range repulsive glasses. Soft Matter. 2013;9:11618. [Google Scholar]
- 50.Heinen M, Holmqvist P, Banchio AJ, Nägele G. Pair structure of the hard-sphere Yukawa fluid: An improved analytic method versus simulations, Rogers-Young scheme, and experiment. J Chem Phys. 2011;134:044532. doi: 10.1063/1.3524309. [DOI] [PubMed] [Google Scholar]
- 51.Scala A, Voigtmann T, De Michele C. Event-driven Brownian dynamics for hard spheres. J Chem Phys. 2007;126:134109. doi: 10.1063/1.2719190. [DOI] [PubMed] [Google Scholar]
- 52.Henrich O, Weysser F, Cates ME, Fuchs M. Hard discs under steady shear: Comparison of Brownian dynamics simulations and mode coupling theory. Phil Trans R Soc A. 2009;367:5033–5050. doi: 10.1098/rsta.2009.0191. [DOI] [PubMed] [Google Scholar]
- 53.Weysser F, Hajnal D. Tests of mode-coupling theory in two dimensions. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;83:041503. doi: 10.1103/PhysRevE.83.041503. [DOI] [PubMed] [Google Scholar]
- 54.Florescu M, Torquato S, Steinhardt PJ. Designer disordered materials with large, complete photonic band gaps. Proc Natl Acad Sci USA. 2009;106:20658–20663. doi: 10.1073/pnas.0907744106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Man W, et al. Isotropic band gaps and freeform waveguides observed in hyperuniform disordered photonic solids. Proc Natl Acad Sci USA. 2013;110:15886–15891. doi: 10.1073/pnas.1307879110. [DOI] [PMC free article] [PubMed] [Google Scholar]