Full atomistic reaction mechanism with kinetics for CO reduction on Cu(100) from ab initio molecular dynamics free-energy calculations at 298 K

Significance

Converting CO₂ to fuels is of great interest nowadays. Copper (Cu) is the only metal that produces hydrocarbon products, making it of interest for learning the reaction mechanisms underlying the selectivity and activity of Cu catalysts. In this report, we examine the reaction mechanism of CO reduction on Cu(100) at pH 7 including explicitly the aqueous solvent with ab initio molecular metadynamics simulations (AIMμD) free-energy calculations, which we find to explain all experimental observations. We expect that this understanding will suggest how to modify the Cu catalyst or replace it with a new material to enhance production of just a single such product while reducing the energy requirements (overpotential).

Abstract

A critical step toward the rational design of new catalysts that achieve selective and efficient reduction of CO₂ to specific hydrocarbons and oxygenates is to determine the detailed reaction mechanism including kinetics and product selectivity as a function of pH and applied potential for known systems. To accomplish this, we apply ab initio molecular metadynamics simulations (AIMμD) for the water/Cu(100) system with five layers of the explicit solvent under a potential of −0.59 V [reversible hydrogen electrode (RHE)] at pH 7 and compare with experiment. From these free-energy calculations, we determined the kinetics and pathways for major products (ethylene and methane) and minor products (ethanol, glyoxal, glycolaldehyde, ethylene glycol, acetaldehyde, ethane, and methanol). For an applied potential (U) greater than −0.6 V (RHE) ethylene, the major product, is produced via the Eley–Rideal (ER) mechanism using H₂O + e^–. The rate-determining step (RDS) is C–C coupling of two CO, with ΔG^‡ = 0.69 eV. For an applied potential less than −0.60 V (RHE), the rate of ethylene formation decreases, mainly due to the loss of CO surface sites, which are replaced by H*. The reappearance of C₂H₄ along with CH₄ at U less than −0.85 V arises from *CHO formation produced via an ER process of H* with nonadsorbed CO (a unique result). This *CHO is the common intermediate for the formation of both CH₄ and C₂H₄. These results suggest that, to obtain hydrocarbon products selectively and efficiency at pH 7, we need to increase the CO concentration by changing the solvent or alloying the surface.

To reduce the carbon footprint while converting renewable energy sources (such as the wind or solar) into stable chemical forms, we need to develop an economical process for the CO₂ reduction reaction (CO₂RR) to chemicals and fuels. Copper (Cu) is the only nonalloyed metal that can electrochemically catalyze the formation of significant amounts of hydrocarbons (1). However, Cu leads to an overpotential of almost 1 V for a reasonable current (5–10 mA⋅cm⁻²) and faradaic efficiency (>69%) (2), and it leads to a fairly broad mixture of major and minor products, including hydrogen (H₂), ethylene (C₂H₄), and methane (CH₄) as major products plus small amounts of other C₂s and oxygenates (3). Although Cu remains far from ideal for CO₂ reduction, it provides a benchmark for determining and validating the mechanism underlying Cu’s unique ability to catalyze hydrocarbon formation. This mechanism can then provide a basis for designing new catalysts that increase product selectivity and rates while simultaneously lowering overpotentials.

Some excellent reviews summarize previous research associated with CO₂RR on copper (4–6). Although many aspects of the mechanism remain unknown, CO is established as an important intermediate producing both C₂H₄ and methane CH₄ as major products. Indeed electroreduction of CO leads to similar product distributions and onset potentials as observed for CO₂RR (5–8). Online electrochemical mass spectrometry (OLEMS) was used to identify the products formed from the electroreduction of various compounds that might be intermediates on the C₂H₄ and ethanol (C₂H₅OH) pathways (3, 9).

The formation of CH₄ from CO depends on pH in such a way that the rate-determining step (RDS) must involve the transfer of a proton and an electron (10, 11). Recent experiments and density functional theory (DFT) calculations suggested that the key intermediate in the formation of CH₄ are *CHO on Cu(100) (12) and Cu(211) (13) and *COH on Cu(111) (14). On the other hand, the formation of C₂H₄ from CO does not depend on pH. Therefore, a dimer of CO, whose formation does not involve the transfer of a hydrogen atom but does depend on potential, has been suggested as the key intermediate in the C−C coupling (15).

The selectivity toward C₁ and C₂ production also depends on the surface structure of the copper electrode. For example, the formation of CH₄ is favored on Cu(111), whereas formation of C₂H₄ is dominant on Cu(100) (10, 16), and C₂H₅OH is generated at Cu(110) and Cu(511) (17). Evidence also exists that Cu polycrystalline (PC) generates ample amounts of C₂H₄ (3, 6), indicating that Cu(100) is the dominant crystal facet of Cu PC. Indeed, operando electrochemical scanning tunneling microscopy showed that a Cu PC electrode held at a fixed negative potential undergoes stepwise surface reconstruction to establish the Cu(100) surface (18).

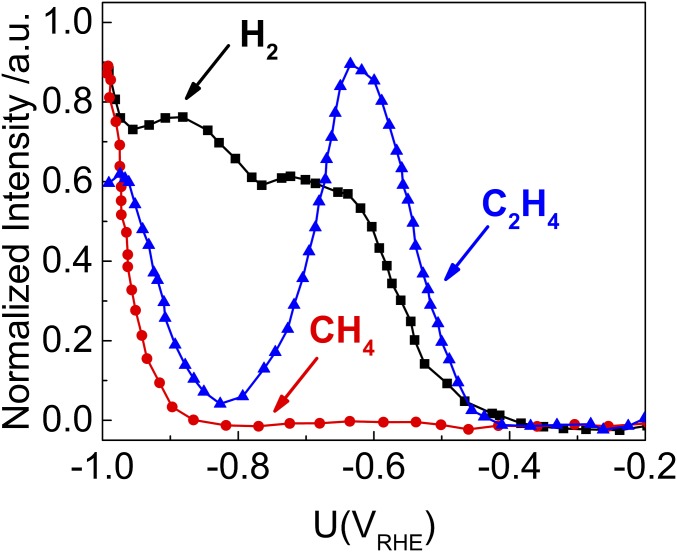
Fig. 1 shows the competition between C₂H₄ formation, hydrogen evolution (HER), and CH₄ formation as a function of applied potential (U) observed experimentally in CO reduction reactions (CORR) on Cu(100) at pH 7 (11). C₂H₄ formation starts at U = −0.40 V [reversible hydrogen electrode (RHE)] and increases to a maximum at −0.60 V with a high current that is hard to explain by the reduction of a surface-adsorbed species (10). Significant H₂ initiates at U = −0.4 V (RHE) and increases monotonically as U becomes more negative, which is the major contribution to current (10, 11). C₂H₄ formation decreases from −0.60 V (RHE) down to 0 at U = −0.80 V (RHE), whereas H₂ production increases but without producing CH₄. At U = −0.85 V (RHE), the formation of CH₄ first appears with C₂H₄ again observed, with both amounts increasing monotonically for more negative potentials.

Fig. 1.

Experimental mass fragments of C₂H₄, H₂, and CH₄, determined with OLEMS for reduction of CO in 0.1 M phosphate buffers (pH 7). C₂H₄ products in blue triangles. H₂ products in black squares and CH₄ products in red circles. This figure is based on the experimental data from Schouten et al. (11).

Quantum-mechanical (QM) calculations can provide atomistic mechanistic insight about CORR (12–15, 19–22). However, previous studies have all been deficient in not fully including solvent effects. Early calculations ignored the solvent in the simulation but corrected afterward (13, 15), whereas later studies used a variety of implicit solvation methods sometimes with a few explicit solvent molecules (14). These various studies led to a range of inconsistent results. For example, the predicted free-energy barriers for CO dimerization range from 0.33 to 1.22 eV, depending on the solvation model (15, 20–22). Consequently, we concluded that it is essential to use multiple layers of explicit water to describe reactions at the catalyst–solvent interface properly.

In this paper, free energies were calculated by metadynamics (23, 24) and further converged using thermodynamic integration by constrained molecular dynamics (blue moon ensemble) (25) to explain the experimentally observed product distribution as a function of U for Cu(100). These free-energy calculations provide a thorough reaction mechanism for major hydrocarbon productions (ethylene and ethane) and minor productions in CORR, which should help guide the design of new generations of catalysts.

Results and Discussion

Applied Potentials Less Negative Than −0.6 V (U greater than −0.6 V).

C₂H₄ is the product with the lowest kinetic barrier.

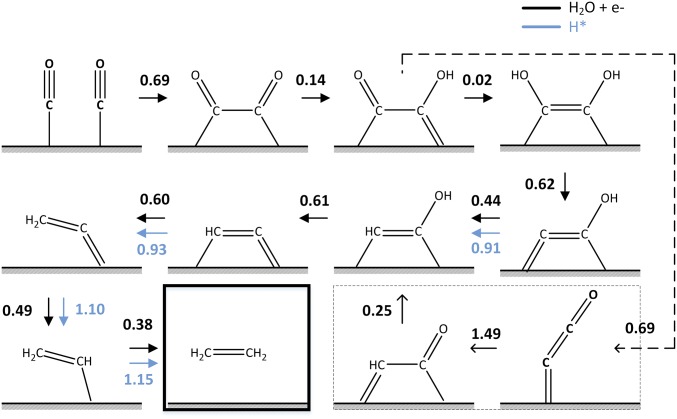
For U = −0.4 to −0.6 V (RHE), our calculations with explicit solvent find that the most favorable reduction of CO is C–C coupling to form *CO–CO, which has a free-energy barrier for the transition state saddle point (ΔG^‡) of 0.69 eV. We find that *CO–CO is quickly hydrated to *CO–COH, which then is quickly reduced to *COH–COH. The reaction barriers for these two steps are both within 0.14 eV. Indeed, we observe these reactions directly in our ab initio molecular dynamics (AIMD) simulation, because the low reaction barriers are surmounted within a few picoseconds. These reactions are via the Eley–Rideal (ER) mechanism using H₂O + e^–. Actually, in our calculations, we found that when adding hydrogen to oxygen, reactions via ER always have lower kinetic barriers than those via Langmuir–Hinshelwood (LH) mechanisms. The formation of *COH–COH explains the experimental observation of C₂ oxygenated products containing two oxygens, such as glycolaldehyde (CH₂OH–CHO) and ethylene glycol (CH₂OH–CH₂OH) (3).

Dihydroxylation of *COH–COH leads to the formation of *C–COH with ΔG^‡ = 0.62 eV via ER. Reduction of *C–COH to *CH–COH has ΔG^‡ = 0.44 eV via ER (0.91 eV via LH). The next step is dihydroxylation of *CH–COH to *CH–C with ΔG^‡ = 0.61 eV via ER by using H₂O + e^–.

The reactions from *CH–C to C₂H₄ seem straightforward, showing selectivity toward hydrocarbon species. Thus, *CH–C is reduced to *CH₂–C instead of *CH–CH, because ΔG^‡ = 0.61 eV (ER) for *CH₂–C formation (ΔG^‡ = 0.93 eV via LH) is lower than the ΔG^‡ = 1.07 eV (ER) for *CH–CH formation (1.41 eV via LH). We find that *CH₂–C is reduced to *CH₂–CH with ΔG^‡ = 0.49 eV (ER) (1.10 eV via LH). Finally, formation of C₂H₄ from *CH₂–CH has ΔG^‡ = 0.38 eV (ER) (1.15 eV via LH).

Summarizing, we find that adding hydrogen to carbon species through the ER mechanisms always has a lower reaction barrier than reactions through LH (Fig. 2) in the C₂H₄ formation pathway. Therefore, at U = −0.59 V (RHE) and pH 7, the lowest kinetic reaction pathway for C₂H₄ formation is purely through the ER mechanism, so that no step requires surface hydrogen (H*). This ER pathway explains the high current for C₂H₄ formation observed experimentally, which is beyond that expected from surface reactions (10). In this ER pathway of C₂H₄ formation, CO dimerization is the RDS with ΔG^‡ = 0.69 eV.

Fig. 2.

Lowest kinetic pathways for the eight-electron reduction of CO to ethylene (C₂H₄). Both Eley–Rideal (ER) (in black) and Langmuir–Hinshelwood (LH) mechanisms (in blue) are considered. In ER, H₂O + e^– (producing OH^–) are the reactants, whereas in LH, H* is the reactant. The reaction free-energy barriers (ΔG^‡) are provided. The slashed line shows the minor pathway for C₂H₄ formation through *C=C=O.

The second pathway to the C₂H₄ product.

A second pathway for C₂H₄ formation is through *CCO, which was first proposed by Calle-Vallejo and Koper (15). Indeed, *CCO formation is energetically more favorable on Cu(100), but ΔG^‡ for *CCO formation (0.69) is 0.67 eV higher than that of *COH–COH formation (0.02), making it kinetically forbidden. Thus, the *CCO pathway provides only a minor contribution to the C₂H₄ formation.

In this *CCO pathway for C₂H₄ formation, *CCO is first reduced to *CH–CO via LH with ΔG^‡ = 0.69 eV. Then, *CH–CO is reduced to *CH–COH with ΔG^‡ = 1.49 eV via LH, which merges into the *COH–COH pathway to also form C₂H₄.

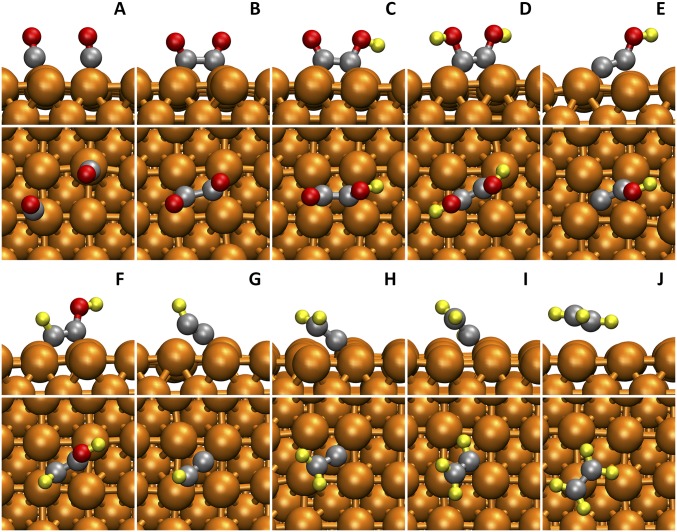
The entire reaction pathway for C₂H₄ formation is shown in Fig. 2. Snapshots of reactive intermediates from AIMD simulations are shown in Fig. 3.

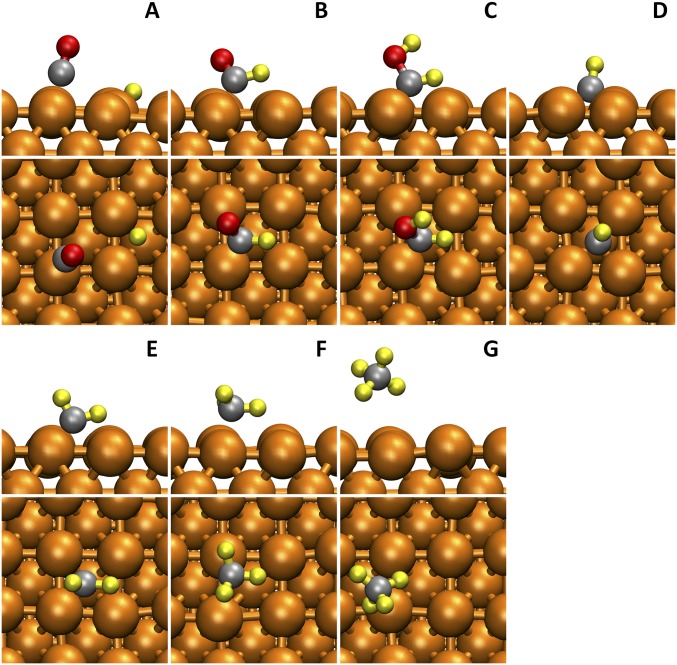
Fig. 3.

Snapshots (side view and top view) of reactants (A), reactive intermediates (B–I), and production (J) in the ethylene (C₂H₄) pathway from AIMD simulations at 298 K. The solvent water molecules are hidden for viewing convenience. The colors are Cu in orange, C in gray, H in yellow, and O in red.

Most kinetic favorable pathway to CH₄ products.

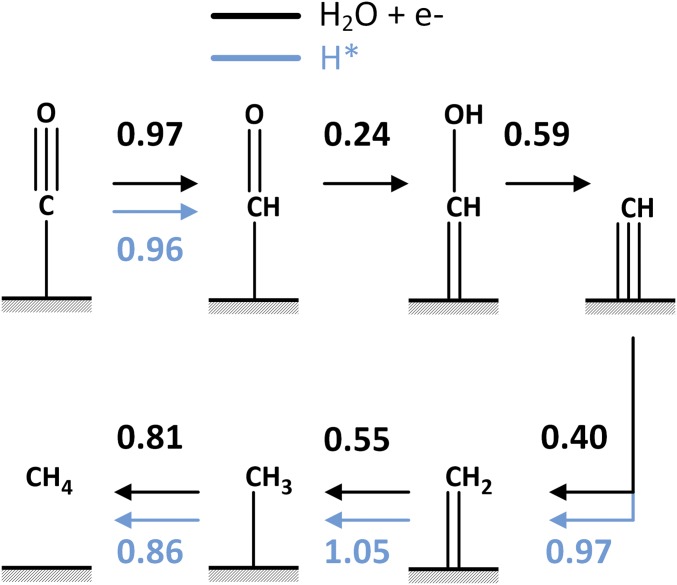
The lowest energy pathway for CH₄ formation at pH 7 is as follows:

• i)Reduction of CO to *CHO with an energy barrier of 0.96 eV via LH (0.97 eV via ER),
• ii)Quick reduction of *CHO to *CHOH with ΔG^‡ = 0.24 eV via ER,
• iii)Then dehydroxylation of *CHOH leads to *CH + OH^– with ΔG^‡ = 0.59 eV via ER.
• iv)Next is *CH reduction to *CH₂ with ΔG^‡ = 0.40 eV via ER (0.97 eV via LH),
• v)Then *CH₂ reduction to *CH₃ with ΔG^‡ = 0.55 eV via ER (1.05 eV via LH),
• vi)And finally, *CH₃ reduction to CH₄ with ΔG^‡ = 0.81 eV via ER (0.86 eV via LH).

The entire reaction pathway for CH₄ formation is shown in Fig. 4. Snapshots of reactive intermediates from AIMD simulations are shown in Fig. 5.

Fig. 4.

Lowest kinetic pathway for the six-electron reduction of CO to methane (CH₄). Both the Eley–Rideal (ER) mechanism (in black) and the Langmuir–Hinshelwood (LH) mechanism (in blue) are considered. In the ER mechanism, H₂O + e^– (producing OH^–) are the reactants, whereas in the LH mechanism, H* is the reactant. The reaction free-energy barriers (ΔG^‡) are provided.

Fig. 5.

Snapshots (side view and top view) of reactants (A), reactive intermediates (B–F), and production (G) in the methane (CH₄) pathway from AIMD simulations at 298 K. The solvent water molecules are hidden for viewing convenience. The colors are Cu in orange, C in gray, H in yellow, and O in red.

At pH 7, *CHO formation is the RDS for CH₄ formation with ΔG^‡ = 0.96 eV via LH, whereas CO dimerization is the RDS for C₂H₄ formation with ΔG^‡ = 0.69 eV. Therefore, at pH 7, C₂H₄ is predominant for U greater than −0.8 V (RHE), as experimentally observed. Note that *CHO formation is pH dependent, whereas C–C coupling is pH independent (20). Thus, at pH 0, ΔG^‡ of *CHO formation decreases to 0.55 eV (0.96 − 0.0592 × 7), whereas the reaction barrier of C–C coupling remains at 0.69 eV. This pH dependency explains why CH₄ is predominant at pH 0, as experimentally observed (11).

HER is the major side reaction competing with CO reduction, which limits the faradaic efficiency. It is known that the presence of CO retards HER due to the stronger binding of CO to Cu metal surface (2). On the Cu(100) surface, our QM calculations with full solvation lead to a binding energy (ΔE_b) of −0.80 eV for CO and −0.11 eV for H atom (hollow site) reference to H₂. Therefore, at zero applied potential (U = 0 V), the binding energy of CO is much larger than that of H*. The maximum CO coverage can reach 1/3 ML, as predicted in a previous DFT calculation (26).

Comparison with experiment and previous calculations.

On the Cu(100) surface, C₂H₄ formation starts at U = −0.4 V and is pH independent (RHE dependent) (11), indicating that the RDS does not involve hydrogen. Additionally, no CH₄ formation is observed at this potential, pointing out that the mechanism is different from at U less than −0.8 V, where there is branching to both C₂H₄ and CH₄. These experimental observations agree with the theory that the first step of C₂H₄ formation is related to coupling of two CO molecules mediated by electron transfer to form *CO–CO.

We find that ΔG^‡ = 0.69 eV for the RDS. Previous calculations of the reaction barrier for CO dimerization have ranged from 0.33 to 1.22 eV, depending on the solvation models and applied potentials (15, 20–22).

Potentials from −0.6 to −0.8 V.

The above tendencies for U greater than −0.8 V are reversed for more negative U. As U becomes more negative, the ΔE_B of H increases with a slope close to 1 eV/V [H₂O(aq) + e^– → OH^–(aq) + H*]. In contrast, more negative U has little impact on ΔE_B of CO, because charges barely transfer during CO adsorption. To validate this, the charge transfers during CO adsorption were calculated under fixed applied potentials by optimizing the number of electrons (N_e) along the reaction path (27) within the framework of joint density functional theory (28), and the solvation effects was handled by the charge-asymmetric nonlocally determined local-electric implicit model (29). We find that, for increasingly negative U, ΔE_B of H* increases, and finally matches the CO binding at U = −0.69 V (RHE). Consequently, at U more negative than −0.69, surface H* and *CO compete for surface sites. Although no experimental data are available about the surface coverage of H under CORR condition, previous experimental studies (analyzed based on Volmer–Heyrovsky pathways and Volmer–Tafel pathways) estimated the surface coverage of H* to range from 0.3 to 1.0 at large negative overpotentials (30, 31).

Furthermore, experiments on Cu(100) starting from U = −0.64 to −0.70 V (saturated calomel electrode) or −0.40 to −0.46 V (RHE) suggest that H* induces reconstruction leading to a concomitant increase in HER (32). A recent in situ surface-enhanced spectroscopic experiment shows that at −0.7 V H* is capable of partially displacing *CO; however, *CO is unable to displace H* to any detectable level (33). This increase in H* coverage causes a decrease in CO surface coverage that significantly slows the CO dimerization and hence C₂H₄ formation. We consider that site-blocking effects explain the decline of C₂H₄ formation down to 0 as U = −0.60 goes to −0.80 V (10, 11). Of course, we cannot exclude that other effects may contribute, such as deposition of metal impurities (34) and mass diffusion limitations (35).

Potentials are more negative than −0.8 V.

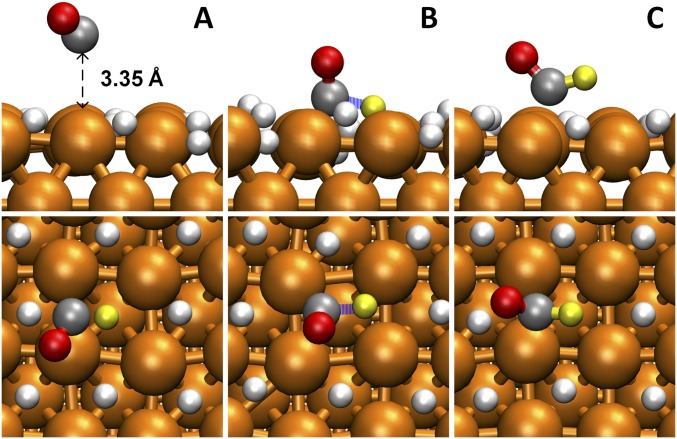
Interestingly, we found that this site-blocking effect at very negative U does not block *CHO formation, which can be explained by *CHO formation proceeding via an ER mechanism from nonadsorbed CO. To demonstrate this, we carried out simulations for the extreme case of full H* (1 ML) coverage to block all available sites for CO adsorption. Under this condition, any CO on the surface would quickly desorb. With explicit solvent, we calculate that at 1-ML H* coverage, the distance of CO from the Cu surface is ∼3.35 Å (as shown in Fig. 6A). We find that ΔG^‡ = 1.01 eV for this solvent CO to react with a surface H* to produce *CHO, very close to the value (ΔG^‡ = 0.96 eV) derived at low H* coverage for adsorbed CO to react with H*. As a consequence, the H* site-blocking effect does not block *CHO formation. Because *CHO formation can proceed from a reaction pathway in which CO is not adsorbed (as shown in Fig. 6), we can understand the appearance of CH₄ at U less than −0.85 V (RHE).

Fig. 6.

Reactive trajectories of *CHO formation for high coverage of surface H (1 ML of H*) from AIMD simulations at 298 K (A) nonadsorbed CO, (B) transition state, and (C) *CHO. The solvent water molecules are hidden for viewing convenience. The colors are Cu in orange, C in gray, H in yellow, and O in red. The reaction barrier is 1.01 eV.

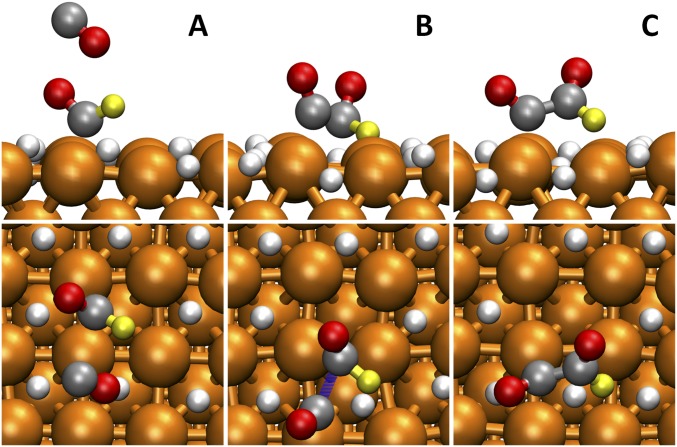
We calculate that recurrence of C₂H₄ for U less than −0.85 arises from the pathway in which nonadsorbed CO reacts with *CHO, as shown in Fig. 7. In this case, a second nonadsorbed CO reacts with *CHO to form *CO–CHO with ΔG^‡ = 0.71 eV. Goodpaster et al. (21) first proposed this reaction pathway to explain the recurrence of C₂H₄ production. Although our predicted ΔG^‡ is close to the Goodpaster value, 0.68 eV, our reaction pathways are significantly different. Goodpaster assumed CO already adsorbed on the Cu surface based on his implicit solvation model, whereas we find that a nonadsorbed CO is a reactant in our explicit solvent calculations. Consequently, our mechanism involves only one surface site (Fig. 7), which we expect to be close to the experimental conditions at U less than −0.85 V (RHE).

Fig. 7.

Reactive trajectories for *CO–CHO formation at the high coverage of surface H (H* in 1 ML) from AIMD simulation at 298 K (A) one *CHO and one nonadsorbed CO, (B) transition state, and (C) *CO-CHO. The solvent water molecules are hidden for viewing convenience. The colors are Cu in orange, C in gray, H in yellow, and O in red. The reaction barrier is 0.71 eV.

Summarizing, we find that the recurrence of C₂H₄ at U less than −0.85 V (RHE) is due to the coupling of nonadsorbed CO with *CHO. Consequently, C₂H₄ and CH₄ formation share a common intermediate, which explains the appearance of C₂H₄ and CH₄ following each other for U < 0.85 V (RHE).

Summary of Reaction Mechanism for CH₄ and C₂H₄ Products for All Potentials.

Armed with the complete free-energy information from above, we can now explain the reaction mechanism of CORR on Cu(100) at pH 7 as follows:

• For U greater than −0.6 V (RHE), C₂H₄ is the major product through CO dimerization with ΔG^‡ = 0.69 eV. We find that H₂O is the hydrogen source for all these reduction steps in C₂H₄ formation, leading to a high current as experimentally observed. CH₄ was not observed at U greater than −0.85 V (RHE), because *CHO formation is unfavorable due to the high reaction barrier (ΔG^‡ = 0.96 eV via adsorbed CO and the ΔG^‡ = 1.01 eV via nonadsorbed CO).

• As U decreases from −0.6 to −0.8 V, the H* binding energy increases, leading to an increased surface concentration of H*, with a concomitant decreased concentration of *CO, which significantly slows C₂H₄ formation and finally totally blocks this reaction for U = −0.80 V.

• At U less than −0.85 V, a nonadsorbed CO hydrogenation pathway contributes to the occurrence of CH4 in addition to the adsorbed CO pathway. The reoccurrence of C₂H₄ formation for U less than −0.85 V in parallel with CH₄ arises from *CO–CHO formation through nonadsorbed CO coupling with *CHO. Thus, *CHO is the common intermediate for both C₂H₄ and CH₄ formation at U less than −0.85 V.

Other Hydrocarbon and Oxygenate Products.

Apart from the two major hydrocarbon products, small amounts of several other C1 to C3 products are observed experimentally under CO₂ reduction conditions (3). The mechanisms for the formation of these minor productions are also an important part of CORR and CO₂RR. We find the lowest kinetic reaction pathways to minor products of C₂ products at pH 7 proceed as follows (in each case, the number below the arrow is the ΔG^‡):

• i)Glyoxal (CHO–CHO):
• $$\begin{array}{l}*\text{COH}–\text{COH}\underset{1.21}{\to }*\text{COH}–\text{CHO}\underset{1.22}{\to }\text{CHO}–\text{CHO}.\end{array}$$ [1]
• ii)Glycolaldehyde (CHO–CH₂OH):
• $$\begin{array}{l}*\text{COH}–\text{COH}\underset{1.07}{\overset{\text{H}*}{\to }}*\text{CHOH}–\text{COH}\underset{1.13}{\overset{\text{H}*}{\to }}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\text{CHOH}=\text{CHOH}\underset{1.22}{\overset{\text{H}*}{\to }}\text{CHO}–{\text{CH}}_2\text{OH}.\end{array}$$ [2]
• iii)Ethylene glycol (CH₂OH–CH₂OH):
• $$\begin{array}{l}\text{CHOH}=\text{CHOH}\underset{1.51}{\overset{\text{H}*}{\to }}*{\text{CH}}_2\text{OH}–\text{CHOH}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\underset{0.83}{\overset{\text{H}*}{\to }}{\text{CH}}_2\text{OH}–{\text{CH}}_2\text{OH}.\end{array}$$ [3]
• iv)Ethanol (CH₃–CH₂OH):
• $$\begin{array}{l}*\text{CH}–\text{COH}\underset{1.05}{\overset{\text{H}*}{\to }}*\text{CH}–\text{CHOH}\underset{1.14}{\overset{\text{H}*}{\to }}{\text{CH}}_2=\text{CHOH}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\underset{1.04}{\overset{\text{H}*}{\to }}{\text{CH}}_3–\text{CHOH}\underset{1.01}{\overset{\text{H}*}{\to }}{\text{CH}}_3–{\text{CH}}_2\text{OH}.\end{array}$$ [4]
• v)Acetaldehyde (CH₃–CHO):
• $$\text{C}{\text{H}}_2=\text{CHOH}\underset{1.22}{\to }{\text{CH}}_3–\text{CHO}.$$ [5]
• vi)Ethane (CH₃–CH₃):
• $$\begin{array}{l}*\text{CH}={\text{CH}}_2\underset{1.21}{\overset{\text{H}*}{\to }}*\text{CH}–{\text{CH}}_3\underset{1.56}{\overset{\text{H}*}{\to }}{\text{CH}}_2–{\text{CH}}_3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\underset{1.24}{\overset{\text{H}*}{\to }}{\text{CH}}_3–{\text{CH}}_3.\end{array}$$ [6]

All these C products share the same reaction intermediate with C₂H₄: *COH–COH. They can be further partitioned into three groups based on how they branch from the C₂H₄ pathway:

• i)Glyoxal (CHO–CHO) leaves the C₂H₄ pathway at *COH–COH by forming *COH–CHO through nonelectrochemical reaction steps, which are much slower than the *C–COH formation in the C₂H₄ pathway.
• ii)Glycolaldehyde (CHO–CH₂OH) and ethylene glycol (CH₂OH–CH₂OH) leave the C₂H₄ pathway at *COH–COH by forming *CHOH–COH, which has a ΔG^‡ of 0.44 eV higher.
• iii)C₂H₅OH, acetaldehyde (CH₃–CHO), and ethane (CH₃–CH₃) leave the C₂H₄ pathway at *CH–COH by forming *CH–COH, which has a ΔG^‡ of 0.43 eV higher. Of these three productions, C₂H₅OH formations are the fastest.

Experimentally, C₂H₄ and C₂H₅OH have similar Tafel slopes patterns, whereas CHO–CH₂OH has a different Tafel slope pattern (3). These observations provide experimental evidence showing that C₂H₅OH branches from the C₂H₄ pathway later than does CHO–CH₂OH, as predicted.

Conclusion

Summarizing, we carried out AIMD reactive dynamics simulations with five layers of explicit water to determine the mechanism of CORR on Cu(100) surface at pH 7. We determined the reaction pathways including free-energy reaction barriers for major products (C₂H₄ and CH₄), and for six minor C2 products (ethanol, glyoxal, glycolaldehyde, ethylene glycol, acetaldehyde, ethane, and methanol). These computations fully explain experimental observations, including the competition between electrochemical reactions and surface sites.

At U greater than −0.6 V, we found that C₂H₄ formation dominates over CH₄ formation. Two *CO couple to form a C–C bond with an energy barrier of 0.69 eV, much lower than for *CHO formation (0.96 eV). Therefore, C₂H₄ is the major hydrocarbon product for U greater than −0.8 V. Interestingly, we find that C₂H₄ proceeds purely via ER mechanisms, explaining why experiments observe high currents associated with the C₂H₄ formation in this regime.

For U less than −0.6V and U greater than −0.8V, H* displaces CO from the surface sites, because H* has a stronger binding energy than CO. Consequently, the surface coverage of H* increases monotonically for more negative potentials, blocking CO adsorption. This decrease of CO surface coverage slows CO dimerization to shut off C₂H₄ production as U = −0.6 V goes to −0.8 V. Of course other factors, such as HER-induced surface reconstruction, deposition of metal impurities (34), and mass diffusion limitation (35), may also contribute to blocking CO adsorption.

At U less than −0.8 V, we found that both CH₄ and C₂H₄ are produced by using nonadsorbed CO. Here, *CHO becomes the common intermediate for both CH₄ and C₂H₄ formation.

Considering this full picture of CORR, we see that U greater than −0.6 V is the optimum region to obtain hydrocarbon products selectivity. To increase the reaction rates in this regime, we need to accelerate CO dimerization. Ways to achieve this include the following: increasing the local concentration of CO (for example, by modifying the electrolyte or by conjoining the Cu with another element such as Ag or Au that can produce CO from CO₂) (36); and increasing the binding energy of CO, perhaps by alloying or using nanotechnologies (37, 38).

Models and Methods

Here, we simulate the water/Cu(100) interface using 48 explicit water molecules on a 4 × 4 Cu(100) surface slab (three layers) as shown in Fig. S1. Two nanoseconds of reactive molecular dynamics (RMD) simulations was carried out to equilibrate the waters interacting with the interface using the ReaxFF reactive force field for Cu and H₂O (39). Starting from this well-equilibrated interface, 10 ps of AIMD simulations were carried out at 298 K. Free-energy barriers for various reaction steps and free-energy differences were obtained by using metadynamics (23, 24, 40, 41) and thermodynamic integration (25) for various reaction steps. The collective variables (CV) for elementary reactions are in Tables S1 and S2 and the calculated free energies are in Tables S3 and S4. Electronic structure calculations were performed within the DFT framework, as implemented in the Vienna ab initio simulation program (VASP) (42–45), a plane-wave pseudopotential package. The exchange and correlation energies were calculated using the Perdew, Burke, and Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) (46, 47). The PBE-D3 method was used to correct van der Waals interaction of water–water and water–Cu (48). The charges on various species were derived using a Bader analysis (49). To compare with the constant potential of experiments, we used the procedure proposed by Chan and Nørskov to remove any artifacts involving work function changes during the chemical reaction (50). The scheme of work function calculation is in Fig. S2. The obtained work functions of elementary reactions are in Tables S5 and S6 and the corrected free energies are in Tables S7 and S8.

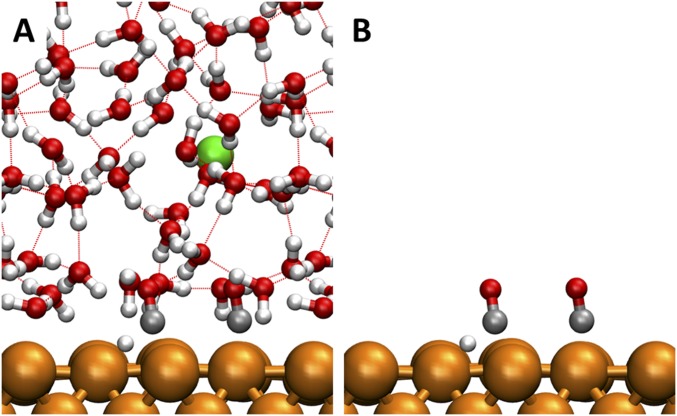
Fig. S1.

Water/Cu(100) interface used in the calculations. A and B show the same system. A shows more details, including explicit water, Na⁺, and hydrogen bond (HB) network. B removes water and Na⁺ to show surface species (2 *CO and 1 H*). The colors are C in silver, H in white, O in red, Cu in orange, and Na in green. HBs are shown with red dashed line.

Table S1.

Collective variables (CVs) for various reduction steps of CH₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	CV
1	$*\text{CO}+\text{H}*\to *\text{CHO}$	R(C–H)
1a	$*\text{CO}+{\text{H}}_2\text{O}+e^{-}\to *\text{CHO}+{\text{OH}}^{-}$	R(C–H)
1b	$*\text{CO}+{\text{H}}_2\text{O}+e^{-}\to *\text{COH}+{\text{OH}}^{-}$	R(O–H)
2	$*\text{CHO}+{\text{H}}_2\text{O}+e^{-}\to *\text{CHOH}+{\text{OH}}^{-}$	R(O–H)
2a	$*\text{CHO}+\text{H}*\to {\text{CH}}_2\text{O}$	R(C–H)
3	$\text{*CHOH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*CH}+{\text{OH}}^{-}$	R(C–O)
3a	$\text{*CHOH}+\text{H*}\to *{\text{CH}}_2\text{OH}$	R(C–H)
4	$\text{*CH}+{\text{H}}_2\text{O}+e^{-}\to *{\text{CH}}_2+{\text{OH}}^{\mathrm{-}}$	R(C–H)
4a	$\text{*CH}+\text{H*}\to *{\text{CH}}_2$	R(C–H)
5	${\text{*CH}}_2+{\text{H}}_2\text{O}+e^{-}\to *{\text{CH}}_3+{\text{OH}}^{-}$	R(C–H)
5a	${\text{*CH}}_2+\text{H*}\to *{\text{CH}}_3$	R(C–H)
6	${\text{*CH}}_3+{\text{H}}_2\text{O}+e^{-}\to {\text{CH}}_4+{\text{OH}}^{-}$	R(C–H)
6a	${\text{*CH}}_3+\text{H*}\to {\text{CH}}_4$	R(C–H)

Each number specifies the reduction step. Reaction IDs with only numbers are major reactions, whereas reaction IDs with a number plus a letter indicates a side reaction. H₂O on arrows are H₂O molecules involved in the Grotthuss hydrogen bond network to tunnel proton.

Table S2.

Collective variables (CVs) for various reduction steps of C₂H₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	CV
0	$\text{*CO}+*\text{CO}+\mathrm{\delta }\cdot e^{-}\to *{\text{CO–CO}}^{\mathrm{\delta }-}$	R(C–C)
1	${\text{*OC–CO}}^{\mathrm{\delta }-}+{\text{H}}_2\text{O}+\left(1\mathrm{-\delta }\right)\mathrm{\cdot }{e}^{-}\to *\text{CO–COH}+{\text{OH}}^{-}$	R(O–H)
2	$\text{*CO–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*COH–COH}+{\text{OH}}^{-}$	R(O–H)
2a	${\text{*OC–CO}}^{\mathrm{\delta }-}+\text{H*}\to *{\text{CHO–CO}}^{\mathrm{\delta }-}$	R(C–H)
3	$\text{*COH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–COH}+{\text{OH}}^{-}$	R(C–H)
3a	$\text{*COH–COH}+\text{H*}\to *\text{CHOH–COH}$	R(C–H)
4	$\text{*C–COH}+{\text{H}}_2\text{O}+e^{-}\to *\text{CH–COH}+{\text{OH}}^{-}$	R(C–H)
4a	$\text{*C–COH}+\text{H*}\to *\text{CH–COH}$	R(C–H)
4b	$\text{*C–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }*\text{C}–\text{C}+{\text{OH}}^{-}$	R(C–O)
4c	$\text{*C–COH}+\text{H*}\to *\text{C}–\text{CHOH}$	R(C–H)
5	$\text{*CH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–CH}+{\text{OH}}^{-}$	R(C–O)
5a	$\text{*CH–COH}+\text{H*}\to *{\text{CH}}_2\text{–COH}$	R(C–H)
5b	$\text{*CH–COH}+\text{H*}\to *\text{CH–CHOH}$	R(C–H)
6	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to *{\text{C}–\text{CH}}_2+{\text{OH}}^{-}$	R(C–H)
6a	$\text{*C–CH}+\text{H*}\to *{\text{C}–\text{CH}}_2$	R(C–H)
6b	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to *\text{CH–CH}+{\text{OH}}^{-}$	R(C–H)
6c	$\text{*C–CH}+\text{H*}\to *\text{CH–CH}$	R(C–H)
7	${\text{*C–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to *{\text{CH–CH}}_2+{\text{OH}}^{-}$	R(C–H)
7a	${\text{*C–CH}}_2+\text{H*}\to *{\text{CH–CH}}_2$	R(C–H)
7b	${\text{*C–CH}}_2+\text{H*}\to *{\text{C}–\text{CH}}_3$	R(C–H)
8	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{C}}_2{\text{H}}_4+{\text{OH}}^{-}$	R(C–H)
8a	${\text{*CH–CH}}_2+\text{H*}\to {\text{C}}_2{\text{H}}_4$	R(C–H)
8b	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_3+{\text{OH}}^{-}$	R(C–H)
8c	${\text{*CH–CH}}_2+\text{H*}\to {\text{*CH–CH}}_3$	R(C–H)

Each number indicates the reduction step. Reaction IDs with only numbers are major reactions, and reaction IDs with a number plus a letter indicates a side reaction. H₂O on arrows are H₂O molecules involved in the Grotthuss hydrogen-bond network to tunnel proton.

Table S3.

Free-energy barriers (ΔG^‡, in electronvolts) and free-energy differences (ΔG, in electronvolts) for various reduction steps of CH₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	ΔG‡, eV	ΔG, eV
1	$\text{*CO}+\text{H*}\to \text{*CHO}$	0.96 (0.10)	0.90 (0.10)
1a	$\text{*CO}+{\text{H}}_2\text{O}+e^{-}\to *\text{CHO}+{\text{OH}}^{-}$	0.98 (0.07)	0.90 (0.08)
1b	$\text{*CO}+{\text{H}}_2\text{O}+e^{-}\to *\text{COH}+{\text{OH}}^{-}$	1.21 (0.13)	1.13 (0.11)
2	$\text{*CHO}+{\text{H}}_2\text{O}+e^{-}\to *\text{CHOH}+{\text{OH}}^{-}$	0.24 (0.15)	0.11 (0.12)
2a	$\text{*CHO}+\text{H*}\to {\text{CH}}_2\text{O}$	1.01 (0.15)	0.51 (0.14)
3	$\text{*CHOH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*CH}+{\text{OH}}^{-}$	0.60 (0.06)	−0.04 (0.07)
3a	$\text{*CHOH}+\text{H*}\to *{\text{CH}}_2\text{OH}$	0.86 (0.09)	0.38 (0.09)
4	$\text{*CH}+{\text{H}}_2\text{O}+e^{-}\to *{\text{CH}}_2+{\text{OH}}^{\mathrm{-}}$	0.41 (0.04)	0.32 (0.11)
4a	$\text{*CH}+\text{H*}\to *{\text{CH}}_2$	0.97 (0.04)	0.19 (0.11)
5	${\text{*CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH}}_3+{\text{OH}}^{-}$	0.56 (0.10)	0.17 (0.13)
5a	${\text{*CH}}_2+\text{H*}\to *{\text{CH}}_3$	1.05 (0.12)	0.01 (0.12)
6	${\text{*CH}}_3+{\text{H}}_2\text{O}+e^{-}\to {\text{CH}}_4+{\text{OH}}^{-}$	0.82 (0.04)	−0.42 (0.11)
6a	${\text{*CH}}_3+\text{H*}\to {\text{CH}}_4$	0.87 (0.14)	−0.69 (0.07)

The errors are in parentheses. All e^– are allowed to rearrange self-consistently during the AIMD simulations.

Table S4.

Free-energy barriers (ΔG^‡, in electronvolts) and free-energy differences (ΔG, in electronvolts) for various reduction steps of C₂H₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	ΔG‡, eV	ΔG, eV
0	$\text{*CO}+\text{*CO}+\mathrm{\delta }\cdot e^{-}\to {\text{*CO–CO}}^{\mathrm{\delta }-}$	0.69 (0.11)	0.59 (0.13)
1	${\text{*OC–CO}}^{\mathrm{\delta }-}+{\text{H}}_2\text{O}+\left(1-\mathrm{\delta }\right)\mathrm{\cdot }{e}^{-}\to \text{*CO–COH}+{\text{OH}}^{-}$	0.14 (0.10)	−0.01 (0.07)
2	$\text{*CO–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*COH–COH}+{\text{OH}}^{-}$	0.02 (0.09)	−0.12 (0.11)
2a	${\text{*OC–CO}}^{\mathrm{\delta -}}+\text{H*}\to {\text{*CHO–CO}}^{\mathrm{\delta -}}$	1.12 (0.12)	0.56 (0.14)
3	$\text{*COH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–COH}+{\text{OH}}^{-}$	0.63 (0.11)	0.43 (0.15)
3a	$\text{*COH–COH}+\text{H*}\to \text{*CHOH–COH}$	1.07 (0.10)	0.80 (0.09)
4	$\text{*C–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*CH–COH}+{\text{OH}}^{-}$	0.45 (0.12)	0.22 (0.15)
4a	$\text{*C–COH}+\text{H*}\to \text{*CH–COH}$	0.92 (0.10)	−0.01 (0.09)
4b	$\text{*C–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–C}+{\text{OH}}^{-}$	1.18 (0.10)	0.79 (0.10)
4c	$\text{*C–COH}+\text{H*}\to \text{*C–CHOH}$	1.01 (0.09)	0.37 (0.11)
5	$\text{*CH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–CH}+{\text{OH}}^{-}$	0.62 (0.11)	−0.11 (0.14)
5a	$\text{*CH–COH}+\text{H*}\to {\text{*CH}}_2\text{–COH}$	1.41 (0.12)	1.22 (0.11)
5b	$\text{*CH–COH}+\text{H*}\to \text{*CH–CHOH}$	1.05 (0.14)	0.83 (0.12)
6	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to {\text{*C–CH}}_2+{\text{OH}}^{-}$	0.61 (0.07)	0.20 (0.08)
6a	$\text{*C–CH}+\text{H*}\to {\text{*C–CH}}_2$	0.93 (0.11)	0.40 (0.09)
6b	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to \text{*CH–CH}+{\text{OH}}^{-}$	1.09 (0.08)	0.87 (0.09)
6c	$\text{*C–CH}+\text{H*}\to \text{*CH–CH}$	1.41 (0.15)	0.68 (0.13)
7	${\text{*C–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_2+{\text{OH}}^{-}$	0.50 (0.08)	0.38 (0.07)
7a	${\text{*C–CH}}_2+\text{H*}\to {\text{*CH–CH}}_2$	1.10 (0.13)	0.42 (0.15)
7b	${\text{*C–CH}}_2+\text{H*}\to {\text{*C–CH}}_3$	1.76 (0.09)	1.76 (0.09)
8	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{C}}_2{\text{H}}_4+{\text{OH}}^{-}$	0.39 (0.09)	−0.07 (0.10)
8a	${\text{*CH–CH}}_2+\text{H*}\to {\text{C}}_2{\text{H}}_4$	1.15 (0.07)	0.02 (0.07)
8b	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_3+{\text{OH}}^{-}$	0.70 (0.13)	0.70 (0.13)
8c	${\text{*CH–CH}}_2+\text{H*}\to {\text{*CH–CH}}_3$	1.21 (0.12)	0.58 (0.11)

All e^– are allowed to rearrange self-consistently during the AIMD simulations.

Fig. S2.

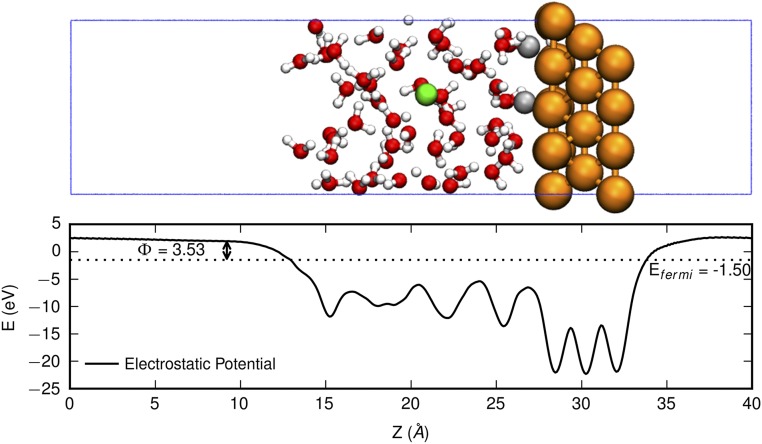
Plane averaged electrostatic potential (in electronvolts) of water/Cu(100) electrode along the z direction. Indicated are the Fermi energy (E_fermi, in electronvolts) and the work function (Φ, in electronvolts). The atomic structure of the water/Cu(100) electrode is shown on the Top for viewing convenience. The colors are C in silver, H in white, O in red, Cu in orange, and Na in green. In this snapshot, E_fermi = −1.50 eV and Φ = 3.53 eV.

Table S5.

Work function (in electronvolts) of the initial state (Φ₀), transition state (Φ_TS), and final state (Φ₁) for various reduction steps of CH₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	Φ0, eV	ΦTS, eV	Φ1, eV
1	$\text{*CO}+\text{H*}\to \text{*CHO}$	3.48 (0.33)	3.49 (0.23)	3.59 (0.24)
1a	$\text{*CO}+{\text{H}}_2\text{O}+e^{-}\to \text{*CHO}+{\text{OH}}^{-}$	3.48 (0.33)	3.60 (0.29)	3.80 (0.27)
1b	$\text{*CO}+{\text{H}}_2\text{O}+e^{-}\to \text{*COH}+{\text{OH}}^{-}$	3.48 (0.33)	3.52 (0.24)	3.75 (0.30)
2	$\text{*CHO}+{\text{H}}_2\text{O}+e^{-}\to \text{*CHOH}+{\text{OH}}^{-}$	3.38 (0.34)	3.48 (0.32)	3.66 (0.20)
2a	$\text{*CHO}+\text{H*}\to {\text{CH}}_2\text{O}$	3.38 (0.34)	3.49 (0.32)	3.47 (0.27)
3	$\text{*CHOH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*CH}+{\text{OH}}^{-}$	3.36 (0.34)	3.55 (0.24)	3.80 (0.34)
3a	$\text{*CHOH}+\text{H*}\to {\text{*CH}}_2\text{OH}$	3.36 (0.34)	3.47 (0.31)	3.49 (0.21)
4	$\text{*CH}+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH}}_2+{\text{OH}}^{-}$	3.23 (0.29)	3.42 (0.25)	3.70 (0.33)
4a	$\text{*CH}+\text{H*}\to {\text{*CH}}_2$	3.23 (0.29)	3.28 (0.32)	3.39 (0.36)
5	${\text{*CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH}}_3+{\text{OH}}^{-}$	3.22 (0.29)	3.41 (0.23)	3.67 (0.29)
5a	${\text{*CH}}_2+\text{H*}\to {\text{*CH}}_3$	3.22 (0.29)	3.25 (0.35)	3.32 (0.33)
6	${\text{*CH}}_3+{\text{H}}_2\text{O}+e^{-}\to {\text{CH}}_4+{\text{OH}}^{-}$	3.26 (0.22)	3.42 (0.29)	3.63 (0.36)
6a	${\text{*CH}}_3+\text{H*}\to {\text{CH}}_4$	3.26 (0.22)	3.38 (0.31)	3.40 (0.22)

Table S6.

Work function (in electronvolts) of the initial state (Φ₀), transition state (Φ_TS), and final state (Φ₁) for various reduction steps of C₂H₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	Φ0, eV	ΦTS, eV	Φ1, eV
0	$\text{*CO}+\text{*CO}+\mathrm{\delta }\cdot e^{-}\to {\text{*CO–CO}}^{\mathrm{\delta -}}$	3.39 (0.24)	3.47 (0.28)	3.67 (0.3)
1	${\text{*OC–CO}}^{\mathrm{\delta -}}+{\text{H}}_2\text{O}+\left(1-\mathrm{\delta }\right)\mathrm{\cdot }{e}^{-}\to \text{*CO–COH}+{\text{OH}}^{-}$	3.67 (0.3)	3.75 (0.21)	3.74 (0.25)
2	$\text{*CO–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*COH–COH}+{\text{OH}}^{-}$	3.32 (0.30)	3.43 (0.35)	3.68 (0.29)
2a	${\text{*OC–CO}}^{\mathrm{\delta -}}+\text{H*}\to {\text{*CHO–CO}}^{\mathrm{\delta -}}$	3.67 (0.3)	3.76 (0.26)	3.83 (0.28)
3	$\text{*COH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–COH}+{\text{OH}}^{-}$	3.13 (0.28)	3.27 (0.22)	3.50 (0.24)
3a	$\text{*COH–COH}+\text{H*}\to \text{*CHOH–COH}$	3.13 (0.28)	3.28 (0.28)	3.19 (0.25)
4	$\text{*C–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*CH–COH}+{\text{OH}}^{-}$	3.43 (0.31)	3.61 (0.34)	3.80 (0.22)
4a	$\text{*C–COH}+\text{H*}\to \text{*CH–COH}$	3.43 (0.31)	3.55 (0.35)	3.56 (0.35)
4b	$\text{*C–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–C}+{\text{OH}}^{-}$	3.43 (0.31)	3.48 (0.24)	3.72 (0.25)
4c	$\text{*C–COH}+\text{H*}\to \text{*C–CHOH}$	3.43 (0.31)	3.56 (0.22)	3.60 (0.27)
5	$\text{*CH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–CH}+{\text{OH}}^{-}$	3.28 (0.27)	3.42 (0.35)	3.65 (0.35)
5a	$\text{*CH–COH}+\text{H*}\to {\text{*CH}}_2\text{–COH}$	3.28 (0.27)	3.36 (0.32)	3.40 (0.21)
5b	$\text{*CH–COH}+\text{H*}\to \text{*CH–CHOH}$	3.28 (0.27)	3.29 (0.35)	3.38 (0.20)
6	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to {\text{*C–CH}}_2+{\text{OH}}^{-}$	3.43 (0.36)	3.60 (0.35)	3.85 (0.26)
6a	$\text{*C–CH}+\text{H*}\to {\text{*C–CH}}_2$	3.43 (0.36)	3.46 (0.27)	3.57 (0.21)
6b	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to \text{*CH–CH}+{\text{OH}}^{-}$	3.43 (0.36)	3.64 (0.25)	3.88 (0.29)
6c	$\text{*C–CH}+\text{H*}\to \text{*CH–CH}$	3.43 (0.36)	3.48 (0.28)	3.60 (0.29)
7	${\text{*C–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_2+{\text{OH}}^{-}$	3.26 (0.30)	3.45 (0.27)	3.64 (0.36)
7a	${\text{*C–CH}}_2+\text{H*}\to {\text{*CH–CH}}_2$	3.26 (0.30)	3.32 (0.25)	3.44 (0.23)
7b	${\text{*C–CH}}_2+\text{H*}\to {\text{*C–CH}}_3$	3.26 (0.30)	3.35 (0.29)	3.48 (0.26)
8	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{C}}_2{\text{H}}_4+{\text{OH}}^{-}$	3.24 (0.21)	3.38 (0.35)	3.65 (0.30)
8a	${\text{*CH–CH}}_2+\text{H*}\to {\text{C}}_2{\text{H}}_4$	3.24 (0.21)	3.30 (0.29)	3.43 (0.24)
8b	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_3+{\text{OH}}^{-}$	3.24 (0.21)	3.44 (0.20)	3.67 (0.32)
8c	${\text{*CH–CH}}_2+\text{H*}\to {\text{*CH–CH}}_3$	3.24 (0.21)	3.34 (0.26)	3.44 (0.28)

Table S7.

Corrected free-energy barriers (ΔG^‡, in electronvolts) and corrected free-energy differences (ΔG, in electronvolts) for various reduction steps of CH₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	ΔG‡, eV	ΔG, eV
1	$\text{*CO}+\text{H*}\to \text{*CHO}$	0.96	0.89
1a	$\text{*CO}+{\text{H}}_2\text{O}+e^{-}\to \text{*CHO}+{\text{OH}}^{-}$	0.97	0.82
1b	$\text{*CO}+{\text{H}}_2\text{O}+e^{-}\to \text{*COH}+{\text{OH}}^{-}$	1.21	1.07
2	$\text{*CHO}+{\text{H}}_2\text{O}+e^{-}\to \text{*CHOH}+{\text{OH}}^{-}$	0.24	0.05
2a	$\text{*CHO}+\text{H*}\to {\text{CH}}_2\text{O}$	1.01	0.50
3	$\text{*CHOH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*CH}+{\text{OH}}^{-}$	0.59	−0.19
3a	$\text{*CHOH}+\text{H*}\to {\text{*CH}}_2\text{OH}$	0.86	0.37
4	$\text{*CH}+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH}}_2+{\text{OH}}^{-}$	0.40	0.15
4a	$\text{*CH}+\text{H*}\to {\text{*CH}}_2$	0.97	0.17
5	${\text{*CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH}}_3+{\text{OH}}^{-}$	0.55	0.01
5a	${\text{*CH}}_2+\text{H*}\to {\text{*CH}}_3$	1.05	0.00
6	${\text{*CH}}_3+{\text{H}}_2\text{O}+e^{-}\to {\text{CH}}_4+{\text{OH}}^{-}$	0.81	−0.53
6a	${\text{*CH}}_3+\text{H*}\to {\text{CH}}_4$	0.86	−0.71

The work functions are referenced to the initial states.

Table S8.

Corrected free-energy barriers (ΔG^‡, in electronvolts) and corrected free-energy differences (ΔG, in electronvolts) for various reduction steps of C₂H₄ formation on Cu(100) at pH 7 and 298 K

ID	Reaction equation	ΔG‡, eV	ΔG, eV
0	$\text{*CO}+\text{*CO}+\mathrm{\delta }\cdot e^{-}\to {\text{*CO–CO}}^{\mathrm{\delta -}}$	0.69	0.56
1	${\text{*OC–CO}}^{\mathrm{\delta -}}+{\text{H}}_2\text{O}+\left(1-\mathrm{\delta }\right)\mathrm{\cdot }{\text{e}}^{-}\to \text{*CO–COH}+{\text{OH}}^{-}$	0.14	−0.01
2	$\text{*CO–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*COH–COH}+{\text{OH}}^{-}$	0.02	−0.17
2a	${\text{*OC–CO}}^{\mathrm{\delta -}}+\text{H*}\to {\text{*CHO–CO}}^{\mathrm{\delta -}}$	1.12	0.55
3	$\text{*COH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–COH}+{\text{OH}}^{-}$	0.62	0.38
3a	$\text{*COH–COH}+\text{H*}\to \text{*CHOH–COH}$	1.06	0.80
4	$\text{*C–COH}+{\text{H}}_2\text{O}+e^{-}\to \text{*CH–COH}+{\text{OH}}^{-}$	0.44	0.17
4a	$\text{*C–COH}+\text{H*}\to \text{*CH–COH}$	0.91	−0.02
4b	$\text{*C–COH}+e^{-}\to \text{*C–C}+{\text{OH}}^{-}$	1.18	0.76
4c	$\text{*C–COH}+\text{H*}\to \text{*C–CHOH}$	1.00	0.36
5	$\text{*CH–COH}+e^{-}\stackrel{{\text{H}}_2\text{O}}{\to }\text{*C–CH}+{\text{OH}}^{-}$	0.61	−0.16
5a	$\text{*CH–COH}+\text{H*}\to {\text{*CH}}_2\text{–COH}$	1.41	1.21
5b	$\text{*CH–COH}+\text{H*}\to \text{*CH–CHOH}$	1.05	0.83
6	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to {\text{*C–CH}}_2+{\text{OH}}^{-}$	0.60	0.13
6a	$\text{*C–CH}+\text{H*}\to {\text{*C–CH}}_2$	0.93	0.39
6b	$\text{*C–CH}+{\text{H}}_2\text{O}+e^{-}\to \text{*CH–CH}+{\text{OH}}^{-}$	1.07	0.79
6c	$\text{*C–CH}+\text{H*}\to \text{*CH–CH}$	1.41	0.67
7	${\text{*C–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_2+{\text{OH}}^{-}$	0.49	0.32
7a	${\text{*C–CH}}_2+\text{H*}\to {\text{*CH–CH}}_2$	1.10	0.41
7b	${\text{*C–CH}}_2+\text{H*}\to {\text{*C–CH}}_3$	1.76	1.74
8	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{C}}_2{\text{H}}_4+{\text{OH}}^{-}$	0.38	−0.14
8a	${\text{*CH–CH}}_2+\text{H*}\to {\text{C}}_2{\text{H}}_4$	1.15	0.01
8b	${\text{*CH–CH}}_2+{\text{H}}_2\text{O}+e^{-}\to {\text{*CH–CH}}_3+{\text{OH}}^{-}$	0.68	0.63
8c	${\text{*CH–CH}}_2+\text{H*}\to {\text{*CH–CH}}_3$	1.21	0.56

The work functions are referenced to the initial states.

Supporting Information includes models and simulation details, free-energy results, and constant potential corrections.

SI Models and Methods

Here, we simulate the water/Cu(100) interface using 48 explicit water molecules (five layers, 1.21 nm thick) on a 4 × 4 Cu(100) surface slab (three layers) with an area of 1.02 nm². To equilibrate the waters interacting with the interface, we carried out 2 ns of reactive molecular dynamics (RMD) simulations using the ReaxFF reactive force field for Cu and H₂O (39). Starting from this well-equilibrated interface, we carried out 10 ps of ab initio AIMD simulation at 298 K. After that, we used metadynamics and thermodynamic integration to calculate free-energy barriers for various reaction steps (the results were averaged over three independent calculations). We find that including one extra Na solvated in the solution leads to a work function of 3.40 (±0.25) eV, which corresponds to −0.59 V (RHE) (3.40 − 4.40 + 0.0592 × 7 = −0.59 V), close to the potential [−0.60 V (RHE)] with maximum C₂H₄ production at pH 7 (11). The simulation box is 40 Å along the z axis with a vacuum of 24 Å. The lateral dimensions of the slab were fixed using the 3.61-Å lattice constant. Two CO molecules and one H atom were placed on the 4 × 4 unit cell (on top site) corresponding to a surface coverage of 1/8 and 1/16 ML, respectively. A snapshot of the simulation box is shown in Fig. S1. We consider that this model of QM with explicit treatment of the water dynamics at operating temperature provides a representative description of the reaction kinetics.

We considered both the Eley–Rideal (ER) and Langmuir–Hinshelwood (LH) reaction mechanisms. In ER, H₂O + e^– are used in the reduction reaction (e^– is used implicitly). In LH, surface hydrogen (H*) is used in the reduction reaction. For LH, the formation of H* implicitly involves either H₃O⁺ or OH^–, so that both the reaction barrier (ΔG^‡) and the energy (ΔG) are pH dependent. At pH 7, the ΔG^‡ and ΔG of reactions via LH are corrected by 0.41 eV (0.0592 × 7) to compare with the ER reactions.

Electronic structure calculations were performed within the DFT framework, as implemented in the Vienna ab initio simulation program (VASP) (42–45), a plane-wave pseudopotential package. The exchange and correlation energies were calculated using the Perdew, Burke, and Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) (46, 47). Spin polarization did not have an appreciable effect on the overall energies. For example, the total energies are different by less than 0.01 eV for adsorbed hydrogen (H*) on Cu(100) surface. The calculations were therefore carried out without spin polarization to reduce computational demands.

We used a plane-wave cutoff energy of 400 eV and the first-order Methfessel–Paxton scheme with a smearing width of 0.2 eV. Dipole corrections were applied along the z axis. The PBE-D3 method was used to correct van der Waals interaction of water–water and water–Cu (48). The energy minimization criterion was that all forces on free atoms be <0.02 eV/Å. The charges on various species were derived using a Bader analysis (49).

We used a 1.2-fs time step in the molecular dynamics (MD) simulations with the hydrogen mass set to 2 atomic mass units. These MD simulations used only the gamma point of the Brillouin zone with no consideration of symmetry. The velocities were rescaled every 20 MD steps to readjust the target temperature to equilibrium. We used a Nose–Hoover thermostat for the free-energy calculations with a temperature damping parameter of 100 fs.

Enhanced sampling methods can increase the timescale of brute force simulations. We calculated the free energies using metadynamics (14, 15) and constrained molecular dynamics (16) (blue moon ensemble). Three parameters are controllable and relevant to the accuracy of a metadynamics simulation: height of a Gaussian hill (h), the width of the Gaussian hill (ω), and frequency to update the bias potential (t_G) (40, 41). We used an ideal double-well model with a transition barrier of 0.9 eV to derive the optimal parameters for the best balance of accuracy and efficiency. In this work, these parameters are h = 0.08 eV, ω = 0.18 Å, and t_G = 24 fs. For the constrained molecular dynamics, we used an increment of 0.67 × 10⁻³ Å/fs to the collective variables. We found that simulation times of 2.4–9.6 ps were sufficient to complete the reaction, depending on the reaction pathways.

From the reactive trajectories, we selected 11 windows for thermodynamic integration calculations. The 2.4-ps simulations were carried out at each window to produce the potential of mean force (PMF). Energy profiles were obtained by integrating the PMF. More simulation details and definitions of collective variables (CVs) for elementary reactions are in SI CVs and Free-Energy Barriers. In this work, we calculate the Helmholtz free energies (F), which we assume are similar to the Gibbs free energies (G).

The strategies used to enhance ensemble averaging were as follows: (i) We carry out 2 ns of reactive molecular dynamics (RMD) simulations using the ReaxFF reactive force field to equilibrate the water/Cu(100) interface. This ReaxFF simulation is necessary because the relaxation time of water at the interface is much longer than in bulk. (ii) We carry out three independent simulations to reduce any bias that might arise from specific water configurations. (iii) We use thermodynamic integration (TI) as an efficient way to extend the short metadynamics simulations. These TI calculations convert the serial calculation into windows that can be calculated in parallel.

In all of the cases (except C–C coupling), the difference between the current step and next step is only one hydrogen, which we consider as a too small perturbation to induce large surface reorientations. The most significant change we observe in the water structure at the surface is the readjustment of hydrogen bond network, which is captured within 2 ps in our explicit water description, which facilitates proton transfer to the stable position by formation hydrogen bond network (an advantage of simulations with explicit H₂O). At each step, one additional hydrogen was added either on the surface (if H* was consumed) or in bulk (if H₂O provides the proton). In the case of adding H*, the closest available hollow (fourfold) site was chosen to deposit the H*. A 2-ps AIMD simulation was then carried out to equilibrate the system. In the case of adding a proton to bulk solvent, one H was added to one surface H₂O (vacuum/H₂O interface) to form H₃O⁺, which was neutralized during the AIMD by the OH^– produced through the hydrogen-bond network in a 2-ps AIMD equilibration. The configuration produced provides a reasonable representation of the reactant for the next reduction step.

For steps where the surface H (H*) model was used to locate transition states, we referenced the initial states back to the H⁺(H₃O⁺/H₂O) + e^– pair through free-energy differences between H* and H₂(g), based on the half-cell reactions (H⁺ + e^–→ H*). Thus, the pH effect is introduced by applying a correction of 0.41 eV (7 × 0.0592) to free-energy barriers and free-energy differences.

For reactions where H₂O acts as the proton source with the release of OH^–, the pH enters the free-energy profiles naturally as the reactant or product (no correction).

To compare with the constant potential of experiments, we used the procedure proposed by Chan and Nørskov (50) to remove any artifacts involving work function changes during the chemical reaction. Because we considered the charges in plane-wave calculations to be suspect, we replaced the charge with the calculated capacitance (more details in SI Constant Potential Corrections). For the cases reported here, these corrections of the free-energy barriers were insignificant (<0.02 eV).

SI Metadynamics

The metadynamics Hamiltonian $\stackrel{\sim }{H}(p,q,t)$ is written as follows:

$$\stackrel{\sim }{H}\left(p,q,t\right)=H\left(p,q\right)+\stackrel{\sim }{V}\left(t,\xi \right),$$ [S1]

where p, q, and t is generalized momenta, generalized coordinate, and time. H(p,q) is the Hamiltonian for the original (unbiased) system, ξ is the CV, and $\stackrel{\sim }{V}(t,\xi )$ is the time-dependent bias potential. The bias term is defined as a sum of deposited Gaussian functions as follows:

$$\stackrel{\sim }{V}\left(t,\xi \right)=h{\displaystyle \sum _{i=1}^{t/t_{\mathrm{G}}}\exp \left\{-\frac{|{\xi }^t-{\xi }^{(i\cdot t_{\mathrm{G}})}{|}^2}{2{\varpi }^2}\right\}}.$$ [S2]

Here, h and ω are the height and width of the Gaussian function. t_G is the time interval to add a new Gaussian. The summation represents the history-dependent potential acting on the current values of the ξ. The biased potential is related to the free energy via the following:

$$A\left(\xi \right)=\underset{t\to \infty }{\lim }\stackrel{\sim }{V}\left(t,\xi \right)+\text{const}.$$ [S3]

In principle, smaller perturbations would lead to better accuracy, but this would require longer simulation times. Although many papers have been published discussing how to choose the parameters (23, 24), there is still no general rule. One must consider each specified case. In this work, we used an ideal double-well model with a transition barrier of 0.9 eV to derive the optimal parameters for the best balance of accuracy and efficiency, as shown in the following: h = 0.08 eV; $\omega$ = 0.18 Å; and t_G = 20 time steps.

We carried out metadynamics simulations until the first barrier crossing.

SI Constrained Molecular Dynamics (25)

The correct (unbiased) average for a quantity α(ξ) of constrained (biased) molecular dynamics can be obtained as follows:

$$\alpha \left(\xi \right)=\frac{{\langle \sqrt{Z}\cdot \alpha \left({\xi }^{\ast }\right)\rangle }_{{\xi }^{\ast }}}{{\langle \sqrt{Z}\rangle }_{{\xi }^{\ast }}},$$ [S4]

where Z is a mass metric tensor defined as follows:

$$Z_{\alpha ,\beta }={\displaystyle \sum _{i=1}^{3N}{m}_i^{-1}{\nabla }_i{\xi }_{\alpha }\cdot {\nabla }_i{\xi }_{\beta }},\hspace{0.17em}\alpha =1,...,N,\hspace{0.17em}\beta =1,...,N,$$ [S5]

and the free-energy gradient can be computed using the following equation (25):

$${\left(\frac{\partial A}{\partial {\xi }_k}\right)}_{{\xi }^{\ast }}=\frac{1}{{\langle \sqrt{\left|Z\right|}\rangle }_{{\xi }^{\ast }}}{\langle \sqrt{\left|Z\right|}\left[{\lambda }_k+\frac{k_{\mathrm{B}}T}{2\left|Z\right|}{{\displaystyle \sum _{j=1}^r\left(\frac{1}{Z}\right)}}_{kj}{\displaystyle \sum _{i=1}^{3N}\frac{{\nabla }_i{\xi }_j\cdot \nabla \left|Z\right|}{m_i}}\right]\rangle }_{{\xi }^{\ast }},$$ [S6]

The free-energy difference between states 1 and 2 can be calculated by integrating the free-energy gradients over a connecting path:

$$\mathrm{\Delta }{A}_{1\to 2}={{\displaystyle \underset{\xi \left(1\right)}{\overset{\xi \left(2\right)}{\int }}\left(\frac{\partial A}{\partial \xi }\right)}}_{{\xi }^{\ast }}d\xi .$$ [S7]

We first used slow growth to generate the reaction path. We applied an increment of 0.0008 Å/step (or 0.00067 Å/fs) to CVs to drive the chemical reactions. We found that simulation times of 2.4–9.6 ps were necessary to complete the reaction, depending on the length of reaction pathways. From the reactive trajectories, we selected 11 windows for thermodynamic integration calculations. Simulations of 2.4 ps were carried out at each window to produce the PMF. Energy profiles were obtained by integrating the PMF.

SI CVs and Free-Energy Barriers

In free-energy calculations, the CVs are the distance between hydrogen (H) and carbon (C) [R(C–H)], the distance between H and oxygen (O) [R(O–H)], or the distance between C and O [R(C–O)]. The distances are a natural choice for the LH model. The ER model is more complex than LH model because the proton transfer procedure involves a hydrogen-bond (HB) channel established by several water molecules. In our previous work with H₃O⁺ (pH 0), we used a CV defined by HB bond network. In this work, the simulation is at pH 7. Therefore, the proton is provided by an H₂O. For example: at pH 7, the Volmer reaction is H₂O + e^– → H* + OH^–. In this condition, we found R(O–H) or R(C–H) [C (or O) is from intermediates and H is from the nearest water] is sufficient for defining a CV, because the subsequent proton transfer reactions can occur in brute-force simulation due to the low energy barriers of proton transfer (about 0.15 eV based on our previous calculation) (12).

The CV and ΔG^‡ of elementary reaction in CH₄ formation and C₂H₄ formation are shown in Tables S1 and S2.

SI Constant Potential Corrections

The simulations are done at constant charge [the number of electrons (N_e) is fixed], which means that the work functions (Φ) change along the reaction pathway. For a simulation starting with Φ₁ and ending with Φ₂, the electrostatic energy change ($\mathrm{\Delta }{E}_{{\mathrm{\Phi }}_2-{\mathrm{\Phi }}_1}^{electrostatic}$) can be determined by the modification of the charges (Δq = q₂ − q₁) and the change in the work functions (ΔΦ = Φ₂ – Φ₁) by using the correction method proposed by Chan and Nørskov (50):

$$\mathrm{\Delta }{E}_{{\mathrm{\Phi }}_2-{\mathrm{\Phi }}_1}^{\mathrm{electrostatic}}=\frac{\left(q_2-q_1\right)\left({\mathrm{\Phi }}_2-{\mathrm{\Phi }}_1\right)}{2}=\frac{\mathrm{\Delta }q\cdot \mathrm{\Delta }\mathrm{\Phi }}{2}.$$ [S8]

However, for plane-wave calculations, the atomic charges are ambiguous. Instead, we use the capacitance (C) to replace change (q), which can be calculated from the work function change as the total number of electrons is varied:

$$C=\frac{\mathrm{\Delta }q}{\mathrm{\Delta }\mathrm{\Phi }}.$$ [S9]

We calculate C from the shift in the work function as the number of total electrons is varied. For the Cu(100) bare surface, the calculated C is 0.79 e/V. The reaction intermediates have a slight influence on C ranging from 0.79 e/V to 0.83 e/V. Therefore, we use one C value (0.79 e/V) in our calculation. Φ is related to the absolute potential (U) vs. the standard hydrogen electrode via the following:

$$U=\frac{\mathrm{\Phi }-{\mathrm{\Phi }}_{\mathrm{SHE}}}{e}.$$ [S10]

Therefore,

$$\mathrm{\Delta }\mathrm{\Phi }=\mathrm{\Delta }U\cdot e.$$ [S11]

Inserting Eqs. S9 and S11 into Eq. S8 leads to the following:

$$\mathrm{\Delta }{E}_{U_2-U_1}^{\mathrm{electrostatic}}=\frac{C\cdot e^2\cdot \mathrm{\Delta }{\mathrm{\Phi }}^2}{2}.$$ [S12]

SI Formation of Acetate

The noticeable amounts acetate (CH₃COO^–) formation was observed in the work of Li et al. (37) using oxide-derived Cu nanoparticle as catalysts for CO reduction. In their work, the authors proposed that the formation of acetate probably arises from an attack of OH^– on a surface-bound ketene or another carbonyl-containing intermediate after C–C bond formation. Instead, we propose that the acetate formation may involve surface O* attacking surface-bond α-hydroxy ketone (*COH–C=O) as follows:

$$*\text{COH}–\text{C}=\text{O}+{\text{O}}^{\ast }+e^{-}\underset{1.07}{\to }*\text{COH}–{\text{COO}}^{-},$$ [S13]

$$*\text{COH}–{\text{COO}}^{-}+e^{-}\underset{0.91}{\to }*\text{C}–{\text{COO}}^{-}+{\text{OH}}^{-},$$ [S14]

$$*\text{C}–{\text{COO}}^{-}+{\text{H}}^{\ast }\underset{1.01}{\to }*\text{CH}–{\text{COO}}^{-},$$ [S15]

$$*\text{CH}–{\text{COO}}^{-}+{\text{H}}^{\ast }\underset{1.29}{\to }*\text{C}{\text{H}}_2–{\text{COO}}^{-},$$ [S16]

$$*\text{C}{\text{H}}_2–{\text{COO}}^{-}+{\text{H}}^{\ast }\underset{1.59}{\to }{\text{CH}}_3{\text{COO}}^{-}\left(\mathrm{aq}\right).$$ [S17]

SI Probe Molecules

Ethylene oxide (C₂H₄O) and glyoxal (C₂H₂O₂) were used experimentally as probe molecules to supply auxiliary information about the mechanism of ethylene formation. The following are the lowest kinetic pathways for the ethylene formation from ethylene oxide and acetaldehyde or ethanol formation from glyoxal predicted from free-energy calculations.

Ethylene Oxide.

$${\text{C}}_2{\text{H}}_4\text{O}\left(\mathrm{aq}\right)+{\text{H}}_2\text{O}+e^{-}\underset{0.48}{\to }*\text{C}{\text{H}}_2–{\text{CH}}_2\text{OH}+{\text{OH}}^{-},$$ [S18]

$$*\text{C}{\text{H}}_2–{\text{CH}}_2\text{OH}+e^{-}\underset{0.17}{\to }*\text{C}{\text{H}}_2={\text{CH}}_2+{\text{OH}}^{-}.$$ [S19]

Glyoxal.

$$\text{CHO}–\text{CHO}\left(\mathrm{aq}\right)+{\text{H}}_2\text{O}+e^{-}\underset{0.75}{\to }*\text{CHOH}–\text{CHO}+{\text{OH}}^{-},$$ [S20]

$$*\text{CHOH}–\text{CHO}+{\text{H}}^{\ast }\underset{1.21}{\to }*{\text{CH}}_2\text{OH}–\text{CHO},$$ [S21]

$$*{\text{CH}}_2\text{OH}–\text{CHO}+e^{-}\underset{0.43}{\to }*{\text{CH}}_2–\text{CHO}+{\text{OH}}^{-},$$ [S22]

$$*{\text{CH}}_2–\text{CHO}+{\text{H}}_2\text{O}+e^{-}\underset{0.58}{\to }{\text{CH}}_2=\text{CHOH}+{\text{OH}}^{-}.$$ [S23]