Persistence-driven durotaxis: Generic, directed motility in rigidity gradients

Abstract

Cells move differently on substrates with different elasticities. In particular, the persistence time of their motion is higher on stiffer substrates. We show that this behavior will result in a net transport of cells directed up a soft-to-stiff gradient. Using simple random walk models with controlled persistence and stochastic simulations, we characterize this propensity to move in terms of the durotactic index measured in experiments. A one-dimensional model captures the essential features of this motion and highlights the competition between diffusive spreading and linear, wavelike propagation. Since the directed motion is rooted in a non-directional change in the behavior of individual cells, the motility is a kinesis rather than a taxis. Persistence-driven durokinesis is generic and may be of use in the design of instructive environments for cells and other motile, mechanosensitive objects.

Cells are acutely aware of the mechanical properties of their surroundings. The rigidity, or lack thereof, of the substrate to which a cell is adhering informs a number of crucial processes: Differentiation, gene expression, proliferation, and other cellular decisions been shown to be — at least in part — affected by the stiffness of the surrounding matrix [1-6]. Cells also move differently depending on the elasticity of the substrate. One of the more striking manifestations of this is the near-universal tendency of motile cells to travel up rigidity gradients; a process generally referred to as durotaxis [7-14], a term that emphasizes the similarity to chemotaxis, the tendency of cells to move directedly in chemical gradients. Chemotaxis — generally believed to offer significant evolutionary advantage — allows cells, for instance, to move towards sources of nutrients. For durotaxis, this advantage is less clear. Motion in stiffness gradients could allow neutrophils and cancer cells to seek out optimal locations for extravasation [15-17], and very similar behavior of stem cells could contribute to mitigation or regeneration of stiff scars and injured tissues [18]. Durotactic motion is quite universal: without exception it is away from softer, towards stiffer. In addition to an overall motion in a gradient, the nature of cellular motion itself was shown to change quantitatively depending directly on the local rigidity of the substrate, with cells moving more persistently on more rigid substrates. In this Letter, we demonstrate that soft-to-stiff durotaxis is a necessary consequence of stiffness-dependent persistence, with or without any rigidity-dependent crawling speed.

Definitions and experimental observations

For cells moving on uniformly elastic substrates, most experiments record the paths of motile cells by tabulating, at fixed time intervals Δt = t_i+1 – t_i, their position $\overrightarrow{r}\left(t_i\right)=\left\{x\right(t_i),y(t_i\left)\right\}$. The resulting time series constitutes a discrete-time Random Walk (RW). Provided that the interval Δt is sufficiently small, these cellular RW paths display a certain amount of persistence, reflecting the tendency to keep moving along the same direction (or, equivalently, the cell’s inability to turn on very short timescales). This persistence is quantified by the persistence time τ_p. For cells moving at a constant linear velocity (i.e., the velocity along their path) v_c, this persistence time may be obtained by analyzing the displacement statistics of the path, either as the decay time the tangent autocorrelation, or by fitting to the formula for the mean squared displacement for a persistent random walk (PRW) [19]

$$\langle \mid {\overrightarrow{r}}^2\mid \rangle \left(t\right)=2v_c^2{\tau }_p^2\left(\frac{t}{{\tau }_p}+e^{-t∕{\tau }_p}-1\right).$$ (1)

The average, here, is taken over many different trajectories at the same time point t_i = t or, equivalently, over many points separated by the same time interval t = t_j – t_i along the same cell trajectory. We note, that while the PRW correctly describes cellular motility in 2D, it fails in 3D [20] — one of many important differences between 2D and 3D processes of cellular adhesion and migration. Although Raab et al. showed [11] that cells migrate more frequently into a soft collagen overlay when they start from a soft gel compared to a stiff gel, which is consistent with 3D durotaxis, we restrict ourselves to the case of 2D motility here, to make our general point. The limiting behavior of this equation is instructive: for short times t << τ_p it describes ballistic motion $\langle \mid {\overrightarrow{r}}^2\mid \rangle \left(t\right)\approx {\left(v_{c}t\right)}^2$, whereas for long times t >> τ_p the motion is a pure random walk; $\langle \mid {\overrightarrow{r}}^2\mid \rangle \left(t\right)\approx 2v_c^2{\tau }_{p}t$. Thus, the persistence time is the characteristic timescale for the crossover between ballistic and diffusive motion. A trivial point, which nonetheless bears repeating here, is that the first moment of the vectorial displacement vanishes, for RW and PRW alike: $\langle \overrightarrow{\mathrm{r}}\rangle \left(t\right)=\overrightarrow{0}$ – this is no longer the case for durotactic processes. A meaningful question, now, is to ask how the parameters that quantify persistence and directed displacement change with the properties of the substrate. While the tendency to move from soft to stiff substrates has been broadly noted and characterized [21-25], the persistence of cells as they do so has only recently begun to be quantitatively addressed. A potential relation between the two has been hinted at in passing, but not further substatiated. In experiments recording the motility of fibroblasts on uniformly elastic PEG hydrogels, Missirlis and Spatz [12] demonstrate that the persistence time - quantified by a Directionality Index $\Delta \left(t\right)=\sqrt{\langle \mid {\overrightarrow{r}}^2\mid \rangle }\left(t\right)∕\left(v_{c}t\right)\propto {\tau }_p$ recorded at the same time on substrates coated with different ligands, rises by about a factor of 3 when the substrate stiffness is increased from 5.5 to 65.7 kPa. Over the same range of stiffnesses, a decrease of v_c by about 33% (from 60 μm/hr to 40 μm/hr) is reported. House et al [26] place fibroblasts on uniformly elastic PAM hydrogels, and report that their persistence time increases by a factor of 3 when the gel stiffness is varied from 10 kPa to 150 kPa. Interestingly, and in contrast to Missirlis and Spatz, House et al. report an increase of v_c with substrate stiffness by a factor of about 2 from 21.6 μm/hr to 42.7 μm/hr over the same stiffness range. A preliminary test, reported in [26], suggests the cells move in the direction of increased persistence. In earlier work [11], Raab et al. quantify the motility of mesenchymal stem cells on uniform PAM substrates - likewise showing an increase in persistence time of about a factor of 3 from 0.7 hrs to 2.1 hrs when the substrate stiffness is varied from 1 kPa to 34 kPa. Raab et al. report no significant change in the cell velocity v_c over the entire range of stiffnesses they study. Importantly, however, Raab et al. also show that the same cells, on the same substrates that are now gradiented in stiffness from 1 kPa to 34 kPa, the cells move towards the stiff side with a durotaxis index equal to about 0.2. In summary, experiments unanimously suggest that cells move more persistently on stiffer substrates, and that when they do, they move from soft to rigid. This behavior is independent of the relation between velocity and stiffness, which appears to be more cell-type dependent although a recent work suggests that speed and persistence may be correlated [14]. As persistence is linked to microtubule (re)positioning with respect to the nucleus, and this process is greatly hampered in 1D motility (cells in narrow channels), the correlation between cell speed and persistence may well be different in different dimensions, but we stress that our results are largely unaffected by the variations in cell speed (cf., Fig 3), stiffness dependent or not. The empirical fact that two behaviors – increasing persistence and soft-to-stiff motion – coincide suggests they might not be independent. To examine whether there is indeed a causation underlying the correlation, we perform stochastic simulations of PRW’s with spatially varying persistence times.

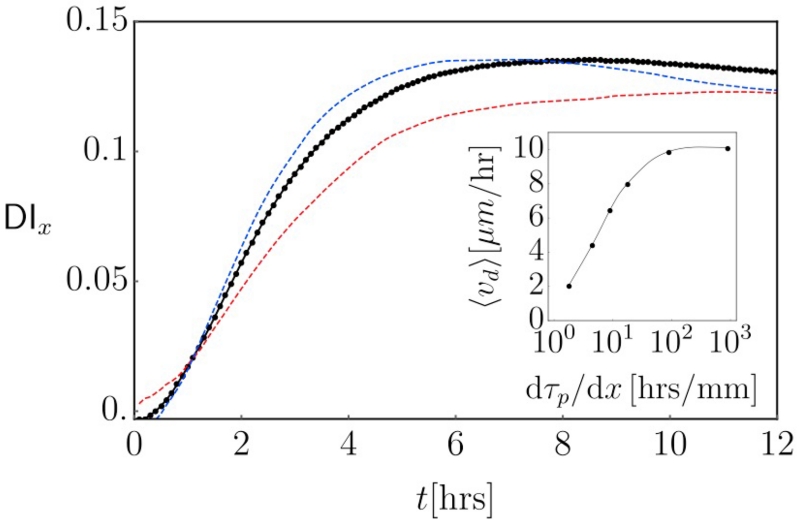
FIG. 3. Durotactic index as function of time.

Main figure: x-component of the durotactic index vs time for cells moving in a rigidity gradient, with τ_p increasing linearly from 0.2 to 2 over the x-range [−0.1, 0.1] mm. Averages computed over 5·10⁴ trajectories. Black line, black dots: stiffness-independent velocity v_c = 50μm/hr everywhere. Red-dashed line: the same system, but with a velocity that rises with persistence; v_c = 20 – 80μm/hr accross the gradient region. Blue-dashed line: velocity decreases with persistence; v_c = 80 – 20μm/hr accross the gradient region. Inset: The effective velocity over the 12 hr window as a function of the gradient strength. All gradients had τ_p varying from 0.2 to 2, but over different spatial ranges.

Simulation setup and results

We consider a 2D substrate, endowed with a gradient in stiffness that manifests itself as a position-dependent persistence time τ_p(x) and a position-dependent velocity v_c(x). To simulate the variable-persistence, variable cell speed PRW in this gradient, we generate trajectories as follows: Starting in the origin at t = 0, a random initial direction θ₀ is chosen, along which the cell is displaced by a distance Δr₁ = v_c(0)Δt. For all subsequent steps, a deviation angle −π < δθ < π is picked randomly from a Gaussian distribution centered around δθ = 0 with variance σ² = 2 Δt/τ_p(x) using the Box-Muller transform, x being the instantaneous x-position. The next point is placed a distance Δr₂ = v_c(x)Δt in the θ₀ + δθ direction, this last step is repeated N = t_tot/Δt times to complete a trajectory representing a total time t_tot. The substrate has a persistence time and velocity τ_p,min and v_c,left at x = −∞, τ_p,max and v_c,right at x = ∞, with both τ_p and v_c transitioning linearly, with variable steepness, between their asymptotic values symmetrically around x = 0. Much like most experimental settings, the gradient thus occupies only part of the system, and is flanked by uniformly elastic regions to either side. We will always choose left to right to be the direction of increasing persistence but will, for demonstrational purposes, allow the velocity to decrease or increase from left to right. For each realization of the gradient, on the order of 10⁵ trajectories are generated to obtain accurate averages.

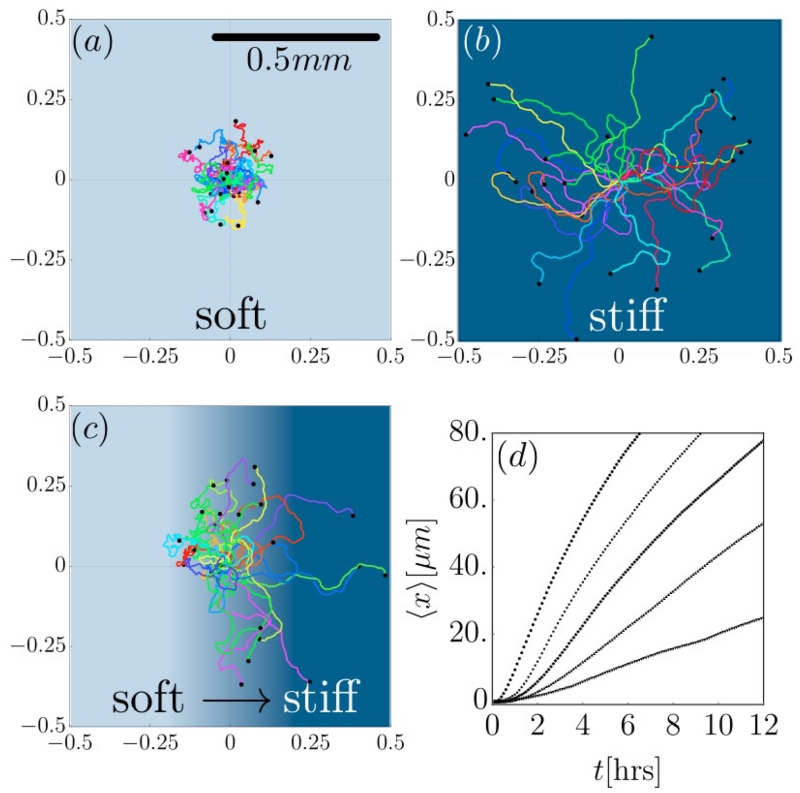
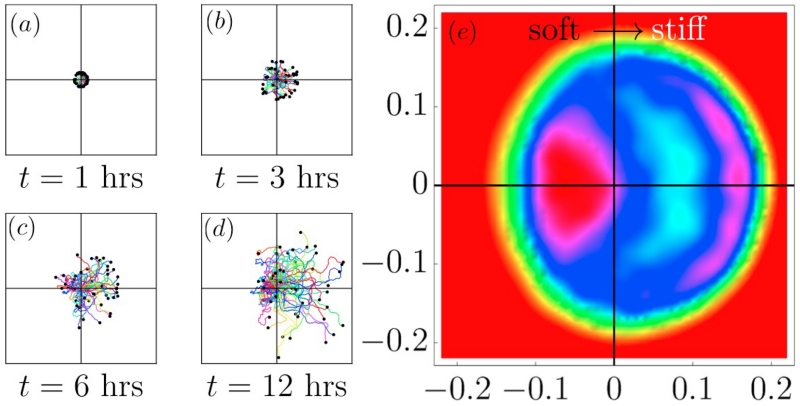
We assume, for now that v_c(x) ≡ v_c; a constant (later on, we will briefly demonstrate that our findings are largely insensitive to increases or decreases in v_c with stiffness). Our main finding is summarized in Fig. 1: a gradient in persistence produces a soft-to-stiff flux of cells, and confers upon them, for typical values, an effective velocity up the stiffness gradient of 2-10 μm/hr. The origin of the effect is readily read off from Fig. 1 (a)-(c); PRW trajectories become asymmetric in the gradient, and those trajectories that either depart up the gradient, or at some point in time first turn towards the stiff direction, travel further in the stiff direction, on average. This leads to a nonzero 〈x〉(t), and the effective velocity - over the ~ 12 hr course of a typical experiment, increases with increasing gradient steepness. Fig. 2(e) plots the probability distribution P(x, y) of finding a cell at position x, t after t = 4 hrs and shows the crucial statistical feature that gives rise to the nonzero center-of-mass motion. On the left, less persistent, side of the substrate the distribution resembles that of a diffusive process. On the right side, where motion is more persistent, a narrower peak moves outward at constant velocity.

FIG. 1. Persistence-dependent motility.

Simulated trajectories of 25 cells, departing from the origin at t = 0 with a linear velocity of 50 μm/hr. Total time is 12 hrs, cellular positions are recorded at 6-minute intervals. A black dot marks the end of each cell trajectory. (a) Cells on a soft substrate, with a low persistence time τ_p = 0.2 hrs. (b) stiff substrate; persistence time τ_p =2 hrs. (c) Gradient substrate, with persistence time increasing linearly from 0.2 to 2 over the x-range [−0.1, 0.1] mm (i.e., Δτ_p/Δx = 9 hrs/mm). (d) averaged x-displacement in in the gradient, for different gradient steepnesses (top to bottom: Δτ_p/Δx = 90 hrs/mm, 18 hrs/mm, 9 hrs/mm, 4.5 hrs/mm, 1.8 hrs/mm).

FIG. 2. Evolution of probability with time.

Simulated trajectories of 50 cells, departing from the origin at t = 0 with a linear velocity of 50 μm/hr on a persistence gradient, increasing linearly from 0.2 to 2 over the x-range [−0.1, 0.1] mm (i.e., Δτ_p/Δx = 9 hrs/mm). The cells were tracked for 12 hrs, their positions recorded at 6-minute intervals. A black dot marks the end of each cell trajectory. (a)-(d) As time progresses, the asymmetry becomes increasingly clear. (e) The probability distribution P(x, y) at t = 4 hrs clearly shows a double-peaked structure: a diffusive peak on the soft side, and a wavefront further out on the rigid side.

The net motion that results from differentially persistent PRW’s executed in a stiffness gradient is reminiscent of the motion that chemotactic bacteria execute in, for instance, a gradient in nutrient concentration [27]. To be sure, in both cases an environmental gradient sets up a flux, but to what extent are these processes truly similar? Following [24, 25], it is instructive to scrutinize the motility using a durotactic (vector-)index

$$\overrightarrow{\mathrm{DI}}\left(t\right)=\left\{{\mathrm{DI}}_x\right(t),{\mathrm{DI}}_y(t\left)\right\}\equiv \frac{\langle \overrightarrow{r}\rangle \left(t\right)}{v_{c}t}.$$ (2)

For all - persistent and non-persistent - non-directional processes $\overrightarrow{\mathrm{DI}}\left(t\right)=\overrightarrow{0}$. For the gradients studied here DI_y(t) = 0; we report only the x-component. In the main panel of Fig. 3, we plot DI_x(t) for a representative set of parameters (listed in the caption). The general behavior is, that DI_x(t) initially rises, peaks at a few times the persistence time, and then slowly drops back down, proportional to t^−1/2 (cf., inset Fig. 4). Fig 3 also shows, that this behavior remains qualitatively the same regardless of whether v_c increases, decreases or stays the same through the gradient. Since the DI is directly proportional to the effective velocity in the direction of the gradient, this is also the expected behavior for the effective velocity which is thus a time dependent quantity for this processes. This is in contrast to the ‘run-and-tumble’ behavior that underlies chemotaxis in, for instance, E. coli, which acquires a finite drift velocity in a gradient by modifying the tumble frequency [27]. Thus, the presence or absence of a plateau in DI_x(t) for longer times could be a reliable way to discriminate the motion we discuss here from a ‘regular’ taxis.

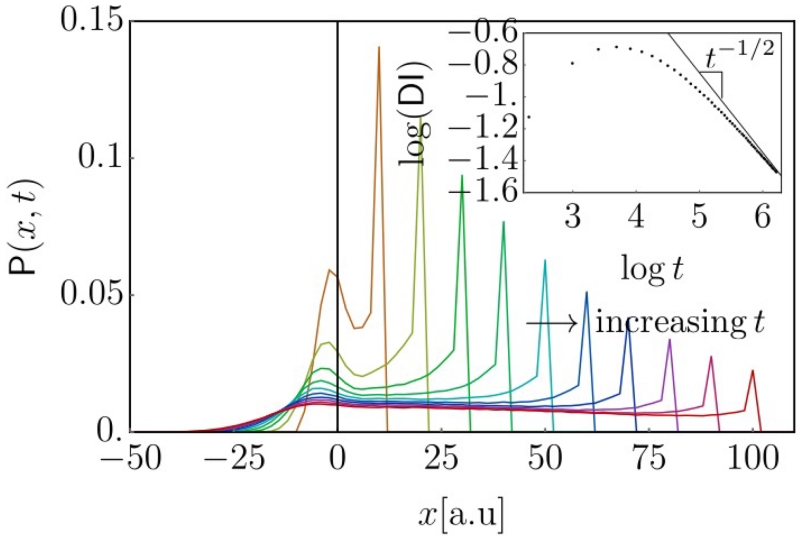
FIG. 4. Evolution of 1D inhomogeneous telegraph probability.

Probability distributions P(x, t) determined by direct integration of Eq. 5. The turning probability λ(x) decreased linearly from 0.4 to 0.02 over the x-interval [−5, 5]. From left to right, we plot distributions for t = 10 … 100 with 10 unit time intervals. Clearly visible is the diffusive spreading on the left, vs. the wave-like propagation to the right. The inset shows the long-time t^−1/2 behavior of DI(t).

1D model and an inhomogeneous telegraph equation

We map the process to one dimension by studying the dispersal of walkers on a line. The equivalent of a spatially dependent persistence, here, is a spatially dependent turning frequency λ(x). Typical behavior in a gradient is collected in Fig. 4 and confirms the dual behavior also seen in two dimensions: the softer side is diffusion-dominated while the more rigid side displays a wavelike propagation. To derive the appropriate continuum equation, we apply a similar approach to the one presented for uniform turning rates in [24], and consider separately the two densities of left- and right movers; ρ₊(x, t) and ρ₋(x, t), normalized such that P(x, t) = ρ₊ + ρ₋, is the total probability density. After a time step Δt, each walker reverses direction with a probability π = λ(x)Δt, or continues (with probability 1 – π(x)) along the previous direction. During each time step, it travels a distance Δx = v_cΔt. The densities ρ₊ and ρ₋ then obey

$${\rho }_{+}(x,t+\Delta t)=[1-\lambda (x-\Delta x\left)\Delta t\right]{\rho }_{+}(x-\Delta x,t)+\left[\lambda \right(x-\Delta x\left)\Delta t\right]{\rho }_{-}(x-\Delta x,t),$$ (3)

$${\rho }_{-}(x,t+\Delta t)=\left[\lambda \right(x+\Delta x\left)\Delta t\right]{\rho }_{+}(x+\Delta x,t)+[1-\lambda (x+\Delta x\left)\Delta t\right]{\rho }_{-}(x+\Delta x,t).$$ (4)

Expanding these two equations to first order in Δx and Δt and combining them using P = ρ₊ + ρ₋ yields the following governing PDE

$${\partial }_t^2\mathrm{P}+2\lambda \left(x\right){\partial }_t\mathrm{P}=v_c^2{\partial }_x^2\mathrm{P}.$$ (5)

A spatially varying velocity may be included by replacing v_c → v_c(x). This inhomogeneous telegraph equation is also the appropriate mode to use for effectively one-dimension migration experiments. To connect with the two-dimensional case, we may identify $2\lambda \left(x\right)\simeq {\tau }_p^{-1}$. The two competing behaviors are readily recognized in the PDE; for large turning frequencies (i.e., short persistence times) the second order time derivative is dominated by the first order term, and diffusive behavior emerges. For low turning frequencies – highly persistent motion – a wave equation is recovered. In principle, this equation, supplemented with a specific form for the persistence gradient λ(x), and the appropriate boundary conditions (generally, P(x, 0) = δ(x) and ∂_tP(x, 0) = 0), allows one to compute averaged displacements as moments in this distribution. Due to the x-dependent λ-term this is far from trivial – we will address this in an upcoming publication.

Conclusions and Outlook

In this Letter, we demonstrate how a broadly reported feature of cellular motility – a dependence of the persistence of movement on the rigidity of the substrate – leads, without further assumptions, to universal soft-to-stiff motion on gradiented substrates. The motion is faster, on experimental timescales, for steeper gradients though over timescales much longer than the persistence time, the effective velocity (and the associated durotactic index) decreases (cf., inset Fig. 4), in contrast to what happens in bacterial chemotaxis. For the type of motion we report here, the term durotaxis may be a bit of a misnomer. Following the suggestions laid out in [28], the flux set up by gradients in the local, substrate-informed persistence is perhaps more accurately described as a (positional) kinesis – an “almost instantaneous response induced by a purely positional signal”. That is, a non-directional change in behavior as opposed to the directional changes typical for chemotaxis. This distinction goes beyond semantics: it suggests that durotaxis in a stiffness gradient is not to be interpreted as the existence of a preferred stiffness for the cell, which it is purposefully migrating towards. Without dismissing the possibility that other mechanisms not considered here could lead to such properly durotactic motion, we show here that – at the very least to an extent that is worth determining in much greater detail – soft-to-stiff migration is an unavoidable consequence of stiffness-dependent persistence. The generic nature of durokinesis suggests it as a potentially worthwhile mechanism to pursue in the development of instructive environments (for an early demonstration see, for instance, [29]); our results show that any stochastic, particulate system whose persistence is informed, locally, by some external parameter has the potential to harness this kinetic transport mechanism.