Periodic assembly of nanoparticle arrays in disclinations of cholesteric liquid crystals

Significance

Linear defects-disclinations in thermotropic liquid crystals are known to serve as templates for self-assembly of nanoparticles and molecules into continuous thread-like structures. Here, we show that disclinations in lyotropic cholesteric liquid crystals can act as templates for nanoparticle dispersions, producing both continuous and discontinuous morphologies, with discrete beads of the dispersion periodically organized along the disclination axis. The beading effect is rooted in the anisotropic properties of the cholesteric phase. The observed mode of assembly expands the design spectrum of architectures of soft materials. The lyotropic nature of the liquid crystal formed by an aqueous suspension of cellulose nanocrystals broadens the range of materials used for the self-assembly of periodical structures.

Abstract

An important goal of the modern soft matter science is to discover new self-assembly modalities to precisely control the placement of small particles in space. Spatial inhomogeneity of liquid crystals offers the capability to organize colloids in certain regions such as the cores of the topological defects. Here we report two self-assembly modes of nanoparticles in linear defects-disclinations in a lyotropic colloidal cholesteric liquid crystal: a continuous helicoidal thread and a periodic array of discrete beads. The beads form one-dimensional arrays with a periodicity that matches half a pitch of the cholesteric phase. The periodic assembly is governed by the anisotropic surface tension and elasticity at the interface of beads with the liquid crystal. This mode of self-assembly of nanoparticles in disclinations expands our ability to use topological defects in liquid crystals as templates for the organization of nanocolloids.

The most extensively studied liquid crystalline phase, the so-called nematic, has been so named after the linear defect-disclinations that appear as flexible threads in optical microscopy textures; “thread” is “νεμα” in Greek (1, 2). The disclinations represent singularities of the director that describes the local orientation of molecules. As one approaches the “core” of the defect, director deformation becomes so strong that the degree of orientational order varies in space. Disclinations can attract additives, e.g., colloidal particles (3–8) and even small molecules (9, 10). Such an attraction is energetically favored, as the strongly distorted disclination core region is replaced with the additive (4). The unique templating ability of disclinations has stimulated the exploration of their applications, such as the fabrication of optical materials (11), conductive microwires (12), soft magnets (13), and electrooptical devices (5, 14, 15).

Disclinations in nematic liquid crystals are generally one-dimensional structures, as the director pattern repeats itself along the line. When an additive is attracted to the disclination core, two possible morphologies are expected: (i) continuous thread-like assembly, or (ii) a linear array of discrete beads. The disclination-templated assemblies reported so far had a thread-like shape, as observed for polymers in the so-called blue phases (15) and for molecular amphiphiles at the cores of nematic disclinations (9, 10).

Here, we report the templating behavior of disclinations in the chiral version of the nematic liquid crystal, the so-called cholesteric (Ch) phase. The local director $\widehat{\mathbf{n}}$ in this phase undergoes helicoid twisting around a helical axis $\widehat{\mathbf{\chi }}$ while being perpendicular to this axis (1, 2). Continuous twist leads to a pseudolayered structure, with a well-defined pitch but no modulation of density. Experiments were performed for spherical Ch droplets, in which disclinations correspond to the equilibrium state, thus ensuring reproducible templating conditions (16, 17). Droplets of thermotropic Ch liquid crystals were proposed for applications as omnidirectional lasers, microresonators, Bragg–Berry optical elements, and photonic crystals (18–23). Here, we focus on the lyotropic droplets formed by an aqueous Ch suspension of cellulose nanocrystals (CNCs) and refer to this Ch phase as the Ch-CNC phase. Lyotropic Ch liquid crystals offer a different dimension of applications because (i) they are hydrophilic, in comparison with their hydrophobic thermotropic counterparts, and (ii) the micrometer size of the core of topological defects is significantly larger (24, 25) than ∼10-nm core size in droplets of thermotropic liquid crystals (10). The implications of these features are in a potentially broader range of hydrophobicity/hydrophilicity and sizes of additives templated by disclinations.

We used a dispersion of negatively charged spherical latex nanoparticles (NPs) as an additive. Recently, we have shown (24) that in large (>80-μm diameter) Ch-CNC droplets latex NPs exhibit an intriguing ability to compartmentalize into an isotropic NP-rich droplet core and into the disclinations. In the present work, we show that NP-rich assemblies templated by Ch disclinations can form either continuous (locally cylindrical and globally helicoidal) thread-like structures, or discontinuous, one-dimensional arrays of discrete beads. We attribute the beading effect to the periodic modulation of the director along the Ch disclination, associated with the twisted structure of the Ch phase and coupled with the anisotropy of interfacial tension and elasticity. Such a modulation and thus the beading effect has not been observed for nematic disclinations. The number of beads and periodicity of linear arrays are determined by the number of concentric Ch pseudolayers in the droplets and by the Ch pitch, respectively. These results provide an insight into the role of anisotropic surface tension and elasticity in the morphology of assemblies templated by linear topological defects in liquid crystals.

Results

An aqueous 7 wt % suspension of negatively charged, rod-like CNCs (Fig. S1) was equilibrated for 21 d. The suspension separated into an isotropic top phase and a Ch-CNC bottom phase with the CNC volume fraction of 5 × 10⁻², in which the CNCs exhibited orientational order combined with a helical director alignment (26). The Ch-CNC phase was separated and emulsified in a microfluidic droplet generator (Fig. S2) (27). Droplets of the Ch-CNC phase with a radius of ∼50 μm and polydispersity ≤2.5% were generated in fluorinated oil containing 0.5 wt % of block copolymer surfactant of perfluoropolyether-co-poly(ethylene oxide-co-polypropylene oxide)-co-perfluoropolyether, and subsequently equilibrated for 72 h in a sealed fluid cell with a height of 400 μm.

Fig. S1.

TEM images of dry CNCs. (Scale bar, 500 nm.)

Fig. S2.

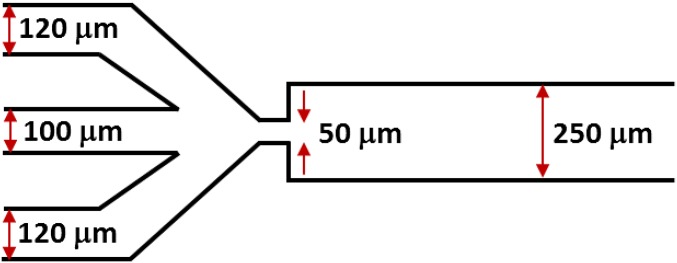
Design of MF device for the preparation of Ch-CNC droplets. The height of channels in the device is 70 μm.

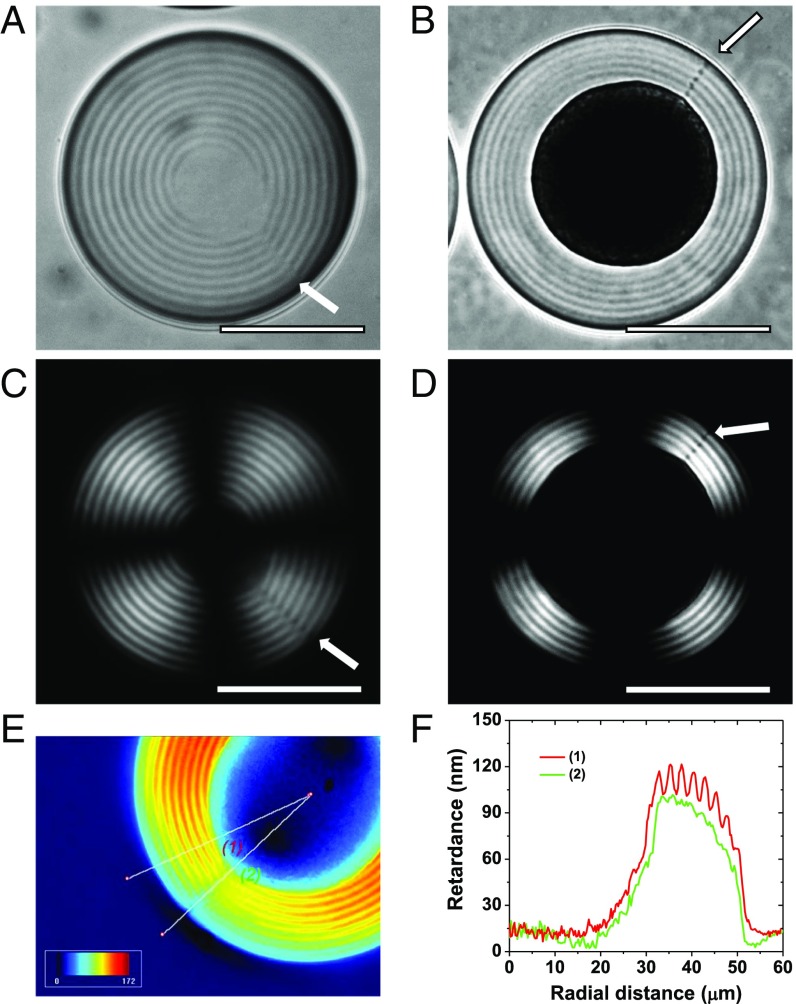
The bright-field (BF) microscopy and polarized optical microscopy (POM) images of a Ch-CNC droplet are shown in Fig. 1 A and C, respectively (a large droplet population is shown in Fig. S3). The POM images of the droplets (Fig. 1C) exhibited characteristic Ch features: a Maltese cross and alternating bright and dark concentric rings corresponding to the twisted director $\widehat{\mathbf{n}}$ (24). The droplets had a core–shell morphology, that is, an isotropic micrometer-size central region (a core) and a Ch shell with a concentric packing of the CNC pseudolayers (24). The average spacing between two adjacent bright or two dark concentric lines of the Ch shell in the POM or BF images corresponded to half-pitch, P/2, of ∼3.1 μm.

Fig. 1.

Disclinations in Ch-CNC droplets. (A and B) BF and (C and D) POM images of Ch-CNC droplets (A and C) and Ch-CNC droplets loaded with latex NPs at ϕ_NP = 2.35 × 10⁻² (B and D). The CNC volume fraction, ϕ₀, in the droplets was 4.5 × 10⁻². The arrows show the disclinations. (Scale bars, 50 μm.) (E) PolScope image of the droplet with pseudocolors showing the variation of optical retardance. (F) Optical retardance plotted vs. radial distance as in E for defect-free direction (1) and for the direction (2) along the +2 core.

Fig. S3.

BF (A) and POM (B) images of Ch-CNC droplets. The volume fraction of CNCs in the droplets was 0.045. (Scale bar, 100 μm.)

When the droplet radius R is significantly larger than the Ch pitch P, spherical confinement leads to the equilibrium structure with concentric packing of Ch layers and either one or two disclinations emanating from the droplet center (2, 16, 28, 29). These lines are called $\chi$-lines to stress that they carry no singularity of the helical axis $\widehat{\mathbf{\chi }}$ (2). Here and below, we follow the Kleman–Friedel classification of Ch defects (2), which considers three mutually perpendicular vectors, namely, $\mathbf{\chi }$ along the helicoidal axis, $\mathbf{\lambda }$ along the director, and $\mathbf{\tau }=\mathbf{\chi }\times \mathbf{\lambda }$. Disclinations, at the core of which one of the vectors is continuous, are labeled by this vector, that is, $\chi$-disclinations are nonsingular in $\mathbf{\chi }$, $\lambda$-disclinations are nonsingular in the director, and $\tau$-disclinations are nonsingular in $\mathbf{\tau }$.

The structure with one disclination of strength 2, the ${\chi }^{+2}$-line, is expected to be energetically preferable over the structure with two ${\chi }^{+1}$-disclinations of strength 1, each based on numerical simulations (16). In agreement with this expectation and experiments for thermotropic Ch droplets (16, 29), we observed disclinations running perpendicularly to the Ch layers (shown in Fig. 1 A and C with white arrows). A single ${\chi }^{+2}$-disclination was observed in ∼90% of the Ch droplets (the remaining ∼10% of droplets exhibited two radial ${\chi }^{+1}$-lines).

In the next step, 50-μm-radius droplets were generated from the mixture of the Ch-CNC phase and latex NPs. Carboxylated polystyrene 184-nm-diameter latex NPs labeled with fluorescein isothiocyanate were mixed with the Ch-CNC phase at a volume fraction ϕ_NP = 2.35 ×10⁻². The mixture was immediately emulsified in the microfluidic device and the resultant droplets were equilibrated for 72 h. Notably, an equilibrated macroscopic mixture of the Ch-CNC phase and NPs phase-separated into an isotropic NP-rich phase and a Ch-CNC–rich phase.

The Ch-CNC droplets laden with NPs adopted a core–shell morphology with an isotropic core and a Ch shell (Fig. 1 B and D). The droplet core was significantly larger than in the latex-free Ch-CNC droplets, due to the phase separation of the Ch-CNC phase and NPs and partition of the isotropic NP-rich phase into the droplet core. A significantly darker core than in the latex-free droplets and a periodic array of small dark round regions in the disclinations of the latex-loaded droplets suggested that the NPs preferentially segregated in these regions (Fig. 1 B and D). The PolScope image (Fig. 1E) demonstrates that the ${\chi }^{+2}$-core was associated with a weaker optical retardance than the rest of the shell (Fig. 1F), which resulted from the predominant director alignment along the disclination axis. In the rest of the shell, the director was perpendicular to the radial direction. This arrangement produced the optical compensating effect along the line (2) at the defect core (Fig. 1F), which was consistent with the core model of ref. 16.

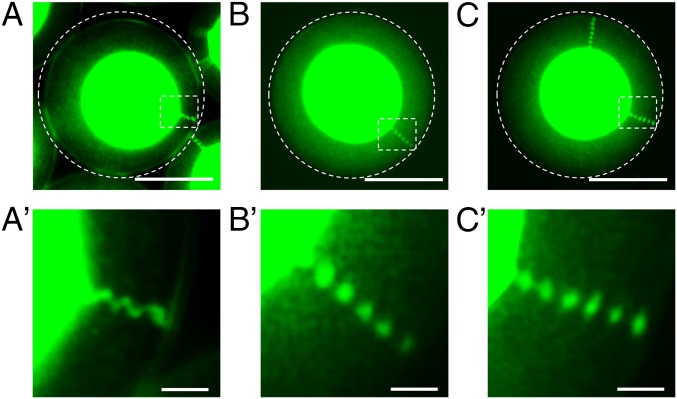
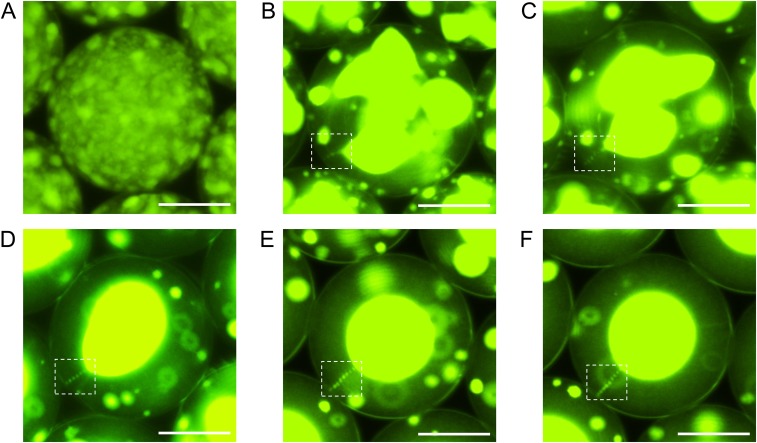
The compartmentalization of the NPs in the Ch-CNC droplets was examined by fluorescence microscopy (FM). In droplets with a ${\chi }^{+2}$-disclination, the NPs organized into two principally different structures: (i) a continuous helicoidal thread with an approximately constant cross-section, observed only in ∼1% of droplets (Fig. 2 A and A'), and (ii) a linear array of discrete beads (Fig. 2 B–C'). Droplets with two ${\chi }^{+1}$-disclinations exhibited only periodic arrays of beads (Fig. 2 C and C' and Movie S1). The equilibrium bead structure was reached via transient states (2, 24). The latex beads appeared at the periphery of the droplets, because the spherical concentric Ch-CNC layers started to form at the droplet/oil interface. As the concentric Ch-CNC packing propagated toward the droplet center, so did the beads arrays (Fig. S4).

Fig. 2.

Organization of latex NPs in the Ch-CNC droplets. (A–C) FM images of the Ch-CNC droplets loaded with 184-nm latex NPs at ϕ_NP = 1.19 × 10⁻². (Scale bars, 50 μm.) (A′–C′) Corresponding enlarged FM images of the areas highlighted in white boxes in A–C. ϕ₀ = 4.5 × 10⁻². (Scale bars, 5 μm.)

Fig. S4.

Fluorescence images of the droplets of the mixture of the Ch-CNC phase and latex NPs. The images were taken 30 min (A), 2 h (B), 4 h (C), 8 h (D), 32 h (E), and 48 h (F) after emulsification of the mixture. The bright-green color corresponds to the phase-separated latex-rich isotropic regions. The bead arrays are highlighted by white dotted boxes. (Scale bars, 50 μm.) The volume fraction of CNCs in the droplets was 0.045; the volume fraction of 184-nm latex NPs in the droplets was 1.19 × 10⁻².

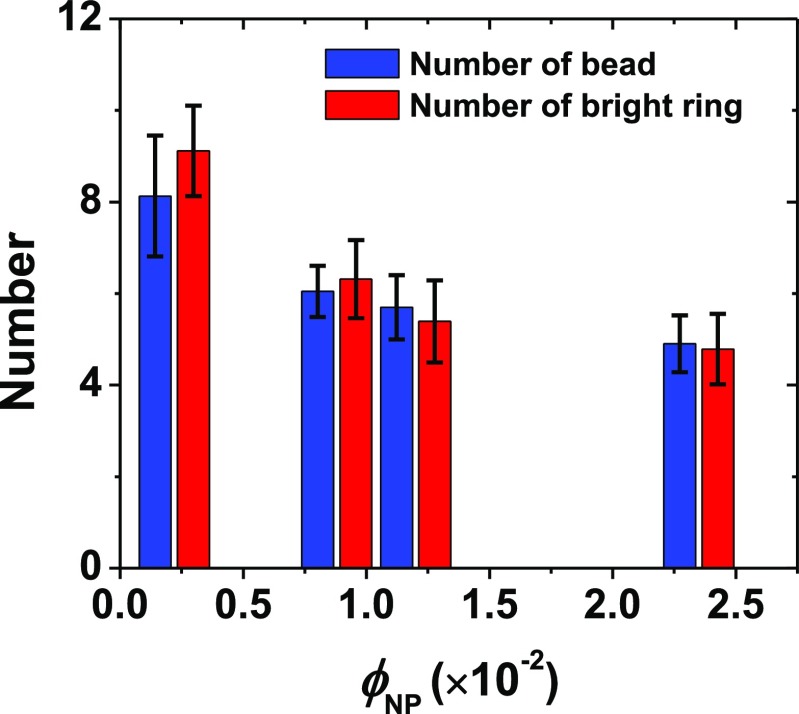
Inspection of the FM images of the Ch-CNC droplets at a varying NP volume fraction, ϕ_NP, revealed that the NPs resided in the isotropic droplet cores, the disclination cores, and the Ch shells. In the disclinations, small ∼2-μm-diameter latex-enriched regions (beads) formed a periodic array (Fig. 2 B–C'). The number of beads was controlled by the pitch and the number, N, of the concentric Ch pseudolayers (Fig. S5). The value of N depended on the volume fraction of NPs in the droplets. For example, when ϕ_NP increased from 2.2 × 10⁻³ to 2.35 × 10⁻² at P/2 ∼ 3.1 μm, the thickness of the Ch shell reduced from 30 to 19 μm, with N decreasing from 9 to 5 (Fig. S5). Consequently, the number of beads in the disclinations reduced from 9 to 5 (Fig. S5); however, the bead diameter did not change with ϕ_NP and was ∼2 μm.

Fig. S5.

Numbers of bead and bright ring in the Ch-CNC droplets as a function of ϕ_NP. In each column, at least 30 droplets were analyzed. The error bar represents the SD.

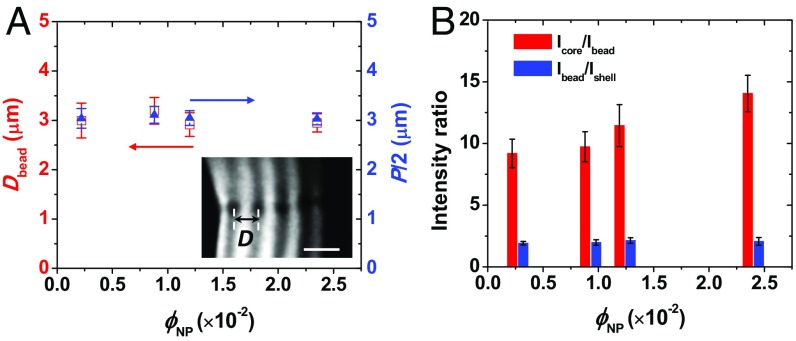
The periodic interbead spacing was measured as the average distance, D, between the centers of two adjacent beads localized in the disclination (Fig. 3A). Because disclinations could adopt different spatial orientations, measurements were carried out only for the droplets, in which the thickness of the Ch shell was equal to the disclination length. With an ∼10-fold increase in ϕ_NP, the value of D remained at ∼3.0 ± 0.2 μm and was equal to P/2 (Fig. 3A).

Fig. 3.

Properties of the arrays of beads in Ch-CNC droplets. (A) Variation of half-pitch, P/2, of the Ch shells (blue triangles) and the interbead spacing, D, in the disclination (red open squares), both plotted as a function of ϕ_NP. (Inset) Enlarged POM image of the fragment of bead array in the Ch-CNC shell at ϕ_NP = 2.35 × 10⁻². (Scale bar, 5 μm.) (B) Variation in the ratios of core-to-bead and bead-to-shell fluorescence intensities, plotted as a function of ϕ_NP in the Ch-CNC droplets. ϕ₀= 4.5 × 10⁻². In A and B, for each value of ϕ_NP, at least 30 droplets were analyzed. The error bars in A and B represent the SDs.

Segregation of the NPs was characterized by the ratio of the isotropic core-to-bead and bead-to-Ch shell fluorescence intensities. With an increasing ϕ_NP, NP partition in the cores was favored, whereas the ratio between the NP segregation in the beads and the Ch shells was almost invariant (Fig. 3B). More specifically, the ratio of the NP partitions in the droplet core, the beads, and the Ch shell varied from 17.5:1.9:1–28.8:2.1:1, when ϕ_NP increased from 2.2 × 10⁻³ to 2.35 × 10⁻², respectively (Fig. 3B). The NP volume fraction in the beads (calculated using fluorescence intensity ratios) increased from 2.1 × 10⁻⁴ to 1.5 × 10⁻³, when ϕ_NP on the droplet increased from 2.2 × 10⁻³ to 2.35 × 10⁻², respectively.

We also varied the thickness of the Ch shells and thus the number of beads in disclinations by changing the diameter of the Ch-CNC droplets. Droplets were generated by vortexing the mixture of the Ch-CNC phase and NPs at ϕ_NP = 2.35 ×10⁻². With the radius of the Ch-CNC droplets increasing from 40 to 105 μm at P/2 = 3.1 μm, the thickness of shells increased from 16 to 43 μm, respectively, with N changing from 5 to 10 and the number of beads increasing from 5 to 10 (Fig. S6).

Fig. S6.

(A and B) BF images of the Ch-CNC droplets with 50-μm (A) and 75-μm (B) radius. The volume fraction of 184-nm latex NPs is 2.35 × 10⁻² in the Ch-CNC droplets. (Scale bar, 50 μm.) (C) Numbers of NP bead and bright ring as a function of droplet radius. The data analysis is based on 200 droplets. The error bar represents the SD.

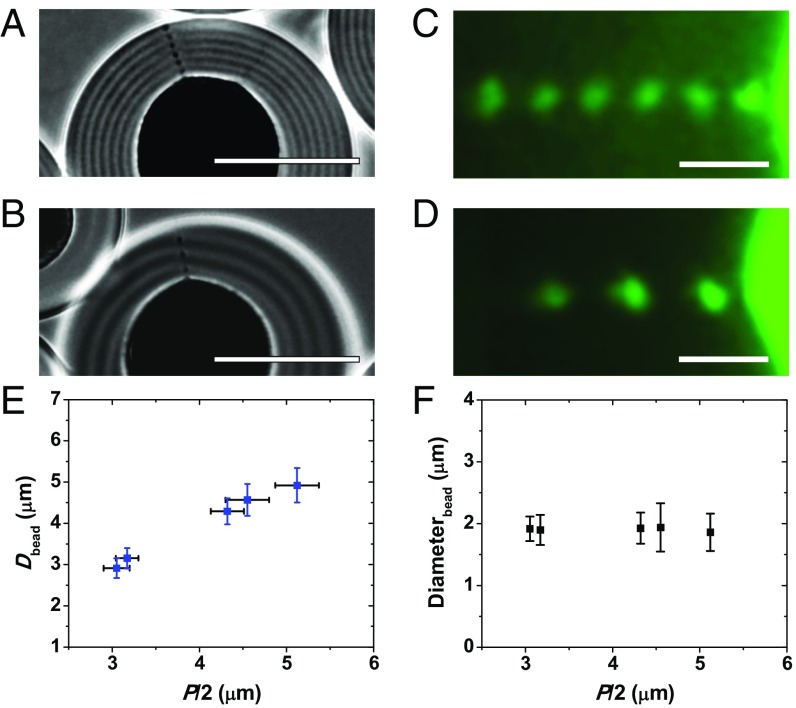
To explore the relationship between the interbead separation, D, and P/2, we applied ultrasonic treatment at varying energy to the CNC suspension before its phase separation into an isotropic and Ch phases and in this manner achieved the variation in pitch of the Ch-CNC phase (30). Fig. 4 A–D shows representative images of the arrays of beads in the disclinations. With P/2 increasing from 3.1 to 5.1 μm, the average interbead spacing increased from 3.0 to 5.0 μm, respectively (Fig. 4E); however, the bead diameter was invariant (Fig. 4F).

Fig. 4.

Variation in periodicity of the bead array. (A and B) BF images of fragments of the Ch-CNC droplets containing disclinations. Before phase separation, the CNC suspension was subjected to ultrasonication at energy of 340 (A) and 1364 J/g CNCs (B). (Scale bar, 50 μm.) (C and D) FM images of the arrays of beads shown in A and B, respectively. (Scale bar, 5 μm.) (E and F) Variation in the periodicity of the bead array (E) and bead diameter (F), both plotted as a function of P/2. For each data point in E and F, at least 30 droplets were analyzed. The error bars represent the SDs. ϕ_NP =1.19 × 10⁻²; ϕ₀= 4.9 × 10⁻² (A and C) and ϕ₀ = 5.5 × 10⁻² (B and D). The results of Student’s t test showed that the average diameter of beads did not change with pitch variation (P > 0.05).

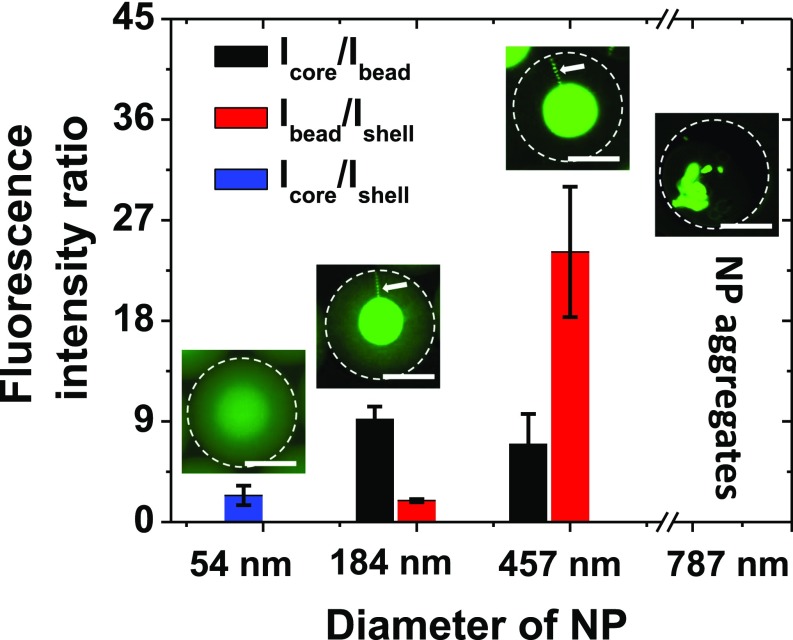
To examine the effect of NP size on disclination-templated bead assembly, we generated Ch-CNC droplets laden with latex NPs with an average diameter of 54, 184, 457, or 787 nm and examined the ratio of fluorescence intensities of the Ch shell, the droplet core, and the beads. The segregation of NPs in the disclinations and droplet core was favored when NP diameter increased from 54 to 457 nm (Fig. 5). For the droplets loaded with 54-nm NPs, NP partition in the disclinations was not observed (Fig. 5, Inset and Fig. S7). In contrast, for droplets loaded with 457-nm NPs, most of the NPs resided in the core and the disclinations (Fig. 5, Inset), with a very small NP fraction localized in the Ch shell. In contrast, 787-nm NPs formed aggregates randomly distributed in the droplets (Fig. 5, Inset). These NPs were kinetically trapped in the out-of-equilibrium state when the Ch-CNC phase was mixed with the NPs. Large NPs perturbed the Ch director around them and exhibited attraction through long-range elastic forces (31, 32). In addition, these NP clusters did not relax their irregular shape to equilibrium shape, due to large (compared with thermal energy) energy barriers (33).

Fig. 5.

Ratios of core-to-bead and the bead-to-shell fluorescence intensities of Ch-CNC droplets loaded with 54-, 184-, 457-, and 787-nm-diameter latex NPs, ϕ_NP = 2.2 × 10⁻³; ϕ₀= 4.5 × 10⁻². For each NP size, at least 30 droplets were analyzed. The error bars represent the SDs. The images above the bars show the Ch-CNC droplets laden with NPs of a particular size. (Scale bars, 50 μm.)

Fig. S7.

(A and B) Ch-CNC droplets loaded with latex NPs of 54-nm diameter. (Scale bar, 200 μm in A; 100 μm in B.) The volume fraction of CNCs in the droplets was 4.5 × 10⁻². ϕ_NP=2.2 × 10⁻³.

Discussion

The accumulation of inclusions at the cores of disclinations is a general phenomenon reported for thermotropic liquid crystals (3, 4, 8–12, 15). Inclusions replace the strongly distorted director field and thus reduce the associated elastic energy of the system (4). Generally, in nematic disclinations, inclusions assemble into a thread with a cylinder-like shape. The most probable reason for the formation of a continuous thread is the elastic nature of the director field: A breakup of the cylinder into beads would lead to additional director distortions and thus a higher elastic energy.

Our experiments show that NP assemblies templated by the $\chi$-disclinations in the Ch-CNC droplets can either be of a continuous type, or of a discontinuous (bead-like) type, with a linear periodic array of beads (Fig. 6A). The latter effect is different from the liquid crystal-templating assemblies previously reported. The periodic arrays resemble in their appearance the rows of droplets formed from a fluid thread surrounded by an isotropic medium, as a result of celebrated Plateau-Rayleigh (PR) instability (34–37). The governing mechanism for the PR instability is the reduction of the (isotropic) surface energy (38). Coalescence of the resulting beads into a single large droplet is hindered by the absence of direct contact between the droplets. The distance between the droplets in the PR instability is controlled by the kinetics of the breakup and by the radius R of the initial cylindrical thread (34, 35). The breakup is triggered by the fastest-growing mode of a wavelength $\lambda \approx 11R$ (39) that sets the period of the resulting array (40). The beading effect observed in our work differs from the PR instability in the following important respects.

Fig. 6.

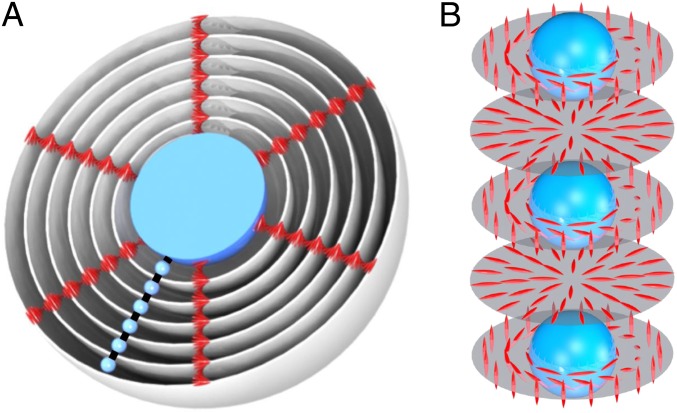
(A) Schematic of the Ch-CNC droplet loaded with NPs. (B) Illustration of the periodic director structure along the ${\chi }^{+1}$-disclination and the resulting periodic array of NP inclusions in the regions that yield predominantly tangential anchoring at the inclusion surface (shown as blue beads). In A the concentric shells represent the Ch-CNC layers and the black line represents the disclination. In A and B, the blue spheres represent the NP-rich regions and the red whisker-like features in B represent the CNCs.

First, the interbead spacing in disclinations is determined entirely by the period P/2 of the Ch-CNC structure. Because the radius of the $\chi$-disclination cores is expected to be on the order of P/2 (2), this spacing is notably smaller than the period $\lambda \approx 5.5P$ that may be naively anticipated on the basis of PR instability in an isotropic medium (39, 40). Second, because the Ch-CNC phase is orientationally ordered, the interfacial tension between the beads and the Ch-CNC phase is anisotropic, rather than isotropic, as it depends on the CNC orientation on the bead surface. Third, the orientational order of the Ch-CNC phase governs the elastic response of the disclination structure to the shape of the self-assembled structure; that is, there is a feedback between the accumulation of inclusions at the defect core and the director structure.

As described above, the droplets contain either one disclination ${\chi }^{+2}$ or two ${\chi }^{+1}$-lines. Their cores are expected to have a region with the director parallel to the disclination (the so-called “escape into the third dimension” effect) (1, 2), which is supported by Fig. 1 E and F. Numerical simulations of an additive-free Ch phase predict that the fine structure of these cores can be different (16), that is, the ${\chi }^{+2}$-core comprises two intertwined ${\lambda }^{+1}$-disclinations of a helicoidal shape. The director pattern rotates along the radial direction. In contrast, the core of a ${\chi }^{+1}$-disclination splits into a linear row of small alternating ${\tau }^{-1/2}$ and ${\lambda }^{+1/2}$-loops (16). The distance between the neighboring ${\tau }^{-1/2}$ and ${\lambda }^{+1/2}$-loops is P/4. As one moves from one loop to another, the local director alternates from the circular to radial +1 configuration within the distance P/4 (Fig. 6B) (16).

In our work, the helicoidal model of the ${\chi }^{+2}$-core with two intertwined ${\lambda }^{+1}$-disclinations (16) is supported by the observation of the helicoidal assembly of latex NPs in a very small fraction of droplets (Fig. 2 A and A'). Most of the droplets with disclinations contained linear arrays of beads separated by P/2. The problem of finding the exact shape of the NP-rich dispersion attracted to $\chi$-disclinations requires numerical simulations. Here, we illustrate qualitatively the role of two factors, namely, the surface energy anisotropy and elasticity that favor the formation of discrete beads, instead of the continuous, thread-like NP self-assembly.

Consider, first, the ${\chi }^{+1}$-lines and imagine a small bead placed at different locations along the disclination (Fig. 6B). Assume that the director field does not respond to the bead placement. Depending on the bead position, the alignment of the director at the bead surface would change from a predominantly tangential to a tilted one to a predominantly perpendicular. Because the bead surface favors the tangential alignment of CNCs, the energetically favored bead position along the disclination will be the one in which the surface alignment of the CNCs is as close to the tangential as possible. These locations are separated by the distance P/2, thereby explaining the beading effect with the interbead spacing of D = P/2 along the ${\chi }^{+1}$-lines.

The periodic beading with a period of P/2 in the case of ${\chi }^{+1}$ can also be favored by the elastic effects. The ${\chi }^{+1}$-line is split into a periodic array of ${\lambda }^{+1/2}$ and ${\tau }^{-1/2}$-loops, with a period P/2. Because the ${\lambda }^{+1/2}$-disclinations are not associated with the director discontinuities, their energy is smaller than the energy of the singular ${\tau }^{-1/2}$-disclinations by a quantity (per unit length) of ∼K, where K is the Frank elastic constant (2). Thus, the ${\chi }^{+1}$-core exhibits a periodic variation of the elastic energy density with the period P/2, which is also likely to support formation of the discrete beads. The fact that we have never observed continuous assemblies at the ${\chi }^{+1}$-cores strongly suggests that these cores exhibit a periodically changing director field, as envisioned in ref. 16.

The case of ${\chi }^{+2}$-lines is even more complex than that of ${\chi }^{+1}$-lines. Numerical simulations predict that in the absence of impurities, the ${\chi }^{+2}$-cores contain a continuously rotating director field (16). In other words, the director pattern remains the same along the disclination, as it only rotates in the plane perpendicular to the defect. If a continuous thread is placed at such a core, the local interfacial tension would not depend on the location along the disclination axis. This geometry is very different from that of the ${\chi }^{+1}$-lines, in which the director periodically varies from circular to radial along the disclination. The existence of a small fraction of droplets with continuous helicoidal assemblies (Fig. 2 A and A') offers a strong support of the model, in which the ${\chi }^{+2}$-core represents a continuously rotating director with no splitting into a periodic array of the loops. Because the director field rotates along the disclination, so does the organization of the NP-rich dispersion.

The beading effect observed in most of the ${\chi }^{+2}$-disclinations suggests that accumulation of NPs modifies the director structure of their cores. Such a modification can be driven by the tendency of the director to be tangential to the interface between the Ch-CNC phase and the NP-rich dispersion, as qualitatively explained below.

Consider a short segment of the helicoidal bead assembly and approximate it by a cylinder of a radius R and a length $L$. The surface energy of such a segment is $2\pi RL{\sigma }_c$, where ${\sigma }_c$ is the interfacial tension between the Ch-CNC phase and the NP-rich dispersion shaped as a cylinder. If such a cylinder is transformed into a sphere of the same volume, the sphere radius and the surface energy would be $b={\left(3R^{2}L/4\right)}^{1/3}$ and $4\pi b^2{\sigma }_s$, respectively, where ${\sigma }_s$ is the interfacial tension at the spherical interface, different from ${\sigma }_c$, because of the anisotropy of the interfacial tension. Neglecting for a moment the elastic energy change, we conclude that the cylinder would be unstable if $L>\left(9/2\right)R{\left({\sigma }_s/{\sigma }_c\right)}^3$. For ${\sigma }_s/{\sigma }_c=1$, this result corresponds to the isotropic fluid (38). In the case of the bead surrounded by the Ch-CNC environment, the instability is enhanced if ${\sigma }_s/{\sigma }_c<1$. The latter condition is fulfilled when the director is predominantly tangential to the spherical surface. With $R\approx L\approx P/2$, this condition reduces to ${\sigma }_s/{\sigma }_c<0.6$. If ${\sigma }_s\approx {\sigma }_{\left|\right|}$ and ${\sigma }_c\approx \left({\sigma }_{\left|\right|}+{\sigma }_{\perp }\right)/2$, where the ${\sigma }_{\left|\right|}$ and ${\sigma }_{\perp }$ are the values of interfacial tension for the director aligned parallel and perpendicular to the interface, respectively, the appearance of the array of beads is favored if ${\sigma }_{\left|\right|}<0.43{\sigma }_{\perp }$. Realigning the director at the core implies that the elastic energy also changes. The increase of elastic energy can be estimated as $\sim Kb$ per bead. For $Kb<4\pi b^2{\sigma }_s$, the modified condition of beading becomes $L>\left(4/3R^2\right){\left(\left(3R{\sigma }_s/2{\sigma }_c\right)+\left(K/4\pi {\sigma }_s\right)\right)}^3$. The latter condition is still likely to be fulfilled if $K/4\pi {\sigma }_s$ is on the order of R or smaller. The typical elastic constants of the lyotropic liquid crystals are on the order of 10 pN (41), whereas the experimentally determined surface tension of the Ch phase of CNCs in contact with their isotropic phase is in the range of 10⁻⁷–10⁻⁶ J /m² (42), which makes $K/4\pi {\sigma }_s\sim \left(1-10\right)\hspace{0.5em}\text{μm}$, of the same order of magnitude as $P/2$. Thus, it can be expected that the anisotropy of surface tension provokes a reconstruction of the ${\chi }^{+2}$-core by the accumulated NPs and the formation of an array of discrete beads with a period P/2. To confirm this scenario, one would need to perform numerical simulations similar to those in ref. 16 but with an explicit inclusion of NPs component.

We note that the templating ability of the disclinations was observed only for a specific NP size. Small 54-nm latex NPs do not show a high propensity to partition in defects: They can fit between the CNCs separated with the distance of ∼30 nm (43) and thus do not strongly disrupt the Ch-CNC structure. Medium-size 184- and 457-nm NPs distort the director and thus partition in the Ch-CNC droplet core and disclinations, where they exhibit the beading effect. Large 787-nm NPs form kinetically trapped irregularly shaped clusters in the Ch-CNC shells that do not relax into equilibrium shapes (33) and the effect of beading is not observed.

Conclusion

We demonstrate that topological defect-disclinations in spherically confined lyotropic Ch colloidal liquid crystals can serve as templates for NP organization. We describe two different geometries of NP-rich dispersions assembled at the disclination cores: (i) a continuous thread with a helicoidal shape and (ii) a periodic array of discrete beads with the spacing equal to half a pitch of the Ch pseudolayers. Control over the number of beads and the interbead spacing was achieved by varying the size and composition of the Ch-CNC droplets. The effect is attributed to the anisotropy of the interface between the phase-separated NP-rich dispersion and the surrounding director field, that is, to the dependence of surface tension and elastic properties on the director orientation at this interface. Anisotropy of Ch properties sets the period of the templated structures equal to the Ch half-pitch. The experimental observations of the continuous and discrete assemblies at the Ch disclinations support the core models proposed by numerical simulations (16).

We stress that all of the disclinations used for NP self-assembly in our work correspond to the equilibrium or, at least, a metastable state of the Ch droplets. This feature ensures that the resulting morphologies are robust and reproducible, potentially making them suitable as elements of more complex architectures. The results extend our understanding of the structure of topological defects and of the mechanisms of hierarchical assembly of nanocolloids in complex orientationally ordered environments, thus paving the way for new approaches in the design of soft composite materials.

Materials and Methods

Preparation of CNC Droplets.

The Ch-CNC phase was emulsified in the flow-focusing microfluidic droplet generator (27) using a syringe pump (PhD 200 Harvard Apparatus PHD 2000 syringe pump). The continuous-phase, fluorinated oil HFE-7500 mixed with 0.5 wt % of the copolymer surfactant (denoted as F-oil) was supplied to the microfluidic device using the second syringe pump (PHD 200 Harvard Apparatus). The flow rate of F-oil and of the Ch-CNC phase was 0.6 mL/h and 0.2 mL/h, respectively. The droplets were collected in a 2-mL vial and transferred into a glass cell consisting of two parallel glass slides separated with a 400-μm-thick spacer. The cell was sealed with epoxy glue.

Preparation of Ch-CNC Droplets Loaded with Latex NPs.

The Ch-CNC droplets laden with NPs were prepared by microfluidic emulsification of the mixture of the Ch-CNC phase and NPs. The procedure was identical to that used for the preparation of NP-free Ch-CNC droplets. The mixture of 60 μL of NP suspension and 540 μL of the Ch-CNC phase was prepared by shaking at 50 Hz for 2 min at 25 °C in a vortex mixer and then immediately emulsified.

To prepare NP-loaded Ch-CNC droplets with a broad size distribution and diameters up to 105 μm, 200 μL of the mixture of the Ch-CNC phase and NPs and 1 mL of F-oil was shaken at 50 Hz for 3 min at 25 °C in a vortex mixer. The resultant suspension was introduced in the cell, the cell was sealed with epoxy glue, and the droplets were equilibrated for 5 d.

Characterization of Droplets.

The BF and POM images were taken on an optical microscope (Olympus BX51) in the transmission mode. The diameters of the droplets and the pitch of the Ch phase in the droplets were measured using the software ImageJ. The fluorescence images of the Ch-CNC droplets loaded with FITC-labeled latex NPs were acquired on an inverted microscope (Nikon Eclipse-Ti). The fluorescence intensity profiles of these droplets were measured using software (NIS-Elements AR Analysis). The Z-stack fluorescence images of the Ch-CNC droplets loaded with FITC-labeled latex NPs were taken by Nikon A1 confocalc microscope.

SI Materials and Methods

An aqueous dispersion of CNCs with the CNC concentration of 11.8 wt % was supplied by the Process Development Center of the University of Maine. The CNCs with an average length and diameter of 183 and 23 nm, respectively, were produced by acid hydrolysis of wood pulp. The polydispersity in the CNC diameter and length were 22% and 29%, respectively, determined by transmission electron microscope (TEM) images (Fig. S1) The electrokinetic potential of the CNCs was −47 ± 9 mV, measured by dynamic light scattering. The photoresist SU-8 was purchased from MicroChem. Poly(dimethylsiloxane) (PDMS, Sylgard 184) was supplied by Dow Corning. The FITC-labeled polystyrene latex particles (Fluoresbrite YG Carboxylate Microspheres) were purchased from Polysciences. The polydispersity of the latex nanoparticles with an average diameter of 54, 184, 457, and 787 nm was 10%, 1.0%, 2.0%, and 6.6%, respectively. The electrokinetic potential of the latex nanoparticles with an average diameter of 54, 184, 457, and 787 nm was −48 ± 6, −41 ± 6, −37 ± 13, and −35 ± 8 mV, respectively. Fluorinated oil HFE-7500 3M Novec was purchased from MG Chemicals. The perfluoropolyether-co- poly(ethylene oxide-co-polypropylene oxide)-co-perfluoropolyether copolymer was used as a surfactant. The copolymer was synthesized as described elsewhere (44). All other chemicals were purchased from Aldrich Canada.

A 7 wt % (10 mL, volume fraction of 0.048) CNC suspension with or without ultrasonication was introduced into a glass vial with a diameter of 2.5 cm. Following equilibration for 21 d, the dispersion phase-separated into a top isotropic phase and the bottom Ch phase. The Ch phase was removed from the vial with a syringe using a 22G needle.

Fabrication of Microfluidic Devices

The microfluidic devices were fabricated in PDMS, using a standard soft lithography procedure (45). Photoresist (SU-8) masters were prepared by photolithography on the silicon wafers. After fabrication, the microfluidic devices were maintained in an oven at 140 °C for 12 h to increase hydrophobicity of the microchannel surface. The schematic of the microfluidic device, along with its dimensions, is shown in Fig. S2.

Fig. S1 shows TEM images of dry CNCs. The CNCs show needle-like structures.

Fig. S2 shows the schematic of the microfluidic (MF) device used for droplet generation.

Fig. S3 shows low-magnification images of the Ch-CNC droplets.

Fig. S4 shows the formation of bead arrays in the droplets formed by the aqueous mixture of the Ch-CNC phase and latex NPs. The array grew from the periphery of the droplets, because the spherical concentric packing of the Ch-CNC layers started tangentially at the droplet/oil interface. With equilibration time, the bead array gradually propagated toward the droplet center, as the Ch-CNC layers packed toward the droplet center.

Fig. S5 shows the number of beads and bright rings in the droplets, plotted as a function of the volume fraction of latex NPs. Occasional skewing of the latex-rich core in the Ch-CNC droplets loaded with latex NPs at ϕ_NP = 2.2 × 10⁻³ led to the difference between the number of beads and bright rings.

Fig. S6 shows that the number of beads in the Ch shell increased with increasing droplet radius.

Fig. S7 shows the Ch-CNC droplets loaded with 54-nm latex NPs. The Ch shell shows a homogeneous green color. Latex NP partition in the disclinations was not observed.