Liquid behavior of cross-linked actin bundles

Significance

The interior of biological cells is composed of soft, macromolecular-based materials. The semiflexible biopolymer actin cross-links into networks and bundles with diverse architectures to form the actin cytoskeleton. Actin networks have been traditionally thought to be viscoelastic gels, whose rigidity controls cell morphogenesis. Here we demonstrate that cross-linked actin filaments also form liquid droplets. Because these liquids are composed of rod-like polymers, they form anisotropic liquid droplets with a spindle-like shape, whose morphology can be controlled by cross-link concentration. Actin-based liquid bundles also display shape instabilities characteristic of fluids. These shape dynamics reveal a mechanism to control subcellular compartmentalization and dynamics, with implications for mitotic spindle shape and molecular motor-independent contractility.

Abstract

The actin cytoskeleton is a critical regulator of cytoplasmic architecture and mechanics, essential in a myriad of physiological processes. Here we demonstrate a liquid phase of actin filaments in the presence of the physiological cross-linker, filamin. Filamin condenses short actin filaments into spindle-shaped droplets, or tactoids, with shape dynamics consistent with a continuum model of anisotropic liquids. We find that cross-linker density controls the droplet shape and deformation timescales, consistent with a variable interfacial tension and viscosity. Near the liquid–solid transition, cross-linked actin bundles show behaviors reminiscent of fluid threads, including capillary instabilities and contraction. These data reveal a liquid droplet phase of actin, demixed from the surrounding solution and dominated by interfacial tension. These results suggest a mechanism to control organization, morphology, and dynamics of the actin cytoskeleton.

The cellular cytoplasm is a hierarchical array of diverse, soft materials assembled from biological molecules that work in concert to support cell physiology (1). The actin cytoskeleton constitutes a spectrum of materials constructed from the semiflexible polymer actin (F-actin) that are crucial in diverse physical processes ranging from cell division and migration to tissue morphogenesis (2, 3). Cross-linking and regulatory proteins assemble actin filaments into bundles and networks with varied composition, mechanics, and physiological function (4). The mechanical properties of actin assemblies regulate force generation and transmission to dynamically control morphogenic processes from the subcellular to tissue length scales (5, 6).

A mechanistic understanding of cytoplasmic mechanics is obscured by the rich complexity of in vivo cytoskeletal assemblies (7) and has been investigated via in vitro model systems (8, 9). Vastly different material properties have been accessed through varying filament length, concentration, and cross-linking. For semidilute concentrations of long actin filaments (>1 μm), the mean spacing between actin filaments, or mesh size, is much smaller than the filament length. In this case, cross-linking proteins mechanically constrain actin filaments to result in space-spanning networks that are viscoelastic gels (10). The structure of cross-linked actin networks is kinetically determined, reflecting a metastable state (11, 12) that requires motor-driven stresses for significant shape changes (13). In contrast, highly concentrated solutions of short actin filaments (<1 μm) align due to entropic effects and form equilibrium liquid crystal phases (14). Liquid crystal theory has been introduced as a framework to understand actin cortex mechanics and mitotic spindle shape (5, 15), but the existence of liquid crystal-like phases at physiological conditions is uncertain.

Liquid-like phases of proteins and nucleic acids have been found within the cytoplasm and are thought to be important in subcellular organization (16). Weak and transient interactions trigger these biomolecules to phase separate from the cytoplasm into droplets, with shape and dynamics dominated by interfacial tension and viscosity (16). Here we demonstrate liquid droplets comprised of cross-linked, short actin filaments. We focus on dilute actin concentrations where cross-linkers are critical to induce phase separation of actin into droplets with tunable tactoid shape. Consistent with a liquid composed of rods, we can describe the droplet shape and dynamics with an anisotropic liquid continuum model. Finally, we demonstrate actin bundles that exhibit shape changes reminiscent of fluid threads, with interfacial tension driven pearling and shortening. This reveals a liquid droplet phase of actin, demixed from the surrounding solution, with shape dominated by interfacial tension.

Results

Liquid Droplets Formed by Short Actin Filaments Cross-Linked by Filamin.

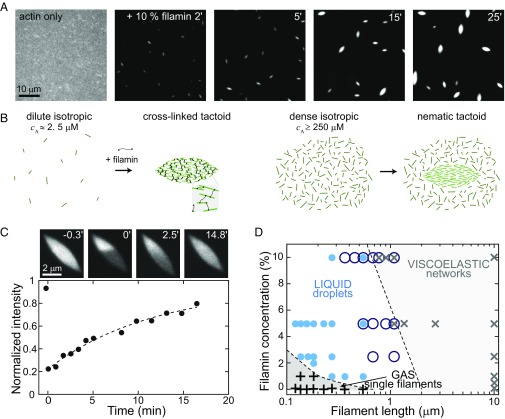
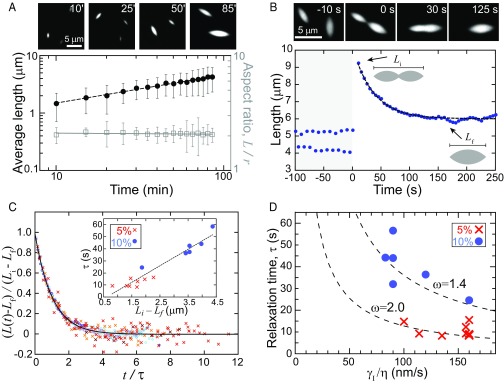
We polymerize actin filaments beginning with a dilute (2.6 µM) suspension of actin monomers in the presence of capping protein, which limits filament growth (17). Under these conditions, the average distance between filaments, or mesh size, is ∼1 µm (18) and much larger than the average F-actin length, ∼180 nm, such that filaments freely diffuse and form a uniform, isotropic mixture (Fig. 1A, Left; SI Text; and Movie S1). Adding 0.26 µM of the F-actin cross-linker filamin (19) triggers sudden density changes in the mixture. Actin filaments rapidly assemble into spindle-shaped aggregates of high density, estimated to be 250-µM monomeric actin; a negligible density of filaments remain in the bulk (Fig. 1B, Left). The tactoids grow over time, increasing in length from ∼1 to 4 µm during the first 60 min after filamin addition (Fig. 1A and Movie S1).

Fig. 1.

Liquid droplets of cross-linked and short F-actin. (A) Fluorescence images of tetramethylrhodamine-labeled actin (TMR-actin) (1 mol % capping protein) before (actin only) and after addition of 10 mol % filamin (added at t = 0). (B) Tactoids are the shape of entropically formed liquid crystal droplets near the isotropic–nematic phase transition (Right). Here we observe tactoids induced by the addition of cross-linkers (Left). (C) Images of TMR-actin within a tactoid (1.5 mol % capping protein and 5 mol % filamin; Upper), with photobleaching occurring at t = 0 min. Average normalized TMR-actin intensity of the photobleached region over time (dashed line indicates exponential fit with τ_R = 880 s). (D) Phase diagram of solid, liquid, and gas phases of cross-linked actin. Black plus symbols are data where dispersed filaments are observed, blue filled circles are samples exhibiting tactoid droplets, dark blue open circles are samples with fluid bundles (Fig. 4), and black crosses are samples where space spanning networks are observed.

These aggregates have a characteristic spindle shape, mathematically described as a tactoid, which is a signature shape of liquid crystal droplets (20). Liquid crystal phases form in highly concentrated suspensions of rods where entropic effects drive the nucleation of orientationally ordered droplets within a dense isotropic background (Fig. 1B, Right) (21, 22). For actin filaments of the length in our experiments, these phases occur at concentrations of ∼250 μM (23) (SI Text). Here we find that filamin induces the formation of tactoids at 100-fold lower actin concentration. In further contrast to traditional liquid crystal tactoids, cross-linked tactoids are surrounded by an undetectably low concentration of F-actin (Fig. 1B, Left).

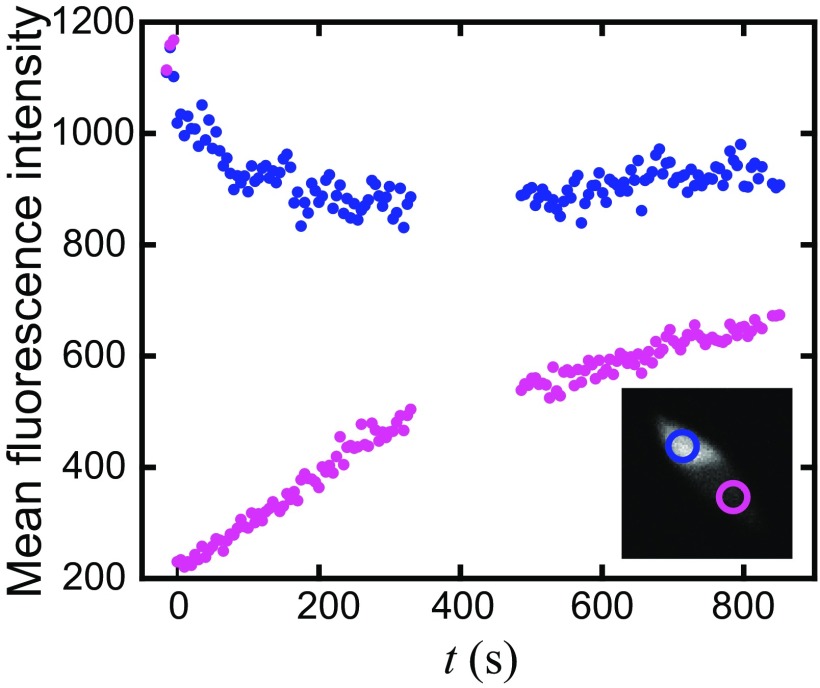
To probe whether cross-linked actin tactoids are fluid, we investigate the actin filament mobility via fluorescence recovery after photobleaching (Fig. 1C, images, and Movie S2). After photobleaching a region of the tactoid, the F-actin fluorescence intensity recovers in the bleached region, suggesting that filaments rearrange within the tactoid (Fig. 1C and Fig. S1). We quantify the recovery by plotting the ratio of the fluorescence intensity on the bleached side to the unbleached side as a function of time. The increasing intensity ratio with time is fit to a rising exponential, yielding a recovery time of τ_R ∼ 900 s. From this, we estimate a diffusion coefficient of D ∼ 0.3 × 10⁻² µm²/s and a viscosity, η ∼ 3 Pa⋅s (SI Text), comparable to viscosities reported in other protein and colloid systems (24).

Fig. S1.

Fluorescence intensity after photobleaching data. The mean intensity, background subtracted and corrected for tactoid angle, is plotted for regions (Inset) on the bleached side (purple) and unbleached side (blue). As the fluorescence intensity of the tactoid on the bleached side increases, the intensity on the unbleached side decreases, indicating diffusive mixing of actin filaments.

We observe tactoids over a range of actin filament lengths (0.1–1 µm) and filamin concentrations (1–10 mol %) (Fig. 1D). At longer filament lengths, we observe the formation of space-spanning actin networks, which have a viscoelasticity that has been well studied (25). At extremely low filament lengths or cross-link concentrations, tactoids do not form, and actin filaments freely diffuse in solution, analogous to a gas phase.

Tactoid Shape Can Be Modulated by Filament Cross-Linking.

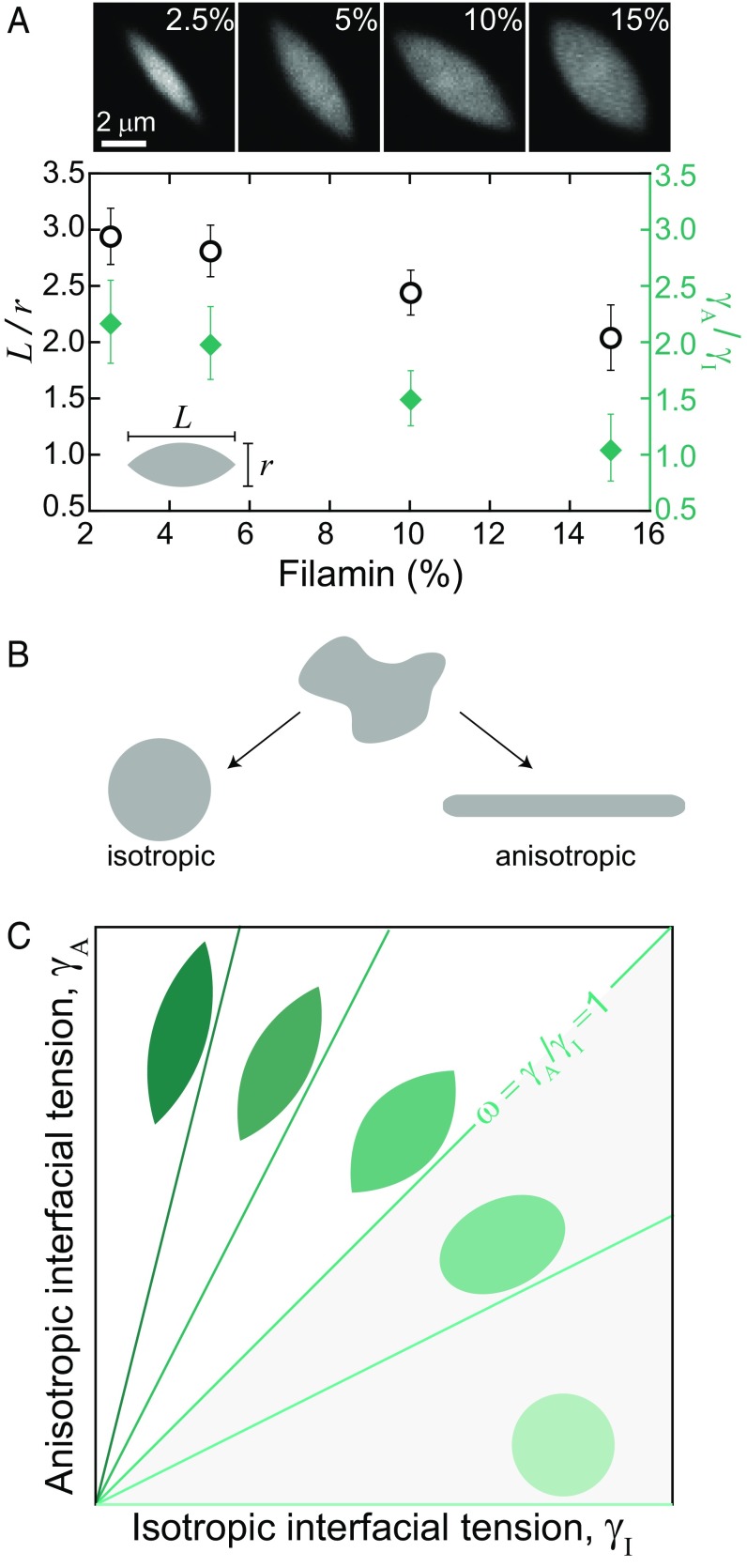
Thus far, we have only observed tactoid formation with filamin. Cross-links are typically thought of as interacting with the filaments in an anisotropic fashion, by promoting actin filament alignment. However, filamin is a long (∼150 nm) and flexible actin cross-linker, with transient binding kinetics (19). This may allow for a less orientationally constrained, long-range attractive interaction between filaments. Thus, cross-links may serve as a source of isotropic or anisotropic cohesion between filaments. To explore this, we form tactoids with variable filamin concentration from 2.5 to 15 mol % (Fig. 2A, images and open circles). We describe the resulting tactoid shape by the aspect ratio, L/r, where L and r are the major and minor axes lengths, respectively. At low filamin concentration, tactoids are elongated (L/r ∼ 3 for 2.5 mol % filamin). Strikingly, we find that as the concentration of filamin cross-links increases, the tactoid aspect ratio decreases (L/r ∼ 2 for 15 mol % filamin).

Fig. 2.

Cross-linking regulates tactoid interfacial tension. (A) Tactoid (1.5 mol % capping protein) images, visualized with TMR-actin for filamin concentration from 2.5 to 15 mol %. Aspect ratio (black open circles) and ratio of anisotropic to isotropic interfacial tension, γ_A/γ_I (green diamonds), as a function of filamin concentration. (B) An arbitrary shaped liquid droplet with purely isotropic interfacial tension relaxes to an equilibrium shape of a sphere, whereas a droplet with purely anisotropic interfacial tension relaxes to an elongated, cylindrical equilibrium shape. (C) Model predictions of liquid droplet shape for varying isotropic and anisotropic interfacial tension ratios.

To understand tactoid shape, we model the tactoid as a fluid droplet using a continuum theory (SI Text). An ordinary liquid droplet has purely isotropic interfacial tension, and the optimal equilibrium shape is a sphere (Fig. 2B). In contrast, a liquid crystal droplet is made of anisotropic particles, which gives rise to an anisotropic interfacial tension (21). A collection of rods with purely anisotropic interactions would have a preferred equilibrium shape of a cylinder (Fig. 2B), with a tendency of rod-like particles to align with the interface. Thus, we model a tactoid as a droplet with both isotropic, γ_I, and anisotropic, γ_A, interfacial tension components (20, 21) (SI Text and Fig. S2). The optimal shape of the droplet is determined by minimizing the interfacial energy, controlled by a single dimensionless parameter, ω = γ_A/γ_I. The balance of anisotropic and isotropic interfacial tensions yields elongated shapes for ω > 0, which become increasingly elongated as ω grows and sharp features emerge for ω > 1 (Fig. 2C).

Fig. S2.

(A) Schematic of a homogeneous tactoid droplet defining the local surface normal $\widehat{\mathit{N}}$ and the nematic director field $\widehat{\mathit{n}}$. (B) Tactoid shape parameters: major axis (L), minor axis (r), radius (R), and the central angle ($\mathit{\alpha }$). (C) Dependence of the rescaled free energy, $\mathit{F}/{\mathit{\gamma }}_{\mathit{I}}{\mathit{V}}^{2/3}$, on the tactoid angle $\mathit{\alpha }$, at various values of the anchoring strength $\mathit{\omega }$. (D) Dependence of the droplet aspect ratio on the anchoring strength. Solid circles represent points obtained via numerical minimization of the free energy. Solid curves denote asymptotic scaling relations predicted by the continuum theory.

We calculate ω from the experimentally observed aspect ratios using the theoretical relation $L/r=2{\omega }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ for ω≥ 1 (20) (SI Text). We observe that ω is inversely proportional to filamin concentration (Fig. 2A, diamonds). Thus, filamin alters ω such that the relative contribution of isotropic interfacial tension increases with respect to the anisotropic interfacial tension. This indicates that filamin serves primarily as cohesion between F-actin, rather than to enforce F-actin alignment within droplets.

Cross-Link Concentration Modulates Tactoid Shape Dynamics.

Over 100 min, the average tactoid length increases as a power law, $L\hspace{0.17em}\sim t^{\text{α}}$, where α = 0.47 ± 0.01 (Fig. 3A, dashed, and Movie S3). Notably, as the average size increases, the tactoid aspect ratio remains constant (Fig. 3A, open squares). This is consistent with theory and experiments on tactoids with homogeneous nematic alignment (26, 27) (SI Text).

Fig. 3.

Cross-link density regulates interfacial tension and viscosity. (A) Fluorescence images of tactoid growth (1.5 mol % capping protein and 5 mol % filamin), visualized by TMR-actin. Average tactoid length (black closed circles) and aspect ratio (open squares) are shown as a function of time after filamin addition, and dashed line indicates a power law fit L ∼ t ^α, where α = 0.47 ± 0.01 for four datasets. Error bars represent $\pm 1$ SD. (B) Fluorescence images of tactoids (1 mol % capping protein and 10 mol % filamin) coalescence. Tactoid length, along the major axis, is shown as a function of time as two initially separate tactoids coalesce. Dashed line is an exponential fit. (C) Tactoid length, rescaled by the deformation length, as a function of time, rescaled by the characteristic relaxation time, for 14 coalescence events (1 mol % capping protein and 5 and 10 mol % filamin) collapses into a master curve. The solid line represents an exponential decay. (Inset) Linear scaling between relaxation time and deformation length from exponential fits of length relaxation. (D) The interfacial tension to viscosity ratio obtained from continuum model fits to the experimental data falls on the theoretically predicted curve for anisotropic droplets.

Tactoid growth likely occurs via coarsening mechanisms associated with conventional liquid droplets, including Ostwald ripening and droplet coalescence (28). At the earliest observed stages of tactoid formation, there is a negligible concentration of F-actin in the bulk. This suggests that tactoid growth via single filament accretion, or Ostwald ripening, is unlikely. Instead, we observe individual coalescence events where two initially separate tactoids merge into a single elongated droplet that relaxes, within minutes, into a larger tactoid (Fig. 3B, images, and Movie S4). Moreover, the scaling exponent we measure in growth dynamics is consistent with that expected for coarsening of isotropic liquid droplets via interfacial tension-driven coalescence (α = 0.5) (28).

As a further test that liquid properties dominate tactoid growth via coalescence, we probe the droplet deformation dynamics. We measure the tactoid length, L, along the major axis, over time as two initially separate tactoids coalesce (Fig. 3B). After initial coalescence (L = L_i), the length rapidly decreases as the merged droplet shape relaxes toward a steady-state tactoid shape with L = L_f. The length shortening is consistent with an exponential decay from which we extract a single characteristic relaxation time, τ, using L(t) = L_f + (L_i − L_f)exp(−t/τ), where τ is a characteristic relaxation time (Fig. 3B, line). Data from multiple coalescence events collapse onto a single master curve upon rescaling the length by the deformation length, L_i − L_f, and time by τ (Fig. 3C).

Using our continuum model for anisotropic fluids (SI Text), we can determine the tactoid shape dynamics during coalescence as function of γ_I, γ_A, and η and extract the characteristic shape relaxation timescale $\tau$ (SI Text). From the model, we calculate $\tau$ as a function of η/γ_I for varying values of ω= γ_A/γ_I (Fig. 3D, dashed lines). We find that τ obtained from experimental data for 5 and 10 mol % filamin is consistent with those predicted for ω = 2 and 1.4 (values corresponding to those in Fig. 2A), respectively (Fig. 3D, symbols). Thus, the shape dynamics during droplet coalescence events can be quantitatively described with a continuum fluid model containing both isotropic and anisotropic interfacial tensions. From the η/γ_I obtained in the fit (Table S1), and the viscosity estimated from photobleaching, we estimate γ_I ∼ 300 nN/m. This interfacial tension is ∼10 times less than reported for other protein-based liquid droplets (24, 29) but consistent with theoretical predictions for larger particles such as actin filaments (21). Consistent with coalescence in isotropic droplets, we observe a linear scaling when we plot the relaxation time, τ, as a function of the deformation length, L_i − L_f, from the exponential fits (Fig. 3C, Inset). The slope of the line is η/γ_eff, where γ_eff is an effective interfacial tension with contributions from both γ_I and γ_A (SI Text). The data from the two different filamin concentrations fall on the same line, suggesting that that cross-link density modifies viscosity and the effective interfacial tension proportionally. Together, the droplet shape and dynamics demonstrate that filamin cross-link concentration modulates both the interfacial tensions and the viscosity of F-actin droplets.

Table S1.

List of mechanical parameters obtained by fitting the continuum model to the experimental data on droplet shape dynamics

Event	Filamin, mol %	$\omega ={\gamma }_A/{\gamma }_I$	${\gamma }_I/\eta$, $\mathrm{\mu }\text{m}/\text{s}$	$L_{\text{equilibrium}}$, $\mathrm{\mu }\text{m}$
Coalescence	5	1.90 ± 0.53	0.14 ± 0.02	2.74 ± 0.52
Coalescence	10	1.87 ± 0.07	0.11 ± 0.03	6.04 ± 0.38
Contraction	2.5	23.9 ± 14.4	2.5 ± 0.9$\hspace{0.17em}$ $\times {10}^{-3}$	5.77 ± 0.55
Contraction	5	11.9 ± 5.48	4.5 ± 0.7 $\times {10}^{-3}$	5.87 ± 2.01
Contraction	10	15.0 ± 7.78	3.5 ± 0.7 $\times {10}^{-3}$	5.68 ± 0.54

Interfacial Tension Drives Pearling and Contraction of Bundles.

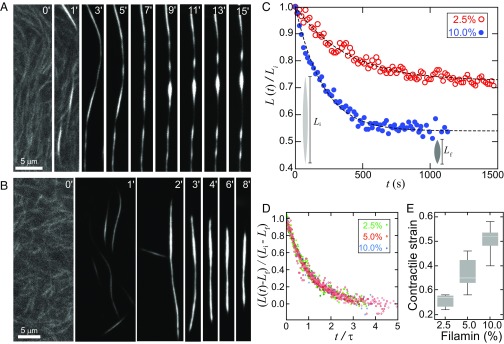
Actin bundles formed with passive cross-linkers are typically thought to be kinetically trapped structures with few structural rearrangements at long times (12). However, our findings suggest that when the actin filaments are sufficiently short, we may be able to observe bundles displaying fluid-like behavior. We explore this in our system by constructing bundles near the liquid–solid boundary (Fig. 1D). We increased the actin filament length such that the initial assembly conditions create long (>50 µm), thin (radius ∼200 nm) bundles of cross-linked F-actin within ∼1 min (Fig. 4 A and B). After rapid assembly, these bundles continue to change shape over ∼10 min timescales. Some bundles develop pearling instabilities along their length that evolve into periodically spaced bulges, which grow circumferentially in time (Fig. 4A and Movie S5). Such behavior is characteristic of a Rayleigh–Plateau instability observed in fluid columns, where interfacial tension drives the growth of periodic bulges that arise from fluctuations (SI Text and Fig. S3). In contrast to simple fluids, where capillary instabilities result in droplet breakup (30), we observe instabilities that evolve into chains of tactoids bridged by thin bundles. This is reminiscent of polymer fluids, where droplet breakup is arrested by polymer entanglements in the thinning bridges (31) (SI Text). The characteristic length scale of pearling is longer than that expected from a simple fluid, consistent with our theoretical model based on anisotropic interfacial tension (SI Text).

Fig. 4.

Interfacial tension drives instabilities and contraction in fluid F-actin bundles, visualized with TMR-actin. (A) Fluorescence images of an F-actin bundle (0.5 mol % capping protein and 10 mol % filamin) that exhibits instabilities that grow over time. (B) Fluorescence images of an F-actin bundle (0.25 mol % capping protein and 10 mol % filamin) that shortens over time. (C) Bundle length (0.25 mol % capping protein and 2.5 mol %, and 10 mol % filamin) as a function of time. (D) Bundle length, rescaled by the deformation length, as a function of time, rescaled by the characteristic relaxation time collapses on to a single master curve (0.25 mol % capping protein and 2.5, 5, and 10 mol % filamin). (E) Contractile strain increases with cross-linker concentration. Contrast is separately adjusted for prebundled actin images (A, 0′, 1′; B, 0′).

Fig. S3.

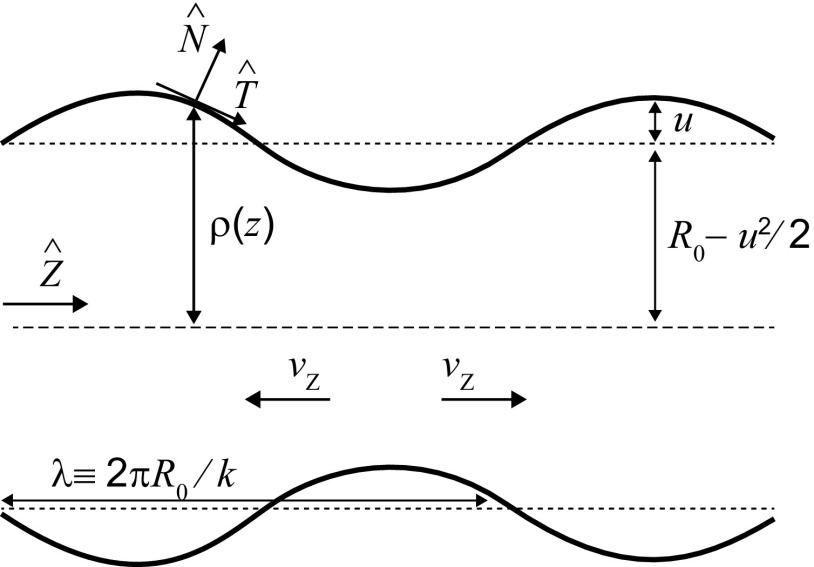
Schematic illustration of the geometry showing shape instability. The rod-like actin filaments are oriented along the z direction (long axis of the cylinder of initial radius ${\mathit{R}}_0$) in a homogeneous nematic configuration. The sinusoidal perturbation of wavelength $\mathit{\lambda }$ and amplitude u to the initial cylindrical geometry grows for $\mathit{\lambda }\ge \sqrt{1+\mathit{\omega }}\mathit{\hspace{0.17em}}\left(2\mathit{\pi }{\mathit{R}}_0\right)$, as the surface energy of the cylinder is reduced. As the capillary instability develops, liquid from the constricted regions have to flow into the bulging regions, thereby causing viscous dissipation.

We also observe bundles that contract (Fig. 4B and Movies S6 and S7). The bundle length, L(t) shortens exponentially in time, reducing in length by 20–60% over ∼10 min (Fig. 4C) toward a tactoid shape. This length contraction is captured by our dynamic continuum model of a droplet relaxing to its equilibrium shape (SI Text and Fig. 4C). Upon rescaling L(t) by deformation length, L_i − L_f, and time by the relaxation time, τ, we find that bundles across a range of cross-linking concentrations collapse onto a single exponential decay (Fig. 4D). This suggests that contracting bundles are also liquid columns that relax to their equilibrium shapes with a characteristic timescale. We find that the extent of cross-linking provides a tunable parameter to modulate bundle contractile strain and strain rates (Fig. 4E). Thus, if cross-linked F-actin bundles are fluidized, interfacial tension is sufficient to drive their contractility.

Discussion

The experimental characterization of cytoskeletal liquid crystal phases is a nascent field (15, 23, 32, 33). Here we describe a liquid crystal droplet, induced by the addition of cross-links and phase separated from a dilute suspension of anisotropic particles. We find that the physiological cross-linker filamin cross-links short F-actin into liquid crystalline droplets at concentrations 100-fold less than the critical concentration expected for entropic ordering. In this unusual, cross-linked liquid crystal, cross-linkers provide attractive interactions, allowing for the modulation of liquid properties such as interfacial tension and viscosity. The liquid phase is likely supported by filamin’s biophysical properties: filamin is a long (∼150 nm) and flexible actin cross-linker, with transient binding kinetics (19). We hypothesize that these cross-link properties are crucial to allowing filament orientational and translational mobility to support a liquid phase. Understanding the molecular mechanisms to control macromolecular liquid phases is an exciting avenue of future research.

Evidence of liquid phases of cross-linked biopolymers in vitro potentially has significant implications for cytoskeletal architecture and mechanics. Liquid crystal physics has been invoked to describe the meiotic spindle shape (15) and actomyosin flows (5). Cross-linked biopolymer tactoids provide a minimal model system to explore biopolymer liquid crystals. Our data provide evidence for a liquid crystal description of spindle shape (15, 34, 35), physical properties (15), and scaling with system size (36). These results suggest that liquid crystal theory has the potential to describe diverse biopolymer assemblies beyond the actin and microtubule cytoskeleton, including amyloid fibrils, intermediate filaments, and bacterial homologs of actin and microtubules.

Transitions between solid and liquid phases change the underlying physical properties of materials. Regulatory proteins in vivo provide dynamic control of biopolymer filament length and cross-link affinity, which could potentially drive the system between a gel and liquid phase to alter bundle mechanics and shape. Most notably, we find that bundles of fluid cross-linked filaments relax their shape by contracting, without requiring molecular motor activity. These results demonstrate that interfacial tension is sufficient to drive shortening and shape instabilities of bundles, suggesting a mechanism for previously reported motor-independent contraction in cells (37). Future research will elucidate the extent to which liquid phases of biopolymer filaments organize the interior of living cells and how such biological structures can inform novel soft materials design.

Experimental Assay

The sample chamber is a glass cylinder (catalog number 3166-10; Corning) affixed to a clean microscope coverslip (number 1.5; Fisherbrand) via vacuum grease (silicone high vacuum grease; Dow–Corning). Glass is cleaned by rinsing with pure water (milliQ), then pure ethanol (200 proof; Decon Laboratories), evaporating residual ethanol under a stream of air, and finally exposing to UV/ozone (UVO cleaner; Jetlight) for 20 min. The sample chamber is then immediately hydrated with vesicle buffer (10 mM sodium phosphate buffer, pH 7.5, 140 mM sodium chloride). To passivate the glass surface against protein adsorption, the chamber is incubated with 100 µM vesicle suspension for at least 15 min to allow formation of a supported lipid bilayer on glass surfaces. Vesicles are prepared at ambient temperature (∼20 °C, well above the gel transition temperature of the phospholipid) by repeated extrusion (Liposofast extruder, through 200 and 50 nm pore polycarbonate membranes; Avestin) of phospholipid (1,2-dioleoyl-sn-glycero-3-phosphocholine; Avanti Polar Lipids) resuspended in vesicle buffer following previously detailed methods (38), and stored at 4 °C until use. After bilayer is formed, excess vesicle suspension is exchanged for actin polymerization buffer (10 mM imidazole, 1 mM MgCl₂, 50 mM KCl, 0.2 mM EGTA, pH 7.5) by rinsing with 15 volumes.

To form actin filaments, monomeric actin [2.64 µM, purified from rabbit skeletal muscle acetone powder (39); Pel-Freez Biologicals; stored at 4 °C in 2 mM Tris, 0.1 mM CaCl₂, 1 mM NaN₃, 0.5 mM DTT, 0.2 mM ATP] is added to actin polymerization buffer in the presence of 300 µM ATP. A small amount of fluorescently labeled actin [0.32 µM labeled with tetramethylrhodamine-6-maleimide (TMR); Life Technologies] sufficed to allow imaging. To change filament length, the monomeric actin is incubated with capping protein [mouse, with a HisTag, purified from bacteria (40); gift from the Dave Kovar laboratory, University of Chicago, Chicago, IL] for 1 min before polymerizing. Oxygen scavenging system [0.5 vol % β-mercaptoethanol (Sigma), 4.5 mg/mL glucose, 2.7 mg/mL glucose oxidase (catalog number 345486; Calbiocchem), and 1,700 units/mL catalase (catalog number 02071; Sigma)] minimizes photobleaching. Depletion agent (0.3 wt % methylcellulose, 15 cp; Sigma) crowds actin filaments (longer than ∼2 µM) to the surface. After allowing actin filaments to polymerize for 20 min, cross-linking is initiated by adding the protein filamin [smooth muscle, purified from chicken gizzard, protocol adapted from (41)].

The sample is imaged using a spinning disk confocal microscope (Nikon), equipped with a CCD camera (Zyla; Andor) and a 60× or 100×, 1.49 NA objective (Zeiss). The sample is illuminated with a 561-nm laser, and images are shuttered to reduce photodamage.

Image Analysis

Tactoid shape is approximated by an ellipse. We describe the elliptical shape using two parameters, the major axis length, L, and the minor axis length, r, which we extract by applying ImageJ’s built-in Analyze Particles function (42) to thresholded images of tactoids. In measurements of average tactoid shape, tactoids that are partially out of focus or visibly merging are excluded. To analyze bundle contraction, images of bundles are skeletonized to a single pixel line, following thresholding. The bundle length is defined as the length of the skeletonized line.

Filament Length, Mesh Size, and Filament Spacing

Actin filament length is modulated through capping protein, a protein that binds to F-actin and inhibits filament growth. Capping protein yields an exponential distribution of filament lengths. Accordingly, in the limit of strong capping protein binding, we approximate the average number of actin monomers in a filament to be given by the proportion of actin monomers to capping protein. We convert the number of actin monomers to a filament length through the known actin monomer density in F-actin, ∼1 monomer per 2.7 nm.

We approximate the mesh size in micrometers, ξ, of actin filaments before cross-linking from the concentration of actin in mg/mL, c, using the relation ξ = 0.3c^−1/2 (18). After cross-linking, we estimated filament spacing within a tactoid from fluorescence intensity, which is approximately proportional to the amount of actin. The intensity associated with a single filament is given by the average integrated intensity associated with the cross-sectional lines along the axis of single filament that is crowded to the surface. The number of filaments in a cross-sectional area of tactoid is estimated by the ratio of the integrated intensity associated with a line across the tactoid minor axis, to average intensity of a single filament. The area is estimated to be a rectangular section, with the width corresponding to the tactoid radius and the height corresponding the depth of field associated with a confocal section (∼1 µm). We estimate the spacing between filaments to be the length scale associated with the average cross-sectional area associated with a filament.

Liquid crystal phases form in highly concentrated suspensions of rods where entropic effects drive the nucleation of nematically ordered droplets within a dense isotropic background (21, 22). For actin filaments, these phases occur at concentrations of ∼250 μM (23).

Fluorescence Recovery After Photobleaching and Viscosity Estimate

To verify the ability of filaments to rearrange or diffuse within a tactoid, a portion of the bundle is selectively photobleached using a 405-nm laser directed by an array of mirrors (MOSAIC; Andor). Shuttered images are captured at 15-s intervals while monitoring the fluorescence recovery (Movie S4).

The recovery of a photobleached spot arises from mobility of the fluorescent units mixing through diffusion with the photobleached units. We can extract an order of magnitude estimate of the viscosity by assuming the spot recovery is due to anisotropic particles diffusing in a simple liquid. Tactoids undergo both translational and rotational diffusion, which influence their absolute fluorescence intensity in a systematic way. Additionally, tactoids diffuse in and out of the focal plane, which results in the overall intensity fluctuating. The mean intensity, corrected for background and angular intensity variations, increases as the corrected mean intensity in the unbleached region decreases (Fig. S1). To minimize the error associated with intensity correction on the estimates of the spot fluorescence recovery, we instead plot the ratio of the average intensity in a region in the bleached portion of the tactoid to the average intensity in the region of the unbleached portion of the tactoid (Fig. 1C). The recovery of the bleached spot or the ratio is fit to a single exponential, where the characteristic recovery time, τ ∼ 900 s. Scaling by the approximate size of the bleached region, this translates to a diffusion coefficient of D ∼ 0.3 × 10⁻² µm²/s. Approximating the tactoid as a Newtonian fluid and actin filaments as elliptical particles, with axes lengths 2L and 2r, allows us to relate D to the viscosity, η, using the Stokes–Einstein relationship for an elliptical particle diffusing in a medium of η (43),

$$D=\frac{k_{B}T\ln \left(\frac{2L}{r}\right)}{6\pi \eta L}.$$

For our sample conditions (where a typical actin filament has length L ∼ 90 nm and diameter 2r ∼ 7 nm), this yields a viscosity η ∼ 3 Pa⋅s.

Continuum Theory of Elongated Droplets

The equilibrium shape of a liquid droplet is determined by minimizing the interfacial energy for a given volume of the fluid. If the interfacial energy is determined by an isotropic interfacial tension, the equilibrium shape is a sphere. In contrast, materials that are composed of highly elongated, anisotropic particles, such as the F-actin in our experiments, can exhibit nematic liquid crystalline phases and consequently form elongated droplets. The surface energy of an elongated droplet made of rod-like filaments is given by

$$F={{\displaystyle \int }}^{}dA\hspace{0.17em}{\gamma }_{ij}{\widehat{N}}_i{\widehat{N}}_j,$$

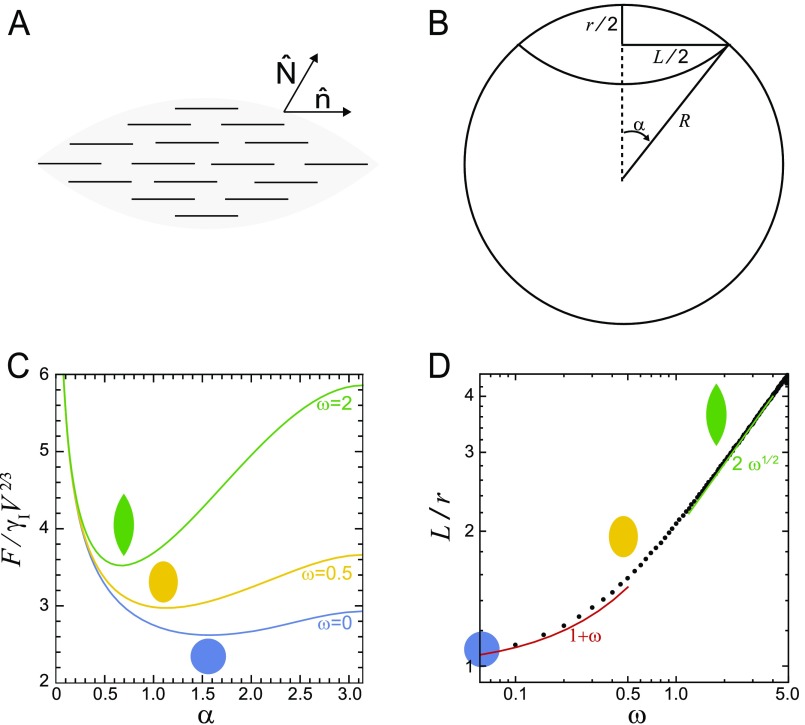
where $\widehat{N}$ is the outward unit normal to the surface of the droplet (Fig. S1A) and ${\gamma }_{ij}$ is the surface stress tensor given by ${\gamma }_{ij}={\gamma }_I{\delta }_{ij}+\hspace{0.17em}{\gamma }_A{n}_i{n}_j$ (21, 44), with i, j denoting spatial coordinates. Here ${\gamma }_I$ describes an isotropic liquid-like interfacial tension, whereas ${\gamma }_A$ describes an anisotropic surface anchoring energy (21, 44). The unit vector $\widehat{n}$ defines the local direction along which the F-actin filaments are aligned (Fig. S2A).

Short actin filaments, such as in our experiments (average lengths between 180 nm and 2 μm), behave as rigid rods because they are much shorter than the persistence length of F-actin (∼10 μm). In the absence of further experimental information on the alignment of actin filaments inside the droplets, we assume homogeneous arrangement of filaments, aligned parallel to the long axis of the droplet (Fig. S2A). Although the experimentally observed nematic configurations in tactoids nucleated from colloidal suspensions are mostly found to be bipolar (45), the continuum theory predicts a crossover to homogeneous director alignment (26), controlled by the dimensionless parameter, ${\gamma }_A{V}^{1/3}/K$, where $V$ is the droplet volume and $K$ is the familiar Frank elastic constant describing the energy cost of deforming the nematic director field (21). For ${\gamma }_A{V}^{1/3}\ll K$, which corresponds to small surface anchoring, large $K$, or small volume, the director field arrangement is expected to be homogeneous. The experimentally observed lack of dependence of the aspect ratio on the size of the droplet provides further support for the homogeneous picture (Fig. 2A). Therefore, we neglect any bulk elastic energies associated with distortions in the director field that are expected to be negligible for small sized droplets.

Equilibrium Droplet Shapes

The equilibrium shape of a droplet with a homogeneous director field, where $\widehat{n}$ is spatially uniform, can be obtained by minimizing the surface free energy F. The minimization procedure can be analytically carried out using the Wulff construction (20, 46), to show that the equilibrium shape is a tactoid, which is defined as the surface of revolution of a circular arc with radius R about its chord (Fig. S2B). The surface area of the droplet can then be readily expressed in terms of the tactoid shape parameters, R and $\alpha$ (Fig. S2B), $A=4\pi R^2(\sin \alpha -\alpha \cos \alpha )$. The effective surface area due to surface anchoring is given by $A_{\omega }={{\displaystyle \int }}^{}dA{(\widehat{n}.\widehat{N})}^2=2\pi R^2(\sin \alpha -\alpha \cos \alpha -\frac{1}{3}{\text{sin}}^3\alpha )$. By minimizing the total interfacial free energy, $F(R,\alpha )={\gamma }_{I}A+{\gamma }_A{A}_{\omega }$, with respect to $\alpha$, subject to the constraint of fixed volume. The rescaled free energy, $F/{\gamma }_I{V}^{2/3}$, is simply a function of $\alpha$, and their dependence is shown in Fig. S2C at various values of the anchoring strength $\omega ={\gamma }_A/{\gamma }_I$. With increasing $\omega$, the free energy is minimized at lower values of $\alpha$, which corresponds to higher aspect ratio droplets. We can then obtain the following simple relations for the dependence of the aspect ratio on $\omega$ (20):

$$\frac{L}{r}=\{\begin{array}{c}2{\omega }^{1/2}\hspace{1em}\omega \ge 1\\ 1+\omega \hspace{1em}0\le \omega <1.\end{array}$$

In Fig. S2D we show the close agreement between the above scaling relations and the aspect ratios obtained from numerical minimization of the free energy. Using the above equation, $\omega$ can be readily deduced from the experimentally measured aspect ratios of the tactoid droplets. We observe that the aspect ratio decreases with increasing filamin concentration, and the corresponding values for $\omega$ lie in the range: $1.1\le \omega \le 2.2$ (Fig. 2A).

Size Dependence of Tactoid Aspect Ratio

From existing liquid crystal theory, there are predictions about how tactoid aspect ratio will depend on size (20). The theory predicts that the aspect ratio decreases for bipolar tactoids and remains constant for homogeneous tactoids. The transition from homogeneous to bipolar depends on the ratio of the length of the mesogen and the tactoid length (L); the transition has recently been demonstrated with carbon nanotube tactoids (27).

Previously reported actin tactoids (formed at actin filament concentrations comparable to the critical concentration for nematic ordering) have aspect ratios decrease with increasing size, consistent with bipolar tactoids (23), as well as the optical signature of a bipolar director field in polarized light microscopy. These tactoids were of the scale of L ∼ 50 µm and formed with actin filament length ∼ 200 nm, which falls within the bipolar regime.

Here we form tactoids that are L ∼ 5 µm in length with actin filaments of length ∼ 200 nm. Theory predicts that under these conditions we would form homogeneous tactoids, consistent with our observations that the tactoid aspect ratio is independent of tactoid length (Fig. 2A).

Droplet Shape Dynamics

Liquid Droplets with Isotropic Interfacial Tension.

The length of coalescing tactoid droplets decays exponentially in simple fluids with an isotropic surface tension, γ_I, and viscosity. This can be readily concluded by balancing the instantaneous rate of change in mechanical energy, $dE/dt\sim -{\gamma }_{I}rdL/dt$, with the rate of energy dissipation in the droplet, which scales as $D\sim \eta \left(r^{2}L\right){(dL/dt)}^2/L^2$. As a consequence, the droplet length is expected to decay exponentially as $dL/dt\propto -\hspace{0.17em}L(r\eta /{\gamma }_I)$, with a timescale $\tau$ that is proportional to ${\gamma }_I/\eta$. Furthermore, the coalescing droplet undergoes a deformation $L_{\mathrm{i}}-L_f$ over a timescale $\tau$, under a conserved volume, $V$. Conservation of energy then readily implies $\eta V{[(L_{\mathrm{i}}-L_f)/\hspace{0.17em}{L}_{\mathrm{i}}\tau ]}^2\sim {\gamma }_{I}r(L_{\mathrm{i}}-L_f)/\tau$. Therefore, $\tau$ is expected to scale linearly with $L_{\mathrm{i}}-L_f$ with a slope proportional to $\eta /{\gamma }_I$.

Liquid Droplets with Isotropic and Anisotropic Interfacial Tension.

Although the surface energy model can provide predictions for the equilibrium shapes of F-actin droplets, it does not account for the dynamics of droplet shape relaxation. To derive the dynamic equations for tactoid shape parameters, we invoke conservation of energy. We balance the rate of change in surface energy with the dissipated power (energy per unit time), D, due to the deformation of constituent filaments: $\frac{dF}{dt}+D=0.$ The rate of energy dissipation is given by:

$$D={{\displaystyle \int }}^{}dV{\eta }_{ij}{v}_{ij},$$

where ${\eta }_{ij}$ is the viscosity tensor and $v_{ij}=\frac{1}{2}({\partial }_i{v}_j+{\partial }_j{v}_i)$ is the symmetric strain rate tensor with v defining the local velocity field. Our model for viscous dissipation assumes ideal Newtonian behavior, such that the dissipative stress scales linearly with the strain rate. For a tactoid droplet relaxing to its equilibrium shape, the strains arise from radial as well as angular deformations. In our scaling model, the corresponding strain rates are $\frac{1}{R}\frac{dR}{dt}$ and $\frac{1}{\alpha }\frac{d\alpha }{dt}$, which lead to the expression, $D=\frac{1}{2}V[{\eta }_R{\left(\frac{1}{R}\frac{dR}{dt}\right)}^2+{\eta }_{\alpha }{\left(\hspace{0.17em}\frac{1}{\alpha }\frac{d\alpha }{dt}\right)}^2]$, where ${\eta }_R$ and ${\eta }_{\alpha }$ define the radial and angular viscosity parameters and $V$ is the droplet volume.

To minimize the number of parameters, we assume for simplicity ${\eta }_R={\eta }_{\alpha }=\eta$. The time evolution of the radius (R) and the spanning angle ($\alpha )$ are determined by numerically solving the coupled nonlinear equations $\frac{dF}{dt}+D=0$ and $\frac{dV}{dt}=0$ (Mathematica NDSolve), subject to the initial conditions for the shape parameters provided by our experimental data. We specifically analyze two cases of experimental relevance: (i) coalescence of tactoid droplets (Fig. 3B) and (ii) contraction of long bundles (Fig. 4B). The numerical solutions for the shape parameters are then fit to our experimental coalescence and bundle contraction data. Sample fits to the data for coalescence and bundle contraction are shown in Figs. 3B and 4C, respectively, for varying filamin concentrations. The best fit results are summarized in Table S1.

For coalescing tactoids, the timescale of relaxation of tactoid length shortening dynamics, $\tau$, depends on two model parameters: ω = γ_A/γ_I and η/γ_I. To determine the dependence of $\tau$ on η/γ_I as well as ω, we numerically solve for the length dynamics of a coalesced droplet for fixed volume. To calculate $\tau ,$ we fit an exponential function to the numerical solution for $L\left(t\right)$ and extract the time constant, by varying γ_I relative to η for a fixed value of ω. We then repeat the analysis for different values of ω to obtain the family of curves as in Fig. 3D.

Capillary Instabilities in Long Droplets

A stationary capillary of liquid can be destabilized by fluctuations, which ultimately break it up into smaller spherical droplets (47) due to the effect of interfacial tension. In simple liquids, this instability, known as Rayleigh–Plateau instability, grows when the wavelength is comparable to the column radius.

A similar tendency is seen for the thinner and longer bundles of F-actin in our experiment (Fig. 4A). Consider the situation shown in Fig. S3, where an initially cylindrical column of liquid column with radius R is subjected to a sinusoidal perturbation of amplitude, u, and wavelength, $\lambda$ : $\rho \left(z\right)=R_0+u\sin \left(2\pi z/\lambda \right)-u^2/4R_0$, where $\rho$ and $z$ define the cylindrical coordinates, and the correction to the mean radius is obtained by imposing conservation of volume, $2\pi \underset{0}{\overset{\lambda }{{\displaystyle \int }}}dz{\rho }^2\left(z\right)=\pi R_0^2\lambda$. In this parameterization, the surface area is given by $A=2\pi \underset{0}{\overset{\lambda }{{\displaystyle \int }}}dz\rho \left(z\right)\sqrt{1+{\left(d\rho /dz\right)}^2}$. For a nematic liquid capillary, the total interfacial free energy is given by $F={\gamma }_I(A+\omega A_{\omega })$, where the effective surface area of anchoring, $A_{\omega }$, is expressed as $A_{\omega }=2\pi \underset{0}{\overset{\lambda }{{\displaystyle \int }}}dz\rho \left(z\right){\left(d\rho /dz\right)}^2/\sqrt{1+{\left(d\rho /dz\right)}^2}$. To leading order in $u$, the interfacial energy cost for the sinusoidal deformation of the nematic liquid capillary is given by $\delta F=\frac{\pi \lambda u^2{\gamma }_I}{2R_0}[\left(1+\omega \right)k^2-1]$, where the nondimensional wavenumber is defined as $k\equiv 2\pi R_0/\lambda$. The capillary is unstable to perturbations when $\delta F<0$, which occurs for wavelengths $\lambda \ge \sqrt{1+\omega }\hspace{0.17em}\left(2\pi R_0\right)$. Thus, the wavelength of fluctuations required to destabilize a nematic capillary is longer than that for a simple fluid by a factor of $\sqrt{1+\omega }$, such that the capillary would break up into droplets of irregular sizes induced by random thermal fluctuations that excite the system.

However, in the experiments we observe a characteristic length scale of instability (Fig. 3A), which corresponds to the fastest growing mode of the perturbation (48, 49). To predict the length scale of this dynamic instability we have to additionally account for the viscous energy dissipation. To this end, we consider a time-dependent shape perturbation, $u\left(t\right)=u{e}^{\text{Ω}t}$, which leads to a dispersion relation of the form (49) $\text{Ω}\left(k\right)=\text{Λ}\left(k\right)[1-\left(1+\omega \right)k^2]$, where $\text{Λ}\left(k\right)$ is a dynamical factor determined by the equations of hydrodynamic flow and the relevant boundary conditions. The form for $\text{Λ}\left(k\right)$ is obtained by equating the rate of decreasing surface energy of the unstable capillary to the viscous losses of the fluid: $D=-d\left(\delta F\right)/dt.$ The dissipated power through the cylindrical volume of fluid is given by $D\hspace{0.17em}\sim \hspace{0.17em}\eta \left(\pi R_0^2\lambda \right){(v/R_0)}^2$, where the average velocity of the fluid at the capillary center is simply related to the growth rate of the perturbation as $v=2\pi \left(\frac{du}{dt}\right)/k$. Using these relations, we derive the scaling dependence of the dynamic factor on the wavenumber: $\text{Λ}\left(k\right)\hspace{0.17em}\sim \hspace{0.17em}(\gamma /\eta R_0)k^2$. Thus, the wavelength of the fastest growing mode corresponding to the quadratic form of $\text{Λ}\left(k\right)$ is given by $k_{\text{max}}=1/\sqrt{2(1+\omega )}$. Using typical parameter values from the experiments, initial bundle radius $R_0\hspace{0.17em}\sim 200\hspace{0.17em}\text{nm}$, and surface anchoring $\omega \hspace{0.17em}\sim \hspace{0.17em}2$, we get ${\lambda }_{\text{max}}\hspace{0.17em}\sim \hspace{0.17em}4\hspace{0.17em}\hspace{0.17em}\mathrm{\mu }\text{m}$, close to what is observed experimentally (∼10 µm, ∼10–100× longer than the radius). The longer characteristic wavelength arises from anisotropic interfacial elastic stresses counteracting forces due to isotropic interfacial tension. For long actin filaments, as used in this experimental regime, elasticity due to entanglement can further increase this length scale.