Simulating the dynamics of the mechanochemical cycle of myosin-V

Significance

The free-energy landscape of the complete mechanochemical cycle of myosin-V is used in simulating the real-time features of the directional motion. The combination of Langevin dynamics simulations and time-dependent Monte Carlo simulations reproduces the observed trend in terms of stall force and force/velocity profile. The present study also addresses the role of the powerstroke and finds it to be the result of the complete free-energy landscape rather than the driving force of the energy conversion by the system.

Abstract

The detailed dynamics of the cycle of myosin-V are explored by simulation approaches, examining the nature of the energy-driven motion. Our study started with Langevin dynamics (LD) simulations on a very coarse landscape with a single rate-limiting barrier and reproduced the stall force and the hand-over-hand dynamics. We then considered a more realistic landscape and used time-dependent Monte Carlo (MC) simulations that allowed trajectories long enough to reproduce the force/velocity characteristic sigmoidal correlation, while also reproducing the hand-over-hand motion. Overall, our study indicated that the notion of a downhill lever-up to lever-down process (popularly known as the powerstroke mechanism) is the result of the energetics of the complete myosin-V cycle and is not the source of directional motion or force generation on its own. The present work further emphasizes the need to use well-defined energy landscapes in studying molecular motors in general and myosin in particular.

Myosin constitutes a superfamily of molecular motors comprising both the nonprocessive single-headed motors that are efficient in generating force on the actin filaments (e.g., myosin-II) and highly processive double-headed motors that can transport cellular load using tracks laid out by the cytoskeletal actin filaments (e.g., myosin-V, myosin-VI) (1, 2). The generation of force and unidirectional motion in each of the myosin molecules predominantly comprises tightly coupled events involving (i) binding and hydrolysis of ATP, followed by release of the products ADP and inorganic phosphate (P_i), occurring at the nucleotide-binding domain; (ii) binding and release of actin through the actin-binding domain; and (iii) a large conformational change of the lever arm that generates mechanical motion. Although the basic mechanochemical cycle is conserved in all members of the myosin superfamily, the exact nature of the coupling between the above steps in myosins, which decides the force-generating and load-bearing characteristics of different members, is unknown (SI Background).

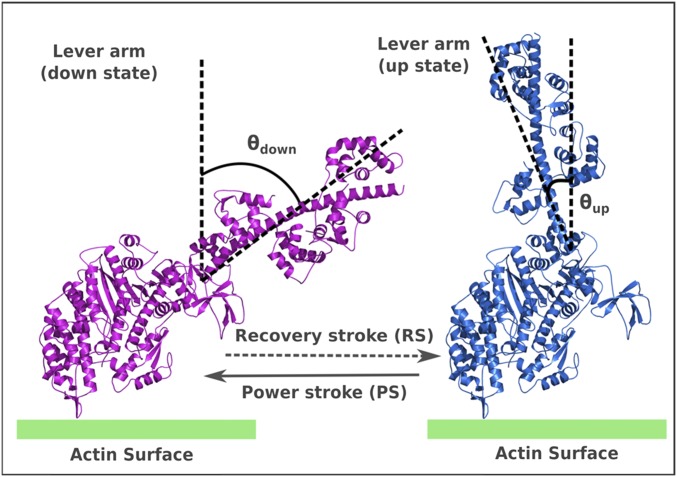
Numerous experiments, including kinetics and thermodynamic studies (3), high-resolution structural studies (4), electron microscopy studies (5), atomic force microscopy (AFM), and single-molecule experiments (2, 6, 7), have advanced our understanding of the action of the system. Although details about the dynamical nature of the myosin-V, along with a quantitative knowledge of the force-response, have been learned from single-molecule studies, the structural studies have provided us with an atomistic knowledge of the key conformational states involved during the cycle, namely, the lever-up (pre) and lever-down (post) states (Fig. S1). In addition, crucial information has been gained on the kinetics of the chemical and ligand-binding/release steps that make up the complete cycle. Based on this experimental information, several theoretical modeling studies (8–17) explored the mechanochemical cycle, mostly using phenomenological modeling approaches, accompanied by some structure-based studies. One of the key ingredients used (almost always) in describing the unidirectionality and behavior under force in myosin-V is the nature of the conformational change, known as the powerstroke (PS), which is generally assumed to generate the force on actin filaments (18–20). The PS occurs in the leading leg (LL), where it changes conformation from the lever-up to lever-down position, although its ADP-bound head is still bound to the actin. On the other hand, the trailing leg (TL), which unbinds actin upon ATP binding, undergoes a conformational change from the lever-down to lever-up position, known as the recovery stroke (RS), and diffuses through the intermittent space between the previous and next actin-binding sites. It is frequently assumed that the PS must release the free energy that provides the basis for the directionality and resistivity of the motor against the force applied in the opposite direction. Unfortunately, the PS idea has not been demonstrated based on a clear, structure-based, free-energy landscape or by considering the principles of microscopic reversibility (21, 22). Apparently, it is extremely challenging to understand the free-energy balance of the myosin-V mechanochemical action. The challenge is due, in part, to the existence of several intermittent states in the cycle and the large size of the system, which make it inaccessible to atomistic simulations even with current computational power. In the absence of a complete understanding of the structure–function relationship of all of the steps in the whole functional cycle, the notion of a strain-dependent, free-energy–releasing PS has become a widely adopted conventional perspective in the field. Motor characteristics, such as directionality, stall force, force/velocity behavior, and other dynamical features of myosin, are usually described through this downhill lever arm movement. It is assumed implicitly that the free-energy release from ATP hydrolysis is transferred into structural strain in the legs (this strain develops especially after P_i release), which is then released through the lever arm movement of the PS (1). However, such a strained intermediate has not been established experimentally.

Fig. S1.

Lever-up and lever-down conformational states of myosin-V. This figure has been adapted from figure 2A of ref. 26, and the details of modeling these structures are provided in the supporting information of ref. 26.

The PS is very difficult to observe experimentally as a separate process, uncoupled from the P_i release events. Most of the direct observations elucidate the strongly coupled nature of the P_i release and the lever arm movement (7, 23). Interestingly, although most experimental groups infer that the P_i must be released just before the PS (1), recent experiments also point to the possibility of the P_i being released after the PS (24). The authors have attempted to resolve these seemingly different observations and have suggested that the P_i might be trapped in another nonspecific protein site away from the catalytic center before it releases to the solvent (25). This argument also highlights the point that the P_i-release free energy is tightly coupled to the PS and that we should understand the PS energetics in the context of the whole cycle. In our previous work (26), we have approached the problem by delineating the energetics of each of the steps that make up the whole cycle and then recombining the energetics and generating the free-energy surfaces for the forward and backward motion of the motor. This analysis has highlighted one interesting fact about the PS; namely, the conformation change from the lever-up to lever-down position is an energy-demanding process, whereas the RS occurring in the TL after ATP binding and actin release is an energy-releasing process. Despite a free energy demanding PS, the correct interweaving of the chemical free energies and actin-binding/release events with the PS and RS can generate several characteristics of myosin-V motion. To establish this finding in a more concrete way, it is important to explore the time dependence of the system. Thus, we studied here the dynamic behavior of the myosin-V model (proposed in ref. 26) under stochastic conditions, performing Langevin dynamics (LD) simulations of a 3D bead model of the motor on an effective free-energy surface and then performing Monte Carlo (MC) simulations of a model with explicit treatment of all chemical steps. Our results agree with the experimental observations of myosin-V and also produce the behavior under external force as indicated in numerous single-molecule studies. The crucial finding from this study is the fact that the PS does not have to be the energy-releasing step in order for myosin-V to function. Rather, in accordance with our previous study, the directionality and the stall force are decided by the relative overall barrier of the forward (plus-ended) over the backward (minus-ended) pathway. In short, our study supports the notion that myosin-V favors a Brownian-ratchet mechanism (21, 22) rather than a mechanical PS mechanism, which relies heavily on coupling the ATP hydrolysis free energy to mechanical strain-mediated conformational change (i.e., downhill PS).

Background

The Forward and Backward Cycle of Myosin-V.

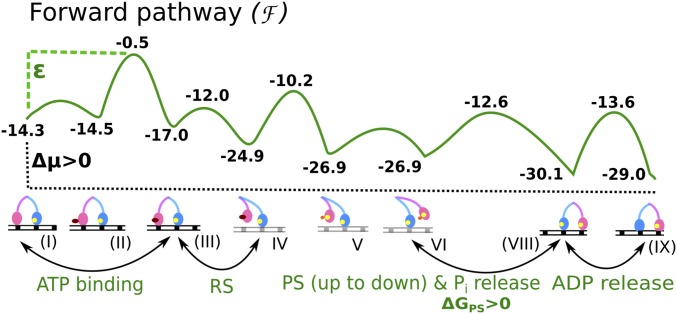
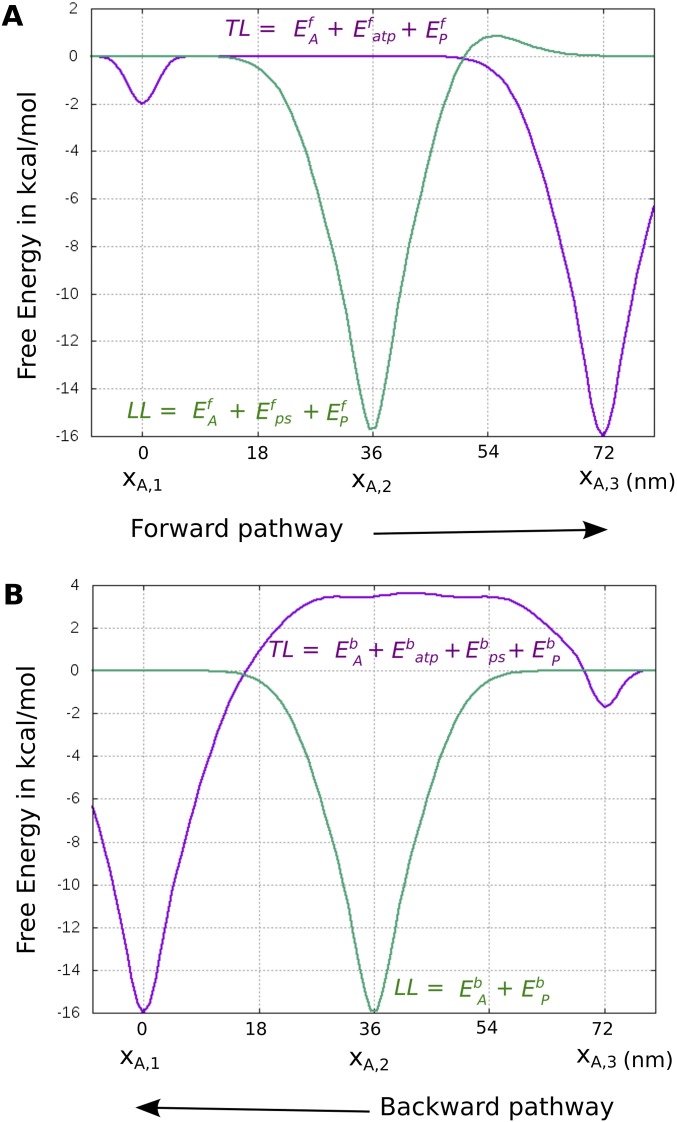
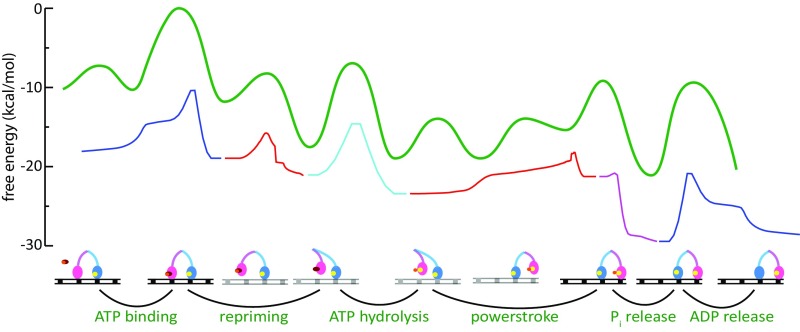
As in our previous study of myosin-V (26), we have delineated the energetics of the steps in the whole cycle using experimental kinetics data. The corresponding energetics were used to generate the free-energy landscape of the motor using a structure-based coarse-grained (CG) model (27, 28) that has been used to simulate various biological machines, such as F_OF₁-ATP synthase (29–31) and other systems (reviewed in ref. 27). The landscape combined the individual chemical and conformational steps in the correct order to produce motion toward the actin plus-end (forward) or minus-end (backward) direction, as shown in Fig. 1 for the forward motion and in Fig. S2 for the backward motion. In both figures, the starting state for the two pathways is the ADP-bound LL and nucleotide-free TL, both bound to actin. The figures involve a modification relative to the version reported by Mukherjee and Warshel (26) in terms of the height of the PS + P_i release barrier, because the observed rates could not discriminate between the two steps; that is, the combined barrier is less than 14.3 kcal/mol [larger than 200 s⁻¹ in ref. (32)], although the results reported by Baker (33) suggested that the barrier for PS + P_i release is higher (additional discussion is provided in Supporting Information).

Fig. 1.

Free-energy profile for a single step of myosin-V over actin filament along the forward positive-ended direction. The rate-limiting barrier along the path is indicated by ε.

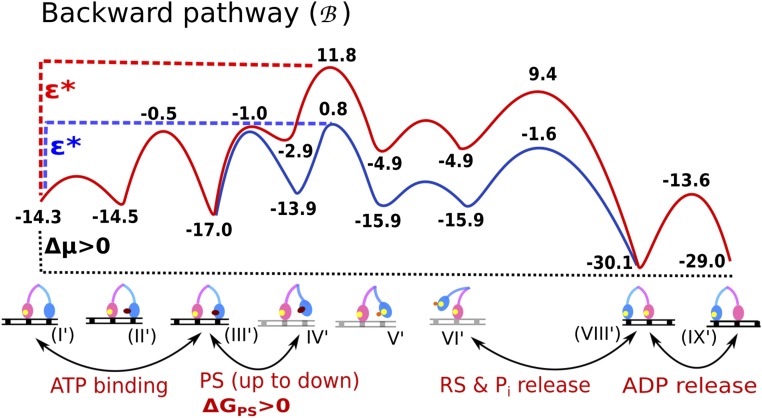
Fig. S2.

The backward pathway of myosin-V. The figure is a modified version of the corresponding figure in the study by Mukherjee and Warshel (26), where the modification involves the reduction of the PS + P_i release barrier (discussed in main text). ΔG_PS is the free energy difference of the lever-up to lever-down conformational change known as the powerstroke.

It is important to note that the forward and backward paths are not just microscopic reverses of each other; rather, the sequence of steps is different in the two pathways. The difference in the two paths stems from the asymmetrical energetics of performing the PS from the lever-up position, actin binding, and P_i release in the forward path [steps VI→(VIII) in Fig. 1] versus performing the ADP release, ATP binding, and PS from the lever-up position in the backward path [steps (VIII′)→(IX′)→(II′)→(III′)→(IV′) in Fig. S2]. The importance of different forward/backward paths in the workings of molecular motors in general has been discussed in depth (21, 22). In our model for myosin-V, the forward path is described by a chain of events starting with the TL binding ATP, releasing actin, performing the RS, and hydrolyzing the ATP, while diffusing in the plus-end direction. Meanwhile, the ADP-bound LL remains strongly bound to actin and attempts to perform the energy-demanding PS conformational change. Until the TL releases its bound P_i and rebinds to its new actin position toward the plus end, the PS in the LL is not completely stabilized in this model. This result is in accordance with experimental observations that the PS in the LL is coupled to the P_i release and actin binding of the TL (7, 23). Once the TL is bound in its new actin position, it becomes the new LL with bound ADP, whereas the formerly called LL releases ADP and is poised to start a new cycle as the TL. The backward path, likewise, starts with the TL binding ATP, releasing actin, and hydrolyzing ATP, but performing the PS unsupported by the P_i release event (as opposed to the case in the forward path). This decoupling of the PS and P_i release can create a high-energy barrier (the red curve in Fig. S2) for the backward path, because the energy-demanding PS is not supported by any energy-releasing P_i release steps. On the contrary, the PS in the forward path is supported by the energy-releasing P_i step, and thus generates a much lower overall barrier along the path. We also note that the ADP release rate from the lever-down state (i.e., post-PS or rigor state) is slower than from the lever-up state (i.e., pre-PS state) (32, 34). The higher ADP release barrier along the backward path may also contribute to establishing directionality. The difference in the overall barrier (Δε = ε* − ε) occurring in the two pathways is sufficient to select the forward path over the backward path (26).

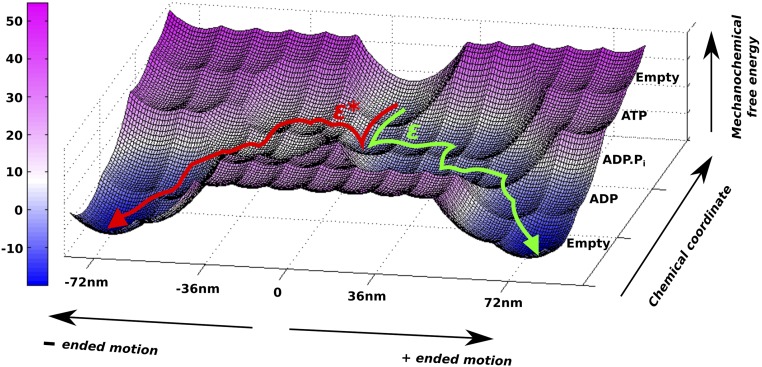
The movement of myosin-V can also be represented on an effective 2D free-energy landscape, as shown in Fig. 2 (details are provided in Supporting Information). Here, the horizontal direction corresponds to movement on the actin filament (plus- or minus-ended), whereas the vertical direction corresponds to the chemical events. The forward and backward paths depicted on the 2D surface also highlight the role of the barrier height (ε* or ε) in determining the overall directionality of the motor. Although the nature of the directionality will be explored below, we also note that there is a current major interest in the reason for the dynamics and force behavior of myosin-V. Thus, we will also examine whether a downhill PS is essential for the dynamics, stall, and force/velocity characteristics of the motor, or if these characteristics emerge because of the complete free-energy landscape with proper mechanical and chemical coupling.

Fig. 2.

Two-dimensional free-energy surface for the forward and backward motions. The green trajectory shows the most probable path taken by myosin-V during a single step over the energy barrier (ε) in the positive-ended direction, whereas the red trajectory is the corresponding backward motion toward the negative-ended direction over the high-energy barrier (ε*) landscape.

Modeling and Simulating Myosin-V.

To explore the dynamics and directionality of myosin-V and its legs under the influence of the free-energy surfaces shown in Fig. 1 and Fig. S2, we used two complementary approaches. In the first approach, we have modeled the 3D system using multiple coarse-grained beads representing the motor legs joined with a common bead at the fork region. The double-legged myosin-V is then simulated using LD to walk over fixed actin-binding sites, separated by a fixed distance of 36 nm. In modeling this system, we had to consider the difficulties in long time simulations (even with CG models); thus, we used two complementary strategies. The first approach used a rather simple effective potential that groups together several contributions and allows one to explore the effect of the rate-limiting barriers in real 3D space with general features resembling phenomenological descriptions but with much more connection to the complete surface. This model allowed us to explore the dynamics of the myosin system by LD simulations, albeit with scaled-down forward and backward barriers and much smaller diffusion coefficients. The details of the LD modeling are given in Supporting Information, Table S1, and Fig. S3.

Table S1.

Parameters used for the LD simulation

Parameter type	Unit	Parameter value
Actin positions
xA,i, i = 20	Nanometers	0,36,72,…
Actin-binding potential
Aa	Kilocalories per mole	−4.0
Wa		1,000
ATP-binding potential
AATP	Kilocalories per mole	2.0
WATP		1,000
Phosphate release potential
Ap	Kilocalories per mole	−12.0
Wp		10,000
Powerstroke (forward)
$A_{PS}^f$	Kilocalories per mole	1.5
$W_{PS}^f$		10,000
xf	Nanometers	14
Powerstroke (backward)
$A_{PS}^b$	Kilocalories per mole	4.5, 5.5, 6.5, 7.5
$W_{PS}^b$		10,000
Xb,n, n = 3	Nanometers	15, 30, 45
Bond
xbond	Nanometers	3.0
Kbond	Kilocalories per mole per (Å)2	3.0
Angle
θangle	Degrees	171.8
Kangle	Kilocalories per mole per (rad)2	30.0
Joint angle
θjoint	Degrees	91.6
Kjoint	Kilocalories per mole per (rad)2	1.5
Nonbonded steric interaction
anb	Kilocalories per mole	200.0
bnb		0.05
rnb	Nanometers	5.0
Effective LD friction		1,000
Effective LD mass		100
LD temperature	Kelvin	300
Time step	Picoseconds	2

Fig. S3.

Effective potentials for (A) forward and (B) backward motion used in the LD simulations.

In view of the difficulties of running the long time LD simulations needed to explore the force/velocity profile, we also introduce a second strategy based on a time-dependent MC approach with a more realistic free-energy surface. The landscape used is much closer to the landscape of Fig. 1 than the landscape used in the LD treatment. In brief, the MC simulations used a simplified myosin-V protein composed of three particles (two particles represent the two heads, and another joint particle represents their connection) moving along an actin filament. The use of only three particles is consistent with the important finding of Hinczewski et al. (12) that the arms behave as rigid rods. Additionally, we performed some calculations in a kinetic MC model, where the energy states (minima and maxima) from Fig. 1 were used to perform a 1D MC simulation, where the system can either move forward or backward along the energy landscape. The energies still had to be scaled down in both MC systems, but much less than in the LD simulations.

Results and Discussion

The Coupling of the P_i Release and the Lever Arm Movement of Myosin-V.

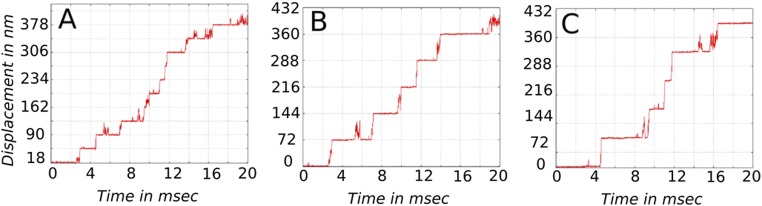
One of our aims has been to explore whether having an energy-demanding PS interweaved with the chemical steps of ATP binding, P_i, and ADP release and actin-binding/release events can produce the myosin-V motion toward the plus end, as has been observed in numerous experiments (35–37). This issue was explored by running LD simulations under different conditions. The results of the simulations are described in Fig. 3, where Fig. 3A describes the motion of the motor center particle (joint) without any external load. Similar trajectories for the head particle starting as the TL and the head particle starting as the LL are shown in Fig. 3 B and C, respectively. It is observed that myosin-V walks in a hand-over-hand fashion with at least one leg bound to the actin filament. We also observe substep features (most evident in single-leg trajectories of Fig. 3 B and C), as found in single-molecule and AFM experiments (35, 36). The motion of the TL follows a substep of ∼40–50 nm, most of which is diffusive in nature after it releases the actin-binding site. The second substep of ∼20–30 nm occurs when the TL releases P_i and rebinds to the next actin-binding site. This rebinding moves the myosin head by one step in the plus-end direction. It is also observed that the completion of the energy-demanding PS occurring in the LL is almost always coupled with the P_i release and rebinding step of the TL, in close accordance with experimental findings (7, 23). Experiments have suggested that the PS can be reversed in the presence of high [P_i] in the bulk. This finding can be interpreted as inhibition of P_i release from the TL, leading to events of PS reversal rather than completion (23). We also note that a PS with large amount of free-energy release (as is often predicted to be the driving force in the PS mechanism) will occur in the LL as soon as the TL unbinds actin due to the presumed release of the mechanical constraint. In this case, inhibition of P_i release should not affect the fate of the PS in a severe way. On the contrary, an energy-demanding PS must be strongly coupled to the P_i release step to stabilize the lever-down state, as has been observed experimentally. It has been difficult to predict the exact sequence of events (P_i release and PS) in the motor during force generation. Most experimental groups favor P_i release before PS, citing structural considerations of difficulty in releasing P_i after the PS (1), although a recent group has reported P_i release after the PS step (24). As mentioned above, a recent review has also hypothesized that the released P_i can reside within the protein (in another distant nonspecific site) until the end of the PS; hence, P_i is released in the solution after the PS (25). Our results indicate that the energy-demanding PS is only stabilized (or ratcheted) with irreversible P_i release (irreversibility imposed under correct thermodynamic conditions of low ADP and P_i concentrations); hence, the PS could not be decoupled from the ligand-release kinetics. In other words, P_i release does not occur as a completely independent step before or after the PS; rather, it is more likely interleaved with the energy-demanding lever arm movement. The idea of intermediate P_i binding within the protein is an interesting concept (25), because it will allow the P_i free energy to release in steps, with a part being released soon after the electrostatic charge separation of the freshly cleaved gamma phosphate from the ADP alpha and beta phosphates and another part released after the P_i release into the solution (entropic in nature). This extended release of the P_i may allow adequate coupling of the P_i release step to the high-energy–demanding PS during the forward motion.

Fig. 3.

Temporal dynamics of myosin-V in the unloaded condition are shown for the central bead (A), for the head particle of the leg starting as the TL (B), and for the head particle of the leg starting as the LL (C). Note that the central particle shows a displacement of 36 nm in a single step, whereas the head particles show displacement of 72 nm per step.

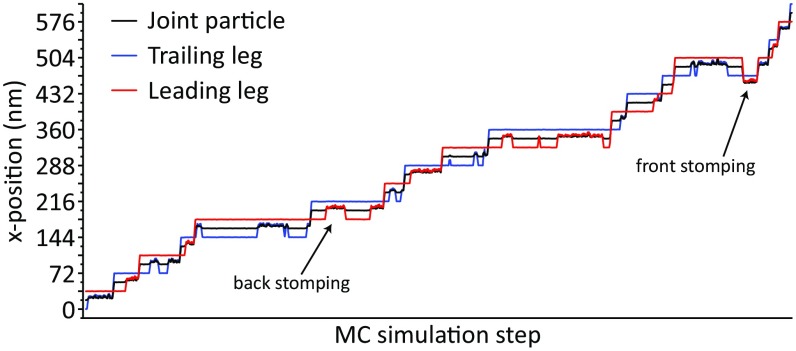
Our simulations show that the TL rotates freely around the joint of the two legs during its diffusive motion before it rebinds to actin. This free rotation of the leg is also a result of the underlying angular constraint used on the joint. It was observed that a strong constraint on the joint led to nonproductive walking motion because the myosin-V was leaving the actin filament much earlier. The free rotation of the TL is in accordance with the motion observed in many single-molecule experiments on myosin-V (35, 36). Some of the trajectories have shown recursive motions of the TL, where the leg, instead of binding to the next actin-binding site, goes back to the previous site. This behavior of the TL has also been observed in the experiments and has been termed “foot stomping” (37). However, similar foot stomping of the LL is observed very rarely, where the LL sometimes rebinds to actin and initiates the walking motion, whereas it falls off and ceases the walking motion at other times. The rarity of LL foot stomping is mostly due to the leg being in a tight ADP- and actin-bound conformation compared with the TL, which releases ADP fast and binds a new ATP molecule to undergo actin release. The difference in ADP release rates in the LL and TL has been observed experimentally and suggested by some to be strain-mediated (32, 34). Overall, the trajectories reveal important mechanistic details about the hand-over-hand motion and substep features that match well-known experimental facts. Our results directly imply that myosin-V is capable of showing directional motion, not due to a free-energy–releasing conformational change (i.e., a downhill PS) but, instead, to proper coupling of the conformational free energies with the binding and product release steps. In this case, a high-energy–demanding PS in the LL is stabilized mostly by the P_i release in the TL, which also implies the strong connection between the PS and P_i release kinetics seen experimentally (23).

Dynamics of Myosin-V Under Constant Load: Dependence of Stall Force on the Pathway Barrier.

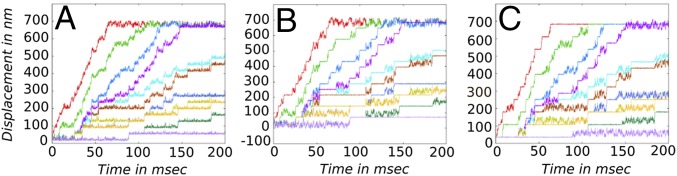
One of our main goals is to reproduce the behavior of myosin-V under load. Accordingly, we carried out LD simulations under a constant load, varying from 0.1 to 1.0 pN, applied on the central particle (joint particle) in the opposite direction of the plus-end motion. Simulated trajectories for the loaded myosin are shown in Fig. 4 for the central particle and for the two head particles. It is observed that as the load increases, the number of steps taken by myosin-V reduces drastically with time, whereas the intermittent dwell times increase between consecutive steps. The nature of the mechanical motion (hand-over-hand motion and substep feature) is similar throughout the force regime explored in this study. All trajectories show a diffusive motion of the TL after it unbinds actin and rotates freely around the central particle before binding to the next site on the actin filament. Application of higher loads increases both the diffusive motion and the bound dwell time for the myosin-V legs. These results reveal that our model of myosin with an energy-demanding PS is actually capable of providing qualitatively similar walking motions as observed in experiments for both unloaded and loaded cases (35, 36). However, it should be noted that the time for a single myosin-V step is much faster in our simulations (especially the phase where both ADP-bound legs are bound to actin) compared with experimental observations. This observation is a result of very fast (almost instantaneous) ADP release and ATP binding in the TL (details are provided in Supporting Information), and has been done to speed up the simulations within reasonable computational resources.

Fig. 4.

Temporal dynamics of myosin-V in the loaded condition where force (F) is applied on the joint particle are shown for the central bead (A), for the head particle of the leg starting as the TL (B), and for the head particle of the leg starting as the LL (C). The color scheme of the trajectory plots with changing F are as follows: red (F = 0), green (F = 0.1 pN), blue (F = 0.2 pN), purple (F = 0.3 pN), cyan (F = 0.4 pN), brown (F = 0.5 pN), dark blue (F = 0.6 pN), olive (F = 0.7 pN), orange (F = 0.8 pN), dark green (F = 0.9 pN), and violet (F = 1.0 pN).

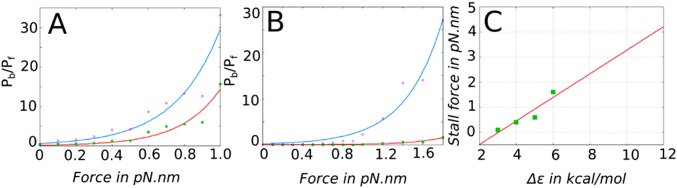
Our next goal is to calculate the stall force from the unloaded and loaded simulations and to determine the dependence of the stall force on the parameters of the energy landscapes shown in Fig. 1 and Fig. S2. According to our model (26) and similar concepts explained elsewhere (21, 22), the most important parameter determining the directionality and stall force of chemically coupled molecular motors like myosin-V is the factor Δε = ε * −ε, namely, the difference in the barrier heights between the forward and backward pathways (further clarification of ε and ε* is provided in Fig. 2).

We note once more, that the difference in the forward and backward barriers might arise from the asymmetry in the lever arm movement (energy-releasing up and energy-demanding down conformations) coupled to P_i release, as well as asymmetry in the ADP-release barriers in the up and down states. Whatever the exact origin of the higher barrier in the back motion, we explore the role of Δε under stochastic conditions by conducting forward and backward simulations using different values of Δε. The stall force for each specific Δε value (obtained from forward simulation with ε and backward simulation with ε*) is given by the force at which the ratio of backward (P_b) and forward (P_f) steps is 1 (i.e., P_b/P_f = 1). Fig. 5 A and B shows the exponential behavior of the P_b/P_f ratio for the force regime studied in this work and for different Δε values. It is seen that stall force increases with increasing Δε. Due to the need for long time simulations to acquire sufficient statistics using a realistic 3D stochastic model, we have only calculated stall forces for Δε = 3, 4, 5, or 6 kcal/mol. The calculated stall forces are plotted in Fig. 5C, and the linear extrapolation yields a stall force of 2.3 pN for Δε = 8 kcal/mol, whereas 11 kcal/mol (the value shown in Fig. 1) is on the higher end, giving a stall force of >3.5 pN. Because the experimental estimate on the stall force for myosin-V is in the range of 1–3 pN, we conclude that Δε should be in the range of 7–9 kcal/mol.

Fig. 5.

P_b/P_f ratio (no. of forward steps/no. of backward steps calculated from trajectories of 200 ms) is plotted from trajectories of forward motion with force applied on the opposite direction (as in Fig. 4) and trajectories of backward motion with force applied on the same direction. Exponential fits for Δε = 3 kcal/mol (blue) and 4 kcal/mol (red) (A) and for Δε = 5 kcal/mol (blue) and 6 kcal/mole (red) (B) are shown. The stall force for each Δε is calculated as the force where P_b/P_f = 1. (C) Linear fit of these stall forces (plotted as green dots) for different Δε values.

Higher Barrier MC Simulations.

As stated in Background, in view of the difficulties of simulating long times, particularly in exploring the force/velocity profile, we introduced a time-dependent MC approach. The difficulties mentioned in Background are not so crucial while looking at the stall force that depends mainly on the overall rate-limiting barriers ε and ε* and while investigating the dynamics of the legs during walking. However, the simulations of the force/velocity dependence may require a more detailed mechanochemical free-energy surface. Thus, in our MC approach, we use a more realistic free-energy surface, because we are not attempting to simulate the real-space 3D dynamics of the motor. The landscape used for the MC is presented in Figs. S4 and S5.

Fig. S4.

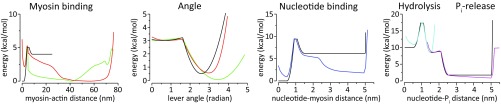
Free-energy landscape for the MC simulations (discussed in main text) and its correspondence to Fig. 1 (in green). The curves are colored as follows: blue for nucleotide binding/unbinding to the myosin heads, red for myosin binding/unbinding to actin particles, cyan for ATP hydrolysis, and magenta for P_i-release. Note that although they are the same chemical process (going in opposite directions), the two red curves are not exactly the same because the entropy of the processes is not symmetrical. Some of the curves were horizontally stretched in a disproportional way to make it easier to see the barriers; the unmodified curves can be seen in Fig. S5.

Fig. S5.

Potential energies used for the MC simulations' coordinates and the output free-energy curves calculated using the distribution. Note that hydrolysis of ATP and P_i release were normalized separately, even though they use a continuous coordinate (nucleotide-P_i distance), because the barrier of both reactions together was too high to obtain good sampling. The green and red curves represent the TL or the LL in the angle curves, and binding to the previous actin particle (i − 1) or next actin particle (i + 1) for the free head, respectively, where i is the index of the actin particle to which the other myosin head is attached.

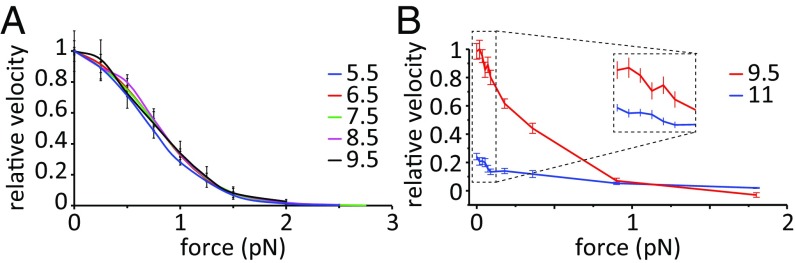
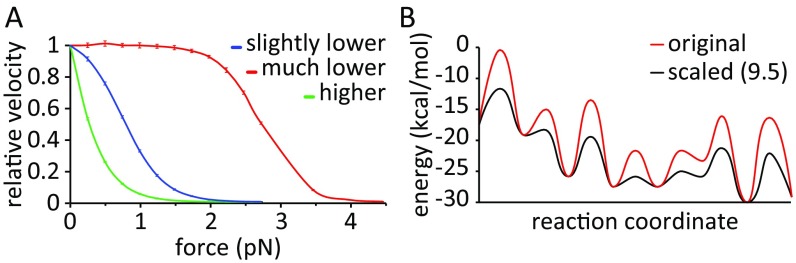
With the MC model, we can explore the nature of the observed force/velocity curve. Here, one can explore the possibility of interplay between different barriers to determine the rate. The most effective way to explore this issue is to use a 1D landscape in our MC model and to solve the kinetic problem. Doing so, we observed that it is not the absolute height of the barriers that defines the force/velocity profile but, rather, the difference between the highest barrier and the barrier where the force is applied (ΔΔg^‡). This fact is revealed by obtaining similar curves regardless of barrier scaling (Fig. 6A). To understand the criteria that dictate the shape of the force/velocity profile, we repeated this analysis using effective surfaces in which the height of the barrier where the force is applied is different, and it is apparent from Fig. S6A that a sigmoidal relationship requires a barrier that is relatively force-independent to be the rate-limiting barrier (e.g., the ADP release barrier compared with the PS + P_i release barrier).

Fig. 6.

(A) Force/velocity profile in the scaled 1D MC simulation as a function of the height of the highest barrier (ADP release). Scaling was done such that the ΔG values and the ΔΔg^‡ were maintained as much as possible (Fig. S6B). (B) Force/velocity profile in the 3D MC simulations. A zoom-in with vertical translation is provided for clarity.

Fig. S6.

(A) Force/velocity profiles obtained in the 1D MC testing of different heights for the barrier, where the force is applied (with respect to the ADP release barrier). Each color presents results of simulations where the force is applied to a different barrier, as indicated in the legend. (B) Comparison between the scaled (black; 9.5 kcal/mol as an example) and unscaled (red; Fig. 1) energy landscapes for the 1D MC simulations.

Further, note that the effect of the force on the ADP release barrier may depend on the ADP concentration, because this concentration changes the relative height of the ADP release barrier and the PS + P_i release barrier (and this change can be reflected in the force effect). Interestingly, a broad plateau is achieved if ΔΔg^‡ > ∼5 kcal/mol, whereas in our case, ΔΔg^‡ = ∼3 kcal/mol.

Intuitively, the energy gap between the highest barrier (ADP release) and the barrier where the work is done to overcome the applied force (the PS + P_i release) is not large enough to make the latter barrier entirely negligible. Thus, the velocity is determined by a combination of both barriers. Initially, the highest barrier, which is relatively force-independent, is the dominant one, and the effect of the force is shielded by it; however, as the force increases, the dominant barrier becomes the PS + P_i release plus the work done to move against the force, and we encounter a decay in the velocity.

The use of the 3D CG model produced similar force/velocity profiles, where a sigmoid shape that is ΔΔg^‡-dependent can be seen (compare Fig. 6B, blue and red curves). The 3D MC trajectories are depicted in Fig. 7, with observed hand-over-hand and occasional foot-stomping dynamics.

Fig. 7.

Temporal dynamics in the 3D MC, presenting the x position of the myosin particles. Typically, a rough line indicates an unbound myosin head particle. Note that the TL and LL are colored based on the initial position and alternate roles on each step.

Concluding Remarks

This work used a CG landscape of the myosin-V system and reproduced the directionality and other key observables by LD and MC simulations. These key observables include the stall force, the hand-over-hand dynamics, and the force/velocity profile. These findings add credibility to our view that the energetics of the lever arm movements (i.e., lever-up and lever-down conformational changes) in the RS and PS of the myosin are key ingredients for establishing the directionality, with another key ingredient being the asymmetry in ADP release rates in the different conformations.

Our study also allows us to explore the nature of the PS proposal; that is, although the PS proposal has not been formulated in a unique way in terms of the corresponding energy barriers and the way the force is generated, we may try to define and examine the main premises of this proposal. The central assumption of the PS proposition is that the strain developed in the actin-bound lever-up structure (assumed to occur after P_i release) is released during the lever-up to lever-down conformational change. This proposition leads to a free-energy–releasing PS that drives the load-dependent directional motion in myosin-V (1, 7, 16, 19, 38). However, our analysis shows that the energy of the lever-up to lever-down conformation is, in fact, increasing rather than decreasing [because the lever-up or pre-PS is the low-energy conformer, whereas the lever-down or post-PS is the high-energy conformer (26)].

We note that a significant part of the support in the PS model seems to come from the implicit assumption that the free-energy difference of the lever movement determines the directionality and efficiency, ignoring several aspects such as the intermediate barriers, coupling to chemical steps and imposing microscopic reversibility on correctly coupled mechanochemical events (21, 22). It also seems to us that some researchers assume that the forward lever arm movement involves an inertial motion [e.g., the statement that “rapid changes are essential” (39)], where the kinetic energy drives the directionality and generates force against a load. This assumption has some similarity to the assumption that dynamics drive enzyme catalysis by having an inertial model in which the kinetic energy of the binding process is used to drive the motion in the chemical direction (40). However, in the case of enzyme dynamics, it is simple to show that the kinetic energy fully dissipates before we have the chance for a stochastic fluctuation that climbs over the chemical activation free energy. It may be harder to see why the situation should be different in the case of the PS. The PS and related ideas imply a release of strain that is generally associated with van der Waals interactions. However, in biological systems, it is much more likely that the energy changes will be associated with slowly varying electrostatic energy, especially for those energy changes that involve long-range movements where the kinetic energy arising due to any van der Waals steric clashes are dissipated very quickly.

Another problematic assumption is the idea (e.g., ref. 20) that the effect of the PS is defined as the ratio between the input energy from ATP hydrolysis and the resulting work; that is, as shown in our study of the torque generation in ATPase (31), the relation of the work to the chemical energy is determined by the shape of the landscape in the conformational and chemical space. Of course, there are many dimensions, except the axis of the actin, where the chemical energy can be dissipated without doing any work along the PS coordinate (e.g., opening of the ATP site is perpendicular to this motion). In fact, recent work of Muretta et al. (24) agrees that the most important energetics are associated with P_i release and not with the large structural reorientation of the light-chain domain. Similarly, our finding supports the idea (21, 22) that the downhill strain-releasing PS motion is not the origin of the directionality or the basis of other motor characteristics.

The present work found that the observed force/velocity profile can be reproduced with the profile of Fig. 1. Notably, the sigmoidal profile is reproduced only when the PS + P_i release is not rate-limiting under low force. This finding further establishes the key role of the landscape in controlling the efficiency and force-dependent action of myosin motors. Considering the role of myosins, and specifically myosin-V, a landscape that is not too heavily dependent on the force is beneficial. In biological terms, when myosin-V is pulling different loads, it might experience a fairly large range of forces at time, and from a regulation point of view, having stable velocity, which probably affects the processibility as well, is better.

Our LD simulations indicated that the difference between the backward and forward barriers can be smaller than predicted in our previous work (26), although still allowing for the observed hand-over-hand dynamics, substep features, stall force, and dynamical behavior under force. To explore this issue more fully, we need to have more details about the landscape for the backward motion. In this respect, we note an interesting point that has not been resolved fully in the present work, that is, the nature of the barrier in the backward motion. As indicated in Fig. S2, the height of the backward barrier can depend on the point where the lever arm changes from a lever-up to lever-down conformation, leading to an increase in energy. If the lever-up to lever-down conformation occurs late and in concert with the P_i release, we may obtain the blue line in Fig. S2. In this case, it is likely that the combined PS + P_i release barrier of the backward-walking leg will not be so high, and it is also possible that the backward motion is controlled by the asymmetry in the ADP release barriers in the lever-up and lever-down states. On this subject, it is interesting to note that although ADP release rates have been proposed to be strain-dependent (32, 34), we hypothesize that the difference in ADP release rates for the prestate and poststate is a result of the conformational changes imposed in and around the binding sites of TL or LL, and might not be directly coupled to the applied force. Rather, the applied force in the opposite direction on the LL can act to populate the prestate more than the poststate, and thus might affect the ADP release rates differently in the LL compared with the TL. In any case, exploring the actual origin of the backward barrier would require more careful and explicit simulation studies involving structural considerations of the motor. It will also be exciting to find experimental ways to explore this issue. Whatever may be the origin of the high back barrier, our study highlights that a relative barrier difference (between forward and backward paths) can produce the observed directional motion and the stall force. Additionally, the high-energy–releasing PS is completely consistent with the myosin dynamics and its coupling to the P_i release step further allows control of its force-dependent characteristics by altering the ligand release kinetics in different subfamilies of myosin. Overall, we believe that the present work should further emphasize the crucial need of having a clear idea of the complete mechanochemical free-energy landscape when exploring the action of molecular machines.

Methods

This work uses the CG landscape of the study by Mukherjee and Warshel (26) and explores the corresponding dynamics by LD simulations that are described in the main text and Supporting Information. The nature of the long time behavior of the system was explored by an MC approach that is also described in the main text, Supporting Information, and Figs. S6B and S7.

Fig. S7.

Exemplary potential from the MC simulations. The potential is shown in red, edge truncation is shown in cyan, and the plateau to prevent tunneling is shown in blue.

SI Background

Due to page limitations, we provide here some important information about the systems studied. The myosin superfamily comprises several members of the nonprocessive and processive molecular motors that use a centrally conserved mechanochemical cycle to ensure force generation and directional motion on actin filaments. The central mechanochemical cycle is a result of intricately coupled ATP hydrolysis, actin binding/release, and conformational changes occurring in the neck linker of the myosin molecule. The neck linker conformational changes produce two key conformational states of the myosin, namely, the lever-up and lever-down states, which are illustrated in Fig. S1. The conformational change from the lever-up to the lever-down state, while the myosin leg is bound to the actin filament, is known as the PS and is thought to be the most important element in force generation or directional movement in myosin motors. The exact nature of the coupling between the chemical, binding/release, and conformational steps in myosin decides the force-generating and load-bearing characteristics of different members of this family. For example, nonprocessive myosin-II shows slightly different kinetics of the product release steps, and these different kinetics result in a low-duty ratio (the time that the molecule remains bound to actin within a complete cycle) compared with the high-duty ratio of processive myosin-V. The high-duty ratio in myosin-V results in one of its legs being bound to the actin for most of the cycle time, while the other leg undergoes the stepping motion. Extensive research on the dynamics of myosin-V in the past few decades has revealed that it moves toward the plus end of the actin filament using a hand-over-hand mechanism, where one of the myosin-V legs releases the actin upon ATP binding and diffuses to the next actin-binding site, while the other leg remains strongly bound to the actin until ADP is released from its nucleotide-binding pocket. The high-duty ratio also allows the motor to take multiple consecutive steps of 36 nm over the actin filament by performing the coupled chemical and conformational alternations in its legs with a well-maintained time lag between the events occurring in each of the legs. Furthermore, the motor with a stalling force (the force applied in the opposite direction that stops the forward motion) of around 1–3 pN can work as a load bearer and an intracellular transporter for the cell by performing unidirectional motion against resistive loads lower than the stall force.

In our previous work on myosin-V (26), we have calculated the free-energy change of the lever-up to lever-down conformational change and observed that the traditionally accepted PS is an energy-demanding process just by itself. We then coupled the conformational free energies to the ATP binding, hydrolysis, product release (P_i and ADP), and actin-binding/release kinetics obtained from the experimentally observed rates of the corresponding process. This coupling provided the quantitative free-energy landscape of a single walking step of myosin-V moving in the plus-end direction (26) (Fig. 1). A similar landscape was also constructed for the back step of the myosin motor (26) (Fig. S2). Comparison of the plus- ended (forward) and negative-ended (backward) free-energy landscapes provided the basis for unidirectionality in myosin-V. We observed especially that the correct coupling of the energy-demanding PS with the appropriate chemical steps can provide a forward pathway that has a lower effective barrier when compared with the backward pathway. We should mention that a few of the barriers in Fig. 1 and Fig. S2 are set more intuitively, whereas most of the other energies are based on experimentally observed kinetics and structure-based theoretical calculations. For example, the assumed barrier for steps highlighting the diffusive motion of the unbound leg toward its next actin-binding site (V→VI in Fig. 1 and (V′→VI′ in Fig. S2) is set to a very low value (not specifically mentioned) in the figure to describe the diffusive event. The energy barrier for the lever-up to lever-down change (PS), and vice versa (RS), is obtained from the free-energy calculations using the CG model. The intermediate conformers were generated using a linear extrapolation scheme, which most likely does not represent the least free-energy path traversed by myosin-V while going from the lever-up to lever-down state. Hence, we emphasize that the free-energy difference of the up and down conformers is much more reliable because it is obtained from calculations using crystal structures with good resolution, whereas the energy barrier of the path is not optimal. The barrier has been scaled down to a value that is just below the rate-limiting ADP release barrier (figure 2 of ref. 26). In our Fig. 1, we have also represented the PS and P_i release barriers as a single event [step VI→(VIII) in Fig. 1] that relates to the experimentally observed rate for the combined PS + P_i step. Finally, we would like to emphasize that the origin of the difference between the effective barrier of the forward and backward paths (noted as ε and ε*, respectively, in the main text and figures) is not completely known at this point. In this work, we have highlighted two major contributors to Δε. The first contribution could arise due to the PS being tightly coupled to the P_i release step in the forward path (green path of Fig. 1), although it is completely decoupled or partially coupled to any energy-releasing step in the backward path (closer to the red path in Fig. S2). Here, we note that a blue path (Fig. S2) could also emerge for the case where ATP hydrolysis and P_i release occur concurrent to the energy-demanding PS in the back step. This scenario would necessarily lead to a negligible Δε solely arising due to the energetic asymmetry of the conformational changes. However, a second contribution arising from the asymmetrical ADP release rates (larger ADP release barrier in the actin-bound up state compared with the relatively load-free down state), which has been observed experimentally, would still allow a sizeable Δε between the forward and backward paths, leading to processive plus ended motion. Although the main text explores the directionality, the focus of this work is on examining the role of a high-energy–demanding PS toward the relation of Δε on stall force and the relation of the detailed free-energy landscape on the force/velocity profile. In this respect, our findings questioned the abundantly held idea that the PS must release the necessary free energy needed for the directionality and resistivity of the motor against force. Instead, they indicated that the PS is the result of the energy landscape of the system that arises due to correct coupling between the ligand release kinetics and conformational transitions.

The concept of Δε arising due to different effective barriers along the forward and backward paths is further explained through the 2D free-energy landscape shown in Fig. 2. This landscape shows the motion of myosin-V along the horizontal axis and the chemical steps along the vertical axis. This effective 2D free-energy surface has been generated using a multiminima empirical valence bond (EVB)-type approach, where the Hamiltonian of the system is defined using multiple diabatic states. Each diabatic states describe the system in any one of the chemical states (no nucleotide or empty, ATP-bound, ADP- and P_i-bound, or ADP-bound) and positional states (each state describes a movement of 6 nm along the actin filament). The diagonalization of the Hamiltonian composed of these diabatic chemical/positional states gives rise to the effective 2D free-energy surface of Fig. 2. The state energies and barriers have been fitted to provide forward and backward paths resembling the green path in Fig. 1 and the red path in Fig. S2. All other off-path state energies are set higher than the highest barrier along the forward and backward paths. The mathematical approach to derive such a multiminima EVB-type surface has been described in detail in many of our previous works (29, 41, 42).

SI Methods

LD Modeling.

We have modeled myosin-V using beads connected through springs to describe the two legs and the joint particle connecting them. Each leg was modeled using eight spherical particles (two represent the head and the convertor regions, and six more represent the long lever arm), which resulted in a total of 17 particles for the whole myosin-V motor (two legs and one joint particle).

The potential energy of the motor is described as

$$E_{myo}^{tot}={\displaystyle \sum _{i,j}{E}_{bonds}}+{\displaystyle \sum _{i,j,k}{E}_{angle}}+{\displaystyle \sum _{i,j,k}{E}_{joint}}+{\displaystyle \sum _{i,j}{E}_{nb}}+E_A+E_{ATP}+E_P+E_{PS},$$ [S1]

where the sum corresponds to the interparticle bond/angle energies (E_bond and E_angle) and the angular constraint around the fork region (E_joint), the short-range repulsion between nonbonded beads (E_nb), and the chemical and conformational energies (E_A, E_ATP, E_P, and E_PS). Here, the stiffness of the myosin legs is modeled using high interparticle bond and angle constraints, whereas the angular constraint of the joint between the two legs is very labile, and thus can show unabated rotational/torsional motions. We find that without stiffening of the legs and by allowing free rotational movement along the joint, myosin-V is not capable of showing directional motion and falls off from the actin filament frequently. A description of the chemical and conformational energy terms is provided in detail below, and the parameters used for the LD simulations are given in Table S1. Note that the parameters are derived intuitively based on the free-energy landscapes of Fig. 1 and Fig. S2. To observe myosin stepping motions within a reasonable computational time, the exact free-energy barriers of Fig. 1 and Fig. S2 are not used; instead, a drastically scaled-down effective barrier is used for the simulations. Also, a very small friction coefficient has been used to speed up the motion of myosin-V. It is useful to note that the focus of the LD simulation is to explore the role of different Δε values on the stall force and overall myosin-V dynamics using a 3D model, whereas the MC simulation examines the role of a detailed chemical/conformational landscape on the nature of the force/velocity profile.

An illustration of the energy surfaces used to model the movement of myosin-V through one forward step is shown in Fig. S3A, where the TL starts from the actin site $x_{A,1}$ and rebinds to the site $x_{A,3}$ that is 72 nm away from the starting position in the plus-ended direction. At the beginning of its journey, the TL feels the $E_A^f$ and $E_{ATP}^f$ potentials applying on $x_{A,1}$. On the other hand, the LL experiences the $E_A^f$ and $E_P^f$ potentials at the site $x_{A,2}$, and it additionally starts to feel the $E_{PS}^f$ potential once it is committed to undergo the PS transition. The cycle ends when the TL experiences the $E_A^f$ and $E_P^f$ potentials at the site $x_{A,3}$ and binds strongly to it after which its status changes from TL to the new LL. Concurrently, the previously called LL finishes its PS and is poised to start a new cycle as the new TL.

A similar illustration of the energy surfaces for the backward step is shown in Fig. S3B, where the TL starts from the actin site $x_{A,3}$ and rebinds to the site $x_{A,1}$ that is 72 nm away from the starting position in the minus-ended direction. The TL initially feels the $E_A^b$ and $E_{ATP}^b$ potentials applying on $x_{A,3}$, but it also experiences the $E_{PS}^b$ potential soon after, and this added potential raises the overall barrier of the backward path. The cycle ends when the TL experiences the $E_A^b$ and $E_P^b$ potentials at the site $x_{A,1}$ and binds strongly to it after which its status changes from TL to the new LL. Concurrently, the previously called LL undergoes a barrierless RS transition and is poised to start a new cycle as the new TL.

Using the potential of Eq. S1 and changing the status of the legs (TL→LL and LL→TL), depending on whether a specific leg has undergone the necessary transitions, we have performed LD simulations for the forward and backward cycles in an unloaded condition [applied force (F) = 0)] and with constant loads (F = 0.1–1.0 pN) applied on the joint particle in the direction opposite to the plus-ended motion. These simulations were run for a much reduced overall barrier, ε = 3 kcal/mol and ε* = 6–9 kcal/mol, to obtain a large enough number of steps within reasonable available computer resources. These simulations allow us to observe the dynamical nature of the myosin-V movement, and also provide an opportunity to explore the role of the path barrier in deciding the major features of the motor. We compare simulations with Δε ranging from 3 to 6 kcal/mol and extrapolated the behavior of the motor for the actual higher barrier difference of around 8–11 kcal/mol reported in our previous work (26).

The different terms in Eq. S1 are described below.

The actin-binding potential energy ($E_A$) is represented by

$$E_A={\displaystyle \sum _i-A_a{e}^{-{\left(x-x_{A,i}\right)}^2/W_a}},$$ [S2]

where the inverse Gaussians are centered on the actin-binding sites $x_{A,i}$ and are felt by the head particle of the TL and LL only (the first particle of each leg), whereas other particles move under the influence of the bond and angle constraints described in Eq. S1.

The ADP release and ATP-binding potential ($E_{ATP}$) for the leg that has weakly bound ADP are represented by

$$E_{ATP}=A_{ATP}{e}^{-{(x-x_{A,i})}^2/W_{ATP}}.$$ [S3]

This potential is felt by the head particle of the TL bound to site $x_{A,i}$, which represents the weak ADP-bound leg (or the lever arm in the down or post-PS state). As ADP is released and ATP binds quickly, the TL releases the actin. The LL that is bound strongly to $x_{A,i+1}$ does not experience this potential of fast ADP release and ATP-binding potential.

The parameters A_a and A_ATP in Eqs. S2 and S3 represent the strength of actin binding and ATP binding, respectively. Because these two potentials apply together on the head particle of the TL, the values (especially A_a) have been chosen to generate an overall ATP-induced actin release barrier of 2 kcal/mol. The parameters W_a and W_ATP denote the width of the Gaussian functions and are kept small to describe the local nature of ATP and actin binding.

For the strong ADP-bound leg (or the lever arm in the up or pre-PS state), the P_i release and ADP release potential $E_P$ are represented by

$$E_P=-A_P{e}^{-{(x-x_{A,i+1})}^2/W_P}-A_P{e}^{-{(x-x_{A,i+2})}^2/W_P}.$$ [S4]

This potential is applied to the head of the LL centered on the actin-binding site $x_{A,i+1}$. The high barrier on the right side of this potential represents the high ADP release barrier of the strongly bound LL. This potential keeps the LL bound to $x_{A,i+1}$ until the TL binds the new actin position. A similar type of potential is also felt by the head particle of the TL only after it is centered on the new actin-binding site $x_{A,i+2}$, after diffusing in the forward or backward direction (whichever direction is being modeled). The free-energy drop of the left wall of this potential represents the downhill P_i release energy, whereas the uphill right wall represents the high ADP release barrier faced by the leg after P_i release. Once the TL is at the bottom of this potential, it is relabeled as the new LL. Similarly, the old LL is relabeled as the new TL and starts to feel the potential, $E_{ATP}$. This change represents the change from the strong ADP-bound state to the weak ADP-bound state. Note that to increase sampling and obtain data on a larger number of steps within a reasonable simulation time, we have assumed this change to be almost instantaneous. In reality, however, myosin-V spends a considerable time with both of its legs bound to ADP and to actin.

Here, the free energy of P_i release is denoted by the parameter A_P, whereas W_P denotes the width of the Gaussian. The width W_P also reflects the start of the P_i release potential energy minima, and hence is important to capture the diffusing TL toward the new actin-binding site. W_P is larger than W_A or W_ATP because it also reflects the coupled nature of P_i release with the long-range mechanical motion of the PS.

$E_{PS}^f$ is the energy-demanding conformational change of the PS during the plus-ended motion (forward), and it is given by

$$E_{PS}^f=A_{PS}^f{e}^{-{(x-\left(x_{A,i+1}+x_f\right))}^2/W_{PS}^f},$$ [S5]

where the term is modeled in the 3D Cartesian space by assuming a Gaussian potential that applies on the tip of the leg (joint particle) when the LL tries to change its position from the lever-up to lever-down state (up or pre-PS to down or post-PS state), while its head is still centered on the actin-binding site $x_{A,i+1}$ and is under the strong ADP-binding potential, as described in Eq. S4.

Here, the free-energy cost of the PS is denoted by the parameter $A_{PS}^f$, whereas $W_{PS}^f$ denotes the width of the Gaussian. The width $A_{PS}^f$ is the same as W_P to simulate the coupled nature of P_i release with the long-range mechanical motion of the PS. To simulate the myosin-V walking motion within reasonable computer resources, the value of $A_{PS}^f$ is kept small (around 1.5 kcal) so that the overall effective barrier along the forward path is small.

Similarly, $E_{PS}^b$ is the energy-demanding conformational change of the PS during the minus-ended motion (backward), and it is given by

$$E_{PS}^b={\displaystyle \sum }_{n=\mathrm{1,3}}{A}_{PS}^b{e}^{-{(x-\left(x_{A,i}-x_{b,n}\right))}^2/W_{PS}^b}.$$ [S6]

This term is modeled in the 3D Cartesian space by assuming the Gaussian potential that applies on the head of the TL when it tries to change its position from the lever-up to lever-down position after it has undergone ATP binding and actin release from $x_{A,i}$.

Here, the free-energy cost of the PS in the back pathway is denoted by the parameter $A_{PS}^b$, whereas $W_{PS}^b$ denotes the width of the Gaussians. Note that multiple Gaussians have been used to model the free-energy cost of the PS unsupported by P_i release (unlike the forward pathway, where the PS and P_i occur in a coupled way). Although, it is not certain at which point along the pathway the PS free-energy cost is finally supported by P_i release, our simulations have maintained high back barriers until halfway through the complete 72-nm path. Simulations with different ε* values have been conducted by changing the parameter $A_{PS}^b$, as noted in Table S1. Comparison of simulations with different ε* values with that of the forward simulations with a single ε value allows us to calculate the P_b/P_f and derive the stall force for different Δε values.

The parameter values used to define the potentials from Eqs. S1–S6 is given in Table S1.

MC Simulation Details.

In the 1D MC simulations, each simulation was run for 1 million steps and each data point represents the average of at least 20 independent runs. In the 3D MC simulations, each simulation was run for at least 100 million steps and each data point represents the average of 32 independent runs. All error bars represent the SD of the mean.

The Energy Landscape for the 3D MC Model.

The MC system is composed of three myosin particles (two heads and one joint), two ADP particles per head (total of four ADP particles), one P_i particle per ADP (total of four P_i particles), and two effective angle “particles” (discussed below). In each MC step, one particle is selected at random and is translated in a random direction by 0–1 nm (randomly as well). This translation is accepted or rejected based on the Metropolis acceptance criteria (43). In the simulations, we determine whether different elements are bound or not bound based on cutoffs [median point (r_M) below] and the energy landscape changes according to the binding state of the entire system (i.e., actin–myosin interactions, nucleotide–myosin interactions, and ADP/ATP state). Certain constraints are introduced to make the system run faster:

• i)The myosin joint particle is restrained to z-values above a set threshold. This limitation emulates the constraint deriving from the position of the cargo vesicle with respect to the actin filament.
• ii)We automatically move the ADP and P_i particles when the MC step selects their associated head particle, and we automatically move the P_i particle when the MC step selects its associated ADP particle. This treatment does not affect the energy landscape because the so-called “child” particle only affects the energy by its relative position with respect to the so-called “parent” particle. The reason for this treatment is to avoid lagging of the system, where the parent particle is being dragged (in energetic terms), waiting for its child particle to be randomly selected and moved in the same direction. In other words, this treatment is done to save a lot of futile MC steps wherein one particle is being moved back and forth constantly until by chance, its associated particle is also moved in the same direction (which is energetically favorable anyway).
• iii)When ADP or P_i particles are selected to move, their movement step is only 0–0.1 nm. The reason is that although the myosin motor is required to move fairly great distances, a large step is not necessary for the nucleotide components.
• iv)We do not allow the ADP particles or the P_i particles to move further than 5 nm away from the myosin head particles or the ADP particles, respectively. This limitation prevents particles from escaping the system completely and emulates the concentration of the entities.
• v)The lever-up and lever-down angles are calculated with respect to the actin filament (discussed more below).
• vi)A repulsive term was introduced between the two nucleotide particles that are associated with one myosin head to prevent double binding. Then, to emulate the constant concentration of ATP and ADP during the process time of myosin-V, whenever a myosin head does not bind a nucleotide (i.e., both nucleotide particles associated with it are in the unbound state), the two particles are always exactly one ATP particle and one ADP particle. The program maintains these values by moving one P_i particle, if needed, regardless of the acceptance criteria. This treatment is important to replenish ATP that is hydrolyzed during the simulation.
• vii)ADP release was not allowed when the lever angle is at an intermediate angle. This limitation was done to prevent premature release of the nucleotide, which often resulted in complete detachment of the myosin.

Another important aspect of generating the MC potential is the incorporation of entropic effects by a specialized energy normalization; that is, to account for entropic contributions and to move from potential energy to free energy, we conducted long MC simulations focusing on one structural parameter at a time (e.g., distance between two particles). For each parameter, we used the distribution obtained throughout the MC simulation to get free-energy profiles. The effective potential was then modified until the free-energy profiles agreed reasonably with Fig. 1. The full energy surface is shown in Fig. S4 and a comparison of the free energy and the potential is provided in Fig. S5.

The energy landscape used in the MC model is based on Fig. 1, except that we compute the ATP binding as a single step. Because the MC model uses a simplified system composed of point particles for the myosin motor, the angle between the ATP-binding domain and the arm could not be represented explicitly. Instead, we compute the angle between the myosin arm and the actin filament, and use this angle to determine whether the angle is lever-up or lever-down.

To account for the angle when the myosin particle is unbound, we use an indirect implicit treatment as follows: The angle is stored as an effective angle parameter λ (one for each head), and the MC movement and potential are applied to λ. To ensure that the geometric angle (θ) follows the correct energy curve, we apply a harmonic constraint that is distance-dependent, such that λ ≈ θ when the myosin is bound. This procedure allows the MC simulation to treat the angle of bound particles accurately, and allows the unbound myosin particle to switch between lever-up and lever-down states based on the free-energy profile. This treatment was tested over long simulations and using various potentials, and it produced no bias and allowed prefect coupling as explained above. The importance of this treatment is to allow the unbound myosin particle to move freely and not be constrained by a geometric angle that has no physical meaning.

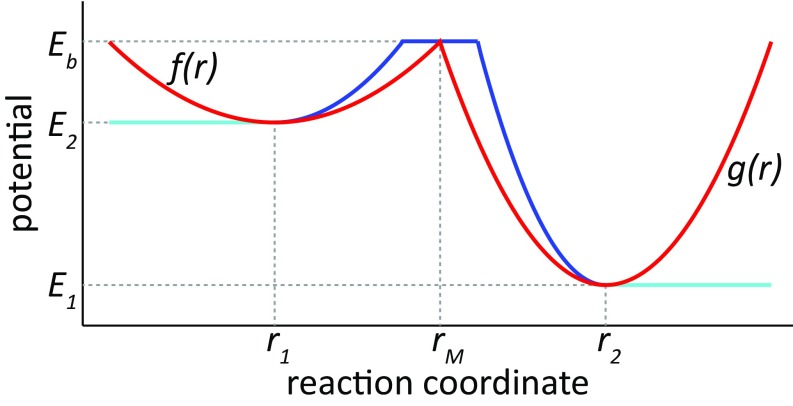
In building the potential, we used modified Marcus parabolas as is done in the two states of EVB treatment (44). In brief, the potential connecting two energy states, E₁ and E₂, via a barrier E_b, is composed of two parabolas, f(r) and g(r), with minima at E₁ and E₂, respectively, whose intersect point is at the median point (r_M) along the reaction coordinate (typically distances r₁ and r₂) such that f(r_M) = g(r_M) = E_b. Then, the energy is given by

$$E=(f+g-\sqrt{{(f-g)}^2})/2.$$ [S7]

We did not include the mixing term H₁₂, because the energy is never derived in the MC model, and H₁₂ is therefore not mandatory. Lastly, we used up to two types of truncations in this function:

• i)In many profiles, the energy outside the range [r₁:r₂] should be flat, so we used f(r₁) and g(r₂), respectively, instead of computing E.
• ii)By using a translation step of up to 1 nm in the MC step, it would have been possible for the system to undergo tunneling under the tip of the peak in the above E profile. To prevent this tunneling, we added to the profile a 1-nm-long plateau, with a range of [r_M − 0.5:r_M + 0.5], with an energy of E_b. A representative potential is given in Fig. S7. The same r_M is also used as the cutoff point to define bound/unbound states.

With the above landscape, we performed time-dependent MC simulations with the following strategy: The Cartesian coordinates of the system were changed in a uniform way, where we used steps of up to 1 nm. The conversion of the MC steps to time steps was done in a rather qualitative way by assuming that each MC step corresponds to 0.1 fs. This calibration is based on running MC simulations for regions with a set free-energy barrier and comparing the number of MC steps needed to overcome this barrier with the time predicted from transition state theory. It also reflects the fact that the MC movement of each particle is allowed only once in N movements where N is the number of independent coordinates (the x, y, and z positions of each bead are changed at the same step). This treatment is not fully justified for the motion in the diffusion region of the PS, and would require a more careful comparison with the corresponding LD results.