Strong signal increase in STED fluorescence microscopy by imaging regions of subdiffraction extent

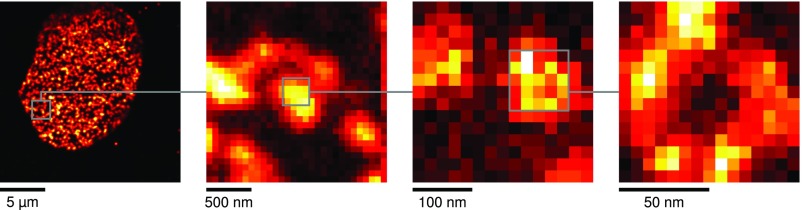
Significance

In stimulated emission depletion (STED) fluorescence microscopy, the diffraction resolution barrier is overcome by applying a doughnut-shaped light beam that transiently switches fluorescence off, confining molecular emission to subdiffraction-sized regions around the doughnut center. Unfortunately, the doughnut intensities required for high resolution exacerbate photobleaching. Our remedy, called MINFIELD, exploits the fact that fluorescence off-switching by STED does not require the high intensities of the doughnut crest. By recording subdiffraction-sized areas or volumes in the sample, molecular exposure to high intensities is avoided and photobleaching is reduced by more than 100-fold. Fluorescence analysis of cellular structures becomes possible in unprecedented detail. Providing larger signal and faster recording times, MINFIELD-STED microscopy should open a unique range of superresolution imaging applications in the life sciences.

Abstract

Photobleaching remains a limiting factor in superresolution fluorescence microscopy. This is particularly true for stimulated emission depletion (STED) and reversible saturable/switchable optical fluorescence transitions (RESOLFT) microscopy, where adjacent fluorescent molecules are distinguished by sequentially turning them off (or on) using a pattern of light formed as a doughnut or a standing wave. In sample regions where the pattern intensity reaches or exceeds a certain threshold, the molecules are essentially off (or on), whereas in areas where the intensity is lower, that is, around the intensity minima, the molecules remain in the initial state. Unfortunately, the creation of on/off state differences on subdiffraction scales requires the maxima of the intensity pattern to exceed the threshold intensity by a large factor that scales with the resolution. Hence, when recording an image by scanning the pattern across the sample, each molecule in the sample is repeatedly exposed to the maxima, which exacerbates bleaching. Here, we introduce MINFIELD, a strategy for fundamentally reducing bleaching in STED/RESOLFT nanoscopy through restricting the scanning to subdiffraction-sized regions. By safeguarding the molecules from the intensity of the maxima and exposing them only to the lower intensities (around the minima) needed for the off-switching (on-switching), MINFIELD largely avoids detrimental transitions to higher molecular states. A bleaching reduction by up to 100-fold is demonstrated. Recording nanobody-labeled nuclear pore complexes in Xenopus laevis cells showed that MINFIELD-STED microscopy resolved details separated by <25 nm where conventional scanning failed to acquire sufficient signal.

Fluorescence nanoscopy or superresolution microscopy methods (1, 2) allow minimally invasive imaging with a resolution far beyond that of ordinary light microscopes. Recent advances open the possibility to resolve details at 20–50 nm and below (see examples in refs. 3–7). In stimulated emission depletion (STED) nanoscopy (8, 9)—as in all other fluorescence microscopy methods—the achievable resolution and contrast are largely determined by the total fluorescence signal, which is in turn limited by photobleaching. As a matter of fact, all superresolution concepts providing resolution at the 20- to 50-nm level are restricted to using specific fluorophores or buffers due to the signal limitation. Approaches previously developed to reduce photobleaching have therefore led to significant advances. Specifically, in STED nanoscopy, using long (>100-ps) laser pulses (10), reducing numbers of unnecessary state transition cycles (11), and allowing the relaxation of bleaching-prone dark fluorophore states (12) have already reduced photobleaching severalfold.

In STED microscopy (Fig. 1), resolution is increased by confining the capability of a fluorophore to emit fluorescence to a predefined subdiffraction-sized region. This is accomplished with the STED light, which forces excited fluorophores into their ground state through stimulated emission before fluorescence emission. Thus, the presence of STED light of a given intensity switches the fluorescence capability of the fluorophore off (Fig. 1A). To use this effect in a point-scanning microscope for superresolution, the focal-plane intensity distribution of a beam of STED light is typically formed to exhibit a central intensity zero (“doughnut”), switching off all fluorophores outside the vicinity of the focal center (Fig. 1 B and C). Both beams are jointly scanned through the specimen to successively probe neighboring subdiffraction sample regions where fluorophores may reside. We choose here to define the STED beam intensity $I_S$ as the intensity at which the probability of deexciting a fluorophore by stimulated emission is $p_{\mathrm{stim}}=0.5$. If the fluorophore is exposed to the intensity $I_S$, its fluorescence is reduced to 50% of its normal value (Fig. 1A).

Fig. 1.

The MINFIELD concept: Lower local deexcitation intensities in STED nanoscopy for image sizes below the diffraction limit. (A) In STED imaging with pulsed lasers, the ability of a fluorophore to emit fluorescence decreases nearly exponentially with the intensity of the beam deexciting the fluorophore by stimulated emission. We here define $I_s$ as the intensity at which the fluorescence signal is reduced by 50%. Fluorophores delivering higher signal are defined as on, whereas those with smaller signal are defined as off. (B) The STED beam is shaped to exhibit a central intensity zero in the focal region (i.e., a doughnut), so that (C) molecules can show fluorescence only if they are located in a small area in the doughnut center. This area decreases with increasing total doughnut intensity. Due to its diffraction-limited nature, the intensity distribution of the STED focal beam extends over more than half of the STED beam wavelength and exhibits strong intensity maxima, significantly contributing to bleaching. By reducing the size of the image field to an area below the diffraction limit, where the STED beam intensity is more moderate (i.e., around the doughnut minimum; compare image area indicated in B), one can reduce the irradiation intensities in the area of interest, inducing lower photobleaching and allowing the acquisition of more fluorescence signal at higher resolution. (Scale bar: 200 nm.)

We can now define $I_S$ as the threshold intensity that separates fluorophores that are “on” from those that are “off.” In other words, if the fluorescence signal of a fluorophore is 50–100% of its normal signal, we define it as on; if it is <50%, we define it as off. Clearly, this definition is somewhat arbitrary, because we could also have chosen 6$I_S$ as the threshold intensity, in which case off would have implied a signal reduction to only 1.56%. However, choosing $I_S$ has the advantage that it directly relates to the full width at half-maximum (FWHM) of the subdiffraction-sized region of fluorescence emission created by the doughnut-shaped STED beam, which is usually taken as a resolution measure. It is now important to realize that, although the fluorophores are off also for STED beam intensities that are higher than $I_S$, such higher intensities are actually not needed for keeping the fluorophore off, because the on/off difference is already created at $I_S$ (Fig. 1).

However, intensities much greater than $I_S$ are applied in STED microscopy because tightly confining the region of possible fluorescence emission inevitably necessitates maxima (doughnut “crests”) that are orders of magnitude stronger than what is required to switch the fluorophores off (Fig. 1C). Actually, these excess intensities only pay tribute to the fact that the doughnut profile is dictated by diffraction. Present over an area of several 100 nm in diameter, with maxima ∼250 nm from the doughnut center, they do not define the on/off state contrast. However, they are the major cause for photobleaching at the periphery of the excitation spot.

The issue of these excess STED beam intensities has been recently addressed by driving fluorophores to an additional light-inert “protected” state in a concept termed “multiple off-state transitions” (MOST) nanoscopy (13). The rationale of MOST is that the process of fluorophore separation and hence resolution enhancement occurs in the immediate vicinity of the minimum (zero) of the state-separating switching light distribution. This long-standing insight (14), that information about the fluorophore(s) residing at the coordinate of the intensity minimum can be obtained right at the minimum by defining this coordinate with many photons, is also at the heart of the recently presented MINFLUX concept (15), enabling tracking and nanoscopy of fluorophores with minimal fluorescence fluxes.

Here, we demonstrate an approach leading to an improvement in total available fluorescence signal by two orders of magnitude on features <100 nm in size, by confining the imaged region almost to the spatial dimensions of the subdiffraction feature itself. Our approach maximizes the fluorescence signal attainable from the structure of interest, and enables imaging at higher resolution with higher signal-to-noise ratio (SNR). By reducing the image size (i.e., the field of view), the irradiation dose on the region of interest can be significantly reduced, as the strong light fields of the STED beam maxima (doughnut crests) are not scanned over the object to be imaged (Fig. 1 B and C). We have dubbed our approach MINFIELD because of two reasons. First, it reminds of the fact that our field of view is minimized to capture only the structure of interest and, second, it alludes to the fact that the molecules are exposed to those parts of the STED beam having minimal light fields. Depending on the image size and applied laser power, MINFIELD thus yields a strong reduction of photobleaching within the imaged region.

Results

Fast Addressing and Recording of Scanning Fields Below the Diffraction Limit.

The nanoscopy setup (SI Materials and Methods, Fig. S1, and Table S1) developed for our demonstration of the MINFIELD approach roughly followed the design considerations for red and far-red emitting dyes as reported previously (7). It used a 775-nm, 20-MHz pulsed STED laser, pulsed laser diodes at 595 and 635 nm for fluorescence excitation, and detection windows at 600–630 and 660–720 nm. However, scanning small areas poses additional challenges to the scanning system. Scaling down the typical scan parameters of a regular STED recording (10-nm pixel size, 100-µs pixel dwell time) to a total scan area of 100 × 100 nm² leads to a line frequency on the order of 1 kHz. As the whole imaged area is illuminated during the sequential acquisition of the pixels, photobleaching for subsequent positions increases. This can be avoided by repeatedly scanning the image at a timescale much shorter than the average fluorophore’s survival time and summing the signal of consecutive image frames to acquire sufficient signal. The linearity of the scan process should be maintained despite the high imaging speed.

Fig. S1.

Optical setup. The specifications of the lenses and filters used are given in Table S1.

Table S1.

List of filters and lenses

Identifier	Type	Description
L1	Achromat	f = 60 mm
L2	Achromat	f = 25 mm
L3	Achromat	f = 250 mm
L4, L5	Achromat	f = 200 mm
TL1	Achromat	f = 180 mm
TL1′	Achromat	f = 50 mm
TL2, TL2′	Achromat	f = 200 mm
TL3	Achromat	f = 100 mm
TL3′	Achromat	f = 400 mm
CL1, CL2′	Cylinder lens	f = −400 mm
CL2, CL3′	Cylinder lens	f = 500 mm
DM1	Dichroic mirror	Z650 SPRDC
DM2	Dichroic mirror	Z770 RDC
F1, F2	Bandpass filter	685/80 ET
F3	Bandpass filter	615/20 nm Brightline
Notch filter		633 nm StopLine
Objective		PL APO 100×, NA 1.4–0.7 oil

DM1, DM2, F1, and F2 are manufactured by Chroma Technology. F3 and notch filter manufactured by Semrock. Objective is by Leica Microsystems.

The focus positioning accuracy and repeatability of the beams must be better than 10 nm to allow nanometer-scale imaging. The accurate placement of the excitation and STED light foci at the desired scan position is especially challenging, because mechanical scanners can have a certain lag between the set and actual position due to their momentum. This lag may vary with the scan speed and scan position, and is typically several 100 nm. Approaching a target with an accuracy <50 nm, however, is crucial for the usability of the setup. These requirements are best satisfied by electro-optic scanners. They use the linear electro-optic effect to deflect the beam almost instantaneously when a voltage is applied, albeit by small angles. The scan range is therefore limited to a few micrometers. We used two electro-optic scanners for deflection in x and y, allowing line frequencies above 100 kHz and reducing the positioning error to a negligible amount. To acquire larger overview images, a piezo stage with a scan range of 200 µm was used for scanning and positioning the sample in x, y, and z. Further details of the implementation can be found in SI Materials and Methods.

To select areas of interest for a STED scan, a large low-resolution image was first acquired with the piezo stage. The desired scan positions were then selected and approached with the piezo stage. A high degree of automation proved essential for productive imaging, as several imaging steps are required to reliably correct for sample drift or inaccurate positioning by the piezo stage. If required, several imaging iterations of decreasing size and increasing STED power could be combined to image the detailed structure on a small scale without losing the context on the large scale (Fig. S2). Dedicated imaging acquisition routines were programmed with Python. As a future development, this iterative scanning with adaptive levels of STED resolution could be beneficially coupled with feature recognition and even machine-learning schemes that automate the selection of (biological) features of interest. Large datasets for hypothesis testing could thus be acquired with minimal input from the user.

Fig. S2.

Iterative reduction of image size. To target the desired structure with a small scan, it is often helpful to increase the imaging resolution iteratively while reducing the image size. From Left to Right: Confocal overview scan (piezo driven) of a nucleus; confocal scan (electro-optic scanners) for drift correction; low-resolution STED scan (electro-optic scanners, 300 × 300-nm scan size) to identify individual NPCs; high-resolution STED image (electro-optic scanners, 100 × 100-nm scan size) reveals the substructure of a single NPC.

MINFIELD Imaging: Small Scan Fields Yield Major Signal Increases.

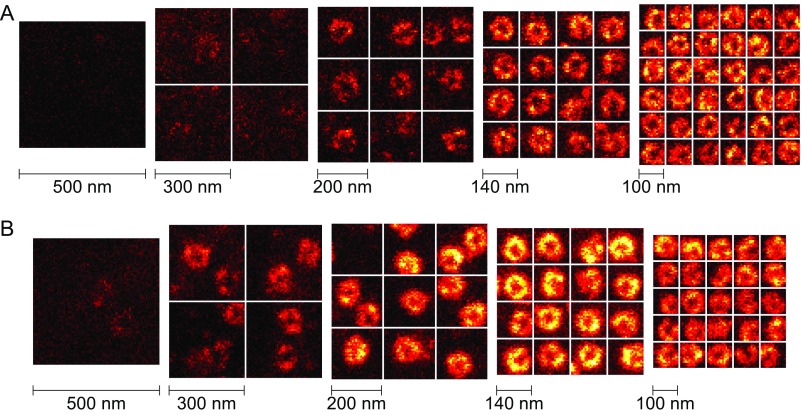
Fig. 2 demonstrates the potential of the altered scanning strategy on two-color STED images of immunolabeled nuclear pore complexes (NPCs). Although it is possible to image the whole nucleus in a single large scan, high laser intensities cause photobleaching; the same structures could not be imaged repeatedly (Fig. 2A and Fig. S3). In contrast, when the scan range was reduced to an area of 200 × 200 nm², more than 10 frames with sufficient signal were acquired (Fig. 2B), using otherwise unchanged imaging parameters (168-mW STED power, 100-µs pixel dwell time, 6.6-nm pixel size). It is thus possible to acquire an order of magnitude more signal from the structure than in a regular scan, opening up the way to image more complex samples with higher demand on resolution and SNR.

Fig. 2.

Fluorescence signal increases when limiting the image field of STED nanoscopy to subdiffraction dimensions. The MINFIELD bleaching reduction is exemplified on amphibian nuclear pore complexes (NPCs) labeled with an anti-gp210 (red) and an anti-FG repeat Nup (green) antibody. (A) Details of the NPC structure are easily resolved in a conventional STED recording (full image in Fig. S3). However, due to photobleaching, acquiring several images was precluded in this case; the images a1–a3 show the fluorescence signal of the highlighted area in subsequent recordings. (B) MINFIELD STED microscopy: reducing the scan area to the structure of interest increases the signal, as long as the area is smaller than the focal extent of the excitation and STED beams. To determine areas of interest, a low-resolution confocal image is acquired first. The selected area is then scanned multiple times (b1–b10) with high resolution. The signal can be summed up (SUM) or evaluated frame by frame. Color scale values (min, max) for this and all other image data are provided in Table S2, and the color scales are in Fig. S8. (C) Signals upon repeated imaging in the red and green channel of the images shown in a1–a3 and b1–b10. (Scale bars: 200 nm.)

Fig. S3.

Complete image of the anti-gp210 and anti-FG repeat indirectly labeled sample. Larger areas were imaged for scan 2 and scan 3 to include unbleached parts of the sample. The presence of fluorescent signal in the additionally imaged areas excludes focus drift as a possible cause for the signal loss. (Scale bars: 1 μm.)

Single-Fluorophore Assessments of Bleaching Reduction by MINFIELD.

To quantify the feasible improvements in signal yield under STED imaging conditions in more detail, we chose to investigate the photobleaching behavior of the dye Atto647N (Fig. 3 and Figs. S4 and S5). Atto647N is already established in STED imaging and has previously been used for bleaching experiments (4, 11, 16, 17). The bleaching dynamics of fluorescent dyes strongly depends on their molecular environment, including the dye density (18, 19) and oxygen concentration (20, 21). To achieve high reproducibility and control over the conditions in the sample, we prepared single-molecule samples of Atto647N-labeled double-stranded DNA (dsDNA) in PBS as described in refs. 16 and 22; the dye was attached at a 10-nm-long dsDNA strand with the opposing end immobilized on the coverslip. This configuration ensured free rotation of the dye molecule and removes it sufficiently from the influence of the coverslip surface.

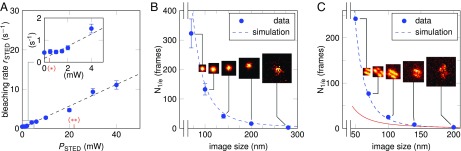
Fig. 3.

Bleaching of the fluorophore Atto647N and the bleaching reduction brought about by MINFIELD recording. Bleaching was investigated by measuring single Atto647N molecules (in A and B) and Atto647N-labeled DNA-origami (in C). Dots represent experimental results, and lines are modeled according to Eq. S1 (SI Materials and Methods). Error bars indicate the derived SEM. (A) The bleaching rate r_STED scales approximately linearly with the STED intensity, for constant excitation (3 µW). (Inset shows enlarged view of data for <5 mW.) The power levels indicated by (*) and (**) are associated with the I_s and the doughnut crest intensity, respectively, used for the measurements in B. (B and C) Average number of frames $N_{1/e}$ before photobleaching of a single fluorophore (B) or DNA origami structure (C) vs. size of the scanned image field. (B) Decreasing the scan size of a STED measurement allows the acquisition of considerably more frames before the fluorophores bleach. (C) The increase in signal yield is readily observable also for more complex structures, such as labeled DNA origami. For comparison, the red curve shows a linear scaling with the inverse image area (normalized to the data point at 200 nm). It indicates the expected bleaching behavior if the average laser intensities in the imaged area were not to change with the image size (i.e., a bleaching reduction purely based on shorter exposure due to fewer-pixel scans). Here, a reduction from 200-nm image size to 50 nm (16-fold smaller area) allowed the acquisition of 100 times more frames.

Fig. S4.

Single-molecule bleaching measurements (Atto647N). The fluorescence signal (A) was acquired (integrating over 16 ms) while the STED laser was periodically blocked to acquire fluorescence signal (probe the fluorescent state). The data were then separated into a “confocal” part, where the STED laser was blocked, and the “STED” part. Note that no doughnut profile was used in these measurements, but (Gaussian) excitation and STED foci were overlaid to study the bleaching at different intensities (B). Data points with signal above a threshold were considered to belong to the fluorophores’ fluorescent state. The total time the molecule is in the fluorescent state (above threshold) before bleaching was averaged over ∼100 molecules (C). Alternatively, the signal of all measured molecules was summed and fit with an exponential decay yielding the bleaching constant (D).

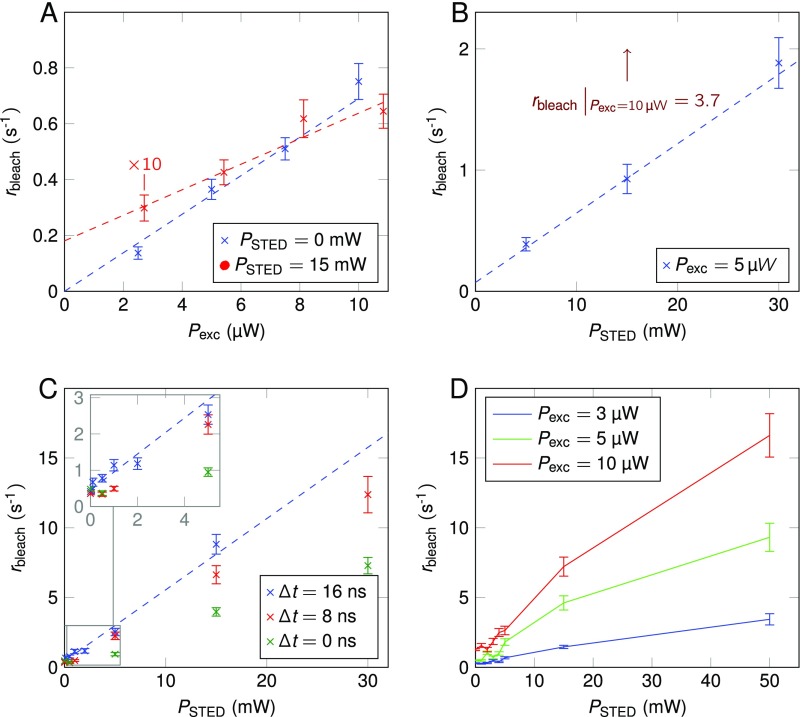
Fig. S5.

Power dependence of the bleaching rate measured on single Atto647N fluorophores. The dashed lines provide a guide to the eye. (A) Varying excitation power at a STED power of 0 and 15 mW. Please note that the data points for 15-mW STED power were divided by 10 to fit into the same graph. (B) Bleaching rate caused by the STED laser alone. During the measurement, the excitation and STED laser alternatingly illuminated the sample. The bleaching rate depended strongly on the excitation laser and the chopper frequency (data not shown). A doubling of the excitation power from 5 to 10 µW, at 15-mW STED power (arrow), increased the bleaching rate to 3.7 s⁻¹. (C) The timing delay between excitation and STED laser pulses were offset by up to 16 ns. (D) Independent bleaching series at varying STED and excitation power.

For the experiment, fluorophores distributed at low density were individually identified in a confocal overview scan, their positions approached and the fluorescence signal measured for 20 s. As the survival time before photobleaching is on the order of a few seconds, most fluorophores bleach within this period. To ensure well-defined irradiation intensities, the vortex phase plate (VPP) (Fig. S1) responsible for the doughnut-shaped focus was removed from the beam path, and the excitation and only slightly larger STED foci were overlaid. To discriminate between reversible fluorescence preclusion and irreversible bleaching, the STED laser was blocked periodically with a chopper (30 Hz), while the fluorophore was illuminated with the excitation laser. The time $\tau$ until the molecule bleaches was derived from the data, and the bleaching rate calculated by averaging over ∼100 molecules: $r_{\mathrm{combined}}=1/\overline{\tau }$, with $\overline{\tau }$ denoting the average time until bleaching. The bleaching rate under STED conditions was calculated as follows:

$$r_{\mathrm{STED}}=r_{\text{combined}}-r_{\text{probe\hspace{0.17em}only}},$$

where $r_{\text{probe\hspace{0.17em}only}}$ is the bleaching rate caused by the excitation beam alone. The photobleaching rate was observed to scale roughly linearly with the applied STED intensity (Fig. 3A). In separate measurements (Fig. S5A), the bleaching rate was found to depend linearly on the excitation intensity (3-µW average power for Fig. 3A) and to be comparatively low when the excitation laser was switched off completely. The excitation cross-section of the molecular ground state $S_0$ is negligibly low at the STED wavelength. A more detailed discussion of the bleaching behavior can be found in SI Materials and Methods, with additional data in Figs. S4 and S5.

A basic model intended to capture these observations considers (i) photobleaching from the $S_1$ state, and (ii) bleaching from higher states $S_n$ populated by further absorption of STED beam photons from $S_1$ (SI Materials and Methods). With this model, we simulated the bleaching behavior at various scan sizes (Fig. 3B)—now considering scanning with the STED doughnut configuration for nanoscopy—and compared the predictions to the experimental data. The bleaching probability of a single frame was calculated using the model by simulating the irradiation intensities at the image center for each pixel in the scan. The excitation laser focus was approximated with a Gaussian of 250 nm FWHM, whereas the doughnut-shaped STED beam intensity was described by

$$I\left(d\right)=I_0{d}^2\exp \left(-{\left(\frac{2d}{d_0}\right)}^2\right),$$

where $I_0$ denotes the intensity scaling factor, $d$ is the distance from the center, and $d_0$ = 468 nm defines the peak-to-peak width of the STED doughnut.

The data points in Fig. 3B each represent the average number of frames $N_{1/e}$ before photobleaching of a single fluorophore. For each data point, ∼100 molecules were measured. The STED average power was kept constant at 53 mW, and the pixel size was set to 10 nm. The Insets show representative images, with the signal of the first $N_{1/e}$ frames summed and the color scale scaled to the minimum and maximum pixel values (Table S2). Considerably more signal could be acquired when the scan range was reduced. Here, the difference between a scan range of 280 nm ($N_{1/e}=3$) and 70 nm ($N_{1/e}=320$) was more than 100-fold.

Table S2.

Upper and lower photon count values of image color scales

Image	Lower value	Upper value
Fig. 2 A, a0–a3, and b1–b10	Red: 3; green: 9	Red: 40; green: 54
Fig. 2B	15	352
Fig. 2, SUM	Red: 20; green: 30	Red: 300; green: 450
Fig. 3B, scan range
280 nm	0	7
200 nm	0	30
140 nm	0	82
100 nm	5	179
70 nm	31	471
Fig. 3C, scan range
200 nm	0	11
140 nm	0	23
100 nm	0	49
70 nm	7	127
50 nm	48	376
Fig. 4B	10	120
Fig. 5B	0	67

The model is readily applicable to other structures labeled with Atto647N, as exemplified on labeled DNA origami nanorulers (GATTA-STED 27R; GATTAquant), shown in Fig. 3C, basically consisting of two line-shaped fluorophore arrays arranged in parallel to each other at 27-nm distance. Although previously reported resolution values (3, 7) for STED microscopes would, in principle, have been sufficient to discern the two lines, our attempts failed in this case due to bleaching. The structure could be resolved, however, for a scan size of 200 nm. In this case, the signal was already reduced to less than a half after the first scan frame. To measure the 27-nm distance between the lines, a stronger signal was required, which was readily achieved by reducing the image size further. Providing absolute values for the improvement in signal yield is challenging, as fast photobleaching at large image sizes precludes accurate analysis. According to the model, a scan range of 200 nm would yield a fivefold increase in signal over that of a large scan, suggesting a 500-fold improvement at an image size of 50 nm. The origamis were imaged at a STED time-averaged power of 280 mW, 2.1-μW excitation power, 5-nm pixel size, and 100-μs pixel dwell time. The signal of ∼100 single independently measured structures was summed up and the signal evolution with time in the image’s central 2 × 2 pixels was fitted by an exponential decay with the bleaching constant $N_{1/e}$. The Insets of Fig. 3C show representative structures, with the signal summed over $N_{1/e}$ image frames and a normalized color scale. The dashed line describes the modeled bleaching behavior, scaled by a constant factor of 1.7. The need to slightly adjust the model to the experimental data are likely due to the different embedding media affecting the photobleaching.

Enabling Nanoscale Imaging of Structures Labeled with Small Numbers of Fluorophores.

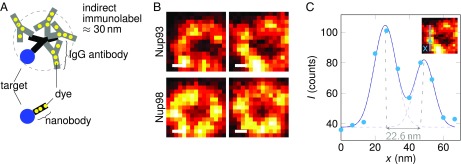
MINFIELD is especially relevant when using small camelid-derived single-domain antibodies (nanobodies) as labels. Although immunolabeling using primary and secondary antibodies gives high signal (>10 dyes per target), the resolution of STED nanoscopy already exceeds the size of the labeled antibody tree (Fig. 4A). Nanobodies are ∼10-fold smaller than conventional antibodies and can therefore deliver fluorescent dyes very close to the actual target protein, offering an outstanding level of accuracy for superresolution microscopy (23, 24). However, because they can be tagged with only a few dyes, samples labeled via nanobodies provide lower signal, reducing the STED resolution attainable in practice. In Fig. 4 B and C, we demonstrate MINFIELD STED nanoscopy of nanobody-labeled NPCs resolving structures separated by as little as ∼20 nm. Imaging with a larger scan size fails to acquire high-resolution images of sufficient quality (Fig. S6). The images show nuclear pores in Xenopus laevis X177 cells, labeled with recently developed nanobodies (23) against the nucleoporins Nup93 and Nup98. The laser powers were 252 mW for the STED and 2.1 µW for the excitation laser, the pixel size was set to 6.6 nm, and the cumulative pixel dwell time was 2 ms. The use of electro-optic scanners to image small areas reduces the need for extensive positioning correction by software and eliminates the overhead of turning points required to accelerate mechanical scanners. Although useful, electro-optic scanning is not critical for the implementation of MINFIELD, as shown in the next demonstration.

Fig. 4.

MINFIELD STED nanoscopy of samples with low fluorophore-to-protein ratio. Here, Abberior Star Red-labeled nanobodies are used to visualize the arrangement of Nup93 and Nup98 within the amphibian NPC. Nup93 forms a ring around the center of the nuclear pore with a diameter of ∼70 nm. Its substructure (A) would be obscured by the size of the antibody tree in conventional indirect immunolabeling. Using nanobodies reduces the number of dye molecules per protein considerably. (B) Limiting the scan field compensates this effect and images detailed cellular structures with high SNR at ∼20-nm resolution. C shows a line profile through the Nup93 image at the indicated position. The data were fitted with two Gaussians, yielding a peak-to-peak separation smaller than 23 nm and a full width at half-maximum of ∼15 nm for the individual Gaussians. (Scale bars: 20 nm.)

Fig. S6.

STED imaging of Xenopus NPCs stained with Abberior Star Red-labeled anti-Nup98 nanobody TP377. (A) Comparison of images with different scan sizes. STED power: 336 mW. Cumulative pixel dwell time: 500 μs. Color scale: 0–50 (for all). (B) Comparison of images with different scan sizes. STED power: 147 mW. Cumulative pixel dwell time: 500 μs. Color scale: 0–80 (for all).

MINFIELD Is Especially Beneficial for STED Imaging Along the Optic Axis.

Fig. 5 demonstrates the MINFIELD approach in 3D, on a STED system using galvanometer scanners for image acquisition (Abberior Instruments; QUAD Scan superresolution microscope, modified with a home-built pulsed STED laser, operating at 40 MHz and 775 nm). Here, the laser light is turned off by acousto-optical modulators during the turning points of the scan mirrors. For the STED beam, a partial beam passing a 2π phase vortex and another one passing a top-hat phase pattern are overlaid incoherently. The relative powers are chosen for the focal STED light intensity distribution to yield approximately isotropic resolution increase in 3D (Fig. 5A). Compared to a configuration with similar 2D (lateral) resolution improvement, the laser intensities are much larger and spread over a wider area, indicating that in 3D STED microscopy confining the scanned region is especially advantageous.

Fig. 5.

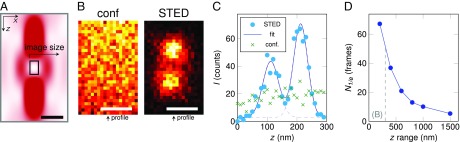
MINFIELD is especially advantageous for STED imaging along the optic axis (z) and in 3D. (A) The focal STED intensity distribution for confining molecular fluorescence along the optic axis (z) and hence in 3D extends well over >1 μm in z. Achieving similar resolution as in the focal plane requires higher laser intensities. (B) Three-dimensional imaging is demonstrated on Atto647N-labeled DNA origami with two spots designed to be separated by 91 nm. The resolution improvement with STED is immediately apparent when comparing the confocal xz image with its MINFIELD STED counterpart. (C) Analyzing the line profile along the z axis yields a peak-to-peak separation of ∼100 nm at a full width at half-maximum of ∼60 nm for the Gaussian fits. (D) Number of image frames that could be acquired before the fluorescence signal dropped below 1/e of its original brightness, depending on the scan range along the z axis. The data were acquired by imaging antibody-labeled microtubules in an x–z scan, using a “top-hat”–only phase pattern and keeping the x-range constant at 5 μm (see data in Fig. 3 B and C, where the imaged fields were squares, and, consequently, the relative area reductions stronger than for the data shown here). The indicated z range (dashed line) corresponds to the size of the images in B. [Scale bars: 500 nm (A), 100 nm (B).]

Fig. 5B demonstrates the resolution improvement of STED compared with conventional confocal microscopy on Atto647N-labeled DNA origami (GattaQuant; custom structure according to ref. 25), with a line profile analysis revealing the resolution increase along z (Fig. 5C). The total STED power of 294 mW was split between the phase patterns, with 10% used for the vortex phase pattern and 90% for the top-hat pattern. The pixel dwell time was set to 10 μs (STED) and 1 µs (conf), with a pixel size of 10 nm. Ten frames were summed for display in Fig. 5B. Fig. 5D demonstrates the bleaching reduction per acquired frame using the pure top-hat pattern with a constant scan range of 5 μm in the x direction. The data were acquired by repeatedly imaging immunolabeled microtubules of Vero cells with a STED average power of 168 mW, yielding a resolution of ∼80 nm in z. Confining the scan range in z to 200 nm readily reduced the bleaching per frame 10-fold.

SI Materials and Methods

Image Processing.

All image data shown is raw data, mapped to a linear color scale (Fig. S8). The lower and upper count values for each image are given in Table S2.

Fig. S8.

Color scales used for data representation. Upper and lower count values are given in Table S2.

Laser Power.

For image data, all powers stated refer to the sample plane. Powers were measured at a reference point before the objective. Powers given for the single-molecule experiments (Fig. 3A and Figs. S4 and S5) directly refer to the measured power.

Microscope Setup.

A sketch of the setup is shown in Fig. S1. The specifications of the lenses and filters are given in Table S1.

The microscope used a pulsed STED laser at 775-nm wavelength, 20-MHz repetition rate, and with pulses of 1.2-ns length (ELP-5-775-DG; IPG Photonics Corporation). The fluorescence was excited by two picosecond laser diodes (LDH-D-TA-595, LDH-PC 635B; PicoQuant), lasing at 595 and 635 nm. The excitation lasers were triggered by an electronic signal, which was emitted upon detection of a STED pulse before coupling the STED laser into a fiber. Separation of the color channels was achieved by pulse-interleaved excitation and detection, as described in ref. 7.

The STED beam passed a vortex phase plate (VPP) (RPC Photonics) imprinting a 2$\pi$ vortex phase pattern on its wave front, which led to the well-known STED doughnut intensity profile in the focus. Two pairs of cylindrical lenses (CL1, CL1′, CL2, CL2′) were used to correct for astigmatism. As the pairs were composed of a positive and a negative lens, the STED beam was compressed in one direction when passing only one pair. This would result in a bad doughnut zero in the focus. The second pair was therefore arranged in reverse order to stretch the beam accordingly. The positioning of the pairs thus allowed independent astigmatism correction of the excitation and the STED beam. A polarizing beam splitter (PBS1) ensured a clean polarization state of the STED beam before entering the electro-optic deflectors.

Dichroic mirrors (DM1 and DM2) were used to overlay the excitation, STED and detection beam paths. The beam was then narrowed with a telescope (lenses TL1 and TL1′) to fit it through the aperture of the electro-optic deflector. The electro-optic deflectors (EOD1, EOD2) deflected the beam apparently at the pivot points (P1 and P2), which were projected on the objective’s back aperture by the lenses TL2, TL2′, TL3, and TL3′. Thus, beam deflection without displacing the beam center was achieved in the back aperture. EOD1 (ED-3, Leysop) is made of lithium tantalite with an aperture of 3 mm and deflected the beam by 1.5 μrad/V, the deflector EOD2 (M-311A, customized; Conoptics) of potassium dideuterium phosphate (KD*P) with a 2.5-mm aperture, deflecting the beam by 7.1 μrad/V. The voltage was delivered by two high-voltage amplifiers providing ±2,000 V at EOD1 (2220-CE; Trek) and ±700 V at EOD2 (PZD700A; Trek). The configuration used allowed a scan range of ±1.75 µm with EOD1 and $\pm$ 2.4 µm with EOD2. EOD2 was used as fast scan axis, providing a bandwidth of >100 kHz.

EODs are birefringent and may slightly rotate the laser polarization. Thus, the polarization was cleaned up again before entering the objective, using a polarizing beam splitter (PBS2). A quarter-waveplate (600–900 nm achromat; B. Halle Nachfl.) circularized the polarization, which is necessary to achieve the intensity zero at the center of the STED focus.

Three fiber-coupled avalanche photodiodes (SPCM-AQRH13; Excelitas) were used for detecting the fluorescence signal. The core of the connected fibers (diameter, 62 µm) acted as confocal pinhole of ∼1 Airy unit in size.

APD1 and APD2 counts constituted the “red” channel with a detection window of 645–725 nm (filters F1 and F2). The fluorescence was split in two orthogonal polarization channels by PBS2. Fluorescence passing through the PBS was descanned by the EODs, filtered by wavelength with F1, and focused onto the multimode fiber with the lens L3. The other polarization was directly filtered and focused. The fluorescence in the “orange” detection path was selected with a notch filter (designed for 633 nm at normal incidence) and filtered by wavelength with F3. Both filters were angle-tuned for optimal suppression of the excitation wavelength and maximum fluorescence signal. The beam path of APD2 and APD3 was not descanned. Thus, the fluorescence signal was suppressed by the pinhole when a deflection of >200 nm was used. As the electro-optic scanners are mostly used for scanning smaller areas however, this was not a strong disadvantage.

A piezo scanning stage (P-562.3CD with E712-driver; Physik Instrumente) was used to image large areas of the sample and to center areas of interest for small area scans.

Three-Dimensional STED Microscopy.

The basic microscope for the 3D STED measurement was a commercial system (2C QUAD Scan Super-Resolution Microscope) from Abberior Instruments. The microscope was customized with a home-built STED laser working with a repetition rate of 40 MHz at a wavelength of 775 nm and a pulse width of roughly 500 ps. The STED beam phase was modulated by a spatial light modulator (LCOS-SLM; Hamamatsu Photonics), which was imaged into the back aperture of the objective lens (Olympus UPLANSAPO 100XO). By passing the SLM twice and in-between turning the polarization by 90°, the beam was incoherently split into two parts, which were independently modulated with a vortex and a top-hat phase mask. Both corresponding intensity profiles were overlaid in the focal spot of the objective lens to achieve an isotropic resolution in all three dimensions.

For excitation at 635 nm, a pulsed picosecond laser with a pulse width around 80 ps was used (PiLas OEM, version 1.1; Advanced Laser Diodes Systems). The fluorescence was detected with an avalanche photodiode (SPCM-AQRH13; Excelitas). The detection window ranged from 650 to 720 nm, and the confocal pinhole was set to 0.75 AU.

The scanning in the xy plane was performed via galvanometer mirrors (Cambridge Technology) and along the z axis with a piezo stage (P-736.ZR2S; Physik Instrumente). The control signal for the scanning mirrors was generated on a field programmable gate array. The scanners were carefully calibrated to achieve reliable positioning between regions of different size. To this end, we took images at different line frequencies and adjusted the scanner lag time such that the spatial shift between these images was negligible. This also resulted in repeatable nanometer precision when scanning the same sample area multiple times. After finishing a scan in the z direction, a return and settling time of 200 ms for the z piezo allowed a precise rescan of the same sample area. To minimize the light overhead during the return motion of the galvanometer mirrors and the z piezo, the excitation and STED laser were blocked via an acousto-optical modulator (AOM) (AA Opto Electronic). The light dose during the experimentally determined rise and fall time of the AOM of 0.7 µs was negligible compared with the overall dwell time of 300 µs per line used.

Indirect Immunolabeling (Fig. 2).

The samples were prepared according to established protocols as described in refs. 7 and 35. Cultured Xenopus laevis X177 cells were fixed with 2.4% (wt/vol) formaldehyde at room temperature for 5 min. Following extraction in 0.3% Triton X-100 in PBS and blocking in 5% (wt/vol) BSA in PBS, the cells were incubated with a mouse monoclonal antibody specific for Xenopus gp210 (36) and panspecific rabbit antibodies for most Xenopus FG repeat nucleoporins. These primary antibodies were detected using secondary antibodies (Dianova) custom labeled with the fluorescent dyes Abberior STAR Red (Abberior) and Alexa Fluor 594 (Thermo Fisher Scientific).

Single-Molecule Sample (Fig. 3).

The samples were prepared according to a modified protocol described in refs. 16 and 22. To reduce fluorescent contaminations, cover glasses were sonicated in 2% (vol/vol) Hellmanex III (Hellma Analytics) solution for 30 min. A simple flow chamber was built by gluing a coverslip onto an object slide with two strips of double-sided adhesive tape, leaving a central channel. To prevent drying of the sample and diffusion of glue into the chamber, silicone grease was added next to the tape before gluing.

The chamber was filled with biotinylated BSA solution (0.5 mg/mL; Sigma-Aldrich) and incubated for 5 min, then washed with 200 µL of PBS. The PBS was replaced with 30 µL of streptavidin solution (0.5 mg/mL; Roche Diagnostics) and washed after 5 min. The streptavidin attached to the biotin on the cover glass, providing binding sites for more biotin molecules. Thirty microliters of labeled dsDNA solution was added (10 pmol; IBA). The dsDNA consisted of 31 bp with the 5′ end of each strand tagged with one Atto647N and one biotin molecule. The biotin attached to a streptavidin molecule, immobilizing the DNA on the cover glass. The sample was analyzed on the microscope, and the last step was repeated until the desired density was reached. Following a washing step with PBS, the sample was sealed with silicone grease. The sample was observed to be stable over several weeks.

The final density of Atto647N molecules was selected to reduce the probability of two dyes being in one confocal volume to a negligible amount. The overabundance of streptavidin in the sample made it improbable that two dsDNA constructs attached to the same molecule.

Nanobody Sample (Fig. 4).

The labeling follows the protocol described in ref. 23. Purified nanobodies with engineered cysteines on their surface were labeled with the dye Abberior Star Red using a maleimide reaction. Specifically, we used nanobodies targeting Xenopus Nup98 (Nanobody TP377) and Nup93 (Nanobody TP179), respectively.

Xenopus laevis X177 cells were grown on cover glasses and prefixed for 30 s with 2.4% (wt/vol) paraformaldehyde (PFA) in transport buffer (TB) (20 mM Hepes, pH 7.5, 110 mM KAc, 1 mM EGTA, 250 mM sucrose), followed by two washing steps with the TB at room temperature. The plasma membranes of the cells were then selectively permeabilized on ice for 8 min with TB containing 25 µg/mL Digitonin, followed by two washing steps with TB containing 1% (wt/vol) BSA (TBA) for 5 min each. The cells were incubated on ice with 100 nM labeled nanobodies in TBA. After two washing steps with TBA at room temperature, the cells were fixed with 3% (wt/vol) PFA in TB for 10 min at room temperature, followed by two washing steps with 1× PBS. Permeabilization of nuclear envelopes was then induced with 0.3% Triton X-100 in 1× PBS for 3 min, followed by two washing steps with 1× PBS for 5 min each. Afterward, the cells were incubated with 50 nM labeled nanobodies for 30 min, washed twice for 15 min with 1× PBS, and mounted in Mowiol containing DABCO.

Simple Model of Photobleaching.

A basic model (analogous to ref. 37) intended to capture these observations considers (i) photobleaching from the $S_1$ state, and (ii) bleaching from higher states $S_n$ populated by further absorption of STED beam photons from $S_1$. The experimental data (Fig. 3A and Fig. S5) suggest (sequential) one-photon processes. Under the experimental condition of no excitation saturation, the probability for excitation during a single pulse repetition period $t_{\text{rep}}$ is independent of the excitation laser pulse length. We therefore simplify the probability of $S_1$ occupation by steady-state assumptions with uniform excitation probability in time (quasicontinuous excitation). The same simplification is applied to the STED beam, as the pulse duration $t_{\text{STED}}\approx 1\text{ns}$ is large compared with the higher state lifetimes [less than picoseconds (38)], while being shorter than the $S_1$ lifetime ${\tau }^{S_1}=3.5\hspace{0.5em}\text{ns}$ (datasheet provided by AttoTec). The bleaching rate can then be written as follows:

$$r_{\mathrm{bleach}}=\left(k_{\mathrm{bleach}}^{S_1}+{\delta }_{\mathrm{STED}}\ast I_{\mathrm{STED}}\right)\ast {\sigma }_{\mathrm{exc}}{I}_{\mathrm{exc}}{\tau }^{S_1},$$ [S1]

where ${\sigma }_{\mathrm{exc}}=2.5\ast {10}^{-16}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^2$ is the absorption cross-section (datasheet), $k_{\mathrm{bleach}}^{S_1}$ is the bleaching rate constant of the $S_1$ state, and ${\delta }_{\mathrm{STED}}=k_{\mathrm{bleach}}^{S_n}\ast {\sigma }_{\mathrm{STED}}^{S_1}{\tau }^{S_n}$ describes bleaching from higher states through STED beam photon absorption. The applied powers can be related to the sample-plane intensities. Assuming a Gaussian focal spot of 250-nm full width at half-maximum (FWHM) for the excitation laser and 300 nm for the STED laser, we calculated the intensities in the focal center. As a reference, 1.4*10⁹ W⋅cm⁻² (excitation beam) and 0.98*10⁹ W⋅cm⁻² (STED beam) correspond to 1 W of time-averaged power, with the photon flux 4.5*10²⁷ cm⁻²⋅s⁻¹ and 3.8*10²⁷ cm⁻²⋅s⁻¹ for excitation and STED, respectively (1-W reference). Fitting the model (Eq. S1) to the data of Fig. 3A yielded values of $k_{\mathrm{bleach}}^{S_1}=21{\mathrm{s}}^{-1}$ and ${\delta }_{\mathrm{STED}}=8.7\ast {10}^{-24}{\mathrm{s}}^{-1}$.

Single-Molecule Bleaching Experiments.

To measure the bleaching rate, a fluorophore molecule’s position was approached and the fluorescence signal measured (Fig. S4A). As the STED laser inhibits the fluorescence, the laser was blocked periodically with a chopper (indicated in green). The analysis was performed on the signal with blocked STED laser. The bleaching caused by the STED laser was calculated as ${\tau }_{\text{STED}}={\tau }_{\text{probe}\hspace{0.17em}\text{only}}{\tau }_{\text{combined}}/\left({\tau }_{\text{probe\hspace{0.17em}only}}-{\tau }_{\text{combined}}\right)$, where ${\tau }_{\text{combined}}$ is the bleaching time of the described measurement and ${\tau }_{\text{probe\hspace{0.17em}only}}$ is the bleaching when only the probing of the fluorescent state was performed. Two possible methods for extracting $\tau$ from the data have been considered: averaging the time each fluorophore is in the fluorescent state (Fig. S4 B and C), or fitting the sum of all fluorescence time traces with an exponential decay (Fig. S4D).

Both methods provided consistent results. However, averaging the individual bleaching times was preferred, as the exponential fit did not provide a good estimate for the experimental error. The error bars were calculated assuming an exponential distribution of the individual bleaching times ${\tau }_i$ and a normal distribution of their average $\overline{\tau }$. Thus, $\mathrm{\Delta }\overline{\tau }=\sqrt{\text{var}\left({\tau }_i\right)/N}=\overline{\tau }/\sqrt{N}$. The error for the STED bleaching time then became: $\text{Δ}{\tau }_{\text{exc}+\text{STED}}=\left({\tau }_{\text{probe\hspace{0.17em}only}}/\left({\tau }_{\text{probe\hspace{0.17em}only}}-{\tau }_{\text{combined}}\right)+{\tau }_{\text{combined}}{\tau }_{\text{probe\hspace{0.17em}only}}/{\left({\tau }_{\text{probe\hspace{0.17em}only}}-{\tau }_{\text{combined}}\right)}^2\right)\text{Δ}{\tau }_{\mathrm{combined}}$, disregarding the error of ${\tau }_{\text{probe\hspace{0.17em}only}}$, as the value had been measured with higher accuracy and was considered constant throughout the analysis. Please note that the measured values for $\tau$ were roughly constant for weeks yet scattered more than implied by the error analysis on a measurement-to-measurement basis. Other observables, such as brightness and STED depletion, did not correlate with the observed scattering of the bleaching rate.

Summarizing the results, the bleaching rate scales roughly linearly with both the excitation and STED power. Against expectation, it is not trivial to identify the specific bleaching pathways involved. Photobleaching of a fluorophore occurs from an electronically excited state, caused by a chemical reaction or dissociation of the molecule. There may be a number of states involved, including dark states, which are challenging to probe as no fluorescence is emitted.

To reduce complexity, several independent experiments were performed (Fig. S5). First, the bleaching dependence on the excitation power was investigated (Fig. S5A). Without the STED laser, the bleaching rate scaled linearly with the excitation power, which suggests no states excited above the first singlet ($S_1$) or triplet ($T_1$) states are involved.

With involvement of the STED laser, the bleaching rate was approximately 10 times higher and still strongly dependent on the excitation power. The extrapolation of the data in Fig. S5A suggests a bleaching component solely caused by the STED laser. The data presented in Fig. S5B elaborate this possibility further: the excitation laser was switched off when the STED laser passed through the chopper. A linear relationship between the STED power and the bleaching rate was observed. Upon first inspection, these data would lead to the conclusion that ∼25% of the bleaching events are caused by absorption of a STED photon from the molecule’s ground state $S_0$. However, the bleaching rate strongly depended on the excitation power and the chopper frequency. This result suggests the involvement of a long-lived dark state (approximately millisecond lifetime), into which the molecule may transition after excitation by the excitation laser, contributing to further photobleaching upon absorption of a STED photon. The involvement of a long-lived nonfluorescent state is further supported by the data in Fig. S5C. Here, the STED pulse was delayed by up to 16 ns with respect to the excitation pulse. The lifetime of the fluorescent $S_1$ state is much shorter, and no fluorescence was observed after 16 ns. However, the bleaching caused by the STED laser was even stronger than in the case of temporally overlapping laser pulses. This can be explained by the shortened lifetime of the $S_1$ state due to the transition $S_1\to S_0$ being stimulated by the STED laser. Thus, the probability of photobleaching and transitioning to the triplet state is reduced. Fig. S5D is an independent measurement series of the bleaching rate at various STED and excitation powers. Again, a strong dependence of the bleaching rate on the excitation intensity was observed. These results suggest that the STED laser does not cause significant photobleaching in the absence of the excitation laser, without excitation from the ground state $S_0$.

One feature that was repeatedly observed, yet could not be sufficiently analyzed due to strong scattering of the data points, is an apparent plateau of the bleaching rate for low STED powers. Below 1-mW STED power, the bleaching rate did not scale linearly with the STED power, yet appeared to be constant. The influence of the STED laser on photobleaching in this power regime may be counteracted by the forced transition $S_1\to S_0$ induced by the STED laser. Thus, reducing the $S_1$ lifetime, leading to a lower probability for photobleaching from $S_1$ and intersystem crossing. The results are in good agreement with a study published recently by Wu et al. (17) on photobleaching in STED microscopy.

Nanobody Images.

Imaging nanobody-labeled samples is especially challenging for superresolution microscopy, as one protein is only labeled by one nanobody with a low degree of labeling (DOL ≈ 1–3). As exemplified in Fig. S6 on nanobody-labeled nuclear pore complexes (NPCs), a large STED scan cannot acquire sufficient signal to take advantage of the high resolution. Therefore, small image sizes are required to investigate the detailed distribution of the labeled protein within an individual NPC. The lower the STED power, the less of an advantage can be gained by reducing the image size.

The major drawback of reducing the image size is the loss of information from the area surrounding the targeted position, as the large STED intensities will bleach any fluorescence in this region. For many cases, however, it is sufficient to image the larger-scale distribution of the labeled structure at a lower resolution and decrease the image size when a structure of interest was identified. Indeed, this procedure is often necessary, as exemplified in Fig. S2: as individual NPCs are usually not distinguishable in the confocal image, an image with low STED power is acquired before centering the scan area at a single NPC.

Calculation of the Number of Useful Pixels.

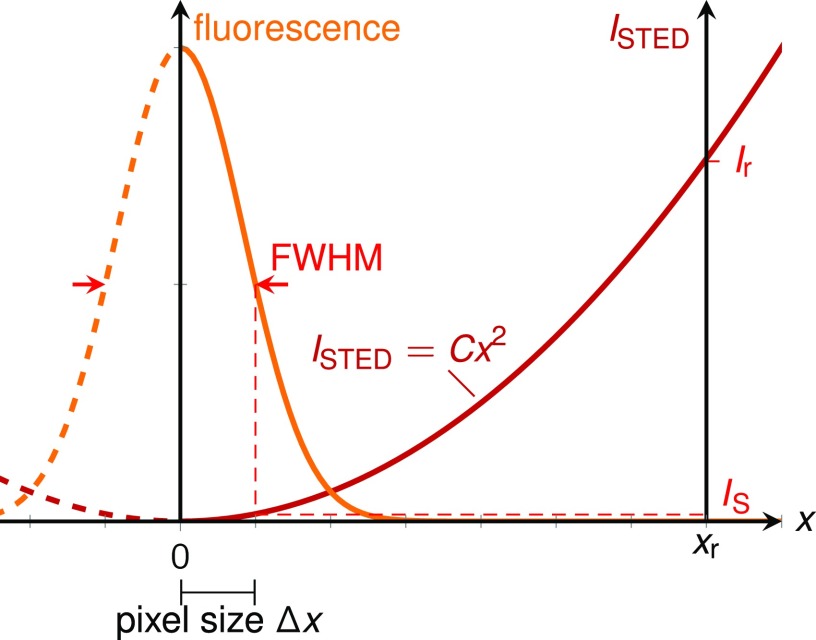
MINFIELD nanoscopy operates near the intensity minimum of the light driving the on–off transition (typically a sinusoidal or doughnut intensity profile). Considering the situation in one dimension (1D) around the minimum, the intensity is therefore well described by the quadratic approximation (Fig. S7), I(x) = C·x², where C is I_max·k² for approximation of a sinusoidal intensity profile I(x) = I_max·sin²(kx) (with k = 2π/λ as the wave number and λ as the wavelength). An additional constant form factor (slightly smaller than unity) would be included in C for a doughnut profile.

Fig. S7.

Intensity dependence of state-switching light (here: STED light) near the minimum in the quadratic approximation. The useful number of pixels is derived in SI Materials and Methods.

To derive the number of useful pixels, we consider the intensity minimum being moved from one edge of the MINFIELD image region (x = 0) to the other edge (x = x_r). At either extreme, the edge opposing the minimum faces an intensity I_r, that is, the maximal intensity to occur in the imaged region. As the key feature of the MINFLUX concept, I_r is reduced manifold relative to the much larger maximal intensity I_max of the on–off driving light pattern. Let Δx be the position from the minimum at which the intensity reaches I_S. In line with a conventional definition of the resolution as the FWHM = 2Δx, we define the pixel size as half the FWHM, that is, Δx (thus fulfilling the Nyquist sampling condition). Therefore, I_s = C·Δx². Likewise, for the maximal permissible intensity found at the edge of the scanned field, we have I_r = C·x_r². Relating the two spatial intensity dependencies directly yields the number of useful pixel steps within the MINFIELD image as N_pix = x_r/Δx = $\sqrt{(I_{\text{r}}/I_{\text{s}})}$. Note that the constant C containing λ, I_max, and the potential form factor cancels out, meaning that, in the quadratic approximation, the useful number of pixels does not depend on the wavelength or on the chosen resolution, which is given by FWHM = 2Δx = λ/[π $\sqrt{(I_{\text{max}}/I_{\text{s}})}$].

Discussion and Conclusions

We have shown that STED nanoscopy can yield over 100 times more signal than usual when the imaged region is limited to a size well below the diffraction limit. The potential of our MINFIELD approach was demonstrated on different sample types, from single molecules to complex structures such as NPCs. We investigated the bleaching behavior of Atto647N in single-molecule experiments and found a linear relationship between the bleaching rate and the light intensities for the studied regime. These results agree well with published data (17) and can be used to estimate the bleaching rate in STED measurements. It should be noted, however, that the bleaching behavior strongly depends on the dye used and on the sample type. Dyes other than Atto647N may be more prone to bleaching by the STED laser alone, which would even increase the benefit of the MINFIELD strategy. At present, our approach appears important for STED imaging of samples labeled with organic fluorophores at a low dye-per-protein ratio, such as nanobodies or SNAP tags. In these cases, plain STED nanoscopy scanning of a large field of view cannot acquire sufficient signal at high resolution, yet the reduction of image size should reveal details separated by only 20 nm with sufficient contrast levels. The increase in signal yield will also be beneficial to applications requiring high photon counts, such as the counting of molecules (22).

Furthermore, a simple estimation (SI Materials and Methods and Fig. S7) shows that the minimal number of pixels per dimension fulfilling the Nyquist sampling condition is given by the square root of the ratio of the highest intensity allowed within the imaging range divided by $I_S$. Note that neither the wavelength nor the maximum intensity of the (doughnut- or standing-wave–shaped) STED light affect this number. Obviously, the resolution and the maximum field of view are tightly connected. Intensity-induced limitations can be avoided if the ratio of the image size (edge length) to the resolution is kept constant. It should also be noted that in MINFIELD scanning the exposure of the fluorophores to (high) intensities varies across the field of view, with the field of view center experiencing the lowest intensities on average.

A fundamental concept, MINFIELD will also be applicable to other types of coordinate-targeted superresolution variants, such as ground-state depletion (26) and reversible saturable/switchable optical fluorescence transitions (RESOLFT) nanoscopy using photoswitchable fluorescent proteins (27–29) and switchable (photochromic) synthetic-organic fluorophores (30). Moreover, MINFIELD will be relevant for superresolution modalities that use light patterns for switching fluorophores on rather than off. This applies not only to the methods that saturate the activation of fluorescent proteins using a pattern of light (31, 32), but also to those that rely on depleting the ground state by pumping the fluorophore to a higher-lying state, in particular the fluorescent state, as is the case in so-called saturated structured illumination microscopy (33, 34), which is substantially more prone to photobleaching than STED microscopy. For all of these ground-state depletion-type approaches (26, 32–34), confining the imaging to subdiffraction-sized regions (around the intensity minimum) should be beneficial. Last but not least, our MINFIELD strategy can be combined with other approaches to reduce photobleaching, such as optimizing the sample buffer (4), dark-state relaxation (12), and reducing the number of state transition cycles (11). Confining the image size to an area below the diffraction limit will extend the capabilities of superresolved fluorescence analysis toward applications where high signal-to-noise and superior resolution are of essential importance.

Materials and Methods

Detailed descriptions of the optical setup, image acquisition, and sample preparation including nanobody labeling, as well as single-molecule bleaching measurements and a calculation of the number of useful pixels, are provided in SI Materials and Methods. In brief, MINFIELD nanoscopy was demonstrated with a custom-built point-scanning dual-color STED setup (7) adapted to incorporate electro-optic rapid scanning of subdiffraction-sized image fields. Piezo scanning was used to image large areas of the sample and to center areas of interest for small-area scans. The minimum at the center of a doughnut-shaped focal intensity distribution for fluorescence deexcitation was formed as previously by imprinting a 2$\pi$ vortex phase pattern on the STED beam’s wave front with a dedicated phase plate.