Modeling the two-way feedback between contractility and matrix realignment reveals a nonlinear mode of cancer cell invasion

Significance

The mechanical cross talk between intracellular and extracellular forces can promote the invasive potential of tumor cells in tumors. Using a quantitative model, we elucidate the two-way feedback loop between stress-dependent cell contractility and matrix fiber realignment and strain stiffening, which enables the cells to polarize and enhance their contractility to break free from the tumor and invade into the matrix. Our model predicts that intermediate matrix stiffness is optimal for invasion, and we find a positive correlation between cell elongation and alignment of fibers in the matrix. Importantly, our model can be used to explain how morphological and structural changes in the tumor microenvironment, such as elevated rigidity and fiber alignment prior to cell invasion, are prognostic of the malignant phenotype.

Abstract

Cancer cell invasion from primary tumors is mediated by a complex interplay between cellular adhesions, actomyosin-driven contractility, and the physical characteristics of the extracellular matrix (ECM). Here, we incorporate a mechanochemical free-energy–based approach to elucidate how the two-way feedback loop between cell contractility (induced by the activity of chemomechanical interactions such as Ca²⁺ and Rho signaling pathways) and matrix fiber realignment and strain stiffening enables the cells to polarize and develop contractile forces to break free from the tumor spheroids and invade into the ECM. Interestingly, through this computational model, we are able to identify a critical stiffness that is required by the matrix to break intercellular adhesions and initiate cell invasion. Also, by considering the kinetics of the cell movement, our model predicts a biphasic invasiveness with respect to the stiffness of the matrix. These predictions are validated by analyzing the invasion of melanoma cells in collagen matrices of varying concentration. Our model also predicts a positive correlation between the elongated morphology of the invading cells and the alignment of fibers in the matrix, suggesting that cell polarization is directly proportional to the stiffness and alignment of the matrix. In contrast, cells in nonfibrous matrices are found to be rounded and not polarized, underscoring the key role played by the nonlinear mechanics of fibrous matrices. Importantly, our model shows that mechanical principles mediated by the contractility of the cells and the nonlinearity of the ECM behavior play a crucial role in determining the phenotype of the cell invasion.

Cell invasion into the surrounding matrix from nonvascularized primary tumors is the main mechanism by which cancer cells migrate to nearby blood vessels and metastasize to eventually form secondary tumors. This process is mediated by an intricate intercoupling between intracellular forces (such as cell contractility) and extracellular forces (adhesions and protrusions) that depend on the stiffness of the surrounding stroma and the alignment of matrix fibers. Previous experimental studies have examined the influence of these forces on the migratory behavior of cells during invasion. For example, the comparison between cell contractility in malignant and normal tissues has shown that the cells with malignant phenotype have a higher level of contractility (1–4). This elevated contractility is directly proportional to factors such as the stiffness of the extracellular matrix (ECM) and the fiber realignment (5–7), suggesting that the cross talk between ECM and intracellular contractility mediated by mechanosensory signaling pathways is also implicated in metastasis. Specifically, the activity of Rho, a myosin GTPase that regulates the activity of myosins, is elevated in proportion to the stiffness of the surrounding matrix (1, 8, 9), and inhibition of Rho-associated protein kinase (ROCK) has been known to reduce the invasiveness of the tumor (1, 10), demonstrating that the Rho pathway is a key promoter of cell invasion (11, 12).

Cells within tumor spheroids are held together by strong cadherin-mediated junctions that preserve the integrity of clusters against external perturbations. Therefore, cells require high contractility to break intercellular adhesions and invade within the matrix. At the periphery of the spheroid, cells can sense and respond to the stiffness of the matrix by forming actin-rich focal adhesions with the matrix ligands. The cell–matrix interactions depend on the mechanical and microstructural properties of the matrix such as matrix rigidity (13, 14), fiber alignment (5, 6, 15, 16), interfibrillar pore size (17), and density of cell-adhesive ligands (18). Previous computational models of cell invasion have examined cellular interactions (19, 20) and the interplay between protrusion forces (generated due to the polymerization of actin), traction forces (at the cell–matrix adhesions), and resisting forces (mostly the drag force caused by the viscosity of the matrix) (19, 21–24). However, these models do not account for (i) cell-induced realignment of the fibers in the matrix and how stiffening due to realignment, in turn, can lead to increased contractility of the cells, and (ii) how the microstructural properties of the matrix (pore size and stiffness) and fiber alignment impact cell motility and morphology.

Here, we present a mechanochemical model to study cell invasion from tumor clusters, with the main focus on the role of the nonlinear mechanics of matrix in enhancing cell contractility and providing the driving force for invasion. We identify a two-way feedback loop between stress-dependent cell contractility and matrix properties, including fiber realignment and strain stiffening, and show that this mechanism is critical to predict several key features of invasion including the existence of a critical stiffness for invasion of cells and the positive correlation between the elongation of the invading cells and the degree of cell-induced fiber alignment. When the impact of the matrix microstructure on cell motility is considered, we predict a biphasic relationship between the degree of invasion and the concentration of the matrix. The predictions of our model are validated by using melanoma cells grown in 3D spheroids and embedded in collagen of increasing concentration. Imaging both tumor cell migration from the spheroid, as well as the morphology of the cells leaving the spheroid, demonstrates that the density of the collagen plays an integral role in defining the mechanics of tumor cell invasion.

Results

Cell Polarization in Fibrous Matrices Increases with Collagen Concentration.

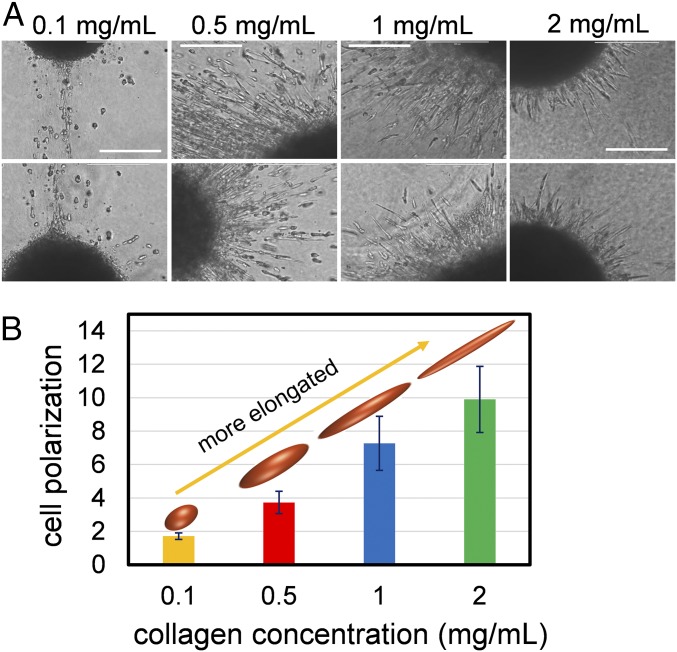
To examine the dependence of the cell elongations on the ECM concentration and stiffness, we studied isolated melanoma cell spheroids (of radius ∼200 µm) cultured inside collagen matrix, and measured the polarization of the invading cells (defined as the ratio of the major axis to the minor axis of the elongated cells) as the concentrations of collagen varied from 0.1 to 2 mg/mL (Fig. 1A). Two-photon microscopy of collagen adjacent to the spheroids of tumor cells shows that, at higher concentrations of collagen (1 and 2 mg/mL), there is an increase in the density of the fibers and cross-links of the matrix, when viewed both in 2D and 3D (Fig. S1). To eliminate the effect of cell proliferation from the measurements of cell polarization and invasiveness, the cells were treated with 1 µg/mL mitomycin C (comparisons between mitomycin C-treated cells and vehicle are shown in Fig. S2). At low concentrations (0.1 mg/mL), the cells located at the periphery of the spheroid have a rounded morphology. With increase in the collagen density (0.5 and 1.0 mg/mL), cells become considerably elongated. At very high concentrations, the cluster shows a sprouting morphology with highly elongated, spindle-like cells protruding from the cluster. Overall, these results show that, by increasing the concentration of collagen, cells become more elongated (Fig. 1B). Cell elongation is directly proportional to migratory potential of the cells and reflects the onset of the epithelial-to-mesenchymal transition (EMT). Therefore, these results indicate that there could be a direct correlation between the driving force underlying EMT and the concentration of collagen. We next incorporated these observations into our model to determine the mechanism underlying the increase in the cell polarization with the stiffness of the matrix.

Fig. 1.

Cell polarization increases with collagen concentration. (A) Melanoma cells invading collagen matrices exhibit strong polarization, which increases with the concentration of collagen. (Scale bars: 100 µm.) (B) The elongation of cells (ratio of the major to the minor axes of the cells) increases with collagen concentration.

Fig. S1.

The (A) 2D and (B) 3D images of collagen fibers adjacent to the spheroids of tumor cells show that, at higher concentrations of collagen (1.0 and 2.0 mg/mL), there is an increase in the density of the fibers and the cross-links of the matrix. Collagen concentrations lower than 1.0 mg/mL could not be imaged due to the loose, flimsy nature of the matrix, which caused significant blurring of the image.

Fig. S2.

Comparison between the mitomycin C-treated cells and vehicle cells invading collagen matrix. Mitomycin C does not appear to affect the rate of invasion of melanoma cells, demonstrating that, at these time points, the spread of cells is due largely to invasion, and not cell proliferation.

The Driving Force of Cell Invasion Is Enhanced by the Interplay Between Matrix Fiber Realignment and Cell Contractility.

Our model consists of a closely packed spheroidal cluster of contractile cells with radius (R = 200 μm) embedded in a nonlinear fibrous material representing the ECM (Fig. 2A). The 3D system of the spheroid and the surrounding matrix can be modeled by adopting the spherical coordinate system $(r,\theta ,\hspace{0.17em}\phi )$, where $r$, $\theta$, and $\phi$ correspond to the radial, angular, and azimuthal directions, respectively.

Fig. 2.

Model of cell invasion from a tumor spheroid into a fibrous matrix. (A) The total free energy (U_total) of cells within a tumor spheroid embedded in a matrix is a function of the chemomechanical energy of the cells (U_cell), the mechanical energy of the matrix (U_matrix), and the adhesion energy associated with cellular adhesions (U_adhesion). The Ca²⁺ pathway and the Rho pathway, which affect cell contractility and the ability of cells to move through a matrix, are implemented in our model. (B) Realignment of the matrix fibers in response to the contractility of the cells. The red curve shows the radial stress, and the blue curve shows the magnitude of the transverse stress (without the negative sign). Radial and transverse directions are shown in the matrix. The stiffness of the matrix in the radial and transverse directions are denoted $E_r^m$ and $E_{\theta }^m$, respectively. (C) The concentration profile of the cells, c(r), as a function of the distance from the center of the cluster, r. The initial radius, R, is marked by the dashed line. For the invasive cluster, three regions are defined: cluster (r < r₀), invaded region (r₀ < r < r₁), and the matrix (r₁ < r). The parameter λ governs the extent of the invaded region in such a way that, with increasing λ the size of the invaded region increases.

Cell contractility, required to force the cells through the matrix, is generated by cross-bridge sliding of the actin filaments due to the activity of myosins. Because each myosin motor behaves like a force “dipole,” the volume averaged density of the motors, or the contractility is treated as a symmetric tensor, ${\rho }_{ij}$ (25). In the quiescent state, that is, in the absence of external mechanical forces, the attachment of the myosins to the cytoskeleton has an intrinsic turnover rate that is determined by the molecular binding and unbinding of myosins to the cytoskeleton, leading to a steady-state contractility that is isotropic. In this case, the contractility tensor is isotropic with the components that are denoted by ${\rho }_0$. On the other hand, as cells respond to the mechanical loads, mechanotransductive feedback mechanisms that alter the concentration of the attached myosins to the actin network can be triggered. In Fig. 2A, we have illustrated two such mechanisms, namely, the Ca²⁺ and the Rho pathways. When the cell is subject to tensile forces, the cell activates the mechanotransductive ion channels and increases intracellular Ca²⁺ concentration, leading to the formation of Ca/calmodulin complex and phosphorylation of the myosin regulatory light chain (MLC), which leads to an increase in the binding rate of myosin to the actin network (26). Similarly, the activation of the Rho pathway via the ROCK-mediated phosphorylation of myosin phosphatase target (MYPT), up-regulates the binding of the myosins to the actin filaments and enhances the contractility of the cell. Under homeostatic conditions, the stress fiber network applies tensile forces on the molecular complex at the focal adhesions, which causes a conformational change of vinculin and p130Cas and exposes the binding sites of Src family kinases SFKs (27). SFKs influence Rho-GTPases by controlling the activity of guanine nucleotide exchange factors (GEFs) and GTPase-activating proteins (GAPs). The increased activity of Rho promotes ROCK-mediated phosphorylation of MYPT, which ultimately results in increased contractility (28). This dependence of the contractility tensor on the cellular strains ${\epsilon }_{ij}^c$ can be obtained from the free energy, $U_{\mathrm{cell}}({\epsilon }_{ij}^c,{\rho }_{ij})$. By implementing this stress-dependent contractility in our model, we can obtain the evolution of cell-morphological characteristics such as the polarization and the elongation as the cells leave the spheroid and invade into the matrix. Following our previous work (25), we have presented the derivation of this energy function in SI Materials and Methods, The Chemomechanical Model for the Response of the Cell to the External Stresses, and shown that the free energy decreases with increasing external stresses as a consequence of increased and polarized recruitment of myosins.

Collagen fibers in the ECM are oriented randomly in the absence of external stresses. In the presence of the contractile forces exerted by the tumor spheroid, the matrix is in the state of tensile strain in the radial direction (perpendicular to the tumor–matrix boundary), whereas the strains are compressive in the angular (transverse) direction. When the local strain in the matrix is tensile and is above a critical threshold (${\epsilon }_{cr}\sim 5\%$), the fibrous matrix becomes considerably aligned (anisotropic) and undergoes “strain stiffening” in the direction of the maximum principal strain (29, 30) (Fig. 2B). Strain stiffening refers to the increase in the stiffness of the matrix due to the transition from random to aligned fiber arrangement. To incorporate the realignment of the fibers caused by the spheroid contractility, as shown in Fig. 2B, we express the elastic modulus of the matrix in the aligned (radial direction) ($E_r^m$) and angular (transverse direction) ($E_{\theta }^m$) directions with two distinct parameters that depend on the radial strain (30):

$$E_r^m=\{\begin{array}{cc}{E}_{\theta }^m=E^m& {\epsilon }_{rr}^m<{\epsilon }_{cr}\\ E_{\theta }^m{\left(\frac{{\epsilon }_{rr}}{{\epsilon }_{cr}}\right)}^n& {\epsilon }_{rr}^m>{\epsilon }_{cr}\end{array},$$ [1]

where ${\epsilon }_{rr}^m$ is the radial strain and $E^m$ is the linear elastic modulus of the matrix. Here, we have introduced a parameter ($n$), which represents the degree of the matrix strain stiffening due to realignment of the fibers, in such a way that $n=0$ corresponds to the matrices that are mechanically isotropic in all directions (such as nonfibrous matrices). The strain energy function of the matrix is presented in SI Materials and Methods, Model for Fiber Realignment and Strain Stiffening of the Matrix and Fig. S3.

Fig. S3.

Radial displacement field in the matrix surrounding a cell spheroid. Displacement decays rapidly in randomly oriented matrices, whereas the displacement field is long-ranged in the aligned matrices. We have used the parameters $r_0=0.75R$ and $\lambda =1$. Also, $E_r^m/E_{\theta }^m=1$ and $E_r^m/E_{\theta }^m=4$ in the random and aligned matrices, respectively.

By incorporating the interplay between matrix fiber realignment and strain stiffening with the activation of Rho and Ca²⁺ molecular pathways, our model predicts the driving force for cell invasion. Specifically, in response to the fiber realignment and subsequent strain stiffening of the matrix due to the intrinsic contractility of the spheroid, large tensile stresses are exerted on the cells. Consequently, the Ca²⁺ and Rho pathway are activated, and the cell contractility is increased. In turn, in the presence of highly contractile cells, the matrix is further stretched and more fibers become realigned, perpendicular to the surface of the spheroid. This process initiates a two-way feedback loop between the cell contractility and the matrix realignment and strain stiffening. As this process progresses, the matrix fibers become highly aligned and the cells become sufficiently contractile to break free from intercellular adhesions and move within the matrix (1, 6).

Our computational model employs an energy-based approach, where the total free energy ($U_{\mathrm{total}}$) of the system is calculated to determine the dynamics of the cell invasion (Fig. 2A). Here, instead of tracking each cell individually, we adopt a homogenized model, where, for a representative element located at the distance $r$ from the center of the cluster, $c\left(r\right)$ represents the local concentration of the cells (defined as the volume of the cells divided by the volume of the total element). In the representative element, we have assumed that cells are placed in “series” with the ECM. This homogenized description of the representative element is detailed in SI Materials and Methods, Homogenized Description of the Cell Invasion Region and Fig. S4. At the time denoted by $t$, we assume that this cell concentration follows the profile that depends on three variables: the radius of the spheroid $r_0\left(t\right)$, cell invasion distance $r_1\left(t\right)$, and a dimensionless parameter $\lambda \left(t\right)$, which governs the extent and spatial variation of cell concentration in the invaded region (Fig. 2C):

$$c\left(r\right)=\{\begin{array}{ccc}1& r<r_0& \text{cluster}\\ \frac{r_1-r}{r_1-r_0}{e}^{-\lambda \hspace{0.17em}\frac{r-r_0}{r_1-r_0}}& r_0<r<r_1& \text{invaded region}\\ 0& r_1<r& \text{matrix}\end{array}.$$ [2]

Fig. S4.

The arrangement of the contractile cells and the matrix elements in the invaded region. The cell–matrix representative unit cell is shown. Cell element is composed of the active and passive parts and is placed “in series” with the matrix element. Cell concentration decays gradually along the radial direction and reaches zero at $r=r_1$.

In the invaded region, we assume that the concentration of the cells decays exponentially with distance and finally reaches zero at the point denoted by $r_1\left(t\right)$. As shown in Fig. 2C, $\lambda \left(t\right)=0$ and $\lambda \left(t\right)>0$ correspond to linear and the exponential profiles for the cell densities, respectively. In our experiments, because the cells are treated with mitomycin C, cell proliferation is negligible. Because the total number of cells remains constant, we can reduce the number of the independent variables that characterize the cell concentration profile from three [$r_0\left(t\right)$, $r_1\left(t\right)$, $\lambda \left(t\right)$] to two [$r_0\left(t\right)$, $\lambda \left(t\right)$], by using the following:

$$\frac{4}{3}\pi \left(R^3-r_0^3\right)={\displaystyle \underset{r_0}{\overset{r_1}{\int }}}\frac{r_1-r}{r_1-r_0}{e}^{-\lambda \hspace{0.17em}\frac{r-r_0}{r_1-r_0}}\hspace{0.17em}4\pi r^{2}dr.$$ [3]

The left-hand side of Eq. 3, accounts for the difference between the volumes of the intact and invasive spheroids, and the right-hand side is the volume of the cells within the invaded region.

Next, we calculate the free-energy density stored in the representative element located at point $r$, as a function of the concentration $c\left(r\right)$, by considering the following contributions to the free energy of the system (Fig. 2A):

• i)The chemomechanical energy associated with the deformation, intrinsic contractility, and the activation of the molecular signaling pathways of the cells [denoted by $U_{\mathrm{cell}}\left({\epsilon }_{ij}^c\left(r\right),{\rho }_{ij}\left(c\right),c\left(r\right)\right)$, where ${\epsilon }_{ij}^c\left(r\right)$ and ${\rho }_{ij}\left(c\right)$ are the strain and polarization tensors of the cells at point $r$].
• ii)The mechanical energy due to deformation, realignment, and strain stiffening of the matrix fibers [$U_{\mathrm{matrix}}\left({\epsilon }_{ij}^m\left(r\right),c\left(r\right)\right)$, where ${\epsilon }_{ij}^m\left(r\right)$ is the mechanical strain in the matrix].
• iii)The adhesion energy associated with the cellular adhesions, $U_{\mathrm{adhesion}}\left(c\left(r\right)\right)$. This term is determined from the dissociation of cell–cell junctions followed by the formation of new adhesions between the cells and the matrix. To calculate this energy, we determine the change in the cellular adhesions during the cell invasion and use cell–cell (${\gamma }_{c-c}$) and cell–matrix (${\gamma }_{c-m}$) adhesion energy densities (detailed in SI Materials and Methods, Adhesion Energy Accounting for the Cell–Cell and Cell–Matrix Junctions).

For a given cell concentration profile $c\left(r\right)$, the total free energy of the system ($U_{\mathrm{total}}$) is calculated from the following:

$$U_{\mathrm{total}}\left({\epsilon }_{ij}^{c,m}\left(r\right),{\rho }_{ij}\left(c\right),c\left(r\right)\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}}\left(U_{\mathrm{cell}}\left({\epsilon }_{ij}^c\left(r\right),{\rho }_{ij}\left(c\right),c\left(r\right)\right)+U_{\mathrm{matrix}}\left({\epsilon }_{ij}^m\left(r\right),c\left(r\right)\right)\right)4\pi r^{2}dr+\hspace{0.17em}{U}_{\mathrm{adhesion}}\left(c\left(r\right)\right).$$ [4]

For an invasive spheroid at time t, the strain and the contractility of the cells can be determined by minimizing this total free-energy function with respect to the strains (${\epsilon }_{ij}^c,{\epsilon }_{ij}^m$) and cell polarization (${\rho }_{ij}$). We solved the evolution equations using the parameters given in Table S1. By obtaining the displacement field, the total free energy of the system can be calculated from Eq. 4. Furthermore, by repeating this process for different cell concentration profiles $c\left(r\right)$, the evolution of the total free energy as the function of the cell concentration and at different stages of the cell invasion can be obtained.

Table S1.

The parameters used in the model

Parameter	Symbol	Value	Reference
$E$	Cell elastic modulus	0.3 kPa	Refs. 57 and 58
$\nu$	Cell Poisson’s ratio	0.3	Estimated
$K$	Cell bulk modulus	0.25 kPa	Ref. 25
$\mu$	Cell shear modulus	0.12 kPa	Ref. 25
${\rho }_0$	Cell initial motor density	0.15 kPa	Estimated
${\epsilon }_0$	Cell stress-free contractility	0.6	Calculated
${\alpha }_v$	Chemomechanical feedback parameter	15 kPa−1	Estimated
${\alpha }_d$	Chemomechanical feedback parameter	25 kPa−1	Estimated
$\beta$	Motor turnover parameter	30 kPa−1	In the range given in ref. 25
$R$	Cluster initial radius	200 μm	Measured
${\gamma }_{c-c}$	Cell–cell adhesion energy	1 mJ/m2	In the range given in refs. 32–34
${\gamma }_{c-m}$	Cell–matrix adhesion energy	0.1 mJ/m2	In the range given in refs. 32–34
$r_{\mathrm{cell}}$	Radius of a single cell	5 μm	Ref. 59
$\phi$	Cell packing density	70%	Estimated
$E^m$	Matrix linear elastic modulus	0.02–1.5 kPa	Estimated
${\nu }_p,{\nu }_{tp}$	Matrix Poisson’s ratios	0.3	Estimated
$n$	Matrix strain stiffening	2.5	In the range given in ref. 30
${\epsilon }_{cr}$	Matrix critical strain	0.05	Ref. 30

The Interplay Between Cell Contractility and Matrix Fiber Realignment Induces Polarization in the Invading Cells.

The increased stiffness of the matrix in the direction of fiber alignment (radial direction $E_r^m$; Fig. 2B) leads to large tensile forces on the cells, which in turn results in the activation of molecular pathways and the up-regulation of contractility in the radial direction (${\rho }_{rr}$). On the other hand, in the transverse direction ($E_{\theta }^m$, perpendicular to the radial direction) where the matrix stiffness is smaller, the contractility (${\rho }_{\theta \theta }$) is significantly smaller compared with the radial direction (${\rho }_{rr}>{\rho }_{\theta \theta }$). This difference in the radial and transverse directions, proportional to the degree of the matrix fiber alignment, induces polarization of the cells. The polarization, which is a measure of the aspect ratios of the elongated cells, can be calculated from the ratio of the contractility in these directions (${\rho }_{rr}/{\rho }_{\theta \theta }$). As cells align the fibers in the matrix, the enhancement in the recruitment of myosin motors that follows, leads to the reduction in the total free energy of the system (Fig. 3A). This decrease in the energy is more pronounced in stiffer matrices (Fig. 3A). As the fibers align in the radial direction, the cell polarization increases and cells adopt an elongated morphology. The polarization of the cells also increases with the stiffness of the matrix (Fig. 3B). We have pictorially depicted how the two-way feedback loop induces the highly aligned organization of the fibers and elongation of the cells at the periphery of the spheroid in Fig. 3C.

Fig. 3.

The two-way feedback loop between cell contractility and matrix fiber realignment. (A) As the cells align the fibers, up-regulation in the recruitment of myosin motors that follows leads to a reduction in the total free energy of the system. (B) Meanwhile, the cells adopt a polarized morphology in proportion to the stiffness of the matrix. The green arrow shows that, with increasing elastic modulus of the matrix (E^m), the polarization increases. (C) Schematic showing the direct reciprocity between fiber alignment and cell polarization. r₀ = 0.75R and λ = 1 in all figures. Fiber alignment is calculated from $E_r^m$ = $E_{\theta }^m$ and cell polarization is ρ_rr/ρ_θθ. Energies are normalized with respect to the energy of E^m = 0.3 kPa when $E_r^m$/$E_{\theta }^m$ = 1.

In agreement with the previous fibrosarcoma studies (31) and our melanoma cell invasion studies (Fig. 1A), our model shows that, at optimal collagen stiffness, the cells within the spheroid have a rounded appearance (${\rho }_{rr}/{\rho }_{\theta \theta }=1$), whereas the cells located at the periphery of the cluster (in the invaded region) are highly elongated (${\rho }_{rr}/{\rho }_{\theta \theta }>1$) (Fig. 4A). Furthermore, by increasing the elastic modulus of the matrix from E^m = 0.3 to 0.9 kPa, the model shows an increase in cell polarization (Fig. 4A), in agreement with our experiments. Moreover, increasing matrix stiffness decreases the realignment of the fibers (Fig. 4B), because stiffer matrices show larger resistance to deformations. We also find that, once the cells invade into the matrix, those located close to the spheroid are more elongated than the cells that have invaded further into the matrix. This agrees with the spatial variation of the fiber alignment and that the fibers are highly aligned near the spheroid and become random with increasing distance from the spheroid (as the elastic stress decays with the distance from the surface of the spheroid) (Fig. 4B), therefore losing the ability to polarize the cells in regions far from the spheroid ($r>0.8\hspace{0.17em}{r}_1$). In addition, temporal evolution of cell polarization shows that fiber realignment (Fig. 4B) and therefore cell elongation (Fig. 4A) increase with time. With the progression of the cell invasion, the extent of the invaded region [$r_1\left(t\right)$ in Fig. 2C] increases. Due to the contractility of the cells, the matrix in this region has highly aligned fibers with enhanced stiffness in the radial direction. Therefore, for the cells located at the periphery of the spheroid, the resistance to the contraction in the radial direction increases, which leads to elevated recruitment of myosins and therefore the increase in matrix realignment and cell elongation with time. Overall, our model shows that cells adopt a more elongated morphology as we increase the stiffness of the matrix. We next incorporate our model to show that, along with the cell polarization, the driving force for cell invasion also increases with the stiffness of the matrix.

Fig. 4.

Cell contractility and matrix realignment increase cell polarization of invading cells. (A) Polarization of the cells located at (r) as the function of the elastic modulus of the matrix. Cells inside the cluster (r < r₀) are not polarized (ρ_rr/ρ_θθ = 1). Cells in the invaded region (r > r₀) are highly polarized (ρ_rr/ρ_θθ > 1). The green arrow shows that the polarization increases with the stiffness of the matrix (E^m). Note that, within the invaded region, the polarization decays with the distance from the spheroid. The top and the bottom rows correspond to two different time instances of the cell invasion. The current radius of the spheroid (r₀) is r₀ = 0.75R and r₀ = 0.65R in the top and bottom rows, respectively. These results show that the cell polarization (or elongation) is increasing with the progression of the cell invasion. (B) Matrix realignment also increases with time, suggesting that cell polarization is directly proportional to the matrix realignment. Matrix alignment is determined from the ratio of the matrix elastic moduli in the radial and transverse directions. Also, λ = 1 in all of the figures.

The Driving Force of Cell Invasion Increases with the Stiffness of the Matrix.

Total free energy of the system ($U_{\mathrm{total}}$) described above is used to calculate the driving force for cell invasion. Specifically, the change in the total energy associated with a change in the cell concentration [$c\left(r\right)$], or the derivative of the energy with respect to the local cell concentration [$\partial U_{\mathrm{total}}({\epsilon }_{ij},{\rho }_{ij},c)/\partial c$], gives the driving force. To examine the dependence of the driving force on the matrix stiffness, we varied the stiffness of the matrix and calculated the change in the total free energy as a function of the change in cell concentration, parametrized by the current radius of the spheroid $r_0\left(t\right),$ and the extent of the cell invasion within the matrix $\lambda \left(t\right)$. If the change in the energy is negative, cell invasion is favorable. Alternatively, a positive change in energy indicates that the spheroid is stable against invasion.

The difference between the cell–cell and the cell–matrix adhesion energies determines the integrity of the cell clusters in the matrix in the absence of the cellular contractility. In the current model, we assume that the adhesion energy associated with the cell–cell junctions is higher than the energy of the cell–matrix adhesion (${\gamma }_{c-c}=10\hspace{0.17em}{\gamma }_{c-m}=1$ mJ/m² in the range given in refs. 32–34), indicating that, in the absence of the external mechanical forces, cells prefer to adhere to other cells and thus the spheroid is stable against dissolution. Therefore, if the contractility of the cells is ignored, our model shows that the energy change associated with the spheroid dissociation is positive, and thus in this case the cell invasion is energetically unfavorable (Fig. 5A). This is in agreement with many studies showing that the cell contractility is required to initiate the cell invasion (1, 4, 11, 35). By including cell contractility, the effect of the matrix alignment and stiffness in promoting the cell invasion becomes evident. When the stiffness of the matrix is small ($E^m=0.02$ kPa in Fig. 5A), adhesions between the cells prevent the dissolution of the cluster because the change in energy associated with cell invasion is positive. In this case, cells in the spheroid contract easily and realign the matrix fibers in the radial direction; however, the matrix is not sufficiently stiff to induce large tensile forces to activate the mechanosensitive pathways in the cells. By increasing the elastic modulus of the matrix to E^m = 0.15 and 0.6 kPa, the role of the two-way feedback loop between the matrix stiffness and cell contractility in providing the cell invasion driving force becomes more significant. In this case, in response to the high resistance from the matrix, cells can recruit more myosin motors through the activation of the Ca²⁺ and Rho molecular pathways, a process that lowers the overall free energy. Once the cell contractility is large enough to disengage the cell–cell adhesions, invasion occurs spontaneously. Therefore, based on this criterion, we can identify a critical elastic modulus for the ECM ($E^m=0.15$ kPa), below which the tumor spheroid is stable and beyond which cell invasion becomes favorable. Together, these results show that, by increasing the stiffness of the matrix, the driving force for cell invasion increases. Below the critical stiffness, this driving force cannot overcome the cell adhesions and therefore the spheroids remain stable. Although beyond the critical stiffness, the driving force can break the adhesions and induce invasion.

Fig. 5.

Biphasic effect of matrix concentration on cell invasion. (A) Change in the total free energy of the system (ΔU_total) as a function of the radius of the spheroid (r₀) and the parameter that governs the extent of the invaded region (λ). The elastic modulus of the surrounding matrix is varied between 0.02 and 0.60 kPa. The change in the energy is normalized with respect to the initial energy of the system (at r₀ = R, λ = 0). The metastatic pathway starting from the full spheroid is also shown (green arrow line connecting the origin to an arbitrary point shown by the yellow cross). In the absence of cell contractility or for the spheroid placed in the soft matrix (0.02 kPa), cell invasion is accompanied by an increase in the free energy. Alternatively, increasing the matrix stiffness beyond the critical stiffness (0.15 kPa) leads to the reduction of the energy and spontaneous invasion of the cells. (B) Increasing ligand density decreases the matrix critical elastic modulus (blue line). (C) At the concentration of collagen beyond the critical value (0.5 mg/mL), melanoma cells leave the cluster and invade into the 3D collagen matrix. (Scale bars: 500 µm.) The tangent elastic modulus between 3 and 7% axial strains (∼0.16 to ∼0.75 kPa) at 0.5, 1.0, and 2.0 mg/mL collagen concentrations is also shown from ref. 53. (D) Quantitative analysis of the melanoma cell invasion shows a biphasic response to the concentration of collagen. **P < 0.0018, ***P < 0.0009, and ****P < 0.0001. (E and F) Three-dimensional imaging of the tumor cells leaving the spheroid and invading the surrounding matrix with (E) 1.0 mg/mL and (F) 2.0 mg/mL collagen. Cells (red) are aligned with collagen fibers (green) in the radial direction, perpendicular to the boundary of the spheroid (blue dashed line). At 1 mg/mL collagen, cells invade rapidly away from the sphere, whereas at 2 mg/mL collagen, cells are located closer to the spheroid.

In addition to enhancing the stiffness of the matrix, increasing collagen concentration in the ECM also increases the density of the cell-adhesive ligands, which also promotes cell invasion. In the current model, the adhesion energy associated with the cell–matrix junctions (${\gamma }_{c-m}$ in Fig. 1A) represents the strength and number of the cell–matrix adhesions and, therefore, can be increased in proportion to the density of the available ligands. As shown in Fig. 5B, the model predicts that, by increasing the ligand density, the measured matrix critical stiffness decreases and cells exhibit more preference to invade the matrix. In agreement with this finding, previous experimental studies aimed to alter ligand density independent of the matrix protein concentration have shown that increasing ligand density from dilute to intermediate densities, induces cell migration (18).

Tumor Cell Invasion Exhibits a Biphasic Response to the Stiffness of the ECM.

Next, we determine the invasiveness of melanoma cells within collagen matrices as a function of concentration. At low concentrations of collagen (0.1 mg/mL), the melanoma spheroids are stable over time and the integrity of the cluster is maintained (Fig. 5 C and D). At higher concentrations (0.5 and 1.0 mg/mL), the spheroids disintegrate into elongated motile cells invading the matrix, an indicator of a metastatic phenotype. In agreement with our model results (Fig. 5A), a critical collagen concentration (∼0.5 mg/mL) can be identified, which demarcates the spheroids into stable vs. invasive phenotypes. We further increased the collagen concentration to examine the stability of the spheroids placed in highly dense matrices (2.0 mg/mL). In this case, although the cells located at the periphery of the spheroids show the elongated morphology characteristic of a motile phenotype (Figs. 1A and 5C), cell invasion within the matrix is reduced significantly. Furthermore, by labeling the spheroids with calcein and using multiphoton imaging, we show that, at 1 mg/mL collagen, cells are aligning as predicted with the collagen fibers and invade rapidly away from the sphere, whereas at 2 mg/mL collagen, the cells are restricted in their motion by the density of the collagen and remain closer to the surface of the spheroid (Fig. 5 E and F). This suggests a biphasic behavior for the response of the cell clusters with respect to the concentration of collagen. To eliminate the possibility that activation of matrix metalloproteinases (MMPs) was affected by the changing density of collagen, we repeated these assays in the presence of MMP inhibitors. We found that, although overall invasion decreased in the presence of MMP inhibitors, the biphasic behavior of the cells did not change (Fig. S5). We also examined the dependence of the cell invasion on the activity of the Rho pathway and validated the predictions of our model with experiment. In the presence of the Rho inhibitor, Y27632, invasion of melanoma cells in the two concentrations of collagen that are the most invasive (0.5 and 1.0 mg/mL) is reduced (Fig. S6A). In agreement, our model also shows that, in the absence of the feedback mechanisms (mediated by the Rho pathway), the total free energy of the system increases as the cells invade and therefore invasion is not favored (Fig. S6B). Furthermore, in this case, our model shows that increasing the matrix stiffness cannot promote the driving force for invasion, underscoring the role played by the two-way feedback in increasing the driving force for the invasion.

Fig. S5.

Biphasic invasive behavior of cells does not change in the presence of MMP inhibitors. (A) Quantification of invasion of 1205Lu melanoma cells, treated with 500 nM MMP2/9 inhibitor, from a 3D spheroid into a fibrous matrix of increasing collagen concentration. (B) Quantification of invasion of 1205Lu melanoma cells, treated with 1 μM MMP2/9 inhibitor, from a 3D spheroid into a fibrous matrix of increasing collagen concentration. ****P < 0.0001; **P < 0.007.

Fig. S6.

(A) Treating the cells with the Rho inhibitor, Y27632, leads to lower levels of cell invasion. In the presence of the Rho inhibitor, Y27632, invasion of melanoma cells in the two concentrations of collagen that are the most invasive (0.5 and 1 mg/mL) is inhibited. (**P < 0.0018, ***P < 0.0009.) (B) In agreement with the experiment, by inhibiting the molecular pathways such as Ca²⁺ and Rho in our model, cell invasion leads to an increase in free energy, and therefore invasion is less favorable. The change in the energy is normalized with respect to the initial energy of the system (at $r_0=r_1=R$).

Invasion Rate Is Determined by the Two-Way Mechanochemical Feedback and the Matrix Pore Size.

In order for the cells to invade, the driving forces from cell contractility and matrix alignment have to overcome the opposing forces that resist the movement of the cells within the matrix (Fig. 6A). These resisting forces arise from various factors such as the drag force generated due to the viscosity of the matrix (21), the ability of the cells to probe the surrounding matrix (through filopodia, for example) and establish adhesions with ligands (23), the stiffness and shape of the cell nucleus (36), and the pore size of the matrix. Here, we model the effect of these factors by introducing a parameter, $M$, which represents the “effective” kinetic mobility of the cells within the matrix. Therefore, to obtain the rate of the cell invasion, we solve the kinetic equations for the cell concentration profile characterized by the radii of the shrinking spheroid ($r_0$) and the region invaded by the cells ($r_1$):

$$\begin{array}{c}\frac{\partial U_{\mathrm{total}}\left(r_0,r_1\right)}{\partial r_0}=-\frac{1}{M}\hspace{0.17em}\frac{\partial r_0}{\partial t}\\ \frac{\partial U_{\mathrm{total}}\left(r_0,r_1\right)}{\partial r_1}=-\frac{1}{M}\hspace{0.17em}\frac{\partial r_1}{\partial t}\end{array}.$$ [5]

Fig. 6.

The kinetics of the cell invasion as a function of the matrix stiffness. (A) Schematic showing the dynamics of the forces involved in cell invasion. The driving force from cell contractility has to overcome the forces resisting cell movement, leading to the invasion of the cells into the matrix. (B) The shrinking of the spheroid radius r₀ and (C) the advance of the front line r₁ as the function of the matrix elastic modulus and time. The rate of the cell invasion shows the biphasic behavior in response to the stiffness of the matrix. Also, the metastatic cell migration predicted by our model follows superdiffusive behavior (with the exponent larger than 0.5). Time is normalized by multiplying by M U_total(r₀ = r₁ = R, E^m = 0.3 kPa)/R².

In these equations, the left- and right-hand sides represent the driving and opposing forces, respectively. To include the steric hindrance effects associated with the decrease in interfibrillar pore size ($d$) at high concentrations of collagen, we use the experimental data that suggest that permeability is proportional to the area of the voids, $M\propto d^2$ (37). Given that the pore size scales with collagen concentration ($\rho$) such that $d\propto {\rho }^{-1/2}$ (38), and the matrix stiffness scales with collagen concentration such that $E^m\propto {\rho }^{1.7}$ (39), we assume that the permeability at high matrix stiffnesses $\left(E^m>0.6\mathrm{kPa}\right)$ decreases with the matrix stiffness, $M\propto {\left(E^m\right)}^{-0.6}$. The total free energy, $U_{\mathrm{total}}$ in the left-hand side, was also evaluated as a function of the cell concentration profile characterized by $r_0$ and $r_1$.

By solving Eq. 5, we obtain the rate of the cell invasion as a function of the matrix stiffness. To compare the rate of the invasion obtained for different matrices, we fit a power-law to relate the change in the radius of the spheroid ($r_0$) and the extent of the invasion region ($r_1$) with time ($r_0\sim t^{-\tau }$ and $r_1\sim t^{\tau }$) and compare the calculated rate exponents ($\tau$) as a function of the matrix stiffness. As we showed earlier, by increasing the stiffness of the fibrous matrix, the driving force of invasion increases and cells become more elongated. Correspondingly, by increasing the elastic modulus of the matrix from $E^m=0.3$ kPa, the rate of the invasion predicted by our model also increases, until reaching a maximum value at $E^m=0.6$ kPa (Fig. 6 B and C). Meanwhile, increasing the matrix stiffness also has the effect of decreasing the size of the interfibrillar voids available for the movement of the cells. Specifically, at very high matrix elastic moduli, the opposing forces caused by the small pore size impose considerable restrictions on the movement of the cells and hinder the invasion of the cells (beyond $E^m=0.6$ kPa in Fig. 6 B and C). Therefore, highly elongated cells create sharp protrusions at the periphery of the spheroid, similar to the invading melanoma cells (2.0 mg/mL in Fig. 1A). These results predict an increase and decrease in the invasion rate with the matrix stiffness in addition to the earlier determined critical stiffness corresponding to the onset of the cell invasion (Fig. 5A) and provide a quantitative explanation for the biphasic response of the tumor spheroids to the stiffness of the ECM (Fig. S7).

Fig. S7.

The biphasic response of the cell invasion to the stiffness of the surrounding matrix predicted by our model.

Tumor Cell Migration Within Collagen Matrices Is Superdiffusive.

Comparison between the rate of the cell invasion with the velocity for free diffusive motion of the cells in 3D matrices can explain the kinetics of cell migration. Free diffusion corresponds to the movement of the noninteracting cells in the absence of external guiding factors. In this case, the migration of the cells follows Brownian motion where the propagation distance ($r$) increases with time ($t$) as $r\propto t^{0.5}$. On the other hand, “directed” motion (or superdiffusion) refers to the persistent movement of the cells under the influence of an imposed field, such as the driving force caused by the two-way feedback mechanism. In this case, we expect that the propagation distance (r) increases with time (t) with an exponent that is bigger than 0.5 ($r\propto t^{\tau }$ and $\tau >0.5$). Our model shows that the predicted rate exponents corresponding to the change in $r_0\left(t\right)$ and $r_1\left(t\right)$ are bigger than 0.5, implying that the cell movement is directed (Fig. 6 B and C). Although the rate of the cell invasion is changing with the stiffness of the matrix, our model predicts that cell migration is superdiffusive, independent of the stiffness of the matrix. We also examined the migration of imaginary “tracers” (or cells) initially located in the cluster (at $r^{\ast }/R=0.9$ and $r^{\ast }/R=0.8$) and monitored their movement as they left the spheroid and entered the matrix. The movement of the tracers also shows the superdiffusive behavior, directed by the influence of the matrix mechanics dependent on the mechanochemical driving forces (Fig. S8).

Fig. S8.

The movement of two tracers initially located at $r^{\ast }/R=0.9$ (Top) and $r^{\ast }/R=0.8$ (Bottom) in the matrix with normalized time. Tracers leave the cluster as they become exposed to the matrix. The propagation of the tracers in the matrix follows the superdiffusive behavior, indicating that the cell migration process is directed under the driving force generated by the matrix.

Cells Are More Elongated in Matrices with Lower Critical Strain and Higher Strain-Stiffening Response.

The parameters controlling matrix realignment such as the matrix critical strain (${\epsilon }_{cr}$) and strain stiffening ($n$) depend on the microstructural properties of the matrix, and can be tuned based on collagen concentration, gelation temperature, and pH. For example, by decreasing the gelation temperature, the matrix critical strain (${\epsilon }_{cr}$) decreases (40–42). Also, at certain gelation temperatures (for example, 37 °C), increasing collagen concentration increases the critical strain (${\epsilon }_{cr}$) (41, 43). Therefore, we can use our model to predict the shape of the cells, at different levels of ${\epsilon }_{cr}$ and $n$. As shown in Fig. S9A, the model predicts that, upon reducing the critical strain (${\epsilon }_{cr}$), the cells adopt a more elongated morphology, because the matrix with lower critical strain shows higher propensity for fiber realignment and therefore can induce higher polarization of the cells. The strain-stiffening parameter ($n$) can also be tuned based on the ability of the matrix to polarize in the direction associated with alignment of the fibers. Fig. S9B shows that decreasing this parameter decreases the matrix realignment and therefore cell polarization.

Fig. S9.

Effect of the matrix critical strain and strain stiffening on cell polarization and matrix alignment. (A) Decreasing the matrix critical strain (ε_cr) and (B) matrix strain stiffening (n) increases the matrix fiber realignment and cell polarization. This is consistent with cells cultured in nonfibrous matrices such as BME (n = 0), adopting a more rounded morphology. E^m = 0.6 kPa, r₀ = 0.75R, and λ = 1 in all figures.

Our model can also be used to explain the rounded morphology of the cells embedded within nonfibrous matrices such as basement membrane extracts (BMEs) (44, 45). The model predicts that, in this case (Fig. S9B with $n=0$), cell polarization decreases substantially, demonstrating that matrix fiber realignment is the main driver of the elongated morphology and confirming the experimental observations (44, 45). In fibrous matrices, increase in the matrix stiffness increases contractility only in the radial direction, leading to the emergence of the highly elongated and polarized cells. On the contrary, in the case of isotropic nonfibrous ECMs, increase in the matrix stiffness leads to a comparable increase in contractility in all directions, which does not lead to substantial polarization of the cells. This explains why epithelial cells in BME could have significantly lower velocity and polarization, and therefore BME can separate the layers of epithelial cells from the underlying connective tissue stroma (45, 46).

SI Materials and Methods

The Chemomechanical Model for the Response of the Cell to the External Stresses.

The cells are treated using a combination of passive mechanical and active chemomechanical elements. The passive element represents the stiffness arising from the cytoskeleton in resisting cellular deformations. We assume that the cytoskeleton is elastic and its elastic modulus and Poisson’s ratio are denoted by$E$ and $\nu$, respectively.

Following our previous work (25), the total energy [$U_{\text{cell}}({\epsilon }_{ij}^c,{\rho }_{ij})$] of the cell associated with the elastic strain, external force, and the myosin motor works can be written as follows:

$$U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)=\frac{K}{2}{\left({\epsilon }_{kk}^c\right)}^2+\mu {\stackrel{\sim }{\epsilon }}_{ij}^c{\stackrel{\sim }{\epsilon }}_{ij}^c-\frac{1}{3}{\displaystyle \underset{0}{\overset{{\epsilon }_{kk}^c}{\int }}{\sigma }_{kk}^{c}d{\epsilon }_{kk}^c}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{\epsilon }}_{ij}^c}{\int }}{\stackrel{\sim }{\sigma }}_{ij}^{c}d{\stackrel{\sim }{\epsilon }}_{ij}^c}+\frac{1}{3}{\rho }_{kk}{\epsilon }_{kk}^c+{\stackrel{\sim }{\rho }}_{ij}{\stackrel{\sim }{\epsilon }}_{ij}^c.$$ [S1]

Here ${\epsilon }_{kk}^c$, ${\sigma }_{kk}^c$, ${\rho }_{kk}$, and ${\stackrel{\sim }{\epsilon }}_{ij}^c$, ${\stackrel{\sim }{\sigma }}_{ij}^c$, ${\stackrel{\sim }{\rho }}_{ij}$, are the volumetric and deviatoric components of the strain, stress, and contractility tensors, which can be related to the stress and strain tensors as follows:

$${\sigma }_{ij}^c={\stackrel{\sim }{\sigma }}_{ij}^c+\frac{1}{3}{\sigma }_{kk}^c{\delta }_{ij},$$

$${\epsilon }_{ij}^c={\stackrel{\sim }{\epsilon }}_{ij}^c+\frac{1}{3}{\epsilon }_{kk}^c{\delta }_{ij},$$

$${\rho }_{ij}={\stackrel{\sim }{\rho }}_{ij}+\frac{1}{3}{\rho }_{kk}{\delta }_{ij}.$$ [S2]

Also, $K=E/3(1-2\nu )$ and $\mu =E/2(1+\nu )$ are the bulk and shear moduli of the cell.

In addition to the cellular deformations, external forces activate the signaling pathways that regulate the recruitment of the molecular motors inside the cell. Under tensile loading, the influx of the Ca²⁺ from the mechanotransductive channels and the activation of the Rho pathways as described in Fig. 2A, up-regulate the recruitment of the myosins and increase the contractility. This chemomechanical recruitment of the myosins reduces the total energy of the system. Therefore, we modify Eq. S1 by including the reduction in the energy from the mechanical feedback as follows:

$$\begin{array}{l}{U}_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)=\frac{K}{2}{\left({\epsilon }_{kk}^c\right)}^2+\mu {\stackrel{\sim }{\epsilon }}_{ij}^c{\stackrel{\sim }{\epsilon }}_{ij}^c-\frac{1}{3}{\displaystyle \underset{0}{\overset{{\epsilon }_{kk}^c}{\int }}{\sigma }_{kk}^{c}d{\epsilon }_{kk}^c}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{\epsilon }}_{ij}^c}{\int }}{\stackrel{\sim }{\sigma }}_{ij}^{c}d{\stackrel{\sim }{\epsilon }}_{ij}^c}+\frac{1}{3}{\rho }_{kk}{\epsilon }_{kk}^c+{\stackrel{\sim }{\rho }}_{ij}{\stackrel{\sim }{\epsilon }}_{ij}^c\\ -\frac{1}{3}{\displaystyle \underset{0}{\overset{{\rho }_{kk}}{\int }}{\alpha }_v{\sigma }_{kk}^{c}d{\rho }_{kk}}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{\rho }}_{ij}}{\int }}{\alpha }_d{\stackrel{\sim }{\sigma }}_{ij}^{c}d{\stackrel{\sim }{\rho }}_{ij}}.\end{array}$$ [S3]

Here, we have introduced two parameters, ${\alpha }_v$ and ${\alpha }_d$, which relate the volumetric ${\sigma }_{kk}^c$ and deviatoric ${\stackrel{\sim }{\sigma }}_{ij}^c$ stress components to the change in the volumetric ${\rho }_{kk}$ and the deviatoric ${\stackrel{\sim }{\rho }}_{ij}$ components of the contractility tensors, respectively.

Although the mechanical feedback mechanism varies the concentration of the engaged myosin motors, the attachment of the myosins to the cytoskeleton has an intrinsic binding and unbinding rate that emanates from the molecular mechanism of binding and forces the concentration of the attached myosins to remain at a certain concentration (denoted by ${\rho }_0$). Any perturbation in the concentration of the myosin from this value increases the total energy and needs to be added to the total energy:

$$\begin{array}{l}{U}_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)=\frac{K}{2}{\left({\epsilon }_{kk}^c\right)}^2+\mu {\stackrel{\sim }{\epsilon }}_{ij}^c{\stackrel{\sim }{\epsilon }}_{ij}^c-\frac{1}{3}{\displaystyle \underset{0}{\overset{{\epsilon }_{kk}^c}{\int }}{\sigma }_{kk}^{c}d{\epsilon }_{kk}^c}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{\epsilon }}_{ij}^c}{\int }}{\stackrel{\sim }{\sigma }}_{ij}^{c}d{\stackrel{\sim }{\epsilon }}_{ij}^c}+\frac{1}{3}{\rho }_{kk}{\epsilon }_{kk}^c+{\stackrel{\sim }{\rho }}_{ij}{\stackrel{\sim }{\epsilon }}_{ij}^c\\ -\frac{1}{3}{\displaystyle \underset{0}{\overset{{\rho }_{kk}}{\int }}{\alpha }_v{\sigma }_{kk}^{c}d{\rho }_{kk}}-{\displaystyle \underset{0}{\overset{{\stackrel{\sim }{\rho }}_{ij}}{\int }}{\alpha }_d{\stackrel{\sim }{\sigma }}_{ij}^{c}d{\stackrel{\sim }{\rho }}_{ij}}+\frac{{\beta }_v}{2}\frac{1}{3}{\left({\rho }_{kk}-3{\rho }_0\right)}^2+\frac{1}{2}{\beta }_d{\stackrel{\sim }{\rho }}_{ij}{\stackrel{\sim }{\rho }}_{ij}.\end{array}$$ [S4]

The last term represents the chemical energy due to the perturbation of the concentration of the attached myosin from ${\rho }_0$. In this term, we have introduced two parameters, ${\beta }_v$ and ${\beta }_d$. ${\beta }_v$ is proportional to the rate of the binding and unbinding of the myosins, and ${\beta }_d$ is the entropic term proportional to the tendency of the myosins to orient randomly in the cytoskeleton. For simplicity, we assume that $\beta ={\beta }_d={\beta }_v$.

The derived energy function $U_{\text{cell}}({\epsilon }_{ij}^c,{\rho }_{ij})$ can be used to obtain the response of the contractile cell to the external loadings exerted from the matrix. To this end, first we derive the time-dependent variation of the cell energy:

$$\begin{array}{l}\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial t}=\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\rho }_{kk}}\frac{\partial {\rho }_{kk}}{\partial t}+\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\stackrel{\sim }{\rho }}_{ij}}\frac{\partial {\stackrel{\sim }{\rho }}_{ij}}{\partial t}+\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\epsilon }_{kk}^c}\frac{\partial {\epsilon }_{kk}^c}{\partial t}+\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\stackrel{\sim }{\epsilon }}_{ij}^c}\frac{\partial {\stackrel{\sim }{\epsilon }}_{ij}^c}{\partial t}\\ =\left(\frac{1}{3}{\epsilon }_{kk}^c+\frac{1}{3}\beta \left({\rho }_{kk}-3{\rho }_0\right)-\frac{1}{3}{\alpha }_v{\sigma }_{kk}^c\right)\frac{\partial {\rho }_{kk}}{\partial t}+\left({\stackrel{\sim }{\epsilon }}_{ij}^c+\beta {\stackrel{\sim }{\rho }}_{ij}-{\alpha }_d{\stackrel{\sim }{\sigma }}_{ij}^c\right)\frac{\partial {\stackrel{\sim }{\rho }}_{ij}}{\partial t}\\ +\left(K{\epsilon }_{kk}^c+\frac{1}{3}{\rho }_{kk}-\frac{1}{3}{\sigma }_{kk}^c\right)\frac{\partial {\epsilon }_{kk}^c}{\partial t}+\left(2\mu {\stackrel{\sim }{\epsilon }}_{ij}^c+{\stackrel{\sim }{\rho }}_{ij}-{\stackrel{\sim }{\sigma }}_{ij}^c\right)\frac{\partial {\stackrel{\sim }{\epsilon }}_{ij}^c}{\partial t}.\end{array}$$ [S5]

As cells respond to the tensile stress, they reduce their energy by recruiting more myosins. To ensure that the energy is decreasing with time [or $\partial U_{\text{cell}}({\epsilon }_{ij}^c,{\rho }_{ij})/\partial t<0$], we define the following rates for the elastic strain and the recruitment of the myosin:

$$\frac{\partial {\epsilon }_{kk}^c}{\partial t}=-k_{\epsilon }^v\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\epsilon }_{kk}^c}=-k_{\epsilon }^v\left(K{\epsilon }_{kk}^c+\frac{1}{3}{\rho }_{kk}-\frac{1}{3}{\sigma }_{kk}^c\right),$$

$$\frac{\partial {\stackrel{\sim }{\epsilon }}_{ij}^c}{\partial t}=-k_{\epsilon }^d\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\stackrel{\sim }{\epsilon }}_{ij}^c}=-k_{\epsilon }^d\left(2\mu {\stackrel{\sim }{\epsilon }}_{ij}^c+{\stackrel{\sim }{\rho }}_{ij}-{\stackrel{\sim }{\sigma }}_{ij}^c\right),$$

$$\frac{\partial {\rho }_{kk}}{\partial t}=-k_{\rho }^v\frac{\partial U_{\text{cell}}\left({\epsilon }_{ij}^c,{\rho }_{ij}\right)}{\partial {\rho }_{kk}}=-k_{\rho }^v\left(\frac{1}{3}{\epsilon }_{kk}^c+\frac{1}{3}\beta \left({\rho }_{kk}-3{\rho }_0\right)-\frac{1}{3}{\alpha }_v{\sigma }_{kk}^c\right),$$

$$\frac{\partial {\stackrel{\sim }{\rho }}_{ij}}{\partial t}=-k_{\rho }^d\frac{\partial U_{\text{cell}}({\epsilon }_{ij}^c,{\rho }_{ij})}{\partial {\stackrel{\sim }{\rho }}_{ij}}=-k_{\rho }^d\left({\stackrel{\sim }{\epsilon }}_{ij}^c+\beta {\stackrel{\sim }{\rho }}_{ij}-{\alpha }_d{\stackrel{\sim }{\sigma }}_{ij}^c\right).$$ [S6]

Here, $k_{\rho }^v>0$ and $k_{\rho }^d>0$ are the kinetic rate constants associated with the recruitment of the volumetric and deviatoric components of the motors, and $k_{\epsilon }^v>0$ and $k_{\epsilon }^d>0$ are the rates that govern the volumetric and deviatoric component of the strain tensor.

In the kinetic equilibrium, and when the recruitment of the myosins has reached the steady state ($\dot{\epsilon }=0$, ${\dot{\rho }}_{kk}=0$), we can simplify Eq. S6 and obtain the stress–strain and contractility–strain relations:

$$\begin{array}{l}{\rho }_{kk}=3{\overline{\rho }}_0+3{\overline{K}}_{\rho }{\epsilon }_{kk}^c{\stackrel{\sim }{\rho }}_{ij}=2{\overline{\mu }}_{\rho }{\stackrel{\sim }{\epsilon }}_{ij}^c\\ {\sigma }_{kk}^c=3{\overline{\rho }}_0+3\overline{K}{\epsilon }_{kk}^c{\stackrel{\sim }{\sigma }}_{ij}^c=2\overline{\mu }\hspace{0.17em}{\stackrel{\sim }{\epsilon }}_{ij}^c.\end{array}$$ [S7]

In Eq. S7, the effective contractility ${\overline{\rho }}_0$, effective bulk modulus $\overline{K}$, effective shear modulus $\overline{\mu }$, effective modulus for motor density ${\overline{K}}_{\rho }$ and effective modulus for the polarization ${\overline{\mu }}_{\rho }$ are defined as follows:

$$\begin{array}{l}{\overline{\rho }}_0=\frac{\beta {\rho }_0}{\beta -{\alpha }_v},3\overline{K}=\frac{3K\beta -1}{\beta -{\alpha }_v},3{\overline{K}}_{\rho }=\frac{3K{\alpha }_v-1}{\beta -{\alpha }_v}\\ 2\overline{\mu }=\frac{2\mu \beta -1}{\beta -{\alpha }_d},2{\overline{\mu }}_{\rho }=\frac{2\mu {\alpha }_d-1}{\beta -{\alpha }_d}.\end{array}$$ [S8]

The contractility of the cells in the absence of the surrounding matrix (${\sigma }_{kk}^c=0$ in Eq. S7) is given by the following:

$${\epsilon }_0=-{\overline{\rho }}_0/\overline{K}=-\beta {\rho }_{\text{0}}/\left(K\beta -1/3\right).$$ [S9]

Because the timescale associated with the activation of the molecular feedback pathways is relatively fast [in the order of seconds (54)], it is assumed that the myosin concentration equilibrates rapidly and the cell’s response to the external loadings is instantaneous.

Model for Fiber Realignment and Strain Stiffening of the Matrix.

To model the matrix with radially aligned fibers, we incorporate the stress–strain relations used for transversely isotropic materials (55):

$${\sigma }_{rr}^m=\mathrm{\Delta }\left(E_r^m\left(1-{\nu }_p^2\right){\epsilon }_{rr}^m+2E_{\theta }^m\left({\nu }_{tp}+{\nu }_p{\nu }_{tp}\right){\epsilon }_{\theta \theta }^m\right),$$

$${\sigma }_{\theta \theta }^m=\mathrm{\Delta }\left(E_{\theta }^m\left(1+{\nu }_p\right){\epsilon }_{\theta \theta }^m+E_{\theta }^m\left({\nu }_{tp}+{\nu }_p{\nu }_{tp}\right){\epsilon }_{rr}^m\right),$$ [S10]

where $E_r^m$ and $E_{\theta }^m$ are the elastic moduli in the radial and transverse directions, and ${\nu }_p\mathrm{and}{\nu }_{tp}$ are the associated Poisson’s ratios. Also, $\mathrm{\Delta }=1/(1-{\nu }_p^2-2{\nu }_{pt}{\nu }_{tp}-2{\nu }_{pt}{\nu }_p{\nu }_{tp})$ and ${\nu }_{pt}\hspace{0.17em}{E}_r^m={\nu }_{tp}\hspace{0.17em}{E}_{\theta }^m$.

By using these stress–strain relations, we can obtain the strain energy function for the fibrous matrix, which has strong polarization along the radial direction $r$:

$$U_{\text{matrix}}\left({\epsilon }_{ij}^m\right)=\frac{\mathrm{\Delta }}{2}\left(E_r^m\left(1-{\nu }_p^2\right)\hspace{0.17em}{\epsilon }_{rr}^m{\epsilon }_{rr}^m+4E_{\theta }^m\left({\nu }_{tp}+{\nu }_p{\nu }_{tp}\right){\epsilon }_{\theta \theta }^m{\epsilon }_{rr}^m+2E_{\theta }^m\left(1+{\nu }_p\right){\epsilon }_{\theta \theta }^m{\epsilon }_{\theta \theta }^m\right).$$ [S11]

Here, for simplicity, we assume that the matrix has the same Poisson’s ratio in all directions and ${\nu }_p,{\nu }_{tp}={\nu }^m$; therefore, we rewrite Eq. S11 as follows:

$$U_{\text{matrix}}\left({\epsilon }_{ij}^m\right)=\frac{\mathrm{\Delta }}{2}\left(1+{\nu }^m\right)\left(E_r^m\left(1-{\nu }^m\right){\epsilon }_{rr}^m{\epsilon }_{rr}^m+4E_{\theta }^m{\nu }^m{\epsilon }_{\theta \theta }^m{\epsilon }_{rr}^m+2E_{\theta }^m{\epsilon }_{\theta \theta }^m{\epsilon }_{\theta \theta }^m\right).$$ [S12]

Here, for simplicity, we assume that the collagen concentration does not change by reorganization of the fibers and only consider the nonlinear mechanical effects arising from the realignment of the fibers. Also, due to the relatively fast timescales associated with the stress relaxation of the collagenous matrix [in the order of 100 s (56)] compared with the migration of the cells in the matrix [in the order of 10 h (31)], the viscoelastic effects are ignored and the matrix is considered to have elastic behavior in response to the mechanical loadings.

We have previously shown that the extent of the displacement propagation from the cell boundary into the surrounding matrix depends on the alignment of the fibers (30). The displacement field decays rapidly with the distance from the cell, in the matrix with randomly oriented fibers [$u\left(r\right)\propto r^{-2}$]. On the other hand, fiber realignment and strain stiffening promote long-range displacement propagation in the matrix with aligned fibers [$u\left(r\right)\propto r^{-n}$, where the exponent (n) is close to −1 (30)]. The dependence of the displacement propagation on the alignment of the fibers surrounding the cell cluster is plotted in Fig. S3. The comparison between the displacement decays in random and aligned matrices shows that the fibrous constitutive model (Eq. S10) reproduces the long-range displacement propagation associated with strain-stiffened matrices and captures the nonlinear behavior of the fibrous matrices.

Homogenized Description of the Cell Invasion Region.

To capture cell polarization and matrix alignment and their interplay in the invaded region, we adopt a homogenized model and introduce a representative element, containing the cells (treated with the mechanochemical model described in The Chemomechanical Model for the Response of the Cell to the External Stresses) placed in “series” with the ECM (treated using the fibrous material model in Model for Fiber Realignment and Strain Stiffening of the Matrix) (shown in Fig. S4). For a given representative element with length $l$, the lengths of the cell and matrix elements in each direction (in the 3D setting of the problem) are denoted by $l^c$ and $l^m$, respectively, and the relative volume fraction of the cell (or cell concentration) $c\left(r\right)$ can be written as follows:

$${\left(\frac{l^c}{l}\right)}^3=c\left(r\right),$$ [S13]

where $0<c\left(r\right)<1$.

For this series arrangement, because the cells and the matrix transmit the same force,

$${\sigma }_{rr}^m={\sigma }_{rr}^c,$$

$${\sigma }_{\theta \theta }^m={\sigma }_{\theta \theta }^c,$$ [S14]

where ${\sigma }_{rr}^{m,c}$ and ${\sigma }_{\theta \theta }^{m,c}$ are the radial and polar stress components, and superscripts $c$ and $m$ represent the cell and the matrix elements, respectively. The total strain of the cell–matrix unit cell is the sum of the strains of the cell and the matrix:

$$l{\epsilon }_{rr}=l^c{\epsilon }_{rr}^c+l^m{\epsilon }_{rr}^m,$$

$$l{\epsilon }_{\theta \theta }=l^c{\epsilon }_{\theta \theta }^c+l^m{\epsilon }_{\theta \theta }^m.$$ [S15]

The radial and polar strains can be related to the displacement in the radial direction $u$ through the following:

$${\epsilon }_{rr}=\frac{\partial u}{\partial r},$$

$${\epsilon }_{\theta \theta }=\frac{u}{r}.$$ [S16]

Adhesion Energy Accounting for the Cell–Cell and Cell–Matrix Junctions.

Cell invasion involves concurrent breaking of the intercellular adherens and tight junctions followed by the formation of the new adhesions between the focal adhesions and the matrix ligands at the leading edge of the migrating cells. In the spheroid–matrix system, the presence of the strong intercellular adhesions impedes the invasion of the cells and lead to the formation of stable spheroids.

In the current model, we obtain the interfacial energy based on the experimentally measured adhesion energies of the cell–cell and cell–matrix junctions. Here, depending on the cell concentration profile [$c\left(r\right)$], the total adhesion energy can be written as follows:

$$\begin{array}{l}{U}_{\text{adhesion}}\left(c\left(r\right)\right)=\left({\gamma }_{c-c}\frac{4\pi }{3}\left(R^3-r_0^3\right)-{\gamma }_{c-m}{\displaystyle \underset{r_0}{\overset{r_1}{\int }}c\left(r\right)4\pi \hspace{0.17em}{r}^{2}dr}\right)\times \frac{\varphi \hspace{0.17em}}{\frac{4}{3}\pi \hspace{0.17em}{r}_{\mathrm{cell}}^3}4\pi \hspace{0.17em}{r}_{\mathrm{cell}}^2\hspace{0.17em}\\ =\frac{4\pi \hspace{0.17em}\varphi \hspace{0.17em}}{r_{\text{cell}}}\left(R^3-r_0^3\right)\hspace{0.17em}\left({\gamma }_{c-c}-{\gamma }_{c-m}\right).\end{array}$$ [S17]

The first term represents the cost associated with the dissociation of the intercellular adhesions, and the second term represents the gain in the energy from the creation of the new adhesions between the cells and the matrix. The parameters ${\gamma }_{c-c}\mathrm{and}\hspace{0.17em}{\gamma }_{c-m}$ are the associated adhesion energies, $\varphi =70\hspace{0.17em}\%$ is the estimated density of packing of cells in the cluster, and $r_{\mathrm{cell}}=5$ μm is the radius of a single cell. The factor $\varphi /(4/3\hspace{0.17em}\pi \hspace{0.17em}{r}_{\mathrm{cell}}^3)$ is used to convert the calculated bulk volumes (in the parentheses) to the number of the cells, and $4\pi \hspace{0.17em}{r}_{\mathrm{cell}}^2$ is used to obtain the total surface area of the contacting cells. Here, by using ${\gamma }_{c-c}=10\hspace{0.17em}{\gamma }_{c-m}=1$ mJ/m² (in the range given in refs. 32–34), we ensure that the change in the interfacial energy because of the cell invasion is positive [or $U_{\text{adhesion}}\left(c\right)>0$], meaning that the invasion is energetically improbable and the cells prefer to stay in the cluster.

Discussion

Migration of tumor cells within fibrous matrices involves an interplay between cellular adhesions such as cell–cell and cell–matrix junctions, cell contractility induced by the activity of myosins, and realignment and strain stiffening of matrix fibers. Our mathematical model determines the driving force underlying cell invasion and predicts its dependence on matrix properties. Specifically, central to our model is the direct reciprocity between stress-dependent cell contractility induced by molecular pathways such as Ca²⁺ and Rho, and matrix fiber realignment and strain stiffening, which enables the cells to acquire the contractility required to break retracting cellular adhesions and move within the matrix.

Existing mathematical models to study the migration of the cells generally focus on the dynamics between protrusion forces due to the polymerization of actin at the leading edge of the cell and the traction forces generated at the cell–matrix adhesions (19, 21–24). The direction of cell movement in these models is calculated from the orientation of the surrounding matrix fibers (24) and the random direction associated with the protrusion forces (21, 47). After obtaining the direction of the cell migration, the assumed asymmetric distribution of the receptors at the front and rear edges of the cell, creates a net traction force, which moves the cells within the matrix (21, 22). However, these models do not consider how cell contractility impacts and alters fiber alignment and how matrix mechanics impacts contractility. By ignoring these feedback mechanisms, current models fail to explain the increase in the cell contractility due to the concurrent realignment of matrix fibers, which is needed to generate intracellular contraction required to overcome the cellular adhesions during cell invasion. In addition, the two-way feedback loop is also required to explain the morphological features of the cells such as elongation, which creates a front–rear polarity to enable the protrusions to establish adhesions with the matrix.

Recently, the migratory behavior of individual cells leaving spheroids and moving within the ECM were tracked to obtain the temporal evolution of the cell morphology (31). In the case of fibrosarcoma HT1080 cells in collagen, the elongation of the cells and the percentage of elongated cells increases spatially from the center of the spheroid toward the invasive front. Although the cells located closer to the spheroid center have rounded appearance, invading cells at the periphery are highly elongated and oriented radially with respect to the spheroid (31), a trend that helps at different collagen densities. By incorporating the two-way feedback, our model is able to show that the cell elongation is proportional to the realignment of the fibers in the surrounding matrix (Figs. 3 and 4) and increases with the stiffness of the matrix. This result also agrees with our melanoma experiments, where increasing the concentration of collagen showed an increase in the elongation of the cells at the periphery of the spheroids (Fig. 1). Because the elongated morphology is indicative of EMT in the cells, we used our model to determine the relation between the driving force underlying EMT and matrix stiffness. Our model shows that this driving force is directly proportional to the stiffness of the surrounding matrix (Fig. 5A). These findings explain our experimental results on the dissolution of the melanoma spheroids with increase in the concentration of collagen in the surrounding matrix (Fig. 5 C and D). Increasing the collagen density from dilute to the intermediate concentrations in our experiments increases the stiffness of the matrix, which, according to our model, enhances the driving force of the cell invasion, leading to the dissociation of the spheroids. Interestingly, we were able to identify a critical stiffness required by the matrix to overcome cell–cell adhesions and initiate the cell invasion (Fig. 5A). This is consistent with our current experiments on the invasion of melanoma cells in collagen matrices (Fig. 5C), where cell invasion occurs only if the concentration of collagen in the surrounding matrix exceeds a critical value (0.5 mg/mL).

The critical stiffness predicted by our model has also been observed in other experimental studies, although this key result has not been captured in previous mathematical models. For example, to study the integrity of multicellular clusters in response to the stiffness of the surrounding matrix, previous in vitro studies have examined the stability of mammary gland acini cultured in collagen matrices at different collagen concentrations (48, 49). Guo et al. (48) have shown that, at low concentrations (less than 0.1 mg/mL), the acini remain stable over time. On the other hand, by increasing collagen concentration (higher than 0.3 mg/mL), cells begin to invade the matrix and move toward the nearby acini. This process continues until a peculiar branching morphology with cell tracks connecting neighboring acini appears in the whole matrix. In agreement with our results, this concentration-dependent acini dissociation can be characterized by defining a critical collagen concentration (0.3 mg/mL in this case), below which the acini are stable and beyond which they turn into motile cells.

Increasing collagen concentration in these experiments also increases the density of cell-adhesive ligands, which in turn controls the migration of the cells in the matrix. Therefore, to examine the increase of the density of ligands with increase in the collagen concentration, we calculated the dependence of the critical stiffness on the ligand density. Interestingly, in agreement with the previous experimental studies (18), our model shows that increasing ligand density alone, decreases the critical stiffness, meaning that cell invasion is facilitated with an increase in the ligand density.

Although the driving force of invasion and cell polarization increases with the stiffness of the matrix, cell invasiveness shows a different behavior. Measurements of the cell invasiveness in our melanoma experiments show that, by increasing collagen concentration from dilute to intermediate concentrations, cell invasion increases (Fig. 5C). On the other hand, beyond the intermediate concentrations, cell invasiveness decreases with collagen concentration. By solving the kinetic equations of cell motion (Eq. 5), and including the effect of the resisting forces against the cell movement, our model also shows that the cell invasiveness has a biphasic behavior with the largest invasion rate occurring at an intermediate level of matrix stiffness. In very stiff matrices, although cells are highly elongated, the small pore size between the fibers hinder the movement of the cells. For this reason, for a spheroid placed in highly dense matrices, our model predicts the formation of a pattern with highly elongated cells protruding from the interface of the spheroid similar to our experimental observations (Fig. 5C; collagen concentration, 2.0 mg/mL).

These key findings are also in agreement with the behavior observed in previous experimental studies (17). For example, Lang et al. (17) used glutaraldehyde to enhance the stiffness of the gel, while maintaining the concentration of the ligands. They showed that adding glutaraldehyde to collagen matrices with dilute concentration of collagen, increases the cell invasion, suggesting that the stiffness of the matrix promotes cell invasion. On the other hand, adding glutaraldehyde decreases the pore size and can also possibly hinder invasion. This effect is more evident when the concentration of collagen is high and the pore size in the matrix is small. Therefore, by altering the stiffness of the matrix, this study shows that the cell invasion exhibits the biphasic response with respect to the stiffness of the matrix, identical to the behavior we observe in our model and experimental study.

By altering the material parameters controlling the realignment of the fibers in the ECM [such as critical strain (${\epsilon }_{cr}$) or strain stiffening ($n$)], we can predict the shape of the cells as a function of the fiber realignment of the ECM. For example, by increasing the critical strain (${\epsilon }_{cr}$) or reducing the strain stiffening ($n$), we can elucidate the migration of the cells within nonfibrous matrices (such BME), where the matrix behaves isotopically in all of the directions. In agreement with the previous experimental observations (44, 45), our model shows that, in this case, cells have more rounded appearance ($n=0$ in Fig. S9), demonstrating that matrix fiber realignment is crucial to induce polarization in the cells in this case.

Although our model has considered a multitude of key elements involved in cell invasion (such as cellular adhesions, cell chemomechanical stress-dependent contractility, matrix stiffness, realignment and strain stiffening, matrix ligand density, pore size, and …), future work should focus on extending the current model to include parameters such as matrix proteolytic degradation and cell proliferation and apoptosis. Cells secrete metalloproteinase enzymes (such as MMPs) to dilute the concentration of collagen and increase the size of the pores to facilitate cell invasion. This effect is more pronounced when the density of the fibers is high and the voids between the fibers are significantly smaller than the cell body (5). Including the effect of the MMPs in our model results in an increase in the cell invasion at higher collagen densities, in agreement with our melanoma observations (Fig. S5). MMP-dependent remodeling of the fibers also provides the required space for cell proliferation in the vicinity of the cells. Therefore, abrogation of MMPs has been shown to result in reduced cell proliferation (50). Matrix rigidity also alters the proliferation of the cells in a Rho-dependent manner. Increase in the matrix stiffness and Rho activity induces phosphorylation of cells focal adhesion kinase (FAK) at Y397 sites, which has been linked to increase in the cell proliferation and differentiation (8, 51). This point suggests that the increased matrix stiffness due to the fiber realignment in our model can promote cell division. In agreement with this prediction, previous measurements of cell–matrix traction forces have also shown that the cell division is accompanied by matrix remodeling and realignment of the fibers along the long axis of the dividing cell (52).

In summary, our model presents a mathematical explanation for the role of the interplay between intracellular and extracellular forces in the initiation and progression of cell invasion from tumor clusters. Notably, the predictions of the model can be used to explain how the morphological changes (such as fiber realignment and remodeling) before cell invasion predict the malignant transformation and tumor development (6).

Materials and Methods

Cell Culture.

1205Lu and WM858 cells were maintained in MCDB153 (Sigma)/L-15 (Cellgro) supplemented with 2% FBS (Invitrogen) and 1.6 mM CaCl₂ (tumor growth media). All cells were cultured at 37 °C in 5% (vol/vol) CO₂.

Three-Dimensional Spheroid Assay.

Tissue culture-treated 96-well plates were coated with 50 µL of 1% Difco Agar Noble (Becton Dickinson). 1205Lu and WM858 cells were seeded at 2 × 10³ and 5 × 10³ cells per well, respectively, and allowed to form spheroids over 72 h. Spheroids were harvested and placed in a collagen plug containing Eagle’s minimal essential medium, FBS, l-glutamine, sodium bicarbonate, and collagen type I (Gibco; A1048301) as previously described. The collagen plug was allowed to set, and 1 mL of tumor growth media was added to the top of the plug. Quantitation of invasive area was performed using NIS Elements Advanced Research software. For mitomycin treatment, 1 μg/mL mitomycin was added to the collagen plug and to the media. For MMP 2/9i (EMD Millipore; 444241) treatment, inhibitor was added directly to the collagen plug and to the media for a final concentration of either 500 nM or 1 μM.