Significance
Accurate climate predictions on 10-y time scales are commonly assumed to require climate models with interactive ocean dynamics. This paper shows that the most predictable components in climate models without interactive ocean dynamics are remarkably similar to those in models containing interactive ocean dynamics. In addition, linear models trained on either type of climate model can skillfully predict observed temperature variations a year or two in advance. The results suggest that mechanisms of decadal climate predictability might be much simpler than previously thought, in particular, that they are dominated by thermodynamic ocean physics coupled to a stochastic atmosphere without interactive ocean dynamics.
Keywords: decadal prediction, decadal predictability, average predictability time, CMIP
Abstract
This paper shows that the most predictable components of internal variability in coupled atmosphere–ocean models are remarkably similar to the most predictable components of climate models without interactive ocean dynamics (i.e., models whose ocean is represented by a 50-m-deep slab ocean mixed layer with no interactive currents). Furthermore, a linear regression model derived solely from dynamical model output can skillfully predict observed anomalies in these components at least a year or two in advance, indicating that these model-derived components and associated linear dynamics are realistic. These results suggest that interactive ocean circulation is not essential for the existence of multiyear predictability previously identified in coupled models and observations.
In recent years, climate prediction on decadal time scales has gained increased attention because of its growing scientific, geopolitical, and societal importance (1–5). Sources of decadal predictability often are divided into two kinds: predictability caused by external forcing, such as changes in solar insolation, volcanic aerosols, and anthropogenic greenhouse gases, and predictability due to internal variability arising naturally from the coupled atmosphere–ocean–land–ice climate system (6). Climate models suggest that certain structures of internal variability in sea surface temperatures (SST), such as the Atlantic Multidecadal Oscillation (AMO) and Pacific Decadal Oscillation (PDO), are predictable on decadal/multidecadal time scales (5, 7–9). The precise mechanisms for this decadal predictability are not clear, although the dynamics of ocean circulation are widely believed to play a major role (10–17).
Recently, a few studies have challenged the notion that interactive ocean dynamics play a dominant role in decadal predictability (18, 19). These studies are based on integrations of atmospheric global circulation models coupled to a slab ocean mixed layer, in which ocean circulation is a prescribed function of time and the ocean interacts with the atmosphere only thermodynamically, through radiative, sensible, and latent heat fluxes. Despite the absence of interactive ocean dynamics, these models can produce realistic variability that is predictable on interannual and longer time scales. For example, El Niño–Southern Oscillation (ENSO)-like variability can arise on interannual and decadal time scales from such models (20–22). Also, the main features of the observed AMO (e.g., spatial pattern, power spectra, and associated atmospheric circulation) have been reproduced in models without interactive ocean dynamics (23). However, not all details of these simulations are perfect: In some locations, the lag correlation between AMO and surface heat flux has the opposite sign relative to coupled models and observations (14, 15). On the other hand, these heat fluxes tend to be nearly canceled by the ocean heat transport convergence on long time scales (24), raising questions as to their true role. In any case, the fact that many features of AMO variability can be reproduced without interactive ocean dynamics suggests that the accompanying surface heat fluxes in coupled models may not be playing a driving role. Moreover, the existence of competing hypotheses for the same phenomena suggest that the mechanisms of the AMO, and decadal predictability in general, are far from settled science.
Despite the above suggestive results, there exists no comprehensive assessment of decadal predictability without interactive ocean dynamics. What are the dominant patterns of decadal variability in systems without ocean dynamics? Are these patterns similar to those of systems that capture ocean dynamics? Do the patterns derived from systems with and without interactive ocean dynamics have similar time scales? Do they have similar dynamics? How would multiyear predictions by the two systems compare in terms of skill? The purpose of this paper is to answer these questions. We will show that the dominant patterns of decadal variability in atmosphere–slab ocean models are remarkably similar to those in fully coupled atmosphere–ocean models, not only in terms of spatial scale but also in time scale and predictability. We also will show that empirical models derived from these dynamical models can produce skillful predictions of observed SSTs.
To answer the above questions, we analyze two different sets of simulations from the Coupled Model Intercomparison Project 3 (CMIP3). Both sets are “control” runs in which external forcing is held fixed at their preindustrial settings, ensuring that the only mechanism for decadal predictability is internal variability. The first set comes from fully coupled climate models with interacting atmosphere, land, ocean and sea ice components; these models will be called “coupled.” The other set of simulations uses the same atmospheric model as in the coupled simulations, but the ocean model is a 50-m-deep slab mixed layer model; these models will be called “slab.” Although the slab model has a periodically varying ocean heat transport (the so-called “Q-flux”), this transport is noninteractive in the sense that it is a prescribed function of time and is independent of the ocean–atmosphere variability. Thus, the slab model contains no interactive ocean dynamics. Further details of the models are given in Table 1.
Table 1.
List of CMIP3 models used for this study
| Model | Length of slab ocean models in years | Length of fully coupled models in years | Resolution | |
| CCCMA_CGCM3_1 | 30 | 500 | ||
| CCCMA_CGCM3_1_T63 | 30 | 350 | ||
| CSIRO_MK3_0 | 60 | 380 | ||
| GFDL_CM2_0 | 50 | 500 | ||
| GFDL_CM2_1 | 100 | 500 | ||
| GISS_MODEL_E_R | 120 | 500 | ||
| INMCM3 | 60 | 330 | ||
| MIROC3_2_HIRES | 20 | 500 | ||
| MIROC3_2_MEDRES | 60 | 100 | ||
| MPI_ECHAM5 | 180 | 1,000 | ||
| MRI_CGCM2_3_2A | 100 | 350 | ||
| NCAR_CCSM3 | 450 | 500 | ||
| UKMO_HADGEM1 | 70 | 240 |
Next, we determine the most predictable components in coupled and slab models using a procedure called average predictability time (APT) analysis (25). This procedure determines an uncorrelated set of components ordered by predictability, where predictability is measured by an integral time scale of the predictable variance (see Data and Method). This optimization method allows decadal predictability to be identified in monthly data, as opposed to annual mean data that are used in most other studies on decadal predictability. Accordingly, we analyze monthly mean 2-m temperature, although, for completeness, we note that repeating our calculations using annual mean data yields similar results. Predictability is maximized in a multimodel sense by pooling simulation data together. As a result, the sample size in our statistical analysis is very large, even though individual model simulations may be relatively short (e.g., some slab simulations last only for 20 y).
To render APT analysis well posed and to mitigate overfitting, maximization of APT is performed in a low-dimensional subspace. Specifically, all temperature fields are projected onto a small number of predetermined patterns. These patterns are the leading eigenfunctions of the Laplace operator over the analysis domain, which capture large-scale features and filter out small spatial structures. These patterns depend only on the geometry of the domain, in contrast to commonly used empirical orthogonal functions, and hence are independent of data, thereby facilitating comparisons across models and data sets. These patterns are obtained from a recently developed Green’s function technique (26), and are projected onto monthly temperature fields to yield time series. The resulting time series are then linearly combined to maximize APT.
An interesting question in our analysis design is whether the basis vectors for maximizing predictability should be global or restricted to individual ocean basins. If decadal predictability in the Atlantic and Pacific arise from different mechanisms, then global basis vectors may lead to failure to detect localized predictability, or may give a misleading impression of the spatial extent of predictability. To investigate this issue, APT analysis was applied to the union of five Laplacian eigenfunctions from the Pacific plus five Laplacian eigenfunctions from the Atlantic. If predictability were localized in each basin separately, then APT analysis would indicate that fact by producing predictable components with loadings in just the Atlantic or just the Pacific. When we perform this calculation, APT analysis always yields global patterns, suggesting that the most predictable components in climate models have global expressions. This result does not necessarily imply that the mechanisms are global. For instance, the mechanism could be local, whereas the response may be global. Indeed, ENSO arises from coupled dynamics localized in the equatorial Pacific, yet it has a global expression through Rossby wave teleconnection mechanisms. Similarly, climate models show that, when one basin is forced on multidecadal time scales, the other oceans (which are free to adjust) vary in synchrony (27). If a predictable component has a global expression, then it is beneficial from a statistical point of view to use global basis vectors to improve the signal-to-noise ratio, even if the mechanisms giving rise to that predictability are local. Moreover, the mechanisms that dominate decadal predictability could very well be global (28). In any case, analyzing global basis vectors is not incompatible with the hypothesis of local mechanisms of predictability. For the above reasons, we chose global basis vectors to maximize predictability.
Data and Method
The model data analyzed in this study are monthly 2-m temperatures from simulations of 13 models from CMIP3. The model details are given in Table 1. The observed monthly SST is from the Extended Reconstructed Sea Surface Temperature dataset, version 3b (ERSSTv3b) (29) for the period 1901–2015. The observed Nino3.4 index is from the UK Met Office Hadley Centre’s Sea Ice and Sea Surface Temperature dataset (HadISST1) (30); it is the area averaged SST from 5°S to 5°N and 170°W to 120°W (https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Nino34/). The observed AMO index is the 12-mo running mean index using Kaplan SST V2 (https://www.esrl.noaa.gov/psd/data/timeseries/AMO/). The PDO index is downloaded from University of Washington/JISAO (http://research.jisao.washington.edu/pdo/PDO.latest.txt). All indices have been smoothed using a 12-mo running mean. We have used monthly SSTs because the difference between 2-m air temperature and surface temperature is negligible on monthly or longer time scales.
Laplacian eigenfunctions were derived on a domain bounded by 50°S to 60°N. The eigenfunctions are orthogonal with respect to an area-weighted norm, and thus the least-squares amplitude of each eigenfunction can be obtained by projection. The eigenfunctions were truncated to 10 and projected onto monthly temperature fields of each model and simulation. The resultant time series were centered, detrended, and seasonally adjusted, yielding a data matrix of dimension , where is the number of months. The time-lagged covariance matrix of a single model is computed as , where denotes time series shifted by lag , and superscript T denotes the matrix transpose. Covariances were computed for each model and simulation separately. A similar procedure was performed on monthly observed SST data, except that, instead of removing a trend, a best-fit third-order polynomial was subtracted to remove most of the forced signal, yielding Laplacian time series and time-lagged covariance matrix .
Decadal predictions from CMIP3 dynamical models are not available. Accordingly, prediction skill is estimated by regression methods. Specifically, a linear model that predicts the future amplitude of 10 Laplacian eigenfunctions based on their present values is defined as
| [1] |
where is lead month and the caret denotes a prediction. The least-squares estimate of the prediction operator is
| [2] |
where denotes the multimodel average covariance matrix. The prediction operator is estimated from dynamical model simulations without using any observations, and is estimated for each lead month separately.
We seek the most predictable component of the linear regression model Eq. 1. This component is derived by finding coefficients of a linear combination of variables (hereafter, weights) that maximize APT. Let the weights be the vector , so that taking a linear combination yields the time series . The predictability of a component is measured by the correlation between predicted and actual value,
| [3] |
The quantity measures the fraction of variance predictable by the regression model Eq. 1 at lead time . We are interested in a measure of predictability that is independent of lead time; therefore, instead of maximizing predictability at an arbitrary lead time , we maximize summed over 60 mo, which yields a quantity called APT,
| [4] |
APT is, effectively, an integral time scale as commonly used in turbulence studies to measure eddy time scales. Theoretically, a component remains predictable until vanishes. Maximizing APT leads to a generalized eigenvalue problem (31) in which the eigenvalues give the APT values (in units of the time step, here 1 mo) and the corresponding eigenvectors give the weights for deriving the most predictable component time series . Similarly, the projection of a predictable component on observations is defined as . Once the weights are known, the predictability of the predictable components can be computed using Eq. 3.
Forecast skill in observations is measured in two ways. First, the normalized mean-square error (NMSE) is defined as,
| [5] |
where is the Euclidean distance. The other metric is the , where is the forecast correlation skill measured as
| [6] |
Results
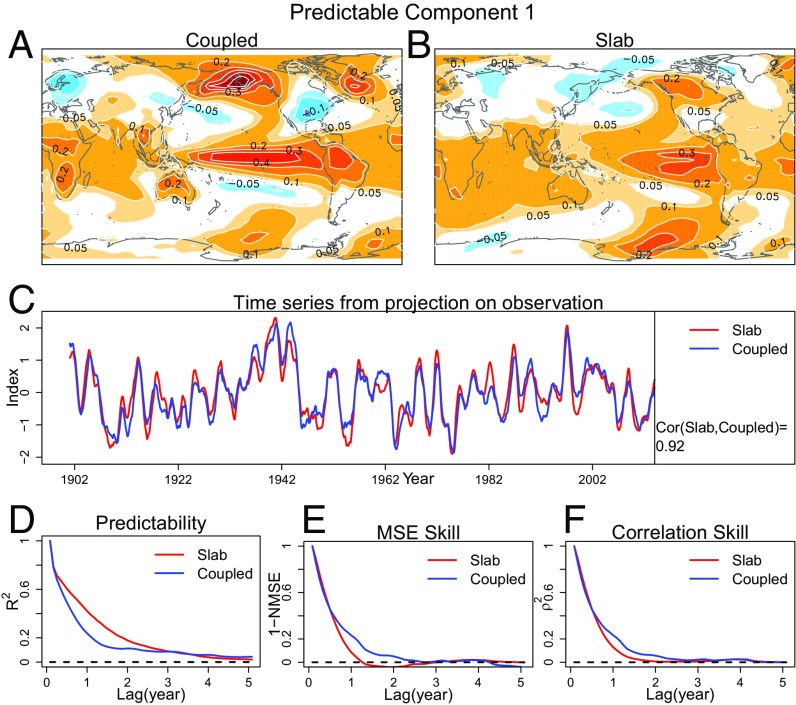
The most predictable component in coupled and slab models is shown in Fig. 1. Although some differences can be seen between the two patterns, especially in the northern latitudes, the large-scale structures are remarkably similar. An immediate question is whether the differences in spatial structure are important. One approach to quantifying the importance of these differences is to project the pattern onto observations and compare the resulting projection coefficients. If the projection coefficients for the two patterns are close, then differences in spatial structure can be said to be minor, in the sense that they have a minor impact on their corresponding time series, which are the central quantities in predictability theory. The time series obtained by projecting these patterns on observations are shown in Fig. 1C. As can be seen, the two time series are very similar—their correlation is 0.92—indicating that differences in spatial structure are relatively minor in terms of their corresponding time series (and thus their predictability). Thus, the differences in spatial structure seen in Fig. 1 A and B should not be interpreted too literally. The spatial patterns resemble the PDO, but the corresponding projected time series are modestly correlated with the observed PDO index (0.56 in slab and 0.35 in coupled models).
Fig. 1.
Most predictable component in coupled and slab models. Most predictable component is derived by maximizing the APT separately in coupled and slab models. (A and B) Spatial pattern of the most predictable component in the (A) coupled and (B) slab models. Each pattern is normalized such that the time series multiplied by the pattern gives the temperature variations (in degrees Celsius) due to this component. (C) Projection of the most predictable pattern onto monthly observed SST, smoothed with a 1-y running mean (blue and red curves, respectively). The correlation between coupled and slab projected time series is indicated in the bottom right legend. (D) The predictability (Eq. 3) of a linear prediction model that predicts the component in dynamical models. (E and F) The forecast skills (Eqs. 5 and 6) of a linear prediction model that predicts the component in observations. In D–F, the dashed line shows the mean-square error of a forecast based on the climatological mean. The time scale of the predictability and forecast skills is defined by the time (lag) when the red and blue curves intersect the dashed curve.
The predictability of the most predictable component is shown in Fig. 1D and is nonzero even after 5 y, confirming that this component is predictable on multiyear time scales in the coupled and in the slab model.
Next, we use the prediction model Eq. 1 to predict the observed amplitude of the most predictable component. Because observations were not used for model estimation, observational data constitute genuinely independent verification data for the prediction model. This approach avoids questions related to fitting and validating regression models with the same observational data. The skill based on NMSE (Fig. 1E) hits the zero line in a couple of years, demonstrating that this component can be skillfully predicted a couple of years (1 y to 2 y) in advance. Similar conclusions are obtained using correlation skill (Fig. 1F). The fact that the skill of the regression model derived from slab models is comparable to that from coupled models is striking considering that the slab model does not contain any interactive ocean dynamics, aside from simple thermodynamic mechanisms associated with heat storage.
Because the most predictable pattern can be predicted skillfully for only a couple of years, one might question whether the term “decadal” is appropriate. In fact, many components with multidecadal time scales, such as the AMO and PDO (after the forced response has been removed), appear to be predictable for only a few years, despite having significant power on multidecadal time scales (32–35). The time scale of a variable is sometimes identified with the period at which the power spectrum peaks, but this period should not be confused with the predictability time scale, which is more associated with the relative width of the peak (36–38).
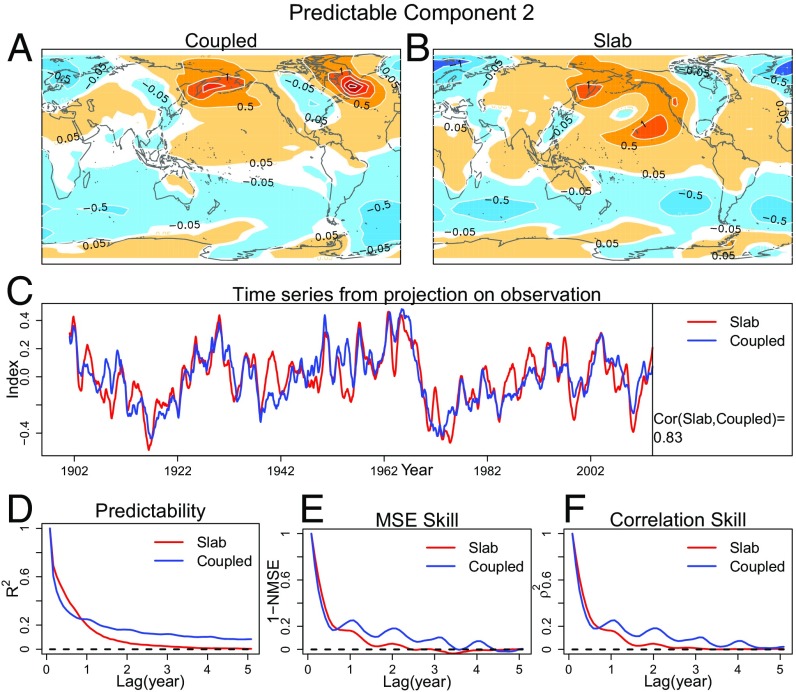
The second-most predictable component in coupled and slab models is shown in Fig. 2. Both components have amplitudes concentrated in high latitudes and opposing signs across hemispheres (Fig. 2 A and B). Such predictable, interhemispheric asymmetric patterns often are claimed to be driven by the Atlantic Meridional Overturning Circulation (AMOC), but the fact that the slab model can produce this pattern demonstrates that interhemispheric asymmetric patterns can be generated without invoking the AMOC. Projection of these patterns onto observations yields similar time series, as indicated by the correlation value of 0.83 (Fig. 2C). The projections are modestly correlated with the observed AMO index (0.4 in coupled and slab models). The coupled system has stronger predictability and forecast skill than its slab counterpart (i.e., the blue curves lie above the red in Fig. 2 D–F), suggesting that interactive ocean dynamics play a larger role than in the first component. Nevertheless, the slab models provide predictability beyond 2 y and skillfully predict observations beyond 1 y. Interestingly, the regression model uses only surface information, so whatever ocean dynamics may be at play can be inferred from surface variables.
Fig. 2.
The second predictable component in coupled and slab models. Same as in Fig. 1, except for the second-most predictable component.
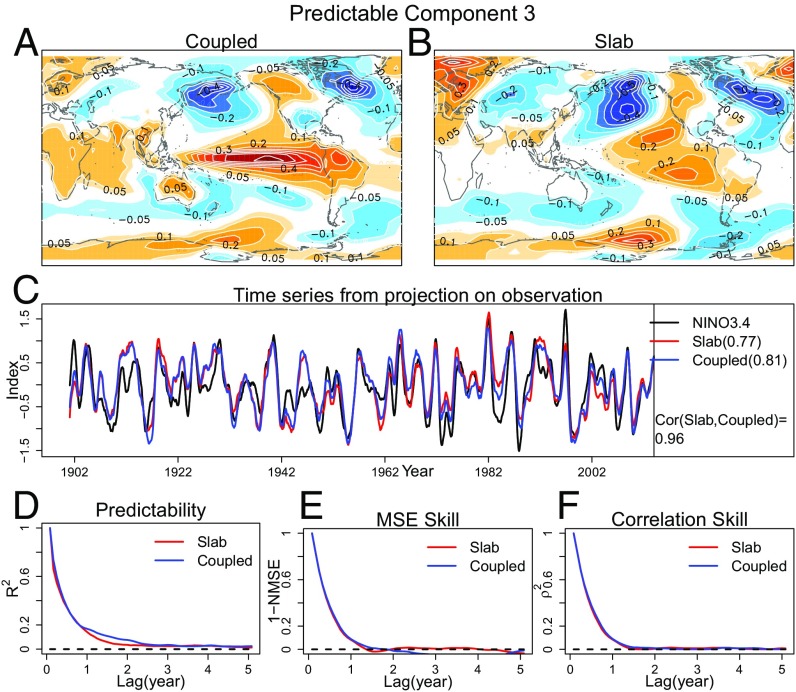
The third-most predictable component in coupled and slab models is shown in Fig. 3. This component resembles the observed ENSO pattern. Incidentally, components 1 and 3 look similar, but their projection on observations differ, and their predictabilities differ (indeed, their time series are orthogonal in the models). Although the pattern in the slab run does not have maximum loading along the equatorial Pacific, its projection time series is very similar to that of the coupled model pattern (correlation of 0.96). Interestingly, the component in slab models is correlated with the observed 1-y smoothed ENSO index almost as well as the component in coupled models. Slab models provide as much predictability and forecast skill (1 y) as coupled models, which is surprising because slab models do not contain the oceanic Rossby and Kelvin waves associated with ENSO mechanisms. Also, the prediction skill of ENSO in current dynamical and statistical models is less than a year (39–41). Subsequent predictable components (i.e., components 4, 5, and 6) in slab and coupled models show similar spatial structure, predictability, and skill, but these are not shown, for brevity.
Fig. 3.
The third predictable component in coupled and slab models. Same as in Figs. 1 and 2, except for the third-most predictable component. The black curve in C shows the observed 1-y-smoothed Nino3.4 index; the correlation between each projected time series and the observed ENSO index is indicated in the parentheses after “slab” and “coupled” in the right legend, and the correlation between coupled and slab projected time series is indicated in the bottom right legend.
We emphasize that the two curves shown in Figs. 1 D–F, 2 D–F, and 3 D–F show the skill and predictability of two different patterns. Testing statistical significance of a difference in skill or predictability of two different quantities is not straightforward. Nevertheless, physically, the range of skill and predictability of the two components are “comparable.” It is also important to recognize that, even if the predictable components were not similar component by component, this would not necessarily imply that the predictabilities differ. For instance, the patterns could be identical but have different rankings. Alternatively, the leading pattern of one model could be a linear combination of leading patterns of another model, or the patterns of one model could be rotated in the same space as those of the other model. In any of these cases, a component-by-component comparison would be unsatisfactory, and a more comprehensive comparison would be required.
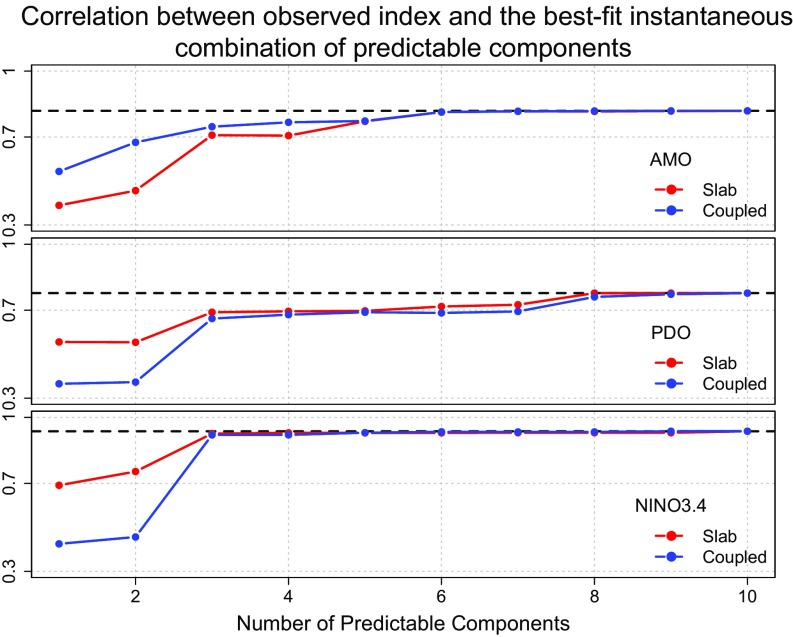
The above comment is pertinent to relating our results to traditional indices like the AMO or PDO. As mentioned earlier, these latter indices have modest correlations with individual model components, but this fact does not imply the two sets of components are unrelated. For instance, the traditional indices could be some linear combination of the components derived here. To investigate this question, the observed AMO index was fit to a linear combination of predictable components. The correlation between the observed and best-fit AMO index is shown in Fig. 4, Top, where the correlation is computed from a 12-mo running mean of the two time series. The correlation based on all 10 predictable components is 0.82, indicating that much of the AMO variability can be captured by a linear combination of predictable components. The figure shows that only six predictable components are needed to achieve this correlation. For the PDO (Fig. 4, Middle), the maximum correlation is 0.78, again indicating that much of the PDO variability is captured by the most predictable components. Noticeably, the maximum correlation for the ENSO (Nino3.4) index in Fig. 4, Bottom, is 0.94, and the first three components are sufficient to capture this correlation. It is important to note that, in contrast to the Nino3.4 index, the traditional AMO and PDO indices are not captured by just the first two or three components, suggesting that the AMO and PDO indices may not be the best indices of decadal predictability as the leading predictable components. This conclusion is not necessarily surprising, because traditional indices were not designed to maximize predictability; for instance, the AMO is merely a spatial average over the Atlantic, and the PDO is merely a leading empirical orthogonal function, which maximizes variance, not predictability. In contrast, ENSO seems to be better identified with the most predictable components, and hence is an appropriate target for predictability.
Fig. 4.
Correlation between observed index and the best-fit instantaneous combination of predictable components. The correlation is computed using a 12-mo running mean for the observed index and for the best-fit instantaneous combination of predictable components. The horizontal axis shows the number of predictable components used to fit the observed index. The blue and red curves show results for coupled and slab predictable components, respectively. The black dashed line shows the maximum correlation when all 10 predictable components are used.
Admittedly, removing a third-order polynomial from the observed SST data may not perfectly remove the forced signal. Any leftover forced signal may contaminate our results, but the fact that the predictable components have real forecast skill of the order of years lends legitimacy to our conclusions.
Also, climate models suffer from significant biases that may reduce or distort the influence of ocean dynamical processes. For example, many coupled models tend to be too cold and fresh in the North Atlantic, which may impact the forcing of the AMOC by the North Atlantic Oscillation, and impact the coupling of the AMOC with the surface ocean. Reducing these biases has been found to change the character of decadal variability in coupled models (42). Also, the above biases can alter the AMOC from being thermally driven to being salinity driven, which also likely impacts predictability (43). Despite these shortcomings, this paper shows that empirical models derived from dynamical models can skillfully predict observations for a few years, suggesting that coupled and slab models still capture realistic aspects of decadal predictability, despite certain biases and inconsistencies with observations.
The similarity of predictable patterns, predictability time scales, and forecast skills derived from coupled and slab models strongly suggests that interactive ocean dynamics is not essential for the existence of multiyear predictability previously identified in coupled models and observations. Instead, the essential mechanisms of decadal predictability appear to involve atmospheric processes and thermodynamic air–sea coupling. One often-cited mechanism is the fact that the ocean mixed layer acts as an integrator of short-period stochastic forcing from the atmosphere, producing red power spectra from white noise forcing (44). Other mechanisms such as cloud–SST feedback (45) and wind–evaporation–SST feedback (46) may further redden the spectrum. We emphasize that we do not claim that ocean dynamics play no role in decadal predictability. For instance, the skill derived from coupled models tends to be higher than that from slab models (Figs. 1 E and F and 2 E and F), although the difference is small in many cases. In the other cases, interactive ocean dynamics appear to simply enhance or modulate decadal predictability without significantly altering the spatial structure. Indeed, components like the AMO and PDO are highly persistent and can be predicted with skill by univariate regression models, but can be predicted with somewhat more skill if predictors associated with ocean dynamics (e.g., ocean meridional circulation or ENSO) are included as predictors (47, 48). There is no doubt that ocean dynamics can produce variability over a huge range of time scales, from days to millennia, but the degree to which subsurface variability on decadal and multidecadal time scales influences the atmosphere and continental land masses (where humans live) remains to be quantified.
Acknowledgments
This research was supported primarily by the National Science Foundation (Grants CCF-1451945 and AGS-1622295). Additional support was provided by the National Science Foundation (Grant AGS-1338427), National Aeronautics and Space Administration (Grant NNX14AM19G), and the National Oceanic and Atmospheric Administration (Grant NA14OAR4310160). The views expressed herein are those of the authors and do not necessarily reflect the views of these agencies.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Latif M, Collins M, Pohlmann H, Keenlyside N. A review of predictability studies of Atlantic sector climate on decadal time scales. J Clim. 2006;19(23):5971–5987. [Google Scholar]
- 2.Meehl GA, et al. Decadal prediction: Can it be skillful? Bull Am Meteorol Soc. 2009;90(10):1467–1485. [Google Scholar]
- 3.Mehta V, et al. Decadal climate predictability and prediction: Where are we? Bull Am Meteorol Soc. 2011;92(5):637–640. [Google Scholar]
- 4.Lienert F, Doblas-Reyes FJ. Decadal prediction of interannual tropical and North Pacific sea surface temperature. J Geophys Res Atmos. 2013;118(12):5913–5922. [Google Scholar]
- 5.Ding R, Li J, Zheng F, Feng J, Liu D. Estimating the limit of decadal-scale climate predictability using observational data. Clim Dyn. 2016;46(5-6):1563–1580. [Google Scholar]
- 6.Kirtman B, et al. Near-term climate change: Projections and predictability. In: Stocker T, et al., editors. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge Univ Press; Cambridge, UK: 2013. pp. 953–1028. [Google Scholar]
- 7.Griffies SM, Bryan K. Predictability of North Atlantic multidecadal climate variability. Science. 1997;275(5297):181–184. doi: 10.1126/science.275.5297.181. [DOI] [PubMed] [Google Scholar]
- 8.Pohlmann H, et al. Estimating the decadal predictability of a coupled AOGCM. J Clim. 2004;17(22):4463–4472. [Google Scholar]
- 9.Collins M, et al. Interannual to decadal climate predictability in the North Atlantic: A multimodel-ensemble study. J Clim. 2006;19(7):1195–1203. [Google Scholar]
- 10.Saravanan R, McWilliams JC. Advective ocean-atmosphere interaction: An analytical stochastic model with implications for decadal variability. J Clim. 1998;11(2):165–188. [Google Scholar]
- 11.Delworth T, Manabe S, Stouffer R. Interdecadal variations of the thermohaline circulation in a coupled ocean-atmosphere model. J Clim. 1993;6(11):1993–2011. [Google Scholar]
- 12.Kushnir Y. Interdecadal variations in North Atlantic sea surface temperature and associated atmospheric conditions. J Clim. 1994;7(1):141–157. [Google Scholar]
- 13.Latif M, et al. Reconstructing, monitoring, and predicting multidecadal-scale changes in the North Atlantic thermohaline circulation with sea surface temperature. J Clim. 2004;17(7):1605–1614. [Google Scholar]
- 14.Gulev SK, Latif M, Keenlyside N, Park W, Koltermann KP. North Atlantic Ocean control on surface heat flux on multidecadal timescales. Nature. 2013;499(7459):464–467. doi: 10.1038/nature12268. [DOI] [PubMed] [Google Scholar]
- 15.Zhang R, et al. Comment on “The Atlantic Multidecadal Oscillation without a role for ocean circulation”. Science. 2016;352(6293):1527–1527. doi: 10.1126/science.aaf1660. [DOI] [PubMed] [Google Scholar]
- 16.O’Reilly CH, Huber M, Woollings T, Zanna L. The signature of low frequency oceanic forcing in the Atlantic Multidecadal Oscillation. Geophys Res Lett. 2016;43(6):2810–2818. [Google Scholar]
- 17.Buckley MW, Marshall J. Observations, inferences, and mechanisms of the Atlantic Meridional Overturning Circulation: A review. Rev Geophys. 2016;54(1):5–63. [Google Scholar]
- 18.Deser C, Phillips AS, Hurrell JW. Pacific interdecadal climate variability: Linkages between the tropics and the North Pacific during boreal winter since 1900. J Clim. 2004;17(16):3109–3124. [Google Scholar]
- 19.Clement A, DiNezio P, Deser C. Rethinking the ocean’s role in the Southern Oscillation. J Clim. 2011;24(15):4056–4072. [Google Scholar]
- 20.Dommenget D. The slab ocean El Niño. Geophys Res Lett. 2010;37(20):L20701. [Google Scholar]
- 21.Dommenget D, Haase S, Bayr T, Frauen C. Analysis of the Slab Ocean El Nino atmospheric feedbacks in observed and simulated ENSO dynamics. Clim Dyn. 2014;42(11-12):3187–3205. [Google Scholar]
- 22.Dommenget D, Latif M. Generation of hyper climate modes. Geophys Res Lett. 2008;35(2):L02706. [Google Scholar]
- 23.Clement A, et al. The Atlantic Multidecadal Oscillation without a role for ocean circulation. Science. 2015;350(6258):320–324. doi: 10.1126/science.aab3980. [DOI] [PubMed] [Google Scholar]
- 24.Clement A, et al. Response to comment on “The Atlantic Multidecadal Oscillation without a role for ocean circulation”. Science. 2016;352(6293):1527–1527. doi: 10.1126/science.aaf2575. [DOI] [PubMed] [Google Scholar]
- 25.DelSole T, Tippett MK. Average predictability time. Part II: Seamless diagnoses of predictability on multiple time scales. J Atmos Sci. 2009;66(5):1188–1204. [Google Scholar]
- 26.DelSole T, Tippett MK. Laplacian eigenfunctions for climate analysis. J Clim. 2015;28(18):7420–7436. [Google Scholar]
- 27.Zhang R, Delworth TL, Held IM. Can the Atlantic Ocean drive the observed multidecadal variability in the Northern Hemisphere mean temperature? Geophys Res Lett. 2007;34(2):L02709. [Google Scholar]
- 28.Kucharski F, et al. Atlantic forcing of pacific decadal variability. Clim Dyn. 2016;46(7-8):2337–2351. [Google Scholar]
- 29.Smith TM, Reynolds RW, Peterson TC, Lawrimore J. Improvements to NOAA’s historical merged land–ocean surface temperature analysis (1880–2006) J Clim. 2008;21:2283–2296. [Google Scholar]
- 30.Rayner N, et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atmos. 2003;108(D14):4407. [Google Scholar]
- 31.DelSole T, Tippett MK. Average predictability time: Part II: Seamless diagnosis of predictability on multiple time scales. J Atmos Sci. 2009;66:1188–1204. [Google Scholar]
- 32.Newman M. Interannual to decadal predictability of Tropical and North Pacific sea surface temperatures. J Clim. 2007;20:2333–2356. [Google Scholar]
- 33.Zanna L. Forecast skill and predictability of observed North Atlantic sea surface temperatures. J Clim. 2012;25:5047–5056. [Google Scholar]
- 34.Newman M. An empirical benchmark for decadal forecasts of global surface temperature anomalies. J Clim. 2013;26:5260–5269. [Google Scholar]
- 35.Suckling EB, Smith LA. An evaluation of decadal probability forecasts from state-of-the-art climate models. J Clim. 2013;26(23):9334–9347. [Google Scholar]
- 36.Chang P, Saravanan R, DelSole T, Wang F. Predictability of linear coupled systems. Part I: Theoretical analyses. J Clim. 2004;17:1474–1486. [Google Scholar]
- 37.DelSole T, Tippett MK. Predictability: Recent insights from information theory. Rev Geophys. 2007;45:RG4002. [Google Scholar]
- 38.DelSole T. Decadal prediction: Achievements and future prospects. Curr Clim Change Rep. in press. [Google Scholar]
- 39.Collins M, Frame D, Sinha B, Wilson C. How far ahead could we predict El Nino? Geophys Res Lett. 2002;29(10):130-1–130-4. [Google Scholar]
- 40.Zheng F, Zhu J, Zhang RH, Zhou GQ. Ensemble hindcasts of SST anomalies in the tropical Pacific using an intermediate coupled model. Geophys Res Lett. 2006;33(19):L19604. [Google Scholar]
- 41.Li J, Ding R. Temporal–spatial distribution of the predictability limit of monthly sea surface temperature in the global oceans. Int J Climatol. 2013;33(8):1936–1947. [Google Scholar]
- 42.Park T, Park W, Latif M. Correcting North Atlantic sea surface salinity biases in the Kiel climate model: Influences on ocean circulation and Atlantic multidecadal variability. Clim Dyn. 2016;47(7-8):2543–2560. [Google Scholar]
- 43.Menary MB, et al. Exploring the impact of CMIP5 model biases on the simulation of North Atlantic decadal variability. Geophys Res Lett. 2015;42(14):5926–5934. [Google Scholar]
- 44.Hasselmann K. Stochastic climate models I. Theory. Tellus. 1976;28:473–485. [Google Scholar]
- 45.Bellomo K, Clement A, Mauritsen T, Rädel G, Stevens B. Simulating the role of subtropical stratocumulus clouds in driving Pacific climate variability. J Clim. 2014;27(13):5119–5131. [Google Scholar]
- 46.Park S, Deser C, Alexander MA. Estimation of the surface heat flux response to sea surface temperature anomalies over the global oceans. J Clim. 2005;18(21):4582–4599. [Google Scholar]
- 47.Trenary L, DelSole T. Does the Atlantic Multidecadal Oscillation get its predictability from the Atlantic Meridional Overturning circulation? J Clim. 2016;29(14):5267–5280. [Google Scholar]
- 48.Newman M, Compo GP, Alexander MA. ENSO-forced variability of the Pacific decadal oscillation. J Clim. 2003;16(23):3853–3857. [Google Scholar]