Two types of amorphous protein particles facilitate crystal nucleation

Significance

The formation of the nuclei of protein crystals has been suggested to occur within protein-rich mesoscopic clusters. The existence of such clusters has been revealed for many proteins; however, their role in crystallization is still unclear. Our live images in a protein crystallization solution using transmission electron microscopy reveal that protein-rich mesoscopic clusters are solid amorphous particles that work as heterogeneous nucleation sites. The nucleation event for the crystal starts via another noncrystalline particle, which appears only a few seconds before crystal nucleation, that is, there are two types of amorphous particles that have different roles in protein crystallization.

Abstract

Nucleation, the primary step in crystallization, dictates the number of crystals, the distribution of their sizes, the polymorph selection, and other crucial properties of the crystal population. We used time-resolved liquid-cell transmission electron microscopy (TEM) to perform an in situ examination of the nucleation of lysozyme crystals. Our TEM images revealed that mesoscopic clusters, which are similar to those previously assumed to consist of a dense liquid and serve as nucleation precursors, are actually amorphous solid particles (ASPs) and act only as heterogeneous nucleation sites. Crystalline phases never form inside them. We demonstrate that a crystal appears within a noncrystalline particle assembling lysozyme on an ASP or a container wall, highlighting the role of heterogeneous nucleation. These findings represent a significant departure from the existing formulation of the two-step nucleation mechanism while reaffirming the role of noncrystalline particles. The insights gained may have significant implications in areas that rely on the production of protein crystals, such as structural biology, pharmacy, and biophysics, and for the fundamental understanding of crystallization mechanisms.

Crystallization can be divided into two processes: nucleation and crystal growth. The crystal growth process has been well examined for a long time, yet the nucleation process is not understood; for example, the nucleation rate of crystals provides a textbook example of order-of-magnitude discrepancies between theoretical predictions and experimental results. Recent proposals have attributed these discrepancies to a nonclassical nucleation pathway, along which a structured crystalline embryo forms within a highly concentrated disordered precursor (1). This mechanism was first proposed for protein crystals (2, 3). Direct observations have demonstrated its applicability to organic (4), inorganic (5, 6), and colloidal (7) crystals. In proteins, clusters of protein molecules have been suggested as precursors; these clusters have mesoscopic sizes from several tens to several hundreds of nanometers and are considered to behave like liquids. It has also been suggested that the precursor is thermodynamically stable with respect to the mother liquid phase but is metastable or unstable with respect to the crystalline phase. The latter nature of the precursor differs from the stable macroscopically dense liquid formed as a result of the liquid–liquid phase separation (8). Such protein-rich mesoscopic clusters have been observed for many proteins, primarily using optical techniques, and have been tentatively identified as precursors for crystal nucleation (9–12). Several important questions concerning this mechanism remain unanswered. First, are the observed mesoscopic clusters actually liquid-like or solid-amorphous? Second, do they play an active role in crystal nucleation? In addition, finally, do the clusters serve as classical heterogeneous nucleation centers or as loci of enhanced nonclassical nucleation? To address these questions, we used time-resolved in situ transmission electron microscopy (TEM) with a liquid cell (Fig. S1) to directly observe crystal nucleation with the protein lysozyme, arguably the most closely studied enzyme (13).

Fig. S1.

Schematic image of the liquid-cell for in situ TEM observations. The crystallization solution is located between the small and large plates. Observations are performed through the solution layer formed by 150- or 500-nm-thick spacers sandwiched between a pair of amorphous silicon nitride windows in the path of the electron beam. The size of the available observation area perpendicular to the electron beam is 50 × 50 μm. The growth solution entering the liquid cell flows between the large plate and the small plate. (Scale bar: 1 mm; the thicknesses of the spacers are not to scale.)

Results and Discussion

Analysis of the Crystallization Solutions.

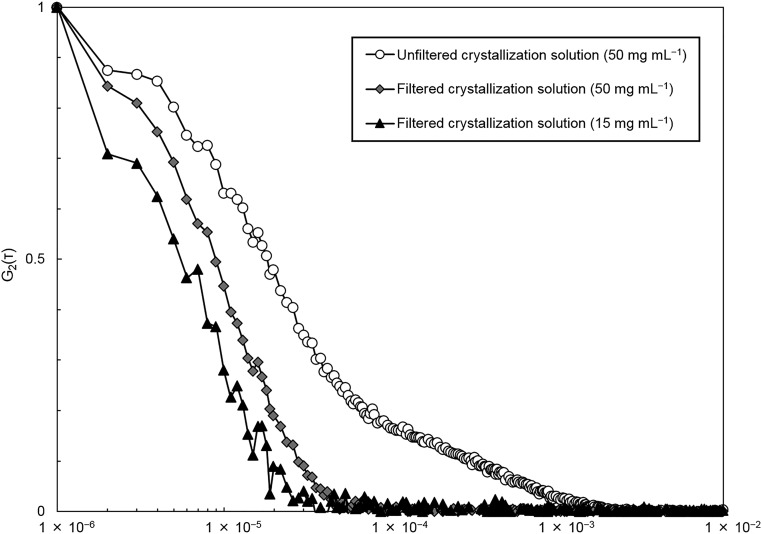
To accelerate nucleation, the liquid cell was initially charged with an unfiltered crystallization solution (50 mg⋅mL⁻¹ of lysozyme and 5 wt% NaCl in a sodium acetate buffer solution); subsequently, a filtered growth solution (15 mg⋅mL⁻¹ lysozyme and 5 wt% NaCl in a sodium acetate buffer solution) was continuously passed through the liquid cell to maintain a constant concentration. Both solutions were analyzed using dynamic light scattering (DLS) (Fig. S2). The DLS signal from the unfiltered solutions is nearly identical to numerous published datasets collected under similar conditions that reveal the presence of mesoscopic (diameters, >100 nm) clusters, which have been suggested to act as precursors for crystal nucleation (9, 10). These solutions clearly lie outside the liquid–liquid coexistence region of the phase diagram, indicating that stable macroscopic dense liquids should not form under these conditions (8). The DLS characterization of the filtered solutions reveals the presence of only lysozyme monomers (Fig. S2).

Fig. S2.

Normalized intensity correlation functions of lysozyme solutions. The three solutions exhibit a decay with characteristic delay time about 20 μs, corresponding to the diffusion time of lysozyme molecules. The unfiltered solution with concentration 50 mg⋅mL^–1 in the only one that exhibits a second decay with characteristic time of about 0.1 ms that suggests the presence of a population of aggregates.

In Situ TEM Observations.

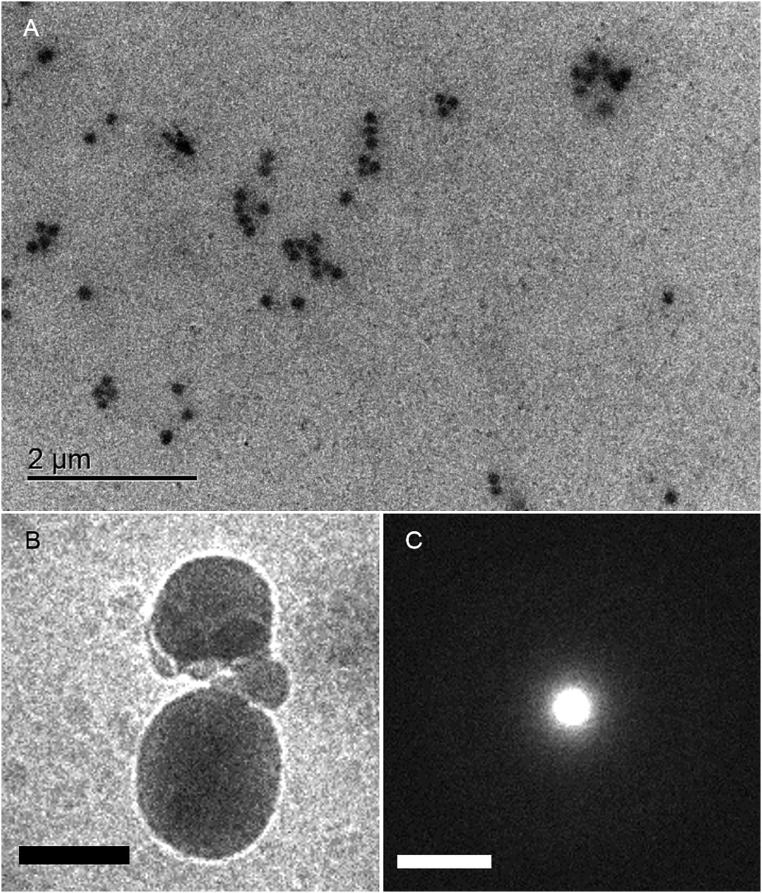
In situ TEM observations (Fig. 1A) demonstrate particles with a range of sizes similar to those identified using DLS. Most of the particles were immobile because they were attached to the liquid-cell windows. The mean diameter of the particles was estimated directly from the TEM images to be ∼170 nm (Fig. S3A). The electron diffraction patterns of the particles exhibit halo rings and no diffraction contrast in the bright-field images (Fig. 1D). Furthermore, they did not coalesce even though many of them were in direct contact with each other. Amorphous particles were also confirmed by corresponding diffraction patterns from the cryo-TEM observations (Fig. S3 B and C). Note that the particles could not be observed in the filtered solutions. From these observations, we conclude that the particles are amorphous solid particles (ASPs) of lysozyme. The ASPs are similar in size to the mesoscopic clusters, which have been suggested to be precursors for crystal nucleation, as reported in previous studies (9, 10). However, crystals never formed within the ASPs during our observations.

Fig. 1.

The amorphous and crystal phases in supersaturated lysosome solutions. In situ TEM images of (A) numerous amorphous solid particles (ASPs); (B) an elongated orthorhombic lysozyme crystal; and (C) a tetragonal lysozyme crystal. The corresponding electron diffraction patterns are shown in D–F, respectively. The arrows in B and C indicate the <001> direction. In C, the (110) face of the tetragonal lysozyme crystal faces upward. [Scale bars: 500 nm (A), 1 μm (B), and 200 nm (C).] In E and F, the crystal zone axes are [10314] and [1 –1 0], respectively.

Fig. S3.

Representative TEM images of ASP. (A) Bright-field in situ TEM image of dispersed ASPs in the liquid cell. The mean diameter of the ASPs in the solution was calculated from the number and total area of the ASPs, assuming that each ASP is a sphere. (B) Cryo-TEM image of ASPs and (C) corresponding electron diffraction pattern. The halo pattern shows amorphous structure of the particles. (Scale bars: 200 nm in B and 2 nm⁻¹ in C, respectively.)

In multiple experiments, we observed both orthorhombic and tetragonal crystals in addition to the ASPs (Fig. 1). The morphologies of the crystals were similar to those of corresponding macroscopic crystals that form under similar conditions (14, 15). For additional identification, we analyzed the electron diffraction patterns generated by these crystalline phases (Fig. 1 E and F). The long-term evolution of two crystals growing in close proximity (Fig. S4) revealed that the orthorhombic crystals grew while the tetragonal crystals dissolved, indicating that the former are more stable polymorphs under the tested experimental conditions. In addition, we observed orthorhombic lysozyme crystals and ASPs in the same view (Fig. S5). The ASPs dissolved completely as opposed to the stably existing orthorhombic lysozyme crystals, suggesting the lower solubility of the orthorhombic lysozyme crystal than that of the ASPs, that is, orthorhombic crystals are more stable than ASPs under the experimental conditions.

Fig. S4.

The stabilities of the observed crystal phases. Bright-field in situ TEM images show an orthorhombic (Upper) and a tetragonal (Lower) lysozyme crystals at 0 and 200 s. The orthorhombic crystal grew by about 400 nm in the <001> direction (white arrow). In contrast, the tetragonal crystal dissolved by about 70 nm in the <001> direction (yellow arrow) but did not grow or dissolve in the <110> directions. This image sequence demonstrates that the orthorhombic phase is more stable than the tetragonal phase under the tested experimental conditions. (Scale bar: 200 nm.)

Fig. S5.

The stabilities of the observed phase between orthorhombic crystal and ASPs. Bright-field in situ TEM images show the two orthorhombic lysozyme crystals and the aggregate of ASPs that exists next to crystals. These ASPs gradually dissolved and completely disappeared within 240 s. In contrast, the orthorhombic lysozyme crystals stably remained. This image sequence demonstrates that the orthorhombic crystal is more stable than the ASPs under the tested experimental conditions. (Scale bar: 500 nm.)

During more than 60 h in 30 separate experiments under optimized experimental conditions, we monitored the nucleation events of an orthorhombic lysozyme crystal attached to a silicon nitride window (Fig. 2A and Movie S1). First, a spherical particle (indicated by an arrowhead in Fig. 2A) formed. As it grew, the particle attained crystal facets and, finally, transformed into an orthorhombic crystal with a characteristic shape elongated in the <001> direction. In other experiments, we observed the nucleation of orthorhombic crystals on ASPs (Fig. 2B and Movie S2). A spherical particle (indicated by an arrowhead in Fig. 2B) was observed to nucleate and transform into an orthorhombic crystal. Because the initial particle has a weaker contrast than that of an ASP at the same size, the nucleated particle may have a different internal structure and density, or shape, than that of the ASPs. This observation clearly indicates that the nucleation event did not start within the ASP; instead, the ASP acted as a heterogeneous substrate that enhanced the nucleation event.

Fig. 2.

The nucleation of lysozyme crystals monitored by time-resolved in situ TEM. (A) A spherical particle observed at 0.1 s (yellow arrowhead) transforms into an orthorhombic crystal. A second crystal nucleates at 10 s. The size, L1, is defined by two dashed lines and a bidirectional arrow at 1 s. (Scale bar: 200 nm.) (B) A spherical particle, indicated with a yellow arrowhead, forms at 0.17 s near an amorphous solid particle (ASP) and transforms into an orthorhombic crystal. The size, L2, is defined similarly to L1 in A. (Scale bar: 200 nm.)

To test the role of the ASPs in the nucleation process, we filtered the crystallization solution. TEM and DLS observations (Fig. S2) indicated that the ASPs were removed from the filtered solutions. Then, the nucleation rates were drastically reduced, likely as a result of the lack of heterogeneous substrates (9). Therefore, the participation of the ASPs as heterogeneous substrates is crucial to crystal nucleation in this system.

Evolution of the Growth Rates of Nucleated Particles.

For additional insight into the nucleation process, we compared the evolution of the lysozyme particle growth rates with known crystal growth rates. We measured the time dependence of the size (L) of the two nucleated particles defined by the bidirectional arrows in Fig. 2 A and B. The size evolutions in Fig. 3 demonstrate that, immediately after nucleation as the first stage of growth, both particles grew to a size of over 100 nm within ∼0.1 s, that is, the growth rate was close to 1 μm⋅s⁻¹; then, the particles grew nearly constantly, and the growth rates of this stage were approximately 1.72 ± 0.22 and 1.73 ± 0.23 nm⋅s⁻¹, as obtained from the datasets of L1 and L2, respectively, in Fig. 3 at 10–30 s. The growth rates at the initial stage are faster by over two orders of magnitude than those during the steady state, which are the same as macroscopic lysozyme (or any other protein) crystals at similar supersaturations (15–17).

Fig. 3.

The size evolution of nucleated particles. The size evolutions of particles L1 in Fig. 2A (circles) and L2 in Fig. 2B (diamonds) reveal decreasing growth rates on average. (Inset) Zoom-in of 0–10 s. Dotted lines are logarithmic fits to each dataset.

To analyze the evolution of the growth rate after nucleation, we first evaluated the effects of the electron beam, which increases the temperature of the specimen (18) and generates chemical species (19), on our system. We observed the growth of orthorhombic lysozyme crystals under different electron fluxes (Fig. S6 and Movie S3). At an electron flux of 3.2 × 10² electron⋅nm⁻²⋅s⁻¹, the crystal grows continuously. However, when we increased the electron flux to 2.9 × 10³ electron⋅nm⁻²⋅s⁻¹, the crystal started to dissolve. In addition, we observed that the growth rate at 3.2 × 10² electron⋅nm⁻²⋅s⁻¹ is constant, at least for 60 s, at a rate of 1.68 ± 0.03 nm⋅s⁻¹ (Fig. S7 A and B). We also measured the growth rate of orthorhombic lysozyme crystals in a non–electron-irradiated environment using optical microscopy (Fig. S7C). At the same conditions as the TEM, the growth rate measured by optical microscopy is 1.7 nm⋅s⁻¹, indicating that the electron beam does not have a significant effect on our system at 3.2 × 10² electron⋅nm⁻²⋅s⁻¹.

Fig. S6.

The electron beam effects to the orthorhombic lysozyme crystal. Bright-field in situ TEM images show the orthorhombic lysozyme crystal (A) growing at 3.2 × 10² electron⋅nm⁻²⋅s⁻¹ of the electron flux and (B) dissolved after irradiated 2.9 × 10³ electron⋅nm⁻²⋅s⁻¹ of the electron flux. (Scale bars: 500 nm.)

Fig. S7.

Growth rates of the orthorhombic crystals in the presence of electron irradiation. (A) Bright-field in situ TEM image of an orthorhombic lysozyme crystal. The bidirectional arrows labeled L < 001> and L′ indicate the sizes along the <001> direction and the direction perpendicular to the <001> direction, respectively. (Scale bar: 200 nm.) (B) The evolution of L <001> and L′ for the crystal shown in A. The growth rate in the <001> direction, measured by linear fitting of the appropriate data, was 1.68 ± 0.03 nm⋅s^–1. The growth rate in the L′ direction was below the limit of detection. (C) Growth rates of orthorhombic lysozyme crystals measured by optical microscopy as a function of supersaturation σ. The numbers above the diamonds show the corresponding experimental temperature in degrees Celsius.

Between 0.1 and 10 s, the growth rates of the two particles sharply decreased from several hundreds of nanometers per second to the bulk growth rate. This appears to be the same tendency as in the case of the nucleation of inorganic materials, such as AgNO₃ (20) and CaCO₃ (21). Based on the Lifshitz–Slyozov–Wagner theory, which can evaluate whether the crystal growth is controlled by diffusion or surface kinetics, these growth rates were limited by diffusion processes because the growth units around the particles were depleted due to the more rapid incorporation of the growth units into the crystals compared to the supply of the growth units to the particle surfaces by diffusion. However, it is well known that the growth of lysozyme crystals is not limited by the diffusion process. Therefore, we first evaluated the possibility of solution depletion as a result of particle formation as a process underlying the slowdown of growth. We used the fact that lysozyme is a relatively small molecule with a hydrodynamic diameter of approximately 3.2 nm and a diffusivity D of approximately 100 μm²⋅s⁻¹. The Stokes–Einstein relation, l² = D ∆t, reveals that diffusion over the characteristic length l = 100 nm, the particle size, would occur over times, ∆t, of an order of 0.1 ms. This estimation indicates that the solution concentration at the particle growth interface is replenished within times much shorter than those probed in Fig. 3. Detailed numerical calculations of the diffusive solute supply (where buoyancy-driven convection is suppressed in cells with a height of 150 or 500 nm, as used here) and the decrease in growth rate support this conclusion (Supporting Information and Fig. S8). Accordingly, we attribute the growth slowdown to the evolution of the particle structure.

Fig. S8.

Evaluation of concentration variations around a growing particle. (A) Schematic of the model geometry. A particle of radius r (shown in green) nucleates and grows with the observed growth rate. The volume of the growth solution that contributes to the crystal growth is defined by the diffusion length $l=\sqrt{Dt}$, where D is the diffusivity of the lysozyme molecule in the growth solution, which is 1.1 × 10⁻¹⁰ m²⋅s^–1 (34). The thickness of the growth cell is 500 nm. (B) The evolution of the lysozyme concentration C* in contributing growth solution for 8 s after nucleation. The largest decrease in C* is 0.05% for an initial concentration of 15 mg⋅mL^–1. This decrement should decrease the growth rate by only 0.04 nm⋅s^–1.

Growth rates faster than those recorded for faceted crystals at similar conditions (15–17) suggest that molecules encounter lower barriers en route to the particle surface. There are three barriers to the growth of a new phase: an enthalpy barrier related to the creation of bonds in the condensed phase, solid, or liquid (22), and two entropy barriers, which account for the search for an incorporation site, via translational diffusion, and a proper crystallographic orientation, via rotational diffusion (23). Molecular incorporation into faceted crystals, where the growth sites on the smooth crystal surfaces are few and distant, and relatively strong crystal bonds are created, maximizing the values of all three barriers. Associations with liquid droplets or clusters encounter minimal entropic barriers and a reduced activation enthalpy. Incorporation into rough crystals, in which the growth site density is close to 1, is an intermediate case, where the enthalpy and rotational barriers are close to those of a facetted crystal, whereas the translational barrier is minimal. Therefore, the initial growth rates (several hundreds of nanometers per second) recorded immediately after nucleation suggest the growth of noncrystalline particles, and the intermediate growth rates (several tens to several nanometers per second) recorded between 1 and 10 s suggest the growth of rough crystals, as expected for crystals emerging from noncrystalline particles. This conclusion is supported by the growth rate of steps on the surface of an orthorhombic lysozyme crystal, 44 nm⋅s⁻¹ (Fig. S9); the steps are always rough and offer the same barriers for molecular incorporation as rough crystals. Therefore, in the case of protein crystallization, entropic restrictions are important due to the large size and complex shape of these molecules. This is one of the reasons why the kinetic coefficients of proteins are 10–1,000 times lower than those of inorganic crystals (24). Therefore, it is reasonable to assume that the very large growth rates measured for the initial particles are only achievable for noncrystalline structures (i.e., eliminating part of the entropic restrictions).

Fig. S9.

Measurement of the step velocity of the orthorhombic lysozyme crystal. A step on a (110) face of an orthorhombic lysozyme crystal was continuously observed at the same position by phase contrast microscopy (A–E). The black arrowhead in A indicates the position where the step is generated. The blue arrowheads in B–E indicate the tip of the step. We measured the step velocity in the <001> direction from the rate of displacement of this tip. A time–space plot image (F) along the X–X′ line in E shows the movement of the tip of the step along the white arrow in F. The slope of the step trace yields a step velocity of 44 nm⋅s^–1. [Scale bar: 50 μm (A).]

At times longer than 30 s, the growth rate of the two crystals dropped to 1.24 ± 0.11 and 1.37 ± 0.17 nm⋅s⁻¹ (obtained from the each dataset at 30–60 s), respectively. TEM images reveal that the phases present during this later stage are faceted crystals. The growth rates measured from the TEM images are similar to those of bulk crystals (Fig. S7) and suggest that the crystals grew following a layer-growth mode (14).

We use the late-stage growth rates to evaluate potential artifacts due to irradiation by the electron beam. The consistency between growth rates measured by TEM and those measured by optical microscopy (Fig. S7C) indicate that the electron beam irradiation negligibly affects the nucleation and growth processes. Assuming that the gradual slowdowns of late-stage growth are due to solution heating by the electron beam, the roughly estimated value of the maximum temperature elevation at the center of the beam is 1.33 °C under our typical experimental condition (18) (details are provided in Supporting Information). If we use the temperature dependency of the solubility and the growth rate (Fig. S7C) to evaluate the hypothetical temperature increase, the growth rate of ∼1.3 nm⋅s⁻¹ at 30–60 s (Fig. 3) suggests a temperature elevation of 0.3 °C. Typically, to monitor a larger solution volume, we shifted the view field after ∼10 s of observation. Therefore, the solution overheating in these scans was less than 0.1 °C, and the corresponding decrease in the supersaturation was insignificant.

Nucleation Process of Lysozyme Crystals.

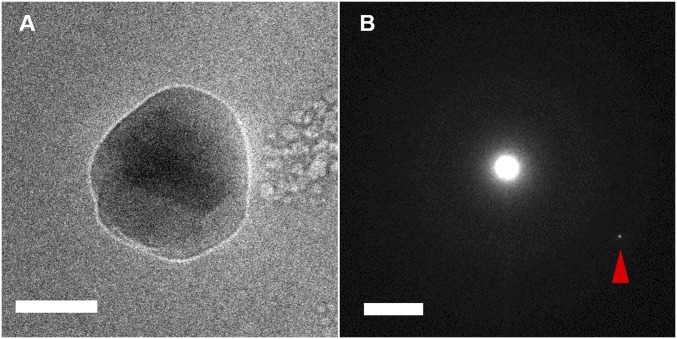
To demonstrate the appearance of a crystal within a noncrystalline particle, we show cryo-TEM images in Fig. 4. The ununiformed contrast can be observed from the particle shown in Fig. 4A. A Laue spot in the corresponding diffraction pattern (Fig. 4B), the faceted shape, and the corresponding diffraction contrast (Fig. S10) represent the crystalline phase. These cryo-TEM images may show that a crystal appears within a noncrystalline particle. To precisely prove the appearance of a crystal in a noncrystalline particle, 3D images may be useful because a TEM image is just a projection. In summary, time-resolved in situ TEM observations of supersaturated solutions of the protein lysozyme demonstrated crystal nucleation following a heretofore-unsuspected modification of the two-step mechanism. Based on the observations, the pathways of this mechanism are schematically illustrated in Fig. 5. In contrast to earlier proposals (2, 3, 9–12), we demonstrate the action of two mesoscopic amorphous phases: amorphous solid particles that serve as heterogeneous nucleation substrates and short-lived (approximately 0.1 s) noncrystalline particles, which form on the container wall or the ASPs and host crystal nuclei. Even though the detailed features of the noncrystalline particles are still unclear, a plausible feature is that of a dense liquid because molecules inside the particles have the flexibility to form crystalline structures, which may be a feature of the liquid phase. Importantly, lysozyme molecules do not directly assemble into crystal nuclei and the ASPs never transform into crystals. This observation gives us insights into the nucleation of not only protein crystals but also other organic crystals. Scattering and spectroscopic techniques reveal the structure evolutions of organic materials in solutions and the existence of clusters (25). To understand the nucleation, our observations suggest the importance of the direct observation of nucleation events at the nanoscale to reveal the role of amorphous particles on crystal nucleation, whether they act as heterogeneous nucleation sites or precursors for nucleation. In addition, numerous organic molecules of sizes larger than 1 nm have become the focus of medicinal and pharmaceutical chemists (26). It is likely that the large size and related flexibility of these molecules may invoke in their solutions behaviors similar to those observed with proteins, including the complex nucleation pathways reported here. Such a complex pathway has also been observed using cryo-TEM in organic materials, where the amorphous material that is initially formed is reorganized into an ordered system (27).

Fig. 4.

Frozen particle with a crystal in its center observed by cryo-TEM. (A) The particle has a different contrast than the faceted faces, indicating a crystalline structure. (Scale bar: 50 nm.) (B) The corresponding diffraction pattern of the particle shows a Laue spot (indicated by a triangle). (Scale bar: 2 nm⁻¹.)

Fig. S10.

Freezed particle with a diffraction contrast observed by cryo-TEM. (A and B) The particle under different focus position shows that the diffraction contrasts indicated by triangles move with the focus position. This particle is the same as the particle in Fig. 4. (Scale bars: 200 nm.)

Fig. 5.

Schematic of the nucleation pathway of lysozyme crystals. Initially, the lysozyme molecules and the ASPs are in the bulk solution. The pathway where molecules assemble into a crystal was not observed. The transformation from the ASP to a crystal was also not observed. Instead, molecules were assembled into noncrystalline particles, for which the detailed features remain undetermined, which heterogeneously nucleate on the container walls or sometimes on the surface of the ASPs. Crystal nucleation was observed only via the noncrystalline particles.

We demonstrate that the crystals emerging from the noncrystalline particles are rough and follow a normal growth mode, with faceting attained at later growth stages. For additional insights, further analyses of observed noncrystalline particles, such as formation kinetics, are required.

Materials and Methods

Materials.

Six-times–recrystallized lysozyme powder (lot no. E40314; Seikagaku Kogyo) was used as a protein sample without further purification. A 50 mM solution of sodium acetate (pH 4.5) was used as the buffer solution. Stock solutions of lysozyme were prepared by dissolving the appropriate amount of lysozyme powder in the buffer solution. The concentration of the lysozyme stock solutions was measured using UV absorption spectrometry (SmartSpec Plus; Bio-Rad Laboratories). NaCl (99.99%; Wako Pure Chemical Industries) was dissolved in the buffer solution to act as a precipitant for the lysozyme. The crystallization solution was prepared by mixing appropriate amounts of the stock solutions. The lysozyme powder sample contained ∼1.5% impurities, which consisted primarily of lysozyme dimer and 18-kDa polypeptide (28).

Solution Preparation and Procedure for Time-Resolved Liquid-Cell TEM Observations.

The supersaturation of the crystallization solution is defined as σ = ln(C/C_e), where C is the bulk concentration of lysozyme and C_e is its solubility at a given temperature. We used two crystallization solutions with different supersaturations. A crystallization solution with a higher supersaturation was used to initially fill the liquid cell before the observation. This solution was prepared by mixing the lysozyme solution and NaCl solution immediately before filling the liquid cell. The resulting solution contained 50 mg⋅mL⁻¹ lysozyme and 50 mg⋅mL⁻¹ NaCl and was not filtered. The crystallization solution, with a lower supersaturation, contained 15 mg⋅mL⁻¹ lysozyme and 50 mg⋅mL⁻¹ NaCl, and flowed through the liquid cell during the TEM observations. This crystallization solution was filtered through a cellulose acetate filter with 0.20-μm pores. During the observations, the solution was passed continuously through the liquid cell at a rate of 1–3 μL⋅min⁻¹ by means of a syringe pump. All of our experiments were performed at 24 °C; as a result, the degree of supersaturation, σ, in the liquid cell was constant. We used values of 3.19 and 3.30 mg⋅mL⁻¹ as the solubilities at 24 °C for the orthorhombic (29) and tetragonal phases (30), respectively, to maintain consistency with our observations of the stability of these phases (Fig. S4). The supersaturations of the crystallization solution with the lower supersaturation were σ = 1.55 and σ = 1.51 for the orthorhombic and tetragonal forms, respectively.

Electron Microscopy.

We used two Hitachi transmission electron microscopes: an H-8100 and an HF-3300. The H-8100 with a LaB₆ filament was operated at an acceleration voltage of 200 kV. Images and movies were recorded using an XR-611 TEM camera (Advanced Microscopy Techniques), which has a recording interval of 157 ms. The HF-3300 with a field-emission gun was operated at an acceleration voltage of 300 kV. Movies were recorded using an ORIUS SC1000 CCD TEM camera (Gatan), which had a recording interval of 100 ms. The electron flux was measured using a combination of a probe-current detector and a Model 6485 Picoammeter (Keithley Instruments) installed in the H-8100.

The TEM Holder and the Assembly of the Liquid Cell.

We used a TEM holder (Protochips) in combination with a liquid cell to image the liquids. The liquid cell consisted of a pair of semiconductor-based plates with an electron-transparent window consisting of an amorphous silicon nitride membrane and two Viton O-rings. These components permitted the preparation of the sample solution under high-vacuum conditions in the TEM (Fig. S1) and allowed the solution to be passed through the liquid cell by means of a syringe pump during the observations. The plates were separated by 150-nm-thick or 500-nm-thick spacers to form the flow path for the sample solution. The thickness of the observed solution layer was larger than the thickness of the spacer due to the expansion resulting from the vacuum present in the electron microscope (31). Before assembling the liquid cell, the plates were subjected to a hydrophilization treatment using plasma-ion bombardment.

Rates of Growth of the Lysozyme Crystals Examined Using Optical Microscopy.

We observed orthorhombic lysozyme crystals using phase contrast microscopy (PCM), and we measured their growth rates for comparison with those observed using TEM. For these measurements, we used a growth cell (32) in which a seed crystal and the growth solution were sealed. Seed crystals for the PCM observations were produced using a crystallization solution (100–120 mg⋅mL⁻¹ lysozyme plus 25 mg⋅mL⁻¹ NaCl in the buffer solution). The solution was sealed in a glass tube (∼400 mL) and kept in an incubator at 40 °C to produce orthorhombic crystals. After 2–3 d, several crystals measuring 100–200 µm were formed, and these were used as seed crystals. A seed crystal was placed in the cell and aligned with its c axis parallel to the focal plane. The growth solution, which contained 15 mg⋅mL⁻¹ lysozyme and 50 mg⋅mL⁻¹ NaCl, was identical to that used in the experiments in the TEM. Before the growth solution was sealed in the cell, it was filtered using a syringe filter with a pore size of 0.20 µm. For the growth rate measurements, the temperature of the cell was maintained in the range of 24–28 °C using Peltier elements on the cell stage. The range of supersaturation σ of the solutions was 1.38–1.55 for the orthorhombic crystals. The temperature at which we measured the step velocity for the orthorhombic crystal (Fig. S7) was 24 °C; the corresponding supersaturation σ was 1.55.

DLS Characterization of the Solutions.

The correlation functions of light scattered by the tested solutions were recorded using an ELS-Z1TK instrument (Otsuka Electronics) equipped with a semiconductor laser (wavelength, 660 nm). We used a quartz cuvette. The respective correlation functions of these solutions are shown in Fig. S2.

Cryo-TEM Observations.

We used a field emission TEM, JEM-2200FS, operated at an acceleration voltage of 200 kV. Images were corrected using a MSC model 794 (Gatan). The sample solution was put on a micro grid, moved to a cryotreatment, and was placed on the cryo-TEM holder. After the treatment, the grid was maintained continuously under −170 °C to prevent crystallization of the water.

Determination of the Size of the ASPs.

From the TEM images, we measured the mean diameter of the ASPs in the experimental solution. An example image is shown in Fig. S3. The ASPs were counted, and the surface area occupied by the ASPs in the plane was measured. By assuming that each particle was spherical, we calculated the mean diameter of the ASPs to be 170 nm from the number and total area of the particles.

SI Text

Calculation of the Concentration Changes Around a Growing Crystal.

When a crystal of lysozyme is growing in solution, the concentration of lysozyme molecules in the solution should decrease because of incorporation of molecules into the crystal surface. To evaluate the effect of this concentration decrement on the growth rate under TEM, we calculated the concentration of lysozyme molecules around a growing crystal on the basis of our experimental setup and results.

Consider a simple model in which a spherical crystal of radius r nanometers is nucleated in a growth solution in which r enlarges (grows) isotopically with time. The moment when nucleation commences (r = 0) is defined as t = 0 s, where t is the time from the nucleation. Molecules for the growth of the crystal are provided by diffusion from the growth solution to the crystal, and the volume of the growth solution is defined by r, the diffusion length l, and the thickness of the fluid cell (500 nm). A schematic representation of this model at time t is shown in Fig. S8A. We applied this model to the crystallization of the orthorhombic crystal.

The radius r(t) was calculated using the logarithmic function from fitting in Fig. 3 of L2. The mass of lysozyme in a particle at time t [M_c(t)] can be expressed as follows:

$$M_c\left(t\right)=V_c\left(t\right)\rho =\frac{4}{3}\text{π}{r}^3\rho ,$$ [S1]

where V_c(t) is the volume of the crystal and ρ is its density. From the structure of the unit cell of the orthorhombic lysozyme crystal [four molecules in 5.644 × 7.373 × 3.043 nm (33)], the molecular weight of the lysozyme (14,300), and the Avogadro constant (6.02 × 10²³), the density ρ is calculated to be 0.75 g⋅cm^–3. The diffusion length l can be expressed as $l=\sqrt{Dt}$, where D is the diffusivity of the lysozyme molecule in the growth solution, which is 1.1 × 10⁻¹⁰ m²⋅s^–1 (34).

We now consider the mass M_s of lysozyme molecules that can contribute to crystal growth in the growth solution. The time at which L exceeds 500 nm, the thickness of the liquid cell, is about 0.005 s. Because this time is much smaller than the time resolution of the TEM movies (recording interval, 157 ms), we can ignore the vertical direction and assume a cylindrical geometry for the purposes. From the volume of the cylinder described above and the volume of the nucleated crystal, the volume of the growth solution V_s that contains molecules that contribute to crystal growth can be expressed as follows:

$$V_s\left(t\right)=4\text{π}{\left(r+l\right)}^{2}h-\frac{4}{3}\text{π}{r}^3.$$ [S2]

The total mass M of lysozyme molecules in this cylinder is V_sC (where C is the initial concentration of the growth solution ∼15 mg⋅mL^–1). The value of M_s can then be obtained by using M and M_c, as follows:

$$M_s\left(t\right)=M-M_c=4\text{π}{\left(r+l\right)}^{2}hC-\frac{4}{3}\text{π}{r}^3\rho .$$ [S3]

Finally, the concentration C* in the cylinder at t is given by the following expression:

$$C^{\ast }\left(t\right)=\frac{M_S}{V_s}=\frac{3{\left(r+l\right)}^{2}hC-r^3\rho }{3{\left(r+l\right)}^{2}h-r^3}.$$ [S4]

The description of C*(t) is shown in Fig. S8B.

According to this calculation, C*(0.15) = 14.992 mg⋅mL^–1 is lowest in the range 0 < t ≤ 8. This decrease in comparison with the initial concentration is only 0.05%. After t = 0.15, the concentration gradually increases because of the decrease in the growth rate. As a result, the concentration recovers to C*(8) = 14.998 mg⋅mL^–1. The difference in supersaturation ln(C/C_e) – ln{C*(8)/C_e} is about 0.0005. The expected decrease in the growth rate of orthorhombic crystals for this difference in supersaturation is about 0.04 nm⋅s^–1 in the <001> direction under our experimental conditions. Note that this change in growth rate is too small to explain the decrease in growth rate immediately after the nucleation under TEM. The change in concentration around the crystal is therefore too small to affect the growth rate under our experimental conditions.

Estimation of the Temperature Elevation of the Liquid Cell.

To evaluate the temperature elevation by electron beam, we calculated the temperature in the center of the beam. According to the Grogan et al. (18), the maximum temperature elevation at the center of the beam is as follows:

$$\mathrm{\Delta }{T}_{\max }=\frac{{10}^{2}SI}{\pi \alpha C_p}\left\{\frac{1}{4}-\frac{1}{2}\ln \left(\frac{L}{a}\right)\right\},$$ [S5]

where $S$ is the electron stopping power (in megaelectronvolts⋅centimeters²⋅gram⁻¹⋅electron⁻¹), $I$ is the beam current (in coulombs⋅second⁻¹), $\alpha$ is the thermal diffusivity of water (in meters²⋅second⁻¹), $C_p$ is the specific heat at constant pressure of water (in joules⋅gram⁻¹⋅kelvin⁻¹), L is the radius of a disk that has the same area of the Si₃N₄ window (in meters), and a is the radius of the beam (in meters). For calculation, we used $S=$ 2.8 at 200 keV (35), $\alpha =1.4\times {10}^{-7}$ (36), $C_p=4.18$ (37), $L=5.6\times {10}^{-5}$, and $a=2.8\times {10}^{-6}$ as typical values, and obtained $\mathrm{\Delta }{T}_{\max }$ = 1.33 for our experimental condition.