Significance
Efficient thermal transport is critical for applications ranging from electronics and energy to advanced manufacturing and transportation; it is essential in emerging domains like wearable computing and soft robotics, which require thermally conductive materials that are also soft and stretchable. However, heat transport within soft materials is limited by the dynamics of phonon transport, which results in a trade-off between thermal conductivity and compliance. We overcome this by engineering an elastomer composite embedded with elongated inclusions of liquid metal (LM) that function as thermally conductive pathways. These composites exhibit an extraordinary combination of low stiffness (<100 kPa), high strain limit (>600%), and metal-like thermal conductivity (up to 9.8 W⋅m−1⋅K−1) that far exceeds any other soft materials.
Keywords: liquid metal, thermal conductivity, soft materials, soft robotics, stretchable electronics
Abstract
Soft dielectric materials typically exhibit poor heat transfer properties due to the dynamics of phonon transport, which constrain thermal conductivity (k) to decrease monotonically with decreasing elastic modulus (E). This thermal−mechanical trade-off is limiting for wearable computing, soft robotics, and other emerging applications that require materials with both high thermal conductivity and low mechanical stiffness. Here, we overcome this constraint with an electrically insulating composite that exhibits an unprecedented combination of metal-like thermal conductivity, an elastic compliance similar to soft biological tissue (Young’s modulus < 100 kPa), and the capability to undergo extreme deformations (>600% strain). By incorporating liquid metal (LM) microdroplets into a soft elastomer, we achieve a ∼25× increase in thermal conductivity (4.7 ± 0.2 W⋅m−1⋅K−1) over the base polymer (0.20 ± 0.01 W⋅m−1·K−1) under stress-free conditions and a ∼50× increase (9.8 ± 0.8 W⋅m−1·K−1) when strained. This exceptional combination of thermal and mechanical properties is enabled by a unique thermal−mechanical coupling that exploits the deformability of the LM inclusions to create thermally conductive pathways in situ. Moreover, these materials offer possibilities for passive heat exchange in stretchable electronics and bioinspired robotics, which we demonstrate through the rapid heat dissipation of an elastomer-mounted extreme high-power LED lamp and a swimming soft robot.
Materials with high thermal conductivity are typically rigid and elastically incompatible with soft and mechanically deformable systems (1–6). In the general case of nonmetallic and electrically insulating solids, this limitation arises from kinetic theory and the Newton−Laplace equation, which imply that thermal conductivity (k) will increase with a material’s elastic modulus (E) according to the approximation k ≈ (E/ρ)1/2(CV ℓ/3), where CV is the volumetric heat capacity, ℓ is the average mean free path of phonons, and ρ is the density (7, 8). For polymers like polyethylene, thermal conductivity can be enhanced through macromolecular chain alignment (from k ≈ 0.3 W⋅m−1·K−1 to 100 W⋅m−1·K−1), but this also leads to a dramatic increase in elastic modulus from ∼1 GPa to 200 GPa (9). Likewise, glassy polymer blends have been engineered to increase thermal conductivity through interchain hydrogen bonding (1), and relatively higher thermal conductivity has been observed in amorphous polythiophene (k ≈ 4.4 W⋅m−1·K−1) (2), but the high elastic modulus (E ≈ 3 GPa) and low strain at failure (<5% strain) of films make them unsuitable for soft functional materials (3).
To overcome this fundamental tradeoff with thermal transport in soft materials, attempts have been made to engineer composites with various fillers (10), including metals (11, 12), ceramics (13), carbon fibers (14), and nanomaterials such as carbon nanotubes and graphene (4, 15, 16). Anisotropic thermal conductivity can arise in composite systems by using 1D fillers such as carbon fibers where thermal transport preferentially occurs along the major dimension of the filler (14). Thermal anisotropy can also be induced in polymeric materials during drawing processes that increase chain alignment (17). Although these composites exhibit increased thermal conductivity, they typically use rigid fillers that result in mechanically stiff materials that cannot support stretchable functionality (4–6) and, in the case of carbon-based fillers, become electrically conductive even at low-volume loadings, which can interfere with functionality (18). To date, the combination of low elastic modulus on the order of biological tissue, large mechanical deformability, and high thermal conductivity remains elusive.
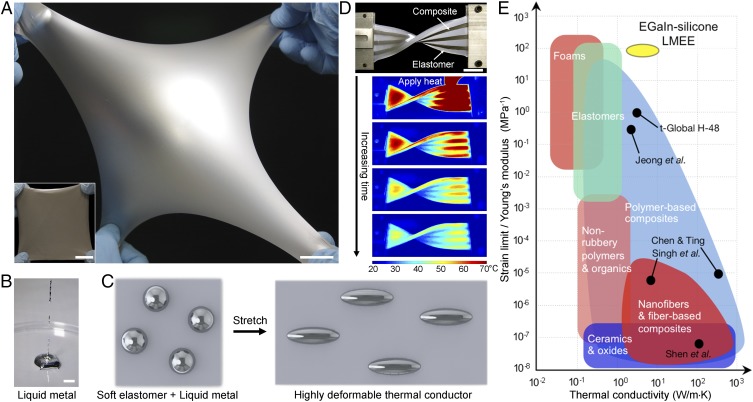
Here, we show that a soft-matter composite consisting of elongated liquid metal (LM) microdroplets dispersed in a highly deformable silicone elastomer (Fig. 1 A−D) exhibits an unprecedented combination of high thermal conductivity (4.7 ± 0.2 W⋅m−1·K−1 under stress-free conditions; 9.8 ± 0.8 W⋅m−1·K−1 at 400% strain) with a low modulus (89 ± 2 kPa after 200% prestrain) and high strain limit (>600%). This approach overcomes the Newton−Laplace scaling because the inclusions have a thermal conductivity that is dominated by electrons, rather than phonons, and can deform with the surrounding matrix to support strain and thermal−mechanical coupling (Electronic Contribution to Thermal Conductivity of EGaIn and Fig. 1 C and D). Previously, we showed that LM-embedded elastomers can be engineered to exhibit dramatic enhancements in electrical permittivity (19) and conductivity (20) without sacrificing the elastic properties of the matrix elastomer. A subsequent effort by another group attempted to show enhanced thermal conductivity with a polydisperse suspensions of irregularly shaped LM inclusions (12). Although an enhanced thermal conductivity of 2.2 W⋅m−1·K−1 was measured at high LM volume fraction (66% by vol.; 92.5% by weight), these samples exhibited an increased stiffness (Young’s modulus increased from 0.65 MPa to 3.3 MPa) and reduced stretchability (strain limit decreased from 150 to 50%), which limits the ability to elongate LM droplets in situ. Comparing previous results with the exceptional performance reported here (Fig. 1E) highlights the critical importance of LM microstructure (and not just material composition) in enabling elastomers to exhibit metal-like thermal conductivity without altering their natural elasticity.
Fig. 1.
Soft, thermally conductive composite. (A) Highly deformable LMEE. (scale bars, 25 mm.) (B) EGaIn alloy is liquid at room temperature and shows fluid characteristics as demonstrated by falling droplets. (Scale bar, 10 mm.) (C) Schematic illustration of the LMEE composite where LM microdoplets are dispersed in an elastomer matrix and, upon deformation, the LM inclusions and elastomer elongate in the direction of stretching. (D) Alternating strips of LMEE and unfilled elastomer are heated with a heat gun, and the IR photo time sequence shows the LMEE dissipating heat more rapidly than the elastomer (images correspond to t = 0, 5, 10, and 15 s after the heat source is removed). (Scale bar, 25 mm.) (E) The ϕ = 50% LMEE composites described here occupy a unique region of the material properties space when comparing thermal conductivity with the ratio of strain limit to Young’s modulus. (Data points are from refs. 2, 9, 12, and 14.)
Electronic Contribution to Thermal Conductivity of EGaIn
The electronic component of thermal conductivity (ke) can be estimated based on the electrical conductivity (σ) and the Weidemann Franz Law, ke/σ = LT, where L = 2.44 × 10−8 W/(S·K) is the Lorenz Number and T is absolute temperature. For EGaIn at room temperature, σ = 3.4 × 106 S/m (21), so ke = 24.9 W⋅m−1·K−1. The total thermal conductivity of EGaIn is 26.4 W⋅m−1·K−1 (23). This implies that the thermal conductivity of EGaIn is largely dominated by electrons.
Experimental Results
The LM embedded elastomer (LMEE) is composed of a Pt-catalyzed silicone elastomer embedded with a randomly distributed, polydisperse suspension of nontoxic (21), liquid-phase eutectic gallium−indium (EGaIn) microdroplets (19, 20, 22). As shown in Fig. 1D and Movie S1, stretched and twisted strips of LMEE exhibit rapid thermal dissipation compared with adjacent strips of unfilled elastomer subject to the same initial heating. Compared with previous attempts with LM-filled elastomers (12), we have discovered that strain creates thermally conductive pathways through the in situ elongation of the deformable liquid inclusions, which significantly enhances thermal conductivity in the stretching direction. For permanent (stress-free) and strain-controlled elongation of the LM inclusions, this enhanced k is nearly 25× to 50× greater than the unfilled elastomer (0.20 ± 0.01 W⋅m−1·K−1) and approaches the limit for the parallel rule of mixtures of an EGaIn−silicone composition (23) without the aid of percolating networks. Referring to Fig. 1E, the exceptional combination of high thermal conductivity, low elastic modulus, and high strain limit allows the LMEE composites to occupy an uncharted region of the material properties space.
The thermal composite is fabricated by shear mixing EGaIn alloy (75% Ga, 25% In, by weight; Gallium Source) with an uncured silicone elastomer (Ecoflex 00-30; Smooth-On) (Methods for material fabrication). During mixing, the LM droplets form a self-passivating Ga2O3 coating that helps prevent coalescence and eliminates the need to add surfactants or other dispersing agents (24). The droplets have a statistically uniform spatial distribution and are polydisperse, with a median diameter of ∼15 μm (19). Thermal conductivity is measured using the transient hotwire (THW) method in which an embedded wire simultaneously acts as a resistive heat source and thermometer that measures the change in temperature (ΔT) as a function of time (t), which is related to thermal conductivity through the cylindrical heat diffusion equation (Methods and Fig. S1). Experimental measurements are presented in Fig. 2A and show that, as LM volume fraction (ϕ) increases, thermal conductivity increases (Fig. S2). These values are in good agreement with theoretical predictions obtained from the Bruggeman effective medium theory (EMT) formulation (25) for a uniform dispersion of spherical EGaIn inclusions [k = 26.4 W⋅m−1·K−1 (23)] in a silicone matrix (k = 0.20 W⋅m−1·K−1).
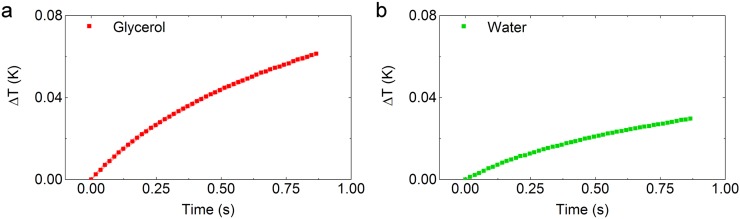
Fig. S1.
Change in temperature (ΔT) versus time for (A) glycerol and (B) water. Data symbols represent the average, and the shaded areas correspond to the SD for the 50 measurements at each condition.
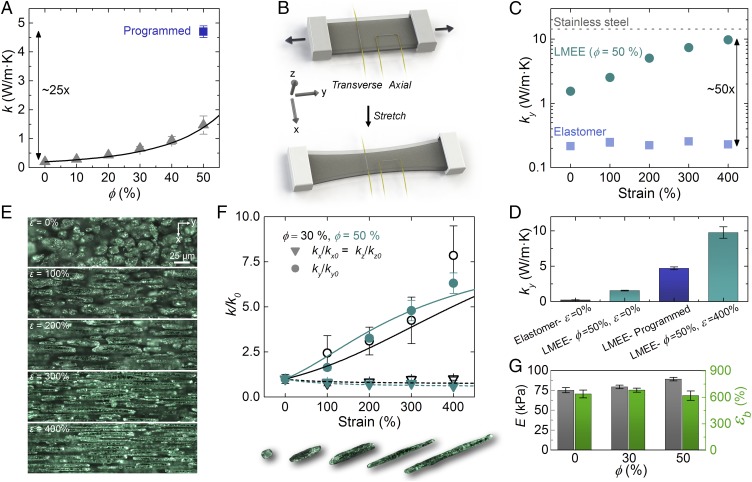
Fig. 2.
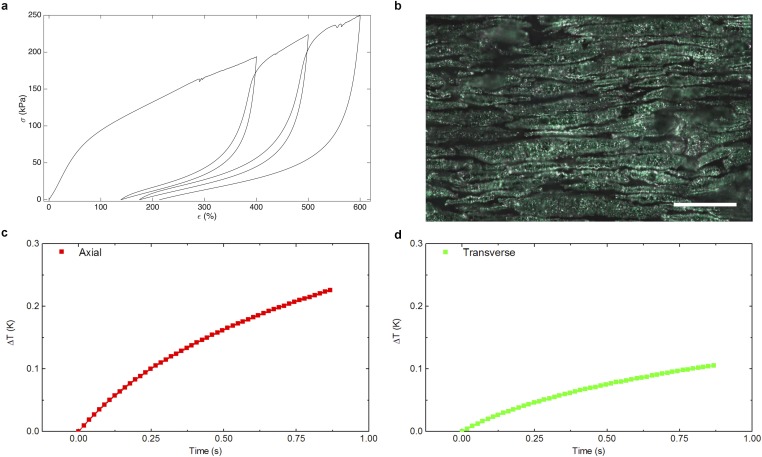
Thermal−mechanical behavior of the LMEE composite. (A) Thermal conductivity versus LM volume fraction (ϕ) in the stress-free state. The programmed sample refers to a composite that has been stretched to 600% strain and then relaxed to an unloaded state. Here the symbols are the experimental measurements, and the solid curve represents the theoretical prediction from the Bruggeman EMT formulation (n = 100 volume fraction dependence, n = 5 programmed samples). (B) Schematic of the THW method to measure anisotropic thermal conductivity under deformation. (C) Plot of thermal conductivity in the stretch direction versus strain for the elastomer and the LMEE composites. Upon stretching, the LMEE approaches the thermal conductivity of stainless steel and is 50× greater than the unfilled elastomer (n = 5). (D) Thermal conductivity comparison for different LM volume fractions (ϕ) and stress states (n = 5). (E) Optical micrographs of the 30% LMEE microstructure during stretching, with the images corresponding to 0 to 400% strain in 100% increments (from top to bottom). (F) Normalized thermal conductivity as a function of strain (blue open symbols are ϕ = 30%, and cyan closed symbols are ϕ = 50%; n = 5). The solid line represents the predicted behavior for the y direction, and the dashed line is the prediction for the x and z direction from our model. The images are representative images of the LM inclusions during the deformation process. (G) Mechanical properties of the LMEE composites with elastic modulus on the left axis and strain at break on the right axis (n = 3). All error bars represent ±1 SD.
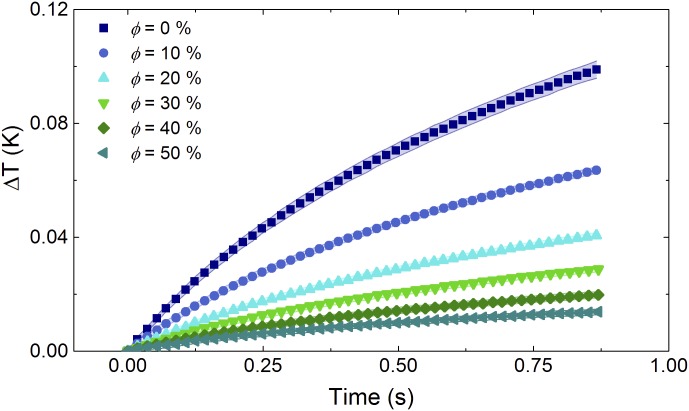
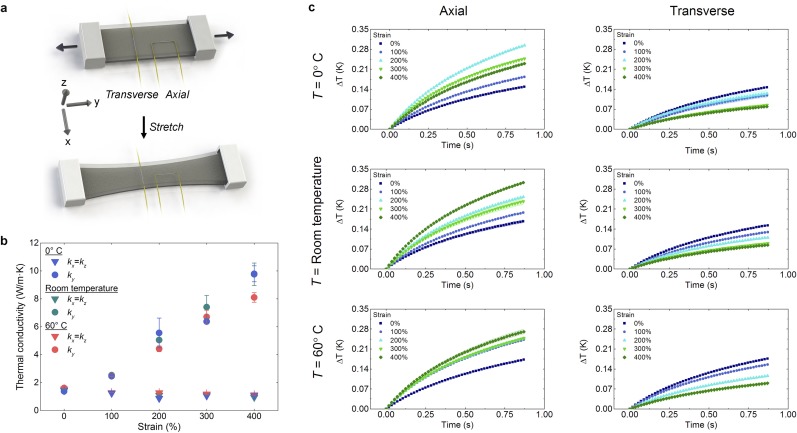
Fig. S2.
Change in temperature (ΔT) versus time for LMEE with ϕ = 0 to 50% volume fraction. Data symbols represent the average, and the shaded areas correspond to the SD for the 100 measurements for each condition.
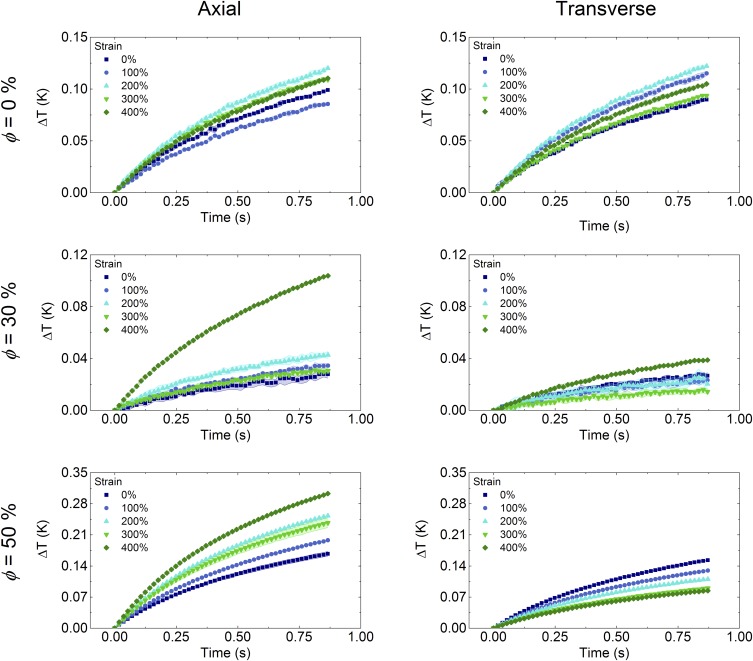
We further configure the THW method to enable directional measurements of thermal conductivity upon deformation by laminating LMEE strips around wires that are parallel (axial) and perpendicular (transverse) to stretch, as shown in Fig. 2B. Ellipsoidal heat spreading yields effective anisotropic thermal conductivities in the axial and transverse directions that can be transformed to measure the orthotropic (kx, ky, kz) bulk values (EMT for derivation) (26, 27). This configuration enables examination of the thermal−mechanical coupling between thermal conductivity and deformation. We find that, upon stretching the unfilled (ϕ = 0%) homogenous elastomer, the thermal conductivity in the direction of stretch (ky ≈ 0.20 W⋅m−1·K−1) remains largely unchanged (Fig. 2C). However, when stretching the ϕ = 50% LMEE, the thermal conductivity in the longitudinal direction (ky) dramatically increases and reaches a value of 9.8 ± 0.8 W⋅m−1·K−1 at 400% strain (Figs. S3 and S4). This represents an increase of ∼50× relative to the unfilled material and a value that approaches the thermal conductivity of some metals like bismuth and stainless steel. These measurements, which were taken at room temperature, are in good agreement with tests performed on samples that were either cooled to 0 °C or heated to 60 °C (Fig. S5). In addition, the material is robust to cyclical loading, with only a slight increase in thermal conductivity measured after 1,000 cycles of 200% strain (Fig. S6). Furthermore, we can “program” the material to achieve permanently elongated LM inclusions in a stress-free state by stretching a virgin sample of LMEE to 600% strain and then unloading to zero stress. An unrecoverable plastic strain of 210% is induced, enabling elongated inclusions in an unloaded (stress-free) state (Methods and Fig. S7). As shown in Fig. 2A, thermal conductivity of the programmed LMEE sample in the longitudinal direction (ky) is 4.7 ± 0.2 W⋅m−1·K−1, which is ∼25× greater than that of the base elastomer (Fig. 2D). It is important to note that, when unstrained, both the ϕ = 0 and 50% samples exhibit values of k that are typically observed in other polymeric composites (12, 28).
Fig. S3.
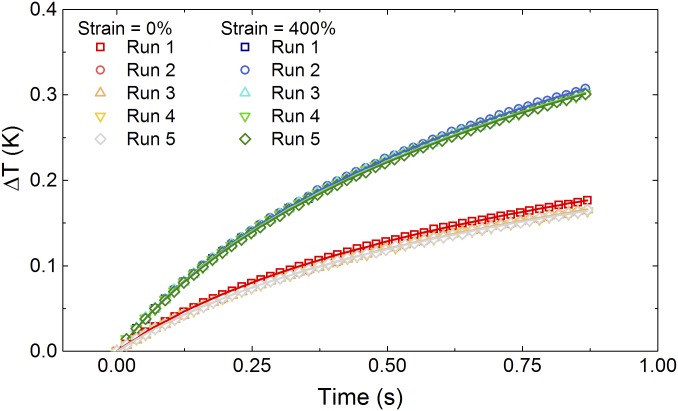
ΔT versus time for ϕ = 50% for the axial wire at ε = 0% and 400%, which demonstrates good agreement with the three-parameter fit explained in Methods, THW Testing. The symbols are the data points for each run, and the lines represent the corresponding three-parameter fit.
Fig. S4.
ΔT versus time of ϕ = 0%, 30%, and 50% for the axial and transverse wire up to 400% strain in 100% strain steps. Data symbols represent the average, and the shaded areas correspond to the SD for the five measurements for each condition. As noted in Methods, THW Testing, a current of 30 mA was applied on the ϕ = 30% experiments except at ε = 400% where 60 mA is applied, which explains the greater temperature rise for these data points relative to the other strain values. Hotwire lengths can vary between tests, resulting in a nonmonotonic temperature change across strain steps. This is accounted for by q, the volumetric heating of the wire per unit length, when calculating thermal conductivity.
Fig. S5.
Temperature dependence. (A) Schematic of the testing setup. (B) Compiled data showing the ϕ = 50% thermal conductivity stretch dependence for 0 °C, room temperature, and 60 °C (n = 5, error bars represent ±1 SD). Good agreement is observed between the three temperatures, with ky varying by an average of 8.3% from the room temperature measurement over all strains (maximum variation of 17% at 400% strain and 60 °C). (C) ΔT versus time of ϕ = 50% for the axial and transverse wire up to 400% strain in 100% strain steps. Data symbols represent the average, and the shaded areas correspond to the SD for the five measurements for each condition. Hotwire lengths can vary between tests, resulting in a nonmonotonic temperature change across strain steps. This is accounted for by q, the volumetric heating of the wire per unit length, when calculating thermal conductivity.
Fig. S6.
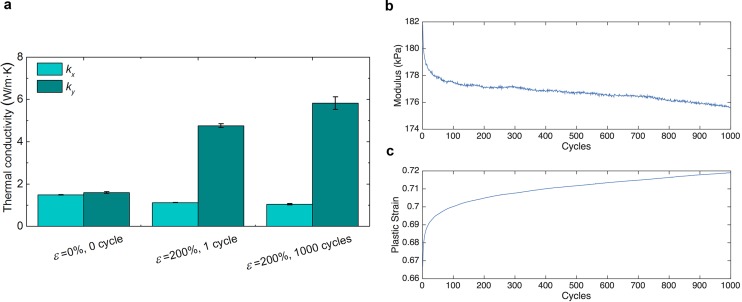
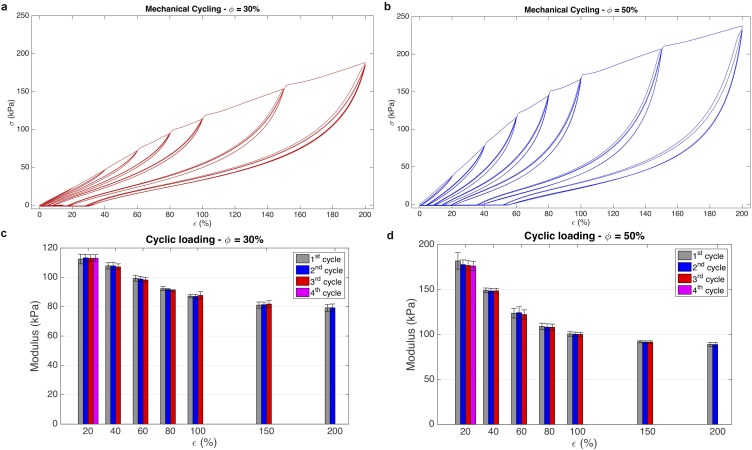
Cyclic testing. (A) Thermal conductivity for a ϕ = 50% composite tested at a strain (ε) of 0% and then stretched to 200%. The sample is then cycled 1,000 times up to a strain of 200%. Thermal conductivity is then evaluated after the 1,000 cycles at a strain of 200% (n = 5, error bars represent ±1 SD). (B) The 10% modulus and (C) induced plastic deformation as a function of number of cycles. The modulus slightly drops and plastic deformation slightly increases with number of cycles. The slight increase in the thermal conductivity ky could be attributed to the Mullins effect and permanently increasing aspect ratio of LM particles.
Fig. S7.
Programmed material. (A) Stress vs. strain curve for fabrication of shape-programmable LMEE with 50% volume ration of LM. (B) Optical micrograph of programmed LMEE with 50% volume ratio of LM. (Scale bar, 50 μm.) (C and D) Change in temperature (ΔT) versus time for (C) axial and (D) transverse wire for the programmed LMEE samples.
Such an unprecedented enhancement in k arises from the discovery of a unique thermal−mechanical coupling in which the deformable LM inclusions elongate into needle-like microstructures along the prestrained or mechanically loaded direction to create enhanced thermally conductive pathways (Fig. 2E). This is further demonstrated in Fig. 2F, in which compositions with ϕ = 30% and 50% EGaIn (by volume) are subject to strains ranging from 0 to 400% in increments of 100% (Methods and Figs. S3 and S4). As shown, the thermal conductivity in the y (stretching) direction increases by greater than a factor of 5 beyond 300% strain. To theoretically capture this behavior, we create an EMT model based on the Bruggeman formulation to explain the relative increase in directional thermal conductivity as a function of axial strain (ε) (EMT for details). As seen in Fig. 2F, we find good agreement between the experimentally measured values (markers) and our theoretical predictions (curves), which capture the large increase in thermal conductivity in the stretching direction (ky) and the slight decrease in the orthogonal directions (kz, kx). The agreement with theory is achieved without data fitting and supports the claim that the observed anisotropic thermal−mechanical response is controlled by the directional change in aspect ratio of the LM inclusions (Fig. 1C). Lastly, for all volume fractions, the composite materials have an elastic modulus less than 90 kPa (Fig. S8) and can support uniaxial strains above 600%, properties that are similar to those of the homogeneous elastomer (Fig. 2G). The modest increase in elastic modulus (<20%) for the LMEE composites can be attributed to surface tension at the liquid−solid interface. For liquid inclusions in a compliant matrix, Style et al. (29) have previously shown that surface tension can induce mechanical resistance to droplet deformation and result in an overall stiffening of the composite. Together, these results show that the EGaIn droplets greatly enhance thermal conductivity of soft materials without degrading their mechanical properties. Significantly, these materials display nearly an order of magnitude enhancement in thermal conductivity and strain at break while possessing an order of magnitude lower modulus than commonly available thermal tapes and previously studied LM-filled composites (12).
Fig. S8.
Mechanical cyclic tests of LMEE. Stress vs. strain curves for (A) 30% and (B) 50% volume ratio of LM and 10% modulus after each strain step for (C) 30% and (D) 50% volume ratio of LM (n = 3, error bars represent ±1 SD).
EMT
As shown in Fig. 1 A and F, the experimental measurements of thermal conductivity are in good agreement with predictions obtained from EMT. The EMT model is based on a Bruggeman formulation that has been adapted to predict the orthotropic bulk values of the thermal conductivity (kx, ky, kz) as a function of both LM volume fraction and stretch. The principal directions are parallel to the sample’s orthogonal surfaces, with the y direction corresponding to the axis along which the sample is stretched.
Modified Bruggeman Formulation.
To explain this experimentally observed thermoelastic coupling, we modify the Bruggeman formulation to account for the stretch-induced deformation of the ellipsoidal LM inclusions. For simplicity, we assume that all particles initially have a spherical shape (initial aspect ratio, p0 = 1) and that the composite is incompressible. During uniaxial stretch in the y direction (λy = λ), the inclusions will become elongated in the direction of loading and have an aspect ratio of . The change in the shape of particles leads to anisotropic thermal conductivity of the effective medium.
Following Sen et al. (35), we use a self-consistent EMT that takes into account the shape of the ellipsoidal particles. We start from a coherent potential approximation with depolarization factor L,
| [S1] |
This equation does not include particle−particle interactions and is more appropriate for a dilute composite. To account for interparticle interactions with the surrounding medium, we use differential EMT (25). In this scheme, we incrementally introduce an infinitesimal suspension of particles to the dispersion medium (step s) and then use this mixture as the reference matrix for evaluating the influence of the next increment (step s + 1). At each incremental step, we assume that the dispersion phase and medium share the same anisotropy in thermal conductivity. This implies the following relationship between thermal conductivity at steps s (ks) and s + 1 (ks+1):
| [S2] |
The differential equation is
| [S3] |
Defining Φ = Vp/(Vm + Vp), it follows that dΦ/dVp = (1 – Φ)/(Vm + Vp). Taking the integral from km to kc for thermal conductivity and from 0 to ϕ for Φ,
| [S4] |
| [S5] |
Here, we modify L to predict the effective thermal conductivity as a function of stretch. For an incompressible material under uniaxial extension (λy = λ), the deformations orthogonal to the primary stretching direction are equal, i.e., . Therefore, the aspect ratio of an incompressible particle as a function of is .
| [S6] |
| [S7] |
| [S8] |
For spherical particles with , it follows that , which recovers the original Bruggeman formula.
Comparison with Experiment.
These predictions are compared with experimental values obtained by mapping the axial and transverse components of thermal conductivities (kaxial, ktrans) (36). Values from the transient hotwire measurements are equal to the geometric mean of the thermal conductivity values orthogonal to wire, specifically, and (26, 27, 37). From symmetry, we assume kx = kz and solve for the directional components of thermal conductivity,
| [S9] |
The uncertainty in kaxial and ktrans is propagated when reporting the uncertainty in kx, kz, and ky.
Selected Applications
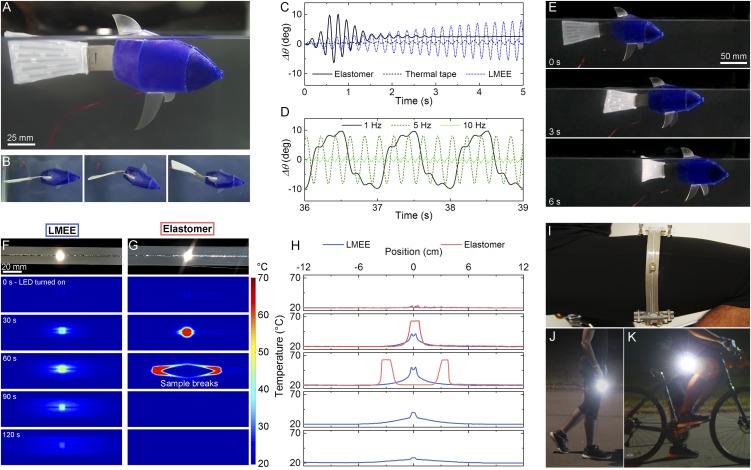
Because the LMEE composites are intrinsically soft and deformable, they can be incorporated as thermal interface materials into wearable computing (30) or thermally activated shape-programmable structures (31) and soft robotic systems (32, 33) without altering the natural mechanics of the host. For such applications, high thermal conductivity is not enough; the material must be sufficiently soft to limit mechanical resistance to deformation. We demonstrate this functionality through a thermally activated soft “artificial muscle” that is actuated with embedded wires of Ni−Ti shape memory alloy (SMA) and used for caudal fin locomotion of a silent, soft swimming robot (Fig. 3 A and B, Figs. S9 and S10, and Movie S2). Compared with thermally insulating silicone and relatively stiff thermal tapes, sealing the SMA wires in LMEE allows for significant enhancements in actuation frequency, deflection, and duration (Fig. 3 C and D). Specifically, the LMEE is able to actuate for more than 10,000 cycles at a frequency of 5 Hz (33.3 min) with no observed degradation in amplitude (14 ± 1 degrees; Fig. S9D). In contrast, the unfilled silicone elastomer becomes saturated with heat and ceases to actuate after 2 s. Although the commercial tape can support cyclical loading, its relatively high mechanical stiffness results in a low steady-state amplitude of ∼3 degrees. When incorporated into the robotic fish, the LMEE-sealed SMA enables forward swimming at ∼0.15 body lengths per second (Fig. 3E).
Fig. 3.
Soft robot and stretchable electronics implementation of the LMEE composite. (A) Soft robotic fish composed of a silicone body and caudal fin connected by an LMEE-sealed SMA actuator. (B) Top-down view during forward caudal fin locomotion. (C) LMEE, unfilled silicone elastomer, and commercial thermal tape actuated at a frequency of 5 Hz. (D) LMEE actuated at 1-, 5-, and 10-Hz signal. (E) Time sequence images of the soft robotic fish swimming with a stroke frequency of 0.7 Hz. (F) XHP LED lamp mounted on an LMEE composite stretched to 400% strain with a sequence of IR images during LED operation. (G) The same experiment on an elastomer sample where the sample breaks at 60 s due to significant localized heating. (H) Temperature versus time plots for the IR image sequence, where the temperature is measured across the sample’s length. LED is turned on and off at t = 0 s and t = 70 s, respectively. (I) An XHP LED is mounted to a strip of LMEE that is wrapped around the leg and shows high brightness during (J) running and (K) cycling.
Fig. S9.
Soft robotic actuator. (A) Rendering of molds for holding antagonistic SMA wires and casting LMEE. (B) Illustration of thermal LMEE actuator with embedded LMEE wires. (C) The actuator bending angle is determined in Tracker. (D) Cyclical deformation of actuator during 5-Hz activation after 5 (solid blue curve) and 30 (dashed red) min.
Fig. S10.
The soft swimming robot is composed of an LMEE SMA thermal actuator, silicone caudal fin, and two silicone-enclosed chambers for the body. The buoyancy is adjusted by filling the body with fluid (water or EGaIn).
Furthermore, we demonstrate the LMEE's potential as an exceptional material for thermal management in stretchable electronics and wearable computing by comparing infrared temperature maps of an extreme high power (XHP) LED lamp on stretched LMEE and unfilled silicone elastomer membranes (Methods). The poor thermal conductivity of the unfilled silicone elastomer results in excessive heat accumulation that leads to thermal degradation and dramatic mechanical failure. In contrast, the LMEE effectively dissipates heat and allows continuous operation of the LED (Fig. 3 F−H and Movie S3). To demonstrate the potential use of LMEEs as heat spreaders for low-profile wearable applications, an XHP LED lamp is mounted to a strip of LMEE that is wrapped around the thigh. This wearable lamp can operate during running, hiking, and cycling to provide exceptional visibility at night without the need for a socket mount (Fig. 3 I−K and Movie S4). It runs at power outputs greater than 1 W and produces substantially more light and heat than standard indicator LEDs, which run on milliwatts of power. The XHP LED is representative of a broader range of heat-generating devices (e.g., processors, transformers, power supplies) that could potentially be used in wearable computing and stretchable electronic circuits.
Discussion and Conclusions
Electrically insulating solids with high thermal conductivity are typically rigid due to the dynamics of phonon transport within an elastic medium. Here, we report a soft elastomer composite that overcomes this constraint and exhibits the highest-ever combined values of thermal conductivity and stretchability (Fig. 1E). This high performance is accomplished by exploiting the unique thermal−mechanical interactions of LM microdroplets that are suspended within a silicone elastomer. The composite achieves an exceptional combination of low elastic modulus (<100 kPa; i.e., softer than human skin), high strain limit (>600%), and high thermal conductivity (k), which ranges from 4.7 W⋅m−1·K−1 (stress-free state) to nearly 10 W⋅m−1·K−1 (when stretched). This represents a 25× to 50× increase in thermal conductivity compared with soft rubbers, i.e., similar in magnitude to some metals (e.g., bismuth, manganese, stainless steel) while having a 105 to 106 lower elastic modulus.
The ability to achieve high thermal conductivity with an elastomer without altering its elastic properties is enabled through LM microstructure and the distinctive thermal−mechanical coupling in which the deformation of an elastomer matrix creates needle-like LM inclusions in situ. Previous studies of LM suspensions in elastomer did not explore such critical factors and hence failed to capture the breakthrough performance presented here. These experimentally measured values are also found to be in strong agreement with predictions from a theoretical model that we derived based on Bruggeman EMT. Such agreement is achieved without the aid of data fitting and provides further evidence for the critical role of in situ elongation of LM inclusions. As previously shown by Style et al. (29), altering the size of liquid inclusions in a compliant matrix can result in changes to the elastic modulus of the composite. However, according to our EMT model, inclusion size has little influence on thermal conductivity (which is instead largely dependent on LM volume loading and inclusion aspect ratio). This difference in dependency can be used for matching the elastic properties of composites without altering the thermal properties (Influence of LM Droplet Size on Elastic Modulus and Fig. S11).
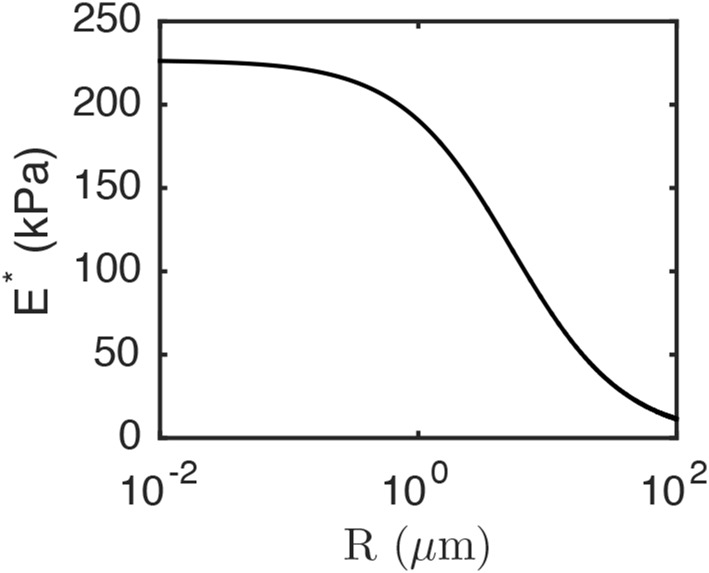
Fig. S11.
Theoretical prediction for dependence of effective modulus of inclusions (E*) on droplet radius (R) for E = 85 kPa and γ = 0.5 N/m. The prediction is based on a theory reported in Style et al. (29).
The combination of high thermal conductivity and elasticity is especially critical for rapid heat dissipation in applications such as wearable computing and soft robotics, which rely on soft and stretchable functionality. We show that LMEE composites can be used to manage heat within an SMA-powered swimming robot and stretchable, body-mounted circuits for high-power illumination. Together, these examples show the potential for LMEEs to dramatically improve thermal management in applications that require electrically insulating materials with both rapid heat conduction and soft elastic functionality. In particular, we anticipate that this class of materials will be enabling for soft robotics, shape-changing programmable matter, stretchable electronics, and soft-matter technologies designed for physical interaction with humans.
Influence of LM Droplet Size on Elastic Modulus
As suggested by Style et al. (29), liquid inclusions suspended in a soft elastomer can exhibit an effective modulus of E* = E⋅[24α/(10 + 9α)], where α = γ/E⋅R, E is the modulus of homogenous elastomer, γ is the interfacial surface energy, and R is the radius of droplets. Hence, we expect that the effective elastic modulus (E*) increases monotonically with decreasing droplet size. This can be seen in Fig. S11, which shows this dependency for an elastic solid of modulus E = 85 kPa and droplets with an interfacial energy γ = 0.5 N/m.
In contrast, it follows from our EMT model that thermal conductivity is not expected to have a significant dependency on droplet size. Instead, the main parameters in our model regarding particle properties are the aspect ratio of the inclusions and the volume fraction in the composite.
Methods
Composite Fabrication.
LMEE composites are composed of a polydisperse suspension of EGaIn microdroplets dispersed in a Pt-catalyzed silicone elastomer (Ecoflex 00-30; Smooth-On). The fabrication method is the same as that reported in Bartlett et al. (19). First, the two-part silicone prepolymer is prepared by combining part A and part B at a 1:1 ratio by mass and then thoroughly mixing and degassing in a planetary centrifugal mixer (THINKY AR-100). EGaIn alloy is prepared by mixing gallium and indium (Gallium Source, LLC) at a 3:1 ratio by mass and then heating and homogenizing at 190 °C overnight on a hot-plate. The LMEE is then prepared by shear mixing the uncured polymer and EGaIn with a mortar and pestle. Components are mixed for 7 min to 10 min until a homogeneous viscous composite is obtained. For volume fractions of LM lower than 30%, the initial mixing is done at higher concentrations and then diluted to maintain similar mixing conditions.
THW Testing.
Thermal conductivity is determined using the THW method and the following analytical solution to the cylindrical heat diffusion equation: k = q/4πξ (34). Here, q is the volumetric heating of the wire per unit length, which is calculated using known current and resistance values (Fig. S1 for reference measurements), and ξ = d(ΔT)/d[ln(t)].
Unstrained measurements.
Test samples are prepared by first suspending a platinum wire (D = 25 µm, ℓ = 40 mm) in a 3D-printed container with dimensions of 40 mm × 7 mm × 7 mm. Next, uncured composite is poured around the wire to ensure conformal contact. The composite is cured with the Pt wire inside in an oven at 50 °C for 16 h. The electrical resistance across the wire is measured before and after curing to ensure that there is no mechanical interference in the wire due to thermal expansion or contraction. To administer the tests, each sample is connected to a Keithley 2700 Digital Multimeter and a Keithley 6221 DC/AC Current Source in a four-point measurement configuration. A Heavyside current input of I = 30 mA is applied, and 50 voltage values (V) are recorded over 0.9 s. With this voltage data and a known current, the resistance (R) is determined as a function of time following Ohm’s Law: R(t) = V(t)/I. This is used to calculate the change in temperature ΔT(t) = [R(t)/R0 – 1]/β and the volumetric heating of the wire per unit length q = I2R0/ℓ. Here, R0 = R(0) is the initial resistance of the wire, β = 3.75 × 10−3 K−1 is the coefficient of thermoresistance of platinum, and ℓ is the length of the wire. Next, we plot ΔT versus time (t) and fit the curves using the following three-parameter model: ΔT = b1ln(t – b2) + b3, where the constants b1, b2, and b3 are the fitting parameters. The fit is performed in MATLAB R2015a (The Mathworks, Inc.) using a nonlinear regression “nlinfit” algorithm. The fitted coefficient b1 corresponds to ξ = d(ΔT)/d[ln(t)], and the thermal conductivity is calculated as k = q/4πξ. Our data acquisition has an arbitrary delay relative to initiation of the Heavyside function, and b2 and b3 represent the delay time and resultant temperature rise that occur during that period.
The thermal conductivities measured for water and glycerol at room temperature are 0.60 ± 0.07 and 0.33 ± 0.02, respectively, and are in good agreement with reference data. The thermal conductivity is reported by taking the average k across all runs, and the error represents ±1 SD. Fig. S1 shows the ΔT versus t plots for these two validation measurements, where the data symbols represent the average and the shaded areas correspond to the SD for 50 measurements.
Average ΔT vs. time for LMEE samples of varied LM volume fraction is shown in Fig. S2. Each measurement is repeated 100 times for each volume fraction of LM composite. The data symbols represent the average, and the shaded areas correspond to the SD for 100 measurements at each volume fraction.
Thermal−mechanical testing.
The thermal conductivity as a function of stretch is measured with two Pt wire probes orientated parallel and perpendicular to the primary stretching direction (Fig. 2B). The probes are laminated between two layers of material, which each have dimensions of 60 mm wide, 40 mm long, and ∼5 mm thick. Tests are performed with composites of ϕ = 0%, 30%, and 50% that are strained (ε = ΔL/L0) to 400% in 100% strain increments. A current of 30 mA is used for ϕ = 0% and 30% (with the exception ϕ = 30% at 400% strain, where 60 mA is applied to improve signal to noise), and 100 mA is used for ϕ = 50%. At each strain increment, five measurements are taken on each wire at 2-min intervals. After each strain increment, the two layers of material are delaminated, freeing the wire probes to prevent damage during stretching, then stretched equally in both directions using linear actuators. At the next position, the layers of composite are relaminated around the wires, with a clamping force applied to ensure conformal contact.
Fig. S3 demonstrates the good agreement with the three-parameter fit for the ϕ = 50% LMEE measured on the axial wire at ε = 0% and 400%. The symbols are the data points for each run, and the lines represent the corresponding three-parameter fit. Fig. S4 presents ΔT vs. t curves for the axial and transverse wires in the ϕ = 0%, 30%, and 50% LMEE. At ε = 0%, the measured thermal conductivity for both the laminated parallel and transverse sensors are in good agreement with the embedded sensors described in Unstrained measurements, proving that the wire is in intimate contact with the LMEE samples.
Strain-dependent thermal conductivity is also evaluated at elevated (60 ± 3 °C) and reduced (0 ± 3 °C) temperatures. A thermocouple embedded in the LMEE is used to monitor temperature, and measurements are conducted when a variance of no more than 0.1 °C is observed over a 1-min period. Thermal conductivity measurements are then performed as described above. In between each strain increment, the LMEE is allowed to reach room temperature and then stretched. The LMEE is then reheated or cooled for the next measurement.
Shape-Programmable LMEE.
We program the shape of the LM particles by inducing plastic deformation in the films. The samples are made in a dogbone shape and tested on an Instron 5969 mechanical testing machine with 10 N load cell. The sample is stretched with a strain rate of 0.17 min−1, up to a strain of 600%, and unloaded to stress-free state. Plastic strain of 210% is induced in the sample, and LM particles are elongated in the direction of stretch (Fig. S7B). THW data are presented Fig. S7 C and D.
Mechanical Testing.
Mechanical samples are prepared in a dogbone shape, and tests are performed on an Instron 5969 mechanical testing machine using a 10 N load cell. Three samples are tested with LM volume ratio of 30% and 50%, under a strain rate of 10 mm/min. Samples are cyclically loaded three times at each of the following sequence of strains: 20%, 40%, 60%, 80%, 100%, 150%, and 200%. Fig. S8 A and B presents the stress−strain curves for LMEE for the 30% and 50% samples, respectively. The elastic modulus is calculated as the slope of the loading curve at a nominal strain of 10%. The nominal strain is defined with respect to the absolute stress-free strain of the sample, which increases during cyclical loading. In general, strain is calculated as a percentage defined with respect to the original length of the virgin sample (before initial loading). The 10% elastic modulus for the 30% and 50% samples is presented in Fig. S8 C and D, respectively.
Soft Robotics Implementation.
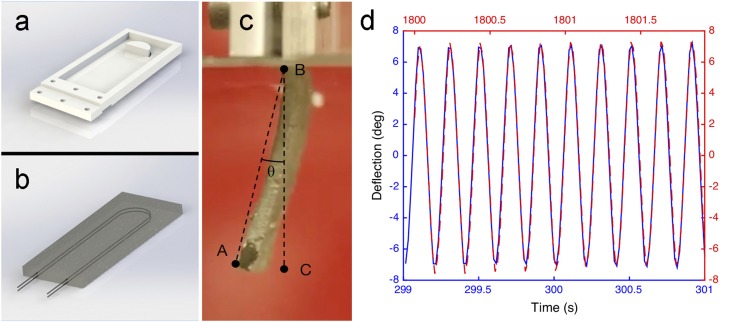
We perform a series of illustrative artificial muscle implementations with SMA wire that enable the propulsion of a bioinspired, silent, soft swimming robot (Fig. 3 A and B and Movie S2). The actuator is composed of two naturally curved loops of SMA wire (0.012 in diameter; Dynalloy) that have an antagonistic arrangement and induce bidirectional bending when serially activated through direct Joule heating. The material encapsulating the SMA actuator is thus required to have both high thermal conductivity to facilitate heat transfer to the outer media and a low Young’s modulus to allow significant deflection (Figs. S8 and S9). This advantage can be seen in Fig. 3C when actuators sealed in either LMEE, unfilled silicon, or commercial thermal tapes are actuated at a frequency of 5 Hz in a water bath. The LMEE-sealed actuator reaches a steady-state amplitude of ∼10 degrees, whereas the unfilled silicone elastomer becomes saturated with heat and ceases to actuate, and the commercial tape reaches a much smaller amplitude of ∼3 degrees because of its high mechanical stiffness. The LMEE-sealed actuator is also able to operate at a range of frequencies (Fig. 3D), with a maximum of 10 Hz. At frequencies above 5 Hz, the electrical pulse duration becomes shorter than the thermal time constant of the fin, and the amplitude of the periodic temperature oscillation within the SMA wire decreases. Details of the SMA actuator fabrication and testing are reported in Thermal Actuator.
When incorporated into a silicone-based soft robotic fish, the LMEE-sealed SMA enables forward caudal fin locomotion at ∼0.15 body lengths per second (0.7 Hz activation). The body of the soft swimming robot is composed of polydimethylsiloxane (PDMS; 1:10 base to curing agent ratio; Sylgard-184; Dow Corning) mixed with a blue pigment (0.3% by weight; Smooth-On); it is an assembly of three parts that are bonded to form two chambers as shown in Fig. S10, which are filled with EGaIn and water, respectively, to balance the weight and buoyancy. Each individual part is produced by casting the dyed PDMS in a 3D-printed mold and then bonded together.
The caudal fin of the robot is composed of Ecoflex 00-30 (Smooth-On). As with the PDMS, the Ecoflex silicone is prepared using a THINKY AR-100 planetary centrifugal mixer. The elastomer is poured into molds for the two halves of the fin. After curing, the two layers of the film are bonded together with an additional layer of Ecoflex. The buoyancy is adjusted by filling the embedded chambers of the caudal fin with water.
LED Demonstration.
LMEE and elastomer (Ecoflex 00-30; Smooth-On) samples are mounted on a frame and stretched to 400% strain. EGaIn traces are applied with a stencil mask and connected to copper leads. XHP LED lamps (Cree XLamp XHP50, 5 mm × 5 mm) are placed onto the EGaIn traces on the stretched samples. The LEDs are connected in parallel with a power supply, and 6 V and 500 mA are supplied at time t = 0 s. IR images are captured with a FLIR A645sc Infrared Camera with a 45° lens at a frame rate of 25 frames per second.
For the wearable electronics demonstration, an XHP LED lamp (Cree XLamp XHP50, 5 mm × 5 mm) is placed on an LMEE layer with 3.5-mm thickness, and is sealed by another layer of LMEE. A thin layer of elastomer is used to seal the EGaIn traces to stop the LM from spreading. EGaIn traces are connected to banana plugs at the terminal end, which are secured in place using silicon adhesive and acrylic clamps. The LED is powered by a 9-V battery.
Thermal Actuator
The actuator used to power the soft robotic fish is composed of a wire of SMA embedded within the LMEE composite. The wire has a diameter of 0.3 mm and reversibly undergoes a phase transition from a martensite to austenite crystal structure when heated to 70 °C. First, the SMA wire (Flexinol; Dynalloy) is “trained” into a naturally curved shape by fixing it into a 3D-printed holder and applying an electrical current of 2.5A for 3 min. The trained wires are then straightened and mounted parallel to each other in an antagonistic configuration using a 3D-printed mold (Objet24; Stratasys) (Fig. S9A). Next, the uncured LMEE is poured into the mold and around the wires. After the material is fully cured, the actuator is demolded and has final dimensions of 20 mm wide, 52 mm long, and 3.2 mm thick (Fig. S9B).
For comparison, studies are also performed with SMA wires embedded in unfilled Ecoflex and a commercial thermal tape (H-48; t-Global). The thermal tape is an elastomer-based pressure-sensitive adhesive with a thickness of 1.1 mm. The layers of thermal tape are bonded together by applying light pressure. Actuators with the H-48 are produced by sandwiching the prestretched wires between three layers of the thermal tape. Actuators with Ecoflex are produced using the same fabrication technique used with the LMEE.
The elastomer-sealed actuators are tested in a tank of water. The thermal actuator is oriented vertically and mounted to an aluminum block. A DC power supply (Electro Industries DIGI360) provides a constant voltage with a power of 19.6 W. The supplied voltage is switched on and off at a defined frequency with a metal-oxide semiconductor field-effect transistor (MOSFET; Digi-Key) controlled through an Arduino Uno microprocessor. Frequencies of 1, 5, and 10 Hz are examined where two square wave pulses (duty ratio: 50%) with a phase difference of 180° are sent to the two SMA wires. Computer vision software (Tracker) is used to track the trajectory of the actuator tip, and the angle of deflection (θ) is automatically calculated by the software (Fig. S9C).
Supplementary Material
Acknowledgments
We acknowledge J. Bartels and E. Markvicka for support with infrared imaging. M.D.B., N.K., and C.M. acknowledge support by the Air Force Office of Scientific Research Young Investigator Program (Mechanics of Multifunctional Materials and Microsystems; Dr. Les Lee; Award FA9550-13-1-0123) and NASA Early Career Faculty Award (NNX14AO49G). J.A.M. acknowledges support from the Army Research Office Grant W911NF-14-0350. Materials characterization was performed on equipment supported through an Office of Navy Research (ONR) Defense University Research Instrumentation Program (DURIP) (Bio-inspired Autonomous Systems; Dr. Tom McKenna; Award N00014140778).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1616377114/-/DCSupplemental.
References
- 1.Kim G-H, et al. High thermal conductivity in amorphous polymer blends by engineered interchain interactions. Nat Mater. 2015;14(3):295–300. doi: 10.1038/nmat4141. [DOI] [PubMed] [Google Scholar]
- 2.Singh V, et al. High thermal conductivity of chain-oriented amorphous polythiophene. Nat Nanotechnol. 2014;9(5):384–390. doi: 10.1038/nnano.2014.44. [DOI] [PubMed] [Google Scholar]
- 3.Wang XS, Tang HP, Li XD, Hua X. Investigations on the mechanical properties of conducting polymer coating-substrate structures and their influencing factors. Int J Mol Sci. 2009;10(12):5257–5284. doi: 10.3390/ijms10125257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Miranzo P, et al. Anisotropic thermal conductivity of silicon nitride ceramics containing carbon nanostructures. J Eur Ceram Soc. 2012;32(8):1847–1854. [Google Scholar]
- 5.Wong CP, Bollampally RS. Thermal conductivity, elastic modulus, and coefficient of thermal expansion of polymer composites filled with ceramic particles for electronic packaging. J Appl Polym Sci. 1999;74(14):3396–3403. [Google Scholar]
- 6.Mamunya YP, Davydenko VV, Pissis P, Lebedev EV. Electrical and thermal conductivity of polymers filled with metal powders. Eur Polym J. 2002;38(9):1887–1897. [Google Scholar]
- 7.Zeller RC, Pohl RO. Thermal conductivity and specific heat of noncrystalline solids. Phys Rev B. 1971;4(6):2029–2041. [Google Scholar]
- 8.Plawsky JL. Transport Phenomena Fundamentals. 3rd Ed CRC Press; Boca Raton, FL: 2014. [Google Scholar]
- 9.Shen S, Henry A, Tong J, Zheng R, Chen G. Polyethylene nanofibres with very high thermal conductivities. Nat Nanotechnol. 2010;5(4):251–255. doi: 10.1038/nnano.2010.27. [DOI] [PubMed] [Google Scholar]
- 10.Bigg DM. Thermally conductive polymer compositions. Polym Compos. 1986;7(3):125–140. [Google Scholar]
- 11.Cong H, Pan T. Photopatternable conductive PDMS materials for microfabrication. Adv Funct Mater. 2008;18(13):1912–1921. [Google Scholar]
- 12.Jeong SH, et al. Mechanically stretchable and electrically insulating thermal elastomer composite by liquid alloy droplet embedment. Sci Rep. 2015;5:18257. doi: 10.1038/srep18257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hill RF, Supancic PH. Thermal conductivity of platelet-filled polymer composites. J Am Ceram Soc. 2002;85(4):851–857. [Google Scholar]
- 14.Chen Y-M, Ting J-M. Ultra high thermal conductivity polymer composites. Carbon. 2002;40(3):359–362. [Google Scholar]
- 15.Biercuk MJ, et al. Carbon nanotube composites for thermal management. Appl Phys Lett. 2002;80(15):2767–2769. [Google Scholar]
- 16.Shahil KMF, Balandin AA. Graphene-multilayer graphene nanocomposites as highly efficient thermal interface materials. Nano Lett. 2012;12(2):861–867. doi: 10.1021/nl203906r. [DOI] [PubMed] [Google Scholar]
- 17.Kurabayashi K. Anisotropic thermal properties of solid polymers. Int J Thermophys. 2001;22(1):277–288. [Google Scholar]
- 18.Stankovich S, et al. Graphene-based composite materials. Nature. 2006;442(7100):282–286. doi: 10.1038/nature04969. [DOI] [PubMed] [Google Scholar]
- 19.Bartlett MD, et al. Stretchable, high-k dielectric elastomers through liquid-metal inclusions. Adv Mater. 2016;28(19):3726–3731. doi: 10.1002/adma.201506243. [DOI] [PubMed] [Google Scholar]
- 20.Fassler A, Majidi C. Liquid-phase metal inclusions for a conductive polymer composite. Adv Mater. 2015;27(11):1928–1932. doi: 10.1002/adma.201405256. [DOI] [PubMed] [Google Scholar]
- 21.Lu Y, et al. Transformable liquid-metal nanomedicine. Nat Commun. 2015;6:10066. doi: 10.1038/ncomms10066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dickey MD, et al. Eutectic gallium-indium (EGaIn): A liquid metal alloy for the formation of stable structures in microchannels at room temperature. Adv Funct Mater. 2008;18(7):1097–1104. [Google Scholar]
- 23.Yu S, Kaviany M. Electrical, thermal, and species transport properties of liquid eutectic Ga-In and Ga-In-Sn from first principles. J Chem Phys. 2014;140(6):064303. doi: 10.1063/1.4865105. [DOI] [PubMed] [Google Scholar]
- 24.Dickey MD. Emerging applications of liquid metals featuring surface oxides. ACS Appl Mater Interfaces. 2014;6(21):18369–18379. doi: 10.1021/am5043017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bruggeman DAG. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann Phys. 1935;416(7):636–664. German. [Google Scholar]
- 26.Ohmura T, Tsuboi M, Tomimura T. Estimation of the mean thermal conductivity of anisotropic materials. Int J. 2002;23(3):843–853. [Google Scholar]
- 27.Borca-Tasciuc T, Kumar AR, Chen G. Data reduction in 3ω method for thin-film thermal conductivity determination. Rev Sci Instrum. 2001;72(4):2139–2147. [Google Scholar]
- 28.Han Z, Fina A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog Polym Sci. 2011;36(7):914–944. [Google Scholar]
- 29.Style RW, et al. Stiffening solids with liquid inclusions. Nat Phys. 2015;11:82–87. [Google Scholar]
- 30.Rogers JA, Someya T, Huang Y. Materials and mechanics for stretchable electronics. Science. 2010;327(5973):1603–1607. doi: 10.1126/science.1182383. [DOI] [PubMed] [Google Scholar]
- 31.Haines CS, et al. Artificial muscles from fishing line and sewing thread. Science. 2014;343(6173):868–872. doi: 10.1126/science.1246906. [DOI] [PubMed] [Google Scholar]
- 32.Morin SA, et al. Camouflage and display for soft machines. Science. 2012;337(6096):828–832. doi: 10.1126/science.1222149. [DOI] [PubMed] [Google Scholar]
- 33.Larson C, et al. Highly stretchable electroluminescent skin for optical signaling and tactile sensing. Science. 2016;351(6277):1071–1074. doi: 10.1126/science.aac5082. [DOI] [PubMed] [Google Scholar]
- 34.Nagasaka Y, Nagashima A. Absolute measurement of the thermal conductivity of electrically conducting liquids by the transient hot-wire method. J Phys Educ. 1981;14(12):1435–1440. [Google Scholar]
- 35.Sen PA, Scala C, Cohen MH. A self-similar model for sedimentary rocks with application to the dielectric constant of fused glass bead. Geophysics. 1981;46(5):781–795. [Google Scholar]
- 36.Mishra V, Hardin CL, Garay JE, Dames C. A 3 omega method to measure an arbitrary anisotropic thermal conductivity tensor. Rev Sci Instrum. 2015;86(5):054902. doi: 10.1063/1.4918800. [DOI] [PubMed] [Google Scholar]
- 37.Reinecke BN, Shan JW, Suabedissen KK, Cherkasova AS. On the anisotropic thermal conductivity of magnetorheological suspensions. J Appl Phys. 2008;104(2):023507. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.