Modeling, Signaling and Integrated Modeling-experimental Frameworks in Cell Migration

Abstract

Cell migration is a complex and multi-step process involved in homeostasis maintenance, morphogenesis and disease development, such as cancer metastasis. Modeling cell migration and the relevant cytoskeleton dynamics has profound implications for studying fundamental development and disease diagnosis. This review focuses on some recent models of both cell migration and migration-related cytoskeleton dynamics, addressing issues such as the difference between amoeboid and mesenchymal migration modes, and between single-cell migration and collective cell migration. There view also highlights the computational integration among variable external cues, especially the biochemical and mechanical signaling that affects cell migration. Finally, we aim to identify the gaps in our current knowledge and potential strategies to develop integrated modeling-experimental frameworks for multi-scale behavior integrating gene expression, cell signaling, mechanics and multi-cellular dynamics.

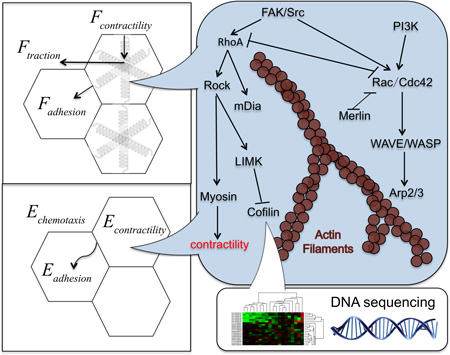
Graphical abstract

Introduction

Cell migration, both at the single-cell and at the collective cell level, plays a significant role in regulating living system behavior. It is a complex process involved in development, tissue formation and engineering, cancer and metastasis.^1,2 From a mechanistic stand point, it is argued that individual cell migration has three key components: protrusion, contractility, and adhesion, for migration in different environments.^3,4 Additionally, single cell migration has been classified into two types,⁵ namely amoeboid and mesenchymal migration. Amoeboid migration commonly refers to the faster movement of rounder cells that lack mature focal adhesion and stress fibers, while cells with high cell-matrix adhesion and high cytoskeleton contractility undergo the fibroblast-like mesenchymal migration.⁶ There are also several modes of collective cell migration, which are observed in vivo and differ from single migration modes.⁵ Cell migration is a result of a balance between cell-environment interaction and intracellular cytoskeleton dynamics. Seeded on a two-dimension (2D) substrate, cells have been shown to migrate towards a stiffer environment, a process that is termed as durotaxis.⁷ Cells in three-dimension (3D) matrices also tends to move faster under stiff environment, however, with a certain limit over which the cell speed will be hindered due to the matrix resistance force.^8–15 Mechanical inputs also play a role in migration, for example, the increased collagen crosslink and extracellular matrix (ECM) stiffening, cooperating with oncogenes such as ErbB2 can promote the invasiveness of mammary epithelial cells,^10,16,17 even with the absence of cellular and soluble tissue and systemic factors.¹⁶ Other than mechanical inputs, chemotaxis, due to growth factors, is important in modulating both 2D and 3D cell migration.^18,19 These and other studies have shown that environmental factors, both chemical and mechanical, are key to developing a comprehensive understanding of single and collective migratory behavior. Observations of these cellular behaviors in experiments inspire computational models aiming to unveil underlying mechanisms that are hard to test directly due to the complexity or to bridge current gaps in our current understanding. A key aim of this review is to understand the current computational models available, and their strengths and weaknesses, in describing both the environment and the migratory behavior at a single and collective level.

With the improved computational power, quantitative cell tracking techniques for cell migration have received an augment as well. Recent studies have used several trackers for migration and cellular reorganization including the nucleus,²⁰ Cytotrackers,²¹ single-particle tracking systems,^20,22–24 the particle image velocimetry (PIV)²⁵ and additional methods such as optical flow tracking.²⁶ Utilization of these tools have made it possible not only to track cellular motion velocity but also directional migration persistence,²⁷ mean squared displacement (MSD),²⁸ the velocity correlation,²⁵ the cell-pair separation distance²⁰ and so on. Nonetheless, more quantified variables are needed to quantify and distinguish different patterns of migration modes in both single-cell and collective cell migration, such as transition between amoeboid and mesenchymal migration, cellular leadership in collective behavior.^29,30 Additionally, not all tools are applicable in native like three-dimensional environments. This review aims to address both the recent developments and future opportunities in integrated modeling-experimental frameworks to understand single and collective cellular behavior in complex environments.

Cellular computational models in cell migration

To investigate microenvironment effects on cell migration, several models have been proposed to quantitatively predict the migration speed due to different external cues for both single-cell and collective cell migration. There include, among others, force balancing models to predict the migration speed for the single-cell migration^10,31, and also the energy based model to predict the collective cell migration for wound healing process, tumor cell invasion and angiogenesis.

Force balancing models in cell migration

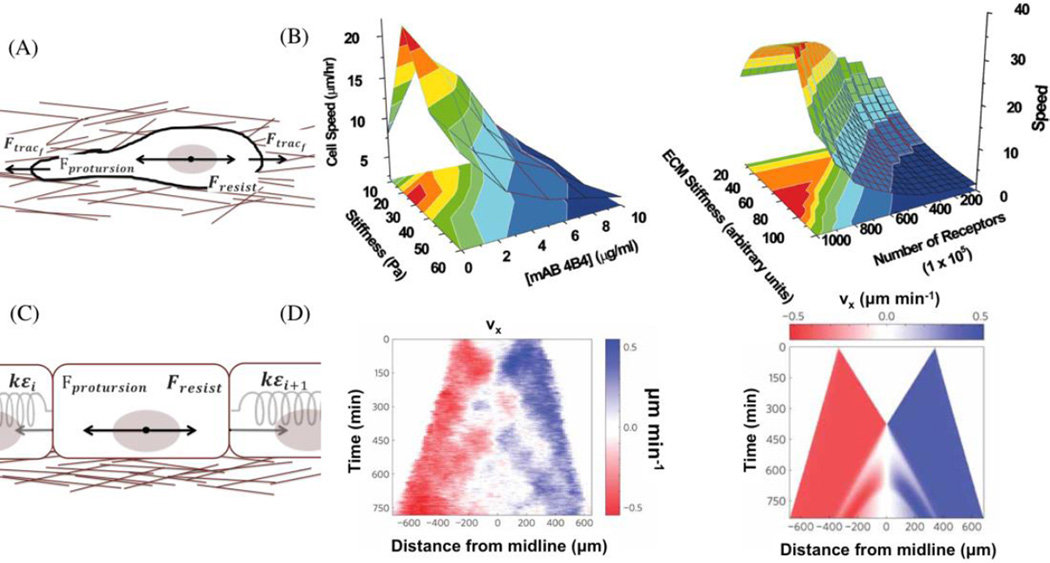
The mechanical interventions due to external stimuli such as changes in physical, chemical or mechanical properties of ECM are intuitively characterized with force balancing models. In 3D single-cell migration, the balance among the cell protrusion force, the cell traction force from both the cell front and back due to cell-ECM interactions, and the resistive force is used to study cell speed change due to different ECM stiffness, density, cell integrin amounts, and matrix metalloproteinase (MMP) expressions (Fig 1A).^8,10,31

$$0=F_{\mathit{\text{protusion}}}+F_{{\mathit{\text{trac}}}_f}(E_{\mathit{\text{mol}}},L{D}_f,IT{G}_f,MMP)-F_{{\mathit{\text{trac}}}_b}(E_{\mathit{\text{mol}}},L{D}_b,IT{G}_b,MMP)-F_{\mathit{\text{resistive}}}(\nu ).$$

Fig 1. Force balancing models of cell migration.

(A) A force balancing model of individual cell migration. (B) The later experimental validation (left) is consistent with the computational predictions (right), which successfully predicted the cell migration speed dependence on both the integrin concentration and the matrix stiffness. Iamges are obtained from Zaman et al.¹⁰ (Copyright (2006) National Academy of Sciences)(C) A force balancing model of collective monolayer cell migration. (D) This model successfully explained the mechanical wave-like cell migration and stress patterns, which are due to the reinforcement and fluidization of cytoskeleton. The experimental measurement is on the left and the numerical simulation is on the right using the force balancing model. Images are obtained from Serra-Picamal et al.³⁴ (Adapted by permission from Macmillan Publishers Ltd: Nat. Phys. (Ref 34), copyright (2012))

Here, cell migration speed ν is determined by solving the F_resistive, given the ECM stiffness E_mol, the ECM ligand density LD, the cell-expressing integrin concentration ITG and MMP density. F_protusion is the cell protrusion force in 3D that is simulated by a vector with constant magnitude but random direction. The traction forces and the resistive force can be mathematically represented as

$$F_{{\mathit{\text{trac}}}_f}=f(E_{\mathit{\text{mol}}})IT{G}_{f}L{D}_f(MMP)$$

$$F_{{\mathit{\text{trac}}}_b}=f(E_{\mathit{\text{mol}}})IT{G}_{b}L{D}_b(MMP)$$

$$F_{\mathit{\text{resistive}}}=6\pi R\eta \nu$$

Here f(E_mol) is a linear function of E_mol until E_mol reaches a threshold and then this function plateaus. The ligand density LD_f(MMP) is linearly dependent on MMP-mediated matrix degradation.⁸ R and η are the cell radius and the effective viscosity of the matrix material. This single-cell force balancing model not only predicts the biphasic dependence of cell speed on ECM density in 3D, but also shifting of such dependence due to changes in integrin-mediated adhesions in vitro (Fig 1B).¹⁰ In this experimental validation single cell speed is measured using a live cell membrane dye and IMARIS (Bitplane, St. Paul, MN) spots/isosurface tracking routines. Here this tool offers major advantages in single particle tracking in 3D and being automated, though like most single particle tracking algorithm it does not deal with cell division/apoptosis. Excluding the matric resistance force enables this model to predict cell migrations in 2D as well.^31,32 Overall, this model is significant because it qualitatively predicts the cellular behavior due to variations in ECM properties in 3D, and unveils the underlying mechanism leading to these variations, though it doesn’t capture the changes in local stiffness or morphology change of the gel due to cell-ECM interactions.³³

Another force balancing model focused on characterizing the collective 1D or semi-2D cell migration (average on one direction) considers cell-cell stress and cell elastic properties, in addition to the cell traction force, cell protrusion force, and resistive force³⁴ (Fig 1C).

$$F_{\mathit{\text{protrusion}}}+k{\epsilon }_i-k{\epsilon }_{i+1}-F_{\mathit{\text{resistive}}}(\nu )=0.$$

Here F_protusion is the cell protrusion force, or the cell self-propelled force in collective migration, ε is the neighbor cell deformation strain, i and i + 1 denotes different neighbor cells, and k is the cell elastic constant. Both the cell-cell stress and cell migration velocity are the outputs of this model. Results from the model showed that only with cell reinforcement (stiffening) and followed soon by a fluidization (softening) when the strain is above a threshold, can the cells have a mechanical wave pattern of migration speed and cell-cell stress observed in experiments.³⁴ Without such a quantitative model, it would be difficult to understand this wave pattern and to further link it to the cytoskeleton reinforcement/fluidization. Here cell speed in a 2D monolayer is measured using the particle image velocimetry (PIV) algorithm. This algorithm offers major advantages in measuring collective cell migration in 2D monolayer using phase-contract images, and do not require any fluorescence staining. Although it does not track motions of each cell but rather identifies average movements of subregions in an image.²⁶ A possible factor that this collective cell migration force balancing model can be extended to capture directly is the cell-cell adhesion,^35,36 which is not always the same as the cell-cell stress.

These force-balance models are mainly deterministic models. The advantage for these types of models is the computational efficiency, since one can directly solve the cell speed in a linear manner. One of the limitations is that when considering chemically relevant effects, or factors that cannot be explicitly expressed in terms of force, this model is unable to capture the chemical complexity. That said, studies have used force-like terms to model the chemotaxis in cell migration.³⁷ This force-like term linearly depends on the cell sensitivity to the chemical gradient. Force balancing models can also be carried out in a stochastic fashion using the Langevin equation with a stochastic noise term.^37,38 Overall, force balancing models are an approximation of equations of motions, in which usually the inertia terms are neglected due to the relative high friction between the cells and their environment for high computational efficiency.

Energy based models in cell migration

To address factors that are chemically relevant or cannot be explicitly expressed in terms of forces, the cellular Potts model³⁹ with energy minimization and Monte Carlo steps offers a major advantage. Its off-lattice alternative, the vertex model, is also well used in morphogenesis and patterning.^40,41 The factors affecting cell migration are evaluated in terms of Hamiltonian or energy form.^42–45

$$E=E_{\mathit{\text{adhesion}}}(\mathit{\text{adhesive sites}})+E_{\mathit{\text{growth}}}(\mathit{\text{cell size}})+E_{\mathit{\text{chemotaxis}}}(\mathit{\text{growth factor concentration gradients}})+E_{\mathit{\text{continuity}}}(\mathit{\text{cell size}})$$

$$E_{\mathit{\text{adhesion}}}(\mathit{\text{adhesive sites}})={\sigma }_{cc}\sum _{\underset{\mathit{\text{adhesion sites}}}{\mathit{\text{cell}}-\mathit{\text{cell}}}}{A}_{cc}+{\sigma }_{cE}\sum _{\underset{\mathit{\text{adhesion sites}}}{\mathit{\text{cell}}-ECM}}{A}_{cE}$$

$$E_{\mathit{\text{continuity}}}(\mathit{\text{cell size}})=\frac{k}{2}\sum _{\mathit{\text{cells}}}{(V-V^0)}^2$$

$$E_{\mathit{\text{chemotaxis}}}(\nabla GF)=\chi \sum _{\mathit{\text{sites}}}\nabla GF$$

Here the adhesion energy term E_adhesion, which was developed from Steinberg’s Differential Adhesion Hypothesis (DAH),^39,46 has two parts: the adhesion among cells, and between cell and ECM or medium.⁴¹ σ is the adhesion energy per unit area, and A is the adhesion area for cell-cell or cell-ECM contacts. E_continuity is the conservation of cell volume V in 3D or surface area in 2D due to cell elasticity and/or contractility,^41,47 and is usually a quadratic function of the change ratio. E_growth captures favorable energy change due to proliferation via the doubling cell volume and surface area.⁴³ In some models however, the effect of proliferation is set within the E_continuity. The chemotaxis energy term E_chemotaxis is simulated to be linearly dependent on the growth factor concentration gradient ∇GF.⁴³ The probability of accepting each Monte Carlo step is given by⁴³

$$P_{\mathit{\text{accept}}}=\{\begin{array}{cc}1,\hfill & \hfill \mathit{\text{if }}\mathrm{\Delta }E<0;\hfill \\ \hfill e^{-\frac{\mathrm{\Delta }E}{kT}},\hfill & \hfill \mathit{\text{if }}\mathrm{\Delta }E>0.\hfill \end{array}$$

The cellular Potts model has addressed multiple cell migration predictions that can be validated by experiments. One of the successes is in predicting endothelial cell migration in angiogenesis.⁴⁸ Shamloo et al⁴⁸ first used an in silico collagen fibrils model to estimate the corresponding matrix density index used in their model via matching collagen area in microscopic and in silico images under different densities. We also have used an in silico collagen fibers model to mimic microscopic collagen images in vitro.³³ With this corresponding matrix density index obtained, the angiogenesis process, that is the migration of endothelial cells, is simulated mimicking different collagen density effect. Shamloo et al⁴⁸ confirmed their previous model predictions⁴³ on endothelial sprout formation morphology under different ECM matrix. Recent studies also consider the effect of MMP and the nucleus compartments in cell migration using cellular Potts models. These models have been able to predict that cell migratory ability in subcellular channels closely depends on proteolytic machinery, and the cancer cell can achieve a sustained locomotion by either a pericellular proteolysis or by deforming its nucleus in a subnuclear track.^42,49 A limitation for these Monte Carlo based energy minimization models is that they can only simulate a relatively small number of cell populations due to the heavy computational task.

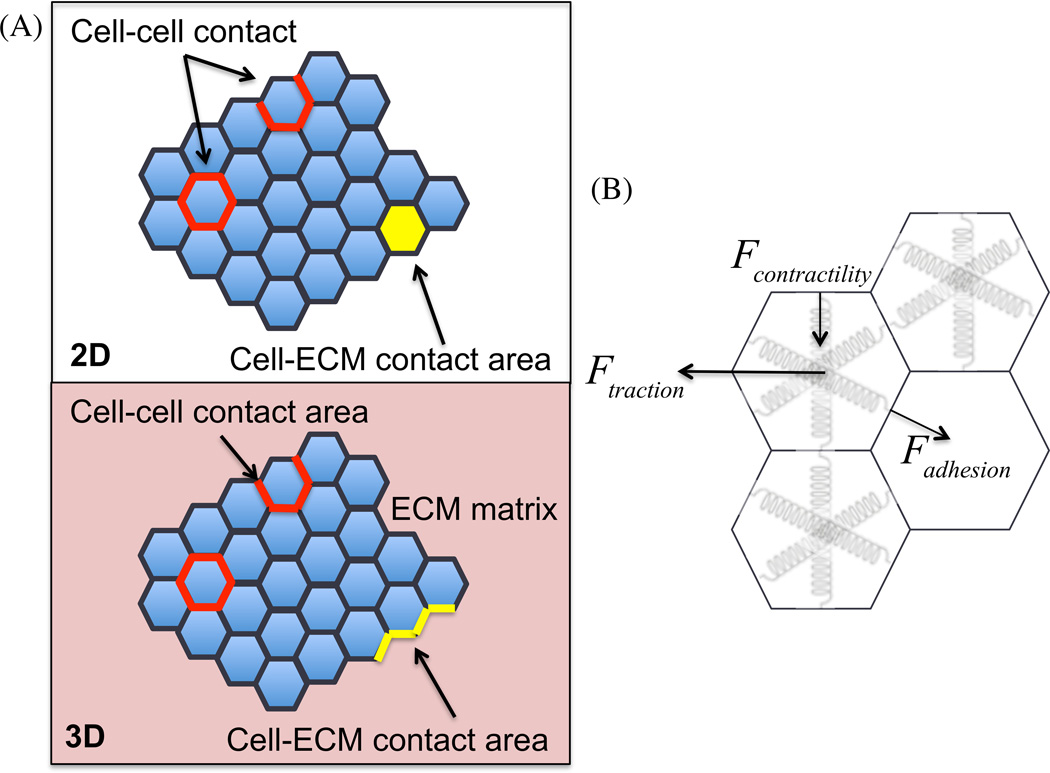
In comparison, the vertex model using the similar form of energy term is solved as an optimization problem. It tracks the movement of vertices during the optimization process. The gradient descent method can help to find the local minima state of the system energy. The steady state of 2D or 3D vertex model (Fig 2B) is close to the force balancing model result. For example, both approaches lead to the equilibrium between the contractility and the cell-cell adhesive force,⁴¹ and so does the Cellular Potts model. However, to fully convert the results between these models, vertex version of force balancing model (Fig 2C), or more generally, an appropriate conversion between the energy based model and the force balancing model is needed.

Fig 2. The vertex model and its potential force balancing correspondence.

(A) The vertex model for collective cell migration in 2D and 3D, with the difference in cell-ECM contact area part and whether to include the elasticity of ECM matrix when cells invading into the matrix. (B) An appropriate analog between the energy based model and force balancing model is needed.

This is a challenging problem, but a significant one. With recent advancements in stress and force measurement techniques, such as cell traction microscopy and cell stress microscopy, the mechanical properties can be measured directly during collective cell migration. A force-based model will have an advantage of direct correspondence with these mechanical measurements, and it can be directly and easily tested, in comparison with the energy based model. During collective cell migration, there exists largely motility, mechanical, molecular signaling heterogeneities within monolayers and cell clusters. The next step of unveiling the collective cell migration patterns is to explain the source and predict quantitatively these heterogeneities.

In addition to the models discussed above, there are also stochastic models on collective cell migration, especially focused on angiogenesis involving tip cell migration, sprouting and anastomosis.⁵⁰ Maclaw et al. developed an evolutionary model of tumor progression regarding cell growth and migration, suggesting that targeting short-range cellular migratory activity could have marked effects on tumor growth rates.⁵¹ There is also a phase-field model, which does not identify cell boundaries and studies cell migration in a relatively deterministic manner.⁵² Additionally cell migration models have been developed that capture how migration affects ECM fibrous structure.³³ There is an opportunity that it can be combined with recent additional ECM fibrous models^53,54 focusing on microenvironment heterogeneity in cell migration.

Signaling pathways in cell migration

Cell signaling plays a central role in single and collective migration. The following section will review recent advancements in modeling signaling during migration. Due to a greater number of models focused on mesenchymal migration, and more data and literature focusing on these modes, the next section will have a greater discussion of mesenchymal modes, compared to amoeboid studies.

Signaling pathways in mesenchymal migration

As previously mentioned, modes of single-cell migration are divided into two broad categories, namely mesenchymal and amoeboid migratory modes. The mesenchymal migration relies mainly on high adhesion and form mature focal adhesion.

In mesenchymal modes, cell migration involves formation of cell-ECM adhesions at the leading edge of protrusions and disassembly of adhesions, mainly at cell rear.^55,56 Integrins bind to the ECM and initially form small, transient matrix contact structures, called nascent adhesions. Proteins are recruited to bind with integrin cytoplasmic domains, such as paxillin.^57,58 During adhesion maturation to focal adhesion, FAK and Src are activated by phosphorylation. FAK activity can be enhanced by the collagen crosslinking and ECM stiffening and further drive invasion of tumor cells.^16,59 Importantly, it has been found recently that for cells in 3D matrices, focal adhesion proteins such as FAK do not form aggregates but are more diffused throughout the cytoplasm, though they still modulate cell motility by affecting protrusion activity and matrix deformation.⁶⁰ Adhesion-relevant kinases regulate Rho-family GTPases, such as Rac and RhoA.^61,62 FAK has been shown to be able to activate^63–65 or inhibit RhoA activity.^66,67 Though with these opposing effects, there is an apparent global increase in FAK and RhoA activity in stiffer 3D ECM environment.⁵⁹ The increased collagen crosslink and ECM stiffening also promote 3D cell migration via up-regulating growth factor dependent PI3K activity.^16,68 Following EGF stimulation, protein complexes containing Src, F-actin, mDia1 and Dia-interacting protein 1 stimulate Rac1.⁶⁶

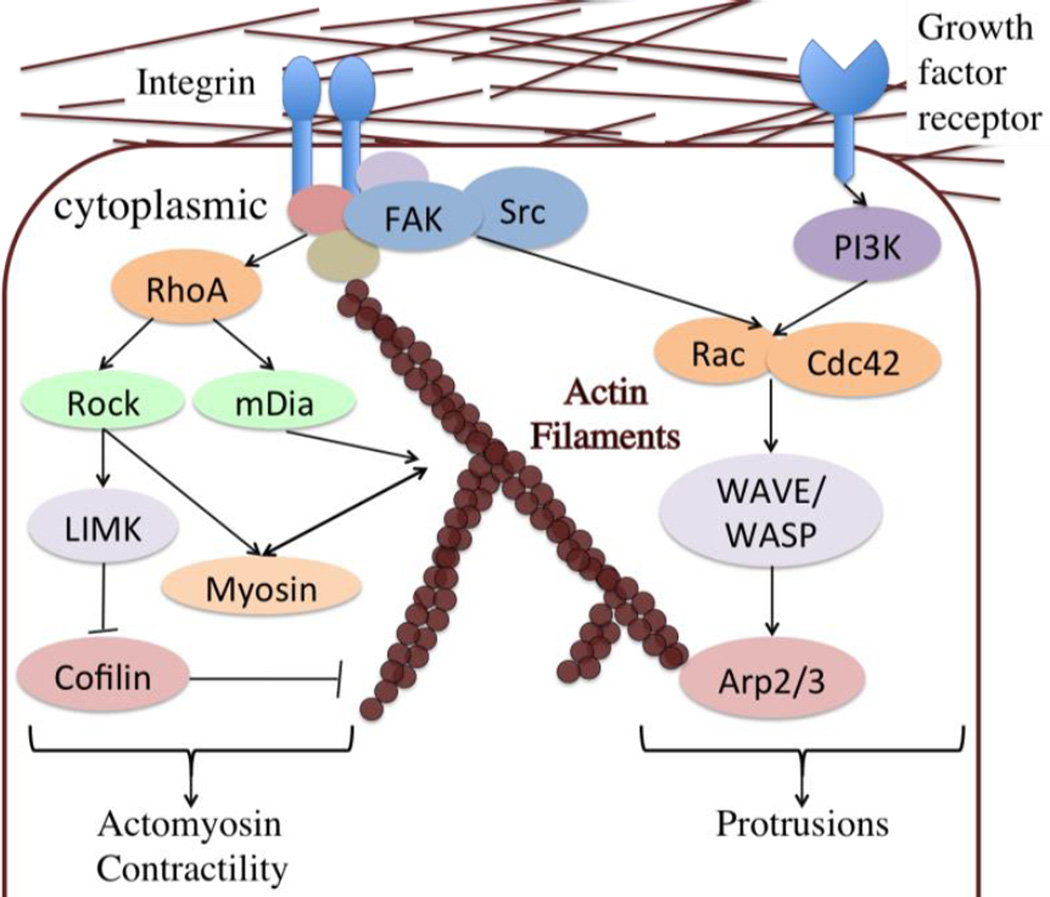
Cell protrusions at leading edge in migration process involves actin polymerization, while at cell rear there are cell contractions.⁵⁶ The cytoskeleton activities are coordinated with formation/disassembly of cell-ECM adhesions. Rho-family GTPases are molecular ‘switches’ within cells bridging adhesion activities and cytoskeleton dynamics by controlling the formation and disassembly of actin cytoskeletal structures (Fig 3). RhoA-GTP can activate formin (mDia)-based actin nucleation^69,70 and ROCK dependent myosin II contractility⁷¹. mDia stimulates the formation of stable microtubules that are capped and oriented towards the wound edge to promote cell migration.^72,73 Rac stimulates branching and polymerization of actin filaments by the Arp2/3 complex via the activation of WAVE,⁷⁴ and it promotes the lamellipodia formation in cell migration.^75,76 Cdc42 activity is also prominent at the tip of the leading edge and regulates the migration direction by regulating the cell polarization.^77,78 WASP, which is autoinhibited, can be activated by binding with Cdc42 and further activates Arp2/3.⁷⁹ Conventionally, Rac promotes membrane protrusions at the leading edge, while RhoA is active in the cell rear and regulates its contractility in 2D cell migration.^80,81 This is most likely due to the antagonism between Rac and RhoA at the leading edge.^82,83 However, it has also been found that in randomly migrating cells, RhoA activity is high in a sharp band directly at the edge of protrusions.⁸⁴

Fig 3. The signaling pathways of cytoskeleton dynamics in cell migration.

Here is a signaling pathway map that represents how external cues regulate cytoskeleton dynamics, and further induce directional cell migration via these downstream signaling molecules. Several modeling work of these signaling pathways have been built upon these interactions and crosstalks, and they further predict or explain the integrated effects of signaling molecules in affecting cell migration.

Signaling pathways in amoeboid migration

In amoeboid cell migration mode, cells migrate in a largely rounded shape, which results from a high cell tension relative to cell adhesions.⁸⁵ In cells that undergo amoeboid migration, actin filaments assemble into a fibrous cortex that is absent from the cell front, but become progressively denser toward the cell rear, and so does myosin.⁸⁶ With myosin II-dependent contraction at the cell rear, cells are even able to squeeze their nuclei through a narrow gap.³ High cell tension, that is, high cortical actomyosin contractility is due to high Rho and low Rac activities.⁸⁵ Relying on increased activity of the RhoA pathway, formin-based actin nucleation and myosin II contractility are activated, which meanwhile promotes a retrograde actin flow during migration process.⁸⁷ A retrograde flow is a translocation and recycling at proximal sites due to actin filament severing and/or disassembly following assembly at nucleation sites.⁸⁸ The cell-scale retrograde flow of actin and myosin II is the driving force for the stable bleb mode in amoeboid migration. The pseudopods mode of amoeboid migration, which has protrusion due local actin assembly at the leading edge, only has the retrograde flow in the front.⁴

Manipulating cytoskeleton regulators, such as Rac,⁷⁴ Rho⁸⁹ and Rock,⁸⁶ cell-ECM adhesion proteins,⁸⁶ can make cells to switch migration modes between the mesenchymal and amoeboid migration. Adding lysophosphatidic (LPA), a serum phospholipid known to activate cortical contractility via the Rho/Rock pathway, also induces amoeboid migration.⁹⁰ After LPA addition, myosin II rapidly redistributed to the cell cortex. The cortical accumulations of myosin II and the size of bleb are correlated with LPA addition. And a gradient of LPA can induce an asymmetric contraction of the cortical cytoskeleton to further influence cell migration. Both the mesenchymal and amoeboid single-cell migration requires a high myosin activity for mechanotransduction and great amount actin assemblies. However, other than the integrin or the external environment regulations, what kinds of direct molecular actin regulators lead to the difference between the cortical actin assemblies and the stress fiber assemblies? Do the stress fiber contractility and the cortical actomyosin contractility depend on the same cascade of myosin II signaling? These are the questions in need to be answered in unveiling the regulation of the single-cell migration signaling.

Signaling pathways in collective cell migration

Though the collective cell migration is ubiquitous in biology, detailed mechanistic and quantitative understanding linking molecular events with collective behavior is lacking compared to single-cell migration due to its complexity. When studying collective cell behavior, velocity correlation is sometimes used,^25,30 to understand collective cellular motion. This correlation is a coefficient of coordination in collective cell migration in addition to cell speed and directional persistence. The tumor suppressor, merlin, plays an important role in coordinating cells interacting with Rac1 in monolayer epithelial collective migration.²⁵ Also results from experiments show that collective migration has largely related to the intercellular stress.³⁴ Within a confluent monolayer cells tend to move along directions with minimal intercellular shear stress, so that cell-cell junctions along these directions carry only minimal shear stresses.⁹¹ In the adherens junctions of epithelial cells, the extracellular domain of E-cadherin interact with cadherin protein on other cells (trans-binding) in a calcium-dependent way,⁹² while the cytoplasmic domain of E-cadherin interacts with p120 catenin, β-catenin and α-catenin, which links with the actin cytoskeleton.⁹³ P-cadherin, whose expression is highly associated with undifferentiated cells in normal adult epithelial tissues and breast cancer, has the similar cadherin-catenin complex structure and actin cytoskeleton connection in cells.⁹⁴ Results from the experiment show that Wnt slows down collective cell migration, which involves with the interaction with β-catenin.³⁰ Substrate stiffness not only regulates cellular migration at a single cell level, but also at a collective level. The stiffer substrate has resulted in higher migration speed and persistence at the edge, which emerge with a higher myosin-mediated contractility.²⁰ Cell coordination relies on a balance between cadherin complex mediated cell-cell adhesion and myosin-mediated contractility during collective motion. Epithelial polarity is another important factor regulating the cooperativity during cell migration, though to our knowledge researchers have not fully studied how the balance of the contractility and cell-cell adhesion interacts with this polarity in this directionality information synchronization. With current molecular assays in collective cell migration, the challenges stem from the investigation of downstream cascade signaling effects and quantification of patterns of collective cell migration in various environments. Thus, the computational models have the ability to provide novel insights to understand these questions.

Modeling signaling in cell migration

In the previous section we mainly reviewed the signaling pathways during cell migration, at the single and collective level. In the following section, we will turn our attention to additional comprehensive modeling work that integrates cell signaling and migration, with an eye towards the future direction and opportunities for computational modeling.

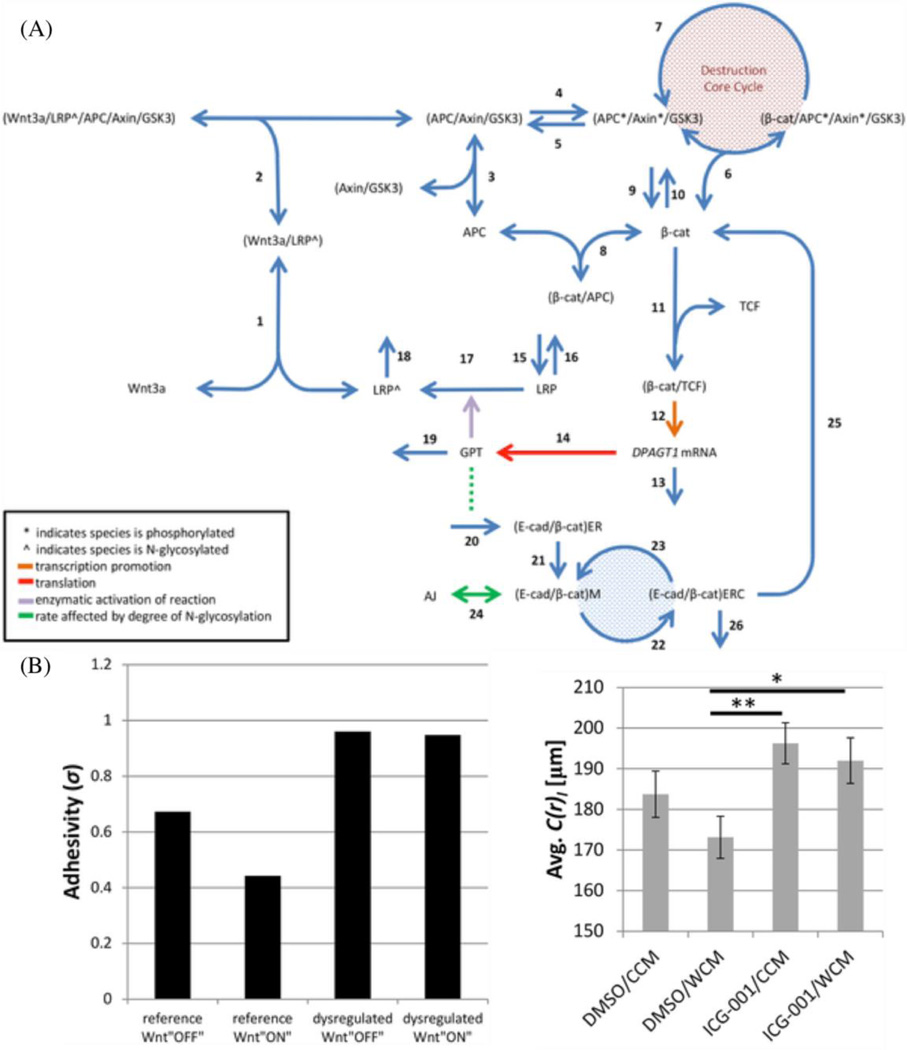
It is of fundamental importance to understand the molecular programmes that regulate cell migration in an integrated modeling-experimental framework. We recently have established an integrated signaling model of N-glycosylation metabolic pathway, Wnt/β-catenin signaling pathway, and cadherin-mediated adhesion in affecting cell migrations (Fig. 4A).³⁰ A fundamental, ER glycosylation enzyme, GPT, is a Wnt/β-catenin transcriptional target that can promote the N-glycosylation of E-cadherin. This glycosylation, in turn, limits the adhesivity of cadherin ectodomains, which, in turn, leads to enhanced β-catenin signaling. This consists of multiple signaling pathways and feedback/feedforward pathways with extensive complexity. With the integrated modeling-experimental framework, we can reduce this complexity and unveil underlying molecular mechanisms regulating cell migration. In this model, binding and dissociation processes are described as linear product of the kinetic rate and the corresponding molecule concentrations: k_iXY and k_−i(X/Y). Here X and Y are the free concentrations of the binding partners, (X/Y) the concentration of the complex in which X and Y binds together, and k_i and k_−i the association and dissociation rates. Syntheses of proteins are described by constant rates (ν_i). Phosphorylation and dephosphorylation processes are described as k_iX and k_iX^*, in which phosphorylated molecules are labeled with *. For example,

$$\frac{d\mathrm{\beta }\text{cat}}{dt}={\nu }_9+k_{-6}(\mathrm{\beta }\text{cat}/\mathrm{A}\mathrm{P}{\mathrm{C}}^{*}/{\text{Axin}}^{*}/\mathrm{G}\mathrm{S}\mathrm{K}3)-k_6(\mathrm{A}\mathrm{P}{\mathrm{C}}^{*}/{\text{Axin}}^{*}/\mathrm{G}\mathrm{S}\mathrm{K}3)\mathrm{\beta }\text{cat}+k_{-8}(\mathrm{\beta }\text{cat}/\mathrm{A}\mathrm{P}\mathrm{C})-k_{8}APC\mathrm{\beta }\text{cat}+k_{-11}(\mathrm{\beta }\text{cat}/\mathrm{T}\mathrm{C}\mathrm{F})-k_{11}\mathrm{\beta }\text{cat}\mathrm{T}\mathrm{C}\mathrm{F}+k_{25}(\mathrm{E}\text{cad}/\mathrm{\beta }\text{cat})-k_{10}$$

$$\frac{d{\sigma }_{AJ}}{dt}=\left(\frac{k_{24}({\sigma }_M){(\mathrm{E}\text{cad}/\mathrm{\beta }\text{cat})}_M}{\mathrm{A}\mathrm{J}}\right)({\sigma }_M-{\sigma }_{AJ})$$

Fig 4. The integrated signaling pathway of N-glycosylation, Wnt/β-catenin and E-cadherin/β-catenin.

The signaling pathway map (A) that integrates model of N-glycosylation, Wnt/β-catenin and E-cadherin/β-catenin represents how signaling molecules interact in a kinetic network. The quantitative predictions of the model (B: left) are validated in experiments of cell migration (B: right). (Copyright 2016 PLoS Comput. Biol.³⁰ :https://creativecommons.org/licenses/by/4.0/)

Here the dynamics of active β-catenin is solved based on the pathway processes that it involves in. The parameters are either taken from the direct measurement of the binding/unbinding rate and the phosphorylation/dephosphorylation rate, or estimated from known cellular responses. And the adhesivity of adhesion junctions is solved by the concentration of the adhesion junctions, the concentration of the (E-caderin/β-catenin) complex in the membrane, and the N-glycosylation degree of E-cadherin in the membrane (σ_M). We also carried out the experimental validation for our signaling pathway model. We not only measured the molecular amount change under the addition of Wnt3a and the β-catenin/TCF binding inhibitor, but also quantify the collective migration pattern change under these conditions in wound assay. The average speed, the movement angle orientations that indicate the coordination and the persistence, and more importantly, the correlation length are calculated based on the PIV measurement, which was previously discussed and offers an advantage in tracking motions in a monolayer. The correlation length quantifies the length scale within which cells have coordination in their motions,²⁵ and the adhesivity predicted in our model has a good agreement with this intercellular coordination measurement in wound assay experiment (Figure 4B). To the authors’ knowledge, this is one of the few successful studies investigating multiple signaling pathways in influencing cell migration in an integrated modeling-experimental framework.

Over the years, a number of additional computational studies have modeled dynamics of signaling molecules to understand cell migration. The enormous complexity of the cell, combined with limited spatial and temporal data at the molecular level and prohibitive cost of detailed molecular modeling, result in models that cannot capture the dynamics of all the key molecules in complex environments. The molecules selected in the computational model are therefore often representative of the questions the researchers want to ask. For example, some models focus on how Rho-family GTPases sense the ECM properties characterizing the adhesion related kinases,⁹⁵ other models have focused on rate of protrusion^96,97 and polymerization⁹⁸ in cell migration using cytoskeletal dynamics. However, most such computational models due to computational complexity and lack of detailed mechanistic data, have focused on single cells and have occasionally incorporated ECM,^33,99,100 suggesting that integrated modeling of cellular interior, cell-cell and cell-ECM interactions continues to be an elusive goal. To this end, one of the most important processes in designing a multi-scale model is the “bridge”. The challenge in creating this bridge is about how to transfer simulation information/results between multiple scales. There have been some efforts, for example, the previous force balancing model inside the cell can potentially coupled with the previous force balancing model of cell migration. Similarly, the signaling pathway of Hippo^95,101 can be combined in the energy based model and characterizing how the cell-cell stress difference can lead to different pattern of collective cell migration.

$$E=E_{\mathit{\text{adhesion}}}(E-\mathit{\text{cadherin}}/P-\mathit{\text{cadherin}})+E_{\mathit{\text{growth}}}(YAP/TAZ)+E_{\mathit{\text{chemotaxis}}}(EGFR)+E_{\mathit{\text{continuity}}}(\mathit{\text{cortical contractility}}/\mathit{\text{myosin}})$$

Yet, the broad based frameworks connecting scales and providing detailed and valuable information at multiple scales continues to be a major challenge.

Outlook

With increasing computational power in the past twenty years, significant effort has been made to study cell migration in complex and clinically relevant environments. Combined with new developments in biomedical engineering, new tools are being developed to effectively characterize cell migration and the associated mechanisms, such as tracking individuals within cell cohorts embedded in three dimensional collagen scaffolding²⁹ and 3D cell traction microscopy.¹⁰² With the help of these quantification tools, corresponding numerical modeling work has also shed light on 3D migratory mechanisms in disease understanding. Availability of this data is revolutionizing modeling strategies and approaches to understand cellular behavior in complex environments and possibly identify new therapeutic targets. Finally, with the development of genome-scale analyses, patient specific and precision medicine strategies will also benefit from integrated experimental and computational models to understand how cell migration alterations may influence clinical outcomes,¹⁰³ Thus while new challenges in understanding cell migration behavior remain, the opportunities to develop new, powerful and potent therapeutic regimens, and create new platforms for multi-scale investigation provide exciting possibilities for fundamental and applied understanding of cellular form, fate and function.