Use of Causal Diagrams to Inform the Design and Interpretation of Observational Studies: An Example from the Study of Heart and Renal Protection (SHARP)

Abstract

Observational studies often seek to estimate the causal relevance of an exposure to an outcome of interest. However, many possible biases can arise when estimating such relationships, in particular bias because of confounding. To control for confounding properly, careful consideration of the nature of the assumed relationships between the exposure, the outcome, and other characteristics is required. Causal diagrams provide a simple graphic means of displaying such relationships, describing the assumptions made, and allowing for the identification of a set of characteristics that should be taken into account (i.e., adjusted for) in any analysis. Furthermore, causal diagrams can be used to identify other possible sources of bias (such as selection bias), which if understood from the outset, can inform the planning of appropriate analyses. In this article, we review the basic theory of causal diagrams and describe some of the methods available to identify which characteristics need to be taken into account when estimating the total effect of an exposure on an outcome. In doing so, we review the concept of collider bias and show how it is inappropriate to adjust for characteristics that may be influenced, directly or indirectly, by both the exposure and the outcome of interest. A motivating example is taken from the Study of Heart and Renal Protection, in which the relevance of smoking to progression to ESRD is considered.

Introduction

In longitudinal analyses of observational studies (including observational analyses done using trial data), a range of possible biases can arise when assessing the relevance of a particular characteristic (exposure) to a particular disease (outcome). Uppermost among these is bias due to confounding, which may be thought of as a spurious statistical association between the exposure and the disease that arises (wholly or partly) because of some other exposure that is associated with a change in both the exposure of interest and the probability of disease. Statistical methods to control for confounding include adjustment (e.g., in a regression model) and stratification (e.g., performing analyses separately in subsets of individuals with similar characteristics). Although it may be thought that increasing levels of adjustment for characteristics not believed to be involved in the causal pathway could only result in an improved estimate of the true etiologic relevance of the exposure to the disease (i.e., a reduction in bias due to confounding), in fact, the opposite may be true. Depending on the nature of the relationship between the exposure of interest and the potential confounders, inappropriate adjustment for some of them can lead to the introduction of a bias that did not previously exist (1).

An understanding of causal diagrams aids the identification of possible sources of bias in epidemiologic analyses (including confounding, reverse causality, and selection bias) and, therefore, facilitates the identification of an appropriate set of characteristics that would need to be taken into account during any statistical analysis. The purpose of this paper is to provide such an understanding, so that the methods can be considered and applied more widely by those who wish to perform such analyses.

A Hypothetical Example

Consider the following hypothetical example. A conference is attended by 500 delegates. All delegates arrive the day before the plenary session, and one half have flown long haul to travel to the conference. Now suppose that everyone who flies long haul will suffer, to some degree, from jet lag the next day. A drinks reception is held on the evening before the morning plenary session, at which a choice of alcoholic and nonalcoholic drinks is available. Suppose the effect of drinking alcohol on jet lag is of interest, and the overall 2×2 contingency table of the relationship is as shown in Table 1, A (from which an odds ratio of 1.00 (95% confidence interval [95% CI], 0.70 to 1.43) is estimated, which makes sense, because jet lag is a result of flying long haul rather than alcohol consumption at the conference reception). However, now suppose that this analysis had been done separately among those who had attended the plenary session and those who did not attend. On the face of it, this seems reasonable, because both drinking alcohol and being jet lagged may be associated with missing the plenary session. After stratifying by whether the delegate attended the plenary session, the contingency tables could plausibly look like those in Table 1, B. The estimated Mantel–Haenszel odds ratio (which takes into account the stratification) is now 0.63 (95% CI, 0.42 to 0.93), which suggests, quite wrongly, that drinking alcoholic rather than nonalcoholic drinks at the conference reception has a strongly protective effect on the risk of jet lag.

Table 1.

Hypothetical example illustrating the association between drinking alcohol at the conference reception and suffering from jet lag the next day before and after stratification for whether the delegate attended the plenary session

Delegate Classification	Jet Lag
	Yes	No
A
Drank alcohol at reception
Yes	100	100
No	150	150
B
Delegate missed plenary session
Drank alcohol at reception
Yes	80	60
No	100	30
Delegate attended plenary session
Drank alcohol at reception
Yes	20	40
No	50	120

Odds ratio for A is 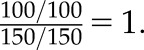Mantel–Haenszel odds ratio for B is .

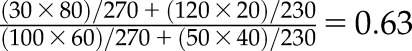The problem is caused by inappropriate stratification by whether the delegate missed the plenary session. In this case, stratification for missing the plenary session introduces bias into the assessment of the relationship between drinking alcohol and jet lag, because missing the plenary session could be influenced by both alcohol consumption and jet lag (i.e., is a collider; see below). To understand how this happens and how it can be avoided, one needs to appreciate the basic theory of causal diagrams.

An Introduction to Causal Diagrams

A detailed description of the theory of causal diagrams in epidemiologic studies can be found elsewhere (2,3); only a basic introduction is provided here. We start with some terminology.

A causal diagram is a graphical tool that enables the visualization of the relationships between the exposure of interest, the outcome being studied, and all other characteristics (variables) that are associated in some way with at least two other variables in the diagram. It encodes the assumptions underlying the epidemiologic analysis and should include all relevant variables (even if they have not been measured). Causal diagrams, therefore, comprise a set of variables (nodes: often represented by letters) with arrows drawn between them to show the directions of the assumed causal relationships. No other assumptions, however, about the nature of these relationships are made (for example, whether the exposure increases or decreases the value of the outcome or the magnitude of such an effect). The lack of an arrow between a pair of variables, therefore, represents the assumption that there is no direct relationship between them.

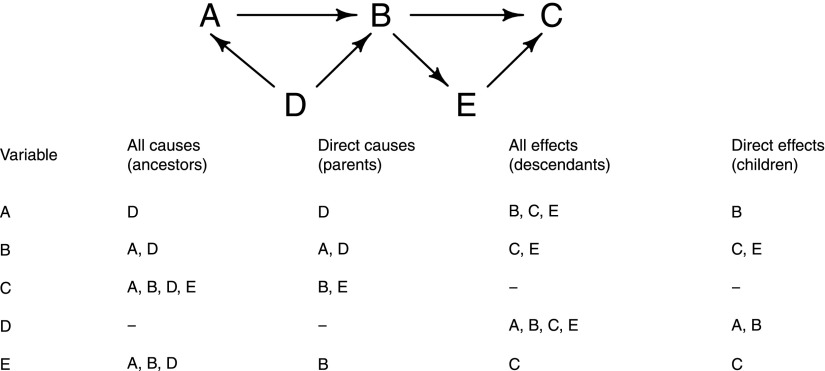
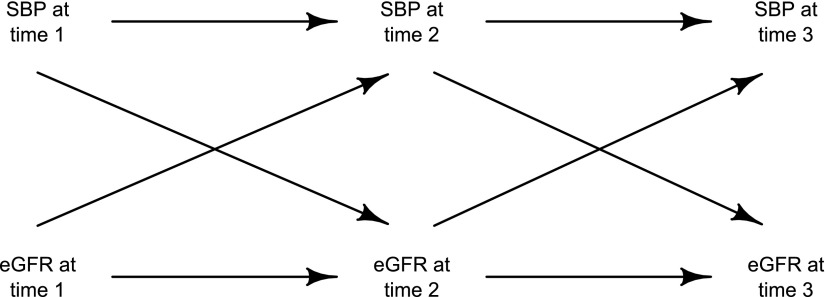
In a causal diagram, a cause is a variable that influences, either directly or indirectly, the value of another variable. Causes are often referred to as ancestors of the other variable, with direct causes (Figure 1) called parents. By contrast, effects are variables that are influenced, either directly or indirectly, by another variable. Effects are often referred to as descendants, with direct effects (Figure 1) called children. For example, consider the relationships between the five variables A–E shown in Figure 1. Looking at variable E, it has A, B, and D as causes (or ancestors), but only B is a parent of E. Similarly, the variable A has B, C, and E as effects (or descendants), but only B is a child of A. A path is said to exist between two variables in a causal diagram if they can be joined through a sequence of single-headed arrows, irrespective of their direction, possibly passing through other variables on the way. The paths of most interest in epidemiologic studies are generally the causal pathways, which are paths starting at the exposure and ending at the disease that do follow the direction of the arrows. Directed acyclic graphs (DAGs) are a special form of causal diagram that does not contain any directed cycles. That is, in a DAG, it is not possible to connect any variable through a path of single-headed arrows, when following the direction of the arrows, back to itself. (Time ordering is important in causal diagrams; any causes must precede effects, and therefore, no variable can be both the cause and the effect of any other variable in the graph.) However, that is not to say that DAGs cannot be used to represent bidirectional biologic relationships where feedback loops exist, providing that the temporality is preserved (e.g., Figure 2 shows how a bidirectional relationship between systolic BP and eGFR could be represented in a DAG). (Note that the analysis of data with time-varying treatments or exposures may require specialist statistical methods to be used, such as marginal structural models [4,5].)

Figure 1.

Causal diagram to illustrate causes (ancestors and parents) and effects (descendants and children).

Figure 2.

Example of how to represent a possible bidirectional relationship in a directed acyclic graph. SBP, systolic BP.

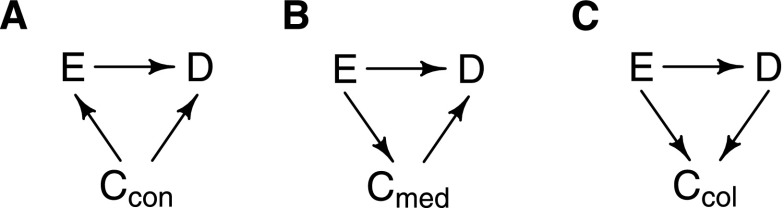
When considering a single exposure of interest (E), an outcome of interest (D), and a single covariate (C) that is associated in some way with both the exposure and the outcome, there are three possible sets of relationships (Figure 3). The first scenario (Figure 3A) is that the covariate C is a cause of both the exposure and the outcome (i.e., it is a confounder). The second scenario (Figure 3B) is that the covariate is on the causal pathway from the exposure to the outcome. In this case, C is called an effect mediator. The final situation (Figure 3C) is where the covariate is a common effect of both the exposure and the outcome. In this case, C is called a collider.

Figure 3.

Causal diagrams showing possible underlying relationships for a covariate that is associated with both the exposure of interest and the outcome of interest. (A) C is a confounder. (B) C is an effect mediator. (C) C is a collider. C, covariate; E, the exposure of interest; D the outcome of interest.

Paths can be characterized into causal pathways and noncausal pathways. Because the causal pathways represent the associations of interest, they should typically remain open in any statistical analysis. (An open path in a DAG is merely a path along which an association can be transmitted.) By contrast, if a path is blocked, then no association can be transmitted along it. Consequently, it is typically the goal to perform a statistical analysis that blocks all noncausal pathways. If not, then the open noncausal pathway that remains is referred to as a biasing pathway. An association (or a possible association that is to be tested) between two variables requires at least one open path between the variables. An open path can become blocked and vice versa by conditioning on particular variables along that path (conditioning typically means statistical adjustment [e.g., through a regression analysis] or stratification [as in the hypothetical example]). The rules in Table 2 can be used to establish whether a particular causal or noncausal path in a given DAG is open or blocked (6,7).

Table 2.

Rules to establish whether a pathway in a causal diagram is open or blocked

Rule No.	Type of Path	No. of Colliders on Path	Aim of Adjustment	How to Establish if Path is Open or Blocked
1	Causal	N/A	Leave open (for estimation of total causal effect)	The path will be open providing that no variables along it are conditioned on (otherwise, it will be blocked)
2	Noncausal	0	Block noncausal pathway	The path will be blocked if at least one variable along it is conditioned on (otherwise, it will be open)
3a	Noncausal	1	Block noncausal pathway	The path will be open if the only variable conditioned on is the collidera (otherwise, it will be blocked)
3b	Noncausal	>1	Block noncausal pathway	The path will be open if all of the collider variablesa (and no noncollider variables) are conditioned on (otherwise, it will be blocked)

N/A, not applicable.

^aOr descendant(s) of the collider(s).

Consider now the confounder C_con shown in Figure 3A, the effect mediator C_med in Figure 3B, and the collider C_col shown in Figure 3C. The rules in Table 2 can be used to determine whether the paths from E to D through C in these cases are open and hence, whether they are biasing pathways. In Figure 3A, the path E ← C_con → D is open (rule 2) and therefore, a biasing pathway. Conditioning on C_con blocks the path (rule 2) and provides an unbiased estimate of the effect of E on D. In Figure 3B, the path E → C_med → D is also open, but because this path is a causal pathway, it should be kept open, assuming that the goal is to estimate the total effect of E on D. Conditioning on C_med in this situation would block this path (rule 1) and result in estimation only of the direct effect of E on D (that is, the part that is not mediated through C_med). In Figure 3C, the path E → C_col ← D is already blocked (rule 3a), and there are no other noncausal pathways in the DAG. However, if C_col was conditioned on, then the path E → C_col ← D would be opened (rule 3a), creating a new biasing pathway that did not previously exist.

These rules allow us to establish why the estimate of the (hypothetical) causal effect of alcohol consumption on jet lag above was so clearly wrong. In this case, missing the plenary session is a collider, because it could have been caused by either alcohol consumption or suffering from jet lag. Conditioning on it (by creating the two separate 2×2 contingency tables) opened up a new biasing pathway.

Selecting Appropriate Sets of Covariates for Observational Analyses

Generally, DAGs drawn to represent the relationship between the exposure and the outcome in an epidemiologic study will be much more complex than those shown in Figure 3, because there will be many inter-relationships between the various covariates, exposure, and outcome, making it difficult to identify all of the potentially biasing pathways. Although a simple six–step algorithm exists, allowing one to test whether a proposed set of covariates to control for removes all biasing pathways (8), applying this can require considerable trial and error. Fortunately, freely available software exists to implement these rules, making the selection of an appropriate set of covariates much easier (for example, http://www.dagitty.net/ [9] and R package dagR [10]). It is also worth noting that the theory of DAGs can be combined with traditional selection methods (11,12) to see whether there are any unnecessary covariates that could be removed from the set and, therefore, possibly improve the precision of the estimated effect of exposure on outcome.

A Real Example: Adjustment for Baseline Albumin-to-Creatinine Ratio in Analyses of the Relevance of Smoking to Progression to ESRD

Now that the theory of causal diagrams has been introduced, we shall apply it to a real epidemiologic analysis to illustrate the type of problem that can result if causal relationships are not properly considered. The example chosen is an analysis of the relevance of smoking to progression to ESRD among 6245 patients who were not on dialysis at the time of randomization into the Study of Heart and Renal Protection (SHARP), a large randomized trial of lipid modification in patients with established renal disease (13).

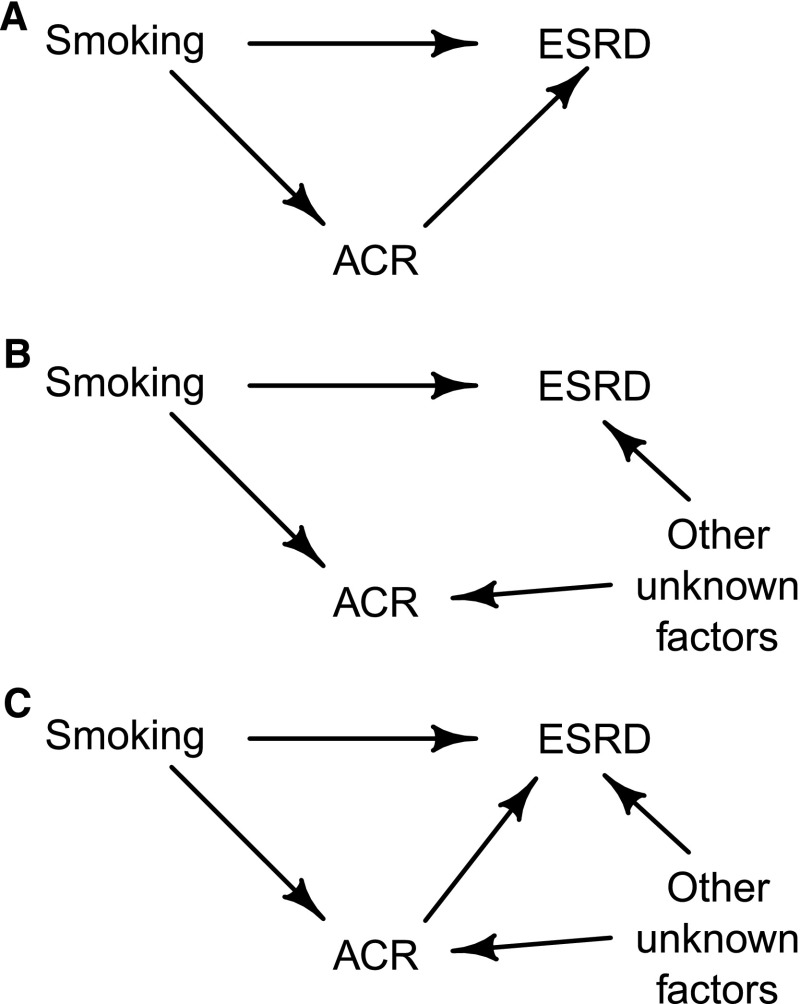
Interest lies in estimating the relevance of smoking to ESRD, and the question is whether to adjust (i.e., condition) for each participant’s urinary albumin-to-creatinine ratio (ACR). Smoking increases ACR (14,15), and higher ACR concentrations are associated with increased risk of progression to ESRD (16,17). However, the causal nature of the association between ACR and ESRD is uncertain. Although it is possible that ACR directly influences (i.e., causes) ESRD, it is also possible that the association between ACR and ESRD is caused by other (unknown) factors that affect both ACR and the risk of reaching ESRD (in which case, ACR would merely be a marker of renal progression). These scenarios are illustrated by the DAGs drawn in Figure 4. (In the latter case, exposure to these unknown factors would have to increase ACR as well as increase ESRD risk for higher ACR to be associated with increased ESRD risk.) For simplicity, we ignore in Figure 4 all covariates that could otherwise confound the relationship between smoking and ESRD risk and assume that adjustment has already been made for any covariates needed to close any biasing paths between smoking and ESRD.

Figure 4.

Causal diagrams that represent three possible relationships between smoking, ESRD, and albumin-to-creatinine ratio (ACR) in the Study of Heart and Renal Protection. (A) ACR is an effect mediator on the causal pathway between smoking and ESRD. (B) ACR is a collider on one the paths between smoking and ESRD. (C) ACR is an effect mediator on one path and a collider on another path between smoking and ESRD.

If Figure 4A represented the truth, then ACR would be an effect mediator, and it would be inappropriate to condition on ACR, because it would block a causal pathway between smoking and ESRD. (If it were done, the effect of this pathway would be removed from the estimate of the total effect of smoking on ESRD.) If Figure 4B represented the truth, however, then ACR would be a collider on one of the two paths between smoking and ESRD, and as such, it would still be inappropriate to adjust for it (because doing so would create a biasing pathway between smoking and ESRD). Specifically, if it were known that someone had an increased level of ACR (the effect of conditioning), then knowing that they were also a smoker would reduce the probability that they have been exposed to the other unknown factors. This is because being a smoker is the more likely cause of their increased value of ACR. In other words, given ACR, smokers will be systematically less likely to have been exposed to the other unknown factors (which of course, cannot be controlled for in the statistical analysis), and their risk of progression to ESRD will, as a consequence, apparently be reduced. Conditioning on ACR in this situation would, therefore, bias the relative risk of ESRD associated with smoking downward and could even result in a relative risk that (wrongly) suggests that smoking has a protective effect on the risk of progression. Another scenario would be that ACR has some direct effect on the risk of ESRD with other unknown factors influencing both ACR and ESRD (i.e., a combination of the scenarios in Figure 4, A and B, which is shown in Figure 4C). In this case, it would still be inappropriate to adjust for ACR (because ACR is both an effect mediator and a collider on another pathway between smoking and ESRD).

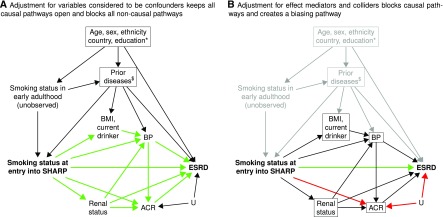
In SHARP, the etiologic relevance of baseline smoking status (current smokers compared with never smokers) to ESRD was estimated using Cox proportional hazards regression (18). After adjustment for a range of assumed confounders (the assumed DAG is in Figure 5A), current smokers had a similar rate of progression to ESRD as never smokers (hazard ratio, 1.02; 95% CI, 0.89 to 1.17). (In DAGs, variables that are conditioned on are usually highlighted by drawing a square around them, as shown in Figure 5.) However, if adjustment is also made for ACR (and other factors associated with smoking and ESRD risk: BP, body mass index, current drinking, and renal status) rather than only the characteristics thought to be confounders, an apparent protective association between current smoking and ESRD risk is observed (hazard ratio, 0.85; 95% CI, 0.74 to 0.98). The DAG in Figure 5B illustrates what has happened. Many of the causal pathways (shown in green in Figure 5A) are now blocked, because all of these additional factors were assumed to be effect mediators. In addition, a new biasing pathway (shown in red in Figure 5B) has arisen by conditioning on ACR, because it is a collider on the path: smoking at entry into SHARP → ACR ← other unknown factors → ESRD. Inclusion of the additional factors (in particular, albuminuria) creates what we believe to be an artificial association between smoking and a reduced risk of ESRD, which is unlikely to reflect a true protective effect.

Figure 5.

Causal diagram showing assumed associations between baseline smoking status, ESRD, and baseline characteristics in the Study of Heart and Renal Protection (SHARP). (A) Adjustment for variables considered to be confounders keeps all causal pathways open and blocks all noncausal pathways. (B) Adjustment for effect mediators and colliders blocks causal pathways and creates a biasing pathway. Boxes around variables indicate that they have been adjusted for in analyses. Open causal pathways are highlighted by green arrows (e.g., smoking status at entry into SHARP → urinary albumin-to-creatinine ratio [ACR] → ESRD in A), and biasing pathways are indicated by red arrows (e.g., smoking status at entry into SHARP → ACR ← other unknown factors [U] → ESRD in B). *Age, sex, ethnicity, country, and education would also be causes of body mass index (BMI), current drinking, BP, renal status, and ACR. ^$Prior diseases would also be causes of renal status and ACR.

Index Event Bias in Studies of Individuals with CKD

Causal diagrams allow sources of bias related to the selection of participants into a study to be identified. One such bias that is particularly relevant to studies of CKD populations is index event bias. Although index event bias is well recognized in the epidemiologic literature (19,20), it is perhaps not sufficiently acknowledged in epidemiologic studies of already diseased individuals. It is usually discussed in the context of recurrent events, because paradoxical findings are often observed where well established risk factors for a disease may seem to not influence recurrence risk among individuals who have already had a first event. Because progression to ESRD among those with CKD is a worsening of a preexisting condition, studies examining causes of ESRD in CKD populations could suffer from similar issues.

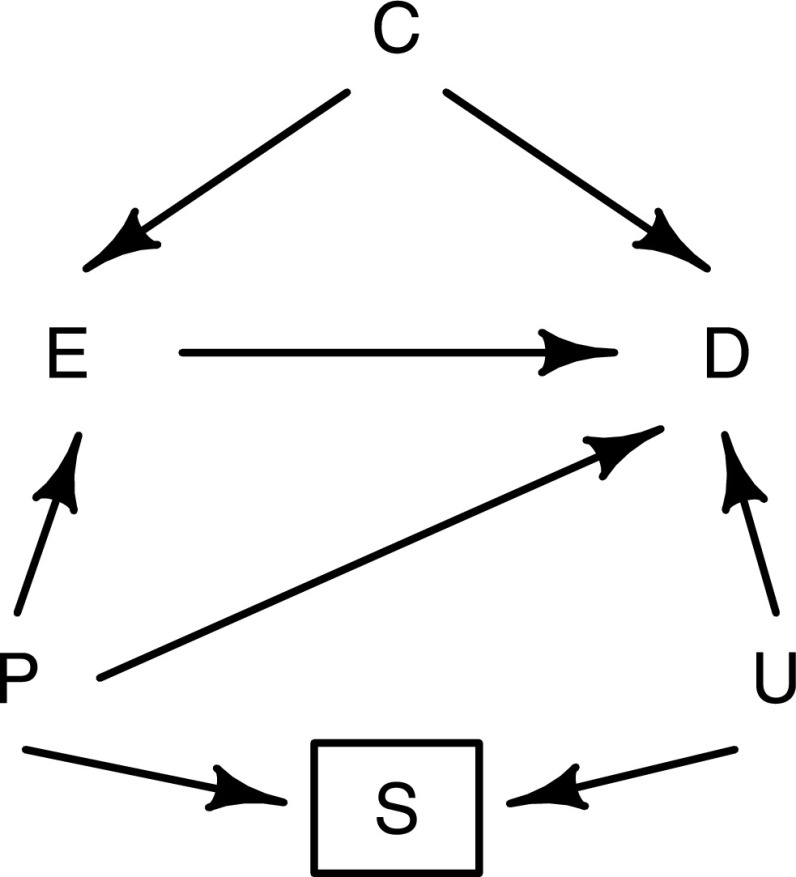
Consider, for example, the causal diagram in Figure 6. The effect of an exposure measured on entry into the study (E) on progression to ESRD (D) is of interest. The variable S represents the selection criteria for the study (which in this case, would be having CKD). Only including individuals who meet this criterion in the study would be the same as conditioning on S. Because progression to ESRD is a worsening of preexisting kidney disease, it is not unreasonable to assume that any risk factors for ESRD will also be risk factors for CKD and hence, be causally related to the selection criteria. The variable U in Figure 6 represents all such risk factors, which may or may not have been recorded in the study. Prior values of the exposure (P) will influence both the risk of CKD and the value of the exposure at time of entry into the study, introducing an association between E and S. The variable S is a collider on the path from E to D that goes through U, and therefore, conditioning on this variable has opened up a biasing pathway between the exposure and the disease. If both the exposure and the unmeasured risk factors are associated with an increased risk of kidney disease, then conditioning on S (which is unavoidable) will create an inverse association between E and U. The consequence of this would be to bias the association between the E and D toward the null.

Figure 6.

Causal diagram to illustrate the issue of index event bias in observational analyses restricted to participants with CKD. E, exposure at study entry; D, progression to ESRD; C, confounders; P, long-term (or usual) values of exposure prior to study entry (unmeasured); S, selection criteria (i.e., having CKD); U, risk factors for kidney disease (possibly unmeasured).

Adjustment for the shared risk factors U would be required to control for index event bias, although it is always possible that residual bias may exist, because some of the risk factors may be unmeasured (or even unknown). However, formulas do exist to estimate the extent of such residual biases (21,22) on the basis of assumptions about the distributions and associations of unmeasured factors.

There is an additional source of bias in the causal diagram in Figure 6 that should also be mentioned. Because P represents the long–term or usual exposure level, this variable could have an effect on progression to ESRD that is not completely explained by the measured baseline value (for example, if this value is measured with error). In this case, the biasing pathway E ← P → D may be thought of as representing regression dilution bias, which can easily be accounted for using other established methods (23,24).

Discussion

Sufficiently large properly randomized trials are generally the preferred method of testing the causal effect of an exposure on an outcome of interest. However, epidemiologic analyses are still often used to estimate causal effects (either to generate hypotheses to be tested in future trials or when trials are not feasible). For observational data, it is necessary to adjust for variables that could confound the causal effect. Causal diagrams provide a graphical representation of all of the assumptions that have been made about the associations between the exposure, the outcome, and any other variables (which should be informed by evidence from the literature as well as expert opinions). On the basis of those assumptions, simple automated methods are available, which will identify the appropriate set of variables to include in a statistical analysis, the aim of which is to minimize bias due to observed confounders. Of course, biases may still exist because of unmeasured confounders of the exposure and the outcome or imprecise measurements of confounders (i.e., residual confounding). Although causal diagrams cannot prevent this residual confounding, they can be used to determine whether the recorded characteristics are likely to be sufficient to adequately adjust for it. Indeed, it may be more likely that the validity of the no residual confounding assumption will be considered if a causal diagram has been constructed.

More generally, causal diagrams allow other potential sources of bias in a study to be recognized, such as index event bias as discussed above. There are many other examples of bias related to the selection of participants in a study or selection bias. For instance, the healthy participant effect is already well established in prospective cohort studies as a potential bias when estimating disease prevalence reliably. Selection bias and its representation using DAGs have been discussed in detail elsewhere (3). Although this article focuses on the use of causal diagrams in observational analyses, they can also be used to detect potential sources of bias in randomized, controlled trials (for example, when participants are unblinded to treatment allocation) (25). One limitation of causal diagrams is that they require the direction of causality between two variables to be stated, which may be difficult to establish when multiple biologic measurements are conducted at the same time.

It is worth noting that the use of causal diagrams is still appropriate, even when there is uncertainty about some of the underlying relationships between the characteristics considered. In such situations, alternative causal diagrams can be considered as sensitivity analyses. Whether explicitly specified or not, every epidemiologic analysis makes assumptions about the underlying causal relationships between the exposure, outcome, and other characteristics. The use of causal diagrams merely states these assumptions and in doing so, helps avoid potential pitfalls through inappropriate adjustments. Causal diagrams should, therefore, be considered at all stages when embarking on such analyses and made available alongside the results to make it clear which assumptions have been made.

Disclosures

None.