Climbing Fibers Control Purkinje Cell Representations of Behavior

Abstract

A crucial issue in understanding cerebellar function is the interaction between simple spike (SS) and complex spike (CS) discharge, the two fundamentally different activity modalities of Purkinje cells. Although several hypotheses have provided insights into the interaction, none fully explains or is completely consistent with the spectrum of experimental observations. Here, we show that during a pseudo-random manual tracking task in the monkey (Macaca mulatta), climbing fiber discharge dynamically controls the information present in the SS firing, triggering robust and rapid changes in the SS encoding of motor signals in 67% of Purkinje cells. The changes in encoding, tightly coupled to CS occurrences, consist of either increases or decreases in the SS sensitivity to kinematics or position errors and are not due to differences in SS firing rates or variability. Nor are the changes in sensitivity due to CS rhythmicity. In addition, the CS-coupled changes in encoding are not evoked by changes in kinematics or position errors. Instead, CS discharge most often leads alterations in behavior. Increases in SS encoding of a kinematic parameter are associated with larger changes in that parameter than are decreases in SS encoding. Increases in SS encoding of position error are followed by and scale with decreases in error. The results suggest a novel function of CSs, in which climbing fiber input dynamically controls the state of Purkinje cell SS encoding in advance of changes in behavior.

SIGNIFICANCE STATEMENT Purkinje cells, the sole output of the cerebellar cortex, manifest two fundamentally different activity modalities, complex spike (CS) discharge and simple spike (SS) firing. Elucidating cerebellar function will require an understanding of the interactions, both short- and long-term, between CS and SS firing. This study shows that CSs dynamically control the information encoded in a Purkinje cell's SS activity by rapidly increasing or decreasing the SS sensitivity to kinematics and/or performance errors independent of firing rate. In many cases, the CS-coupled shift in SS encoding leads a change in behavior. These novel findings on the interaction between CS and SS firing provide for a new hypothesis in which climbing fiber input adjusts the encoding of SS information in advance of a change in behavior.

Introduction

The distinctive morphological and physiological properties of the climbing fiber-Purkinje cell synapse suggest a unique functional role in the cerebellum (Eccles et al., 1967; Ito, 1984). Climbing fiber afferents originate solely from the inferior olive and provide one of two main inputs to the cerebellar cortex. Firing at low rates (∼0.5–2.0/s), a climbing fiber produces a powerful depolarization of a single Purkinje cell through hundreds of glutamatergic synapses along the proximal dendritic tree. This results in a complex spike (CS) consisting of a large Na⁺ somatic spike accompanied by a burst of smaller spikelets as well as Ca²⁺ spikes throughout the entire dendritic tree (Llinás and Sugimori, 1980; Davie et al., 2008). In contrast, a Purkinje cell receives input from >100,000 parallel fibers that modulate the high-frequency simple spike (SS) discharge.

Requisite for elucidating the principles of cerebellar function is an understanding of the interaction between CS discharge and SS firing. Much attention has focused on the long-term effect of CS discharge on SS firing. In the Marr-Albus-Ito hypothesis, LTD of parallel fiber-Purkinje cell synapses resulting from coactivation of parallel and climbing fiber inputs underlies motor learning (for review, see Marr, 1969; Albus, 1971; Ito, 2001). In this context, CSs are evoked by errors and provide a teaching signal that modifies subsequent SS activity to correct the behavior (Gilbert and Thach, 1977; Kitazawa et al., 1998; Medina and Lisberger, 2008; Yang and Lisberger, 2014). Although substantial evidence supports a role for climbing fibers in error signaling and motor learning, CSs are not invariably activated by errors (for review, see Popa et al., 2016). Also, CSs are not essential for cerebellar motor learning (Ke et al., 2009; Nguyen-Vu et al., 2013; Hewitt et al., 2015), SS discharge carries robust error signals (Popa et al., 2012), and there are significant challenges to the role of cerebellar LTD in motor learning (Schonewille et al., 2011).

Moreover, the motor learning/error hypothesis does not account for spontaneous CS firing and the observation that removal of climbing fiber input results in an immediate and dramatic change in the SS firing pattern and a cerebellar-like motor disorder (Llinás et al., 1975; Colin et al., 1980; Montarolo et al., 1982; Cerminara and Rawson, 2004; Horn et al., 2013). Also, spontaneous CSs have been proposed to perturb movements as a probe for initiating plasticity (Bouvier et al., 2016). Therefore, climbing fiber input must play a role in online cerebellar function and motor control. Several hypotheses on CS contribution to real-time motor control emphasize short-term changes in Purkinje cell excitability. The “gain change” and “bistability” hypotheses suggest that CSs control the responses of a Purkinje cell to parallel fiber inputs (Ebner et al., 1983) and switch between “up” and “down” SS firing states (Loewenstein et al., 2005; McKay et al., 2007; Yartsev et al., 2009), respectively. Also, during behavior, CSs and SSs exhibit a reciprocal firing pattern that is mediated by climbing fiber input (Graf et al., 1988; Simpson et al., 1995; Yakhnitsa and Barmack, 2006; Badura et al., 2013). The rhythmicity and synchronicity of climbing fibers suggest a role in movement timing independent of their action on SS firing (Welsh et al., 1995; Lang et al., 1999; Llinás, 2013). However, in the awake, behaving animal, the evidence for strong CS rhythmicity or that CSs act to control gain or bistability is controversial (Keating and Thach, 1995; Simpson et al., 1995; Schonewille et al., 2006; Engbers et al., 2013). Therefore, lacking is a comprehensive understanding of climbing fiber function and its role in cerebellar information processing.

This study evaluates the modulation of SS representations by climbing fiber input. To obtain a comprehensive characterization of the interactions among CS discharge, SS firing, and behavior, we tested this question in a pseudo-random tracking task. The key observation is that CSs are followed rapidly by large increases and decreases in the signals encoded by the SS discharge. These novel findings suggest the global depolarization of a Purkinje cell by climbing fiber input allows for a change in the information conveyed by the SS firing.

Materials and Methods

Behavioral and electrophysiological data were obtained from two rhesus monkeys (Macaca mulatta; female 6.3 kg age 15 years; male 6.8 kg age 8 years) during normal daytime hours. Animals were housed in single cages and kept on a 12 h light/dark cycle. All animal experimentation was approved by the Institutional Animal Care and Use Committee of the University of Minnesota and conducted in accordance with the guidelines of the National Institutes of Health.

Random tracking.

This study used a previously described pseudo-random tracking task (Paninski et al., 2004; Hewitt et al., 2011; Popa et al., 2012); therefore, the paradigm is only briefly detailed here. Two rhesus monkeys were trained to use a robotic manipulandum (InMotion²) that controls a cross-shaped cursor to track a circular shaped target (2.5 cm diameter) on a computer screen (see Fig. 1A). The paradigm started with an initial hold inside a stationary target for a random period of time (1000–2000 ms). The initial target position on the screen was also random. Next, the target moved for 6–10 s along a trajectory selected randomly from 100 trajectories defined a priori. Pseudo-random target paths were generated from a sum of sine waves. Target speed was randomly varied so that the average speed was ∼4 cm/s and conformed to the two-thirds power law (Viviani and Terzuolo, 1982; Lacquaniti et al., 1983). The trajectories were low-pass filtered and selected to avoid sharp turns and large changes in speed, and ended with a final hold period of at least 1000 ms. The paradigm required that the monkey maintain the cursor within the target, and allowed only brief excursions outside the target (<500 ms). Pseudo-random tracking has several advantages compared with other tasks, including providing more comprehensive and uniform coverage of parameter workspaces and dissociating kinematic from error parameters (Paninski et al., 2004; Hewitt et al., 2011). Hand (X and Y, based on cursor position) and target (X_tg, Y_tg) position were sampled at 200 Hz. Cursor velocity (VX, VY) was derived by numerical differentiation, and position error (XE, YE) was defined as the difference between cursor and target positions (see Fig. 1B).

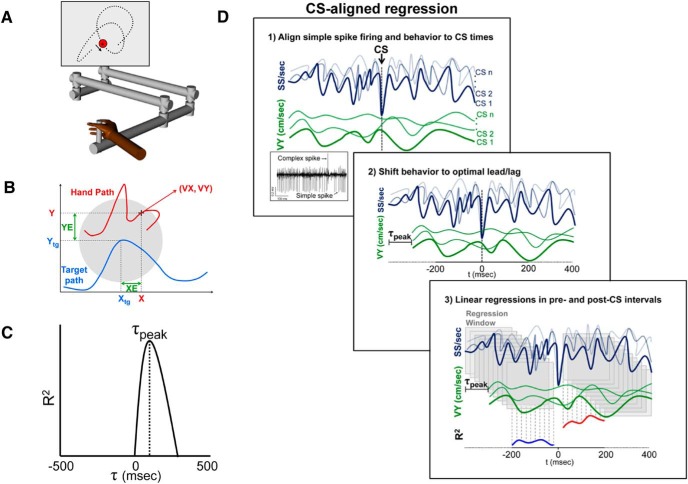
Figure 1.

Experimental paradigm and regression analysis. A, Rhesus macaques use a robotic manipulandum to control a cross-shaped cursor to track a circular target (2.5 cm diameter) on a computer screen (Paninski et al., 2004; Hewitt et al., 2011; Popa et al., 2012). B, Kinematic parameters (X, Y, VX, VY) are based on cursor motion (red trace). Position error (XE and YE) is the difference between cursor (X, Y) and target center position (X_tg, Y_tg). C, Timing of SS signals encoding a parameter was based on the local maxima of the coefficient of determination (R²) profile determined using the temporal linear regression analysis described previously (Popa et al., 2012). D1, Effects of CS discharge on the SS encoding was assessed by aligning the SS firing (dark blue) and the parameter (green) to CS occurrences. D2, Behavior was then shifted by the peak lead or lag (τ-peak) obtained from the non–CS-aligned linear regression (C). D3, Linear regressions were performed 400 ms before and after CS discharge using a 20 ms step sliding window of 200 ms, generating pre (blue) and post (red) R² profiles that quantify encoding strength.

Surgical procedures, electrophysiological recordings, and data collection.

Head restraint hardware and a recording chamber targeting lobules IV–VI of the intermediate and lateral cerebellar zones were chronically implanted over the ipsilateral parietal cortex in each animal using aseptic techniques and full surgical anesthesia. The positions of the electrodes were confirmed by radiographic imaging techniques that combined a CT scan of the skull with an MRI of the cerebellum (Hewitt et al., 2011). After full recovery from chamber implantation surgery, extracellular recordings were obtained during normal daytime hours using Pt-Ir electrodes with parylene C insulation (0.8–1.5 mΩ impedance, Alpha Omega Engineering). Purkinje cells in lobules IV–VI of the intermediate and lateral cerebellar zones were targeted following previously established methods. (Hewitt et al., 2015). After conventional amplification and filtering (30 Hz to 3 kHz bandpass, 60 Hz notch), SSs were discriminated online using the Multiple Spike Detector System (Alpha Omega Engineering). Resulting spike trains were digitized and stored at 1 kHz. The raw electrophysiological data were also digitized and stored at 32 kHz. CSs were sorted offline using a combination of software and manual confirmation (Hewitt et al., 2015). Using the fractional interval method, the SS trains were transformed to a continuous firing rate in 5 ms bins. Importantly, the SS firing rates were not filtered to minimize autocorrelation artifacts. For display and analyses, the mean firing rate for each trial was subtracted from the instantaneous firing rate. The behavioral parameters were filtered (low pass; fourth-order Butterworth with a 5 Hz cutoff). The analyses evaluating the relation among the SS firing, and the behavioral variables were restricted to the tracking period.

Linear modeling of SS firing regardless of CS occurrence.

The first analysis determined for each Purkinje cell the presence and timing of kinematic and error signals in the SS firing during tracking regardless of the time of CS discharge. This involved fitting the SS firing to each kinematic and error parameters using the temporal linear regressions on firing residuals, as described previously (Popa et al., 2012; Hewitt et al., 2015). For each Purkinje cell, this analysis was performed for the tracking periods across all trials and is referred to as the non–CS-aligned linear regression. For a given parameter (e.g., VX), SS variability associated with the rest of the parameters was first removed by determining the firing residuals from a multilinear model that fitted the SS firing to the other kinematic and error parameters (e.g., X,Y,VY, XE, and YE) (Popa et al., 2012). The resulting SS firing residuals were regressed against the individual parameters at 20 ms intervals from −500 to 500 ms, determining the R² and regression coefficient (β) temporal profiles as functions of the lead/lag (τ value). The significance of the R² at each τ value was determined against a noise distribution defined as the mean ± 3 SDs of the R² values obtained from 100 repeats of the same regression analysis performed on firing and behavioral data uncoupled through random trial shuffling. For each parameter, significant correlations were defined if a local maximum of the R² profile at either predictive or feedback timings exceeded the trial shuffled noise level, and the timing (τ value) of the peak lead and/or lag was determined (see Fig. 1C).

CS-aligned analysis of SS encoding.

CS-coupled changes in encoding were determined for each significant SS representation identified by the non–CS-aligned linear regression described above. Next, the SS firing and the behavioral data were aligned to the times of CS firing for the entire recording session (i.e., all trials) as diagrammed in Figure 1D1. Then the behavioral parameter was shifted relative to the SS firing by the peak lead or lag (τ) determined in the non–CS-aligned regression analysis (see Fig. 1D2). To visualize and quantify the CS-coupled changes, the data were partitioned into 64 (8 × 8) equal bins of 0.5 cm ranging from −2 to 2 cm for XE and YE, 3.0 cm/s ranging from −12 to 12 cm/s for VX and VY, and 6 cm from −6 to 6 cm for X and Y, and averaged using a sliding window of 200 ms in 20 ms intervals. The CS-aligned SS firing was averaged in these bins. This partitioning allowed construction of SS firing maps aligned on all CS occurrences at each time interval for position, velocity and position error, respectively (see Fig. 2A), and was also used for the CS-aligned regression analysis described below.

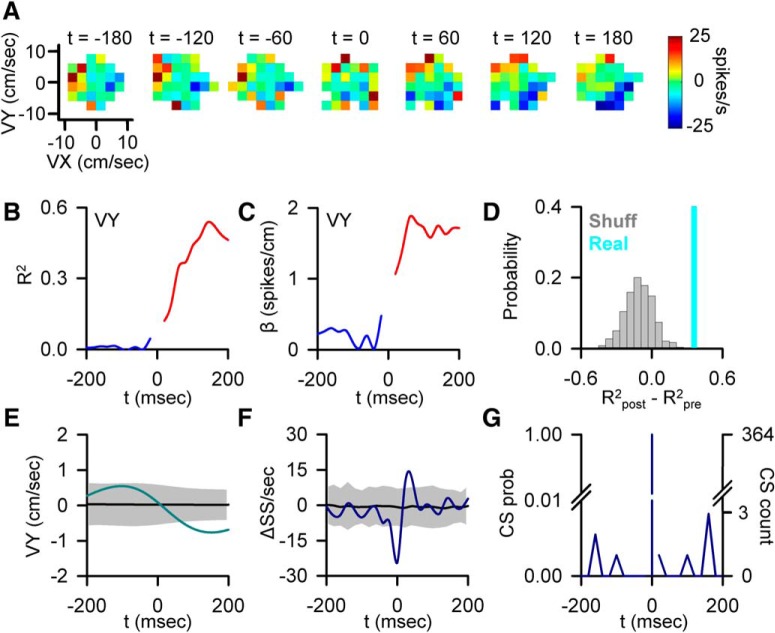
Figure 2.

CS-coupled increase in SS encoding. A, Firing maps illustrating an example of Purkinje cell SS modulation with velocity (VY) relative to CS discharge (t = 0). B, Encoding strength (R²) of VY both pre- (blue trace) and post-CS (red trace). C, Sensitivity (β) of the same Purkinje cell to VY both pre- (blue trace) and post-CS (red trace). D, Magnitude of the CS-coupled change in SS encoding strength as quantified by the difference between R²_post − R²_pre in the ±200 ms window (indicated by the light blue line) relative to the distribution of changes in encoding strength aligned to randomized CS times selected outside the actual CS window (gray bars). Light blue line (in this and subsequent figures) indicates the magnitude of the change in encoding (position along the x-axis) and not a probability (y-axis). E, CS-triggered average of VY (light blue trace) relative to the VY variability from CS-shuffled ISIs (mean ± 3 SDs, gray region). F, CS-triggered average of SS firing (blue trace) relative to the SS variability from CS-shuffled ISIs (mean ± 3 SDs, gray region). Note the brief firing rate reduction (t = 0) due to CS inactivation of the SS discharge. G, Distribution of additional CSs in the −200 to 200 ms intervals centered on CS occurrence (left axis, CS probability; right axis, CS count).

Using this shifted and partitioned behavior, the SS firing was regressed against the behavioral parameter using the same sliding window of 200 ms in ten 20 ms intervals to quantify the SS encoding strength relative to CS occurrence (see Fig. 1D3). To account for the sliding window, the first interval for −200 ms in the pre-CS period was obtained by regressing the firing with behavior data from aligned −400 to −200 ms, and the final pre-CS interval at −20 ms using the data aligned from −220 to −20 ms. The same procedure was used for the post-CS data, with the first post-CS step based on 20 to 220 ms to avoid the brief inactivation period after CS discharge and prevent any overlap between pre- and post-CS periods. The sliding window continued in 20 ms intervals, with the final post-CS interval using the data aligned from 200 to 400 ms. Because the first 20 ms interval following the CS was omitted, we elected to omit the 20 ms interval before the CS to balance the subsequent statistical testing of differences between the pre- and post-CS periods. Therefore, the pre- and post-CS regression analyses were each determined using >10 sliding regression windows of 200 ms duration at 20 ms intervals. The CS-aligned regression analysis resulted in R² and β temporal profiles ranging from −200 to 200 ms before and after CSs for each significantly encoded behavioral parameter (see Fig. 1D3, bottom R² plots). We also assessed whether changes in encoding occurred for parameters that were not significantly modulated based on the results of the non–CS-aligned linear regression analysis. For these data, we performed the same analysis, except that the behavioral data were not shifted relative to the SS firing (i.e., τ of 0 ms).

The significance of the CS-coupled changes in encoding was determined by comparing the difference between mean R² pre- versus mean R² post-CS to a distribution of pre versus post R² changes obtained from 1000 CS-shuffled R² profiles. The data for this CS-shuffled analysis were restricted to time periods that did not overlap with the window used for the CS-coupled regression analysis. The latter ensured that any random changes in encoding were not being driven by overlap with actual CSs. The analysis focused on identifying changes in the R² profile relative to the timing of CSs. Although sharp transitions in SS encoding strength were tightly coupled to CS discharge, the time course to reach the peak change in R² ranged from 100 to 200 ms (for examples, see Figs. 2B, 4B). Thus, the mean differences in encoding were computed by collapsing the data across two different time windows: 100 ms pre-100 ms post (pre-CS window = −100:−20 ms, post-CS window = 20:100 ms) CS and 200 ms pre-200 ms post CS (pre-CS window = −200:−20 ms, post-CS window = 20:200 ms). A CS-coupled change in encoding was determined to be significant if it was above mean ± 2 SDs of the CS-shuffled distribution for either the ±100 ms or ±200 ms windows. Importantly, the majority of significant encoding changes (>70%) met the criteria for significance at both the ±100 ms and ±200 ms windows.

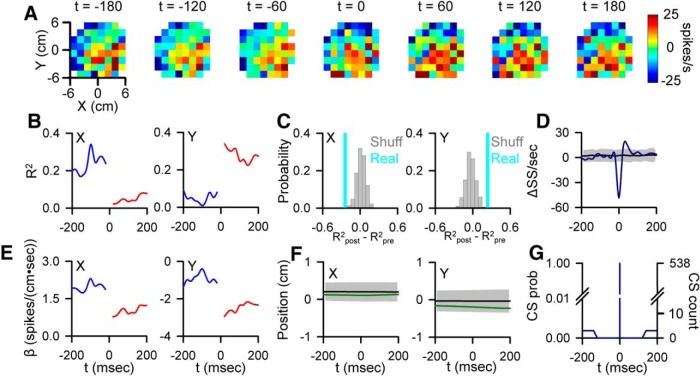
Figure 4.

CS-coupled switch in SS encoding. A, Firing maps illustrating an example cell SS modulation with position relative to CS occurrence (t = 0). B, Pre- and post-CS encoding strength of X and Y (conventions as in Figs. 2, 3). C, Magnitude of the CS-coupled change in SS encoding of X (left) and Y (right) in the ±100 ms window (indicated by the light blue lines) relative to the distribution of profiles aligned to randomized CS times selected outside the actual CS window (gray bars). D, CS-triggered average of SS firing (blue trace) relative to the SS variability CS-shuffled ISIs (mean ± 3 SDs, gray region). E, Pre- and post-CS SS firing sensitivity for this cell to X (left) and Y (right) (conventions as in Figs. 2, 3). F, CS-triggered average of X (left, green trace) and Y (right) relative to the variability from CS-shuffled ISIs (mean ± 3 SDs, gray region). G, Occurrence of additional CSs in the ±200 ms window centered on CS discharge (left axis, CS probability; right axis, CS count).

For the representations with significant CS-coupled changes in encoding, we also quantified the changes in sensitivity by computing the difference between the absolute value of the mean post-CS β values and the absolute value of the mean pre-CS β values (|β_post| − |β_pre|). Positive changes indicate increases in sensitivity, whereas negative changes indicate decreases in sensitivity. Changes in sensitivity were determined using the time window that produced the significant change in encoding strength.

It needs to be emphasized that the temporal linear regression analysis used is highly sensitive to the coverage of the parameter workspace, which is minimal on the single CS level or over the small number of CSs that occur in a single trial compared with the non–CS-aligned regression analysis. Therefore, a meaningful regression analysis on how the SS encoding changes for a single CS or trial was not possible. Instead, the regression analysis over all trials shows the average effect of the CS discharge on the signals in the SS firing.

Relationship between CSs and behavior.

The relationship between CS firing and each behavioral parameter was assessed using CS spike-triggered averaging. The average behavioral trace of each parameter was computed from 500 ms before to 500 ms after each CS occurrence in 20 ms intervals. We elected to use a ±500 ms time window to make certain we captured all significant changes in behavior both before and after CS discharge. The noise level was determined by randomly shuffling the interspike interval (ISI) of CS times within a trial (ISI-shuffled, 50 repeats) and computing the mean and SD of the ISI-shuffled CS-triggered average behavioral trace. For this analysis, we tested for peak changes in behavior relative to the time of CS firing instead of averaging across pre- and post-CS intervals. As such, we used a more stringent criterion for significance. CS-triggered average behavioral parameters with local minima or maxima exceeding a threshold of mean ± 3 SDs of the CS-shuffled noise distribution were considered significant. The magnitude of the behavioral change and timing of the change relative to CS discharge were determined, with negative times indicating behavioral changes occurring before and positive times indicating behavioral changes occurring after CS discharge.

Relationship between CSs and SS firing properties.

The relationship between CS discharge and SS firing was assessed using three methods. For all three analyses described here, we evaluated changes in SS firing properties using both ±200 and ±500 ms windows relative to CS firing, with the post-CS window beginning after the mean ± 1 SD of the CS-induced inactivation period. Again, the rationale for using two time periods was to fully assess whether the SS firing changes in relation to the CS occurrence. One Purkinje cell was excluded from these analyses because of variability in the inactivation period that exceeded 1000 ms. However, removal of this Purkinje cell did not affect the analysis and conclusions, as this neuron did not exhibit any significant CS-coupled changes in SS encoding. First, we compared the mean SS firing pre- and post-CS to evaluate whether CS firing produced significant changes in SS firing rate across the population. Significant changes in SS firing across the population were assessed using Student's paired t test (p < 0.05). Second, we assessed CS-coupled changes in SS firing rate for each Purkinje cell by comparing each 20 ms interval of CS-aligned SS firing in the post-CS interval with the mean ± 3 SDs of the CS-aligned SS firing in the pre-CS interval. Finally, to test for changes in SS firing variability, the Fano factor (Fano, 1947), defined as the ratio of variance over the mean, was calculated. Significant changes in the Fano factor before and after CS occurrence were evaluated for each Purkinje cell also using a paired t test (p < 0.05).

Properties of CS discharge and the encoding changes.

Additional analyses assessed the properties of the CS discharge in relation to the changes in SS encoding. The first of these analyses assessed whether the time course of the encoding changes can be attributed to CS discharge at t = 0 ms, rather than a combination of subsequent CSs. We addressed this by quantifying the number and probability of CS discharges in each bin for the ±200 ms CS-aligned windows. Rhythmicity in CS discharge has been proposed as an essential feature of CS function (Welsh et al., 1995; Lang et al., 1999; Llinás, 2013). To test for rhythmicity, the autocorrelation of the CS discharge was computed over a long time scale (−2000 to 2000 ms) to account for the low CS firing rates in a majority of Purkinje cells. Significance was determined by a change in correlation outside the mean ± 3 SDs of the autocorrelation computed from randomized CS timing (50 repeats). Additionally, the peak amplitudes of the autocorrelation in the 8–12 Hz range, the frequency of the intrinsic rhythmicity in CS firing, were compared with that of randomized CSs.

Results

CSs modulate SS representations of kinematics and errors

Forty Purkinje cells were recorded from two rhesus macaques performing a visually guided, manual pseudo-random tracking task (Fig. 1A,B) (Hewitt et al., 2011; Popa et al., 2012). The overall goal of the analyses is to characterize the effect of CS discharge on the motor signals present in SS firing, specifically on the encoding of position (X and Y), velocity (VX and VY), and position error (XE and YE). The first step in the analyses determined the significant SS representations and their optimal τ values as identified by the non–CS-aligned regression analysis (Fig. 1C; see Materials and Methods). Next, the SS firing and the behavioral data were aligned to the times of CS firing for the entire recording session (i.e., all trials) as diagramed in Figure 1D1. For each significant parameter identified, the parameter was shifted relative to the SS firing by the peak lead or lag (τ values) determined in the non–CS-aligned regression analysis (Fig. 1D2). The alignment on CSs involved a large number of occurrences, as the long duration of the random tracking trials (6–10 s) had an average of 8.06 ± 2.87 CSs per trial. These analyses allowed for visualization of the SS modulation in relation to climbing fiber input by generating firing maps from −200 before to 200 ms after CS occurrence for parameters determined to have significant encoding based on the non–CS-aligned regression analysis. Figure 2A presents an example of CS-coupled increase in SS sensitivity to VY. The firing maps reveal weak SS modulation with VY before CS occurrence (t = 0). Following CS discharge, the SS modulation with velocity greatly increases (Fig. 2A).

The CS-aligned SS firing and shifted behavior were also used to perform the CS-aligned linear regressions that quantified the changes in the SS representations before and after the CSs (Fig. 1D3). The strength and timing of SS modulation are reflected in the R² temporal profile (Fig. 2B), and the changes in SS sensitivity reflected in the β profile (Fig. 2C). The R² and β profiles (Fig. 2B,C) mirror the strong increase in VY encoding visualized in the SS firing maps. The significance of CS-coupled changes in encoding was assessed by comparing the difference between the mean R² for pre- and post-CS encoding (Fig. 2D, cyan bar) to a distribution obtained from 1000 profiles aligned to randomized CS times selected outside the real CS time windows, which provides a measure of the encoding changes occurring independent of the climbing fiber input (Fig. 2D, gray bars). Moreover, the skew of this random distribution can characterize the overall encoding stability of an individual cell. For this example, the change in encoding (R²_post − R²_pre = 0.38) shows the increase in modulation with VY falls far to the right of the noise distribution, exceeding the significance criterion of the mean ± 2 SDs (p < 0.05). Intriguingly, the distribution of encoding changes occurring outside the CS window skews negatively (−0.12 ± 0.12) in contrast to the CS-coupled increase. The CS-coupled increase in the SS encoding is followed by a significant change in VY (Fig. 2E). However, the significant change in VY occurs after the onset of encoding increase, demonstrating that the change in VY representation cannot be attributed to differences in kinematics before CS occurrence.

The SS firing rates are similar before and after CS discharge, with the exception of the inactivation period (Fig. 2F). Therefore, the change in SS encoding is not due to an alteration in firing rate but instead reflects an increase in sensitivity to VY, as demonstrated by the β profile in which the modulation with VY increases markedly following the CS. Finally, the change in encoding is not influenced by other CSs or CS rhythmicity in the ±200 ms window. The probability of another CS within this period is extremely low, with only a very few CSs occurring on the boundaries of the window, reaching a maximum probability of only 1%. Furthermore, there is little evidence of CS rhythmicity (Fig. 2G).

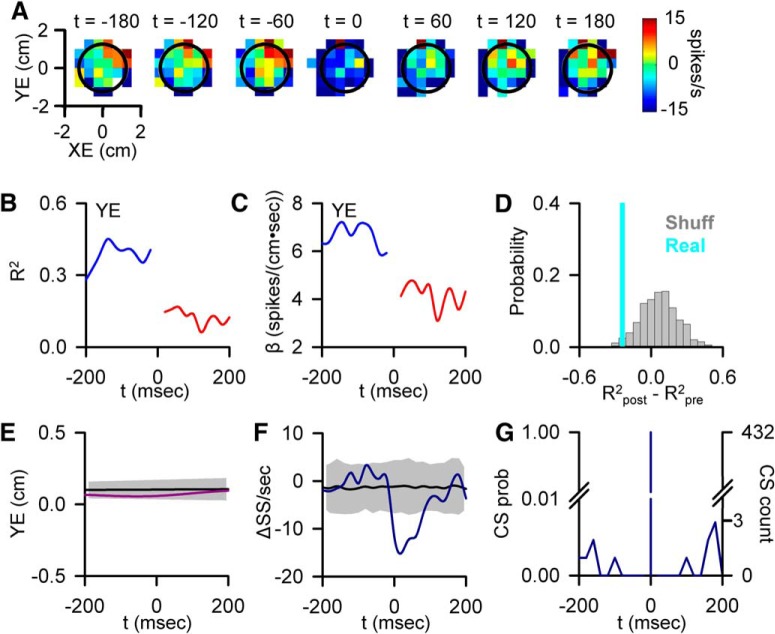
Both increases and decreases in SS encoding were observed for all the parameters evaluated. Figure 3 illustrates an example of a CS-coupled decrease in SS encoding for a Purkinje cell modulated with YE (Fig. 3A–D). Over the 200 ms before a CS, the firing maps show strong SS modulation with YE. After CS discharge, both the strength of the encoding and the sensitivity are significantly attenuated (Fig. 3B–D; R²_post − R²_pre = −0.26). As for the velocity example described above, encoding changes at randomized time points tend to oppose the CS-coupled changes in SS encoding, with a mean change of 0.07 ± 0.16. For this example, the change in encoding is not explained by any significant variations in behavior (Fig. 3E) or SS firing relative to CS (Fig. 3F). As in the previous example, the time course of the encoding change cannot be explained by other CSs in the ±200 ms window or CS rhythmicity (Fig. 3G).

Figure 3.

CS-coupled decrease in SS encoding. A, Firing maps of another Purkinje cell with a change in SS modulation with position errors (YE) relative to CS occurrence (t = 0). Black circle represents target edge. B, Encoding strength (R²) of YE before (blue trace) and after (red trace) CS discharge. C, Sensitivity (β) of the cell to YE, before (blue trace) and after (red trace) CS discharge. D, Magnitude of the CS-coupled change in SS encoding strength in the ±200 ms window (indicated by the light blue line) relative to the distribution of profiles aligned to randomized CS times selected outside the actual CS window (gray bars). E, CS-triggered average of YE (purple trace) relative to the YE variability from CS-shuffled ISIs (mean ± 3 SDs, gray region). F, CS-triggered average SS firing (blue trace) relative to the SS variability from CS-shuffled ISIs (mean ± 3 SDs, gray region) showing SS inactivation following CSs. G, Distribution of additional CSs in the −200 to 200 ms intervals centered on CS occurrence (left axis, CS probability; right axis, CS count).

In some Purkinje cells, the CS-coupled changes in SS encoding are characterized as a shift in the preferred area of the parameter workspace represented. For example, Figure 4A illustrates a Purkinje cell in which the SS firing is strongly modulated by X position in the pre-CS window. After CS occurrence, the SS modulation shifts with Y position strongly encoded. This change in SS modulation is due to a sharp decrease in X encoding (R²_post − R²_pre = −0.23, Fig. 4B,C) and sensitivity (Fig. 4E) and simultaneous increase in Y encoding (R²_post − R²_pre = 0.25) and sensitivity. As with the previous two examples, this shift in encoding cannot be explained by significant changes in either parameter (Fig. 4F), SS firing rates (Fig. 4D), or CS rhythmicity (Fig. 4G).

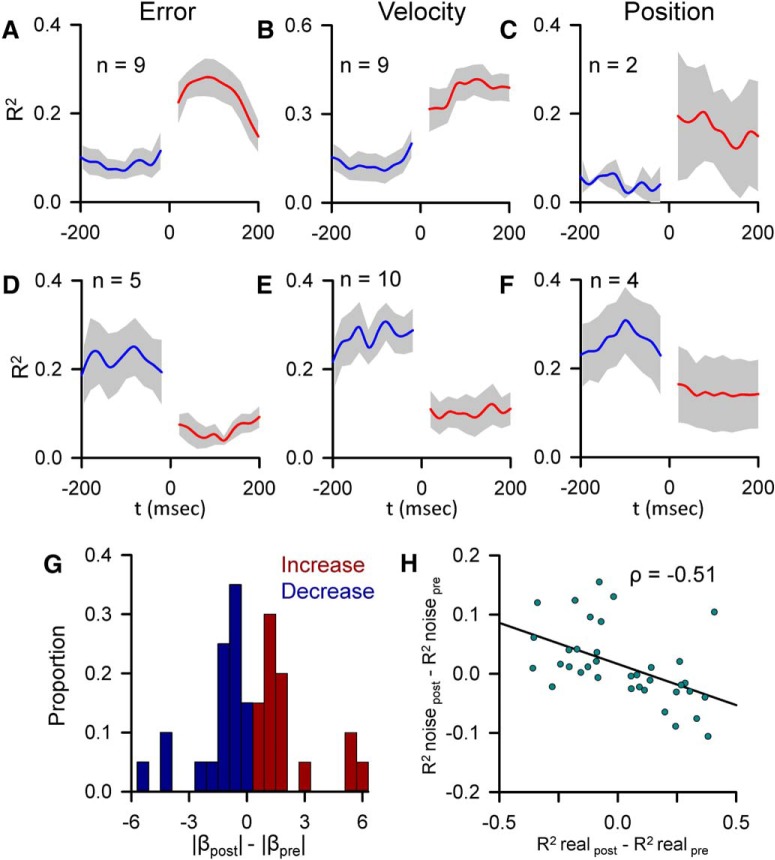
CS-coupled changes in Purkinje cell sensitivity to errors and kinematics

Changes in predictive and feedback SS kinematic and error encoding following a CS are relatively common, occurring in 22 of 40 Purkinje cells. The changes in the strength of encoding across the population were assessed by separately averaging the significantly increased and decreased R² profiles for error, position, and velocity (Fig. 5A–F). The population of R² profiles demonstrate that the transitions in SS encoding, both decreases and increases, are tightly timed to CS occurrence. Changes in SS sensitivity were quantified by calculating the difference between the mean absolute values of the regression coefficients both post- and pre-CS (Fig. 5G). All significant increases in encoding were associated with an increase in sensitivity (Fig. 5G, red bars), and all but one of the significant decreases in encoding were associated with a decrease in sensitivity (Fig. 5G, blue bars). The population summary indicates that most of the SS representations exhibit a positive or negative skew in the distribution of encoding changes not associated with CS discharge. As shown for the examples in Figures 2 and 3, the direction of CS-coupled encoding tends to oppose these average changes. Across the population, these encoding changes not associated with CS discharge show a significant negative correlation with the CS-coupled encoding changes (ρ = −0.51, p = 0.003) (Fig. 5H).

Figure 5.

Population summary of CS-coupled changes in encoding and sensitivity. A–F, Mean of the pre- and post-CS R² profiles for each parameter with a significant CS-coupled encoding change (blue represents pre-CS; red represents post-CS) ± SEM (gray areas). Increases and decreases in encoding are grouped separately. n indicates the number of profiles. G, Population distribution of changes in SS sensitivity with significant CS-coupled changes in encoding (blue bars represent encoding decreases; red bars represent encoding increases). Proportions for increases and decreases were computed separately. H, Distribution of the magnitude of CS-coupled encoding changes versus mean magnitude of encoding changes not associated with CS firing for all significant CS-coupled encoding changes across the population (n = 40). The Pearson correlation coefficient is included. Line indicates the significant trend of the distribution (p = 0.003).

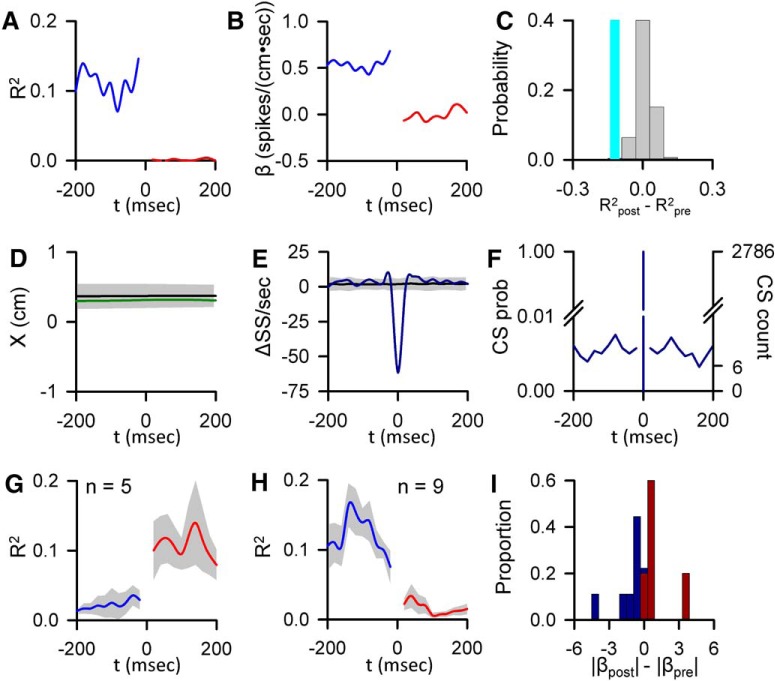
The CS-coupled changes in SS encoding described above (Figs. 2–5) are based on kinematic or position error signals encoded throughout the entire tracking period as determined by the non–CS-aligned linear regression analysis. We also examined CS-coupled encoding changes in the SS firing that did not meet the significance criteria for encoding in the non–CS-aligned regression analysis. In 32% of Purkinje cells (n = 13), climbing fiber discharge significantly alters the encoding of at least one parameter (Fig. 6), finding both increases (5 parameters) and decreases (9 parameters). Changes in signaling are not due to changes in pre- or post-CS discharge SS firing or CS rhythmicity (Fig. 6D–F), and increases and decreases in encoding are associated with increases and decreases in sensitivity, respectively (Fig. 6I). CS-coupled changes in encoding also tend to oppose encoding changes not associated with CS discharge. When combined with the CS-coupled changes in encoding described in Figures 2–5, this inverse relationship is significant (ρ = −0.498, p = 0.002).

Figure 6.

CS-coupled changes in encoding of parameters not initially determined to be significant. A, Encoding strength (R²) of X position before (blue trace) and after (red trace) CS occurrence for an example Purkinje cell. B, Sensitivity (β) of same cell to X, before (blue trace) and after (red trace) CS discharge. C, Magnitude of the CS-coupled change in SS encoding strength in the ±200 ms window (indicated by the light blue bar) relative to the distribution of profiles aligned to randomized CS times selected outside the real CS (gray bars). D, CS-triggered average of X (green trace) relative to the X variability from CS-shuffled ISIs (mean ± 3 SDs, gray region). E, CS-triggered average SS firing (blue trace) relative to the SS variability from CS-shuffled ISIs (mean ± 3 SDs, gray region). F, Distribution of additional CSs in the −200 to 200 ms intervals centered on CS occurrences (left axis, CS probability; right axis, CS count). G, H, Mean of R² profiles showing significant CS-coupled increases (G) and decreases (H) in encoding (mean ± SEM) with the number of profiles denoted by n. I, Population distribution of changes in SS sensitivity to for these parameters with significant CS-coupled changes in encoding (blue bars represent encoding decreases; red bars represent encoding increases).

Overall, CS discharge was followed by a significant alteration in 53 SS representations in 67% of Purkinje cells (n = 27), an average of ∼2 representations per neuron. The CS-coupled changes include 19 increases (18 Purkinje cells), and 18 decreases (16 Purkinje cells). In the remaining 16 profiles (8 Purkinje cells), the CS-coupled changes involved a paired increase and decrease, manifested as a shift in the preferred area of the parameter workspace represented (e.g., Fig. 4). Together, these results illustrate that CS-coupled changes in SS encoding are common during pseudo-random tracking.

CS modulation relative to behavior

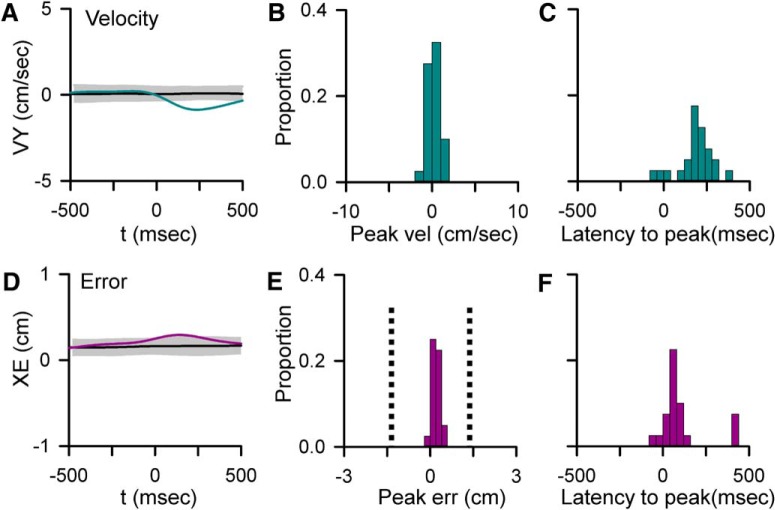
Given previous observations of task-evoked CS discharge (Gilbert and Thach, 1977; Kitazawa et al., 1998; Medina and Lisberger, 2008; Yang and Lisberger, 2014), we assessed the relationship between changes in kinematics and position errors and CS firing using spike-triggered averaging. A peak change in the CS-triggered average of behavior was considered statistically significant if it exceeded mean ± 3 SDs noise level as determined by shuffling the CS ISIs within a trial. Both the magnitude and timing of significant changes were determined (Fig. 7B,C,E,F). In 55% of Purkinje cells (n = 22), there is a significant change in behavior in relation to CS occurrence (4 cells with a change in only kinematics, 2 with only errors and 16 with both kinematics and errors). Intriguingly, the CS discharge is not driven by behavior, as the behavioral changes occur predominantly after CS discharge with a mean lag of 172.5 ± 98.65 ms for velocity and 100.9 ± 147.2 ms for errors (Fig. 7C,F). In only 9% of cases (n = 4 parameters) does the behavioral change occur before CS occurrence. Additionally, the magnitudes of CS-coupled changes are small compared with the overall behavioral variability, ranging from ±1.88 cm/s for velocity and ±0.64 cm for position error (Fig. 7B,E). These small changes in behavior, although significant, are not likely to explain the large changes in sensitivity observed in the SS encoding. Moreover, the transitions in encoding are tightly coupled to CS occurrence, whereas the behavioral changes occur predominantly after CS discharge. Together, these results suggest that neither the CSs nor the SS encoding changes are driven by position errors or changes in kinematics. Instead, climbing fiber discharge is predictive of changes in behavior that may reflect corrective adjustments made during tracking.

Figure 7.

Relationships between CS firing and behavior. A, D, Examples of significant CS-coupled changes in VY (A, blue trace) and XE (D, purple trace) as determined by comparison with mean CS-shuffled control (black trace) ±3 SDs (gray region). B, E, Distributions of peak changes in velocity (B) and error (E) in the 22 Purkinje cells with significant CS-coupled changes in behavior. E, Vertical dashed line indicates the target edge. C, F, Timing of peak changes in velocity (C) and error (F) illustrating that behavioral changes lag CSs.

Relationship between CS-coupled changes in SS encoding and behavior

An essential question is the potential influence of the observed CS-coupled changes in SS encoding on the behavior. Therefore, several analyses evaluated the relationship between CS-coupled modulation of SS encoding and changes in behavior. The first observation is that a CS-coupled change in SS encoding of behavior (e.g., velocity) is associated with a CS-coupled change in that behavior (e.g., velocity) in 38% of profiles (41% of cells). As described, 91% of these changes in behavior occur after the CSs. Therefore, in a large fraction of the neurons, SS encoding and changes in behavior are coupled.

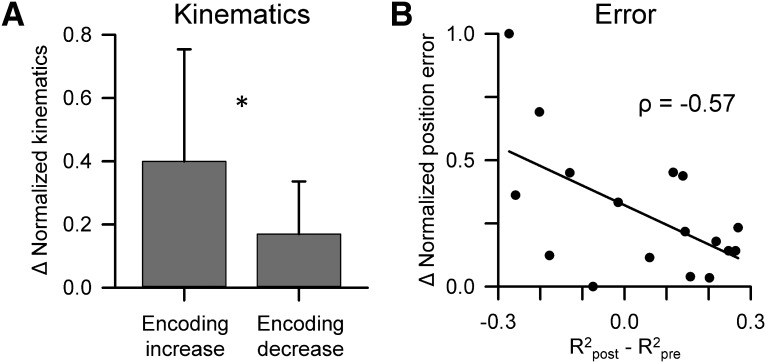
The next analysis was undertaken at the population level and assessed whether behavior changed in a consistent pattern following a CS-coupled change in SS encoding. For example, one possibility is that an increase in SS encoding of a kinematic parameter (e.g., VY) following CSs would be followed by a larger change in that parameter (e.g., VY) than for a decrease in the encoding of the same kinematic parameter. To test this possibility, we evaluated whether a significant CS-coupled change (i.e., increase or decrease) in SS encoding for a behavioral parameter was related to a change in behavior defined as the magnitude of the mean difference in behavior pre- versus post-CS (pre-CS time window: −500 to 0 ms, post-CS time window: 20 to 500 ms). The changes in magnitude were normalized to the maximum change for each parameter. For this analysis, we grouped the four kinematic parameters together because of the relatively small number of SS-encoding changes for any single parameter. The results show that changes in kinematics following CSs correlate with the SS encoding of kinematics with CS-coupled increases in SS encoding of a kinematic parameter (e.g., VY) associated with a significantly larger change in that parameter (e.g., VY) than for CS-coupled decreases (Fig. 8A; unpaired Student's t test, t = 2.61, p = 0.014).

Figure 8.

CS-coupled changes in SS encoding are associated with modulation of behavior. A, Mean ± SD normalized changes in the kinematic parameters (mean_post − mean_pre) for significant CS-coupled increases and decreases in SS encoding. *p < 0.05 (unpaired Student's t test). B, Distribution of all normalized changes in the position error parameters (mean_post − mean_pre) with the magnitude of significant CS-coupled changes in SS encoding. The Pearson correlation coefficient is included and the line depicts the significant trend of the distribution (p = 0.017).

We also observed a significant relationship between SS encoding changes and position errors using the same analysis described above. Even a stronger relation was uncovered, as CS-coupled changes in position error encoding are inversely correlated with position errors, such that the magnitude of performance error decreases as the SS encoding of error increases (Fig. 8B; Pearson correlation, ρ = −0.57, p < 0.05). Together, these results suggest that CS-coupled encoding changes are important for upcoming changes in both kinematics and error performance.

SS firing rates, variability, and CS rhythmicity do not contribute to encoding changes

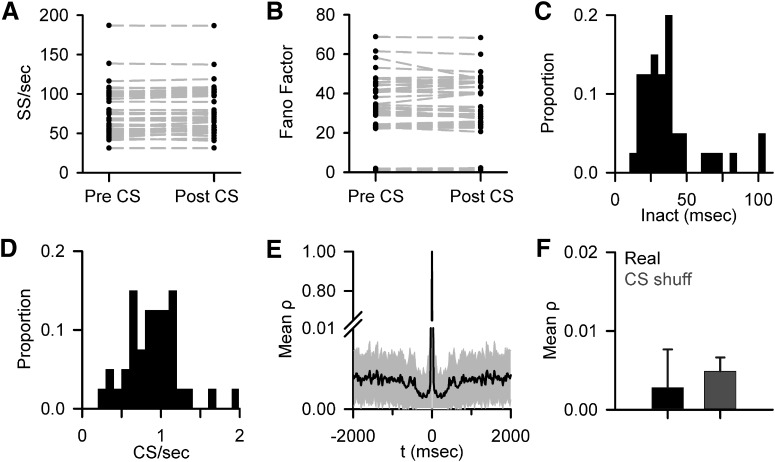
Because both short- and long-term changes in SS firing have been observed following CSs (Ebner et al., 1983; Loewenstein et al., 2005; Yartsev et al., 2009), we evaluated whether alterations in SS firing rates can account for the CS-coupled changes in encoding. The effect of climbing fiber input on the SS firing rates was evaluated over both ±200 and ±500 ms windows (with the post-CS window beginning after the mean ± SD of the inactivation period), determining whether at any time (20 ms bins) after a CS the SS firing differed from the pre-CS rates (mean ± 3 SDs). A change in SS firing was only observed in 5 Purkinje cells. However, the changes in SS firing were single 20 ms bin transient fluctuations in all but one of the Purkinje cells. Additionally, there was not a significant relationship between pre- and post-CS SS firing rate across the population (Fig. 9A). Also assessed was whether the CS discharge altered the SS variability based on the Fano factor, defined as the ratio of the variance of firing over mean firing. The Fano factor both before and after CS were determined using the two different time windows defined above. Significant differences in the Fano factor pre- versus post-CS occurrence were observed in only two Purkinje cells (p < 0.05, paired t test) in either window, suggesting that climbing fiber discharge has little effect on the variability of SS firing during pseudo-random tracking (Fig. 9B). Furthermore, both the increases and decreases in SS encoding persist well beyond the inactivation period (mean = 48.6 ± 85.7 ms; Fig. 9C), further demonstrating that CS-coupled changes in SS firing rates cannot underlie the changes in encoding.

Figure 9.

No evidence for CS-associated changes in SS firing properties or CS rhythmicity. A, Mean SS firing before and after CS discharge based on the 200 ms pre-CS and 200 ms post-CS windows (mean ± SD of the inactivation period) for 39 of 40 recorded Purkinje cells. As described in Materials and Methods, one cell was excluded due to high SS variability following the CS; however, this cell did not have significant SS encoding changes. B, Mean Fano factor pre- and post-CS using the same window in A for 39 of 40 recorded Purkinje cells. C, Distribution of mean SS inactivation periods after CS discharge (Inact) for all 40 Purkinje cells. D, Histogram of mean CS firing rate for all 40 Purkinje cells. E, Population average of CS discharge autocorrelation (mean ± SD). Note the discontinuous y-axis. F, Average maximum autocorrelation in the 8–12 Hz range for CS firing (Real) and randomly shuffled control data (CS shuff). Error bars indicate SD.

A major hypothesis is that CS firing is intrinsically rhythmic (8–12 Hz) and used to organize movement timing (Welsh et al., 1995; Lang et al., 1999; Llinás, 2013), raising the possibility that CS rhythmicity plays a role in the changes in SS encoding. To address whether CS rhythmicity is involved, we determined the autocorrelation of CS discharge for each Purkinje cell over a window of ±2000 ms, which encompasses the vast majority of CS firing with a mean rate of 0.85 ± 0.33 spikes/s (Fig. 9D). There are no significant secondary peaks at any lag or lead for any Purkinje cell, including in the 8–12 Hz range, as determined by comparison to the autocorrelation of randomized CS times. There is no CS rhythmicity in the population average (Fig. 9E). Additionally, the lack of CS rhythmicity in the 8–12 Hz range is evident by the low correlation coefficient (ρ < 0.005) and similarity to the shuffled results (Fig. 9F). As found for spontaneous activity in the awake monkey (Keating and Thach, 1995), there is no evidence for CS rhythmicity during pseudo-random tracking. Therefore, CS rhythmicity does not appear to play a role in the SS encoding changes.

Discussion

This study describes a novel function of climbing fiber input during online motor control. Following CS discharge, rapid increases or decreases occur in SS kinematic and error encoding. The CS-coupled changes in SS encoding are common and occur in all the parameters studied. Importantly, the encoding changes are not related to pre- or post-SS firing rates or variability, CS rhythmicity and firing rates, or the inactivation period. Instead, the powerful synaptic action of a climbing fiber on a Purkinje cell alters the encoding of subsequent parallel fiber inputs, changing the sensitivity to behaviorally relevant measures.

Pseudo-random tracking, CSs, and changes in SS encoding

Pseudo-random tracking allows for the examination of the interactions among CS discharge, SS firing, and behavior in which the correlations between parameters or learning are reduced. Accurate performance on this task requires continuously monitoring the salient behavioral parameters and adjusting for mismatches in hand movement relative to target movement (Hewitt et al., 2011; Popa et al., 2012). This task subverts overly learned, stereotypic behaviors, such as reaching and saccades, in which movement parameters are correlated (Paninski et al., 2004; Soetedjo et al., 2008). It is possible that, during more stereotypic movements, particular aspects of the behavior dominate the CS and SS modulation with little need to adjust the information in the SS firing. In contrast, pseudo-random tracking requires the monitoring of and altering the weights placed on multiple streams of continuously varying kinematic and error information. Therefore, the action of climbing fiber input on SS firing may be markedly different during low dimensional as opposed to high dimensional behaviors.

Intriguingly, in this task, CSs are not strongly driven by position errors or movement kinematics. Instead, the CSs consistently lead changes in behavior (Fig. 7A,D), a finding that is similar to an emerging view that CSs can provide predictive information (Ohmae and Medina, 2015; ten Brinke et al., 2015). In ∼41% of the cells in which the CSs preceded a change in kinematics or position error, the encoding of the parameter changed. This finding offers a link to behavior in which CSs are evoked in anticipation of a change in behavior, and there is a corresponding change in the encoding of the same parameter. In this manner, the change in SS sensitivity that follows CSs provides a way for PCs to dynamically focus on the most salient aspects to the behavior.

Changes in SS encoding are manifest as a change in sensitivity and not firing rate

Several studies demonstrate that climbing fiber input exerts long-term control over the SS firing rate of Purkinje cells (Colin et al., 1980; Montarolo et al., 1982; Cerminara and Rawson, 2004) and the reciprocal pattern of SS modulation to mossy fiber input (Graf et al., 1988; Simpson et al., 1995; Yakhnitsa and Barmack, 2006; Badura et al., 2013). However, the observations described here emphasize a short-term change in the SS encoding not related to SS firing rate. These encoding changes imply that a Purkinje cell responds differently to the same input following a CS. Similar to the gain-change and bistability hypotheses, the effects of a climbing fiber on a Purkinje cell's excitability alter its response to subsequent parallel fiber inputs (Ebner et al., 1983; Loewenstein et al., 2005; McKay et al., 2007; Yartsev et al., 2009). Also, similar to these previous hypotheses, the present findings show that a Purkinje cell changes its state and, therefore, the information present in the SS firing. However, in contrast, the large changes in the SS encoding are not associated with marked changes in the SS firing rate. Only a small number of Purkinje neurons exhibited altered firing rates following CS discharge and in those cells the duration of the change was brief (∼20 ms). Several mechanisms likely explain the lack of CS-coupled changes in SS firing rate. First, as noted in the Introduction, CS-coupled changes in SS firing rates are prominent in reduced or anesthetized preparations but not in the awake animal (Schonewille et al., 2006; Engbers et al., 2013). Second, a large fraction of SS discharge is intrinsic, with parallel fiber input modulating this intrinsic discharge (Raman and Bean, 1997). Third, both increases and decreases in SS encoding occur in single cells. Therefore, in the awake animal, the net effect of climbing fiber input on the SS firing rate is limited. One interpretation of the constant SS firing rate is that climbing fiber activation reallocates the overall bandwidth of a Purkinje cell, with encoding decreases in some parameters to allow increases in others. This reallocation of the bandwidth is consistent with the nearly equal number and magnitude of the increases and decreases (Fig. 5) and the paired increases and decreases in encoding observed in many cells (Fig. 4).

Bidirectional changes in SS encoding

Several mechanisms could explain why both increases and decreases in SS encoding occur. Recent studies show that climbing fiber activation of a Purkinje cell is not all-or-none but instead varies with the properties of the presynaptic climbing fiber burst, the excitability state of the Purkinje cell, and the local inhibitory circuitry. The number of spikes in the incoming climbing fiber modulates the CS burst pattern, dendritic Ca²⁺ spiking and parallel fiber-Purkinje cell synaptic plasticity (Mathy et al., 2009; Bazzigaluppi et al., 2012). Postsynaptically, the Ca²⁺ response to climbing fiber input varies with stimulus properties and is enhanced when triggered by an unexpected sensory event, suggesting that the level of parallel fiber input modulates the Ca²⁺ response (Najafi et al., 2014a, b). The amplitude of the Ca²⁺ transients depends on the location in the dendritic tree, local membrane potential, and concurrent parallel fiber input (Kitamura and Häusser, 2011). GABAergic inhibition generated by cerebellar interneurons locally modifies the conductance changes and Ca²⁺ fluxes evoked by climbing fiber input (Callaway et al., 1995; Kitamura and Häusser, 2011). Decreases in gain occur following a CS when high Ca²⁺ levels reduce parallel fiber input by activation of BK channels and/or endocannabinoid release (Brenowitz and Regehr, 2003; Rancz and Häusser, 2010) and modeling suggests that gain increases occur with local increases in Ca²⁺ (Forrest, 2014). These same sources of variability in the response to climbing fiber input determine whether long-term facilitation or depression results at parallel fiber-Purkinje cell synapses (Coesmans et al., 2004; Medina and Lisberger, 2008; Rasmussen et al., 2013). Also, the timing of climbing fiber discharge may differentially modulate parallel fiber input and thereby determine the direction of synaptic potentiation (Piochon et al., 2012; Suvrathan et al., 2016). Therefore, multiple factors regulate a Purkinje cell's response to climbing fiber input that potentially underlie the bidirectional SS encoding changes.

Do the CSs cause the change in SS encoding?

The present study does not prove unequivocally that the CSs produce the change in SS sensitivity. However, two findings support this view. First, the changes in SS encoding are tightly coupled to and follow the occurrence of a CS, both in individual Purkinje cells (Figs. 2–4) and in the population (Fig. 5). Second, the CSs are rarely preceded by behavioral changes, also arguing against the notion that an unknown factor is driving the sensitivity recalibration (Fig. 7). However, these observations do not imply that the encoding changes are not related to the prior status of the SS representation in Purkinje cells. The direction of CS-coupled encoding changes tends to be in the opposite direction to the state of SS encoding not associated with CS discharge, with CS-coupled increases in encoding associated with net decreases in the shuffled data, and vice versa (Fig. 5H). Together, these observations suggest a role in online motor control in which the CS actively controls the sensitivity of a Purkinje cell, either in anticipation of a change in behavior or in response to an encoding state that is suboptimal.

CS-coupled changes in SS encoding reflect the need to adjust to constantly changing conditions

The motor system produces highly accurate movements under constantly changing conditions and goals. To achieve this level of task performance, the motor system processes and uses different information, including kinematics and errors. For example, the motor system as needed can include or exclude an internal gravitation model from estimations of target motion (Zago et al., 2004). That the cerebellum engages in switching among and using multiple representations can be inferred from the temporal and spatial overlap of activation patterns when subjects use different tools to perform similar tasks (Imamizu et al., 2004). Pseudorandom tracking requires a dynamic representation of behavior with constantly varying target kinematics and a continual effort to minimize performance errors. Consistent with the CSs playing a role, CS-coupled increases in SS encoding of kinematics coincide with larger changes in kinematics than decreases in SS encoding. Furthermore, CS-coupled increases in error encoding correlate with decreases in performance errors. These observations suggest that climbing fiber input adjusts SS encoding in a manner consistent with upcoming changes in behavior. The changes in SS encoding show that the motor information at the level of a single Purkinje cell is highly dynamic, and suggest that climbing fiber input is continually updating the encoding state of Purkinje cells.