Integrating Gene Expression with Summary Association Statistics to Identify Genes Associated with 30 Complex Traits

Abstract

Although genome-wide association studies (GWASs) have identified thousands of risk loci for many complex traits and diseases, the causal variants and genes at these loci remain largely unknown. Here, we introduce a method for estimating the local genetic correlation between gene expression and a complex trait and utilize it to estimate the genetic correlation due to predicted expression between pairs of traits. We integrated gene expression measurements from 45 expression panels with summary GWAS data to perform 30 multi-tissue transcriptome-wide association studies (TWASs). We identified 1,196 genes whose expression is associated with these traits; of these, 168 reside more than 0.5 Mb away from any previously reported GWAS significant variant. We then used our approach to find 43 pairs of traits with significant genetic correlation at the level of predicted expression; of these, eight were not found through genetic correlation at the SNP level. Finally, we used bi-directional regression to find evidence that BMI causally influences triglyceride levels and that triglyceride levels causally influence low-density lipoprotein. Together, our results provide insight into the role of gene expression in the susceptibility of complex traits and diseases.

Introduction

Although genome-wide association studies (GWASs) have identified tens of thousands of common genetic variants associated with many complex traits,¹ with some notable exceptions,^{2, 3} the causal variants and genes at these loci remain unknown. Multiple lines of evidence have shown that GWAS risk variants co-localize with genetic variants that regulate expression—i.e., expression quantitative trait loci (eQTLs).⁴ This suggests that a substantial proportion of GWAS risk variants influence complex traits by regulating expression levels of their target genes.^{4, 5, 6, 7} Analyses of genotype, phenotype, and gene expression measurements from multiple tissues in the same set of individuals can directly investigate this plausible chain of causality. However, doing so is challenging because of cost and tissue availability; therefore, GWAS and eQTL datasets remain largely independent (i.e., no overlapping subjects).^{8, 9} Recent work has shown that one way to integrate GWAS and eQTL data is to predict gene expression levels for GWAS samples and then test for association between the predicted expression and traits.^{10, 11, 12} This approach, referred to as transcriptome-wide association study (TWAS), can increase power over GWAS when the causal mechanism includes genetic variants that regulate the expression of susceptibility genes. TWAS benefits from a lower multiple-testing burden by probing several thousands of genes, whereas GWAS probes several million SNPs. Although TWAS can also be performed with measured gene expression levels directly, using predicted gene expression has several benefits. First, expression measurements are usually not available in GWAS data. Second, predicted gene expression removes environmental noise by focusing on the genetically regulated component, which can increase statistical power. Third, using the predicted expression to test for association can eliminate potential confounding from reverse causation, where traits affect gene expression levels.^{10, 11} However, compared with GWAS, TWAS is underpowered when risk is not mediated through expression or when expression data are not available in the right tissue.

In this work, we introduce methods for estimating the genetic correlation between gene expression and a complex trait from summary GWAS and eQTL data. We utilize the local (cis) genetic variation near a gene (i.e., ±0.5 Mb around the transcription start site [TSS]) to estimate the correlation in the genetic effects between gene expression and the trait. We show that under this framework, TWAS can be viewed as a test for non-zero genetic covariance between expression and a trait from summary association data. In addition to identifying susceptibility genes, the predicted expression can also be used for estimating the genome-wide genetic correlation between pairs of complex traits at the level of predicted expression. This is analogous to computing genome-wide genetic correlation between complex traits,¹³ whereby correlations are determined over predicted gene expression effects rather than SNP effects, and can give insights into the component of genetic correlation mediated through expression. We demonstrate through extensive simulations that our approach is approximately unbiased and well calibrated under the null and slightly conservative when true correlation is near the boundaries. Finally, we utilize estimated effects of predicted expression within a bi-directional regression approach¹⁴ to investigate putative causal direction for pairs of complex traits that are genetically correlated.

We analyze summary statistics from 30 GWASs spanning 2.3 million phenotype measurements^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28} jointly with 45 expression panels^{8, 29, 30, 31, 32, 33, 34} sampled from more than 35 tissues to gain insight into the role of expression in the etiology of complex traits. First, we test each gene-tissue pair across 45 panels to perform a multi-tissue TWAS for each of the 30 traits to identify 1,196 gene associations. For example, at four independent loci, we find 11 genes that do not overlap a genome-wide significant SNP for educational years. Notably, all four loci were replicated in a recent, larger GWAS for educational years.³⁵ Second, we identify 43 pairs of traits showing a genome-wide-significant genetic correlation at the level of predicted expression. Overall, the predicted-expression correlation was highly concordant with SNP-level genetic correlation from cross-trait linkage disequilibrium (LD) score regression, which suggests that a large component of genetic correlation between complex traits is driven by local regulation of gene expression. Finally, we use our bi-directional analysis to provide evidence of putative causal effects between pairs of these traits. Overall, our results shed light on shared biological mechanisms responsible for susceptibility to disease and complex traits, as well as potential downstream effects between traits.

Material and Methods

Datasets

We used summary association statistics from 30 large-scale (n = 20,000 subjects) GWASs, including various anthropometric^{15, 27, 28} (body mass index [BMI], femoral neck bone mineral density [BMD], forearm BMD, lumbar spine BMD, and height), hematopoietic^{23, 25, 26} (hemoglobin, HbA_1c, mean cell hemoglobin [MCH], MCH concentration, mean cell volume, number of platelets, packed cell volume, and red blood cell count), immune-related^{17, 19} (Crohn disease [OMIM: 266600], inflammatory bowel disease [OMIM: 266600], ulcerative colitis [OMIM: 266600], and rheumatoid arthritis [OMIM: 180300]), metabolic^{16, 20, 22, 24} (age of menarche, fasting glucose, fasting insulin, high-density lipoprotein [HDL], HOMA-B, HOMA-IR, low-density lipoprotein [LDL], triglycerides [TG], type 2 diabetes [OMIM: 125853], and total cholesterol [TC] levels), neurological¹⁸ (schizophrenia [OMIM: 181500]), and social²¹ (college and educational attainment) phenotypes (see Table S1). We removed SNPs that were strand ambiguous or had a minor allele frequency (MAF) ≤ 1% (see Table S1).

Gene expression data from RNA sequencing data were obtained from the CommonMind Consortium²⁹ (brain, n = 613), the Genotype-Tissue Expression Project⁸ (GTEx; 41 tissues; see Table S2 for sample size per tissue), and the Metabolic Syndrome in Men study^{31, 32} (adipose, n = 563). Expression microarray data were obtained from the Netherlands Twins Registry³⁴ (NTR; blood, n = 1,247), and the Young Finns Study^{30, 33} (YFS; blood, n = 1,264).

Performing TWAS with GWAS Summary Statistics

We estimated SNP heritability for observed expression levels partitioned into cis-$h_{\text{g}}^2$ (1 Mb region surrounding the TSS) and trans-$h_{\text{g}}^2$ (rest of genome) components. We used the AI-REML algorithm implemented in Genome-wide Complex Trait Analysis (GCTA),³⁶ which allows estimates to fall outside of the (0, 1) boundaries to maintain unbiasedness. To control for confounding, we included batch variables and the top 20 principal components estimated from genome-wide SNPs. Genes with significant cis-heritability in expression data were used for prediction (cis-$h_{\text{g}}^2$ p < 0.05 in a likelihood ratio test between the cis-only and joint models). The average number of genes with significant cis-$h_{\text{g}}^2$ across expression studies was 816 (min = 70 genes from GTEx small intestine samples; max = 3,704 genes from the YFS).

We performed 45 TWASs for each of the 30 GWASs;¹¹ for each trait, we used Bonferroni correction for all gene-tissue pairs tested (see Table S2). In brief, we estimated the strength of association between the predicted expression of a gene and a complex trait (z_TWAS) as a function of the vector of GWAS summary Z scores at a given cis-locus, ${\mathit{z}}_{\text{T}}^{\mathit{\text{'}}}$ (i.e., vector of SNP association Wald statistics), and the LD-adjusted weight vector learned from the gene expression data, w_GE, as

$$z_{\text{TWAS}}=\frac{{\mathit{w}}_{\text{GE}}^{\text{'}}{\mathit{z}}_{\text{T}}}{\sqrt{\text{var}\left({\mathit{w}}_{\text{GE}}^{\text{'}}{\mathit{z}}_T\right)}}=\frac{{\mathit{w}}_{\text{GE}}^{\text{'}}{\mathit{z}}_{\text{T}}}{\sqrt{{\mathit{w}}_{\text{GE}}^{\text{'}}\mathit{V}{\mathit{w}}_{\text{GE}}}},$$

where V is a covariance matrix across SNPs at the locus (i.e., LD). We estimated w_GE by using GBLUP³⁷ from eQTL data and computed $z_{\text{TWAS}}$ by using GWAS summary data for all 30 traits and the ∼36,000 gene expression measurements across all studies. We removed all loci in the human leukocyte antigen (HLA) region as a result of complex LD patterns.

Estimating the Proportion of Trait Variance Explained by Predicted Expression

We use the LD score regression^{38, 39} approach described in Guseve et al.¹¹ to quantify the heritability explained by predicted expression for a complex trait (denoted here as $h_{\text{GE}}^2$). The expected ${\chi }^2$ statistic under a polygenic trait is $E\left[{\chi }^2\right]=1+(N_{\text{T}}\ell /M)h_{\text{GE}}^2+N_{\text{T}}a$, where $N_{\text{T}}$ is the number of individuals in the GWAS, M is the number of genes, $\ell$ is the LD score, and $a$ is the effect of population structure. We estimate $\ell$ for each gene by predicting expression for 503 European samples in 1000 Genomes⁴⁰ by using the GBLUP weights (see above) and then computing sample correlation. For each trait, we perform LD score regression by using $z_{\text{TWAS}}^2$ (which follows a ${\chi }^2$ distribution asymptotically) to infer $h_{\text{GE}}^2$. We estimate heritability for each expression study separately to account for varying sample sizes and repeated gene measurements.

Estimating Genetic Correlation of Expression and Complex Traits from Summary Data

Let expression and traits be modeled as a linear function of the genotypes in a ∼1 Mb locus flanking the gene: ${\mathit{y}}_{\text{GE}}=\mathit{X}{\mathit{\beta }}_{\text{GE}}+{\mathbf{ϵ}}_{\text{GE}}$ and ${\mathit{y}}_{\text{T}}=\mathit{X}{\mathit{\beta }}_{\text{T}}+{\mathbf{ϵ}}_{\text{T}}$, where $\mathit{X}$ is the standardized genotype matrix, ${\mathit{\beta }}_{\text{GE}}$ and ${\mathit{\beta }}_{\text{T}}$ are the standardized effects for expression and traits, respectively, and ${\mathbf{ϵ}}_{\text{GE}}$ and ${\mathbf{ϵ}}_{\text{T}}$ are the environmental noise for expression and traits, respectively. The local covariance between expression and complex traits is

$$\text{cov}\left({\mathit{y}}_{\text{GE}},{\mathit{y}}_{\text{T}}\right)=\text{cov}\left(\mathit{X}{\mathit{\beta }}_{\text{GE}}+{\mathbf{ϵ}}_{\text{GE}},\mathit{X}{\mathit{\beta }}_{\text{T}}+{\mathbf{ϵ}}_{\text{T}}\right)={\mathit{\beta }}_{\text{GE}}^{\text{'}}\text{cov}\left(\mathit{X},\mathit{X}\right){\mathit{\beta }}_{\text{T}}+\text{cov}\left({\mathbf{ϵ}}_{\text{GE}},{\mathbf{ϵ}}_{\text{T}}\right)={\mathit{\beta }}_{\text{GE}}^{\text{'}}\mathit{V}{\mathit{\beta }}_{\text{T}}+\text{cov}\left({\mathbf{ϵ}}_{\text{GE}},{\mathbf{ϵ}}_{\text{T}}\right),$$

where $\mathit{V}$ is the LD matrix. If no individuals are shared between studies, then $\text{cov}\left({\mathbf{ϵ}}_{\text{GE}},{\mathbf{ϵ}}_{\text{T}}\right)=0$ (as in eQTL studies and GWASs). The local genetic correlation between expression and traits can be computed as

$${\rho }_{\text{g},\text{local}}=\frac{{\mathit{\beta }}_{\text{GE}}^{\text{'}}\mathit{V}{\mathit{\beta }}_{\text{T}}}{\sqrt{h_{\text{g},\text{local}}^2\left(\text{GE}\right)}\sqrt{h_{\text{g},\text{local}}^2\left(\text{T}\right)}},$$

where $h_{\text{g},\text{local}}^2\left(\text{GE}\right)$ and $h_{\text{g},\text{local}}^2\left(\text{T}\right)$ are the local SNP heritability⁴¹ for expression and traits, respectively, estimated at the locus. However, this requires knowledge of the true effect sizes. Given association statistics z_T, we estimate an LD-adjusted effect size as ${\hat{\mathit{\beta }}}_{\text{T}}=\frac{1}{\sqrt{N_{\text{T}}}}{\mathit{V}}^{-1}{\mathit{z}}_{\text{T}}$. Hence, an estimate of the local genetic covariance⁴² is given by

$${\hat{\mathit{\beta }}}_{\text{GE}}^{\text{'}}\mathit{V}{\hat{\mathit{\beta }}}_{\text{T}}=\frac{1}{\sqrt{N_{\text{GE}}}\sqrt{N_{\text{T}}}}\left({\mathit{z}}_{\text{GE}}^{\text{'}}{\mathit{V}}^{-1}\right)\mathit{V}\left({\mathit{V}}^{-1}{\mathit{z}}_{\text{T}}\right)={\hat{\mathit{b}}}_{\text{GE}}^{\text{'}}{\mathit{V}}^{-1}{\hat{\mathit{b}}}_{\text{T}},$$

where ${\hat{\mathit{b}}}_{\text{GE}}$ and ${\hat{\mathit{b}}}_{\text{T}}$ are the marginal (i.e., LD-unadjusted) standardized effect-size estimates.^{41, 43} It follows that

$$\frac{1}{\sqrt{N_{\text{T}}}}{z}_{\text{TWAS}}=\frac{1}{\sqrt{N_{\text{T}}}}\frac{{\hat{\mathit{\beta }}}_{\text{GE}}^{\text{'}}{\mathit{z}}_{\text{T}}}{\sqrt{\text{var}\left({\hat{\mathit{\beta }}}_{\text{GE}}^{\text{'}}{\mathit{z}}_{\text{T}}\right)}}=\frac{{\hat{\mathit{b}}}_{\text{GE}}^{\text{'}}{\mathit{V}}^{-1}{\hat{\mathit{b}}}_{\text{T}}}{\sqrt{h_{\text{g},\text{local}}^2\left(\text{GE}\right)}}={\rho }_{\text{g},\text{local}}\sqrt{h_{\text{g},\text{local}}^2\left(\text{T}\right)}.$$

We standardize this estimate to obtain our final local genetic correlation estimate as

$${\hat{\rho }}_{\text{g},\text{local}}=\frac{z_{\text{TWAS}}}{\sqrt{N_{\text{T}}\times h_{\text{g},\text{local}}^2\left(\text{T}\right)}}.$$

In practice, we use the variance explained by the local index SNP (i.e., smallest p value) as a proxy for $h_{\text{g},\text{local}}^2\left(\text{T}\right)$.

Genetic Correlation between Traits at the Level of Predicted Expression

Consider a simple model where the genetic component of a trait can be decomposed into genetic effects that are mediated through cis-gene expressions of k genes plus genetic effects not mediated through expression at other loci in the genome:

$${\mathit{y}}_{\text{T}}=\sum _{i=1}^k\left({\mathit{X}}_i{\mathit{\beta }}_{\mathbf{G}{\mathbf{E}}_{\mathit{i}}}\right){\alpha }_i+{\mathit{X}}_{\mathbf{a}\mathbf{l}\mathbf{t}}{\mathit{\beta }}_{\mathbf{a}\mathbf{l}\mathbf{t}}+{\mathbf{ϵ}}_{\text{T}},$$

where ${\mathit{X}}_{\mathit{i}}$ is a vector of genotypes at the cis-locus of gene i, ${\mathit{\beta }}_{{\text{GE}}_i}$ is the casual eQTL effect vector for gene i, ${\alpha }_i$ is the direct effect of gene expression on a trait, and ${\mathit{X}}_{\mathbf{a}\mathbf{l}\mathbf{t}}$ and ${\mathit{\beta }}_{\mathbf{a}\mathbf{l}\mathbf{t}}$ refer to the genotype and causal effects, respectively, of variants not mediated through expression. We define the genome-wide genetic correlation at the level of expression between two complex traits as the correlation across the gene effects: ${\rho }_{\text{GE}}=\text{cor}\left({\alpha }_{{\text{T}}_1},{\alpha }_{{\text{T}}_2}\right)$. In practice, we do not know $\alpha$, but we can estimate it as

$$\hat{\alpha }=\frac{\text{cov}\left(\mathit{X}{\mathit{\beta }}_{\text{GE}},{\mathit{y}}_{\text{T}}\right)}{\text{var}\left(\mathit{X}{\mathit{\beta }}_{\text{GE}}\right)}=\frac{{\mathit{\beta }}_{\text{GE}}^{\text{'}}\mathit{V}{\mathit{\beta }}_{\text{T}}}{h_{\text{g},\text{local}}^2\left(\text{GE}\right)}={\hat{\rho }}_{\text{g},\text{local}}/\frac{\sqrt{h_{\text{g},\text{local}}^2\left(\text{GE}\right)}}{\sqrt{h_{\text{g},\text{local}}^2\left({\mathit{y}}_{\text{T}}\right)}}$$

to obtain an estimate of expression correlation by using predicted expression $\left({\hat{\rho }}_{\text{GE}}\right)$. In practice, we use the standardized estimates of $\hat{\alpha }$, which are proportional to ${\hat{\rho }}_{\text{g,local}}$. Unlike SNP-based genetic correlation $\left({\rho }_{\text{g}}\right)$, which captures genetic correlation across all common variants in the genome, ${\rho }_{\text{GE}}$ captures only the component of genetic correlation driven by cis genetic effects on expression (see Figure 1). For instance, a pair of traits with highly correlated effects in cis-regions but weakly correlated effects in trans-regions will result in ${\rho }_{\text{GE}}>{\rho }_{\text{g}}$. In the absence of large trans-eQTL effects, we expect ${\rho }_{\text{GE}}\approx {\rho }_{\text{g}}$. Furthermore, because ${\rho }_{\text{GE}}$ accounts for only the shared effect from predicted expression, any genetic effect on a trait not driven through expression in the measured eQTL data will not be represented in ${\rho }_{\text{GE}}$. We test for significance by assuming ${\hat{\rho }}_{\text{GE}}\sqrt{\left(M-2)/(1-{\hat{\rho }}_{\text{GE}}^2\right)}\sim t\left(M-2\right)$, where $M$ is the number of genes and t is the t distribution with M − 2 degrees of freedom. This procedure requires the effects of $M$ genes on the trait to be independent, which could be violated in practice; hence, we compute ${\hat{\rho }}_{\text{GE}}$ by using one gene per 1 Mb locus.

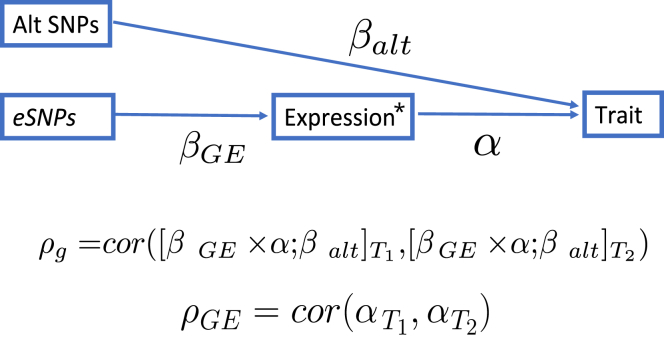
Figure 1.

Causal Diagram Illustrating the Genetic Component of a Trait

The total effect of SNPs on a trait can be partitioned into components that are mediated through cis-regulated (i.e., predicted, indicated by an asterisk) gene expression $\left({\beta }_{\text{GE}}\times \alpha \right)$ or through alternative pathways $\left({\beta }_{\text{alt}}\right)$. In contrast to ${\rho }_{\text{g}}$, which quantifies the correlation of the total SNP effects between two traits (${\beta }_{\text{GE}}\times \alpha$; ${\beta }_{\text{alt}}$), ${\rho }_{\text{GE}}$ focuses exclusively on the effects of cis-regulated gene expression (α).

Estimating Putative Casual Relationships between Pairs of Traits

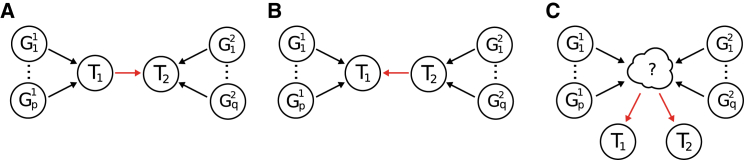
To glean insight into the underlying causal relationship between pairs of traits, we perform a bi-directional regression¹⁴ and estimate two different values of ${\rho }_{\text{GE}}$ by varying gene sets. Before describing the approach, we first review several causal models that explain non-zero ${\rho }_{\text{GE}}$ between two traits (see Figure 2). Models A and B depict causal relationships in which the effects of a gene set are mediated by one trait on the other. We can formally state model A (without loss of generality for B). Let trait 1 (T₁) be defined as ${\mathit{y}}_{{\text{T}}_1}={\mathit{G}}_{{\text{T}}_1}{\mathit{\beta }}_{{\text{T}}_1}+{\mathbf{ϵ}}_{{\text{T}}_1}$, where ${\mathit{G}}_{{\text{T}}_1}$ denotes the matrix of predicted expression at the causal genes, ${\mathit{\beta }}_{{\text{T}}_1}$ is the effect size, and ${\mathbf{ϵ}}_{{\text{T}}_1}$ is environmental noise. We define trait 2 (T₂) as

$${\mathit{y}}_{{\text{T}}_2}={\mathit{y}}_{{\text{T}}_1}{\mathit{\gamma }}_{{\text{T}}_1}+{\mathit{G}}_{{\text{T}}_2}{\mathit{\beta }}_{{\text{T}}_2}+{\mathbf{ϵ}}_{{\text{T}}_2}={\mathit{G}}_{{\text{T}}_1}{\mathit{\beta }}_{{\text{T}}_1}{\mathit{\gamma }}_{{\text{T}}_1}+{\mathit{G}}_{{\text{T}}_2}{\mathit{\beta }}_{{\text{T}}_2}+{\mathbf{ϵ}}_{{\text{T}}_2^{\text{'}}},$$

where ${\mathit{\gamma }}_{{\text{T}}_1}$ is the causal effect of ${\text{T}}_1$ on ${\text{T}}_2$, ${\mathit{G}}_{{\text{T}}_2}$ and ${\mathit{\beta }}_{{\text{T}}_2}$ are the remaining causal genes and their effects, respectively, for ${\text{T}}_2$, and ${\mathit{ϵ}}_{{\text{T}}_2^{\text{'}}}$ is the combined environment component. Under model A, the causal gene set for ${\text{T}}_1$ will have a non-zero effect on ${\text{T}}_2$ (i.e., ${\mathit{\gamma }}_{{\text{T}}_1}\ne 0$); however, if ${\text{T}}_1$ does not cause ${\text{T}}_2$, this effect will be zero given that unrelated genes have no downstream effect. Bi-directional regression provides a test to distinguish between models A and B by regressing estimated effect sizes for gene sets under model A (i.e., ${\mathit{\beta }}_{{\text{T}}_1}\sim {\mathit{\beta }}_{{\text{T}}_1}{\mathit{\gamma }}_{{\text{T}}_1}$) and comparing to estimates under model B (i.e., ${\mathit{\beta }}_{{\text{T}}_2}\sim {\mathit{\beta }}_{{\text{T}}_2}{\mathit{\gamma }}_{{\text{T}}_2}$). Because the causal gene sets for each trait are unknown, we use their identified susceptibility genes as a proxy. We estimate ${\rho }_{\text{GE}}$ by conditioning on the gene set for trait $i$ and denote its value as ${\rho }_{j|i}$. We repeat this procedure by ascertaining the gene set for trait $j$ to obtain ${\rho }_{i|j}$. We perform a Welch’s t test⁴⁴ to determine whether estimates of ${\rho }_{i|j}$ and ${\rho }_{j|i}$ are significantly different, thus providing evidence consistent with a causal direction. To minimize spurious results, we require at least ten genes for estimation in each conditional test. This approach mirrors bi-directional regression analyses of estimated SNP effects on two complex traits.^{45, 46} We stress that although a bi-directional approach is capable of rejecting model A in favor of model B (or vice versa), it cannot rule out model C, in which a shared pathway (or set of pathways) drives both traits independently (see Figure 2).

Figure 2.

Illustration of Several Causal Models That Explain Expression Correlation for Traits 1 and 2 Given Their Causal Gene Sets

(Model A) Trait 1 directly influences trait 2. In this case, the effect of genes $G_1^1,\dots ,G_p^1$ on trait 2 is mediated by trait 1, which implies ${\left\{G_i^1\right\}}_{i=1}^p\mathrm{⊊}{\left\{G_i^2\right\}}_{i=1}^q$.

(Model B) Trait 2 directly influences trait 1. Similarly, the effect of genes $G_1^2,\dots ,G_q^2$ on trait 1 is mediated by trait 2, which implies ${\left\{G_i^2\right\}}_{i=1}^q\mathrm{⊊}{\left\{G_i^1\right\}}_{i=1}^p$.

(Model C) Traits 1 and 2 are influenced independently through an unobserved trait or traits.

Simulation Framework

We simulate gene expression levels by using real genotype data measured in 503 European individuals from the 1000 Genomes Project.⁴⁰ Given a gene locus, we generate expression levels under the linear model E = Xw + $\mathbf{ϵ}$, where E is a gene expression vector of length N, X is the N × 2 mean-centered and variance-standardized genotype matrix over two randomly selected SNPs in the locus, w is the causal effect, and $\mathbf{ϵ}$ is the environmental noise. We sample effect sizes ${\mathit{w}}_i\sim \text{N}\left(0,\left[h_{\text{g}}^2/2\right]\right)$ for i = 1 and 2 and noise from a normal distribution to yield $h_{\text{g}}^2=0.1$ (consistent with what we observe in real gene expression data). We consider only SNPs with a MAF ≥ 0.01 and Hardy-Weinberg equilibrium deviation p ≥ 1 × 10⁻⁵. We simulate a complex trait as a linear function of predicted gene expression for k = 100 genes, given by $\mathit{y}={\sum }_{i=1}^k\left({\mathit{X}}_i{\mathit{w}}_i\right){\alpha }_i+\mathit{ϵ}$, where X_iw_i is the predicted expression of the i^th gene with effect sizes ${\alpha }_i\sim \text{N}\left(0,h_{\text{GE}}^2/k\right)$. For simulations involving ${\rho }_{\text{GE}}$, we simulate the two traits y₁ and y₂ by using the same process, except effects for the i^th gene are drawn from a bivariate normal distribution:

$$\left[\begin{array}{c}{\alpha }_{i,1}\\ {\alpha }_{i,2}\end{array}\right]\sim \text{MVN}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\sigma }_{\alpha ,1}^2& {\rho }_{\text{GE}}{\sigma }_{\alpha ,1}{\sigma }_{\alpha ,2}\\ {\rho }_{\text{GE}}{\sigma }_{\alpha ,1}{\sigma }_{\alpha ,2}& {\sigma }_{\alpha ,2}^2\end{array}\right]\right),$$

where ${\sigma }_{\alpha ,\ast }^2=\left(h_{\text{GE},\ast }^2\right)/k$. Lastly, we perform an association scan on y by using all SNPs at each gene locus to obtain SNP-level Z scores z_T.

Results

Accurate Estimation of Expression-Trait Genetic Correlation in Simulations

To validate our statistical framework for estimating ${\rho }_{\text{g},\text{local}}$, we used real genotype data to perform simulations under various architectures (see Material and Methods). In brief, we simulated gene expression for 100 independent gene loci, which we then used to simulate a complex trait. Using our approach, we performed a GWAS and estimated ${\rho }_{\text{g},\text{local}}$ from TWAS summary statistics (see Material and Methods). We observed unbiased estimates for ${\rho }_{\text{g},\text{local}}$ both when causal variants were typed and when they were masked from the data (see Figure S1). Estimated values of ${\rho }_{\text{g},\text{local}}$ were highly correlated with their true values (r = 0.73; p < 2.2 × 10⁻¹⁶), which indicates that using weights inferred from GBLUP maintains moderate power levels. This slight loss in power extended to $h_{\text{GE}}^2$ estimates, which quantify the total effect of predicted expression on a trait (r = 0.74; p < 6.7 × 10⁻¹²; see Table S3). As eQTL datasets increase in sample size, and predictive models become more accurate, we expect this attenuation bias to decrease.

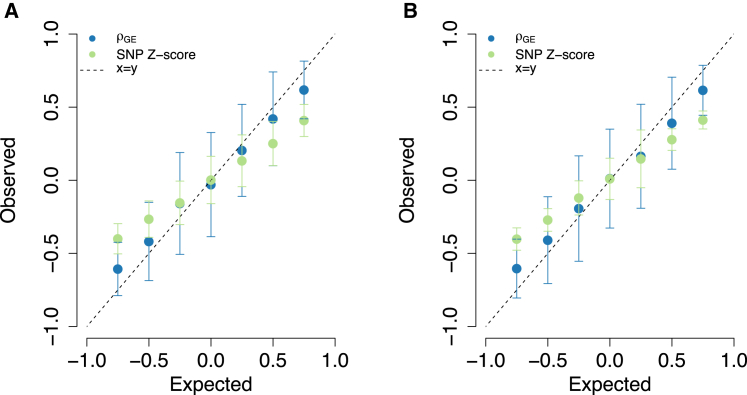
We next performed extensive simulations to validate our procedure for estimating genetic correlation due to predicted expression $\left({\rho }_{\text{GE}}\right)$ between pairs of traits. We simulated genetically correlated complex traits from predicted expression by sampling effects from a bivariate normal distribution with correlation ${\rho }_{\text{GE}}$ (see Material and Methods). We first estimated ${\rho }_{\text{g},\text{local}}$ for each gene-trait pair, which served as input for estimating ${\rho }_{\text{GE}}$. Overall, we observed our estimator to be approximately unbiased, with conservative estimates for ${\rho }_{\text{GE}}$ when its underlying value was near the boundaries (see Figure 3). Importantly, estimates were relatively unbiased when causal variants were untyped in the data. Our method appropriately accounted for LD among variants, resulting in a large improvement over the naive SNP correlation approach (which simply correlates the Z scores by ignoring LD). We also assessed our approach for testing for deviations from ${\rho }_{\text{GE}}$ = 0 and found estimates consistent with the null distribution with ${\lambda }_{\text{GC}}$ = 0.97 (Jack-knife 95% CI = [0.86, 1.08]; see Figure S2). To measure how sensitive our approach is to estimates of $h_{\text{g},\text{local}}^2\left(\text{GE}\right)$ at each gene, we repeated simulations by using variance explained by the top eQTL as a proxy for local heritability. Although estimates were highly similar (r = 0.99; p < 6.6 × 10⁻⁷), our approach produced estimates closer to the ground truth (see Figure S3).

Figure 3.

Simulation Results for ${\hat{\mathit{\rho }}}_{\text{GE}}$ and Correlation of SNP Z Scores

Each point represents the mean estimate over 100 simulations. Error bars represent the 95% confidence interval estimated by the mean SE across simulations. The dotted line represents the identity line.

(A) Causal SNPs for gene expression are typed in the data.

(B) Causal SNPs are untyped.

TWAS Identifies 1,196 Genes Associated with 30 Complex Traits and Diseases

We integrated GWAS summary data of 30 complex traits with gene expression to identify 1,196 susceptibility genes (i.e., genes with at least one significant trait association), comprising 5,490 total associations (after Bonferroni correction; see Material and Methods). Of these associations, we observed 1,789 distinct gene-trait pairs, of which 783 were found in anthropometric traits, 423 in metabolic traits, 215 in immune-related traits, 213 in hematopoietic traits, 137 in neurological traits (e.g., schizophrenia), and 18 in social traits (see Tables 1, S4, and S5). For example, the 137 susceptibility genes found for schizophrenia included SNX19 (e.g., GTEx cerebellum; p < 2.2 × 10⁻⁸) and NMRAL1 (e.g., GTEx skeletal muscle; p < 9.7 × 10⁻⁷); this is consistent with a previously reported study¹² that used different methods and expression data (see Table S6). We did not find susceptibility genes for forearm BMD, HOMA-B, or MCH concentration, consistent with low GWAS signal for these traits (see Table 1). Indeed, the number of GWAS risk loci strongly correlated with the number of identified susceptibility genes (r = 0.99; p < 2.2 × 10⁻¹⁶). Using the PANTHER database,⁴⁷ we explored putative molecular function and pathways enriched with identified susceptibility genes but were underpowered to detect molecular function for most individual traits (see Appendix A).

Table 1.

Summary of GWAS and TWAS Results

Trait	Abbreviation	Number of GWASs				Number of Susceptibility Genes
		Loci	Loci with an eGene	Loci with a Single Susceptibility Gene	Loci with at Least One Susceptibility Gene	Genes Overlapping GWASs	Genes Not Overlapping GWASs
Age at menarche	AM	70	60	14	19	34	9
Body mass index	BMI	76	60	10	18	44	11
College	COL	5	5	2	2	1	4
Crohn disease	CD	50	48	4	17	65	5
Educational years	EY	7	4	2	2	2	11
Fasting glucose	FG	12	11	2	5	8	1
Fasting insulin	FI	0	0	0	0	0	1
Femoral neck bone mineral density	FN	20	20	2	2	2	1
Forearm bone mineral density	FA	3	3	0	0	0	0
Hemoglobin	HB	22	21	2	5	22	3
HbA1c	–	10	10	0	1	4	0
Height	–	482	454	94	225	669	52
High-density lipoprotein	HDL	100	95	11	29	98	4
HOMA-B	–	4	3	0	0	0	0
HOMA-IR	–	0	0	0	0	0	1
Inflammatory bowel disease	IBD	63	59	12	23	70	11
Low-density lipoprotein	LDL	75	72	8	25	84	3
Lumbar spine	LS	24	23	2	3	4	0
Mean cell hemoglobin concentration	MCHC	5	3	0	0	0	0
Mean cell hemoglobin	MCH	35	31	5	17	46	7
Mean cell volume	MCV	43	40	8	20	49	1
Number of platelets	PLT	35	34	6	13	30	8
Packed cell volume	PCV	14	13	1	3	5	1
Red blood cell count	RBC	25	21	3	10	35	2
Rheumatoid arthritis	RA	44	41	7	13	30	5
Schizophrenia	SCZ	95	74	15	31	113	24
Total cholesterol	TC	88	85	13	40	117	0
Triglycerides	TG	70	67	4	18	59	1
Type 2 diabetes	T2D	12	12	0	1	3	0
Ulcerative colitis	UC	37	36	5	9	27	2
Total		1,526	1,405	232	551	1,621	168

The first four numeric columns summarize GWAS risk loci. The last two numeric columns summarize identified TWAS susceptibility genes. The majority (92%) of GWAS risk loci overlap at least one eGene, of which 40% contain at least one susceptibility gene. We report 168 (9%) identified gene-trait pairs that do not overlap a GWAS variant, providing risk loci for follow up.

Next, we quantified the overlap of susceptibility genes and GWAS signals. Of the 1,789 identified gene-trait pairs, 168 (9%) were not proximal (more than 0.5 Mb from the TSS) to any genome-wide-significant SNP for that respective trait (see Table 2). This measure was robust to increases in window size, such that 140 (8%) gene-trait pairs did not overlap a genome-wide-significant SNP within 1 Mb of the TSS. We observed increased SNP association statistics at these genes (mean χ² = 6.5; see Figure S4), which suggests that GWASs with an increased sample size will discover genome-wide-significant SNPs nearby. We tested this hypothesis by assessing the new TWAS loci for educational years²¹ (n = 126,599) in a recent, much larger GWAS for educational years³⁵ (n = 293,723). All four independent loci contained a genome-wide-significant SNP in the larger GWAS (see Table S7). Of the 1,526 GWAS risk loci, 1,405 (92%) overlapped at least one eGene (i.e., a gene with heritable expression levels in at least one of the considered expression panels), and 551 (36%) overlapped at least one susceptibility gene (see Table 1). Focusing on the 1,621 TWAS associations that overlapped a genome-wide-significant SNP, we observed 1,350 (83%) genes that were not the closest, suggesting that the traditional heuristic of prioritizing genes closest to GWAS SNPs is typically not supported by evidence from eQTL data⁴⁸ (see Figure S5). This is also supported by the mean χ² association statistics for genes closest to index SNPs (χ² = 43.9) and the top association (χ² = 72.9; see Figure S6). In addition, lead GWAS SNPs typically have a weaker eQTL effect for the proximal gene than for the TWAS-implicated gene in 1,088 of 1,350 TWAS associations. This result, consistent with earlier reports,^{11, 12} highlights the importance of utilizing the entire locus and estimates of LD to prioritize genes.

Table 2.

Susceptibility Genes That Do Not Overlap a Genome-wide Significant SNP within 0.5 Mb of the Transcription Start and End Sites for Each Trait

Trait	Genes
AM	CCDC65, COG6, INO80E, NUCKS1, PMS2P5, RAB7L1, SLC26A9, STAG3L2, and TMEM180
BMI	CDK5RAP3, CERCAM, DHRS11, GGNBP2, INO80E, RP11-6N17.10, RP11-6N17.9, SLC27A4, STAG3L1, TUBA1C, and URM1
CD	CCDC88B, CISD1, PPP1R14B, RIT1, and SMIM19
COL	ABCB9, AC091729.9, AFF3, and RNF123
EY	ABCB9, EIF3CL, MIR4721, MPHOSPH9, NFATC2IP, RP11-1348G14.4, SDCCAG8, SH2B1, STK24, SULT1A1, and TUFM
FG	MAPRE3
FI	KNOP1
FN	FGFRL1
HB	CCDC117, UBE2Q2, and WNT3
HDL	HRAS, KNOP1, RETSAT, and TYRO3
HEIGHT	ARL17A, ATF1, ATP5J2, C20orf194, C9orf156, CCDC116, CNIH4, COX6B1, CRELD1, CRHR1, DAB2IP, DESI1, DLG5, DUS3L, ECHDC2, FAM35A, FUCA2, H2AFJ, HIBADH, INO80E, IQGAP1, KANSL1, LBX2-AS1, LRRC37A2, MAPT, MAT2A, MED4, MEGF9, MGMT, MORC2-AS1, MSRB2, P4HTM, PHF19, PLEKHA1, PSMD5, PSMD5-AS1, RP11-173M1.8, RP11-455F5.3, RP11-4O1.2, RP11-67A1.2, RP13-39P12.3, RP4-612B15.3, RRN3, SFTPD, SH3YL1, SUSD1, TMEM128, UBE2L3, UTP18, WDR60, YPEL3, and YWHAB
HOMA-IR	KNOP1
IBD	ADCY3, CCDC88B, FAM189B, GBA, GBAP1, HCN3, PPP1R14B, RMI2, SATB2, TMEM180, ZFP90
LDL	DHRS13, ERAL1, and WDR25
MCH	AP003419.16, GSTP1, PABPC4, PTPRCAP, RP11-69E11.4, RP1-18D14.7, and RPS6KB2
MCV	COX4I2
PCV	PLEKHH2
PLT	ACTR1A, BAZ2A, CCDC17, IPP, MUTYH, PRIM1, TESK2, and TMEM180
RA	METTL21B, RNF40, RPS26, SLC26A10, and SUOX
RBC	COX4I2 and FBXL20
SCZ	ALMS1P, ARL14EP, CAD, CBR3, CEBPZ, CORO7, CPNE7, DND1, EMB, ENDOG, EPN2, GRAP, IK, NMRAL1, NRBP1, PCNX, PFDN1, PRR12, PRRG2, RNF112, RP11-135L13.4, SEPT10, SRA1, and TMCO6
TG	L3MBTL3
UC	SATB2 and TNPO3

For details on individual genes, expression studies, and association statistics, see Table S4. Genome-wide significance: p < 5 × 10⁻⁸.

Although GWAS SNPs provide the majority of the power in this approach, the flexibility of TWASs to leverage allelic heterogeneity provides a significant gain.¹¹ We found 219 instances across 19 traits where association signal was stronger (20% higher χ² statistics on average) in TWASs than in GWASs. For example, predicted expression in CCDC88B (OMIM: 611205; a gene involved in T cell maturation and inflammation⁴⁹) exhibited strong association with Crohn disease (p_TWAS = 6.32 × 10⁻⁸), whereas the index SNP (i.e., top overlapping GWAS SNP) at site rs11231774 was only suggestive (p_GWAS = 2.47 × 10⁻⁶). This effect was most dramatic for height, such that 108 susceptibility genes had a stronger signal than GWAS index SNPs. We observed that the χ² statistics for predicted expression in CRELD1 (OMIM: 607170; p_TWAS = 1.55 × 10⁻¹⁰) were 2.6× higher than those for the index SNP rs1473183 (p_GWAS = 6.33 × 10⁻⁵).

Recent work⁵⁰ applied a similar approach¹² that used summary eQTLs from blood and GWAS data to identify 71 genes for 28 complex traits.⁵⁰ Of the investigated traits, 12 overlapped those in our study. Overall, whereas that study reported 63 genes for these traits, we identified 564 genes. Surprisingly, despite using independent methods and expression data, we replicated 40 out of 51 associations for genes assayed in both studies (see Table S8). This increase in power can be attributed to two reasons. First, we integrated many more expression panels sampled from many tissues, leading to many more genes for the assay. Second, we used a method that jointly tests the entire locus rather than the index SNPs. We have shown that many identified susceptibility genes contain signals of allelic heterogeneity; therefore, using individual SNPs will decrease power.

Genes Associated with Multiple Traits

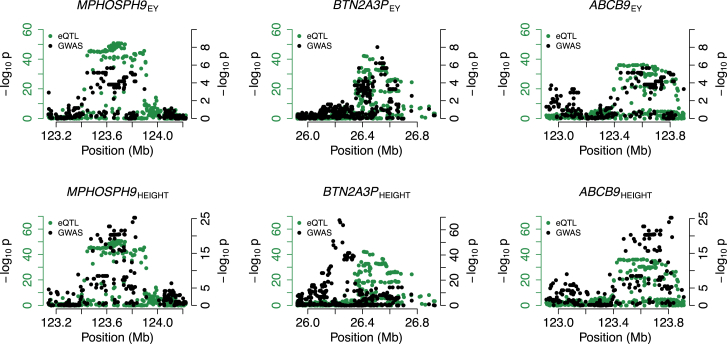
We investigated the degree of pleiotropic susceptibility genes (i.e., genes associated with more than one trait) in our data and found 380 (32%) genes associated with multiple traits (see Figure S7). For example, IKZF3 (OMIM: 606221) displayed strong associations with Crohn disease (NTR; p = 1.6 × 10⁻⁹), HDL levels (NTR; p = 6.6 × 10⁻¹⁵), inflammatory bowel disease (NTR; p = 7.9 × 10⁻¹⁶), rheumatoid arthritis (NTR; p = 6.0 × 10⁻⁸), and ulcerative colitis (NTR; p = 9.2 × 10⁻¹⁰). Indeed, IKZF3 has been shown to influence lymphocyte development and differentiation.^{51, 52} These traits are known to have a strong autoimmune component;⁵³ hence, association with predicted IKZF3 expression levels is consistent with a model where cis-regulated variation in IKZF3 product levels contributes to risk. Similarly, we observed three susceptibility genes shared between educational years (EY) and height (see Figure 4): ABCB9 (OMIM: 605453; GTEx heart left ventricle; p_height = 1.38 × 10⁻¹⁵; p_EY = 1.28 × 10⁻⁶), BTN2A3P (OMIM: 613592; GTEx subcutaneous adipose; p_height = 3.82 × 10⁻¹²; p_EY = 1.90 × 10⁻⁷), and MPHOSPH9 (OMIM: 605501; GTEx thyroid; p_height = 5.84 × 10⁻¹⁸; p_EY = 1.30 × 10⁻⁶). Although not direct evidence of co-localization of educational years and height at these loci, this result is consistent with a recent study¹³ that reported a non-zero genetic correlation between height and educational years (${\hat{\rho }}_{\text{g}}$ = 0.13; p = 3.82 × 10⁻⁶).

Figure 4.

Susceptibility Genes Shared for Educational Years and Height

We indicate –log₁₀ p values for eQTLs in green and trait-specific GWASs in black on separate axes to simplify illustration.

The Effect of cis Expression on Traits Is Consistent across Tissues

Having established the importance of individual predicted gene expression levels for these traits, we next estimated the amount of trait variance explained by predicted expression by using all examined genes, including those not significantly associated, and an LD score regression approach (see Material and Methods). We found 108 tissue-trait pairs across 17 traits and 33 tissues where the cumulative effect of all measured genes on the trait was significantly greater (p < 0.05/45) than for the significant-only set (see Table S9). For example, in height we estimated $h_{\text{GE}}^2$ = 0.07 (Jack-knife SE = 0.02; p = 5.6 × 10⁻⁴) by using all 3,733 measured genes in YFS and $h_{\text{GE}}^2$ = 0.015 (Jack-knife SE = 6.9; p = 0.03) by using only the 169 YFS susceptibility genes (p_all>sig = 5.6 × 10⁻³). This suggests that height has additional susceptibility genes, which we are underpowered to detect. Strikingly, the predicted expression from all YFS genes accounts for 12% of SNP heritability measured in height.⁵⁴ However, for most trait-tissue pairs, we did not observe a significant difference at our given sample sizes. Indeed, we measured a significant association between expression-study sample size and number of eGenes (r = 0.73; SE = 0.10; p = 1.3 × 10⁻⁸), which indicates that smaller studies lack power to find eGenes and thus underestimate the total $h_{\text{GE}}^2$.

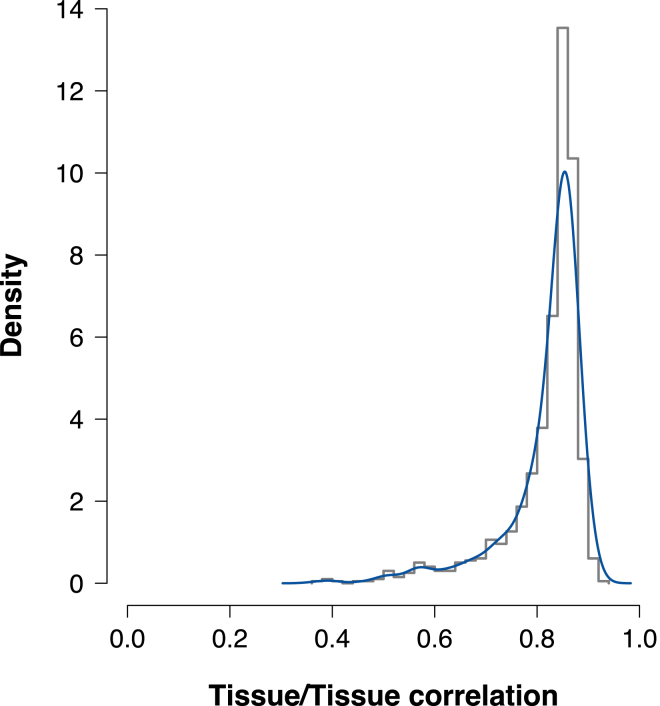
We next asked whether any tissues are burdened with increased levels of risk for a given trait. To test this hypothesis, we examined the difference between estimated trait variance explained per gene and the average. Our results did not suggest tissue-specific enrichment at the current sample sizes (see Table S10). We observed a significant correlation between gene expression sample size and tissue enrichment estimates (p = 62.4 × 10⁻⁶). One explanation for this relationship is that the number of eGenes identified per study increases with sample size, which increases $h_{\text{GE}}^2$ estimates. Given no observable difference in tissue-specific risk, we expect local estimates of genetic correlation to be highly similar across tissues. When estimating ${\rho }_{\text{g},\text{local}}$, we observed consistent effect-size estimates in both sign and magnitude estimates across tissues (mean tissue-tissue r = 0.82; see Figure 5). These results are compatible with earlier work that found that cis effects on expression are largely consistent across tissues.⁵⁵ To obtain a meta-estimate of local genetic correlation for gene-trait pairs with measurements in multiple tissues, we used the mean genetic correlation across all expression panels in all of the following analyses.

Figure 5.

Histogram and Density Estimate for Correlation of ${\rho }_{\text{g},\text{local}}$ across Tissues

We computed the correlation across pairs of different tissues by using local estimates of genetic correlation between expression and traits. Most tissues exhibited a high correlation over the underlying gene effects on traits with an estimated mean of r = 0.82.

Genetic Correlation between Traits at the Level of Predicted Expression

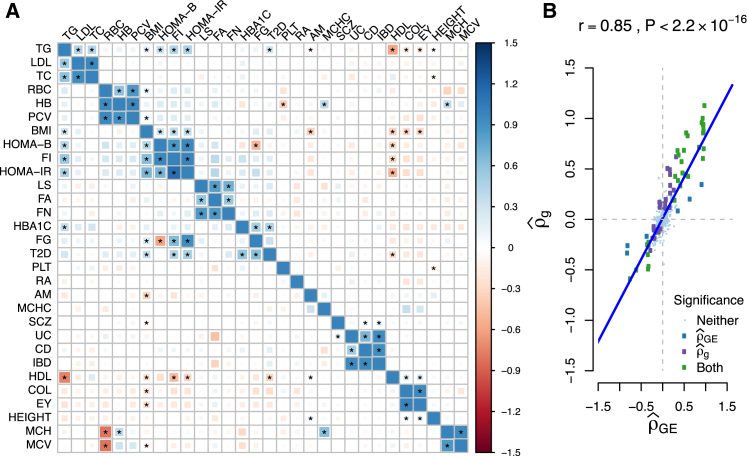
To evaluate the shared contribution of predicted expression on pairs of traits, we used nominally significant (p < 0.05) genes to compute the genome-wide genetic correlation at levels of predicted expression (see Material and Methods). For 435 distinct pairs, we discovered 43 significant expression correlations, 22 of which had previously reported non-zero genetic correlations¹³ (see Figure 6 and Table 3). For example, age of menarche and BMI had ${\hat{\rho }}_{\text{GE}}$ = −0.32 (95% CI = [−0.32, −0.21]; p = 7.97 × 10⁻⁸). This negative correlation is consistent with estimates published in epidemiological studies,⁵⁶ in addition to studies probing genetic correlation across complex traits.¹³ To determine whether estimates were sensitive to changes in scale, we recomputed ${\hat{\rho }}_{\text{GE}}$ by using the top eQTL as a proxy for local heritability of gene expression and observed similar results (r = 0.99; p = 2.2 × 10⁻¹⁶; see Figure S8). Results were also robust to increasing window size for gene pruning, such that there was no significant difference in estimates between 2 and 4 Mb windows (r_2Mb = 0.99; r_4Mb = 0.98). Using estimates of ${\hat{\rho }}_{\text{GE}}$, we clustered traits and observed groups forming naturally in the trait-trait matrix (see Figure 6). Interestingly, BMI clustered with insulin-related traits (HOMA-B, HOMA-IR, and fasting insulin). Our estimates were highly consistent with the results of LD score regression (see Figure 6 and Table S11). Out of 435 pairs of traits, 35 demonstrated significance for ${\hat{\rho }}_{\text{GE}}$ and ${\hat{\rho }}_{\text{g}}$, whereas 8 and 27 were exclusive to ${\hat{\rho }}_{\text{GE}}$ and ${\hat{\rho }}_{\text{g}}$, respectively. Given the high degree of concordance between estimates, we tested for significant differences and found four insulin-related pairs of traits and three blood-related pairs with more extreme values for ${\hat{\rho }}_{\text{GE}}$ (see Table S11). Differences for these pairs of traits can be partially explained by overconfident standard errors for ${\hat{\rho }}_{\text{GE}}$ (see Table S12). Overall, we found ${\hat{\rho }}_{\text{GE}}$ to explain most of the variation in ${\hat{\rho }}_{\text{g}}$ (r² = 0.72). We compared this to the naive approach of computing the correlation of SNP Z scores across susceptibility gene loci and observed a much smaller proportion of variance explained in ${\hat{\rho }}_{\text{g}}$ (r² = 0.46). This reinforces that, compared to the naive approach, our method incorporates LD to aggregate signal.

Figure 6.

Estimates of Genetic Correlation ${\hat{\rho }}_{\text{g}}$ Obtained from LD Scores versus Estimates of Expression Correlation ${\hat{\rho }}_{\text{GE}}$ from Nominally Significant TWAS Results

(A) Correlation matrix for 30 traits. The lower triangle contains ${\hat{\rho }}_{\text{GE}}$, and the upper triangle contains ${\hat{\rho }}_{\text{g}}$ estimates. Correlation estimates that are significantly non-zero (p < 0.05/435) are marked with an asterisk (^∗). The strength and direction of correlation are indicated by size and color. We found 43 significantly correlated traits by using predicted expression and 62 by using genome-wide SNPs.

(B) Linear relationship between estimates of ${\hat{\rho }}_{\text{GE}}$ and ${\hat{\rho }}_{\text{g}}$. We indicate whether individual estimates were significant in either approach by color. Non-significant trait pairs are reduced in size for visibility.

Table 3.

Pairs of Traits with Significant Estimates of ${\mathit{\rho }}_{\text{GE}}$

Trait 1	Trait 2	All Nominally Significant Genes
		${\hat{\mathit{\rho }}}_{\mathbf{GE}}$	95% CI		M
AM	BMI	−0.33	−0.43	−0.21	257
BMI	COL	−0.31	−0.44	−0.18	190
BMI	EY	−0.31	−0.43	−0.18	210
BMI	FI	0.39	0.25	0.51	164
BMI	HDL	−0.34	−0.45	−0.23	256
BMI	HOMA-B	0.31	0.17	0.44	168
BMI	HOMA-IR	0.36	0.22	0.49	162
BMI	TG	0.29	0.17	0.41	233
CD	IBD	0.93	0.91	0.94	366
CD	UC	0.51	0.41	0.60	218
COL	EY	0.95	0.94	0.96	363
FA	FN	0.57	0.44	0.67	149
FA	LS	0.60	0.49	0.69	170
FG	FI	0.65	0.53	0.74	133
FG	HOMA-B	−0.60	−0.70	−0.47	125
FG	HOMA-IR	0.92	0.89	0.94	136
FI	HDL	−0.31	−0.44	−0.17	168
FI	HOMA-B	0.97	0.96	0.98	243
FI	HOMA-IR	0.99	0.99	0.99	383
FI	TG	0.57	0.45	0.66	152
FN	LS	0.86	0.83	0.89	264
HB	MCH	0.37	0.23	0.50	156
HB	MCHC	0.40	0.23	0.55	105
HB	PCV	0.97	0.96	0.97	338
HB	PLT	−0.36	−0.49	−0.20	141
HB	RBC	0.95	0.94	0.96	260
HbA1c	T2D	0.46	0.30	0.59	110
HbA1c	TG	0.37	0.21	0.50	137
HDL	HOMA-IR	−0.32	−0.46	−0.18	159
HDL	T2D	−0.32	−0.45	−0.19	186
HDL	TG	−0.74	−0.79	−0.69	274
HOMA-B	HOMA-IR	0.97	0.96	0.98	227
HOMA-B	TG	0.43	0.27	0.56	127
HOMA-IR	TG	0.48	0.34	0.60	138
IBD	UC	0.96	0.95	0.96	415
LDL	TC	0.97	0.96	0.97	452
LDL	TG	0.54	0.44	0.63	231
MCH	MCHC	0.63	0.51	0.72	127
MCH	MCV	0.96	0.95	0.97	320
MCH	RBC	−0.81	−0.85	−0.76	207
MCV	RBC	−0.80	−0.85	−0.75	208
PCV	RBC	0.96	0.95	0.97	278
TC	TG	0.61	0.53	0.68	248

Estimates were computed with $M$ pruned genes that were nominally significant (p < 0.05) in both traits.

Bi-directional Regression Suggests Putative Causal Relationships

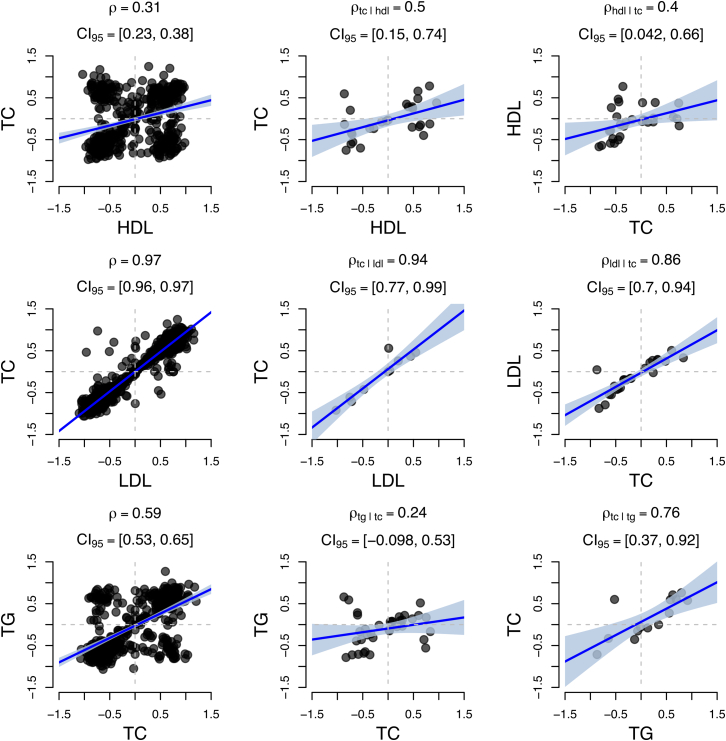
Given pairs of traits with significant estimates of ${\rho }_{\text{GE}}$, we aimed to distinguish among possible causal explanations by performing bi-directional regression analyses (see Material and Methods). To empirically validate our approach, we regressed HDL, LDL, and TG with TC. TC is the direct consequence of summing over TG, HDL, and LDL levels, so we expected to observe higher signal for ${\rho }_{\text{TC }|\text{lipid}}$ than for ${\rho }_{\text{lipid}|\text{TC}}$. Of these three, we found evidence that TG influences TC (p = 2.34 × 10⁻³). We observed consistent, but not significant, evidence for the effects of LDL on TC (p = 0.07) and HDL on TC (p = 0.55; see Figure 7). These results suggest that point estimates from the bi-directional approach favor the correct model but might not have adequate power required for significance.

Figure 7.

Estimates of Expression Correlation ${\mathit{\rho }}_{\text{GE}}$ between TC and HDL, LDL, and TG

(Left column) Estimates of ${\rho }_{\text{GE}}$ with the use of nominally significant genes (p < 0.05).

(Middle column) We repeated the analysis by using only susceptibility genes found in the x axis trait but not found in the y axis trait.

(Right right) Same analysis as in the middle column but with the other trait’s susceptibility genes.

All three analyses resulted in stronger point estimates for ${\rho }_{\text{TC }|\text{lipid}}$ when conditioning on HDL, LDL, and TG genes than for ${\rho }_{\text{lipid }|\text{TC}}$; however, significance was observed only for ${\rho }_{\text{TC}|\text{TG}}$ (p = 2.34 × 10⁻³). Shaded regions indicate the estimated 95% confidence interval for the regression line.

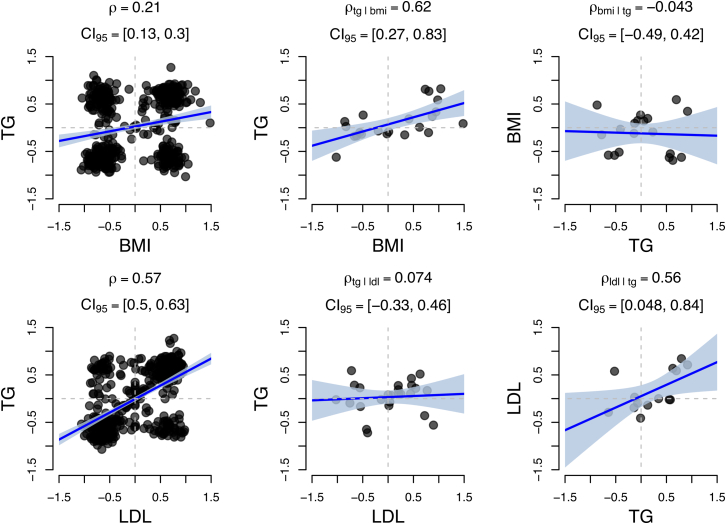
We tested the 43 pairs of traits identified above (see Table 3) while ascertaining susceptibility genes and observed asymmetric effects at p < 0.05 for BMI-TG and LDL-TG (see Figure 8 and Table 4). For example, in the bi-directional analysis on BMI and TG, we observed a significant effect for ${\rho }_{\text{TG}|\text{BMI}}$ = 0.62 (95% CI = [0.27, 0.83]; p = 2.06 × 10⁻³). By contrast, the reverse analysis estimate overlapped 0 at ${\rho }_{\text{BMI}|\text{TG}}=-0.04$ (95% CI = [−0.49, 0.42]; p = 0.86). Individual estimates for ${\rho }_{\text{TG }|\text{BMI}}$ and ${\rho }_{\text{BMI}|\text{TG}}$ were significantly different (p = 0.01, Welch’s t test), which is consistent with a model where BMI directly influences TG levels. In practice, we used susceptibility genes found through a TWAS (p ∼ 1 × 10⁻⁶), but this could be too strict an inclusion threshold for genes for which we lack power to detect. We conducted analyses with weaker thresholds and observed similar results (see Tables S13 and S14). Our results reinforce previous estimates of putative causal effects where BMI influences TG levels.^{45, 57}

Figure 8.

Estimates of ${\hat{\mathit{\rho }}}_{\text{GE}}$ for TG with BMI and for TG with LDL

We present results for pairs of traits that displayed a significant difference (p < 0.05, Welch’s t test) in their conditional estimates. These results are consistent with a causal model where BMI influences TG and TG influences LDL. Shaded regions indicate the estimated 95% confidence interval for the regression line.

Table 4.

Bi-directional Estimates of Genome-wide Genetic Correlation at the Level of Predicted Expression

Trait 1	Trait 2	Results when Ascertaining for Trait 1				Results when Ascertaining for Trait 2				Test for Difference
		${\hat{\mathit{\rho }}}_{\mathbf{GE}}$	SE	p	M	${\hat{\mathit{\rho }}}_{\mathbf{GE}}$	SE	p	M	t	p	∼M
BMI	TG	0.62	0.10	2.06 × 10−3	22	−0.04	0.22	8.62 × 10−1	19	2.74	1.12 × 10−2	25
LDL	TG	0.07	0.19	7.25 × 10−1	25	0.56	0.13	3.55 × 10−2	14	−2.17	3.69 × 10−2	36
TC	TG	0.24	0.14	1.63 × 10−1	36	0.76	0.08	1.79 × 10−3	14	−3.22	2.34 × 10−3	47

We denote the number of ascertained genes used in the test as M. We tested for a difference as a t statistic, where $t=\frac{\left|{\rho }_{\text{GE},1}-{\rho }_{\text{GE},2}\right|}{\sqrt{{\text{SE}}_1^2+{\text{SE}}_2^2}}\sim t\left(\text{df}\right)$ and df is the approximate degrees of freedom determine by the Welch-Satterthwaite equation.

Discussion

In this work, we described an approach to estimate the local genetic covariance and correlation between gene expression and complex traits by using GWAS summary data. We also introduced a method of estimating genome-wide genetic correlation between complex traits at the level of predicted expression. Using simulations, we demonstrated that both approaches are relatively unbiased under realistic scenarios. We used GWAS summary statistics from 30 complex traits and diseases jointly with expression data collected across 45 expression panels to identify 1,196 susceptibility genes for complex traits. Interestingly, susceptibility genes that were identified for educational years and not proximal to a genome-wide significant SNP were validated in a much larger GWAS.³⁵ We leveraged estimates of local genetic correlation between gene expression and traits to compute ${\rho }_{\text{GE}}$ for 435 trait pairs. This quantified the shared effect of predicted expression levels between two complex traits. To provide evidence of possible causal direction, we adapted a recently proposed causality test⁴⁵ to operate at the level of predicted gene expression. Our results suggest that TG influences LDL and that BMI influences TG. As more GWAS and eQTL summary results become publicly available, we expect additional studies to integrate cross-trait information to make inferences about mechanistic bases for complex traits. Indeed, recent work has combined chromatin phenotypes with alternatively spliced introns and total gene expression (the latter of which overlaps expression used in this study) to identify regulatory mechanisms for schizophrenia.⁵⁸

Under the assumption that gene expression mediates the effect of genetics on complex traits, testing for association between predicted gene expression and traits is equivalent to a two-sample Mendelian randomization test for a causal effect of expression on a trait.^{59, 60} This test for causality is valid if SNPs do not exhibit pleiotropic effects, which is difficult to prove; therefore, TWAS associations do not provide direct evidence of causal relationships between gene expression and complex traits but rather reflect associations between expression levels and traits. This set of assumptions extends to our bi-directional approach to inferring causal direction. A bi-directional regression is capable of distinguishing between directions of effect but cannot rule out pleiotropy. Therefore, our results show consistency with a putative causal mechanism and should not be interpreted as direct proof of causality.

We conclude with several caveats. First, we note that using estimates of genetic correlation to find susceptibility genes could still be biased as a result of confounding. The expression weights used for TWASs could tag variants that are causal through other genes or non-genic mechanisms. In principle, this can be partially remedied by joint testing of multiple genes and a trait. In this work, we combined estimates across tissues by taking the mean effect to compute the genetic correlation between traits and expression. This approach is unbiased but could be inefficient. Recent work⁶¹ has described a random-effect model that combines estimates across tissues to increase power. Finally, our method of estimating correlation between traits by using the genetically predicted component of gene expression makes several simplifying assumptions. First, we remedied the non-independence of genes by sampling single genes within a 1 Mb region, an approach that has been used previously.⁴⁶ However, a more powerful approach could take correlations across genes into account. Second, we limited predictive models to the local (or cis) effects on gene expression, which ignores distal (or trans) effects that regulate gene expression. Although the predictive accuracy of models for gene expression used in this study can account for most of the variation due to genetics,¹¹ we believe that incorporating additional sources of genomic information (e.g., functional priors on SNP effects^{39, 62, 63}) could make additional refinement possible.

Published: February 23, 2017

Appendix A: Pathway Analysis

We used the PANTHER database⁴⁷ to explore putative molecular function and pathways enriched with identified susceptibility genes. Using all susceptibility genes across all traits, we found 13 significantly enriched categories, of which seven were related to binding functions. Catalytic activity exhibited the strongest enrichment at 1.3× (GO: 0003824; p = 5.17 × 10⁻⁹; see Figure S9). We next focused on individual traits (see Figure S10); however, most individually tested gene sets did not indicate significant enrichment, except for height, LDL, and TC. For example, height had a significant enrichment of genes with catalytic activity (1.31×; p = 4.77 × 10⁻⁴). We next looked at biological processes and found TWAS genes enriched at 1.2× for metabolic processes (GO: 0008152; p = 7.29 × 10⁻¹¹) and 1.57× cellular catabolic processes (GO: 0044248; p = 2.51 × 10⁻²; see Figures S11 and S12). Enrichment was most pronounced in susceptibility genes specific to height (1.3×; p = 1.03 × 10⁻⁶).

Web Resources

• CommonMind Consortium, https://www.synapse.org

• FUSION software package, http://gusevlab.org/projects/fusion/

• GCTA, http://cnsgenomics.com/software/gcta/

• Gene Ontology, http://www.geneontology.org/

• GTEx Portal, http://www.gtexportal.org/home/

• OMIM, http://www.omim.org

• PLINK, https://www.cog-genomics.org/plink2/

• RhoGE software, https://github.com/bogdanlab/RHOGE

Supplemental Data

Table S2. Sample Size and Number of Association Tests

Sample size and the number of genes tested for association with trait by training set. The per-trait Bonferroni correction factor used to determine significance with traits is listed in the “Total Tests” column. Some GWAS did not have overlapping SNPs to perform expression imputation and thus individual expression/trait association was absent.

Table S5. Significant Gene Associations

The “Expression Study” column denotes the original study used to fit weights. The p values are based on a two-tailed Z score test determined from the TWAS test.

Table S6. Susceptibility Genes Identified in Zhu et al.

Comparison of association strength for genes shared with Zhu et al.¹² The “TWAS Z” and “TWAS P” columns indicate the association strength determined using the TWAS expression study weights. PSMR and PHEIDI correspond to the Zhu et al. findings.

Table S8. Susceptibility Genes Reported in Pavlides et al.

Comparison of association strength for genes and traits shared with Pavlides et al.⁵⁰

Table S9. Estimates of $h_{\text{GE}}^2$ in Real Data

Heritability explained by gene expression computed using all genes measured versus reported susceptibility genes only for each tissue.

Table S10. Tissue Relevance for Each Trait

Mean variance explained in trait per gene. Each estimate was tested for against the cross-tissue mean using a one-sided Z-test.

Table S11. Estimates of Expression Correlation and Genetic Correlation for Pairs of Traits

Comparisons between LD score estimates of genetic correlation (ρ_g) versus genetic correlation using predicted expression (ρ_GE). LD-Score was run genome-wide using the same summary data. The threshold for significance was p < 0.05 / 435, where 435 is the total number of pairwise combinations. Significant estimates are denoted with an asterisk (^∗).

Table S12. Estimates of Expression Correlation Using Jack-knife and Genetic Correlation for Pairs of Traits

Comparisons between LD score estimates of genetic correlation (ρ_g) versus genetic correlation using predicted expression (ρ_GE). Standard error estimates for ρ_GE were obtained by jack-knifing over genes.

Table S13. Bi-directional Estimates of Conditional Genetic Correlations at the Level of Predicted Expression

Bi-directional estimates for all pairs of traits. The number of genes used in the calculation is indicated in the M column. Gene sets included genes that attained p < 1 × 10⁻⁶ exclusively for that trait. We pruned genes by selecting a single gene per 1 Mb locus.

Table S14. Bi-directional Estimates of Conditional Genetic Correlations at the Level of Predicted Expression

The analyses in Table S13 were repeated with relaxed gene sets that attained p < 1 × 10⁻³.