Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Mar 7;7:44024. doi: 10.1038/srep44024

Superconducting gap structure of FeSe

Lin Jiao 1,*, Chien-Lung Huang 1,*,†, Sahana Rößler 1,a, Cevriye Koz 1, Ulrich K Rößler 2, Ulrich Schwarz 1, Steffen Wirth 1,b
PMCID: PMC5339780  PMID: 28266654

Abstract

The microscopic mechanism governing the zero-resistance flow of current in some iron-based, high-temperature superconducting materials is not well understood up to now. A central issue concerning the investigation of these materials is their superconducting gap symmetry and structure. Here we present a combined study of low-temperature specific heat and scanning tunnelling microscopy measurements on single crystalline FeSe. The results reveal the existence of at least two superconducting gaps which can be represented by a phenomenological two-band model. The analysis of the specific heat suggests significant anisotropy in the gap magnitude with deep gap minima. The tunneling spectra display an overall “U”-shaped gap close to the Fermi level away as well as on top of twin boundaries. These results are compatible with the anisotropic nodeless models describing superconductivity in FeSe.

Soon after the discovery of the Fe-based superconductors (Fe-SC) great effort has been devoted to unveil their electron paring mechanism. Even after nearly a decade of intensive research, the symmetry of the superconducting order parameter is still under dispute1,2, nonetheless most theories favor an unconventional s± symmetry with a sign change of the order parameter between the hole and the electron Fermi sheets3,4,5,6.

Among the members of the family of Fe-SC, the binary compound FeSe has attracted considerable attention recently. This is mostly because the crystal structure of FeSe is regarded as representative of the entire family of Fe-SC. Further, the superconducting transition temperature Tc ≈ 8 K7 in bulk FeSe can be enhanced up to 37 K by application of pressure8,9,10,11 and even to 50–100 K by growing it as a monolayer on a SrTiO3 substrate12,13,14,15. Another unique feature of FeSe is that it undergoes a structural phase transition from a tetragonal to an orthorhombic phase at Ts ≈ 87 K16, which is not accompanied or followed by a long-range magnetic order. At Ts, the C4-rotational symmetry of the underlying electronic system is also spontaneously broken. The resulting electronic state with a C2 symmetry is referred to as a nematic phase. It is argued that the symmetry of the superconducting order-parameter should give insight into the collective degree of freedom that governs both superconductivity as well as nematicity in the Fe-SC17.

However, the situation on the experimental front is far from being resolved. Even in the case of single crystalline FeSe with relatively simple crystal structure, different experiments indicated different superconducting gap structures. While most experiments detected two superconducting gaps18,19,20,21,22,23,24,25, no consensus has been reached concerning the magnitude of the superconducting gap as well as on the presence or absence of nodes within the structure. The residual linear component of the thermal conductivity κ0/T in the T → 0 limit, which is particularly sensitive to nodal quasiparticles, revealed contradicting results24,25. Further, surface sensitive scanning tunnelling spectroscopic (STS) measurements, performed on single crystalline24 and thin film samples26, detected “V”-shaped spectra in the superconducting state indicating the presence of nodes. However, STS conducted on the twin boundaries displayed a full gap27, suggesting nodeless superconductivity at the twin boundaries. In order to resolve this issue, it is necessary to perform both bulk and surface sensitive experiments on FeSe. Owing to the marked dependence of the superconducting properties even for FeSe samples grown by the same method24,25, concerted investigations on identical single crystals are required to establish one of its most fundamental properties, viz., the symmetry of the superconducting order parameter.

Here we report on specific heat C(T) combined with low-temperature (T ≥ 0.35 K) scanning tunnelling microscopy (STM) measurements on a stoichiometric FeSe single crystal to establish its superconducting order parameter. As shown below, such a combination of techniques, bulk sensitive C(T) and surface sensitive STM, allows us to unequivocally resolve the superconducting gap structure of FeSe to be nodeless.

Experimental Results

For a general characterization of our single crystal, we measured the temperature dependence of resistivity ρ(T) and magnetization M(T), see Fig. 1. These measurements were carried out on the same single crystal which is shown in the inset of Fig. 2. In Fig. 1(a), ρ(T) measurement along the [100]T direction of the tetragonal structure is presented. The resistivities are ρ300K = 0.51 mΩ cm at 300 K and ρ15K = 0.031 mΩ cm at 15 K. These values give a residual resistivity ratio (RRR) ρ300K/ρ15K = 16.4. The RRR of our crystal is very similar to the FeSe crystal (sample B) investigated by Bourgeois-Hope et al. in ref. 25. A kink at Ts = 87 K marks the structural transition temperature. In the inset, Fig. 1(b), the onset of superconducting transition can be seen at 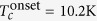Inline graphic. The sample achieves zero resistivity at Tc = 8.5 K, which is the superconducting transition temperature of the bulk. In the inset Fig. 1(c), M(T) measured in a field of 20 Oe, both in the zero-field-cooled (ZFC) and field-cooled protocol (FC) are shown. The sample displays a full diamagnetic shielding in the superconducting state with 4πχ = −1.

Figure 1. Resistivity and magnetization.

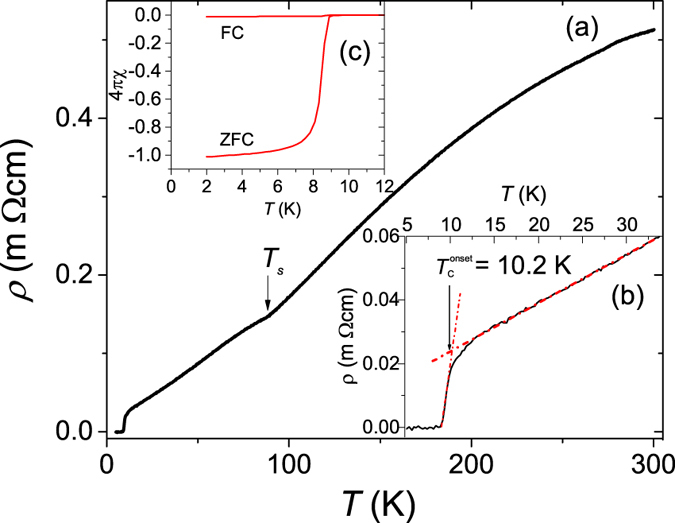
Figure 1

Open in a new tab

(a) Resistivity ρ(T) of FeSe single crystal presented in inset of Fig. 2. The temperature of the structural transition is marked by Ts. (b) The same ρ(T) data in (a) zoomed in for T < 40 K showing the superconducting transition. (c) Magnetization measured in a magnetic field of 20 Oe both in zero-field-cooled (ZFC) and field-cooled (FC) protocols.

Figure 2. Specific heat.

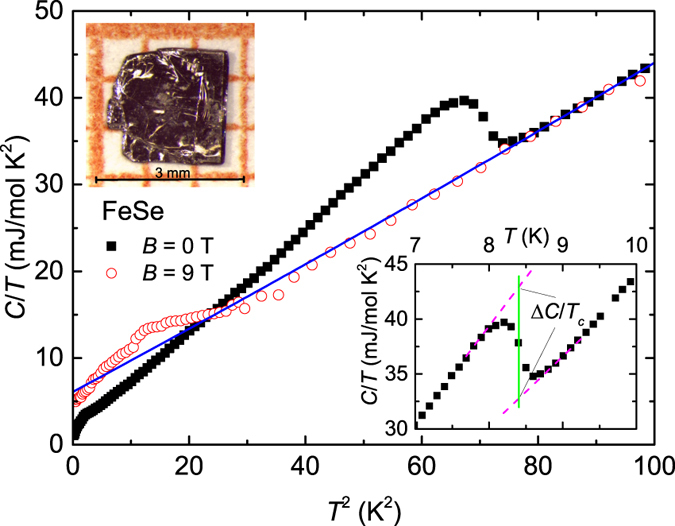
Figure 2

Open in a new tab

Specific heat divided by temperature, C/T vs T2, measured at magnetic fields of zero and 9 T. The solid line represents the normal-state specific heat Cn. Upper-left inset: a photograph of tetragonal FeSe single crystal used for specific-heat measurements. Lower-right inset: zero-field C/T vs T in an enlarged scale around Tc. Lines show how Tc and ΔC/Tc were determined.

The temperature (T) and magnetic field (B) dependence of the specific heat C(T, B) was measured on the single crystal imaged in the inset of Fig. 2. The zero-field C/T vs T2 plot between 0.35 and 10 K presented in Fig. 2 displays two anomalies, a λ-like transition at Tc = 8.4(1) K and a broad shoulder below 2 K, better seen in Fig. 3. This is a typical behaviour of a two-gap superconductor such as MgB228, suggesting the presence of at least two superconducting gaps in FeSe. The Tc was determined via local entropy conservation, i.e., the vertical line in the inset of Fig. 2 segments equal areas in a C/T vs T plot. We describe the normal-state specific heat Cn below 10 K by 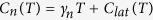Inline graphic, where γnT is the normal electronic contribution and 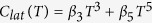Inline graphic represents the phonon contribution. The fit to C/T is shown as a solid line in Fig. 2, which yields γn = 6.5 mJ/mol K2, β3 = 0.365 mJ/mol K4, and β5 = 1.94 × 10−4 mJ/mol K6. The Debye temperature θD calculated from β3 is 242 K. These parameters are comparable to those reported earlier22,29,30,31. The normalized specific-heat jump at Tc, ΔC/γnTc, is estimated to be 1.55, which is slightly larger than the weak-coupling value 1.43 of Bardeen-Cooper-Schrieffer (BCS) theory32. The excess electronic specific heat contribution in the superconducting state given by δC(T) = C(T, B = 0) − Cn(T) is plotted in Fig. 3. The inset illustrates the satisfaction of entropy conservation 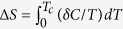Inline graphic justifying the validity of the parameters used to fit Cn(T). In the δC/T plot, the shoulder below 2 K arising due to the second superconducting gap is clearly visible. To our knowledge, such a shoulder feature has been only reported for pure, polycrystalline samples29 with compositions Fe1.01Se and Fe1.02Se. In order to further examine the superconducting order parameter, the data in Fig. 3 were fitted to the one-band BCS equation32 given by

Figure 3. Electronic part of the specific heat.

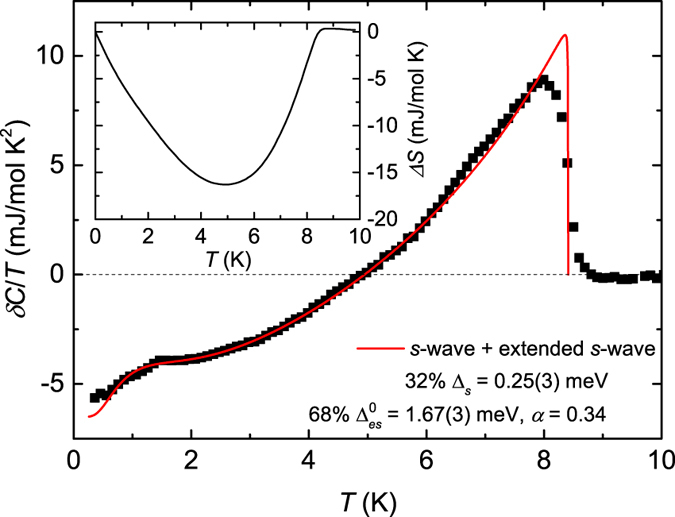
Figure 3

Open in a new tab

Zero-field electronic specific heat (with the normal-state specific heat being subtracted) divided by temperature. The solid line represents a fit by a smaller s-wave plus a larger extended s-wave models of the form 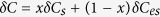Inline graphic with x = 0.32. The inset shows the entropy conservation required for a second-order phase transition.

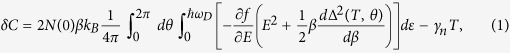graphic file with name srep44024-m5.jpg

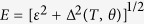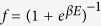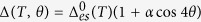where N(0) is the density of states at the Fermi surface, β = 1/kBT, Inline graphic, Inline graphic, and Inline graphic an extended s-wave where α and θ represent the gap anisotropy and polar angle, respectively33,34. Note that in an angle-integrated measurement, the functional forms containing cos 4 θ and cos 2 θ result in the same parameters and hence, it is not possible to distinguish between an extended s-wave and a d-wave symmetry. We found that a single anisotropic s-wave model, either with or without accidental nodes, does not fit to the δC/T data (see Supplementary information, Figs S1–S3). Since δC indicated a signature of two superconducting gaps, we also tried a phenomenological two-gap model35,36,37 by taking a sum of either two s-wave-gaps (see Supplementary information, Fig. S4) or an s-wave + an extended s-wave gaps (s + es), Fig. 3 (see also Supplementary information, Fig. S5), to describe the data. In the fitting, more weight was given to the low-temperature data, i.e., the data below T = 5 K. The reason being, close to Tc the thermal fluctuations become stronger, and may result in increasing deviation of the data from the applied models which are based on a mean-field framework. We found that both models lead to satisfactory fits. Hence, the exact superconducting gap structure of FeSe cannot be unambiguously determined from analyzing the specific-heat data alone. However, as discussed later, with the help of fitting several models also to the tunnelling spectra (see Supplementary information, Figs S8–S11), we could select (s + es) model as a proper model to describe the C(T)-data, with the larger gap assigned to the extended s-wave. The goodness of fit for each model tried here is presented in the Supplementary information Table S1. The gap values in the T → 0 limit estimated from the (s + es) model fitting are: a small s-wave gap of Δs(0) = 0.25(3) meV and a large anisotropic extended s-wave gap of 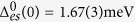Inline graphic with α = 0.34. The value of α < 1 obtained here clearly rules out the presence of accidental nodes38. Since the obtained isotropic gap value Δs(0) is very small, a possible anisotropy of this gap would be beyond the resolution of our experiments. Further, a recent heat capacity study of FeSe single crystals by Wang et al.31 reports a small residual value of the electronic specific heat originating from low-energy quasiparticle excitations indicating either line nodes or deep gap minima. However, their experiment did not show the shoulder in C(T) which we observe below 2 K and interpret as the mark of a second, smaller superconducting gap. In our case, this shoulder limits the analysis of the functional form of δC(T) as T → 0. Therefore, if we consider the data only below 1 K, the presence of accidental nodes can not be ruled out based on the specific heat analysis.

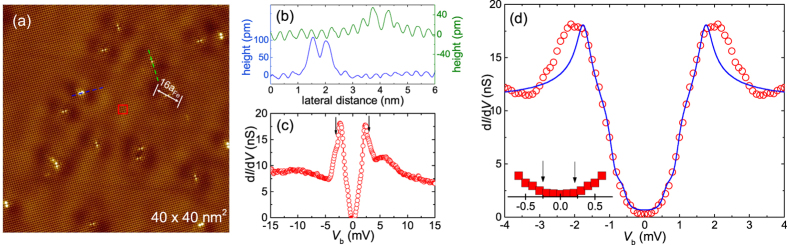
In order to determine the superconducting gap structure of FeSe microscopically, we performed STM measurements at 0.35 K. The topographic images, e.g. Fig. 4(a), revealed atomically resolved clean Se-terminated surfaces indicating good sample quality, very similar to our previous report39. The Se-Se distance aSe−Se = 3.7(1) Å observed here is in line with the distance of 3.7702(5) Å found by x-ray diffraction on our crystals30. A few protrusions (see Fig. 4(b) for line scans across the impurities) on the top of the surface likely correspond to Se-Se bound atoms left over from the top-most counter layer while cleaving, or to an impurity atom occupying the Fe-site underneath the topmost Se-layer. Alternatively, recent density functional theory (DFT) based calculations suggested that Fe-site vacancies can perturb orbitals on neighbouring Se-sites, thereby producing atomic dumbbells40. All these defects act as impurities and induce additional dumbbell-like unidirectional depressions in the topography, known as “electronic dimers”41, marked by the white line in Fig. 4(a). Interestingly, the unidirectional behaviour of these electronic dimers can be unveiled from the fact that the orientation of the dimers is independent of the orientation of the impurities but rotates by 90° across the twin boundary (TB) obvious from the bright stripe in the topography, Supplementary information, Fig. S6. This behaviour represents a broken C4 symmetry in the impurity scattering. The length of the electronic dimers is ≈16 aFe, where aFe is the distance of the Fe-Fe atoms in the crystal structure, which is consistent with a previous report41. We note that all electronic dimers are oriented in the same direction in Fig. 4(a) indicating the entire image consists of a single crystallographic domain.

Figure 4. STM topography and spectroscopy.

Figure 4

Open in a new tab

(a) A topography of FeSe on an area of 40 × 40 nm2 obtained at 0.35 K. The white line mark one of the unidirectional electronic dimer of length ~16 aFe, where aFe is the distance of the Fe-Fe atoms in the crystal structure. The bias voltage and the tunnelling currents were set at Vb = 10 mV and Isp = 100 pA, respectively. The tunnelling conductance is acquired by the standard lock-in technique with a small modulation voltage of 0.05 mVrms. (b) Line scans along the blue and green lines marked in (a) displaying the heights of the impurities. (c) An average tunnelling spectrum measured within the area of 1 × 1 nm2 [red square in (a)] at 0.35 K. The arrows indicate “wing”-like features mentioned in the text. (d) A fit (solid line) of a Dynes gap function to the symmetrized data (open circles) in the Vb range ±3 mV for an (s + es)-wave model. For the fit, the thermal broadening as well as the broadening caused by a finite energy resolution was taken into account. Inset: The tunneling conductance at |Vb| → 0. The arrows mark the voltage range at which dI/dV ≈ 0 (cf. Supplementary information, Fig. S11).

In Fig. 4(c), a tunnelling spectrum averaged over an area marked in Fig. 4(a) is presented. Since the spectra were measured approximately in the middle of Fig. 4(a), a possible TB is at least a minimum distance of 20 nm away. The most prominent feature of the spectrum is that, as Vb → 0, the spectrum attains a “U”-shape. Here, “U”-shape refers to the finite energy range within which the experimental tunnelling conductance is zero, as more clearly seen in Fig. 4(d). Due to the estimated small magnitude of the smaller gap (see above) a zero tunnelling conductance is only expected within a very narrow energy range. A tunnelling conductance of zero indicates the absence of quasiparticle excitations within the superconducting gap, thus providing strong evidence for a nodeless superconductivity in FeSe. However, the spectrum contains additional hump-like features at energies ≈−10 mV and +5.4 mV. These represent either simply the bottom of an electron band and the top of a hole band, respectively, or more complex phenomena such as a density-wave type ordering39 or an electron-boson coupling42. In addition, there are “wing”-like features contained in the coherence peaks at energies Vb ≈ ±2.75 mV, indicated by black arrows in Fig. 4(c). These features may be related to the fine details of the band structure, such as spin-orbit coupling43 induced band-hybridization38,44,45, which is beyond the scope of this paper.

In an attempt to describe the tunnelling spectra, we used a Dynes gap function46 to fit the data. Within the standard picture of the BCS model32, the tunnelling conductance 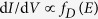Inline graphic, where

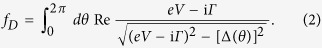graphic file with name srep44024-m11.jpg

Here, the spectral broadening is given by the inverse quasiparticle lifetime Γ. Since the experimental spectra did not indicate the presence of nodes, we first tried a single extended s-wave gap function 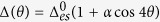Inline graphic to fit the data (see Supplementary information, Fig. S11). Although the fitted curve followed the experimental data well in the applied bias voltage range 0.5 meV < |Vb| < 0.75 meV, below 0.5 meV, the fitted curve deviated from the experimental data as Vb → 0. This suggested the presence of a small second gap as already inferred from the specific heat analysis. However, the coherence peaks corresponding to the smaller gap could not be resolved in our experiments due to its small magnitude, which is at the limits of our instrumental resolution. To take this into account, we included an energy resolution of 0.16 meV in the fit procedure, which accounts for the spectral broadening caused by thermal effects (0.35 K) as well as a finite modulation voltage (0.05 mVrms). In Fig. 4(d), the best fit to the experimental spectrum is presented. This fit corresponds to an (s + es) model with an s-wave gap of Δs = 0.6(1) meV and an extended s-wave gap 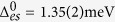Inline graphic and α = 0.30(1). These values are slightly different than those obtained from the specific heat analysis. Here we would like to emphasize that the models considered here should not be taken exhaustive, rather it should be understood as a minimum ansatz to describe the overall behaviour of the spectrum, which agrees semi-quantitatively with the specific-heat analysis. By considering the raw data alone and leaving the models aside, the multigap nature of the superconducting gap is derived from the specific heat measurements, whereas, the nodeless nature of the gap is concluded from the tunnelling spectroscopy measurements.

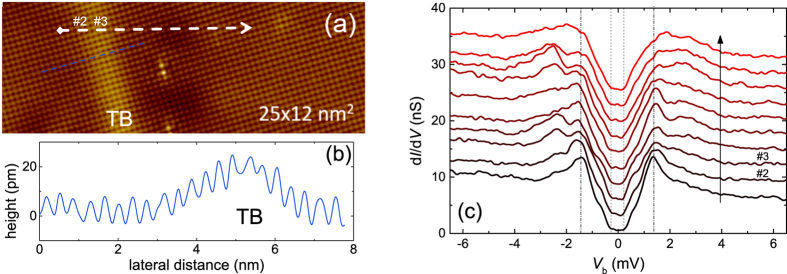
Following this indication towards nodeless superconductivity in FeSe, we now show — using STM/STS — that the gap structure appears to remain nodeless on different crystallographic twin domains as well as at the TB. In Fig. 5(a), an STM topographic image over an area of 25 × 12 nm2 containing a TB is presented. This image is a part of the topography of 40 × 40 nm2 presented in Fig. S6 (Supplementary information). A height scan across the TB is shown in Fig. 5(b). Several spectra were measured along the white line in Fig. 5(a) in such a way that the spectra were distributed on either side as well as on the TB. As can be seen in Fig. 5(c), the spectra retains an overall “U”-shape across the TB, warranting the robustness of the nodeless gap structure in our single crystal. Alternatively, Watashige et al.27 observed a lifting of nodes in the vicinity of a TB and interpreted this finding in terms of time reversal symmetry breaking caused by a π/2 rotation of the crystallographic domains. They also found that the influence of the TB on the superconducting gap structure extends up to a length scale of more than 50 nm. Since the spectra shown in Fig. 5(c) were measured only up to 9 nm away from the twin boundary, our results shown in Fig. 5 do not directly contradict those of ref. 27. However, we did not find any signature of pair-breaking by observing a formation of bound states in the spectra taken on the TB, which was suggestive of a time reversal symmetry breaking. For the sake of confirming the U-shape of the tunneling spectra at small Vb as a common feature of our sample, we performed STM/STS on a second crystal. In this case we conducted our measurements on an area of 100 × 100 nm2 without any TB, see Supplementary information Fig. S7. As can be seen in Fig. S7(b), even the small gap could be resolved in some cases in the tunneling spectra. However, within a small range of Vb, the spectra retain a U-shape indicating the absence of low energy quasiparticle excitations owing to finite superconducting gap over the Fermi surface.

Figure 5. Tunneling spectra at a twin boundary.

Figure 5

Open in a new tab

(a) A 25 × 12 nm2 topography of FeSe with a twin boundary (TB), which is zoomed from Fig. S6 (Supplementary information). (b) A line scan along the blue line depicted in (a). (c) Ten tunnelling spectra measured laterally at equidistant positions along the white dashed line in (a). The black arrow in (c) represents the direction of measurement shown in (a). Spectra #2 and #3 are measured on the TB. Curves are equally shifted vertically for clarity. The bias voltage and the tunnelling currents were set at Vb = 10 mV and Isp = 100 pA, respectively.

Discussion

In the framework of a single-band BCS theory, the zero-temperature upper critical field Hc2(0) is proportional to (Δ/vF)2, vF being the Fermi velocity47. In a phenomenological two-gap model, Hc2(0) is set by the larger gap, and the critical field for the smaller gap H*(0) can be determined by thermodynamic, e.g., specific-heat48 and thermal-conductivity25 measurements. Shubnikov-de Haas oscillation measurements have reported comparable values of vF for the different Fermi sheets in FeSe49. By taking the maximum gap value 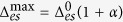Inline graphic and Δs(0) obtained from the C(T) analysis, we estimate, 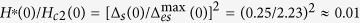Inline graphic. This value is in good agreement with the data reported by Bourgeois-Hope et al.25, thus further supporting the validity of the current analysis. As far as the absence of nodes is concerned, our results are also in good agreement with recent thermal conductivity25, penetration depth50, and microwave conductivity51 measurements on single crystals of similar quality.

It is worthwhile to discuss the possible origin of the discrepancy between the STM results presented here in comparison to those in refs 24,27. The nodes observed in FeSe are considered accidental, i.e., they are not imposed by symmetry1,2. Theoretical investigations of multiorbital microscopic models have suggested that the nodes in the Fermi surface can be lifted by disorder52 or external strain53. One of the ways to get a semi-quantitative estimation of the degree of disorder in a sample is to look at its RRR value. However, we would like to point out that in the particular case of FeSe, the RRR calculated by taking the resistivity values from above and below Ts contain additional contributions other than initial intrinsic disorder of the crystal which exists at room temperature. As observed by Knöner et al.54, cooling the samples through Ts induces different twin states in the samples in question; which together with the finite in-plane anisotropy can produce different resistivity values below Ts. A similar observation was also made in ref. 25. Therefore, the crystals showing lower RRR likely contain more twins, and TB are considered accountable for lifting the nodes27. Nonetheless, a very recent thermal conductivity25 measurement on samples grown by flux-vapour transport55 with the RRR values similar to those used in refs 24,27, exhibited two-gap nodeless superconductivity. It is rather intriguing that such negligibly small differences in the samples appear to be sufficient to influence the superconducting gap structure in FeSe.

Our observation of two superconducting gaps Δs and Δes with strongly different gap magnitudes, i.e. 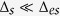Inline graphic, indicates that superconductivity appears presumably in one band (producing a large gap Δes) and may induce a second small gap Δs in another band due to a proximity effect44,56. Nonetheless, both gaps open at the same temperature, but may have different temperature dependencies1. So far in FeSe, only one hole Fermi sheet and one electron Fermi pocket are detected by angle-resolved photoemission spectroscopy (ARPES)57 and quantum oscillation experiments49,58. If this is correct, then an inter-band extended s-wave pairing with a sign reversal of the order parameter between different Fermi surface sheets might be the likely mechanism of superconductivity in FeSe3. However, there are experimental indications for more than one electron pocket crossing the Fermi energy59,60. In this case, a more exotic pairing mechanism such as band-hybridization induced odd frequency pairing can be expected44.

In summary, we have investigated the superconducting gap structure of FeSe in a combined study of scanning tunnelling microscopy and specific heat measurements. The results indicate multigap superconductivity in FeSe single crystals. Our analysis suggests that the gap is of (s + es) type. The isotropic s-wave gap is much smaller than the anisotropic s-wave gap. Additionally, the tunnelling spectroscopy indicate at a superconducting gap which remains nodeless also on twin boundaries. These experimental results are expected to provide important ingredients for a unified theory of the superconducting paring mechanism for all FeSe-related superconductors.

Note added: In the revising stage of this manuscript we became aware of a new STM study on FeSe reported very recently61. Our conclusions presented here are in excellent agreement with these complementary investigations in which the Bogoliubov quasipaticle scattering interference (BQPI) was used to determine the superconducting gap symmetry as extremely anisotropic, but nodeless with an OP changing sign between the hole and electron pockets. In addition, ref. 61 also provides evidence for an orbital-selective Cooper pairing in FeSe.

Methods

The single crystals were grown by chemical vapour transport30,62 of stoichiometric FeSe powder containing α-Fe of less than 300 ppm. The ratio of FeSe to the transport additive AlCl3 was taken as 50:1. Typically, a mixture of 1 g of FeSe powder and 20 mg of AlCl3 was placed in a quartz ampoule of length 10 cm and diameter 2 cm prepared inside an argon-filled glove box. The ampoule containing the mixture was evacuated, sealed, and placed horizontally inside a two-zone furnace at temperatures from T2 = 673 K and T1 = 573 K. The crystal growth was carried out for 2 months. Finally, the ampoule was quenched in water. The product, which contained plate-shaped single crystals with edge lengths up to 400 μm perpendicular to the c axis, was washed repeatedly in ethanol to remove remaining condensed gas phase, dried under vacuum and stored in the glove box. By extending the growth time to one year, larger single crystals with dimensions up to 4 × 2 × 0.03 mm3 could be grown. The specific heat C(T, B) was measured down to 0.5 K using a thermal-relaxation method in a physical property measurement system (Quantum Design) with the magnetic field B applied parallel to the [001] direction of the single crystal. The scanning tunnelling microscopy/spectroscopy measurements were performed in an ultra-high vacuum (p < 3 × 10−9 Pa) cryogenic STM with a base temperature T ≈ 0.35 K. The bias voltage and the tunnelling currents were set at Vb = 10 mV and Isp = 100 pA, respectively. The tunnelling conductance is acquired by the standard lock-in technique with a small modulation voltage of 0.05 mVrms. Given the total energy resolution ΔE of the STM is limited by 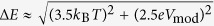Inline graphic63, the low temperature (0.35 K) and the small modulation voltage (0.05 mVrms) used here allows us to resolve the fine structure of the superconducting gap. The FeSe single crystals were cleaved in situ at 20 K before being inserted into the STM-head.

Additional Information

How to cite this article: Jiao, L. et al. Superconducting gap structure of FeSe. Sci. Rep. 7, 44024; doi: 10.1038/srep44024 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep44024-s1.pdf (2.4MB, pdf)

Acknowledgments

Financial support from the Deutsche Forschungsgemeinschaft (DFG) within the Schwerpunktprogramm SPP1458 is gratefully acknowledged. L.J. thanks the Alexander-von-Humboldt foundation for financial support. C.L.H. acknowledges technical support from C. Klausnitzer. We thank A. Akbari, S. Borisenko, Y. Grin, M. Haverkort, P. J. Hirschfeld, P. Thalmeier, and L. H. Tjeng for discussions.

Footnotes

The authors declare no competing financial interests.

Author Contributions S.R. and S.W. conceived the experiments, C.K. and U.S. prepared the samples, L.J. and C.-L.H. conducted the experiments, L.J., C.-L.H., and U.K.R. analysed the results. S.R., L.J., and C.-L.H. wrote the paper. All authors reviewed the manuscript.

References

  1. Hirschfeld P. J., Korshunov M. M. & Mazin I. I. Gap symmetry and structure of Fe-based superconductors. Rep. Prog. Phys. 74, 124508 (2011). [Google Scholar]
  2. Hirschfeld P. J. Using gap symmetry and structure to reveal the pairing mechanism in Fe-based superconductors. C. R. Physique 17, 197–231 (2016). [Google Scholar]
  3. Mazin I. I., Singh D. J., Johannes M. D. & Du M. H. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx. Phys. Rev. Lett. 101, 057003 (2008). [DOI] [PubMed] [Google Scholar]
  4. Kuroki K. et al. Unconventional pairing originating from the disconnected Fermi surfaces of superconducting LaFeAsO1−xFx. Phys. Rev. Lett. 101, 087004 (2008). [DOI] [PubMed] [Google Scholar]
  5. Wang F., Zhai H., Ran Y., Vishwanath A. & Lee D.-H. Inverse proximity effect in superconductor-ferromagnet bilayer structures. Phys. Rev. Lett. 102, 047005 (2009). [DOI] [PubMed] [Google Scholar]
  6. Kontani H. & Onari S. Orbital-fluctuation-mediated superconductivity in iron pnictides: analysis of the five-orbital Hubbard-Holstein model. Phys. Rev. Lett. 104, 157001 (2010). [DOI] [PubMed] [Google Scholar]
  7. Hsu F.-C. et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl. Acad. Sci. USA 105, 14262–14264 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Mizuguchi Y., Tomioka F., Tsuda S., Yamaguchi T. & Takano Y. Superconductivity at 27 K in tetragonal FeSe under high pressure. Appl. Phys. Lett. 93, 152505 (2008). [Google Scholar]
  9. Medvedev S. et al. Electronic and magnetic phase diagram of β-Fe1.01Se with superconductivity at 36.7 K under pressure. Nature Mater. 8, 630–633 (2009). [DOI] [PubMed] [Google Scholar]
  10. Margadonna S. et al. Pressure evolution of the low-temperature crystal structure and bonding of the superconductor FeSe (Tc = 37 K). Phys. Rev. B 80, 064506 (2009). [Google Scholar]
  11. Imai T., Ahilan K., Ning F. L., McQueen T. M. & Cava R. J. Why does undoped FeSe become a high-Tc superconductor under pressure? Phys. Rev. Lett. 102, 177005 (2009). [DOI] [PubMed] [Google Scholar]
  12. Wang Q.-Y. et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 29, 037402 (2012). [Google Scholar]
  13. Ge J.-F. et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nature Mater. 14, 285–289 (2015). [DOI] [PubMed] [Google Scholar]
  14. Fan Q. et al. Plain s-wave superconductivity in single-layer FeSe on SrTiO3 probed by scanning tunnelling microscopy. Nature Phys. 11, 946–952 (2015). [Google Scholar]
  15. Zhang Y. et al. Superconducting gap anisotropy in monolayer FeSe thin film. Phys. Rev. Lett. 117, 117001 (2016). [DOI] [PubMed] [Google Scholar]
  16. McQueen T. M. et al. Tetragonal-to-orthorhombic structural phase transition at 90 K in the superconductor Fe1.01Se. Phys. Rev. Lett. 103, 057002 (2009). [DOI] [PubMed] [Google Scholar]
  17. Fernandes R. M., Chubukov A. V. & Schmalian J. What drives nematic order in iron-based superconductors? Nature Phys. 10, 97–104 (2014). [Google Scholar]
  18. Khasanov R. et al. Evidence of nodeless superconductivity in FeSe0.85 from a muon-spin-rotation study of the in-plane magnetic penetration depth. Phys. Rev. B 78, 220510(R) (2008). [Google Scholar]
  19. Dong J. K. et al. Multigap nodeless superconductivity in FeSex: Evidence from quasiparticle heat transport. Phys. Rev. B 80, 024518 (2009). [Google Scholar]
  20. Khasanov R. et al. Evolution of two-gap behavior of the superconductor FeSe1−x Phys. Rev. Lett. 104, 087004 (2010). [DOI] [PubMed] [Google Scholar]
  21. Ponomarev Ya. G. et al. Andreev spectroscopy of FeSe: Evidence for two-gap superconductivity. J. Exp. Theor. Phys. 113, 459–467 (2011). [Google Scholar]
  22. Lin J.-Y. et al. Coexistence of isotropic and extended s-wave order parameters in FeSe as revealed by low-temperature specific heat. Phys. Rev. B 84, 220507(R) (2011). [Google Scholar]
  23. Abdel-Hafiez M. et al. Temperature dependence of lower critical field Hc1(T) shows nodeless superconductivity in FeSe. Phys. Rev. B 88, 174512 (2013). [Google Scholar]
  24. Kasahara S. et al. Field-induced superconducting phase of FeSe in the BCS-BEC cross-over. Proc. Natl. Acad. Sci. USA 111, 16309–16313 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bourgeois-Hope P. et al. Thermal conductivity of the iron-based superconductor FeSe: nodeless gap with strong two-band character. Phys. Rev. Lett. 117, 097003 (2016). [DOI] [PubMed] [Google Scholar]
  26. Song C.-L. et al. Direct observation of nodes and twofold symmetry in FeSe superconductor. Science 332, 1410–1413 (2011). [DOI] [PubMed] [Google Scholar]
  27. Watashige T. et al. Evidence for time-reversal symmetry breaking of the superconducting state near twin-boundary interfaces in FeSe revealed by scanning tunneling spectroscopy. Phys. Rev. X 5, 031022 (2015). [Google Scholar]
  28. Bouquet F., Fisher R. A., Phillips N. E., Hinks D. G. & Jorgensen J. D. Specific heat of Mg11B2: Evidence for a second energy gap. Phys. Rev. Lett. 87, 047001 (2001). [DOI] [PubMed] [Google Scholar]
  29. McQueen T. M. et al. Extreme sensitivity of superconductivity to stoichiometry in Fe1+δSe. Phys. Rev. B 79, 014522 (2009). [Google Scholar]
  30. Koz C. et al. Synthesis and crystal growth of tetragonal β-Fe1.00Se. Z. Anorg. Allg. Chem. 640, 1600 (2014). [Google Scholar]
  31. Wang L. et al. Physica Status Solidi B, doi: 10.1002/pssb.201600153 (2016). [DOI] [Google Scholar]
  32. Bardeen J., Cooper L. N. & Schrieffer J. R. Theory of superconductivity. Phys. Rev. 108, 1175 (1957). [Google Scholar]
  33. Maier T. A., Graser S., Scalapino D. J. & Hirschfeld P. J. Origin of gap anisotropy in spin fluctuation models of the iron pnictides Phys. Rev. B 79, 224510 (2009). [Google Scholar]
  34. Chubukov A. V., Vavilov M. G. & Vorontsov A. B. Momentum dependence and nodes of the superconducting gap in the iron pnictides. Phys. Rev. B 80, 140515(R) (2009). [Google Scholar]
  35. Suhl H., Matthias B. T. & Walker L. R. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 3, 552 (1959). [Google Scholar]
  36. Moskalenko V. A. Superconductivity of metals taking into account the overlapping of energy bands. Phys. Met. Metallogr+ 8, 25–36 (1958). [Google Scholar]
  37. Zehetmayer M. A review of two-band superconductivity: materials and effects on the thermodynamic and reversible mixed-state properties. Supercond. Sci. Technol. 26, 043001 (2013). [Google Scholar]
  38. Hinojosa A. & Chubukov A. V. Gap structure in Fe-based superconductors with accidental nodes: The role of hybridization. Phys. Rev. B 91, 224502 (2015). [Google Scholar]
  39. Rößler S. et al. Emergence of an incipient ordering mode in FeSe. Phys. Rev. B 92, 060505(R) (2015). [Google Scholar]
  40. Huang D. et al. Dumbell defects in FeSe films: A scanning tunneling microscopy and First-Principle investigations. Nano Lett. 16, 4224–4229 (2016). [DOI] [PubMed] [Google Scholar]
  41. Song C. -L. et al. Suppression of superconductivity by twin boundaries in FeSe. Phys. Rev. Lett. 109, 137004 (2012). [DOI] [PubMed] [Google Scholar]
  42. Song C.-L. et al. Imaging the electron-boson coupling in superconducting FeSe films using a scanning tunneling microscope. Phys. Rev. Lett. 112, 057002 (2014). [DOI] [PubMed] [Google Scholar]
  43. Borisenko S. V. et al. Direct observation of spin–orbit coupling in iron-based superconductors. Nature Phys. 12, 311–317, 3594 (2015). [Google Scholar]
  44. Black-Schaffer A. M. & Balatsky A. V. Odd-frequency superconducting pairing in multiband superconductors. Phys. Rev. B 88, 104514 (2013). [Google Scholar]
  45. Komendová L., Balatsky A. V. & Black-Schaffer A. M. Experimentally observable signatures of odd-frequency pairing in multiband superconductors. Phys. Rev. B 92, 094517 (2015). [Google Scholar]
  46. Dynes R. C., Narayanamurti V. & Garno J. P. Direct measurement of quasiparticle-lifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509 (1978). [Google Scholar]
  47. Shulga S. V. & Drechsler S. -L. Low temperature value of the upper critical field Hc2(0) of isotropic single band metals. J. Low Temp. Phys. 129, 93–102 (2002). [Google Scholar]
  48. Bouquet F. et al. Specific heat of single crystal MgB2: A two-band superconductor with two different anisotropies. Phys. Rev. Lett. 89, 257001 (2002). [DOI] [PubMed] [Google Scholar]
  49. Terashima T. et al. Anomalous Fermi surface in FeSe seen by Shubnikov–de Haas oscillation measurements. Phys. Rev. B 90, 144517 (2014). [Google Scholar]
  50. Teknowijoyo S. et al. Enhancement of Tc by point-like disorder and anisotropic gap in FeSe. Phys. Rev. B 94, 064521 (2016). [Google Scholar]
  51. Li M. et al. Superfluid density and microwave conductivity of FeSe superconductor: ultra-long-lived quasiparticles and extended s-wave energy gap. New J. Phys. 18, 082001 (2016). [Google Scholar]
  52. Mishra V. et al. Lifting of nodes by disorder in extended-s–state superconductors: Application to ferropnictides Phys. Rev. B 79, 094512 (2009). [Google Scholar]
  53. Kang J., Kemper A. F. & Fernandes R. M. Manipulation of gap nodes by uniaxial strain in iron-based superconductors. Phys. Rev. Lett. 113, 217001 (2014). [DOI] [PubMed] [Google Scholar]
  54. Knöner S. et al. Resistivity and magnetoresistance of FeSe single crystals under helium gas-pressure. Phys. Rev. B 91, 174510 (2015). [Google Scholar]
  55. Böhmer A. E. et al. Lack of coupling between superconductivity and orthorhombic distortion in stoichiometric single-crystalline FeSe. Phys. Rev. B 87, 180505(R) (2013). [Google Scholar]
  56. McMillan W. L. Tunneling model of the superconducting proximity effect. Phys. Rev. 175, 537 (1968). [Google Scholar]
  57. Maletz J. et al. Unusual band renormalization in the simplest iron-based superconductor FeSe1−x. Phys. Rev. B 89, 220506(R) (2014). [Google Scholar]
  58. Watson M. D. et al. Dichotomy between the hole and electron behavior in multiband superconductor FeSe probed by ultrahigh magnetic fields. Phys. Rev. Lett. 115, 027006 (2015). [DOI] [PubMed] [Google Scholar]
  59. Watson M. D. et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B 91, 155106 (2015). [Google Scholar]
  60. Huynh K. K. et al. Electric transport of a single-crystal iron chalcogenide FeSe superconductor: Evidence of symmetry-breakdown nematicity and additional ultrafast Dirac cone-like carriers. Phys. Rev. B 90, 144516 (2014). [Google Scholar]
  61. Sprau P. O. et al. Discovery of orbital-selective Cooper pairing in FeSe. arXiv:1611.02134 (2016). [DOI] [PubMed]
  62. Rößler S., Koz C., Wirth S. & Schwarz U. Synthesis, phase stability, structural, and physical properties of 11-type iron chalcogenides. Phys. Status Solidi B, doi: 10.1002/pssb.201600149 (2016). [DOI] [Google Scholar]
  63. Lauhon L. J. & Ho W. Effects of temperature and other experimental variables on single molecule vibrational spectroscopy with the scanning tunneling microscope. Rev. Sci. Instrum. 72, 216–213 (2001). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep44024-s1.pdf (2.4MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES