Learning‐based deformable image registration for infant MR images in the first year of life

Abstract

Purpose

Many brain development studies have been devoted to investigate dynamic structural and functional changes in the first year of life. To quantitatively measure brain development in such a dynamic period, accurate image registration for different infant subjects with possible large age gap is of high demand. Although many state‐of‐the‐art image registration methods have been proposed for young and elderly brain images, very few registration methods work for infant brain images acquired in the first year of life, because of (a) large anatomical changes due to fast brain development and (b) dynamic appearance changes due to white‐matter myelination.

Methods

To address these two difficulties, we propose a learning‐based registration method to not only align the anatomical structures but also alleviate the appearance differences between two arbitrary infant MR images (with large age gap) by leveraging the regression forest to predict both the initial displacement vector and appearance changes. Specifically, in the training stage, two regression models are trained separately, with (a) one model learning the relationship between local image appearance (of one development phase) and its displacement toward the template (of another development phase) and (b) another model learning the local appearance changes between the two brain development phases. Then, in the testing stage, to register a new infant image to the template, we first predict both its voxel‐wise displacement and appearance changes by the two learned regression models. Since such initializations can alleviate significant appearance and shape differences between new infant image and the template, it is easy to just use a conventional registration method to refine the remaining registration.

Results

We apply our proposed registration method to align 24 infant subjects at five different time points (i.e., 2‐week‐old, 3‐month‐old, 6‐month‐old, 9‐month‐old, and 12‐month‐old), and achieve more accurate and robust registration results, compared to the state‐of‐the‐art registration methods.

Conclusions

The proposed learning‐based registration method addresses the challenging task of registering infant brain images and achieves higher registration accuracy compared with other counterpart registration methods.

1. Introduction

During the first year of postnatal development, the human brain grows rapidly in brain volume and also dramatically changes in both cortex and white‐matter structures.^{1, 2} For instance, the whole brain volume increases from ~36% at 2–4 weeks to ~72% of adult volume at 12 months.^{1, 3} Several neuroscience studies aimed to understand the human brain development in this dynamic period. Modern imaging, such as MRI (magnetic resonance imaging), provides a non‐invasive measurement of the whole brain. Hence, MRI has been increasingly used in many neuroimaging‐based studies of early brain development and developmental disorders.^{3, 4, 5}

To quantify structural changes across infant subjects, deformable image registration can provide an accurate special normalization of subtle geometric difference. Although many image registration methods^{6, 7, 8, 9, 10, 11, 12} have been proposed in the last two decades, very few methods work for infant MR brain images acquired during early development, due to the two following difficulties:

• Fast brain development. As shown in Fig. 1, not only the whole brain volume expands, but also the folding patterns in the cortical regions develop rapidly from birth to 1 year old. Hence, infant image registration is required to have the capacity of dealing with this large deformation.

• Dynamic and non‐linear appearance changes across different brain development stages. In general, there are three stages of brain development in the first year,^{13, 14} that is, (a) infantile stage (≤ 5 months), (b) iso‐intense stage (6–8 months), and (c) early adult‐like stage (≥ 9 months). As reflected by different brain time the intensity histograms in Fig. 1, image appearances in WM (white matter) and GM (gray matter) change dramatically due to white‐matter myelination. Since many image registration methods are mainly based on image intensity or local appearance,^{15, 16, 17, 18, 19, 20} such dynamic appearance changes over time can pose significant difficulty for infant brain image registration.

Figure 1.

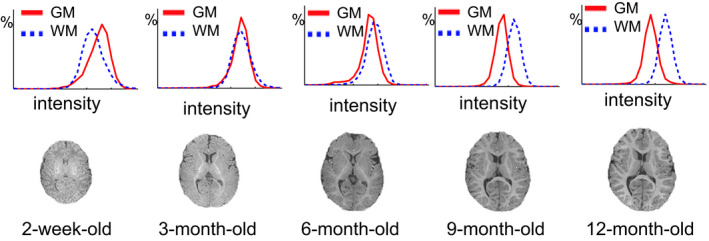
Dynamic infant brain development from 2‐week‐old to 12‐month‐old. The first row shows the histograms of WM and GM intensities for the T1‐weighted MR images shown in the second row, acquired at 2‐week‐old, 3‐, 6‐, 9‐, and 12‐month‐old, respectively. These histograms and images show large anatomical and dynamic appearance changes for the infant MR brain images acquired in the first year of postnatal development. [Color figure can be viewed at wileyonlinelibrary.com]

To address the above two difficulties, we propose a novel learning‐based registration framework to accurately register any infant image in the first year of life (even with possible significant age gap) to a pre‐defined template image. Since volumetric image is in high dimension, we leverage regression forest^{21, 22, 23} to learn two complex mappings in a patchwise manner: (a) Patchwise appearance‐displacement model that characterizes the mapping from the patchwise image appearance to the voxelwise displacement vector, where the displacement at the patch center points to the corresponding location in the template image space; (b) patchwise appearance‐appearance model that encodes the evolution of patchwise appearance from one particular brain development stage to the corresponding image patch in the template domain (of another brain development stage). In the application stage, before registering the new infant image to the template, for each voxel in the new infant image, we predict its initial displacement to the template by the learned patchwise appearance‐displacement model. In this way, we obtain a dense deformation field to initialize the registration of the new infant image to the template. Then, we further apply the learned patchwise appearance‐appearance model to predict the template‐like appearance for the new infant image. With this initialized deformation field and also the estimated appearance for the new infant image under registration, many conventional registration methods, for example, diffeomorphic Demons,^{15, 16, 24, 25, 26} can be used to estimate the small remaining deformations between the new infant brain image and the template.

In our previous work, we have proposed a sparse representation‐based image registration method²⁷ for infant brains, by leveraging the known temporal correspondences among the training subjects to guide the image registration of two new infant images at different time points. Specifically, to register the two new infant images with possible large age gap, we first identify the corresponding image patches between each new infant image and its respective training images with similar age by sparse representation technique. Then, the registration between the two new infant images can be assisted by the learned growth trajectories from one time point to another time point. However, this method is very time consuming to solve the sparse representation problem at each time point, thus making it less attractive in clinical applications.

In this paper, we have comprehensively evaluated the registration performance of our proposed method for infant images at 2‐week‐old, 3‐month‐old, 6‐month‐old, 9‐month‐old, and 12‐month‐old with comparison to the state‐of‐the‐art deformable image registration methods, including diffeomorphic Demons registration method^{15, 16} (http://www.insight-journal.org/browse/publication/154), the SyN registration method in ANTs package (http://sourceforge.net/projects/advants/) using mutual information^{17, 18} and cross correlation^{19, 20} as similarity measures, and 3D‐HAMMER²⁸ using the segmentation images obtained with iBEAT software (http://www.nitrc.org/projects/ibeat/).²⁹ Based on both quantitative measurements and visual inspection, our proposed learning‐based registration method outperforms all other deformable image registration methods under comparison for the case of registering infant brain MR image with large anatomical and appearance changes.

The remaining parts of this paper are organized as follows. In Section Methods, we present technical details of the proposed regression‐forest‐based infant brain registration method. In Section 3, we give experimental results. Finally, in Section 4, the conclusion is provided.

2. Method

The goal of our infant brain registration method is to register any infant brain image in the first year of life with possible large age gap to the template image T. Our learning‐based infant registration method consists of training and application stages, as detailed in the next subsections.

Each subject in the training dataset has both MRI structural and DTI scans at 2 weeks old, 3 months old, 6 months old, 9 months old, and 12 months old. It is worth indicating that no ground‐truth deformation fields between the subject and the template brain images are available, thus difficult to train and validate our learning models. To deal with this critical issue, we use a multimodal longitudinal infant brain segmentation algorithm¹⁴ to segment each time point image into WM, GM, and cerebrospinal fluid (CSF) by leveraging both multimodal image information and the longitudinal heuristics in temporal domain. And then, these segmentation results are manually edited. Since the segmented images are free from appearance difference, we can use these segmented images to estimate the deformation field between each training image and the template image by 4D‐HAMMER registration method.³⁰ Next, the estimated deformation fields (based on the segmented images) can be considered as ground truth (or target deformation fields) for both training and validating our appearance‐displacement model. Although these obtained deformation fields are not the gold standard for training, they can approximately reproduce actual anatomical correspondences, thus giving a way to provide the initial deformation field by our proposed appearance‐displacement model.

2.A. Training stage — learn to predict the deformation and appearance changes by respective regression‐forest models

In the training stage, N MR image sequences $\{I_n^t|n=1,\dots ,N,t=1,\dots ,M\}$, each with M = 5 time points (scanned at 2‐week‐old, 3‐month‐old, 6‐month‐old, 9‐month‐old, and 12‐month‐old), are used as the training dataset. All data are transformed from each subject's native space to a randomly selected template space via affine registration by FSL's linear registration tool (FLIRT) in FSL package.³¹ Note that, although in the application stage, only the T1‐ or T2‐ weighted MR images (depending on the scanning time point) will be used for registration, in the training images, we use multimodal images, such as T1‐weighted, T2‐weighted MR images, and DTI (diffusion tensor imaging), to obtain tissue segmentation images for helping training. Thanks to the complete longitudinal image information and also the complementary multimodal imaging information, we first deploy the state‐of‐the‐art longitudinal multimodal image segmentation method^{29, 32} to accurately segment each infant brain image to WM, GM, and CSF. Since there are no any appearance changes in these segmented images, we use a longitudinal image registration method³⁰ to simultaneously calculate the temporal deformation fields from every time point to a pre‐defined template image T, with the temporal consistency enforced by the estimated spatial deformation fields along time. Thus, we obtain the deformation fields ${\mathrm{\Phi }}_n^t=\{{\mathit{\phi }}_n^t(v)|v\in {\mathrm{\Omega }}_T\}$. It is worth noting that our goal of training patchwise appearance‐displacement model is to predict the displacement vector at the center of subject image patch (prior to image refinement registration) in the application stage. Therefore, we need to reverse each deformation field ${\mathrm{\Phi }}_n^t$ to make its native space correspond with each training image space, that is, ${\mathrm{\Psi }}_n^t=\{{\mathit{\psi }}^t{}_n(u)|u\in {\mathrm{\Omega }}_{I_n^t}\}$. We follow the diffeomorphism principle in³³ to reverse ${\mathrm{\Phi }}_n^t$ by (a) estimating the velocity field from the obtained deformation field and (b) integrating the velocity in the reversed order to obtain the reversed deformation field. Thus, for each voxel u in the training image $I_n^t$, its corresponding location in the template image space is $u+{\mathit{\psi }}_n^t(u)$.

Since the human brain develops dramatically in the first year, we train both the patchwise appearance‐displacement and patchwise appearance‐appearance regression models from 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old to 12‐month‐old domain (used as template time point) separately. In the following, we take the 3‐month‐old phase (i.e., t = 2) as an example to explain the appearance‐displacement learning procedure.

2.A.1. Learn patchwise appearance‐displacement model

Training samples for patchwise appearance‐displacement model consist of pairs of the local image patch $P_n^t(u)$ extracted at the uniformly randomly sampled voxel u of training image $I_n^t$ and its displacement vector ${\mathit{\psi }}_n^t(u)$. Regression forest^{21, 22, 23} is used to learn the relationship between local image patch $P_n^t(u)$ and displacement vector ${\mathit{\psi }}_n^t(u)$. Specifically, we calculate several patchwise image features from $P_n^t(u)$, such as intensity, 3‐D Haar‐like features, and coordinates. The 3‐D Haar‐like features of a patch are computed as the local mean intensity of any randomly displaced cubical region, or the mean intensity difference over any two randomly displaced, asymmetric cubical regions,¹⁴ where the center of the randomly selected region is located in the patch. To train a tree in the regression forest, the parameters of each node are learned recursively, starting at the root node. Then, the training samples are recursively split into left and right nodes by selecting the optimal feature and threshold. Suppose Θ denotes a node in the regression forest, and then its optimal feature and threshold are determined by maximizing the following objective function,

$$E=\mathit{\sigma }(\mathit{\Theta })-{\sum }_{i\in \{L,R\}\frac{W_i}{\mathit{W}}\mathit{\sigma }({\mathit{\Theta }}_i)}$$ (1)

where Θ _i (i ∈ {L, R}) denotes the left/right children node of the node Θ. W _i denotes the number of training samples at the node Θ _i . W is the number of training samples at the node Θ. Z(Θ) is the set of training samples entering the node Θ. σ(Θ) denotes a function that measures the variance of training samples Z(Θ) as below,

$$\mathit{\sigma }(\mathit{\Theta })=\frac{1}{W}{\sum }_{(u,n)\in Z(\mathit{\Theta })}||{\mathit{\psi }}_n^t(u)-\overline{d}(\mathit{\Theta }){||}_2^2$$ (2)

$$\overline{d}(\mathit{\Theta })=\frac{1}{\mathit{W}}{\sum }_{(\mathit{u},\mathit{n})\in Z(\mathit{\Theta })}{\mathit{\psi }}_{\mathit{n}}^{\mathit{t}}(\mathit{u})$$ (3)

where $\overline{d}(\mathrm{\Theta })$ is the mean displacement vector of all training samples at the node Θ. After determining the optimal feature and threshold for the node Θ by maximizing Eq. (1), the training samples are split into left and right child nodes by comparing the selected features with the learned threshold. The same splitting process is recursively applied on the left and right child nodes until the maximal tree depth is reached or the number of training samples at one node is less than a certain amount. When the splitting stops, we consider the current node as a leaf node and store the mean displacement there for future prediction.

2.A.2. Learn patchwise appearance‐appearance model

Training samples for patchwise appearance‐appearance model consist of the local image patch $P_n^t(u)$ centered at a uniformly randomly sampled point u of the training image $I_n^t$ and the corresponding image patch $P_T\left(u+{\mathit{\psi }}_n^t\left(u\right)\right)$ extracted at the location $u+{\mathit{\psi }}_n^t(u)$ of the template T. We use the same regression‐forest learning procedure (as described above) to train the patchwise appearance‐appearance model, except that the mean displacement vector in the above is replaced with the mean of the template image patches from all samples stored at the leaf node. Specifically, to estimate the template‐like patch appearance for the patch $P_s(u)(u\in {\mathrm{\Omega }}_s)$ of the new subject image S, we consider the mean image patch stored at the destination leaf node as the prediction/estimation.

2.B. Application stage — register new infant brain images from the first year of life

We register the new infant subject S to the same template T that is used in the training stage in three steps: 1) predict initial deformation field, 2) predict appearance change, and 3) estimate the remaining deformations. The registration progress is illustrated in Fig. 2.

Figure 2.

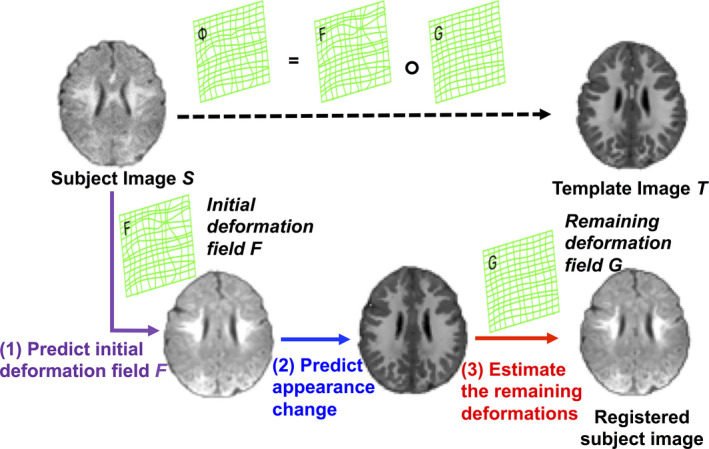
The schematic illustration of the proposed registration process. [Color figure can be viewed at wileyonlinelibrary.com]

2.B.1. Apply patchwise appearance‐displacement model — predict an initial deformation field

We first visit each voxel u of the new infant subject $S(u\in {\mathrm{\Omega }}_s)$ and use the learned patchwise appearance‐displacement model to predict its displacement h(u), pointing to the template image, based on the image patch P _s (u) extracted at u. In this way, we obtain the dense deformation field $H=\{h(u)|u\in {\mathrm{\Omega }}_s\}$ and further calculate the initial deformation field F by reversing the dense deformation field H, since the deformation field (deforming the subject image S to the template space ${\mathrm{\Omega }}_T$) should be defined in the template image space, that is, $F=\{{f(v)|v\in \mathrm{\Omega }}_T\}$.

Given a new image patch P _s (u) ($u\in {\mathrm{\Omega }}_s$) from a testing subject S, we first extract the same patchwise image features from P _s (u). Then, based on the learned feature and threshold at each node, the testing image patch P _s (u) is guided toward leaf nodes of different tree. When it reaches the leaf node of each tree, the mean displacement vector stored in the leaf node is used as the predicted displacement vector. For robustness, we train multiple regression trees independently using the idea of bagging. Thus, the final prediction is the average of the predicted displacement vectors from all different decision trees. The thin‐plate spline (TPS)³⁴ is used to interpolate and smooth the dense deformation field after obtaining the initial deformation on each voxel. Specifically, we first check the histogram of Jacobian determinant values, and then select the points with Jacobian determinant values larger than 0 to calculate the target point set using the learned deformation field. The deformation field can be updated by the TPS smoothness measurement with a fixed regularization term,³⁵ which is used to ensure the topology preservation of the deformation field. Note that the topology preservation is necessary for the invertibility of the deformation field. Several strategies are also used to prevent the potential issues in reversing deformation field: (a) We increase the strength of smoothness regularization term in TPS interpolation. (b) We check the Jacobian determinant of interpolated dense deformation field. If the Jacobian determinant is greater or smaller than a fixed threshold, we will drop the control points in that region and re‐interpolate. We repeat this procedure until all Jacobian determinants in the image domain are within a certain threshold. We believe more advanced interpolation method (e.g., geodesic interpolation^{36, 37}) can better preserve the topology of the deformation field. Figure 3 shows the accuracy of predicted displacement vector at each voxel for intra‐subject registration (from 3‐month‐old to 12‐month‐old) in terms of voxel‐wise residual error w.r.t. the ground‐truth deformation that is obtained by registering the segmented images. According to the accumulative histogram in Fig. 3(b), it is apparent that almost 96.7% residual errors are within 1 mm. Figure 3(c) and (d) show the examples of a ground‐truth deformation field and the learned deformation field during the leave‐one‐out validation procedure.

Figure 3.

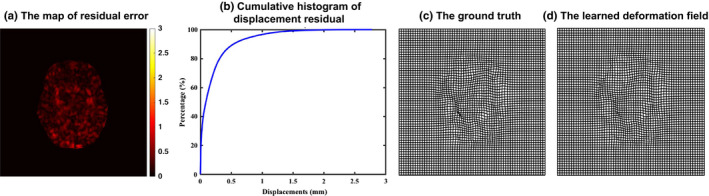
(a) The map of residual error between predicted displacement field at each voxel and its ground‐truth displacement field. (b) The accumulative histogram of residual errors in the whole brain region. (c) A ground‐truth deformation field. (d) Our learned deformation field. [Color figure can be viewed at wileyonlinelibrary.com]

2.B.2. Apply patchwise appearance‐appearance model — predict appearance changes

After deforming the subject image S from its native space ${\mathrm{\Omega }}_S$ to the template space ${\mathrm{\Omega }}_T$, we further use the learned patchwise appearance‐appearance model to convert local image appearance P _s (u) from the time point where the subject image S is scanned to Q(u) at the time point where the template image T is scanned. Thus, we finally obtain the roughly aligned subject image with its template‐like appearance also estimated, which can be denoted as $\widehat{S}$.

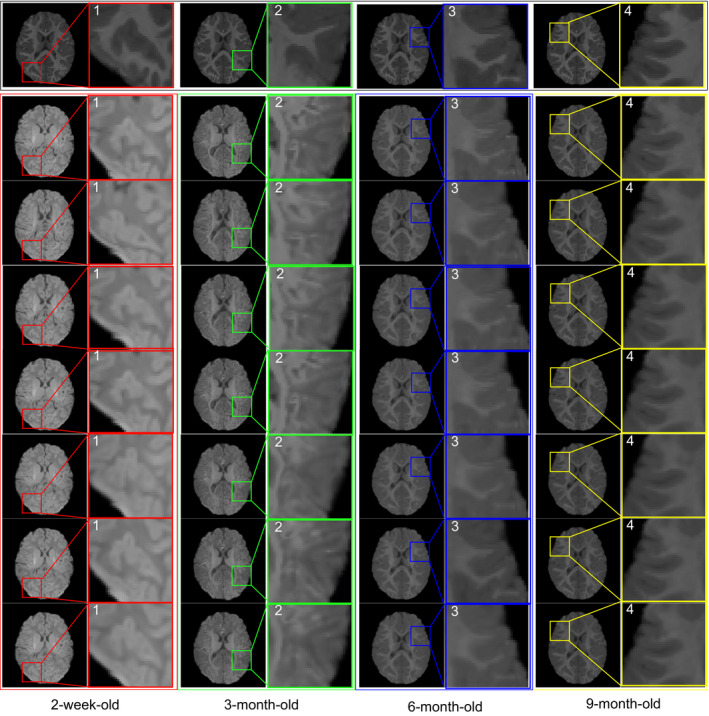
Figure 4 demonstrates the performance of predicting appearance changes from 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old to 12‐month‐old, respectively. Specifically, Fig. 4(a) shows the 12‐month‐old template image. It is clear that both shape and image appearance of this 12‐month‐old template image are quite different from those of 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old images (as shown in the top row of Fig. 4). After applying the patchwise appearance‐displacement model to generate the initial deformation field, we largely remove the shape discrepancies, as shown in the middle row of Fig. 4, but the appearance differences remain. Next, for each (subject) image at 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old, we apply their respective learned patchwise appearance‐appearance models on each image voxel and replace the original local image appearance by the predicted template‐like (12‐month‐old) appearance. As shown in the bottom row of Fig. 4, not only the shape but also the image appearance become similar to the template after sequentially applying the patchwise appearance‐displacement and patchwise appearance‐appearance models at each time point.

Figure 4.

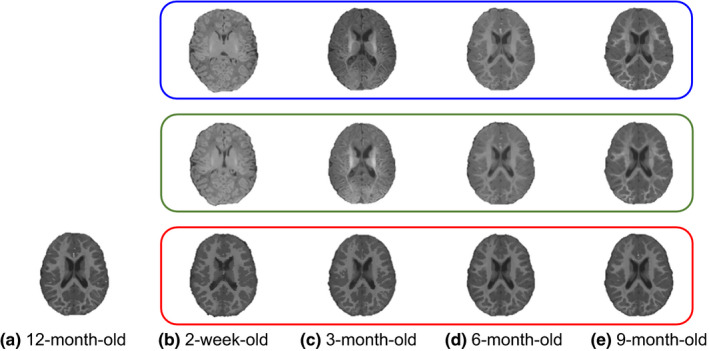
Estimation of estimating both shape and appearance changes from 2‐week‐old, 3‐month‐old, 6‐month‐old, and 9‐month‐old to the 12‐month‐old template image (a). From top to bottom row, we respectively show the original subject images, the deformed subject images after applying the learned patchwise appearance‐displacement model, and the deformed subject images after applying both the learned patchwise appearance‐displacement and appearance‐appearance models at 2‐week‐old (b), 3‐month‐old (c), 6‐month‐old (d), and 9‐month‐old (e). It can be observed that both anatomical and appearance discrepancies have been largely decreased after applying these two learned models. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 5 shows an example in each stage of estimating the deformation field during the intra‐subject registration (from 3‐month‐old to 12‐month‐old). Fig. 5(a) shows the target ground‐truth deformation field, Fig. 5(b) shows the learned deformation field by our appearance‐displacement model, Fig. 5(c) shows the remaining deformation field between the template‐like image and the template image, and Fig. 5(d) gives the final deformation field by composing our learned deformation field and our estimated remaining deformation field. The similarity between deformation fields in (a) and (d) indicates the accuracy of our proposed registration method.

Figure 5.

Estimation of the deformation fields. (a) The target ground‐truth deformation field, (b) the learned deformation field by our appearance‐displacement model, and (c) the remaining deformation field estimated by registering the template‐like image and the template image, and (d) the final deformation field by composing our learned deformation field and our estimated remaining deformation field

2.B.3. Estimate the remaining deformation — finish the registration

Since the anatomical shape and appearance of learned $\widehat{S}$ are almost similar to the template image T, we employ the classic diffeomorphic Demons^{15, 16} to complete the estimation of the remaining deformation G. Finally, the whole displacement vector $\mathrm{\Phi }$ from subject image S to the template image T can be achieved by $\mathrm{\Phi }=F\circ G$, where “$\circ$” stands for the deformation composition.³³ The schematic registration process is shown in Fig. 2.

2.C. Evaluation criterion

We use Dice ratio of combined WM and GM (as well as Dice ratio of hippocampus) as a measurement to quantitatively evaluate the accuracy of registration. The Dice ratio can be obtained as follows:

$$\text{Dice ratio}=\frac{2||\mathrm{A}\cap \mathrm{B}||}{||\mathrm{A}||+||\mathrm{B}||}$$ (4)

where A is the combined WM and GM voxel set of template and B is the combined WM and GM voxel set of registered subject when calculating Dice ratio for the combined WM and GM. We also measure the accuracy of the registration by calculating Dice ratio between the hippocampus voxel set of the template and the hippocampus voxel set of each registered subject. Note that hippocampi in longitudinal images of ten subjects were manually segmented and used as ground truth, with one example shown in Fig. 6. The top row in Fig. 6 shows the original slices (in axial, sagittal, coronal views), and the bottom row shows manually segmented left and right hippocampi in red and green. After registering these images, we can warp their respective manually segmented hippocampi to the template for computing the overlap of hippocampi with Dice ratio.

Figure 6.

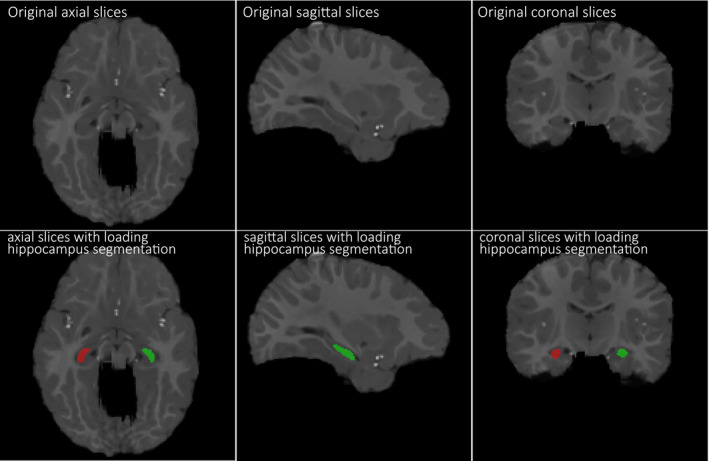
Demonstration of manually segmented hippocampi in a 12‐month‐old infant brain MR image. The top row shows the original slices (in axial, sagittal, coronal views), and the bottom row shows manually segmented left and right hippocampi in red and green. [Color figure can be viewed at wileyonlinelibrary.com]

3. Experiment

Totally 24 infant subjects are included in the following experiments, where each subject has T1‐ and T2‐weighted MR images at 2‐week‐old, 3‐, 6‐, 9‐, and 12‐month‐old. The T1‐weighted images were acquired with a Siemens head‐only 3T MR scanner and had 144 sagittal slices at resolution 1 × 1 × 1 mm³. The T2‐weighted images were obtained with 64 axial slices at resolution 1.25 × 1.25 × 1.95 mm³. For each subject, the T2‐weighted image was linearly aligned to its T1‐weighted image at the same time point using FLIRT^{31, 38} and then further isotropically up‐sampled to 1 × 1 × 1 mm³ resolution. In our experiments, the following parameters are used: (a) Input patch size: 7 × 7 × 7, and extracted from the training subjects; (b) output patch size: 1 × 1 × 1, and extracted from the training template; (c) the length of Haar‐like features: 300; (d) random forest: the number of regression trees is 100, and the maximum tree depth is 50; and (e) the number of sampled patches is 50,000.

The image preprocessing includes three steps: skull‐stripping,^{32, 39} bias correction,⁴⁰ and image segmentation.⁴¹ We compare the registration accuracy of our proposed learning‐based infant brain registration method with several state‐of‐the‐art deformable registration methods under the following three categories:

• Intensity‐based image registration methods. We employ three deformable image registration methods that use different image similarity metrics, that is, (a) diffeomorphic Demons,^{15, 16} (b) mutual‐information‐based deformable registration method (MI‐based),^{17, 18} and (c) cross‐correlation‐based deformable image registration method (CC‐based).^{19, 20}

• Feature‐based image registration method. HAMMER²⁸ is one of typical feature‐based registration methods, which computes geometric moments for all tissue types as morphological signature at each voxel. The deformation of image registration is driven by robust feature matching, instead of simple image intensity comparison. Apparently, the registration performance of this method is highly dependent on the segmentation quality. In the following experiment, we assume that the new to‐be‐registered infant image has been well segmented, which is, however, not practical in real application since segmentation of infant image at single time point is very difficult without complementary longitudinal and multimodal information.

• Other learning‐based registration method. In our previous work, we proposed a sparse representation‐based registration method (SR‐based),²⁷ which leveraged the known temporal correspondence in the training subjects to tackle the appearance gap between the two different time point images under registration.

3.A. Registering images of same infant subject at different time points

In order to investigate subject‐specific brain development, the images of the same infant subject at different time points need to be registered in many longitudinal studies. Thus, for each subject, we register 2‐week, 3‐, 6‐, and 9‐month‐old images to its corresponding 12‐month‐old image. Specifically, we carry out this experiment in a leave‐one‐out manner, where the longitudinal scans of 23 infant subjects are used to train both the patchwise appearance‐displacement and appearance‐appearance models at 2‐week, 3‐, 6‐, and 9‐month‐old separately, by using the corresponding 12‐month‐old image as the template. In the testing stage, we separately register the 2‐week, 3‐, 6‐, and 9‐month‐old images of the remaining infant subject to its corresponding 12‐month‐old image.

Recall that all the longitudinal images of total 24 infant subjects have been well segmented by manually editing segmentation images from automatic tissue segmentation results, and thus can be used as ground truth. To quantitatively evaluate the registration accuracy, we calculate the Dice ratio of WM and GM between the 12‐month‐old segmentation image (used as template) and the registered segmentation image from each of other time points. Table 1 shows the mean and standard deviation of Dice ratios of the combined WM and GM under 24 leave‐one‐out cases by CC‐based, MI‐based, HAMMER, SR‐based, our method after applying the learned patchwise appearance‐displacement model (our method 1), and our full method (our method 2), respectively. It is apparent that (a) our proposed method achieves better Dice ratio. (b) Combining the appearance‐displacement model and appearance‐appearance model is a feasible way to register the images with large anatomical and appearance changes. (c) The improvements are significant to register subject infant brain MR images of 2‐week‐old and 3‐month‐old to the 12‐month‐old template. In order to evaluate the performances of registration methods, Table 2 also shows Dice ratios of hippocampus voxel set between the registered image and the template image. As mentioned, we have ten subjects with their left and right hippocampi manually segmented. Thus, we warp the segmented hippocampus regions by CC‐based, MI‐based, HAMMER, SR‐based, and our method, for calculating the Dice ratios between the hippocampus voxel set of template and the hippocampus voxel set of each registered subject by Eq. (4). As shown in Table 2, our proposed method obtains similar results as the SR‐based method, but much higher hippocampal Dice ratio than other methods. From both (Tables 1 and 2), we can see that (a) the learning‐based method (our method and SR‐based method) can obtain better registration accuracy, and (b) the proposed method is effective in registering infant brain MR images by using both appearance‐displacement model and appearance‐appearance model.

Table 1.

The mean and standard deviation of Dice ratios of the combined WM and GM for intra‐subject registration, by aligning the 2‐week‐old, 3‐, 6‐, and 9‐month‐old images to the 12‐month‐old image via different methods. The best Dice ratio for each column is shown in bold

Method	2‐Week to 12‐month	3‐Month to 12‐month	6‐Month to 12‐month	9‐Month to 12‐month
CC‐based	0.714 ± 0.025	0.687 ± 0.031	0.797 ± 0.028	0.851 ± 0.019
MI‐based	0.709 ± 0.028	0.694 ± 0.030	0.799 ± 0.029	0.850 ± 0.018
3D‐HAMMER	0.764 ± 0.027	0.756 ± 0.028	0.806 ± 0.024	0.848 ± 0.021
SR‐based	0.774 ± 0.015	0.778 ± 0.018	0.818 ± 0.016	0.858 ± 0.015
Our proposed method 1	0.810 ± 0.044	0.783 ± 0.054	0.823 ± 0.056	0.892 ± 0.009
Our proposed method 2	0.833 ± 0.029	0.826 ± 0.026	0.847 ± 0.041	0.892 ± 0.006

Table 2.

The mean and standard deviation of Dice ratios of the hippocampus on ten intra‐subjects, when registering the 2‐week‐old, 3‐, 6‐, and 9‐month‐old images to the 12‐month‐old image via different methods. The best Dice ratio for each column is shown in bold

Method	2‐Week to 12‐month	3‐Month to 12‐month	6‐Month to 12‐month	9‐Month to 12‐month
CC‐based	0.579 ± 0.066	0.585 ± 0.065	0.681 ± 0.064	0.748 ± 0.045
MI‐based	0.581 ± 0.072	0.593 ± 0.070	0.676 ± 0.061	0.751 ± 0.053
3D‐HAMMER	0.601 ± 0.061	0.613 ± 0.062	0.683 ± 0.065	0.736 ± 0.051
SR‐based	0.614 ± 0.063	0.635 ± 0.055	0.702 ± 0.059	0.762 ± 0.049
Our proposed method	0.615 ± 0.024	0.638 ± 0.047	0.702 ± 0.071	0.766 ± 0.052

As shown in Fig. 2, our method first uses the learned patchwise appearance‐displacement and appearance‐appearance models to predict initial deformation field and correct the appearance differences, and then uses a conventional registration method to estimate the remaining deformations. Here, we take diffeomorphic Demons^{15, 16} as a refinement registration method to demonstrate the advantages of our proposed learning‐based registration method. The template image is shown in the first row of (Fig. 7). From left to right columns, we show the registration results for 2‐week‐old, 3‐, 6‐, and 9‐month‐old images by linear registration (2nd row), direct use of diffeomorphic Demons (3rd row), CC (4th row), MI (5th row), HAMMER (6th row), diffeomorphic Demons after applying our learned patchwise appearance‐displacement model (7th row), and our full method (last row), respectively. It is apparent that our learning‐based registration method is effective for infant brain registration and outperforms both linear registration and the direct use of diffeomorphic Demons for registering 2‐week‐old and 3‐month‐old images to the 12‐month‐old image, and (2) using both patchwise appearance‐displacement model and appearance‐appearance model can improve registration performance for infant brain images with large anatomical and appearance changes.

Figure 7.

Intra‐subject registration results on infant brain images at different time points. The first row represents the 12‐month‐old image, which is used as the template. From left to right columns, we show registration results for 2‐week‐old, 3‐, 6‐, and 9‐month‐old images by linear registration (2nd row), direct use of diffeomorphic Demons (3rd row), CC (4th row), MI (5th row), HAMMER (6th row), diffeomorphic Demons after applying our learned patchwise appearance‐displacement model (7th row), and our full method (last row), respectively. The 7th row shows that, after applying our learned appearance‐displacement model, the anatomical structures of different time point images become similar to the template image shown in the first row. Moreover, the last row shows that, after applying both of our proposed learning models (our full method), not only the anatomical structures but also the appearances of different time point images become similar to the template image. [Color figure can be viewed at wileyonlinelibrary.com]

In Fig. 8, we further show cortical surface distances between the template surface and the aligned subject surfaces, by registering the segmented images of template and subject images (used as the target ground‐truth deformation fields in this study; 1st row), and registering the original MR images by linear registration (2nd row), diffeomorphic Demons (3rd row), and our learning‐based method (bottom). As shown in Fig. 8, it is clear that our proposed registration method achieves more accurate registration results than comparison registration methods, especially in the regions inside the red circles.

Figure 8.

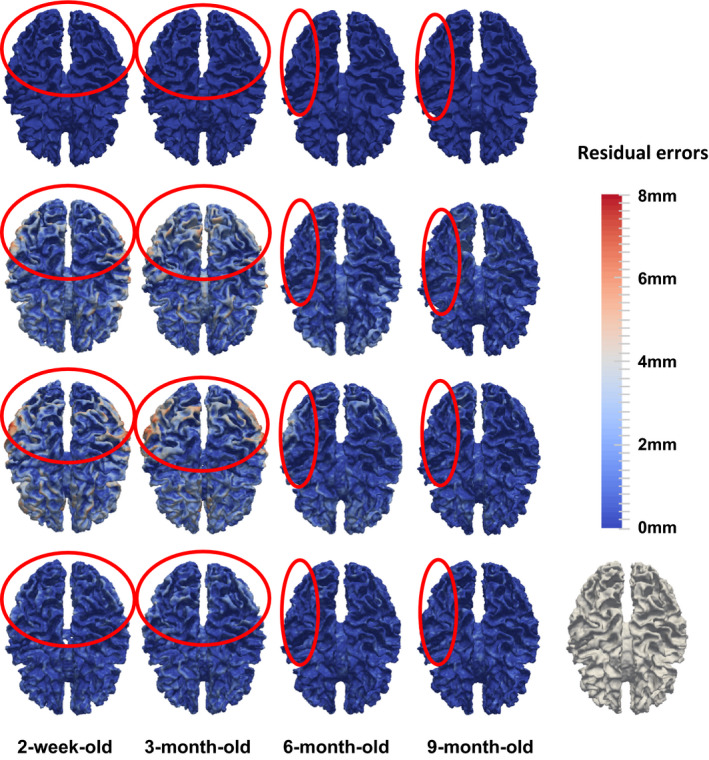
Cortical surface distances between the template surface and the aligned subject surfaces, by registering the segmented images of template and subject images (used as the target ground‐truth deformation fields in this study (1st row), and registering the original MR images by linear registration (2nd row), diffeomorphic Demons (3rd row), and our learning‐based method (bottom). The color‐coding bar shows the template‐to‐aligned surface distance range. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Registering images of different infant subjects with age gap

It is more challenging to register infant brain images of different subjects with possible large age gap. Here, we use a leave‐two‐subjects‐out strategy to evaluate the registration performance. Specifically, longitudinal scans of 22 infant subjects are used as the training dataset to train both the appearance‐displacement and appearance‐appearance models at each time point. The 12‐month‐old image of one remaining infant subject is treated as the template. Then, we register the 2‐week, 3‐, 6‐, and 9‐month‐old images of another remaining infant subject to the template. We repeat such procedure for $C_{24}^2=276$ times and report the averaged Dice ratio of combined WM and GM in Table 3 by the CC‐based, MI‐based, HAMMER, SP‐based, our method after applying just the learned patchwise appearance‐displacement model (our method 1), and our full method (our method 2), respectively. Table 4 further shows the Dice ratios of hippocampus between registered images, on the ten subjects with manually segmented hippocampi. These hippocampal results show that: (a) our proposed method also achieves much better hippocampal Dice ratios for inter‐subject infant brain registration. (b) The best Dice ratios are 0.480 ± 0.078, 0.537 ± 0.059, 0.590 ± 0.050, and 0.631 ± 0.061 for registration of the 2‐week‐old, 3‐, 6‐, and 9‐month‐old images to the 12‐month‐old image. (3) The Dice ratio on hippocampus is still low, indicating the necessity of further improving inter‐subject registration.

Table 3.

The mean and standard deviation of Dice ratios of the combined WM and GM for inter‐subject registration, by aligning 2‐week‐old, 3‐, 6‐, and 9‐month‐old images to the 12‐month‐old image via different methods. The best Dice ratio for each column is shown in bold

Method	2‐Week to 12‐month	3‐Month to 12‐month	6‐Month to 12‐month	9‐Month to 12‐month
CC‐based	0.643 ± 0.030	0.618 ± 0.025	0.684 ± 0.024	0.722 ± 0.020
MI‐based	0.614 ± 0.025	0.602 ± 0.022	0.675 ± 0.030	0.717 ± 0.022
3D‐HAMMER	0.662 ± 0.023	0.642 ± 0.026	0.688 ± 0.025	0.715 ± 0.023
SR‐based	0.673 ± 0.016	0.665 ± 0.017	0.695 ± 0.015	0.718 ± 0.018
Our proposed method 1	0.623 ± 0.029	0.633 ± 0.026	0.661 ± 0.050	0.676 ± 0.039
Our proposed method 2	0.692 ± 0.035	0.684 ± 0.037	0.726 ± 0.069	0.766 ± 0.033

Table 4.

The mean and standard deviation of Dice ratios of the hippocampus on ten INTER‐subjects, when registering the 2‐week‐old, 3‐, 6‐, and 9‐month‐old images to the 12‐month‐old image via different methods. The best Dice ratio for each column is shown in bold

Method	2‐Week to 12‐month	3‐Month to 12‐month	6‐Month to 12‐month	9‐Month to 12‐month
CC‐based	0.442 ± 0.081	0.471 ± 0.078	0.573 ± 0.053	0.627 ± 0.053
MI‐based	0.437 ± 0.073	0.465 ± 0.072	0.569 ± 0.058	0.631 ± 0.061
3D‐HAMMER	0.461 ± 0.071	0.512 ± 0.069	0.568 ± 0.062	0.621 ± 0.050
SR‐based	0.478 ± 0.063	0.535 ± 0.0.67	0.585 ± 0.062	0.625 ± 0.055
Our proposed method	0.480 ± 0.078	0.537 ± 0.059	0.590 ± 0.050	0.628 ± 0.079

Similarly, for visual inspection, the registration results of different infant images are shown in Fig. 9. The template T2‐weighted (left) and T1‐weighted (middle) images are shown in the first row. Also, the blue boxes are used to denote the T2‐weighted images in their original and zoomed‐up scales, and the red boxes are used to denote the T1‐weighted MR images similarly. From left to right columns, we show the registration results for the 2‐week‐old, 3‐, 6‐, and 9‐month‐old images by linear registration (2nd row), direct use of diffeomorphic Demons (3rd row), CC (4th row), MI (5th row), HAMMER (6th row), diffeomorphic Demons after applying our learned patchwise appearance‐displacement model (7th row), and our full method (last row), respectively. Even under these inter‐subject registration cases, it is also apparent that: (a) our learning‐based registration method outperforms both linear registration and the direct use of diffeomorphic Demons for registering the 2‐week‐old and 3‐month‐old images to the 12‐month‐old image, and (b) using both the patchwise appearance‐displacement model and appearance‐appearance model can further improve the registration performance for infant subjects with large anatomical and appearance changes.

Figure 9.

Inter‐subject registration results on infant brain images at different time points. The first row shows the 12‐month‐old template, with T2‐weighted image (left) and T1‐weighted image (middle). In the whole figure, the blue boxes denote the T2‐weighted images, and the red boxes denote the T1‐weighted images. From left to right columns, we show the registration results for the 2‐week‐old, 3‐, 6‐, and 9‐month‐old images by linear registration (2nd row), direct use of diffeomorphic Demons (3rd row), CC (4th row), MI (5th row), HAMMER (6th row), diffeomorphic Demons after applying our learned patchwise appearance‐displacement model (7th row), and our full method (last row), respectively. Similar to Fig. 7, the 7th row in this figure shows that the anatomical discrepancies are decreased, and the 8th row shows that both anatomical and appearance discrepancies are decreased. Even for inter‐subject registration case, as shown in the last row, our proposed method can still obtain good registration results. [Color figure can be viewed at wileyonlinelibrary.com]

Our experiments were done on a computer cluster with 3.1 GHz Intel processors, 12 M L3 cache, and 128 GB memory nodes. The average run times of Demons, MI‐based, CC‐based, 3D‐HAMMER, SR‐based and our proposed method without considering the training time were 3.6, 12.5, 14.6, 28.7, 26.3, and 6.1 minutes, respectively.

4. Conclusion and discussion

In this paper, we have presented a novel learning‐based registration method to tackle the challenging problems of infant brain image registration in the first year of life. To address the rapid brain development and dynamic appearance changes, we employ regression forest to learn the complex anatomical development and appearance changes between different time points. Specifically, to register a new infant image with possible large age gap, we first apply the learned appearance‐displacement and appearance‐appearance models to initialize image registration and also adjust image appearance (becoming similar to the template image). Then, we use the conventional image registration method to estimate the remaining deformation field, which is often small and thus much easier to be estimated, compared to the case of direct estimation from the original images. We have extensively evaluated registration accuracy of our proposed method on 24 infant subjects with longitudinal scans, and achieved higher registration accuracy compared with other counterpart registration methods.

It is worth indicating the potential bias in our current evaluation framework. Although 3D‐HAMMER in iBEAT and 4D‐HAMMER (used to generate ground truth) are both performed on the segmented images, instead of the original intensity images, the mechanisms used to constrain the deformation field are the same when using HAMMER to register either segmented images or original images. Thus, the final results shown in all tables may be biased to those obtained by 3D‐HAMMER (on registering original images). The better way is to use other independent methods for generating the ground truth.

For our future work, we also need to address several challenge. (a) How to obtain more accurate target deformation fields to evaluate the performance of our method. The deformation fields used as ground truth are not the gold standard, which limits the evaluation of our proposed method, specifically for inter‐subject registration. Besides, although the target deformation fields can be used to evaluate the accuracy of our appearance‐displacement model, the final accuracy of our method is difficult to evaluate. Therefore, better validation strategy for infant brain registration is of high demand. (b) How to improve the accuracy of our learning models for further refinement of accuracy registration. Currently, we use simple image features from local subject patch to estimate the displacement or the template image intensities. Other advanced features, that is, estimated with deep learning, should be considered. Besides, we will need to incorporate other registration algorithms into our learning‐based registration framework, and further evaluate our methods with more infant images.

Conflict of interest

The authors have no relevant conflicts of interest to disclose.