Lipid Domain Co-localization Induced by Membrane Undulations

Abstract

Multicomponent lipid bilayer membranes display rich phase transition and associated compositional lipid domain formation behavior. When both leaflets of the bilayer contain domains, they are often found co-localized across the leaflets, implying the presence of a thermodynamic interleaflet coupling. In this work, it is demonstrated that fluctuation-induced interactions between domains embedded within opposing membrane leaflets provide a robust means to co-localize the domains. In particular, it is shown via a combination of a mode-counting argument, a perturbative calculation, and a non-perturbative treatment of a special case, that spatial variations in membrane bending rigidity associated with lipid domains embedded within the background phase always lead to an attractive interleaflet coupling with a magnitude of $\sim 0.01k_{\text{B}}T{\text{/nm}}^2$ in simple model membrane systems. Finally, it is demonstrated that the fluctuation-induced coupling is very robust against membrane tension and substrate interactions.

Introduction

Multicomponent lipid bilayer membranes represent an interesting class of soft matter systems, displaying rich phase transition and associated compositional lipid domain formation behavior (1, 2, 3). In particular, ternary systems featuring coexisting compositional liquid-liquid phases (the so-called “Lo” phase, enriched in cholesterol and saturated lipids, and “Ld” phase, enriched in unsaturated lipids) are often employed as simple model systems of the plasma membrane of mammalian cells, where Lo-like lipid “raft” nanodomains (4, 5) are believed to play a key role in several cellular processes, such as cell signaling and trafficking (6).

Interestingly, when both leaflets of the bilayer membrane contain lipid domains, they are often found co-localized across the leaflets (7, 8, 9, 10), implying the presence of a thermodynamic interleaflet coupling, $\Lambda >0$, defined via $\Delta \mathcal{F}=-\text{ΛΔ}{A}_{\text{o}}$, where $\Delta \mathcal{F}$ and $\Delta A_{\text{o}}$ denote the changes in the system free energy and domain overlap, respectively. To explain this observed registration between domains, several physical mechanisms have been proposed, such as cholesterol flip-flop and dynamic chain interdigitation (11) and complex interplay between chain entropic and energetic effects (12). As for the strength of the interleaflet coupling, $\Lambda$, theoretical predictions range from $\sim 1k_{\text{B}}T{\text{/nm}}^2$ (11, 13) to $\sim 0.01k_{\text{B}}T{\text{/nm}}^2$ (12), while very recent experimental work employing a microfluidics approach in conjunction with a supported bilayer system has obtained a value of $\Lambda \approx 0.016k_{\text{B}}T/$ nm² for a representative ternary lipid system (14). To put these values in perspective, as shown in (12), the characteristic width of the mismatched region resulting from out-of-alignment fluctuations is given by ${\xi }_{\perp }={\left[{\left(k_{\text{B}}T\right)}^2\text{/}\left(\Lambda \tau \right)\right]}^{1/3}$, where $\tau \sim {10}^{-12}N$ denotes the line tension between Ld/Lo domains away from a critical point (2). For a given $\Lambda$, co-localization can thus be sustained for two domains of radius $R\mathrm{\gtrsim }{\xi }_{\perp }$. Hence, $\Lambda \mathrm{\gtrsim }{10}^{-3}{k}_{\text{B}}T\text{/}$nm² is sufficient to co-localize lipid domains $\gtrsim 10\text{nm}$ in radius across the two leaflets.

To date, all existing theoretical work on the interleaflet coupling has focused on planar membranes (11, 12, 13), although one of the hallmark features of soft matter systems is their susceptibility to thermo-mechanical perturbations. A case in point is the development of membrane undulations at finite temperature, which in turn gives rise to algebraically decaying, fluctuation-induced interactions between membrane inclusions that are more rigid or softer than the background phase (15, 16, 17, 18, 19). Importantly for the present problem, it is well-known that the Lo domains are more rigid than the Ld ones, with a bending rigidity of ${\kappa }_{\text{Lo}}\sim 2-3{\kappa }_{\text{Ld}}$ (20, 21). Thus, these lipid domains should experience an entropic interaction mediated by membrane undulations. Indeed, Horner et al. (22) have argued that fluctuations should in general favor the co-localization of domains that are more rigid than the background phase. Although these fluctuation-induced interactions are well-understood by now in the case of large domain separations (corresponding to non-overlapping domains), much less is known about their nature and strength in the case of partially or completely co-localized domains.

In this work, it is demonstrated that membrane-fluctuation-induced interactions between compositional lipid domains embedded within opposing leaflets of a bilayer membrane indeed provide an additional and robust means to co-localize the domains. In particular, it will be shown via a combination of a mode-counting argument, a perturbative calculation for the general case, and a non-perturbative analysis of a special case, that spatial variations in the membrane bending rigidity associated with the Ld/Lo domains lead to an attractive interleaflet coupling with a strength of ${\Lambda }_{\text{fluct}}\sim 0.01k_{\text{B}}T\text{/}$nm² in model membranes. It is argued that, in contrast to interactions between well-separated, non-overlapping domains, Gaussian rigidity variations do not contribute to ${\Lambda }_{\text{fluct}}$ for domains whose overlap area $A_{\text{o}}\gg {\ell }^2$, where $\ell$ denotes a microscopic length comparable to the bilayer thickness. Finally, it is demonstrated that the attractive interleaflet coupling due to fluctuations is very robust against membrane tension and substrate interactions.

Materials and Methods

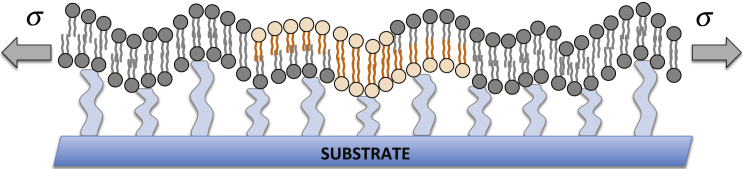
As illustrated in the schematic in Fig. 1, we consider a pair of incompletely co-localized compositional lipid domains of area $A_{\text{d}}$ embedded within opposing leaflets of a bilayer membrane. The membrane is under tension and interacts with a substrate.

Figure 1.

In this work, we consider the effective membrane-fluctuation-induced interaction between two partially co-localized compositional lipid domains (represented by orange particles) embedded within opposing leaflets of a bilayer membrane and characterized by a contrast in the elastic constants between the domains and the background phase. The bilayer is taken to be under tension with magnitude σ and also coupled to a substrate. To see this figure in color, go online.

Our starting point is the Helfrich (23) Hamiltonian describing membrane shape fluctuations in the Monge gauge, augmented with terms describing the effects of membrane tension and coupling with substrate:

$$H\left[h\left(\mathbf{r}\right)\right]=\int d^2\mathbf{r}\left[\frac{\kappa \left(\mathbf{r}\right)}{2}{\left({\nabla }^{2}h\left(\mathbf{r}\right)\right)}^2+\overline{\kappa }\left(\mathbf{r}\right)\left(\frac{{\partial }^{2}h\left(\mathbf{r}\right)}{\partial x^2}\frac{{\partial }^{2}h\left(\mathbf{r}\right)}{\partial y^2}-{\left(\frac{{\partial }^{2}h\left(\mathbf{r}\right)}{\partial x\partial y}\right)}^2\right)+\frac{\sigma }{2}{\left(\nabla h\left(\mathbf{r}\right)\right)}^2+\frac{{\alpha }^2}{2}{\left(h-h_0\right)}^2\right].$$ (1)

In Eq. 1, $h\left(\mathbf{r}\right)$ denotes the local height of the bilayer mid-plane above a reference plane (taken to be the substrate), and $\kappa \left(\mathbf{r}\right)>0$ and $\overline{\kappa }\left(\mathbf{r}\right)<0$ denote the spatially varying bending and Gaussian rigidities, respectively. Furthermore, σ denotes the membrane tension, $h_0$ the preferred height above the substrate ($h_0=0$ without any loss of generality), and ${\alpha }^2$ an effective spring constant describing the coupling between the membrane and the substrate. We expect that the continuum description in Eq. 1 is valid for membrane undulation modes with wavenumbers $q\mathrm{\lesssim }2\pi /\ell$, where $\ell$ denotes a microscopic cutoff comparable to the bilayer thickness; a detailed discussion of the range of validity of continuum theory for membrane undulations can be found in (24).

Upon introducing the shape functions ${\theta }_1\left(\mathbf{r}\right)$ and ${\theta }_2\left(\mathbf{r}\right)$ for the two domains with ${\theta }_1=1$ $\left({\theta }_2=1\right)$ within the first (second) domain and zero elsewhere, we write $\kappa \left(\mathbf{r}\right)={\kappa }_0+\left(\delta \kappa /2\right)\left[{\theta }_1\left(\mathbf{r}\right)+{\theta }_2\left(\mathbf{r}\right)\right]$ and $\overline{\kappa }\left(\mathbf{r}\right)={\overline{\kappa }}_0+\left(\delta \overline{\kappa }/2\right)\left[{\theta }_1\left(\mathbf{r}\right)+{\theta }_2\left(\mathbf{r}\right)\right]$ such that $\delta \kappa ={\kappa }_{\text{dom}}-{\kappa }_0$ and $\delta \overline{\kappa }={\overline{\kappa }}_{\text{dom}}-{\overline{\kappa }}_0$. Given the instantaneous configurations of the two domains, the goal is to evaluate the free energy of the system associated with membrane undulations by employing the standard definition $\mathcal{F}=-k_{\text{B}}T\text{ln}Z$, where the partition function Z is computed as a functional integral, $Z=\mathrm{\oint }Dh\left(\mathbf{r}\right)\text{exp}\left(-\left(H\left[h\left(\mathbf{r}\right)\right]/k_{\text{B}}T\right)\right)$. Although the evaluation of Z is straightforward in the case of elastically homogeneous membranes ($\kappa ={\kappa }_0$ and $\overline{\kappa }={\overline{\kappa }}_0$), the presence of elastic heterogeneities ($\delta \kappa \ne 0$ and/or $\delta \overline{\kappa }\ne 0$) poses technical challenges. In this work, the effect of such elastic heterogeneities is captured via a standard perturbative scheme that assumes $\delta \kappa \ll {\kappa }_0$ and $\delta \overline{\kappa }\ll {\kappa }_0$, as well as via a non-perturbative calculation for the special case of a tensionless membrane decoupled from a substrate with spatial variations in the bending rigidity $\kappa \left(\mathbf{r}\right)$ only.

For the perturbative analysis, we first write $H=H_0+H_{\text{pert}}$, where

$$H_0=\int d^2\mathbf{r}\left[\frac{{\kappa }_0}{2}{\left({\nabla }^{2}h\right)}^2+\frac{\sigma }{2}{\left(\nabla h\right)}^2+\frac{{\alpha }^2}{2}{h}^2\right]$$ (2)

and

$$H_{\text{pert}}=\int d^2\mathbf{r}[\frac{1}{4}\delta \kappa \left[{\theta }_1\left(\mathbf{r}\right)+{\theta }_2\left(\mathbf{r}\right)\right]{\left({\nabla }^{2}h\right)}^2+\frac{1}{2}\delta \overline{\kappa }[{\theta }_1\left(\mathbf{r}\right)+{\theta }_2\left(\mathbf{r}\right)]\times \left(\frac{{\partial }^{2}h}{\partial x^2}\frac{{\partial }^{2}h}{\partial y^2}-{\left(\frac{{\partial }^{2}h}{\partial x\partial y}\right)}^2\right)].$$ (3)

Note that we have dropped the Gaussian curvature term from $H_0$, as it integrates to an unimportant constant in an infinite system. Now, in terms of the cumulant expansion, $\mathcal{F}$ can be expressed as (15, 16, 18, 19)

$$\mathcal{F}={\mathcal{F}}_0-k_{\text{B}}T\text{ln}{\langle e^{-\frac{H_{\text{pert}}}{k_{\text{B}}T}}\rangle }_0={\mathcal{F}}_0-{\langle H_{\text{pert}}\rangle }_0-\frac{1}{2k_{\text{B}}T}\left[{\langle H_{\text{pert}}^2\rangle }_0-{\langle H_{\text{pert}}\rangle }_0^2\right]+\dots ,$$ (4)

where ${\langle A\rangle }_0\equiv \mathrm{\oint }Dh\left(\mathbf{r}\right)A\text{exp}\left(-H_0/k_{\text{B}}T\right)/\mathrm{\oint }Dh\left(\mathbf{r}\right)\text{exp}\left(-H_0/k_{\text{B}}T\right)$. Thermal averages of $H_{\text{pert}}$ are in turn expressed in terms of the derivatives ${\partial }_{ijkl}^{4}G\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)$ of the height-height correlation function of the unperturbed system,

$$G\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)={\langle h\left(\mathbf{r}\right)h\left({\mathbf{r}}^{\prime }\right)\rangle }_0=k_{\text{B}}T{\int }_0^{2\pi /\ell }\frac{d^2\mathbf{p}}{{\left(2\pi \right)}^2}\frac{e^{-i\mathbf{p}\cdot \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)}}{{\kappa }_0{p}^4+\sigma p^2+{\alpha }^2},$$ (5)

and products thereof evaluated via Wick’s theorem. Specifically, ${\langle H_{\text{pert}}\rangle }_0={\nabla }^{4}G\left(0\right)\int d^2\mathbf{r}\delta \kappa \left[\left({\theta }_1\left(\mathbf{r}\right)+{\theta }_2\left(\mathbf{r}\right)\right)/2\right]={\nabla }^{4}G\left(0\right)\delta \kappa A_{\text{d}}$, which is independent of domain overlap, whereas

$${\langle H_{\text{pert}}^2\rangle }_0-{\langle H_{\text{pert}}\rangle }_0^2=2\int d^2\mathbf{r}\int d^2{\mathbf{r}}^{\prime }{\theta }_1\left(\mathbf{r}\right){\theta }_2\left({\mathbf{r}}^{\prime }\right)\{\frac{{\left(\delta \kappa \right)}^2}{8}{\left({\nabla }^{4}G\right)}^2+\frac{1}{2}\delta \kappa \delta \overline{\kappa }\left[\left({\partial }_{xx}^2{\nabla }^{2}G\right)\left({\partial }_{yy}^2{\nabla }^{2}G\right)-{\left({\partial }_{xy}^2{\nabla }^{2}G\right)}^2\right]+\frac{1}{4}{\left(\delta \overline{\kappa }\right)}^2[\left({\partial }_{xxxx}^{4}G\right)\left({\partial }_{yyyy}^{4}G\right)+3{\left({\partial }_{xxyy}^{4}G\right)}^2-4\left({\partial }_{xxxy}^{4}G\right)\left({\partial }_{xyyy}^{4}G\right)]\}\equiv I_1\left(\delta \kappa \right)+I_2\left(\delta \kappa ,\delta \overline{\kappa }\right)+I_3\left(\delta \overline{\kappa }\right).$$ (6)

Equation 6 is responsible for the leading order term in the interleaflet coupling.

It should be noted that a microscopic cutoff $\ell$ has been explicitly included in G in Eq. 5 to reflect the fact that the continuum theory only applies on scales $\mathrm{\gtrsim }\ell$ comparable to bilayer thickness (24), as already noted above. Also, asymptotically, $G\left(\rho \right)\sim \left(k_{\text{B}}T/16\pi {\kappa }_0\right){\rho }^2\text{ln}{\rho }^2$ when $\rho \to \infty$ in the absence of membrane tension and substrate effects, whereas $G\left(\rho \right)\sim -\left(k_{\text{B}}T/4\pi \sigma \right)\text{ln}{\rho }^2$ in the presence of membrane tension but de-coupled from substrate. Finally, in the presence of a substrate, $G\left(\rho \right)\sim \left(k_{\text{B}}T/{\alpha }^2\right)J_1\left(\rho \right)/\rho$ asymptotically, where $J_1$ denotes the Bessel function of the first kind of order one.

Results

In this section, it will be shown via a combination of a mode-counting argument, a perturbative calculation for the general case, and a non-perturbative one for a special case, that spatial variations in the membrane bending rigidity associated with the domains lead to an attractive interleaflet coupling in model membranes.

Mode-counting argument to estimate ${\mathbf{\Lambda }}_{\mathbf{fluct}}$

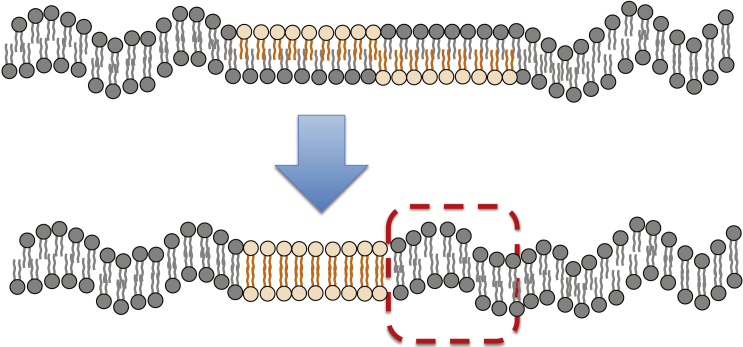
Before embarking on the detailed analysis of the implications of Eqs. 5 and 6 for the interleaflet coupling, $\Lambda$, it is worthwhile to develop physical intuition and estimate the contribution of membrane undulations to $\Lambda$ by way of a mode-counting argument. Following Horner et al. (22), we consider the system illustrated in Fig. 2, which consists of two infinitely rigid domains (i.e., $\delta \kappa /{\kappa }_0\to \mathrm{\infty }$) of area $A_{\text{d}}$ embedded within the bilayer membrane. When the domains are only partially co-localized, they readily suppress membrane undulations over an area $2A_{\text{d}}-A_{\text{o}}$, where $A_{\text{o}}$ denotes the area of overlap between the domains. When the domains achieve a state of more complete co-localization, membrane undulations are enabled within the previously unavailable regions. Thus, starting from two completely co-localized domains and separating them such that they no longer overlap at all will bring about an increase in free energy of magnitude $\Delta \mathcal{F}={\Lambda }_{\text{fluct}}{A}_{\text{d}}\sim k_{\text{B}}T{\rho }_{\text{fluct}}{A}_{\text{d}}$, where ${\rho }_{\text{fluct}}$ denotes the density of undulating modes per unit (projected) area of the membrane. Thus, undulations will contribute a term $\sim k_{\text{B}}T{\rho }_{\text{fluct}}$ to the overall interleaflet coupling, $\Lambda$.

Figure 2.

Effective interaction between two infinitely rigid lipid domains (represented by orange particles) embedded within opposing leaflets of a bilayer. In the case of incomplete domain overlap, membrane undulations are suppressed above and below the domains. When the domains achieve complete co-localization, membrane undulations are enabled within the dashed box, resulting in a decrease in free energy (22). To see this figure in color, go online.

To estimate ${\Lambda }_{\text{fluct}}$, we note that the areal density of modes ${\rho }_{\text{fluct}}=\pi /{\ell }^2$ (25), such that ${\Lambda }_{\text{fluct}}\sim k_{\text{B}}T/{\ell }^2$. Taking $\ell =5\text{nm}$, our simple argument thus suggests that ${\Lambda }_{\text{fluct}}\sim {10}^{-2}{k}_{\text{B}}T\text{/}$nm². Interestingly, the same estimate for ${\Lambda }_{\text{fluct}}$ is obtained if the elastic properties of the domains and the background phase are interchanged, such that two fluctuating, partially overlapping domains are embedded within an infinitely rigid background phase.

Perturbative analysis of membrane undulation effects on ${\mathbf{\Lambda }}_{\mathbf{fluct}}$

Having explored the physical basis for the membrane-undulation induced coupling between the two domains, we next turn to a more quantitative analysis of the problem via the perturbative scheme outlined in Materials and Methods. The calculations are done in a limit opposite to that employed in the mode-counting argument above, such that $\delta \kappa /{\kappa }_0\ll 1$. For completeness, we will discuss separately the cases of non-overlapping and partially overlapping domains; the intermediate-range case, where domain separation is $\rho \approx 2R$, will not be discussed, as it is not amenable to explicit analytic treatment.

Case I: Non-overlapping domains

Using Eq. 6 and the asymptotic form of G, it is straightforward to verify that for two compact domains of area $A_{\text{d}}$ separated by a distance $\rho \gg \sqrt{A_{\text{d}}}$, the leading-order ρ-dependent term in the case of vanishing tension and membrane uncoupled from substrate is given by ${\mathcal{F}}_{\text{coupl}}\sim k_{\text{B}}T{A}_{\text{d}}^2\delta \kappa \delta \overline{\kappa }/\left({\pi }^2{\kappa }_0^2{\rho }^4\right)$, as first shown by Goulian et al. (15) and later by others (16, 17, 18). Similarly, with finite tension but no substrate, ${\mathcal{F}}_{\text{coupl}}\sim -k_{\text{B}}T{A}_{\text{d}}^2{\left(\delta \overline{\kappa }\right)}^2\text{/}\left({\pi }^2{\sigma }^2{\rho }^8\right)$, also in agreement with previous studies (17). In the presence of a substrate, on the other hand, domain interactions become exponentially small beyond a characteristic domain separation, ${\rho }^{\text{∗}}=\text{max}\left[{\left(\sigma /{\alpha }^2\right)}^{1/2},{\left({\kappa }_0/{\alpha }^2\right)}^{1/4}\right]$. Finally, it should be noted that the aforementioned interactions require a heterogeneity in the Gaussian rigidity $\left(\delta \overline{\kappa }\ne 0\right)$, whereas variations in the bending rigidity alone do not induce any long-range algebraic interactions, as explicitly shown by Dean et al. (19).

Case II: Partially co-localized domains

Although the interaction between well-separated domains is well-understood, the case of partially co-localized ones has remained unexplored. From a technical perspective, the most important difference is that in contrast to non-overlapping domains, domain coupling in the case of partial domain overlap is dominated by the short-distance behavior of the pairwise interaction terms, ${\left[{\partial }_{xx}^2{\nabla }^{2}G\left(\mathbf{r}-{\mathbf{r}}^{\prime }\right)\right]}^2$, etc. in Eq. 6. Importantly, these interactions decay rapidly; for example, in the case of $\sigma =0$ and ${\alpha }^2=0$, ${\left({\partial }_{ijkl}^{4}G\right)}^2\sim 1/{\left|\mathbf{r}-{\mathbf{r}}^{\prime }\right|}^{\gamma }$, where $\gamma =4$. Since $\gamma >d$, where $d=2$ denotes the spatial dimension of the membrane, such pairwise interactions are short-ranged in a thermodynamic sense, implying additivity of the interaction energy of the system (see, e.g., (26)). Hence, the double integrals converge rapidly such that ${\langle H_{\text{pert}}^2\rangle }_0-{\langle H_{\text{pert}}\rangle }_0^2=2k_{\text{B}}T{\Lambda }_{\text{fluct}}{A}_{\text{o}}$ when the domain overlap is $A_{\text{o}}\gg {\ell }^2$, regardless of domain shape. Furthermore, in the thermodynamic limit $A_{\text{o}}\to \mathrm{\infty }$, the terms $I_2$ and $I_3$ in Eq. 6 involving the Gaussian rigidity heterogeneity, $\delta \overline{\kappa }$, vanish; that is, these terms do not contribute to ${\Lambda }_{\text{fluct}}$ in this limit. For domains with finite size $R\equiv \sqrt{A_{\text{d}}}$, on the other hand, $I_2\sim I_3\sim {\left(k_{\text{B}}T\right)}^2{A}_{\text{o}}\text{/}{R}^{2+m}$, where $m=0$ when $\sigma ={\alpha }^2=0$, $m=4$ when ${\kappa }_0={\alpha }^2=0$, and $m=8$ when ${\kappa }_0=\sigma =0$.

Now, upon evaluating the term $I_1$ in Eq. 6 by employing cylindrical coordinates in the limit $A_{\text{o}}\gg {\ell }^2$, we obtain

$${\Lambda }_{\text{fluct}}=\frac{2\pi k_{\text{B}}T}{{\kappa }_0^2{\ell }^2}{\int }_0^{\infty }duu\frac{{\left(\delta \kappa \right)}^2}{8}{\left({\nabla }^4\tilde{G}\left(u\right)\right)}^2+\mathcal{O}\left(\frac{\delta \kappa \delta \overline{\kappa }}{{\kappa }_0^2},\frac{{\left(\delta \overline{\kappa }\right)}^2}{{\kappa }_0^2}\right)\frac{k_{\text{B}}T}{R^{2+m}},$$ (7)

where

$${\nabla }^4\tilde{G}\left(u\right)={\int }_0^{1}ds\frac{s^5{J}_0\left(su\right)}{s^4+\frac{\sigma {\ell }^2}{4{\pi }^2{\kappa }_0}{s}^2+\frac{{\alpha }^2{\ell }^4}{16{\pi }^4{\kappa }_0}},$$ (8)

with $J_0$ denoting the Bessel function of the first kind of order zero and $m\ge 0$. Thus,

$${\Lambda }_{\text{fluct}}=\frac{\pi k_{\text{B}}T}{4{\ell }^2}{\left(\frac{\delta \kappa }{{\kappa }_0}\right)}^2\Omega \left(\ell ,{\kappa }_0,\sigma ,{\alpha }^2\right)+\mathcal{O}\left(\frac{\delta \kappa \delta \overline{\kappa }}{{\kappa }_0^2},\frac{{\left(\delta \overline{\kappa }\right)}^2}{{\kappa }_0^2}\right)\frac{k_{\text{B}}T}{R^{2+m}},$$ (9)

where

$$\begin{array}{c}\Omega \left(\ell ,{\kappa }_0,\sigma ,{\alpha }^2\right)\equiv {\int }_0^{\infty }duu{\left({\nabla }^4\tilde{G}\left(u\right)\right)}^2\\ ={\int }_0^{\infty }duu{\left[{\int }_0^{1}ds\frac{s^5}{s^4+\frac{\sigma {\ell }^2}{4{\pi }^2{\kappa }_0}{s}^2+\frac{{\alpha }^2{\ell }^4}{16{\pi }^4{\kappa }_0}}{J}_0\left(su\right)\right]}^2.\end{array}$$ (10)

Equations 9 and 10, which quantify the effects of unrestricted membrane undulations, membrane tension, and substrate effects on the interleaflet coupling, comprise a central result of this study.

First, we note that for domains with $A_{\text{d}}\gg {\ell }^2$, ${\Lambda }_{\text{fluct}}$ is dominated by variations in the bending rigidity, whereas variations in the Gaussian rigidity yield only minute corrections to ${\Lambda }_{\text{fluct}}$. Specifically, for domains with $R\mathrm{\gtrsim }50\text{nm}$, these corrections will be of order ${10}^{-2}{\Lambda }_{\text{fluct}}$ or smaller, assuming $\delta \kappa \sim \delta \overline{\kappa }$. Second, regardless of whether the domains are softer than $\left(\delta \kappa <0\right)$ or more rigid than the background phase $\left(\delta \kappa >0\right)$, the fluctuation-induced interaction in Eq. 9 is always attractive $\left({\Lambda }_{\text{fluct}}\ge 0\right)$ for domains with $A_{\text{d}}\gg {\ell }^2$. This short-range behavior should be contrasted with that at large domain separations, where the interaction can be attractive or repulsive, depending on the signs of $\delta \kappa$ and $\delta \overline{\kappa }$. Third, the interaction between partially overlapping domains is non-zero even in cases where the Gaussian rigidity contrast between the domains and the background phase vanishes $\left(\delta \overline{\kappa }=0\right)$ while $\delta \kappa \ne 0$, in stark contrast with the behavior at large domain separations, where the interaction vanishes (15, 19). Finally, for nanometer-sized domains with $A_{\text{d}}\sim {\ell }^2$, the contributions to ${\Lambda }_{\text{fluct}}$ from spatial variations in the Gaussian and bending rigidities will be of the same order, with magnitudes that cannot be quantitatively assessed within a continuum approach. Moving beyond these general observations, below we explore the effects of bending rigidity of the background phase, membrane tension, and coupling to substrate on ${\Lambda }_{\text{fluct}}$ in the limit $A_{\text{d}}\gg {\ell }^2$, where contributions from the spatial variations in the Gaussian rigidity can be ignored.

To this end, in the absence of both membrane tension and substrate (appropriate for, e.g., freely-floating vesicles), $\Omega ={\int }_0^{\infty }duu{\left[{\int }_0^{1}dss{J}_0\left(su\right)\right]}^2={\int }_0^{\infty }duu{\left(J_1\left(u\right)/u\right)}^2=1/2$, and thus,

$${\Lambda }_{\text{fluct;free}}=\frac{\pi }{8}\frac{k_{\text{B}}T}{{\ell }^2}{\left(\frac{\delta \kappa }{{\kappa }_0}\right)}^2.$$ (11)

To estimate the elastic modulus contrast between the domains and the background phase required to achieve domain co-localization in this case, we set ${\Lambda }_{\text{fluct;free}}={10}^{-3}{k}_{\text{B}}T\text{/}$ nm² and $\ell =5$ nm in Eq. 11, and solve for $\delta \kappa$ to yield a relatively modest bending rigidity heterogeneity, $\delta \kappa \approx \pm 0.25{\kappa }_0$. In light of the fact that ${\kappa }_{\text{Lo}}\sim 2-3{\kappa }_{\text{Ld}}$ in synthetic membranes (20, 21), membrane undulations alone are thus sufficient to co-localize Lo/Ld domains in model membranes. We note that applying Eq. 11 to such systems is suspect, however, as the magnitude of the bending rigidity variation is well beyond the applicability of second-order perturbation theory; we return to this point below. Furthermore, with regard to in vivo systems, although the differences in, e.g., lipid packing (and presumably bending rigidity variations) between the raft and non-raft phases are smaller than those in simple ternary ones (27), it is plausible that membrane undulations contribute to co-localization of sufficiently large domains $\left(R\mathrm{\gtrsim }5\ell \sim 25\text{nm}\right)$, given the rather modest bending rigidity heterogeneity, $\delta \kappa \approx \pm 0.25{\kappa }_0$, required for the mechanism to be relevant.

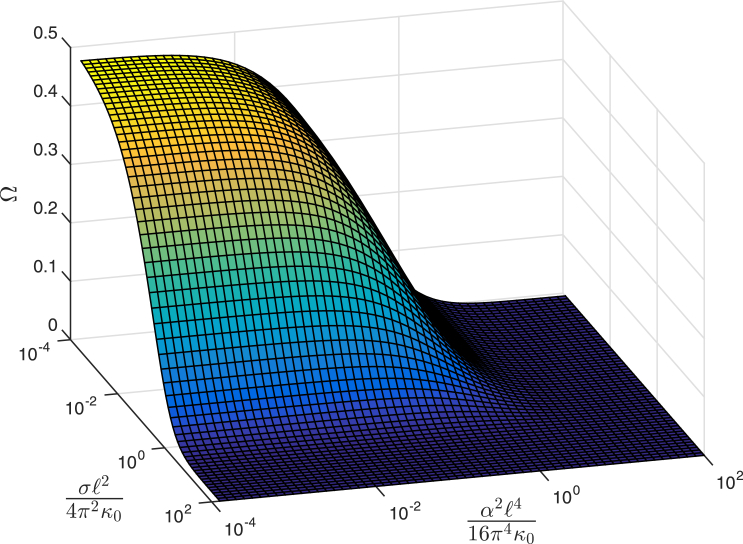
Next, we consider the more general case where both membrane tension and coupling to substrate (or the cytoskeleton in the case of in vivo membranes) are present. Intuitively, both effects should weaken the interdomain interaction by suppressing membrane undulations. Indeed, a closer examination of $\Omega$ from Eq. 10, which is plotted in Fig. 3 over a wide range of representative values of σ and ${\alpha }^2$, confirms this expectation. Increasing either σ or ${\alpha }^2$ decreases the magnitude of $\Omega$ (and thus ${\Lambda }_{\text{fluct}}$). What is perhaps more interesting is the observation that a significant (i.e., a 10-fold) decrease of ${\Lambda }_{\text{fluct}}$ relative to ${\Lambda }_{\text{fluct;free}}$ is obtained only when $\left(\sigma {\ell }^2/4{\pi }^2{\kappa }_0\right)\mathrm{\gtrsim }1$ or $\left({\alpha }^2{\ell }^4/\left(16{\pi }^4{\kappa }_0\right)\right)\mathrm{\gtrsim }1$. In the former case, $\sigma \mathrm{\gtrsim }\left(\left(4{\pi }^2{\kappa }_0\right)/{\ell }^2\right)\sim 20k_{\text{B}}T/$ nm², a value comparable to reported values of the membrane rupture tension (28). In the latter case, ${\alpha }^2\mathrm{\gtrsim }\left(\left(16{\pi }^4{\kappa }_0\right)/{\ell }^4\right)$, or, upon introducing the root mean-square (RMS) height fluctuation, $w^2\equiv {\langle h^2\rangle }_0=\left(\pi k_{\text{B}}T/\left({\alpha }^2{\ell }^2\right)\right)$, the condition becomes $\left(w/\ell \right)\mathrm{\lesssim }{\left[k_{\text{B}}T/16{\pi }^3{\kappa }_0\right]}^{1/2}\sim {10}^{-2}$, where we have employed ${\kappa }_0\approx 20k_{\text{B}}T$, appropriate for the Ld phase (21). Thus, suppression of RMS fluctuations below $w\approx 0.5$ Å is required for the substrate to significantly affect ${\Lambda }_{\text{fluct}}$ in the case of supported bilayers. This is a rather stringent requirement, given that measurements of the RMS height fluctuations in bilayer stacks on a support have yielded values between $\sim 1$ (29) and ∼3–4 Å (30) for the proximal bilayer in single-component systems in the gel and liquid phases, respectively. These considerations thus imply that the interdomain coupling mechanism discussed in this work is very robust against both tension and substrate effects and hence is expected to play an important role in co-localizing domains with $A_{\text{d}}\gg {\ell }^2$ within tension-less free bilayers, bilayers with tension, supported bilayers, or domains with a sufficient elastic heterogeneity in in vivo membranes interacting with the cytoskeleton.

Figure 3.

Dimensionless interleaflet coupling function, $\Omega$ (see Eq. 9 in the main text), versus scaled membrane tension σ and substrate coupling ${\alpha }^2$. To see this figure in color, go online.

Non-perturbative analysis of membrane undulation effects on ${\Lambda }_{fluct}$: special case

Although the above analysis captures the effect of membrane undulations on interleaflet coupling for small elastic heterogeneity $\left(\delta \kappa \ll {\kappa }_0\right)$, drawing quantitative conclusions for Ld/Lo systems (for which elastic heterogeneity can be as large as $\delta \kappa \approx 2{\kappa }_0$ (20, 21)) from a simple perturbative approach becomes questionable. To complement the results of the perturbative analysis leading to Eqs. 9 and 10, we will explicitly consider a special case amenable to a non-perturbative treatment. More specifically, we will focus on an unsupported, tensionless system which contains spatial variations in the bending rigidity, $\kappa \left(\mathbf{r}\right)$, and ignore any variations in the Gaussian rigidity, as the perturbation analysis suggests that Gaussian rigidity has an asymptotically vanishing effect on ${\Lambda }_{\text{fluct}}$ for domains whose overlap $A_{\text{o}}\gg {\ell }^2$.

To this end, following Dean et al. (19), it can be shown that the undulation free energy associated with a given spatial bending rigidity distribution, $\kappa \left(\mathbf{r}\right)$, and spatially uniform $\ell$ is given by $\mathcal{F}=\left(\pi k_{\text{B}}T/2{\ell }^2\right)\int d^2\mathbf{r}\text{ln}\left[\kappa \left(\mathbf{r}\right)/k_{\text{B}}T\right]+\tilde{\mathcal{F}}$, where $\tilde{\mathcal{F}}$ is independent of $\kappa \left(\mathbf{r}\right)$. (This result is readily obtained by first writing H in Eq. 1 in terms of a new variable, $f\left(\mathbf{r}\right)={\nabla }^{2}h\left(\mathbf{r}\right)$, discretizing the system on a square lattice with lattice spacing $\ell /\sqrt{\pi }$ so as to enforce the proper areal density of undulation modes, ${\rho }_{\text{fluct}}=\pi /{\ell }^2$, and evaluating the resulting partition function.)

Now, consider two domains of area $A_{\text{d}}$ that do not overlap at all. For this configuration, ${\mathcal{F}}_{\text{I}}=\left(\pi k_{\text{B}}T/2{\ell }^2\right)\left[\left(A-2A_{\text{d}}\right)\text{ln}\left({\kappa }_0/k_{\text{B}}T\right)+2A_d\text{ln}\left(\left({\kappa }_0+\delta \kappa /2\right)/k_{\text{B}}T\right)\right]+\tilde{\mathcal{F}}$, where A denotes the total area of the system. Next, bring the two domains into partial contact such that they overlap over an area $A_{\text{o}}$. For the second configuration, ${\mathcal{F}}_{\text{II}}=(\pi k_{\text{B}}T/2{\ell }^2)\left[\left(A-2A_{\text{d}}+A_{\text{o}}\right)\text{ln}\left({\kappa }_0/k_{\text{B}}T\right)+2\left(A_{\text{d}}-A_{\text{o}}\right)\text{ln}\left({\kappa }_0+\delta \kappa /2/k_{\text{B}}T\right)+A_{\text{o}}\text{ln}\left({\kappa }_0+\delta \kappa /k_{\text{B}}T\right)\right]+\tilde{\mathcal{F}}\mathrm{.}$ Now, $\Delta \mathcal{F}={\mathcal{F}}_{\text{II}}-{\mathcal{F}}_{\text{I}}=-\left(\pi k_{\text{B}}T/2{\ell }^2\right)\text{ln}\left[{\left[1+\delta \kappa /\left(2{\kappa }_0\right)\right]}^2/\left(1+\delta \kappa /{\kappa }_0\right)\right]A_{\text{o}},$ which implies that

$$\begin{array}{c}{\Lambda }_{\text{fluct;free}}=\frac{\pi k_{\text{B}}T}{2{\ell }^2}\text{ln}\left[\frac{{\left[1+\delta \kappa /\left(2{\kappa }_0\right)\right]}^2}{1+\delta \kappa /{\kappa }_0}\right]\\ =\frac{\pi k_{\text{B}}T}{2{\ell }^2}\text{ln}\left[1+\frac{1}{4}\left(\frac{{\kappa }_{\text{dom}}}{{\kappa }_0}+\frac{{\kappa }_0}{{\kappa }_{\text{dom}}}-2\right)\right],\end{array}$$ (12)

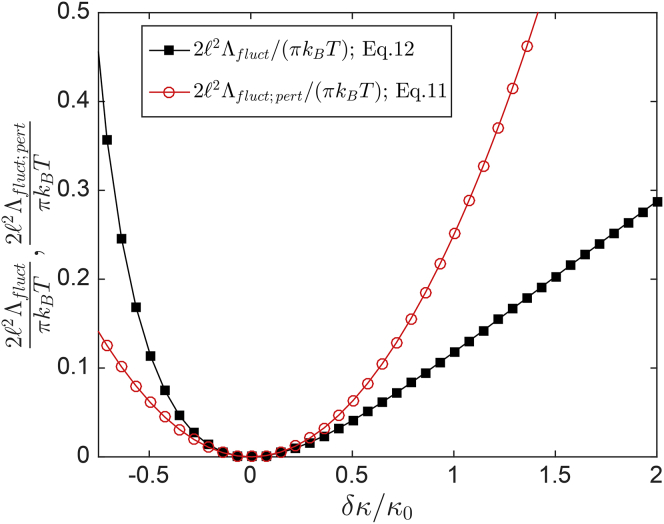
where we have employed the definition $\delta \kappa ={\kappa }_{\text{dom}}-{\kappa }_0$. Equation 12, which accounts for the effects of bending rigidity variations with arbitrarily large contrasts between the domain and the matrix phase in the absence of tension and membrane effects, constitutes the second central result of this study. It is reassuring to note that upon expanding ${\Lambda }_{\text{fluct;free}}$ in Eq. 12 in a Taylor series, we obtain ${\Lambda }_{\text{fluct;free}}=\left(\pi /8\right)\left(k_{\text{B}}T/{\ell }^2\right){\left(\delta \kappa /{\kappa }_0\right)}^2+\mathcal{O}{\left(\delta \kappa \right)}^3$ at leading order, in excellent agreement with the perturbative result in Eq. 11. Finally, Fig. 4 displays the behaviors of ${\Lambda }_{\text{fluct}}$ from Eqs. 11 and 12 over a wide range of $\delta \kappa /{\kappa }_0$ values.

Figure 4.

Comparison between the exact and perturbative expressions for ${\Lambda }_{\text{fluct}}$ in the absence of membrane tension and substrate effects from Eqs. 12 and 11, respectively. To see this figure in color, go online.

To quantitatively compare Eqs. 12 and 11, we set $\delta \kappa ={\kappa }_0$ and $\ell =5\text{nm}$, and obtain ${\Lambda }_{\text{fluct;free}}\approx 0.007k_{\text{B}}T\text{/}$nm² from Eq. 12, whereas Eq. 11 yields $0.016k_{\text{B}}T\text{/}$nm², in reasonable quantitative agreement, given the large elastic heterogeneity. Not surprisingly, the agreement becomes worse for an even larger bending rigidity contrast, $\delta \kappa =2{\kappa }_0$, appropriate for Lo domains embedded within the Ld phase, for which Eqs. 12 and 11 yield ${\Lambda }_{\text{fluct;free}}\approx 0.018k_{\text{B}}T\text{/}$nm² and $0.06k_{\text{B}}T\text{/}$nm², respectively. It is interesting to note that since Eq. 12 is symmetric under the transformation ${\kappa }_0\to {\kappa }_{\text{dom}};{\kappa }_{\text{dom}}\to {\kappa }_0$, ${\Lambda }_{\text{fluct;free}}\approx 0.018k_{\text{B}}T\text{/}$nm² also for the case of softer Ld domains embedded within the more rigid Lo phase. Thus, membrane undulations also promote co-localization of the softer Ld domains, in agreement with experimental observations (31, 32). Such a symmetry is absent when the domains are far apart (17).

Finally, the derivation leading to Eq. 12 assumed that the microscopic cutoff $\ell$ (proportional to membrane thickness) is constant. In cases where $\ell$ does vary between the domain and the background phases, generalizing the approach of Dean et al. (19) yields $\mathcal{F}=\left(\pi k_{\text{B}}T/2{\ell }^{\text{∗}2}\right)\int d^2\mathbf{r}\text{ln}{\left[\kappa \left(\mathbf{r}\right)/k_{\text{B}}T\right]}^{{\ell }^{\text{∗}2}/{\ell }^2\left(\mathbf{r}\right)}+\tilde{\mathcal{F}}$, where ${\ell }^{\text{∗}}$ denotes a reference value, such that

$${\Lambda }_{\text{fluct;free}}=\frac{\pi k_{\text{B}}T}{2{\ell }^{\text{∗}2}}\text{ln}[{\left(\frac{k_{\text{B}}T}{{\kappa }_0}\right)}^{{\ell }^{\text{∗}2}/{\ell }^2}{\left(\frac{{\kappa }_0+\delta \kappa /2}{k_{\text{B}}T}\right)}^{2{\ell }^{\text{∗}2}/{\ell }_1^2}{\left(\frac{k_{\text{B}}T}{{\kappa }_0+\delta \kappa }\right)}^{{\ell }^{\text{∗}2}/{\ell }_{\text{d}}^2}].$$ (13)

Here, $\ell$ denotes the microscopic cutoff for the background phase, and ${\ell }_1$ and ${\ell }_{\text{d}}$ denote the cutoffs for partially overlapping and co-localized domain regions, respectively. It is straightforward to verify that ${\Lambda }_{\text{fluct;free}}$ in Eq. 13 is symmetric under the transformations ${\kappa }_0\to {\kappa }_{\text{dom}};{\kappa }_{\text{dom}}\to {\kappa }_0;\ell \to {\ell }_{\text{d}};{\ell }_{\text{d}}\to \ell$.

To estimate the effects of spatially-varying $\ell$ in Eq. 13, let ${\ell }_{\text{d}}=\ell \left(1+\Delta \right)$ and ${\ell }_1=\ell \left(1+\Delta /2\right)$ with $\Delta \ll 1$, such that ${\Lambda }_{\text{fluct;free}}\approx \left(\pi k_{\text{B}}T/2{\ell }^2\right)\text{ln}\left[{\left(1+\delta \kappa /\left(2{\kappa }_0\right)\right)}^{2-2\Delta }/{\left(1+\delta \kappa /{\kappa }_0\right)}^{1-2\Delta }\right]$. Taking $\ell ={\ell }^{\text{∗}}=5\text{nm}$, $\Delta =0.2$, and $\delta \kappa =2{\kappa }_0$ yields ${\Lambda }_{\text{fluct;free}}\left(\Delta =0.2\right)\approx 0.028k_{\text{B}}T\text{/}$nm², whereas ${\Lambda }_{\text{fluct;free}}\left(\Delta =0\right)\approx 0.018k_{\text{B}}T\text{/}$nm². Hence, a larger cutoff (and, correspondingly, lower areal density of modes) associated with the domains leads to an increase in the interleaflet coupling.

Discussion

In this work, it was demonstrated that entropic interactions between compositional lipid domains embedded within opposing leaflets of a bilayer membrane contribute significantly to the co-localization of domains. In particular, it was shown via a combination of a mode-counting argument, a perturbative calculation for the general case, and a non-perturbative treatment of a special case that spatial variations in the membrane bending rigidity associated with the domains lead to an attractive interleaflet coupling with a strength ${\Lambda }_{\text{fluct}}\sim 0.01k_{\text{B}}T\text{/}$ nm² for a system with an elastic heterogeneity similar to that of an Lo/Ld one. Interestingly, Gaussian rigidity variations do not contribute to ${\Lambda }_{\text{fluct}}$ for sufficiently large domains, in contrast to non-overlapping domains, where such variations are required for a non-vanishing interdomain interaction. Furthermore, the mode-counting argument and the non-perturbative analysis both suggest that ${\Lambda }_{\text{fluct}}$ is symmetric under the exchange of elastic properties between the domains and the matrix phase, implying that ${\Lambda }_{\text{fluct}}$ is the same for both Lo domains embedded within an Ld matrix phase and Ld domains embedded within an Lo phase.

It was also argued that the fluctuation-induced interleaflet coupling is very robust against membrane tension and substrate interactions. Specifically, applied tensions comparable to the membrane rupture tension are required to reduce ${\Lambda }_{\text{fluct}}$ by a factor of 10, and restricting RMS height fluctuations to <$\sim 0.5$Å is necessary for the substrate to significantly affect ${\Lambda }_{\text{fluct}}$. Thus, the results of the non-perturbative calculation for freely suspended bilayers in Eq. 12, which imply that even relatively modest bending rigidity variations significantly contribute to co-localization, should be applicable for bilayers under a wide range of applied tensions and substrate interactions.

Given that ${\Lambda }_{\text{fluct}}$ decreases as the linear dimension, L, of the system decreases (as fewer and fewer membrane undulation modes remain accessible) and vanishes for systems for which L becomes comparable to the bilayer thickness, it is of interest to estimate this size dependence. To this end, replacing the upper limit of the integral in Eq. 7 by $L/\ell$ to reflect the finite system size leads to ${\Lambda }_{\text{fluct}}\left(L\right)\approx {\Lambda }_{\text{fluct}}\left[1-J_0^2\left(L\text{/}\ell \right)-J_1^2\left(L\text{/}\ell \right)\right]$, where $J_0$ and $J_1$ denote Bessel functions of the first kind of orders 0 and 1, respectively. The most rapid variation in ${\Lambda }_{\text{fluct}}\left(L\right)$ occurs between $L=0$ and $L\approx 5\ell$, whereas for $L\mathrm{\gtrsim }10\ell$, ${\Lambda }_{\text{fluct}}\left(L\right)$ differs from ${\Lambda }_{\text{fluct}}$ by only 5% or less. Based on these observations, we therefore expect that membrane undulations fully contribute to the interleaflet coupling in bilayer systems whose linear dimension exceeds $L\mathrm{\gtrsim }10\ell \sim 50\text{nm}$ or so.

It should be noted that although the continuum approach employed in this work quantifies the contribution of membrane fluctuations to the total interleaflet coupling over the range of undulation modes where continuum theory is valid (24), it clearly cannot capture molecular effects. The molecular mean-field approach of Putzel et al. (12), on the other hand, yields explicit predictions for the contributions of gauche bond energy, configurational entropy, and orientational interactions to ${\Lambda }_{\text{mol}}$ for flat membranes. Combining the results from these two complementary approaches should thus yield a predictive expression of the total interleaflet coupling, $\Lambda ={\Lambda }_{\text{mol}}+{\Lambda }_{\text{fluct}}$, which incorporates both molecular-scale and collective fluctuation effects.

With regard to alternative co-localization mechanisms that do not involve any explicit interleaflet coupling (i.e., $\Lambda =0$), effective line tension resulting from hydrophobic thickness variations has recently been proposed by Galimzyanov et al. (33) as a possibility. Although such line tension effects will undoubtedly play a role in the registration/anti-registration behavior of nanoscale domains, as demonstrated very recently by Fowler et al. (34) using coarse-grained molecular dynamics simulations, the vanishing of $\Lambda$ for large (say, $R\sim 10\mu \text{m}$) domains observed in simple ternary systems would require either an almost perfect matching of the bending rigidities of the two phases and simultaneous cancellation of molecular effects discussed above or an almost exact cancellation of the attractive contributions in $\Lambda$ due to membrane undulations and repulsive ones due to molecular effects, with both scenarios appearing very unlikely.

Finally, from a technical perspective, the calculations reported in this article do not explicitly take into account the effects of thermal fluctuations on the bending rigidity. Specifically, it is well-known that fluctuations lead to a scale- and temperature-dependent (renormalized) bending rigidity, ${\kappa }_{\text{R}}\left(\lambda \right)={\kappa }_0-\left(3k_{\text{B}}T/4\pi \right)\text{ln}\left(\lambda /\ell \right)$, where λ denotes the spatial scale at which the system is probed (see, e.g., (35)); it is ${\kappa }_{\text{R}}$ that is measured in experiments. Although the renormalization of the bending rigidity should only lead to small changes in ${\Lambda }_{\text{fluct}}$ (this is because ${\kappa }_0-{\kappa }_R\mathrm{\lesssim }3k_{\text{B}}T\ll {\kappa }_0$ for $\lambda \mathrm{\lesssim }100\mu \text{m}$), the temperature dependence of ${\kappa }_{\text{R}}$ for both the domain and background phases may offer a means to extract $\ell$ from experiments that quantify vesicle shape fluctuations (36)—and thus ${\kappa }_{\text{R}}$—over a range of temperatures. From a simulation perspective, on the other hand, the theoretical predictions presented in this article are amenable to verification via particle-based simulations of membrane systems, in which the elastic properties between the domains and the matrix phase are explicitly tuned, $\ell$ is extracted from simulated membrane undulation spectra (24), and $\Lambda$ is measured from, e.g., out-of-alignment fluctuations (10, 12).

Author Contributions

M.P.H. developed the theoretical framework, analyzed the results, and wrote the article.

Editor: Ana-Suncana Smith.