Two Distinct Actin Networks Mediate Traction Oscillations to Confer Focal Adhesion Mechanosensing

Abstract

Focal adhesions (FAs) are integrin-based transmembrane assemblies that connect a cell to its extracellular matrix (ECM). They are mechanosensors through which cells exert actin cytoskeleton-mediated traction forces to sense the ECM stiffness. Interestingly, FAs themselves are dynamic structures that adapt their growth in response to mechanical force. It is unclear how the cell manages the plasticity of the FA structure and the associated traction force to accurately sense ECM stiffness. Strikingly, FA traction forces oscillate in time and space, and govern the cell mechanosensing of ECM stiffness. However, precisely how and why the FA traction oscillates is unknown. We developed a model of FA growth that integrates the contributions of the branched actin network and stress fibers (SFs). Using the model in combination with experimental tests, we show that the retrograde flux of the branched actin network promotes the proximal growth of the FA and contributes to a traction peak near the FA’s distal tip. The resulting traction gradient within the growing FA favors SF formation near the FA’s proximal end. The SF-mediated actomyosin contractility further stabilizes the FA and generates a second traction peak near the center of the FA. Formin-mediated SF elongation negatively feeds back with actomyosin contractility, resulting in central traction peak oscillation. This underpins the observed FA traction oscillation and, importantly, broadens the ECM stiffness range over which FAs can accurately adapt to traction force generation. Actin cytoskeleton-mediated FA growth and maturation thus culminate with FA traction oscillation to drive efficient FA mechanosensing.

Introduction

Focal adhesions (FAs) are the integrin-based linkages between a cell and its extracellular matrix (ECM) (1). Each FA serves as a mechanosensor through which the cell exerts traction force to sense the local ECM stiffness. Such FA-mediated mechanosensing leads the cell to preferentially migrate toward stiffer substrates. This phenomenon, termed durotaxis (2), underlies many physiological activities, including cancer metastasis (3, 4, 5), nervous system development (6, 7), and tissue formation (8, 9).

From a mechanical standpoint, this mechanosensing is akin to applying force via a spring/sensor with a known spring constant (the FA) to measure the elastic constant of another spring (the ECM). The complication here is that rather than being a static object, the FA evolves constantly (10, 11, 12) and hence is very plastic as a sensor during the mechanosensing process. Typically, many FAs exist within a migrating cell at any time and exhibit different developmental stages in time and space. FAs initiate near the leading edge of cells. Although many nascent FAs disassemble rapidly, some survive and grow proximally toward the cell interior by incorporating more FA components and hence increasing the ECM-contacting area. As these FAs in the cell leading edge become more stable, they transmit traction forces to the ECM, mediating the cell front protrusion and pulling the cell body forward. Meanwhile, the FAs at the rear of the cell undergo a coordinated disassembly to facilitate cell migration. On one hand, the external force tugging an FA drives the growth of the FA in the direction of force application (13). On the other hand, the FA-mediated traction correlates with the FA-ECM contacting area (14). Together, these observations suggest that FA growth, traction force transmission, and mechanosensing of ECM stiffness form an intricate triangular relationship: perturbing one will affect the other two and vice versa. It is unclear how the cell accurately interprets the ECM stiffness while the properties of its mechanosensor keep on evolving. In this context, understanding how FA growth is coupled with the FA traction force will provide the key for deciphering FA mechanosensing, which has not been systematically explored by theoretical models.

The branched actin network and stress fibers (SFs) dictate FA growth, traction generation, and mechanosensing (15, 16). Arp2/3-mediated polymerization of the branched actin network pushes against the cell membrane, which results in a combination of a forward protrusion of the cell leading edge and a backward flow of the branched actin network relative to the ECM, called retrograde actin flux (17). This retrograde actin flux promotes the proximal growth of an FA from its nascent stage (18). Compared with the branched actin network, SFs exist further inside the cell. SFs are comprised of actomyosin filament bundles that emanate from the FA proximal end due to formin-mediated actin polymerization (19). The SF-mediated actomyosin contractility further drives the maturation of the FA in terms of its ECM-contacting area, composition, traction transmission to the ECM, and, importantly, mechanosensing ability (1, 15). Inhibiting actomyosin contraction compromises durotaxis (20, 21), indicating that FAs with fully functional SFs are important for mechanosensing, and nascent FAs may not be directly involved. Seminal work has greatly advanced our understanding of these actin structures and their roles in cell migration on the whole-cell level (22). However, exactly how the growth of individual FAs integrates the effects of the branched actin network and SFs, and consequently contributes to mechanosensing remains unclear.

Intricate FA-localized spatial-temporal patterns of biochemical signaling and mechanical activities provide important clues about FA growth and mechanosensing processes, but have not yet been explained by existing theoretical models (23, 24, 25, 26, 27). Protein tyrosine kinase (PTK) activity, which is essential for cell motility, is concentrated in nascent FAs and remains enriched near the FA distal tip as the FA matures (28). FAs also exert their traction maximum near the distal tip, which shifts toward the FA center as the ECM becomes stiffer (21). Interestingly, the amplitude and position of the FA traction maximum oscillate in antiphase (21): when the FA traction maximum is near the FA distal tip, its magnitude is lower than that near the FA center. Although these oscillations are strictly localized to individual FAs and are asynchronous among FAs within individual cells (21), they collectively confer efficient durotaxis to individual cells (21). The underlying physical mechanisms that drive traction peak oscillation and how this oscillation contributes to mechanosensing are unknown.

In this work, we addressed the questions of how and why FA traction oscillates. Since FAs are not uniform plaques, and since the existing models all assume an internal homogeneity of FAs and obviously cannot explain these spatial-temporal oscillations (23, 24, 25, 26, 27), figuring out how FAs grow is an integral part of understanding traction oscillation and mechanosensing. Toward that end, we established an integrated model of FA growth. By combining modeling and experiments, we found that actin-flux-mediated FA growth set the stage for the formation of FA-engaging SFs. A two-peak traction profile emerged within a growing FA: the distal and central peaks reflected FA-actin-flux mechanical engagement and SF-mediated actomyosin contraction, respectively. The SF elongation-mediated negative feedback with actomyosin contraction caused oscillations of the central traction peak, which competed with the distal traction peak in amplitude and yielded the spatial-temporal oscillation of the FA traction peak evidenced in experiments. Critically, we showed that the central traction peak oscillation, together with the FA structural plasticity arising from FA growth dynamics, increased the range of FA mechanosensing of ECM stiffness. Thus, the growth of an FA is inseparably linked to its mechanosensing ability, and the spatial-temporal FA traction oscillation reflects this underlying mechanism.

Materials and Methods

We used mouse embryo fibroblasts (MEFs) provided by Dr. M. Beckerle (University of Utah). High-resolution traction force microscopy (TFM) was performed to measure FA traction forces. A spinning-disk confocal microscope was used to measure actin flux. SF elongation was measured via photolabeling tracking experiments. Details of these experiments are provided in Supporting Materials and Methods in the Supporting Material.

Results

Model development

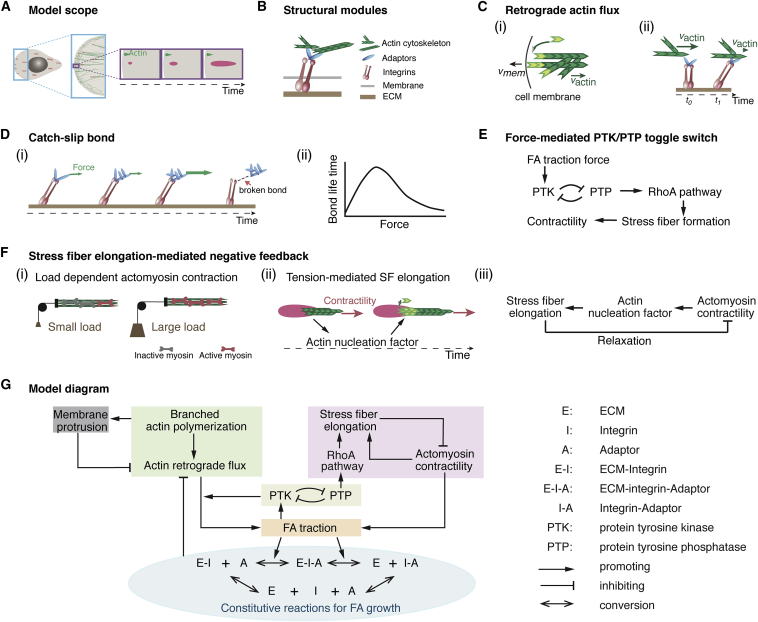
To distill the simplest mechanism, we focused on a single FA growing from a nascent state in a lamellipodium (LP) to a mature state at the LP/lamellum (LM) interface (Fig. 1 A). Although more than 150 individual proteins are involved in FA formation (29), they can be grouped into distinct structural modules according to their functional roles and spatial locations based on the layered structure of an FA (30) (Fig. 1 B). These structural modules are 1) the ECM, 2) integrins, 3) adaptor proteins, and 4) the actin cytoskeleton. Each module can only interact with neighboring layers directly. In addition to these structural modules, the model incorporates the FA-localized signaling effects of PTKs and phosphatases (PTPs) (31, 32, 33, 34, 35), which are essential for the normal physiology of FAs. Characterizing a single FA on the level of modules allowed us to look beyond the roles of individual molecular players and discern the collective behavior of functional modules on a system level. We stressed from the outset that the goal of our model was to offer faithful predictions for in vivo experimental testing, which would require it to integrate all the essential ingredients in this paradigm. Our phase-diagram studies showed that a lack of any of these components in the model resulted in notable FA phenotypes in terms of growth, maturation, and mechanosensing, which either were in line with previous experiments or resolved contradicting experimental observations (see Supporting Materials and Methods for details). This integrated approach distinguishes our model from the previous simplified FA models (23, 27, 36), and could serve as a more realistic starting point to understand FA growth and mechanosensing. Below, we first qualitatively describe the key mechanochemical properties of these functional modules.

• 1)Arp2/3-mediated polymerization of the branched actin network at the cell leading edge results in a combination of membrane protrusion (37) and retrograde actin flux due to resistance from membrane elasticity (17, 38) (Fig. 1 Ci). As the retrograde actin flux passes over the nascent FA, it engages with integrin-bound FA adaptors (Fig. 1 Cii).
• 2)The actin flux-FA engagement assumes behaviors of a catch bond in a low-force regime and a slip bond in a high-force limit. This assumption is based on the following elaborations of the experimental data: due to their catch-bond nature, FA adaptors (e.g., talin (39)) under stretch expose more of the cryptic binding site and promote further actin binding and integrin recruitment (Fig. 1 D). When the actin-flux-mediated pulling becomes large, the actin-adaptor-integrin-ECM linkage falls apart (Fig. 1 D) (40, 41), resulting in mobile FA components that are not anchored to the ECM, e.g., the free FA adaptor in the juxtaposed region right above the FA. This is a slip-bond behavior.
• 3)PTK (i.e., the Src-FAK-CAS functional module (42)) is a mechanosensor: the greater the local traction force, the more its kinase activity increases (Fig. 1 E) (42). PTK-mediated phosphorylation of FA adaptors (e.g., pY-paxillin) potentiates actin-FA engagement (43, 44). Importantly, PTK is in mutual antagonism with PTP, which is upstream of RhoA-mediated SF formation (Fig. 1 E) (31, 32, 33, 34, 35).
• 4)SF-mediated actomyosin contractility is load dependent (45). Resisting loads stimulate stronger myosin II contraction, whereas facilitating loads weaken it (Fig. 1 Fi). On the other hand, actomyosin contraction exerts tension upon the SF. This tension activates the actin nucleation factor (46, 47), and promotes actin polymerization by incorporating actin monomers into the SF ends at the FA (Fig. 1 Fii). The model posits that the resulting SF elongation relaxes and hence turns off the actomyosin contractility, thus constituting a negative feedback (Fig. 1 Fiii).

Figure 1.

Schematic model description. (A) Basic model layout that describes FA growth coupled with actin cytoskeleton dynamics. (B–F) Individual depictions of key model components. (B) FA structural functional modules. (C) Branched actin network polymerization results in a combination of membrane protrusion and retrograde actin flux (i), and the engagement between the actin flux and FA exerts traction on the FA and hence stretches FA components (ii). (D) Catch- and slip-bond behaviors of FA-actin-flux engagement. Actin-flux-mediated stretching initially strengthens the FA mechanical linkage with the actin flux due to the catch-bond nature of the FA. When the stretching becomes sufficiently large, the bond between the flux and FA will break and behave like a slip bond. (E) Changes in the traction force can influence the balance of the toggle switch between FA-localized PTK and PTP activities. In addition, the PTP activity serves as an upstream signal in promoting the RhoA-mediated pathway, which eventually results in SF formation and actomyosin contraction upon the FA. (F) The actomyosin contractility is load dependent (i) and promotes SF elongation (ii). SF elongation negatively feeds back with actomyosin contractility due to the load dependence of myosin II contraction (iii). (G) Wiring diagram of the model summary. To see this figure in color, go online.

The model organically combines these essential elements distilled from the literature into a coherent mechanism of FA growth, as summarized in the wiring diagram of Fig. 1 G. The key point is that FA growth both controls and is dictated by FA-generated traction forces arising from the branched actin network and the SF.

We then translated these qualitative descriptions into a set of coupled partial differential equations (Supporting Materials and Methods). The model focused on a simulation zone that mimicked a patch within the LP (Fig. 1 A). For simplicity, we assumed a constant polymerization rate of the branched actin network at the cell membrane, imposed a fixed width of the LP (∼3 μm), and dictated that the majority of depolymerization of the branched actin network took place around the LP/LM interface (17). The membrane mechanics was governed by a Helfrich-like energy. The membrane protrusion was driven by branched actin network polymerization and was resisted by a boundary effect from the overall membrane resilience of the rest of the cell. The resulting membrane position (the left boundary in Fig. 1 A) was treated as the moving boundary for the retrograde actin flow. The mass balance dictated that the velocity of the retrograde actin flux at the membrane was equal to the constant polymerization rate of the branched actin network minus the membrane protrusion speed (48, 49). The other two boundaries in the simulation box were treated as slip boundaries. The branched actin network is viscoelastic (50, 51): it responds elastically at timescales smaller than the lifetimes of F-actin and actin cross-linkers (typically seconds or tens of seconds), whereas it behaves more viscously at longer timescales, e.g., during FA growth, which typically takes minutes. The model therefore approximated the dynamics of actin flux in the LP by Navier-Stokes hydrodynamics (see Supporting Materials and Methods for detailed considerations). We modeled the FA as a layered structure that was in force balance with actin cytoskeletons. As each FA component also assumed force balance, the actin cytoskeleton-mediated force was transmitted onto the ECM and hence defined as the FA traction (Fig. S1). Any bonds in the ECM-integrin-adaptor linkage could break, e.g., it could break into ECM and integrin-adaptor, or ECM-integrin and adaptor, etc. The model treated these bond breakages and formations as chemical reactions according to the layered FA structure. Among the FA components, only the ECM and ECM-anchored ones were immobile. The rest were mobile, undergoing slow, two-dimensional diffusion and drifting with the actin flux. We modeled the FA-localized biochemical reactions by Michaelis-Menten-type kinetics, the reaction rates of which were modulated by the local traction force (the sum of the actin-flux-mediated traction force and the actomyosin contractility). As all of the tractions were regulated by FA-localized biochemical cascades, the mechanical actions and biochemical pathways were dynamically coupled in the FA growth model.

A two-traction peak profile emerges from a coherent process of FA growth

We first studied the dynamics of our FA growth model by integrating over time the partial differential equations from an initial condition (Supporting Materials and Methods). As part of the initial conditions, 1) the nascent FA was ∼200 nm in diameter; 2) within the nascent FA, all FA modules were in chemical equilibrium with a high PTK activity and a low PTP activity; 3) there were no SFs and no polymerization of the branched actin network; and 4) the membrane was at rest. We then jump-started the simulation by imposing a fixed rate of branched actin polymerization at the membrane. At each time step, the model reported the membrane position and local information, including the densities of the FA components, the traction force, the retrograde flux rate, and the SF elongation rate.

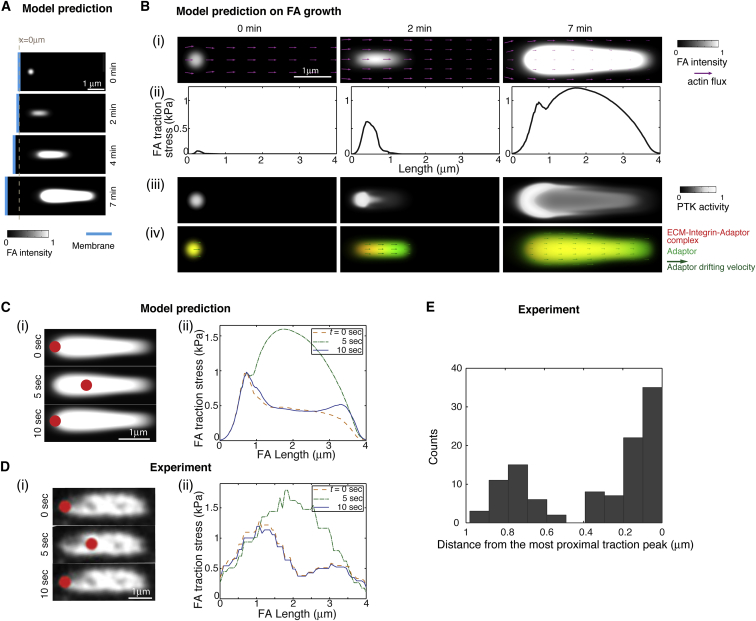
As exemplified by Fig. 2 A, this model recapitulated the observed directional FA growth from the nascent state coupled with membrane protrusion (18) (see Movie S1). The snapshots in Fig. 2 B are the predicted FA-localized spatial-temporal patterns of a growing FA and suggest the following picture of FA growth: as the retrograde actin flux first tugged the nascent FA (Fig. 2 Bi), the initial pulling stimulated the catch-bond behavior of the FA adaptors. This strengthened the FA-ECM linkage by recruiting more adaptors and integrins (Fig. 2 Bii), and stimulating the FA-localized PTK activities that phosphorylated the FA adaptor (e.g., pY-paxillin) (Fig. 2 Biii), which in turn potentiated actin-FA engagement (43, 44). While strengthening the FA-ECM linkage and building up the FA traction (Fig. 2 Bii), this mechanochemical interplay reciprocally slowed down the actin flux within the FA due to force balance (Fig. 2 Bi). This predicted actin flux spatial profile was consistent with previous observations (52, 53, 54). On the other hand, when the actin-flux-mediated pulling became too large, it broke the bonds, resulting in disengaged FA components (e.g., the disengaged adaptor protein A in Fig. 2 Biv). Like a leaf drifting along a creek, these mobile FA components flowed along with the actin flux downstream (Fig. 2 Biv) (54). During the drifting, the disengaged species recruited other FA components, e.g., adaptor A could bind integrin I by forming I-A, which could further anchor onto the ECM by forming E-I-A. These episodes of binding, pulling, breaking, drifting, and rebinding promoted the FA proximal growth downstream of the actin flux (Fig. 2 Bi and Biv). This is in line with observations that the proximal elongation of nascent FAs strongly correlates with the local actin retrograde flux (18, 53). Therefore, upon the mechanical challenge by actin flux, the balance between the self-strengthening catch-bond and drifting slip-bond behaviors of the FA components gave rise to the distal traction peak and the proximal growth of the FA (Fig. 2 Bii and Biv).

Figure 2.

Coherent FA growth and a two-peak traction profile explains FA-localized traction peak oscillation. (A) Centripetal FA growth coupled with membrane protrusion. (B) Predicted FA-localized spatial-temporal profiles of FA components and traction force during FA growth. (i) FA growth coupled with and reciprocally impeding the local retrograde actin flux. (ii) Spatial-temporal evolution of FA traction force that eventually leads to a two-peak traction profile. (iii) Spatiotemporal evolution of PTK activity. (iv) FA drifting components promote centripetal FA growth downstream of the retrograde actin flux. (C) The model predicts that competition between the distal traction peak and the oscillating central traction peak underlies the observed spatial-temporal traction peak oscillation. (D) Traction force microscopy (TFM) experiments illustrate the existence of the two-peak traction profile, with only the central peak oscillating in amplitude. For (C) and (D), the red dots in (i) represent the location of the FA traction maximum, and the FA domains reflect the FA intensity profiles subtracting the fluorescence intensity that is 10% higher than background signals for better contrasts (see Fig. S5 for details). The colored lines in (ii) represent the FA traction profiles along the central line of the FA domains at different times that are not calibrated by backgrounds. (E) Traction peak position distribution. The 0 μm in the x axis indicates the most proximal peak position (toward the center of the FA) for each FA. n = 109 frames from eight FAs in five cells, with each frame taken at 5 s intervals. To see this figure in color, go online.

Because the newly formed FA region contained a less fully anchored FA constituent (i.e., E-I-A at 2 min in Fig. 2 Biv), it was more weakly anchored to the ECM and exerted less traction than the FA distal end (at 2 min in Fig. 2 Bii). Consequently, a traction force gradient emerged as the FA grew proximally, decreasing toward the growing proximal end (Fig. 2 Bii). Due to the mechanosensitivity of PTKs (42), the resulting traction gradient spatially dictated the PTK activity (Fig. 2 Biii). According to the model, this spatial pattern not only explained the FA distal-end-enriched PTK activities (e.g., pY-paxillin) evidenced in experiments (28, 43) but also introduced a transition from branching actin network-mediated FA growth to SF-mediated FA maturation: the proximally tapering of PTK activity tipped the balance of the PTK-PTP toggle switch toward PTP activation at the FA proximal end. As PTP promotes RhoA-mediated SF formation (Fig. 1 E) (31, 32, 33, 34, 35), the PTP activation at the FA growing end drove SF formation locally, consistent with the general consensus that SF emanates from the FA proximal end (1, 15). In contrast to the actin flux that slowed down upon engagement with the FA, the SF-mediated actomyosin contractility was potentiated upon strengthening of the FA and culminated in the central traction peak due to its load dependence (at 7 min in Fig. 2 Bii). Thus, a two-peak traction profile emerged from the growing FA (at 7 min in Fig. 2 Bii), and the spatial separation between the two traction peaks reflected the temporal sequence of the branched actin network and SF engaging with the growing FA.

FA traction maximum oscillation stems from competition between the central and distal traction peaks

Importantly, the FA traction peak oscillation emerged from our model as the FA grew (Fig. 2 Ci and Cii), and was strikingly similar to the observed ones (see Movie S2) (21). Fig. 2 Cii shows the traction force profiles within the FA at different time points (for a more visual presentation, see Movie S3, top). Our model predicted that there were two traction peaks, each at a distinct fixed position: one near the FA distal tip and the other near the FA center. Only the amplitude of the central peak oscillated over time. When the central peak was higher than the distal peak, it marked the location of the traction force maximum. Otherwise, the distal traction peak manifested itself as the traction force maximum for the entire FA. The essence of this two-peak result was typical for the model and preserved within a broad range of the parameter space, as demonstrated by our phase diagram studies (Figs. S2–S4). Thus, instead of a single traction peak oscillating in space, the model predicted that it was the competition in amplitude between the two traction peaks that underlay the observed antiphase oscillations between the magnitude and the location of the FA traction maximum (21).

To test our model, we next performed TFM experiments to measure the traction profiles within FAs. We cultured MEFs on fibronectin-coated coverslips, a condition that promotes FA assembly and traction peak oscillation (21). Our data indicated that for the FAs undergoing spatial-temporal traction peak oscillation, the overall FA traction profile was indeed the overlay of two distinct force distributions peaking at two different locations ∼0.8–1.0 μm apart, a separation that is larger than the spatial resolution of TFM (0.7 μm) (Figs. 2 D and S5). Furthermore, we found that the magnitude of the distal peak remained constant and the central peak oscillated (Fig. 2 C; Movie S3, bottom), thus supporting the model predictions. We then carried out a statistical clustering analysis of FA-localized traction profiles over time. We aligned the TFM images of different FAs according to the position of their respective proximal traction peak. Our results revealed that all of the FA-localized traction peaks clustered around two distinct locations, each with a narrow distribution (Fig. 2 E). Importantly, there was very little population of traction peaks in-between the two locations (Fig. 2 E). We reasoned that if it were the single traction peak that traveled back and forth, the traction peak position would be expected to exhibit a more uniform distribution along the length of the FA. Therefore, this result further favored our two-peak mechanism of FA traction oscillation.

To further test our model, we focused on model predictions that 1) the distal traction peak stemmed from the actin flux-FA engagement, 2) the central traction peak emerged from the SF-mediated actomyosin contractility (Fig. 2 B), and 3) the central peak oscillated because of the off-paced negative feedback between actomyosin contractility and SF elongation (Fig. 1 F).

We set out to experimentally test these model predictions by perturbing the two actin network structures and examining how such perturbations affected the two traction peaks and hence the oscillation. Briefly, we showed that the decreasing gradient of actin flux from the LP toward the LM in control cells correlated with the decreasing propensity of distal traction peaks: the farther away an FA was from the cell leading edge, the less it exhibited a distal traction peak, and the more it exhibited only the central traction peak (Figs. S6 and S7). Moreover, upon Arp2/3 inhibition, the distal peak in the FAs near the cell edge disappeared, whereas the FAs located deep inside the cell body displayed only the central traction peak in control cells and remained unperturbed (Figs. S6 and S7). Together, these results confirmed the prediction that Arp2/3-mediated actin flux contributed to the FA distal traction peak. Below, we discuss how and why the FA central traction peak oscillates.

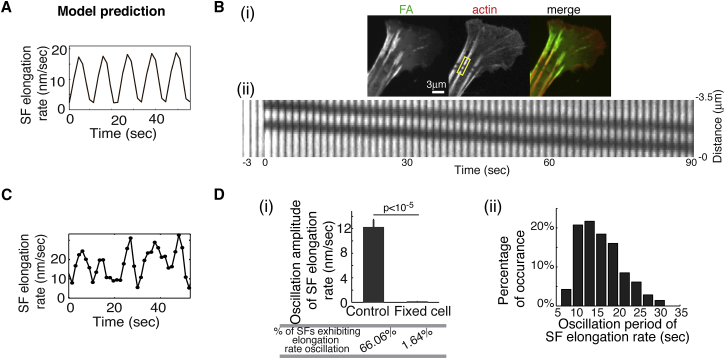
The SF elongation rate oscillates during the central traction peak oscillation

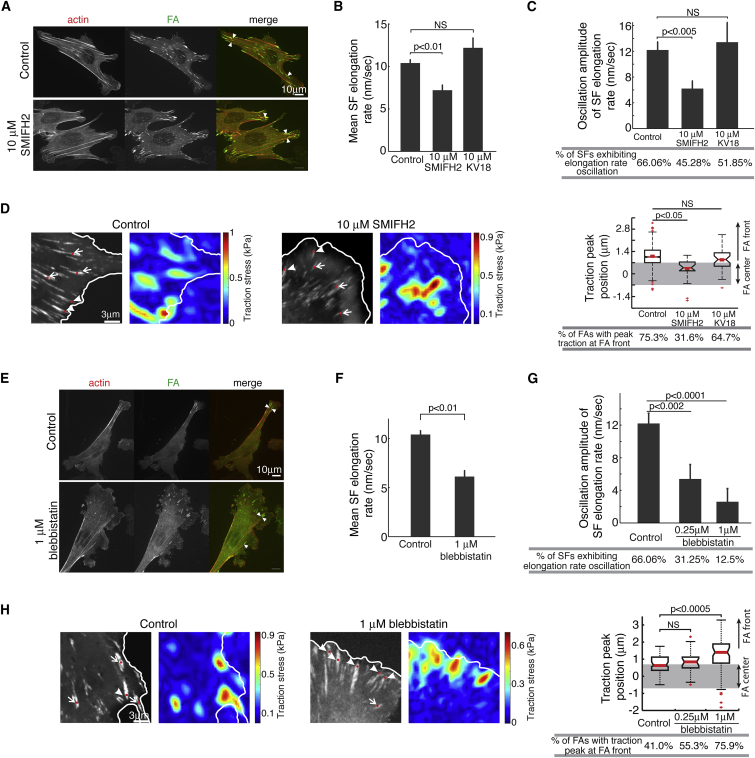
A unique model prediction was that the rate of SF elongating from the FA would oscillate during the traction peak oscillation (Fig. 3 A). To test this prediction, we measured the dynamics of SF elongation in MEFs expressing fluorescently labeled actin and paxillin. We photolabeled individual SFs in these cells by bleaching two diffraction-limited stripes, which created a fluorescent spot between them on a prominent SF near the associated-FA proximal end (Fig. 3 Bi). We used Gaussian fit to pinpoint the centroid position of each fluorescent spot with an accuracy of ∼20 nm (see Fig. S8 for details), and then tracked their positions for 90 s at 1.5 s intervals. From these data (Fig. 3 Bii), we calculated the elongation velocities of individual SFs for every 6 s. We found that whereas the SF elongation rate varied broadly (from 50 to 0 nm/s, with an average value of ∼10 nm/s), the instantaneous SF elongation rate oscillated as predicted (Fig. 3 C), and more than 65% of the SFs (n = 109) exhibited oscillation in the elongation rates (Fig. 3 Di). Importantly, the amplitude of the oscillation was significantly higher in control cells than in chemically fixed cells (by ∼12 nm/s), which reflected random noise (Fig. 3 Di). Moreover, this oscillation amplitude was much higher than the measurement error that arose from the accuracy of the fluorescent spot centroid position, which was 3.3 nm/s (Fig. S8). Further, the period of these oscillations displayed a well-defined mean value of ∼10–20 s (Fig. 3 Dii), the same as that of the observed traction peak oscillations. Together, our experiments thus suggested that the SF elongation rate oscillated during the traction peak oscillation.

Figure 3.

SF dynamics mediates oscillation of the FA central traction peak. (A) The model predicts that the SF elongation rate will oscillate concurrently with the traction peak oscillation. (B) SF photolabeling experiments. (i) Confocal images of MEFs with a photomark bleached onto an SF. Images of eGFP-paxillin, mApple-actin, and color overlay are shown in the left, middle, and right panels, respectively. (ii) Time series (1.5 s interval) of the photomark on the SF labeled with mApple-actin. (C) Measurements of the photomark on the SF show that the rate of SF elongation oscillates over time (see Fig. S8 and Supporting Materials and Methods for more detailed descriptions of SF photolabeling). (D) Statistical analysis of measurements of SF elongation rates. (i) Comparison between control and fixed cells in terms of the oscillation amplitudes of the SF elongation rates. Control: 109 FAs from 66 cells; fixed cell: 61 FAs from 18 cells. Error bars, mean ± SE; p-values, Student’s t-test. (ii) Histogram of oscillation period measurements. Oscillation in the SF elongation rate was counted if there were at least three consecutive significant peaks during the elongation course of individual SFs. Based on this criterion, 72 such SFs were analyzed in (ii), as each SF exhibited elongation rate oscillation. To see this figure in color, go online.

Negative feedback between formin-mediated SF elongation and actomyosin contractility gives rise to central traction peak oscillation

According to our model, the central peak oscillation stemmed from the negative feedback between SF elongation and actomyosin contraction (Fig. 1 F). To further dissect the underlying mechanism, we experimentally perturbed the SF by inhibiting SF elongation and actomyosin contractility. We focused on measuring two observables that faithfully characterized the central traction peak oscillation: 1) the position of the FA traction maximum measured by TFM, and 2) the oscillation amplitude of the SF elongation rate measured by photolabeling.

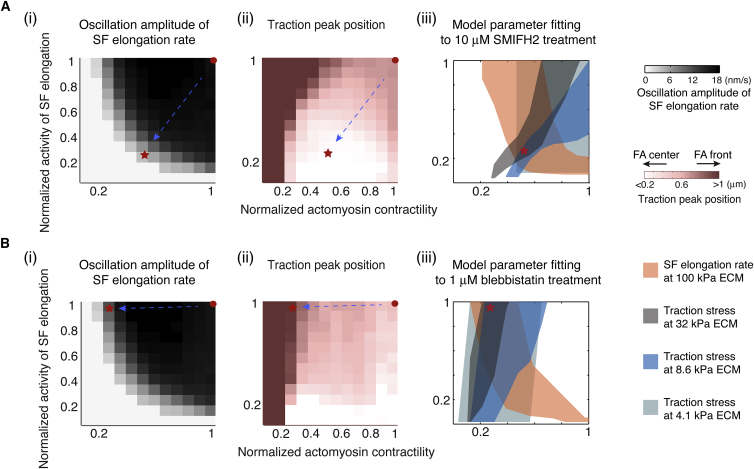
We began with the inhibition of SF elongation. The model predicted that the oscillation amplitudes in SF elongation rates would decrease upon inhibition of the actin nucleation factors for F-actin bundles (Fig. 4 Ai). In addition, for the FAs displaying spatial-temporal traction oscillations in Fig. 2, C and D, the central traction peak would consequently become higher, eventually revealing itself as the sole FA traction maximum (Fig. 4 Aii). To test these predictions, we inhibited formins, which are essential nucleation factors that promote bundled F-actin polymerization (55) and have been implicated in SF elongation from FAs (19). We treated the MEFs for 4 h with SMIFH2, a pharmacological inhibitor of the formin-family FH2 domain (56). Because SMIFH2 is used at 25–100 μM for full SF ablation, we chose a low concentration of SMIFH2, 10 μM, to inhibit formins without completely disrupting the SFs (Fig. 5 A). Using the SMIFH2-treated cells and untreated control cells, we conducted photolabeling experiments and TFM separately. Consistent with previous findings (19), inhibition of formin activity decreased the SF elongation rate by ∼30% (Fig. 5 B). High-resolution tracking of the photomark revealed that formin inhibition decreased the oscillation amplitude of the SF elongation rate by 50% and significantly decreased the fraction of SFs that exhibited oscillating elongation rates (Fig. 5 C). To further validate the effect of SMIFH2, we treated the cells with an inactive form of SMIFH2, KV18. Our data showed that neither the oscillation amplitudes nor the absolute values of the SF elongation rate in KV18-treated cells were significantly different from those in control cells (Fig. 5, B and C). Together with a previous experimental validation of SMIFH2 specificity (57), our experiment suggested that SMIFH2 inhibition of formins was effective. Critically, the FA traction peak position was shifted toward the FA center in SMIFH2-treated cells, whereas the peak in control cells resided at the FA distal tip (Fig. 5 D).

Figure 4.

The negative feedback between SF elongation and actomyosin contractility controls oscillations in the SF elongation rates and the positioning of the FA traction peak. (A) The model phase diagram study predicts that inhibiting actin nucleation factor will critically influence the SF elongation rate oscillation (i) and traction peak position (ii). (iii) Model fitting of parameter changes upon formin inhibition (see Fig. 5, A–D) (marked by the arrows from the red dots to the red stars). (B) The model phase diagram study predicts that inhibiting actomyosin contractility will reduce the oscillation amplitude in the SF elongation rate (i) and shift the position of the traction maximum toward the distal end. (iii) Model fitting of parameter changes upon 1 μM blebbistatin treatment (see Fig. 5, E–H) (marked by the arrows from the red dots to the red stars). To see this figure in color, go online.

Figure 5.

Effects of inhibiting formins or actomyosin contractility on SF elongation rate oscillation and the FA traction profile. (A) Representative images of MEFs in control cells and upon formin inhibition by 10 μM SMIFH2 treatment for 4 h. (B) Statistical analysis of the effects of partial formin inhibition on the SF elongation rate. (C) Statistical analysis of the effects of partial formin inhibition on SF elongation rate oscillation. (B–C) Control: 109 FAs from 66 cells; 10 μM SMIFH2: 53 FAs from 16 cells; 10 μM KV18: 27 FAs from 17 cells. (D) Statistical analysis of the position changes of the FA traction maximum by partial formin inhibition. Left and middle: representative confocal images and the corresponding TFM images for control cells and SMIFH2-treated cells, respectively. Right: statistical analysis of the positions of the FA traction maximum. Control: 270 FAs from 72 cells; 10 μM SMIFH2: 19 FAs from six cells; 10 μM KV18: 34 FAs from nine cells. (E) Representative experimental images of MEFs in control cells and upon nonmuscle myosin II inhibition by 1 μM blebbistatin treatment for 2 h. (F) Statistical analysis of the effects of nonmuscle myosin II inhibition by 1 μM blebbistatin treatment on the SF elongation rate. (G) Statistical analysis of the effects of partial nonmuscle myosin II inhibition on SF elongation rate oscillation. (F and G) Control: 109 FAs from 66 cells; 0.25 μM blebbistatin: 32 FAs from 10 cells; 1 μM blebbistatin: 24 FAs from 14 cells. (H) Analysis of the position changes of the FA traction maximum by partial nonmuscle myosin II inhibition. Left and middle: representative confocal images and corresponding TFM images for control cells and blebbistatin-treated cells, respectively. Right: statistical analysis of the positions of the FA traction maximum. Control: 78 FAs from 10 cells; 0.25 μM blebbistatin: 47 FAs from eight cells; 1 μM blebbistatin: 112 FAs from 10 cells. (A–C and E–G) MEFs expressing eGFP-paxillin and mApple-actin were cultured on individual coverslips coated with 10 μg/mL human plasma fibronectin. (D) MEFs expressing eGFP-paxillin were cultured on an 8.6 kPa PAA gel coated with human plasma fibronectin. (D and H) Top: boxplot of the relative positions of the FA traction maximum within single FAs; bottom: fraction of TFM snapshots of FAs in which the position of the traction maximum was significantly skewed (>0.7 μm) toward the distal tip. The box plots indicate the 25% (lower bound), median (middle line), and 75% (upper bound) confidence intervals, with nearest observations within 1.5 times the interquartile range (whiskers), and the 95% confidence interval of the median (notches) and outliers (+). For all other plots, error bars indicate the mean ± SE; p-values, Student’s t-test. To see this figure in color, go online.

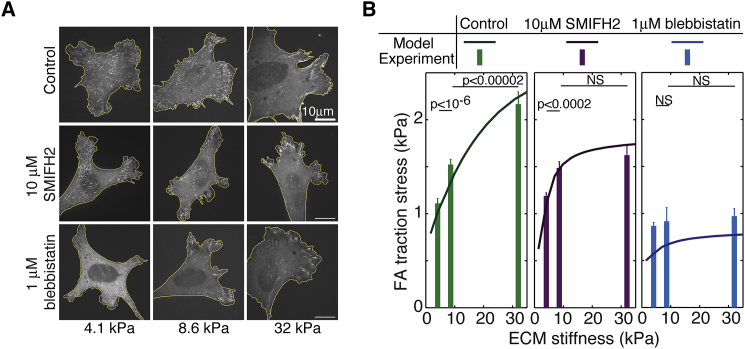
Up to this point, our experiments were in qualitative agreement with the model predictions. As SF elongation and actomyosin contractility were predicted to be in a feedback loop, perturbing one factor by drugs could adversely alter the other. To faithfully test the model, we needed to determine quantitatively how SMIFH2 treatment would alter the model parameters pertaining to SF elongation and actomyosin contractility. Although SMIFH2 treatment also impacted actin fluxes (Fig. S9 A), the resulting changes only marginally altered the traction profile (Fig. S9 A). After incorporating these SMIFH2-mediated actin flux changes into the model, we fitted SF elongation and actomyosin contractility to reproduce the measured SF elongation rates (Fig. 5 B) and traction stresses (Fig. 6) on different ECM stiffnesses under SMIFH2 treatment. The fitting results for each condition are represented by different color zones in Fig. 4 Aiii. The overlapping area of these zones in Fig. 4 Aiii represents the most probable set of the model parameter changes caused by the SMIFH2 treatment. We then used these model parameter changes as inputs (indicated by the arrows from the red dots to the red stars in Fig. 4 A) to pinpoint the quantitative model predictions, which were in quantitative agreement with the effects of SMIFH2 treatment on the oscillation amplitude of the SF elongation rates and the position of the traction maximums (Figs. 4 A and 5, C and D).

Figure 6.

FA traction oscillation contributes to FA mechanosensing. (A) Representative experimental images of control cells and drug-treated cells on ECMs of different stiffnesses. (B) Model prediction (line plots) and experimental measurements (bar graphs) of the FA traction dependence on ECM stiffness. The total cellular traction is normalized to the FA area in cells plated on compliant PAA gels of different stiffnesses (4.1, 8.6, and 32 kPa). We compare this FA mechanosensing of control cells with the conditions that perturb the traction peak oscillations corresponding to those in Figs. 4 and 5. Cells were plated on ECMs of different stiffnesses for 6 h, treated with pharmacological inhibitors for another 2 h, and then imaged. n = >12 cells per condition; error bar, mean ± SE; p-values, Student’s t-test. To see this figure in color, go online.

We next examined the role of actomyosin contractility in the traction peak oscillation. The model predicted that compromising actomyosin contractility would attenuate the oscillation amplitude of the SF elongation rate (Fig. 4 Bi). Further, for the FA on stiff ECMs, decreasing the actomyosin contractility would reduce the central traction peak, allowing the distal traction peak to take over and become the FA traction maximum (Fig. 4 Bii). To examine these two predictions, we treated MEFs with low doses of blebbistatin to partially inhibit the nonmuscle myosin II. The low doses (0.25 and 1 μM) of blebbistatin did not significantly change the FA size, shape, or protein composition, as previously demonstrated (Fig. 5 E) (58). To measure SF elongation rates and minimize the phototoxic effect of blebbistatin (59), we used MEFs that coexpressed eGFP-paxillin and mApple-actin. We used a low intensity of green light (561 nm) to photomark the SFs, and could then follow the dynamics of SF elongation in the red channel. Blebbistatin-mediated inhibition of myosin II indeed reduced the SF elongation rate (Fig. 5 F), supporting our proposal that actomyosin contractility plays a positive role in SF elongation (Fig. 1, F and G). Importantly, blebbistatin treatments reduced the oscillation amplitude in a dose-dependent fashion (Fig. 5 G), in line with model predictions. To determine the effect of myosin II inhibition on the position of the FA traction maximum, we used blebbistatin-treated MEFs that expressed eGFP-paxillin and were cultured on a 32 kPa polyacrylamide (PAA) gel coated with human plasma fibronectin. In control cells, the FA traction maximum was at the FA center (Fig. 5 H). In a dose-dependent manner, the blebbistatin treatments decreased the fraction of FAs with centrally located traction peaks and increased the fraction of FAs with the traction peak at the distal tip (Fig. 5 H). Although blebbistatin impacted actin fluxes (Fig. S9 B), it did not cause notable changes in the overall traction profile (Fig. S9 B). To further quantitatively compare our model predictions with experiments, we used a model parameter fitting procedure similar to that employed for the SMIFH2 treatments, and determined the model parameter changes in SF elongation and actomyosin contractility caused by 1 μM blebbistatin treatments (Fig. 4 Biii). Likewise, the model predictions regarding the oscillations of the SF elongation rate and positions of the traction maximum (marked by the arrows from the red dots to the red stars in Fig. 4 B) were in quantitative agreement with the experimental measurements (Figs. 4 B and 5, G and H).

Taken together, these results indicate that 1) the oscillation in the SF elongation rate underpins and reflects the oscillation of the central traction peak, and 2) the negative feedback between formin protein family activity and actomyosin contractility is actively involved in the generation and oscillation of the central traction peak.

SF elongation-mediated negative feedback confers FA mechanosensing of ECM stiffness

Finally, we addressed the functional role of these traction peak oscillations. Previous experiments suggested a role for this spatial-temporal FA traction peak oscillation in durotaxis (21). As durotaxis entails a collective interplay between different FAs in a cell, it is beyond the scope of the model presented here, which only focuses on the dynamics of a single FA. Nevertheless, the notion that FA traction oscillation correlates with functional roles prompted us to investigate exactly how the SF elongation-mediated negative feedback contributed to FA-mediated mechanosensing. To that end, we examined FA traction stress across the physiological range of ECM stiffnesses (from 4.1 to 32 kPa) under conditions that preserved or perturbed SF elongation-mediated negative feedback (Fig. 6). Our studies showed that in control cells, the FA traction stress increased significantly from 1.1 to 2.2 kPa as the ECM stiffness changed from 4.1 to 32 kPa (Fig. 6). The FA could thus distinguish ECM stiffness by generating a sufficiently distinct traction force, conferring mechanosensitive responses. When actomyosin contractility was inhibited by blebbistatin, the FA traction stress remained low regardless of the ECM stiffness (Fig. 6). The FA in this scenario thus lost its capacity to accurately sense the ECM stiffness, consistent with the observation that myosin II is essential for cell mechanosensing (20). When SF elongation was abated by SMIFH2-mediated inhibition of formin activity, there was no significant difference between FA traction stress values on ECMs with a stiffness of 8.6 versus 32 kPa. In contrast, traction stress values differed significantly on ECMs with a stiffness of 4.1 versus 8.6 kPa (Fig. 6). This result indicated that formin activity is required for the mechanosensing ability of the FA to use increased traction to sense and respond to increases in ECM stiffness. Therefore, we concluded that the negative feedback between formin-mediated SF elongation and actomyosin contractility plays a fundamental role in efficient FA mechanosensing by increasing its working zone of ECM stiffness, and that oscillation of the central FA traction peak is reminiscent of this underlying mechanism.

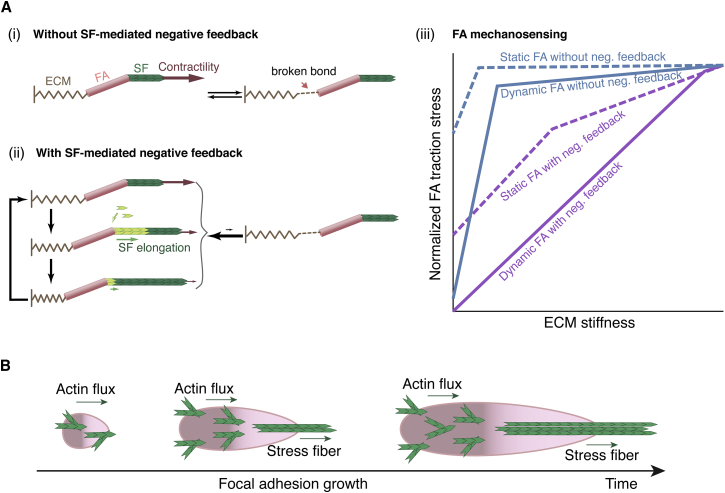
To rationalize the functional role of this SF elongation-mediated negative feedback in mechanosensing, let us consider FA-ECM linkage as a series of springs connected by chemical bonds. The mechanical essence of this spring-like description is captured in our model (Supporting Materials and Methods), as well as in the simplified models developed in previous studies (e.g., (27)). The effective elasticity of this series of connected springs (k) is influenced by the stiffness of each spring, the ECM and FA (k_ECM and k_FA): $k=k_{ECM}\mathrm{\cdot }{k}_{FA}/k_{ECM}+k_{FA}$. The softer the spring, the more it will deform upon pulling, which builds up more strain energy that weakens the chemical bonds within the FA-ECM linkage (27). The strength of the FA-ECM linkage defines the maximum traction upon the FA without breaking the FA-ECM linkage, which is modulated by the overall spring constant k (27). However, the spring constant of the FA-ECM linkage saturates when k_ECM ≫ k_FA, and so does the FA traction (27); that is, the FA is not capable of gauging anything stiffer than itself (Fig. 7 Ai and Aiii). The SF elongation-mediated negative feedback provides a solution. It tunes down the traction on the stiffer ECM while preserving the FA to effectively sense ECM stiffness over a broader range (Fig. 7 Aii and Aiii), just like a decompression valve.

Figure 7.

Model summary. (A) Schematics of the functional roles of SF-mediated negative feedback. (i) Without the negative feedback, the actomyosin contractility eventually matches the mechanical strength of the FA-ECM linkage and becomes saturated when the ECM is stiffer than the FA. (ii) SF-mediated negative feedback downregulates actomyosin contractility. (iii) Schematic comparisons of FA mechanosensing of ECM stiffness under four conditions: with a static or dynamic FA, and with or without SF-mediated negative feedback. (B) Model summary of the sequential actions of the two distinct actin networks in promoting FA growth. To see this figure in color, go online.

Discussion

So far, we have shown that SF elongation-mediated negative feedback and the resulting traction peak oscillation confer efficient FA mechanosensing. A prerequisite of this mechanosensing is the formation of FA-engaging SFs. Instead of forming a priori, the SFs emerge as a natural consequence of the FA maturation process that couples the growing FA to SF formation at the FA proximal end. This points to the intricate relationship between the growth of the FA and its mechanosensing capacity that lies at the heart of the problem. We further elaborated on this key point by leveraging our model.

First, actin flux engagement with nascent FA contributed to a traction peak near the FA distal (Figs. S6 and S7) and promoted the drifting of FA mobile components (Fig. 2 B). Because it took time for the FA drifting components to anchor onto the ECM, this temporal delay led to a proximally decreasing traction gradient as the FA grew. This distinct FA-localized mechanical environment tipped the balance of PTK-PTP antagonism to PTP activation and SF formation. That is, the profile of the actin-flux-mediated FA traction gradient dictated whether and how SFs formed on the FA proximal end (Fig. S10, A–C). When the actin-flux-driven drifting was turned off (Fig. S10 B) or when the E-I-A bond was too strong to break (Fig. S2 H), the FA mobile components had more time to anchor onto the ECM, resulting in less drifting and an increase in flux-mediated FA traction. However, the proximal FA growth was limited. With this small FA size, the tapering of traction force over this short distance was insufficient to tip the balance toward PTP activation. This left little room for SF formation, leading to a compromised mechanosensing (Figs. S2 I and S10 D). A large FA size is a necessary condition for effective FA mechanosensing, but it is not sufficient by itself. For example, in contrast to the nominal case, when FA assembly was speeded up so that the FA drifting components could anchor quickly onto the ECM, no significant traction peak emerged (Fig. S10 C). This more uniform traction distribution dictated that the FA-localized PTK activity would always dominate and suppress PTP activity in growing FAs, and hence SFs could not form upon the growing FA. Consequently, even though the FA could undergo proximal growth in this case, its mechanosensing was compromised (Fig. S10 D), which is similar to the phenotype of blebbistatin-treated cells described in this work (Fig. 5 E) and elsewhere (20).

The above elaborations highlight the necessity of FA growth for SF formation, which is a prerequisite condition for efficient FA mechanosensing. However, does FA growth play more direct roles in efficient FA mechanosensing, other than just paving the way for SF formation? Can we preserve the same FA mechanosensing capacity by treating the mature FA as a static object while keeping the SF elongation-mediated negative feedback? Although fixing an FA and testing its mechanosensing capacity in experiments would be difficult, leveraging our model suggests that FA growth dynamics directly contributes to efficient FA mechanosensing.

To address this issue, we evolved the FA in the model from the nascent to the maturation stage, when SF-mediated actomyosin contractility fully engaged upon the FA. From this mature FA, we modulated the actomyosin contractility to mimic the conditions assigning a traction force upon FA with or without describing FA growth dynamics. We then compared the FA traction transmission onto the ECM and the corresponding FA mechanosensing of ECM stiffness between different scenarios (Fig. S10, E and F). In our nominal case, where FA growth dynamics persisted, the FA traction was largely buffered against variations in actomyosin contractility (Fig. S10 E). This was because the FA traction here reflected the dynamic equilibrium between the catch- and slip-bond behaviors of the FA. Further increasing actomyosin contractility from this balance point broke more ECM-integrin-adaptor linkages, weakening the FA. Conversely, further decreasing actomyosin contractility tipped the equilibrium toward FA strengthening. Either way, the FA traction was buffered, suggesting that FA growth and traction transmission self-regulate each other. Critically, the corresponding FA could effectively sense ECM stiffnesses up to 50–100 kPa (Fig. S10 F). In contrast, when the model treated this mature FA as a static object while preserving the SF elongation-mediated negative feedback, the FA transmitted more traction than the nominal case (Fig. S10 E). However, the corresponding FA mechanosensing zone was decreased (Fig. S10 F). In our nominal case, the FA structure was plastic because of FA growth dynamics, e.g., the slip-bond behavior of the FA and the drifting of FA mobile components. Hence, this dynamic FA may not withstand actomyosin contractility to the same extent as its static counterpart does. Similarly to SF elongation-mediated negative feedback, such FA structural plasticity tunes down the traction transmission onto the ECM, but the gain is a broadened working zone of FA mechanosensing (Fig. 7 Aiii). In fact, this effect of FA structural plasticity adds to that of SF elongation-mediated negative feedback. When the model treated the mature FA as a static object deprived of SF elongation-mediated negative feedback, it predicted an even smaller mechanosensing zone (Figs. 7 Aiii and S10 F).

Taken together, these results suggest that the formation of FA-engaging SFs requires that the FAs grow in a defined manner. Actin-flux-mediated FA proximal growth shapes a proper gradient of the traction profile that tips the PTK-PTP antagonism toward PTP activation near the FA proximal end, which in turn drives SF formation. In this way, actin-flux-mediated FA growth and SF-mediated FA maturation are indispensible sequential events en route to efficient FA mechanosensing (Fig. 7 B). Specifically, the resulting SF-mediated traction oscillation, together with the FA structural plasticity arising from FA growth dynamics, broadens the working zone of FA mechanosensing (Fig. 7 A).

In sum, we have presented a coherent model of FA growth with a number of testable predictions (Figs. S2–S4, S6, S7, and S10). The experiments presented here only validated the model predictions that concerned the FA-autonomous traction oscillations. Although we will experimentally test the rest of the model predictions in future work, we should note that our model captures only the most salient features of FA growth and inevitably is incomplete. In future studies, we plan to more realistically characterize LP and address how the detailed spatial-temporal coupling in actin dynamics between LP and LM influences FA growth and, reciprocally, whether and how FA growth affects the formation of LP and LM in the first place. Moreover, many adaptor proteins and integrin family members exhibit distinct spatial-temporal profiles that correspond to different stages of the FA life cycle (11, 43, 60, 61, 62, 63, 64). Future models will account for these distinct dynamics and may shed light on their functional roles. Additionally, the model only describes a canonical pathway along which nascent FAs grow into maturation steadily without stochastic effects. In reality, many nascent FAs turn over randomly in the LP and the surviving ones may adopt different shapes (18), and mature FAs at the cell rear disassemble upon retraction of the cell edge (65). In the future we will carry out more systematic studies of FA growth and disassembly. Finally, while the model presented here focuses on a single FA, in future efforts we will investigate how migrating cells integrate the information from multiple individual FAs to achieve durotaxis.

Author Contributions

Z.W., S.V.P., C.M.W., and J.L. designed the project. Z.W. constructed and calculated the model. S.V.P. and A.M. performed the experiments. Z.W., S.V.P., A.M., C.M.W., and J.L. analyzed the data. Z.W., S.V.P., A.M., C.W., and J.L. wrote the manuscript.

Editor: Sean Sun.

Supporting Material

Movie S2. FA Traction Peak Oscillation in Time and Space

Top: a typical model result. Bottom: experimental observation. The red dots represent the location of the FA traction maximum.

Movie S3. Temporal Evolution of the FA Traction Profile during the FA Traction Peak Oscillation

Top: a typical model result. Bottom: experimental observation. The FA traction profiles in both movies are along the centerline in the long axis of the FA.