Dynamic Sampling and Information Encoding in Biochemical Networks

Abstract

Cells use biochemical networks to translate environmental information into intracellular responses. These responses can be highly dynamic, but how the information is encoded in these dynamics remains poorly understood. Here, we investigate the dynamic encoding of information in the ATP-induced calcium responses of fibroblast cells, using a vectorial, or multi-time-point, measure from information theory. We find that the amount of extracted information depends on physiological constraints such as the sampling rate and memory capacity of the downstream network, and it is affected differentially by intrinsic versus extrinsic noise. By comparing to a minimal physical model, we find, surprisingly, that the information is often insensitive to the detailed structure of the underlying dynamics, and instead the decoding mechanism acts as a simple low-pass filter. These results demonstrate the mechanisms and limitations of dynamic information storage in cells.

Introduction

Cells utilize cascades of biochemical pathways to translate environmental cues into intracellular responses (1, 2). Due to extensive feedback and cross-talk among these signaling pathways (3, 4, 5, 6), messenger molecules exhibit rich dynamic modes, such as waves, oscillations, and pulses. Recent work in cell biology has suggested a new perspective in cell signaling: the dynamics, or temporal profiles, of messenger molecules allow cells to encode and decode even more rich and complex information than do static profiles (7, 8). For instance, during inflammation response, exposure to tumor necrosis factor α causes the transcription factor NF-κB to oscillate between the nucleus and cytoplasm of a cell (9), whereas bacterial lipopolysaccharide triggers a single wave of NF-κB within the cell (10). Therefore, the dynamics of NF-κB encode the identity of external stimuli. In another example, stimulation of pheochromocytoma cells cells by epidermal growth factor leads to transient mitogen-activated protein kinase activation and cell proliferation, whereas stimulation by nerve growth factor leads to sustained mitogen-activated protein kinase activation and cell differentiation (11). These and other examples raise the question of how one quantifies the information carried by signaling dynamics.

Information theory provides a useful framework for addressing such questions (12, 13, 14). In the simplest case, one calculates the scalar mutual information between states of extracellular stimuli (typically well-controlled discretized values) and states of the cell (typically protein concentrations measured at a certain time). Mutual information characterizes the correlation between environmental cues and cell responses, and conveniently expresses such correlations in units of bits. For example, if the mutual information between an environmental stimulus and a cell response is measured to be ${\text{log}}_{2}2=1$ bit, it means that effectively only two stimulus levels can be resolved by the response variable; any further resolution is not possible given the shape of the stimulus-response curve and the noise in the system (14). Similarly, if the mutual information is ${\text{log}}_{2}3=1.6$ bit, then three stimulus levels can be resolved, and so on. This framework has been successfully employed to quantitatively understand the amount of information that can be transmitted through a biochemical pathway (channel capacity) (15), mechanisms of mitigating errors (16), and design principles of signaling network architectures (17).

Recently, inspired by the fact that cells utilize dynamic signaling to encode and decode information, a multivariate, or vectorial, mutual information has been proposed (18). In this framework, cellular responses are described by vectors of dimension n, which consist of cellular states sampled at multiple time points. The vectorial mutual information is generally higher than the scalar mutual information. Indeed, the scalar mutual information can be thought of as the limit of the vectorial mutual information when the length of the vector is one, and therefore, the vectorial information cannot be lower than the scalar information. This suggests that signaling dynamics allow richer content to be transmitted than does static information processing alone. It has also been shown that sampling cellular states at multiple time points eliminates extrinsic noise—noise that degrades information due to cell-to-cell variability (18).

In light of these results, we ask, what is the optimal strategy for cells to utilize the power of vectorial mutual information? How should a cell sample its own temporal profiles? Can cells use vectorial mutual information to distinguish different dynamic states of the underlying signaling pathways? To address these questions, we combine experimental measurements of ATP-induced Ca²⁺ responses with theoretical analysis to systematically study scalar and vectorial mutual information in a dynamic signaling system. We find that given different physiological constraints, the optimal sampling depends on the starting time, sampling rate, and memory capacity. We characterize how vectorial information is affected by intrinsic and extrinsic noise, in both the experimental system and a simple physical model. Surprisingly, we find that vectorial mutual information is often insensitive to the detailed structure of the underlying dynamics, failing to distinguish between, for example, oscillatory and relaxation dynamics. We explain this observation by deriving the connections between vectorial and scalar information, which reveals that in a particular regime, vectorial encoding acts as a simple low-pass filter.

Materials and Methods

Cell culture and sample preparation

The samples were prepared according to previously reported protocol (19). Briefly, NIH 3T3 cells were cultured in standard growth media (Dulbecco’s modified Eagle’s medium supplemented with 10% bovine calf serum and 1% penicillin). To prepare samples, cells were detached from culture dishes using TrypLE Select (Life Technologies, Carlsbad, CA) and suspended in growth media before being pipetted into the microfluidics devices and allowed to form monolayers. After overnight incubation of the flow-chamber devices containing cell monolayers, fluorescent calcium indicator (Fluo4, Life Technologies) was applied to make the samples ready for imaging.

Fluorescence imaging and data analysis

Fluorescence was detected using an inverted microscope (DMI 6000B, Leica Microsystems, Wetzlar, Germany) coupled with a Flash 2.8 camera (Hamamatsu Photonics, Hamamatsu City, Japan). Movies were taken at a frame rate of 1 fps with a 20× oil immersion objective. Image analysis and data processing were performed in MATLAB.

Results

To investigate properties of dynamic encoding, we focus on the calcium dynamics of fibroblast cells in response to extracellular ATP, a common signaling molecule involved in a range of physiological processes such as platelet aggregation (20) and vascular tone (21). ATP is detected by P2 receptors on the cell membrane and triggers the release of second messenger inositol trisphosphate (IP3). IP3 activates the ion channels on the endoplasmic reticulum (ER), which allows free calcium ions to flux into the cytosol. The nonlinear interactions of Ca²⁺, IP3, ion channels, and ion pumps generate various types of calcium dynamics which may lead to distinct cellular functions (8, 22).

Quantifying information in experimental dynamics

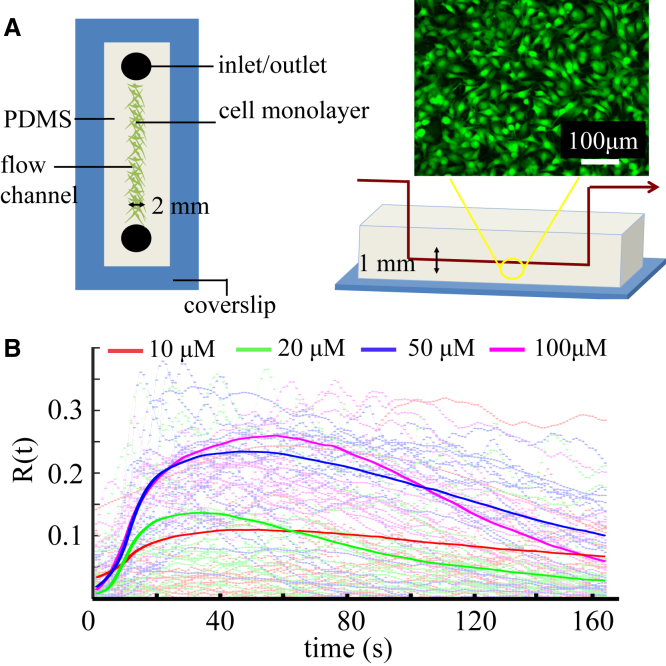
To measure the calcium dynamics of fibroblast cells in response to external ATP stimuli, we employ microfluidic devices for cell culture and solution delivery as described previously (19, 23). In brief, NIH 3T3 cells (ATCC, Manassas, VA) are cultured in polydimethylsiloxane (PDMS)-bounded flow channels, as shown in Fig. 1 A. After attaching the glass bottom for 24 h, the cells are loaded with fluorescent calcium indicators (FLUO-4, Life Technologies) according to the manufacture’s protocol. ATP solutions diluted by Dulbecco’s modified Eagle’s medium to 10, 20, 50, and 100 μM are sucked into the flow channel with a two-way syringe pump (New Era Pump Systems, Farmingdale, NY) at a rate of 90 μL/min. At the same time, we record fluorescent images of the cell monolayer at 1 Hz for a total of 10 min (Flash 2.8, Hamamatsu Photonics).

Figure 1.

Schematics of experimental setup. (A) Top and cross views of the microfluidics device for delivering ATP solution to cultured fibroblast (NIH 3T3) cells. Inset: Fluorescent calcium imaging of a typical experiment. (B) Relative fluorescent intensities indicating the calcium dynamics, $R_i\left(t\right)$, of individual cells (dashed lines) when stimulated by external ATP at four different concentrations, and the average trajectories (solid lines) at each concentration. To see this figure in color, go online.

In all the experimental recordings, ATP arrives at approximately $t=10$ s and stays at a constant concentration. Since most responses happen within 2 min, we use the first 160 s of recording for subsequent analysis. The time-lapse images are postprocessed to obtain the fluorescent intensity, $I_i\left(t\right)$, of each cell, i, at a given time, t. We define the calcium response as $R_i\left(t\right)=\left[I_i\left(t\right)-I_i^{\text{r}}\right]/I_i^{\text{r}}$, where $I_i^r$ is a reference obtained by averaging the fluorescence intensity of cell i before ATP arrives (Fig. 1 B).

To quantify the information encoded in the calcium dynamics of fibroblast cells in response to ATP, we have analyzed a total of >10,000 cells over four different ATP concentrations (10, 20, 50, and 100 μM) as inputs. With the underlying assumption that each input appears at a probability of 1/4, the same number of cells is selected for each ATP concentration. Since the mutual information is bounded from above by the minimum of the entropies of the two variables, the maximal possible mutual information between the input and output is the entropy of the input, or ${\text{log}}_{2}4=2$ bit.

The mutual information can be written in terms of the joint probability distribution between input and output variables, or equivalently as a difference between entropies (24). In our case, we will find the latter more convenient. Denoting the dynamic calcium response as $R_i^{\alpha }\left(t\right)$, where $\alpha =\mathrm{1,2,3,4}$ for each ATP concentration, and $i=\mathrm{1,2},\dots ,N$ for each cell $\left(N\sim 2500\right)$, the scalar mutual information is defined as

$$M{I}_{\text{s}}\left(t\right)=H\left[\left\{R\left(t\right)\right\}\right]-\frac{1}{4}\sum _{\alpha }H\left[\left\{R^{\alpha }\left(t\right)\right\}\right],$$ (1)

where H represents the differential entropy. The first term is the unconditioned entropy calculated from cellular responses at time t for all four ATP concentrations. The second term is the average of the differential entropies conditioned at each ATP concentration. Intuitively, the scalar mutual information, $M{I}_{\text{s}}\left(t\right),$ measures how much the entropy (uncertainty) in the output (cellular responses) is reduced by knowledge of the input (ATP concentration) and, therefore, how much information one variable contains about the other. It is a function of the time, t, at which we take a snapshot of the system and evaluate the differential entropy across the ensemble of cells.

The vectorial mutual information is defined as

$$M{I}_{\text{v}}\left(t_{\text{s}}\right)=H\left[\left\{R\left(\overrightarrow{t}\right)\right\}\right]-\frac{1}{4}\sum _{\alpha }H\left[\left\{R^{\alpha }\left(\overrightarrow{t}\right)\right\}\right],$$ (2)

where $\overrightarrow{t}=\left(t_{\text{s}},t_{\text{s}}+r^{-1},t_{\text{s}}+2r^{-1},\dots ,t_{\text{s}}+T_{\text{d}}\right)$. When generalizing to the vectorial mutual information, $M{I}_{\text{v}}$, one has to specify not only the sampling start time, $t_{\text{s}}$ (equivalent to the time t in the case of $M{I}_{\text{s}}$), but also the sampling duration, $T_{\text{d}}$, and the sampling rate, r, which opens the possibility of complex sampling strategies. In the time between $t_{\text{s}}$ and $t_{\text{s}}+T_{\text{d}}$, a fibroblast cell sampling its calcium concentration at a rate r accumulates a vectorial representation of its calcium dynamics with vector dimension $n=1+r{T}_{\text{d}}$. Since the cell has to store the vector for further processing, n also represents its memory capacity.

To calculate the scalar and vectorial mutual information, we employ the k-nearest neighbor (kNN) method to estimate the differential entropies (18, 25, 26), as we have done in our previous work (27). This method does not require binning of data, and it has been shown to converge quickly even with a small number of data points (26). The kNN method makes the approximation that the probability density, $\rho \left(x\right)$, around a data point $x$ is uniform within the n-dimensional sphere that encloses exactly k other data points. As a result, the performance of the kNN method degrades, particularly for distributions that have long tails or large spatial gradients. Despite these limitations, the kNN method is widely employed in quantitative biology for its ease of implementation and superior performance. That being said, some of the errors will cancel when calculating the mutual information (18, 26), and we have taken $k=50$ (square root of the sample size) based on the suggestions of (25).

Dynamic encoding increases information

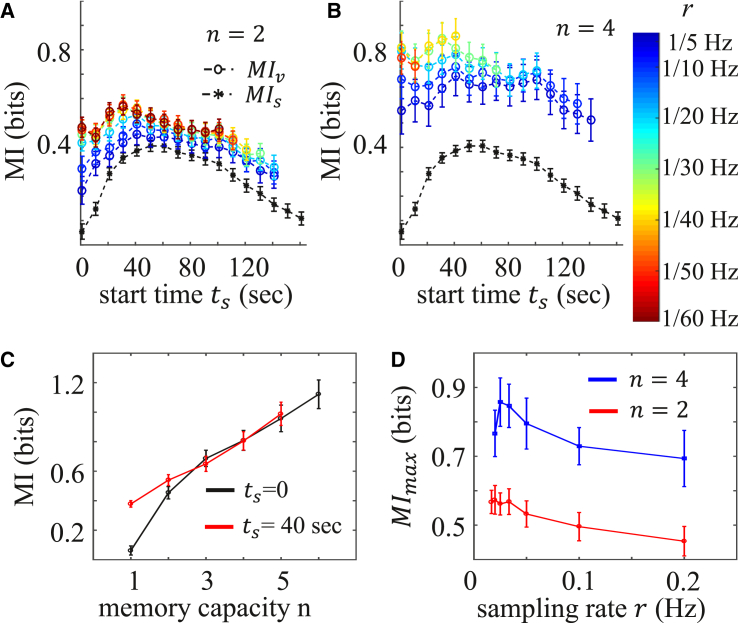
We first consider the situation where the sampling duration, $T_{\text{d}}$, is fixed. Fig. 2 shows the mutual information of both scalar $\left(M{I}_{\text{s}}\right)$ and vectorial encoding $\left(M{I}_{\text{v}}\right)$ from fibroblast calcium dynamics for $T_{\text{d}}=30$ s (Fig. 2, A, C, and E) and $T_{\text{d}}=60$ s (Fig. 2, B, D, and F). As seen in Fig. 2, A and B, $M{I}_{\text{s}}$ first rises, then falls, as a function of time. This is due to the separation, then convergence, of the four ATP-conditioned responses as a function of time, as seen in Fig. 1 B: better-separated responses contain more information about the ATP level. This shape is also reflected in $M{I}_{\text{v}}$, with additional smoothing due to the repeated sampling.

Figure 2.

Information carried by calcium dynamics of fibroblast cells in response to ATP, for fixed sampling duration, $T_{\text{d}}$. (A and B) Vectorial mutual information, $M{I}_{\text{v}}$, as a function of sampling start time, $t_{\text{s}}$, at different sampling rates, r (color bar), for (A) $T_{\text{d}}=$ 30 s and (B) $T_{\text{d}}=$ 60 s. The black curve gives the scalar mutual information, $M{I}_{\text{s}}$, at each time point. (C and D) Mutual information per sample for the same conditions as in (A) and (B). (E and F) Maximal $M{I}_{\text{v}}$ over all $t_{\text{s}}$ values as a function of the memory capacity, n, for (E) $T_{\text{d}}$ = 30 s and (F) $T_{\text{d}}$ = 60 s. Maximal $M{I}_{\text{s}}$ is plotted at $n=1$. Error bars in (A)–(F) represent the mean ± SD of 100 bootstraps. To see this figure in color, go online.

Fig. 2, A and B, also shows that $M{I}_{\text{v}}$ increases with sampling rate r. This is intuitive, since a larger sampling rate produces a larger number of samples, $n=1+r{T}_{\text{d}}$, which increases the amount of information extracted from the dynamics. Although the results in Fig. 2, A and B, are intuitively expected, it is also important to know the efficiency for dynamic encoding. To this end, we have calculated the mutual information per sample, defined as $M{I}_{\text{v}}\text{/}n$, as shown in Fig. 2, C and D. It is evident that higher coding efficiency is achieved at a smaller sampling rate. This is because when the sampling rate is large, samples are spaced closely in time and therefore contain increasingly redundant information, which lowers the coding efficiency. The results shown in Fig. 2, C and D, suggest that although dynamic encoding mitigates intrinsic noise, it is not enough to allow $M{I}_{\text{v}}$ to grow faster than linearly with n. Indeed, scalar encoding generally offers better efficiency than vectorial encoding: as shown in Fig. 2, C and D, $M{I}_{\text{s}}\left(t_{\text{s}}\right)>M{I}_{\text{v}}\left(t_{\text{s}}\right)\text{/}n$, except at very early times when the cellular response has just started.

The results of Fig. 2, A–D, are summarized in Fig. 2, E and F, which plot $M{I}_{\text{max}}$, the maximal mutual information over all possible sampling start times, $t_{\text{s}}$. As seen in Fig. 2, E and F, $M{I}_{\text{max}}$ monotonically increases with n, which shows that dynamic encoding improves the information capture. However, the increase is sublinear, i.e., below the dashed line defined by the scalar mutual information, which shows that the efficiency of dynamic encoding decreases with vector length n. Considering scalar encoding as the limiting case of $r\to 0$, we conclude that as the sampling rate increases, mutual information increases but the coding efficiency per measurement decreases.

Dynamics determine optimal sampling rate

Cells have limited ability to process dynamically encoded information. It is conceivable that a biochemical signaling network processing a vectorial code of high dimension will be complex and expensive, because it requires a high memory capacity, n, for storage and transfer. Therefore, a relevant question is, what sampling strategy can a cell apply when the memory capacity is fixed? Fig. 3, A and B, show the mutual information as a function of sampling start time, $t_{\text{s}}$, when the memory capacity, n, is fixed while the sampling rate, r, and therefore the duration, $T_{\text{d}}=\left(n-1\right)/r$, are allowed to vary. Comparing Fig. 3 A to Fig. 3 B, we see that larger memory capacity n generally allows more information to be transmitted, as was the case in Fig. 2. This trend is quantified in Fig. 3 C, which plots the mutual information as a function of n for a fixed sampling rate and at two particular starting times, $t_{\text{s}}$. We see that the amount of information significantly depends on $t_{\text{s}}$ for small n, whereas the difference diminishes at larger n. Therefore, we see that larger memory capacity not only encodes higher information, but also helps cells to obtain more uniform readouts. We suspect that the convergence is due to the fact that information is upper-bounded (at 2 bit in our case), which requires that all curves, regardless of $t_s$, ultimately saturate with increasing n. Although our current sample size is not large enough to calculate $M{I}_{\text{v}}$ at larger n, the saturation of $M{I}_{\text{v}}$ has been shown in (18) to occur at around $n=12$ for ATP-induced calcium dynamics.

Figure 3.

Information carried by calcium dynamics of fibroblast cells in response to ATP, for a given memory capacity, n. (A and B) Vectorial mutual information, $M{I}_{\text{v}}$, as a function of sampling start time, $t_{\text{s}}$, at different sampling rates, r (color bar) for (A) $n=2$ and (B) $n=4$. The black curve is the scalar mutual information, $M{I}_{\text{s}}$, at each time point. (C) $M{I}_{\text{v}}$ as a function of n at fixed sampling rate $r=1/30$ Hz and sampling start time (black curve, $t_s=0$; red curve, $t_{\text{s}}=40$ s). $n=$ 1 corresponds to $M{I}_{\text{s}}$. (D) Maximal $M{I}_{\text{v}}$ over all $t_{\text{s}}$ values as a function of r for fixed memory capacity (red, $n=2$; blue, $n=4$). Error bars in (A)–(D) represent the mean ± SD of 100 bootstraps. To see this figure in color, go online.

We also see in Fig. 3, A and B, that for a given n, there is an optimal sampling rate, r, that maximizes the information. This is made more evident by considering, as before, the maximal mutual information, $M{I}_{\text{max}}$, over all possible start times, $t_{\text{s}}$, which is plotted as a function of r in Fig. 3 D. Particularly, for $n=4$ (blue curve), we see that $M{I}_{\text{max}}$ is maximal at a particular sampling rate. This is because, for a fixed number of samples n, sampling too frequently results in redundant information, as discussed above, whereas sampling too infrequently places samples at late times, when the dynamic responses have already relaxed (see Fig. 1 B). Therefore, it is generally beneficial to sample at a lower rate except when the sampled points are too far apart, which places samples outside the “high yield” temporal region. The tradeoff between these two effects leads to the optimal sampling rate, where the information gathered is the largest.

Vectorial information is insensitive to detailed dynamic structure

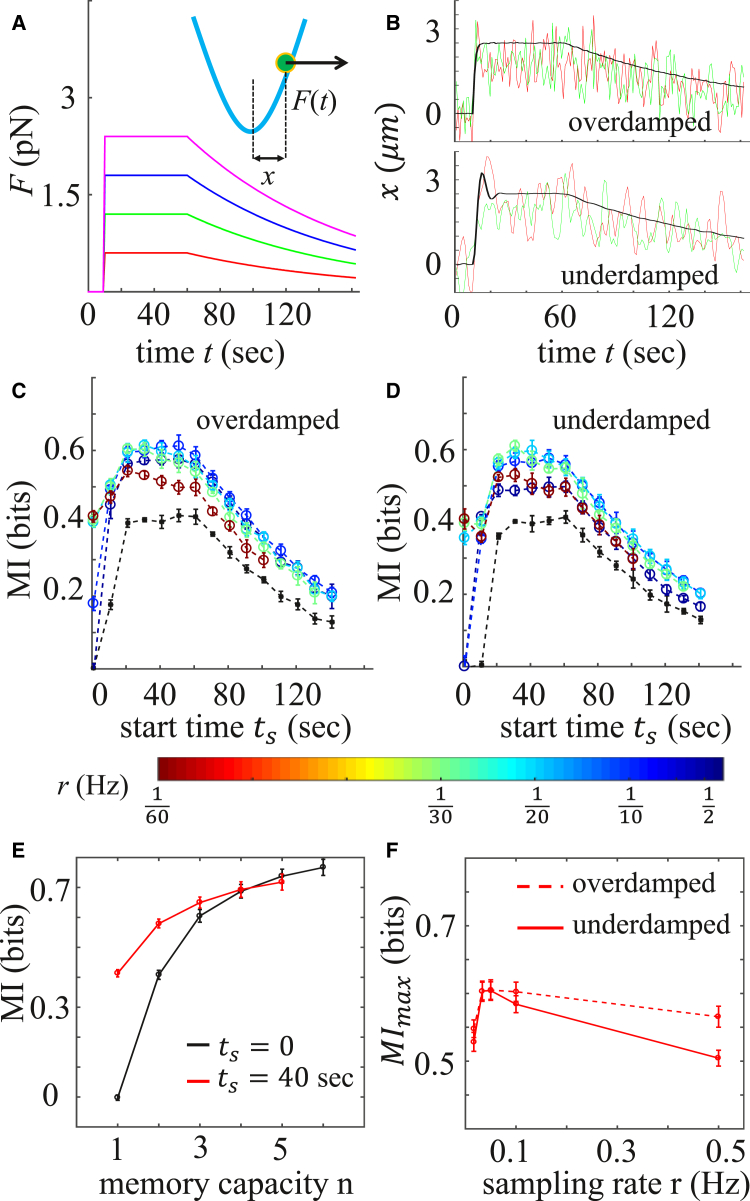
Is vectorial encoding sensitive to the underlying details of the dynamic response? To answer this question, and to provide a mechanistic understanding of dynamic information transmission in biochemical networks, we construct a minimal stochastic model with the aim of recapitulating the key features of the fibroblast response. As a minimal model we consider a damped harmonic oscillator in a thermal bath, driven out of equilibrium by a time-dependent forcing, $F\left(t\right)$. The magnitude of the external forcing is proportional to a scalar input, which is analogous to the ATP concentration. The displacement of the particle $x\left(t\right)$, like the calcium dynamics, can then be analyzed to infer the information that the oscillator encodes about the input.

The equation of motion for the oscillator is given by the Langevin equation (28)

$$m\frac{d^{2}x}{d{t}^2}+\gamma \frac{dx}{dt}+kx=g_{\alpha }F\left(t\right)+\psi \left(t\right),$$

$$\langle \psi \left(t\right)\psi \left(t^{\prime }\right)\rangle =2k_{\text{B}}T\gamma \delta \left(t-t^{\prime }\right),$$

$$F\left(t\right)=\{\begin{array}{cc}0& t<t_1\\ 1& t_1\le t\le t_2\\ e^{-\beta \left(t-t_2\right)}& t>t_2.\end{array}$$ (3)

Here, m is the mass, γ is the drag coefficient, and k is the spring constant. $\psi \left(t\right)$ is the random forcing arising from thermal fluctuations with energy $k_{\text{B}}T$; it is Gaussian and white, and represents intrinsic noise. The form of the external forcing, $F\left(t\right)$, illustrated in Fig. 4 A for four magnitudes, $g_{\mathrm{1,2,3,4}}$, is chosen to reflect the fact that after initial elevation, cells relax to their resting level of cytosolic calcium concentration at the end of experimental recording (see Fig. 1 B). To account for the extrinsic noise observed in our cellular system (27), we have allowed the spring constant for each oscillator trajectory to vary uniformly around $\langle k\rangle$ with a standard deviation of $\delta k$. Fig. 4 B shows sample trajectories, $x\left(t\right)$, for two cases: when the oscillations are overdamped $\left(m<m_c\right)$ and when they are underdamped $\left(m>m_{\text{c}}\right)$, where $m_{\text{c}}\equiv {\gamma }^2/\left(4k\right)$ is the mass at critical damping.

Figure 4.

Information encoding in the noisy harmonic oscillator model. (A) Oscillator at position $x\left(t\right)$ is subjected to random thermal forcing as well as deterministic forcing, $F\left(t\right)$ (Eq. 3). Four force magnitudes, $g_{\mathrm{1,2,3,4}}=\left\{0.6,1.2,1.8,\text{and}2.4\text{pN}\right\}$, serve as input, and $x\left(t\right)$ is output. Other parameters are $t_1=10$ s, $t_2=60$ s, and $\beta =0.01$ s⁻¹. (B) Two sample trajectories (red and green curves) and the average of 5000 trajectories (black curves) corresponding to $g_4=2.4$ pN. Upper: Overdamped oscillators with $m=0.4m_{\text{c}}$, where $m_{\text{c}}={\gamma }^2\text{/}\left(4k\right)=0.25$ mg is the mass at critical damping, $\gamma =1$ pN s/μm, and $k=$ 1 pN/μm. Lower: Underdamped oscillators with $m=9m_{\text{c}}$. Other parameters are $k_{\text{B}}T$ = 0.5 pN μm and $\delta k=0.2$ pN/μm. (C and D) Vectorial mutual information, $M{I}_{\text{v}}$, as a function of sampling start time, $t_{\text{s}}$, at different sampling rates, r (color bar), and memory capacity $n=2$ for (C) overdamped and (D) underdamped oscillators. The black curve represents the scalar mutual information, $M{I}_{\text{s}}$, at each time point. (E) $M{I}_{\text{v}}$ as a function of n at fixed sampling rate $r=1/30$ Hz and sampling start time (black curve, $t_{\text{s}}=0$; red curve, $t_{\text{s}}=40$ s). $n=$ 1 corresponds to $M{I}_{\text{s}}$. (F) Maximal $M{I}_{\text{v}}$ over all $t_{\text{s}}$ values as a function of r for fixed memory capacity $n=2$. Error bars in (C)–(F) represent the mean ± SD of 20 independent trials for each condition. To see this figure in color, go online.

Fig. 4, C and D, shows, for the overdamped and underdamped cases, the scalar and vectorial mutual information between input, $g_{\alpha }$, and output $x\left(t\right)$, as a function of sampling start time, $t_{\text{s}}$, for various sampling rates r and fixed memory capacity $n=2$. Additionally, Fig. 4 E shows the mutual information as a function of n at fixed r for the overdamped case, and Fig. 4 F shows the maximal mutual information as a function of r at fixed n for both cases. Comparing Fig. 4 to Fig. 3, we see that our minimal model is sufficient to capture the key features of the experiments. Specifically, comparing Fig. 4, C and D, to Fig. 3 A, we see that the model captures the non-monotonic shape of the mutual information as a function of start time, $t_{\text{s}}$, as well as the improvement of vectorial encoding (colors) over scalar encoding (black). Comparing Fig. 4 E to Fig. 3 C, we see that the model captures the increase of mutual information with memory capacity n, as well as the large-n convergence of curves with different $t_{\text{s}}$ (although it is evident that the model appears to saturate at an n value lower than the experimental results). Finally, comparing Fig. 4 F to Fig. 3 D, we see that the model captures the presence of an optimal sampling rate, r, that negotiates the tradeoff between samples that are well-separated, yet confined to the high-yield region ($t_1\le t\le t_2$ in the model). These correspondences validate the model, and allow us to use the model to ask how vectorial encoding depends on the structure of the underlying dynamic responses.

The noisy oscillator model allows us to explore two qualitatively different regimes of dynamic structure. In the overdamped regime, the thermal noise overpowers the oscillations, and the dynamics are dominated by fluctuations (Fig. 4 B, upper). In contrast, in the underdamped regime, the oscillations overpower the thermal noise, and the dynamics are dominated by the underlying oscillatory structure (Fig. 4 B, lower). Since vectorial mutual information corresponds to sampling the dynamics at regular intervals, it is natural to hypothesize that the amount of information extracted from underdamped dynamics will be higher than that extracted from overdamped dynamics, because underdamped dynamics have a more ordered structure. Fig. 4, C and D, compares the mutual information in the overdamped and underdamped cases. Surprisingly, we see that the amounts of information are roughly equivalent in the two cases. It is evident from Fig. 4, C and D, that the equivalence holds at varying sampling rates, r, and start times, $t_{\text{s}}$ (including the start time at which the information is maximal (Fig. 4 F)). In particular, the equivalence holds when the sampling rate, r, equals the oscillation frequency of the underdamped oscillator, $\nu =\sqrt{\left(k/m\right)\left(1-m_{\text{c}}/m\right)}/\left(2\pi \right)\approx 1/10$ Hz in Fig. 4. This is true despite the fact that $r\approx \nu$ or nearby frequencies is the regime where one might have expected the vectorial information to benefit most from sampling the periodic dynamics instead of noisy dynamics. We have also checked that the equivalence holds for a large range of intrinsic and extrinsic noise levels. The previously demonstrated correspondence between the model and the experiments suggests that in the fibroblasts as well, ordered dynamics would not provide more information than noisy dynamics, at least as quantified by the vectorial mutual information. We expand upon this conclusion in the Discussion.

Differential effects of intrinsic and extrinsic noise

Vectorial mutual information, $M{I}_{\text{v}}$, is larger than scalar mutual information, $M{I}_{\text{s}}$, in part because repeated sampling helps to mitigate intrinsic noise (18). Yet, in the case of the fibroblast cells, the gain of $M{I}_{\text{v}}$ over $M{I}_{\text{s}}$ is often small. For example, as seen in Fig. 3 A, at $n=2$ and $r=1/10$ Hz, whereas $M{I}_{\text{s}}$ can be as large as ∼0.4 bit, the further increase of $M{I}_{\text{v}}$ over $M{I}_{\text{s}}$ is <∼0.1 bit. We make this observation quantitative by defining the information gain, $M{I}_{\text{v,max}}-M{I}_{\text{s,max}}$, where each is maximized over the start time, $t_{\text{s}}$. Fig. 5 shows the information gain versus $M{I}_{\text{s,max}}$ for the fibroblasts at $n=2$ and $r=1/10$ Hz (pink circle). The fact that the gain is small (0.1 bit) suggests that additional factors, apart from intrinsic noise alone, reduce the efficacy of vectorial encoding.

Figure 5.

Gain of vectorial over scalar mutual information, where each is maximized over start times, $t_{\text{s}}$. For vectorial information, the memory capacity is $n=2$ and the sampling rate is $r=1/10$ Hz. Fibroblast data are compared against the over- and underdamped oscillator model. In the oscillator model, parameters are as in Fig. 4, and the intrinsic noise is governed by $k_{\text{B}}T$, which varies from 0.2 to 1 pN μm, whereas extrinsic noise is governed by $\delta k\text{/}\langle k\rangle$, which varies from 0 to 0.4. Error bars represent the mean ± SD of 100 bootstraps (fibroblast data) for 20 independent trials of 5000 trajectories each (oscillator model). To see this figure in color, go online.

To explore this hypothesis in a systematic way, we again turn to our minimal oscillator model. For both the overdamped and underdamped oscillator, we compute $M{I}_{\text{s,max}}$ and the information gain. In the model, the intrinsic noise is governed by the thermal energy $k_{\text{B}}T$. The model also provides an opportunity to investigate the effects of extrinsic noise, which is governed by $\delta k\text{/}\langle k\rangle$, the relative width of the distribution of spring constants. As shown in Fig. 5, when the intrinsic noise increases while the extrinsic noise is fixed, both the scalar information and the information gain decrease, as expected (dashed lines). The decrease in scalar information is more pronounced than the decrease in the gain, which is consistent with the fact that vector information is beneficial for mitigating intrinsic noise. On the other hand, when the extrinsic noise increases while the intrinsic noise is fixed, the gain decreases more rapidly, whereas the scalar information decreases less rapidly (colored symbols). This implies that the gain is more sensitive to extrinsic noise than to intrinsic noise.

In the context of the fibroblast population, these results suggest that extrinsic noise (cell-to-cell variability), not intrinsic noise, is primarily responsible for degrading the performance of vectorial encoding and producing small information gains.

Redundant information and low-pass filtering

The vectorial mutual information, $M{I}_{\text{v}}$, can never be larger than the sum of the scalar mutual information values, $M{I}_{\text{s}}\left(t_i\right)$, taken individually at each time point, $t_i$. The reason is that there will always be some nonnegative amount of redundant information between the output at one time and the output at another time (29). Denoting the redundant information as $M{I}_{\text{red}}$, we formalize this statement as

$$M{I}_{\text{red}}=\left[\sum _{i=1}^{n}M{I}_{\text{s}}\left(t_i\right)\right]-M{I}_{\text{v}}=n\langle M{I}_{\text{s}}\rangle -M{I}_{\text{v}}\ge 0,$$ (4)

where, as before, $t_i=t_{\text{s}}+i{r}^{-1}$, and in the second step, we rewrite the sum in terms of the temporal average, $\langle M{I}_{\text{s}}\rangle =n^{-1}{\sum }_{i=1}^{n}M{I}_{\text{s}}\left(t_i\right)$. In the limit that the dynamics are approximately stationary, such as in the high-yield regions of Figs. 1 B and 4 B, $M{I}_{\text{s}}$ is approximately independent of time, and $\langle M{I}_{\text{s}}\rangle =M{I}_{\text{s}}$. For $n=2$, as in Fig. 5, Eq. 4 then becomes

$$M{I}_{\text{v}}-M{I}_{\text{s}}\le M{I}_{\text{s}}.$$ (5)

Equation 5 expresses the intuitive fact that the gain upon making an additional measurement can never be more than the information from the original measurement, for a stationary process. Equation 5 is plotted in Fig. 5 (dashed line), and we see that it indeed bounds all data from above, as predicted.

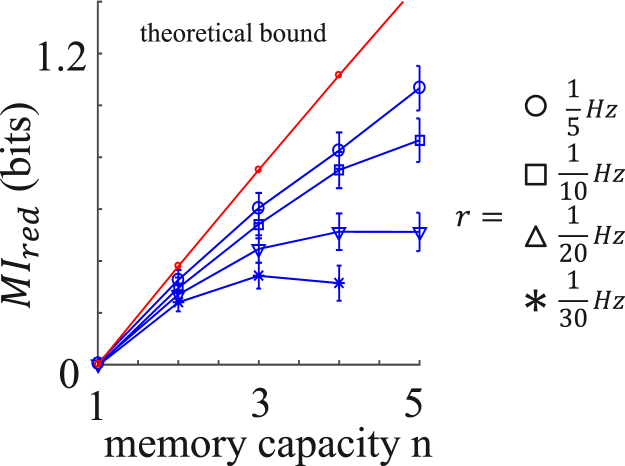
The redundant information in Eq. 4 can be directly measured in the experiments. Fig. 6 shows the redundant information in the fibroblast calcium dynamics as a function of the memory capacity, n, computed from the scalar and vectorial mutual information according to Eq. 4. Here, $t_{\text{s}}=$ 70 s, and for each curve, the sampling rate, r, is fixed, such that the duration, $T_{\text{d}}$, increases with n. We see that the redundant information depends on r and appears to be bounded from above by a roughly linear function of n. Can we understand this dependence theoretically? To address this question, we return to Eq. 4. We rearrange Eq. 4 as $M{I}_{\text{red}}=\left(n-1\right)\langle M{I}_{\text{s}}\rangle -\Delta$, where we define $\Delta =M{I}_{\text{v}}-\langle M{I}_{\text{s}}\rangle$. Since the vectorial information is not smaller than the scalar information corresponding to any of its time points, it is also not smaller than the average scalar information. Therefore, $\Delta \ge 0$, and we have

$$M{I}_{\text{red}}\le \left(n-1\right)\langle M{I}_{\text{s}}\rangle .$$ (6)

Equation 6 is a linear function of n, weakly modified by the fact that $\langle M{I}_{\text{s}}\rangle$ itself depends on n, since it is computed for varying numbers of time points. Equation 6 is compared with the data in Fig. 6, and we see that it indeed predicts the bound well. Equation 6 makes another prediction, namely, that the bound is reached for a stationary process when $\Delta =M{I}_{\text{v}}-\langle M{I}_{\text{s}}\rangle \to 0$, i.e., when the vector information provides vanishing improvement over the average scalar information. We expect this situation to occur in the limit of large sampling frequency, r, when samples occur in close succession and offer little additional information beyond a single scalar measurement. Indeed, we see from the data in Fig. 6 that, consistent with this prediction, the bound is approached in the limit of increasing r.

Figure 6.

Redundant information of dynamic encoding for fibroblast cells. Redundant information, $M{I}_{\text{red}}$ (Eq. 4, $t_{\text{s}}=$ 70 s), is plotted as a function of memory capacity, n, for varying sampling rates, r, and compared with the theoretical bound (Eq. 6). To see this figure in color, go online.

Clearly, the benefit of vectorial encoding is largest when the redundant information is small (the lowest data points in Fig. 6). In the ideal case, there is no redundant information at all, and Eq. 4 becomes

$$M{I}_{\text{v}}=\sum _{i=1}^{n}M{I}_{\text{s}}\left(t_i\right).$$ (7)

Here, we see that the vectorial information is simply the sum of the scalar information at each time point. In this sense, Eq. 7 describes a low-pass filter: vectorial encoding captures the temporal accumulation of scalar information, as long as the sampling is sufficiently slow to remove the redundancy. Therefore, in this limit the vectorial information records only the slow (low-frequency) variations in the dynamics. This feature may help explain the previous counterintuitive result that the vectorial information is insensitive to the detailed dynamic structure, as we expand upon in the Discussion.

Discussion

The dynamic waveforms of signaling molecules offer a useful perspective from which to understand cellular information encoding. Indeed, dynamic encoding, as quantified by the vectorial mutual information, $M{I}_{\text{v}}$, has larger channel capacity than the static encoding, as quantified by the scalar mutual information, $M{I}_{\text{s}}$ (18). From both experimental data and a minimal model we presented here, we find that dynamic encoding has several key advantages over static encoding. First, the maximal vectorial information is larger than the maximal scalar information, suggesting that dynamic encoding provides a more reliable readout of environmental inputs than static encoding does. Second, although the scalar information can vary significantly with sampling time, the vectorial information is more uniform across sampling start times, even with small vector dimensions (Figs. 3 C and 4 E).

However, the benefit of dynamic encoding comes with the cost of increasing the memory capacity, n, of cells. For a fixed memory capacity, we have shown that the best strategy for cells to adopt is to sample as slowly as possible while keeping their samples within a “high-yield” region, where the mean dynamics depend significantly on the input. Nonetheless, we find that within this region, the benefit of dynamic encoding can depend very little on the detailed structure of the dynamics (persistent oscillation versus monotonic relaxation). Moreover, the gain of dynamic encoding over static encoding can be small, largely due to the presence of extrinsic, as opposed to intrinsic, noise.

The finding that vectorial information is largely insensitive to the detailed dynamics is surprising, and is likely a reflection of the type of dynamics we investigate here, as well as the vectorial measure itself. To accurately model the experimental dynamics, we have considered noisy dynamics arising from a driven oscillator. Although this has allowed us to probe both noise-dominated and oscillation-dominated regimes, these dynamics remain mean reverting and confined to a stationary or cyclo-stationary state. It is likely that other classes of dynamics, such as temporal ramps, would emerge as having uniquely higher vectorial information than stationary dynamics. Furthermore, the vectorial information itself, as defined here, reports correlations between a categorical input variable and a regularly sampled output trajectory. It is likely that more sophisticated information-theoretic measures would be more sensitive to dynamic details, such as the mutual information between input and output trajectories that has been argued to play a biological role in cell motility (30, 31).

Our results suggest that dynamic and static encoding mechanisms are deeply connected. By invoking the redundant information, $M{I}_{\text{red}}$ (29), we have made this connection rigorous. Specifically, combining Eqs. 4 and 6 yields $\langle M{I}_{\text{s}}\rangle \le M{I}_{\text{v}}\le n\langle M{I}_{\text{s}}\rangle$, which shows explicitly that the vectorial information is bounded from both above and below by quantities determined by the window-averaged scalar information, $\langle M{I}_{\text{s}}\rangle$. Taking a window average of the scalar information is equivalent to the downstream network acting as a low-pass filter, accumulating temporal measurements at sufficiently low frequencies. We find that such low-pass filtering effects are evident in both the experimental and modeling results.

In this study, we have taken the approach that an understanding of both the static and dynamic encoding behaviors of the fibroblast cells can be obtained from a model based on noisy harmonic oscillators. Despite the simplicity of the model, we find that it reproduces the experimental results very well. The agreement between the experiment and this simple model highlights our central conclusion that the vectorial mutual information is intrinsically connected with the scalar mutual information and therefore has limited capability to distinguish underlying dynamics. Because the model is minimal, we anticipate that it can be extended to answer more general questions about information encoding on a large, multicellular scale. This is particularly desirable, as understanding collective information processing is a new frontier in systems biophysics (19, 23, 27, 32, 33, 34). On the other hand, many interesting questions, such as the precise functional form of $M{I}_{\text{v}}\left(n\right)$ and the dependence of mutual information on nonlinear effects such as feedback, bifurcations, and coupling of multiple timescales, may require more realistic models beyond noisy harmonic oscillators.

Author Contributions

B.S. conceived the research. A.M. and B.S. designed the research. G.D.P., T.A.B., A.M., and B.S. performed the research, analyzed data, and wrote the article.

Editor: Jennifer Curtis.