Design Rules for Membrane-Embedded Voltage-Sensing Nanoparticles

Abstract

Voltage-sensing dyes and voltage-sensing fluorescence proteins have been continually improved and as a result have provided a wealth of insights into neuronal circuits. Further improvements in voltage-sensing dyes and voltage-sensing fluorescence proteins are needed, however, for routine detection of single action potentials across a large number of individual neurons in a large field-of-view of a live mammalian brain. On the other hand, recent experiments and calculations suggest that semiconducting nanoparticles could act as efficient voltage sensors, suitable for the above-mentioned task. This study presents quantum mechanical calculations, including Auger recombination rates, of the quantum-confined Stark effect in membrane-embedded semiconducting nanoparticles, examines their possible utility as membrane voltage sensors, and provide design rules for their structure and composition.

Introduction

To understand the brain, tools need to be developed to allow the investigation of interactions between individual neurons (1, 2). Multielectrode recordings have provided important insights but have limited performance when dense local circuits need to be analyzed or when signals from specific types of near-by neurons need to be distinguished. For this reason, considerable efforts have been invested in developing optical detection methods (3), including the utilization of voltage-sensitive dyes (4, 5, 6). Voltage-sensing dyes (VSDs) could potentially allow simultaneous visualization of neuronal activity over a large number of neurons in a large field-of-view and with superresolution. Moreover, targetable VSDs could report signals from specific types of neurons. As examples, synthetic and genetically encoded fluorescent Ca²⁺ indicators have gained great prominence and are routinely used to study Ca²⁺ signals in cultured neurons, brain slices, and live brains. Such indicators allow the recording of the dynamics of Ca²⁺ signals over large sets of individual neurons of known types. Although Ca²⁺ dynamics is correlated to neuronal spiking, Ca²⁺ signals do not report neuronal spiking signals faithfully due to their slow kinetics and signal saturation. In contrast, VSDs afford direct imaging of cellular membrane action potentials (APs). Indeed, organic VSDs have allowed the functional mapping of brain activities in individual cells, in invertebrates, in mammalian brain slices, and even in whole brains of awake mammals (6). Most VSDs report on voltage changes via changes in their fluorescence intensity, but ratiometric VSDs have also been demonstrated (7). VSDs, however, suffer from some shortcomings. They could alter membrane capacitance, be phototoxic, suffer from photobleaching, have a short retention time in the membrane, and mistarget the membrane, resulting in nonspecific background labeling. More recently, several genetically encoded fluorescent voltage-sensor proteins have been developed and used to detect aggregate neural activity in vivo and single spikes in vitro (8, 9). Hybrid approaches (combining membrane-targeted fluorescent proteins with VSDs) have also been reported (10), but they suffer from slow kinetics, limited dynamic range, low quantum yields, and perturbation to membrane capacitance. Unfortunately, despite these advances, VSDs and voltage-sensing fluorescence proteins (VSPs) are not yet performing at the level of detection where every single AP, in every neuron, in a large field-of-view, in the brain of a live animal, could be recorded (1, 2). Promising results, however, have been recently demonstrated with ArcLight VSP (11).

Recently, we examined bandgap-engineered colloidal semiconductor nanoparticles, dubbed “voltage-sensing nanoparticles” (vsNPs), which display large quantum-confined Stark effect (QCSE) at room temperature on the single particle level. In particular, we have shown that charge separation across one (or more) heterostructure interface(s) with type-II band alignment (and the associated induced dipole) is crucial for an enhanced QCSE (12). The feasibility of utilizing such vsNPs for membrane voltage sensing was soon after theoretically investigated and favorably compared to organic VSDs (13, 14). Here we utilize self-consistent Schrödinger-Poisson calculations for vsNPs embedded in the membrane to further explore the feasibility and performance of vsNPs as voltage sensors, and to provide guiding principles for their design.

A detailed explanation for how these calculations are performed is given in the Materials and Methods section below.

Materials and Methods

All calculations were performed using a home-written code (using the software Python; https://www.python.org/). Two types of vsNPs were examined as model systems: a simple cylindrical homostructure CdSe nanorod (NR) (SI-1, Fig. S1 A) and a heterostructure ZnSe-CdS NR with asymmetric type-II energy band alignment (SI-1, Fig. S1 B). In practice, ZnSe seeded CdS NR are commonly synthesized using the hot injection method (15), yielding a spherical quantum dot (QD) seed that is usually embedded off-center in the CdS NR. This complicated geometry is difficult to model. Instead, we approximate the seeded NR as end-jointed collinear cylinders with a single heterointerface (see Fig. S1). We first calculated the inhomogeneous Poisson equation to obtain the electrostatic potential profile of the NRs embedded in the lipid membrane:

$$-\nabla \times \left({\epsilon }_r\left(r,z\right)\nabla V\left(r,z\right)\right)=\rho \left(r,z\right)/{\epsilon }_0.$$ (1)

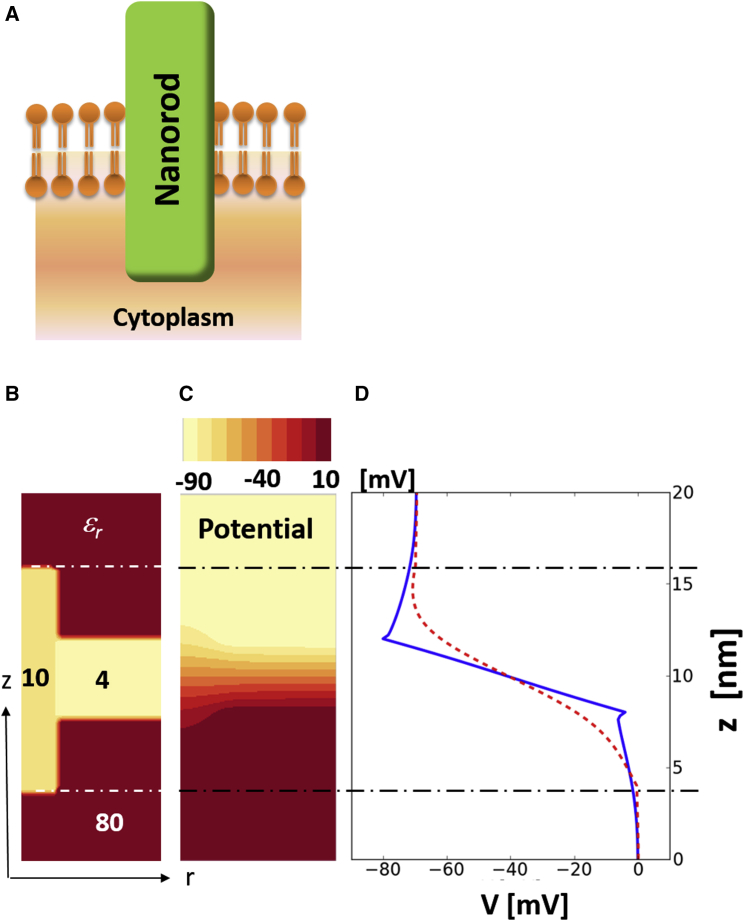
The NRs, the lipid membrane, and the surrounding physiological buffer were modeled in three dimensions (3D) by using two-dimensional (2D) calculations + cylindrical symmetry, and a finite difference method (FDM) with a grid mesh size of 2 Å. The entire simulation space spans 8 × 20 nm (radius × length). The lipid membrane (of 4 nm thickness) is located at the center of the simulated space. The NR (of 2 nm radius) is symmetrically embedded in the membrane and its length is varied from 4 to 12 nm (Fig. 1, A and B). Each region is parameterized with its corresponding dielectric constant (Fig. 1 B). Neumann boundary conditions (ΔV = 0 at the boundaries) were applied in 2D except the cylindrical axis. The singularity at r = 0 caused by operating a Laplacian in cylindrical coordinates is removed by assigning $V\left(r=0,z\right)=V\left(r_1,z\right)$, where $r_1$ is the first mesh point away from the axis ($r_1=2$ Å). The membrane potential $V_m$ is established by applying a thin sheet of charges (C/m²) justified by the very short Debye screening length (≈0.7 nm) of a physiological buffer. Having the sheet of charges and the map of dielectric constants as inputs, the Poisson equation returns the electrostatic potential across the entire simulation space, providing the relation between $V_m$ and electric field $F_{\mathrm{int}}$ inside the NR.

Figure 1.

Calculated potential of the inserted NR in membrane. (A) Schematic of NR embedded in membrane. (B) Dielectric constants: ${\epsilon }_r$, intra- and extracellular (red); 80, lipid (yellow); 4, NR (dark yellow) 10. The ${\epsilon }_r$-values at the boundaries and interfaces are averaged. (C) Color map of the calculated potential profile of geometry (B) when $V_m=70\text{mV}$. (D) One-dimensional potential profile across the NR (dashed red line) and outside of the NR (solid blue line). (Dashed-dotted black lines) Top and bottom of the NR. To see this figure in color, go online.

With the internal electric field $F_{\mathrm{int}}$ at hand, we solved the Schrödinger equation using the two-band $K\times \hat{p}$ (Kane) model and obtained the electron’s and the hole’s wavefunctions $\left({\varphi }_e,{\varphi }_h\right)$ and their ground state energies $\left(E_e^1,E_h^1\right)$ for different electric field values. For this second part, the simulation space is reduced to have it boundaries +2 nm away from the tips of the NR, but with higher density mesh (0.5 Å for calculating Eq. 2 in comparison to 2 Å for calculating Eq. 1). This simulation was implemented in one dimension using FDM (2D FDM with a larger mesh size failed to properly model the excited hole’s plane waves with large k vectors, which are needed for the Auger recombination rate ($k_A$) calculations). The Kane Hamiltonian is given by:

$$\begin{array}{c}H=\left(\begin{array}{cc}{H}_e& K\times \hat{p}\\ K\times \hat{p}& H_h\end{array}\right)\\ \text{with}\\ H_{e,h}=\pm {\hat{p}}^2/2m_{e,h}^{\ast }\pm E_g/2\pm V_{c,v}\pm V_F\mp V_{\text{Coul}}^{h,e},\end{array}$$ (2)

where K is the Kane matrix element; $\hat{p}$ is the momentum operator ($\hat{p}=-i\hslash \nabla$); $E_g$ is the energy bandgap; $m_{e,h}^{\ast }$ comprises the electron (e) and hole (h) effective masses, respectively; $V_{c,v}$ comprises the electron (c) and hole (v) confinement energies, respectively; and $V_F$ is the potential generated by the $F_{\mathrm{int}}$ ($V_F=z\times F_{\mathrm{int}}$, where z is the spatial coordinate along the NR’s long axis). $V_{\text{Coul}}^{h,e}$ is the Coulomb potential, accounting for the attraction between electron and hole and it is solved by Poisson equation $-\nabla \times \left({\epsilon }_r\left(z\right)\nabla V_{\text{Coul}}^{h,e}\left(z\right)\right)=\pm q{\varphi }_{h,e}\left(z\right)/{\epsilon }_0$. The coupled Poisson-Schrödinger equations were self-consistently and iteratively solved until electron and hole energies converged to values that changed less than ΔE < 1 meV between successive iterations (see Supporting Material in Park et al. (12)). All parameters used in the calculations are listed in Fig. S1 and Table S1.

As a validation step, we successfully reproduced previously published calculations for $V_F=0$ (16, 17). Calculations were repeated for varying $F_{\mathrm{int}}$ from −200 to +200 kV/cm. With the calculated electron’s and the hole’s wavefunctions and corresponding energies at hand, we could calculate in a third step the Stark-shift ($\Delta \lambda$), the Auger recombination rate ($k_A$), and the squared overlap integral between the electron and hole wavefunctions ($f={\langle {\psi }_e|{\psi }_h\rangle }^2$). By combining the derived $V_m-F_{\mathrm{int}}$ relation from the Poisson equation in cylindrical symmetry and the derived $F_{\mathrm{int}}-\Delta \lambda$ relation and $k_A$ and f from the self-consistent Schrödinger-Poisson equation, we could extract $\Delta \lambda$, $k_A$, and f for each $V_m$. The calculation of $k_A$ is described in SI-2 in the Supporting Material. The relative radiative recombination lifetime $\Delta {\tau }_r$ and the NRs’ emission intensity $\Delta I$ were then calculated from f and $k_A$. The value ${\tau }_r$ is given by ${\tau }_r=\left(2\pi {\epsilon }_0{m}_e{c}^3{\hslash }^2/\sqrt{\eta }{e}^2{E}_{\text{ex}}{E}_{p}f\right)$, where $m_e$ is the free electron mass, c is the speed of light, $\hslash$ is the reduced plank constant, ${\epsilon }_0$ is the vacuum permittivity, η is the refractive index for the NRs ($\eta =2.5$ for both CdSe and ZnSe-CdS), $E_p$ is the Kane energy (where $E_p=2K^2{m}_o$), and $E_{\text{ex}}$ is the exciton’s photon emission energy (18). The total emission intensity $\Delta I$ was calculated as a weighted sum of the exciton’s state (X) (dominant at low light excitation) and the positive trion’s state (X⁺) (dominant at high light excitation) emission intensities for varying relative weights. This was done to evaluate the contribution of Auger recombination to voltage-sensing performance by voltage-sensing NRs. This sequence of calculations was repeated for resting- and AP-like membrane voltages.

Results

The internal electric field ($F_{\mathrm{int}}$) inside the NR, in response to the external membrane potential ($V_m$), was calculated by solving the inhomogeneous Poisson equation ($-\nabla \times \left({\epsilon }_r\left(r,z\right)\nabla V\left(r,z\right)\right)=\rho \left(r,z\right)/{\epsilon }_0$) for the dielectric distribution depicted in Fig. 1 B. The NRs, the lipid membrane, and the surrounding physiological buffer were modeled in 3D by using 2D calculations (r, radial direction; z, axial direction) and extending to 3D using cylindrical symmetry. As an example, Fig. 1 C shows the 2D potential profile of a 12-nm-long NR at $V_m=70\text{mV}$. For this calculation, 0.8 and 11.4 mC/m² of sheet charges were applied to both sides of the membrane, respectively, corresponding to 7.9 and 117.9 mM ion concentrations. Fig. 1 D shows the potential profile across the long axis of the NR (dashed red line) and across the membrane away from the NR (solid blue line). In the absence of the NR, the potential drops entirely across the lipid membrane, due to the large difference in dielectric constants between water and lipids (${\epsilon }_r=80$ vs. ${\epsilon }_r=4$). Within the NR, the potential still drops across its entire length (confirmed for lengths from 4 to 12 nm) despite the fact that it protrudes from the membrane on both sides. The average $F_{\mathrm{int}}$ inside the NR could therefore be simply approximated to be $F_{\mathrm{int}}=\Delta V/l=V_m/l$ (where l is the length of the NR). The internal electric field in the water-protruding ends does diminish, however, for longer l values. This indicates that a longer NR does not guarantee enlarged QCSE.

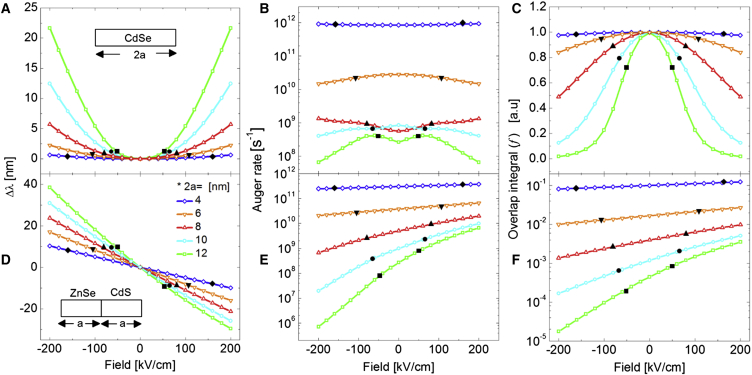
The QCSE observables wavelength shift ($\Delta \lambda$), squared overlap integral (f), and Auger rate ($k_A$) were calculated for type-I CdSe NRs (SI-1, Fig. S1 A) and type-II heterostructure NRs (SI-1, Fig. S1 B) of varying lengths, from 4 to 12 nm (Fig. 2). In the latter case, the hetero-interface between ZnSe and CdS is assumed to be alloyed over ∼1 nm (SI-1, Fig. S1 B). Voltage-dependent spectral shifts and intensity (emission rate) changes in QDs and NRs were experimentally observed and theoretically treated (12, 19, 20, 21, 22). These field-induced photophysical changes depend on the geometry, composition, and heterostructure configuration of these nanoparticles (12). To the best of our knowledge, however, the effect of an applied voltage on the Auger recombination rate was not considered previously. Auger recombination is a three-particles process that results in a nonradiative transition due to the absorption of the exciton’s energy by a spectator particle (see SI-2 and Discussion below). It is a dominant contributor to nonradiative transitions in NPs that results in intermittency (blinking) in their photoluminescence (fluorescence emission) (23, 24).

Figure 2.

Calculated values for $\Delta \lambda$ (A and D), k_A (B and E), and f (C and F) as function of electric field for CdSe NRs (A–C) and type-II ZnSe-CdS heterostructure NRs (D–F). (Blue diamond) 2a = 4 nm; (orange downtriangle) 2a = 6 nm; (red uptriangle) 2a = 8 nm; (cyan circle) 2a = 10 nm; (green square) 2a = 12 nm. (Black symbols) Fields that the NRs (of different lengths) could experience by the maximal field of an AP (160 kV/cm). To see this figure in color, go online.

Compared to bulk semiconductors, the Auger recombination rate in NPs is greatly enhanced (inversely proportional to the NP’s volume). Although blinking can sometimes be advantageously exploited, as for example in superresolution imaging (25), it reduces the NP’s overall emission rate. For this reason, a considerable effort has been invested in designing novel NPs with reduced Auger recombination and blinking, such as via graded shells (16, 26), increased shell thickness (27, 28), type-II shells (29), and alloying (30). These approaches weaken the transition rate of Auger recombination by smoothing the otherwise abrupt changes in the conduction and valence band energies at the interfaces (16). In this study, we examined the field-dependent Auger recombination rate, and its influence on NRs’ emission rates (and intensities).

Fig. 2, A–C, shows the calculated values for $\Delta \lambda$, f, and $k_A$ for the CdSe NR. Fig. 2, D–F, shows the same for the type-II ZnSe-CdS heterostructure NRs. As previously demonstrated (19, 20), a quadratic $\Delta \lambda -\Delta F$ relation and a red shift ($\Delta \lambda >0$) are calculated for the type-I CdSe NR. The quadratic relation is a manifestation of the particle’s (and its bandgap’s) symmetry. It indicates that there is no induced dipole moment upon photoexcitation, and that the exciton’s energy is always reduced under an applied field (i.e., red shift in emission spectrum). In contrast, a roughly linear $\Delta \lambda -\Delta F$ relation and both a red shift ($\Delta \lambda >0$) and a blue shift ($\Delta \lambda <0$) that are dependent on the applied field direction are calculated for the type-II ZnSe-CdS heterostructure NRs. This behavior is a manifestation of the particle’s (and its bandgap’s) asymmetry and the presence of an induced dipole moment after photoexcitation (12, 21).

As can be seen from Fig. 2, A and D, the sensitivity of the QCSE to the field (i.e., $\Delta \lambda /\Delta F$, the slope of the calculated curves) scales with the length of both types of particles. The type-II ZnSe-CdS heterostructure NRs, however, exhibit a larger sensitivity and a larger QCSE shift per given applied field as compared to type-I CdSe NR.

Fig. 2, B and E, shows calculated Auger recombination rates ($k_A$) for the two nanoparticles as a function of applied field. The results were obtained by applying the Fermi golden rule for the Kane (31) electron and hole wave functions (16):

$$k_A=\frac{1}{{\tau }_A}=\frac{2\pi }{\hslash }{\left|M_{if}\right|}^2\rho \left(E_f\right),$$ (3)

where ${\tau }_A$ is the Auger recombination lifetime, $M_{if}$ is the Coulomb potential matrix element, and $\rho \left(E_f\right)$ is the density of states at the energy level of the excited particle. $k_A$ was calculated only for the electron-hole-hole scattering configuration (Fig. S2 A). This configuration is more likely to occur than the electron-electron-hole scattering configuration (Fig. S2 B due to the stronger hole confinement in the smaller volumes of the ZnSe (32) seeds that are embedded in elongated CdS shell. A CdSe (33) seeded CdS nanorod serves as another example for stronger hole confinement.

It is well established that $k_A$ scales inversely with the nanoparticle volume ($k_A\propto {\text{vol}}^{-1}$) (23, 24) and proportionally with the level of abruptness of the heterointerface (26). A narrower wave function in real space contains high spatial frequency components in the momentum (k) space. A spectator hole with high energy and large momentum final (scattered) state is more likely to scatter from high spatial frequency components of a localized hole state, as in the case of a small volume nanoparticle and/or an abrupt core-shell heterointerface. On the other hand, when the initial wavefunction is broad in real space (as in a large volume nanoparticle and/or a graded shell), $k_A$ is suppressed. In addition, Cragg and Efros (16) showed that $k_A$ could be suppressed periodically at precise “magic” QD diameters or NRs lengths. Similar to Cragg and Efros (16), our calculations also capture these diameter/length-dependent oscillations in $k_A$, as shown in Fig. S3 and in Fig. 2 B for the 8 nm CdSe NR at 0 kV/cm (red line).

Our calculations show that $k_A$ is invariant under the field for 4 nm CdSe NR because the electron’s and hole’s Coulomb attraction is strong such that they are not separated under the electric field (Fig. 2 C). For CdSe NRs longer than 6 nm length, $k_A$ is reduced under the electric field due to the reduced Coulomb interaction. The relatively smaller $k_A$ in the 8 nm NRs at $F=0$ is due to the “magic” size effect, where $k_A$ is suppressed. For type-II ZnSe-CdS NRs, $k_A$ increases under positive fields (corresponding to blue shifts of the QCSE, Fig. 2 E), conditions at which the hole wavefunction is narrow with increased Coulomb interaction. On the other hand, $k_A$ is decreased under negative fields (corresponding to red shifts of the QCSE; Fig. 2 E), conditions at which the Coulomb interaction between the electron and the hole is diminished. The influence of the voltage-dependent Auger recombination rate $k_A$ on the relative intensity change $\Delta I/I$ (one of the experimental observable) will be discussed below.

The squared overlap integral is later used to calculate the ${\tau }_r$ (another experimental observable) and I. Especially, ${\tau }_r$ is inversely proportional to the f (see Materials and Methods). The value f is symmetric with respect to F for the type-I CdSe NR (Fig. 2 C) and nonsymmetric for the type-II ZnSe-CdS heterostructure NRs (Fig. 2 F). For a short type-I NR, the electron and the hole are strongly attracted and confined, preventing charge separation (Fig. 2 C, blue). Experimentally, type-II NRs exhibit much larger QCSE as compared to type-I NRs (12), because they better support charge separation. This observation underlines the importance of the Coulomb interaction in these nanosensors.

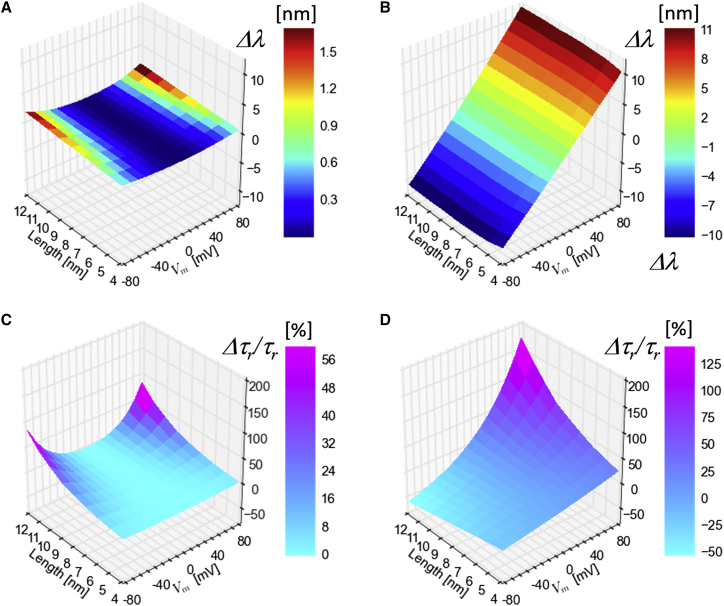
With the approximation $F_{\mathrm{int}}\approx \Delta V/l=V_m/l$ (Fig. 1), the potential energy operator can be written as $V_F\left(z\right)=z\times F_{\mathrm{int}}=z\times V_m/l$ and therefore the Hamiltonians for the two bands are $H_{e,h}=\pm {\hat{p}}^2/2m_{e,h}^{\ast }\pm E_g/2\pm V_{c,v}\pm V_F\mp V_{\text{Coul}}^{h,e}$ (see Materials and Methods). Solving the Schrödinger equation for electron and hole energies directly yields the QCSE’s spectral shift dependence on the $V_m$ (Fig. 3). Fig. 3 A shows $\Delta \lambda$ for different-length type-I CdSe NR. Fig. 3 B shows $\Delta \lambda$ for different-length type-II ZnSe-CdS heterostructure NRs. While longer NRs can give rise to a larger separation between the charges, and hence a larger dipole, $F_{\mathrm{int}}$ is decreased. $\Delta \lambda$ is therefore only moderately increased (in absolute value, for both red and blue shifts) as a function of the NRs’ length (Fig. 3, A and B). A 4-nm-long CdSe type-I NR has 0.4 nm/100 mV (from −70 to +30 mV) or 0.5 nm/70 mV (from −70 to 0 mV) sensitivity, which is similar to the shift Marshall and Schnitzer (13) estimated for a 4 nm CdTe QD). A 12-nm-long CdSe type-I NR has 1.3 nm/100 mV (from −70 to +30 mV) or 1.5 nm/70 mV (from −70 to 0 mV) sensitivity. In contrast, 4-nm-long type-II ZnSe-CdS NR shows 12.8 nm/100 mV red shift and 12.5 nm/100 mV blue shift. A much longer 12-nm-long ZnSe-CdS NR shows 14.5 nm/100 mV red shift and 13.8 nm/100 mV blue shift.

Figure 3.

Stark-shift $\Delta {\lambda }_r$ (A and B) and relative radiative lifetime changes $\Delta {\tau }_r/{\tau }_r$ (C and D) for different length type-I CdSe NR (A and C) and type-II ZnSe-CdS heterostructure NRs (B and D), referenced to $V_m=0$. To see this figure in color, go online.

Fig. 3, C and D, shows the relative change in the radiative lifetime $\Delta {\tau }_r/{\tau }_r$ (%) of CdSe type-I NRs (Fig. 3 C) and type-II ZnSe-CdS NRs (Fig. 3 D). $\Delta {\tau }_r/{\tau }_r$ is decreased by only 1.5%/100 mV (from −70 to 30 mV) for a 4 nm CdSe NR. This is likely due to strong electron and hole confinement in a small volume, with f hardly changing. However, $\Delta {\tau }_r/{\tau }_r$ decreases by 31.5%/100 mV for a 12 nm CdSe type-I NR. While $\Delta \lambda$ changes only weakly as function of length for type-II ZnSe-CdS NR, $\Delta {\tau }_r/{\tau }_r$ exhibits a strong length dependence for these NRs. This is because that f is more sensitive to the electric field than $\Delta \lambda$ (compare Fig. 2, C and F with Fig. 2, A and D). For 4-nm-long type-II NRs, $\Delta {\tau }_r/{\tau }_r$ increases by 31.2%/100 mV for red-shifting field orientation, or reduced by 24.0%/100 mV for blue-shifting orientation. These changes are amplified to 204.0%/100 mV (red shifting) or reduced to 70.2%/100 mV (blue shifting) for 12-nm-long type-II NRs. This $\Delta {\tau }_r/V_m$ sensitivity could be exploited by utilizing conventional fluorescence lifetime imaging microscopy (34) or wide-field fluorescence lifetime imaging microscopy using the single photon counting H33D detector (35).

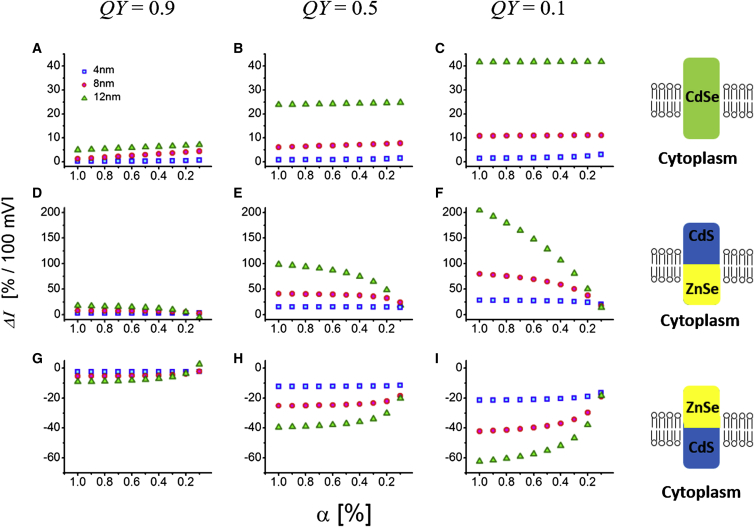
Using the squared overlap integral and the radiative lifetime calculations discussed above, one can estimate the sensor’s fluorescence emission intensity ($I=QY\times \left(\sigma /\hslash \omega \right)$), which is an easily accessible observable of the QCSE. Here σ is the sensor’s absorption cross section at the given excitation wavelength and QY is its quantum yield. To a first approximation, we assume σ not to depend on $V_m$, so that $\Delta I\propto \Delta QY$. The overall QY of the sensor’s fluorescence emission is assumed to be a linear combination of the QY values of the exciton (X) and the positive trion state (X+), $QY=\alpha Q{Y}^X+\left(1-\alpha \right)Q{Y}^{X+}$ with $Q{Y}^X=k_r/\left(k_r+k_t\right)$ and $Q{Y}^{X+}=2k_r/\left(2k_r+2k_t+k_A\right)$, where α is the exciton’s emission partition coefficient (relative weight) between the exciton (X) and the positive trion state (X+), a weight that depends on the excitation intensity (α is close to one at low excitation power and close to zero at high excitation power). $k_r={\tau }_r^{-1}$ is the radiative transition rate, and $k_t$ is the sum of all nonradiative rates, including the charge trapping rate at the particle’s surface (due to surface states). The value $k_t$ is assumed not to depend on the AP. Both the X and X+ states are subjected to surface trapping (i.e., $k_t$ affects both $Q{Y}^X$ and $Q{Y}^{X+}$), but $k_A$ affects only the X+ state. The weights of $k_r$ and $k_t$ are doubled for the X+ state, accounting for the presence of two holes in this state. Fig. 4 gives estimates for the maximum attainable $\Delta I/I$ at 100 mV under a full voltage sweep (−70 to +30 mV). Previously obtained $k_r$ (see Fig. 3) and $k_A$ (see Fig. 2) are reused for this calculation. The $k_t$ values are assigned such that QY at $\Delta V=0$ becomes 0.9 (Fig. 4, A, D, and G), 0.5 (Fig. 4, B, E, and H), and 0.1 (Fig. 4, C, F, and I).

Figure 4.

Relative intensity change $\Delta I/I$ corresponding to a voltage sweep of an AP calculated for 4-nm (blue-square), 8-nm (red-circle), and 12-nm (green-triangle)-long NRs. (A–C) Type-I CdSe NRs. (D–I) Type-II ZnSe-CdS heterostructure NRs. (D–F) Red-shifting geometry. (G–I) Blue-shifting geometry. The $k_t$-values are adjusted such that QY at $\Delta V=0$ are 0.9 (A, D, and G), 0.5 (B, E, and H), and 0.1 (C, F, and I). All subplots (A–I): x ticks are α-values. To see this figure in color, go online.

We found that $\Delta I/I$ [%/100 mV] increases for longer-length type-I CdSe NRs emitting in the trion state (small α) with low QY (Fig. 4 C). Type-II ZnSe-CdS heterostructure NRs, however, exhibit much larger $\Delta I/I$ sensitivity. In addition, their orientation in the membrane affects the sign of $\Delta I$ in response to membrane depolarization. When the hole-trapping part (ZnSe) is facing the cytoplasmic side (Fig. 4, D–F), $\Delta I/I$ is positive (intensity is increased). When it faces the extracellular side (Fig. 4, G–I), $\Delta I/I$ is negative (intensity is decreased). For both orientations, $\left|\Delta I/I\right|$ is larger for α → 1. It is therefore beneficial to run these sensors under weak excitation (favoring emission from the X state). It is also found that longer type-II NRs exhibit larger $\left|\Delta I/I\right|$ than shorter NRs. Both types of particles exhibit larger $\left|\Delta I/I\right|$ sensitivity for lower QY values due to the strong dependence on ${\tau }_r$ (for a given ${\tau }_{\mathit{nr}}$) at low QY (Fig. 4, C, F, and I).

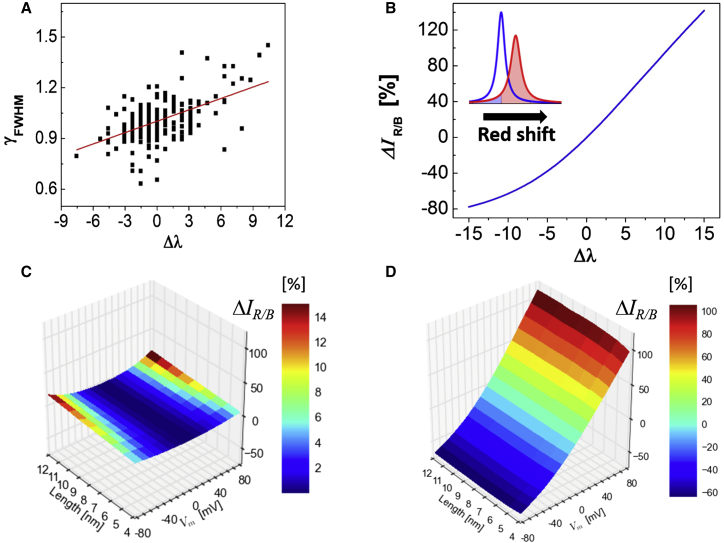
The QCSE can be detected not only by recording a decrease or an increase in the sensor’s (total) fluorescence intensity, but also through a direct measurement of the spectral shift of the sensor’s emission spectrum. This latter approach provides a more noise-immune measurement (12). The spectral shift can be measured by recording the emission spectrum as a function of voltage and extracting the peak position of the spectra by fitting. Alternatively, the shift can be detected by splitting the emission into two halves (using a dichroic mirror) and detecting them with two (or split) detectors. Spectral shifts are thus translated into anticorrelated intensity changes between the two detected signals. The ratio of the two signals (denoted here as $I_{R/B}=I_R/I_B$; see Eq. 4) directly reports the spectral shift, and is more noise robust as compared to a simple intensity measurement (7, 13).

The QCSE results in both a spectral shift $\Delta \lambda$ and a spectral broadening $\Delta FWH{M}_V$. To estimate the dependence of $I_{R/B}$ on $\Delta \lambda$, we reanalyzed our previously published QCSE data taken for 275 individual ZnSe-CdS NRs (12). This data set lacks a voltage calibration. However, due to a distribution of NRs orientations with respect to the field direction, the data set exhibits distributions of Stark shifts and spectral broadenings. Fig. 5 A shows a scatter plot of normalized spectral broadenings ${\gamma }_{\text{FWHM}}=\Delta FWH{M}_V/\Delta FWH{M}_{V=0}$ ($\Delta FWH{M}_{V=0}$ is the zero field spectral width value) as function of spectral shifts $\Delta \lambda$ for the whole data set. From this scatter plot we derive, by linear regression, the relation: ${\gamma }_{\text{FWHM}}\left(\Delta \lambda \right)=1+0.022\times \Delta \lambda$. When the spectrum is red shifted, $\Delta FWH{M}_V$ is increased. When the spectrum is blue shifted, $\Delta FWH{M}_V$ is decreased. Based on the average spectra at zero field, the unperturbed sensor’s emission spectrum can be modeled by a Lorentzian curve:

$$L\left(\lambda \right)=\frac{30\text{nm}}{2\pi \left[{\left(\lambda -600\text{nm}\right)}^2+{\left(30\text{nm}/2\right)}^2\right]},$$ (4)

with $\Delta FWH{M}_{V=0}=30\text{nm}$, and ${\lambda }_{V=0}=600\text{nm}$ (average peak emission wavelength at zero field). This average model spectrum is shown as a red curve in the inset of Fig. 5 B. Under an applied field, this spectrum is altered according to:

$$L\left(\lambda ,\Delta \lambda \right)=\frac{30\text{nm}\times {\gamma }_{\text{FWHM}}\left(\Delta \lambda \right)}{2\pi \left[{\left(\lambda -600\text{nm}-\Delta \lambda \right)}^2+{\left(30\text{nm}\times {\gamma }_{\text{FWHM}}\left(\Delta \lambda \right)/2\right)}^2\right]},$$ (5)

and the ratiometric observable $I_{R/B}$ is estimated from $L\left(\lambda ,\Delta \lambda \right)$:

$$I_{R/B}\left(\Delta \lambda \right)=\frac{I_R\left(\Delta \lambda \right)}{I_B\left(\Delta \lambda \right)}=\frac{\underset{600\text{nm}}{\overset{\infty }{\int }}L\left(\lambda ,\Delta \lambda \right)d\lambda }{\underset{-\infty }{\overset{600\text{nm}}{\int }}L\left(\lambda ,\Delta \lambda \right)d\lambda }.$$ (6)

As shown in Fig. 5 B, $\Delta I_{R/B}$ changes from −78 to +142% when the spectrum is shifted from −15 to +15 nm. For a 4 nm type-I CdSe NRs, $\Delta I_{R/B}$ reduces by ∼3% when $V_m$ changes from −70 to 30 mV (Fig. 5 C). For a 12 nm type-I CdSe NRs, $\Delta I_{R/B}$ reduces by 10% for the same voltage sweep (Fig. 5 C). $\Delta I_{R/B}$ of a 4 nm type-II ZnSe-CdS heterostructure NR reduces by 62% (for a blue-shifting orientation) or increases by 217% (for a red-shifting orientation) when the membrane voltage is swept from −70 to +30 mV (Fig. 5 D). $\Delta I_{R/B}$ is only weakly dependent on the length of these type-II NRs (see also Fig. 3 B). For a 12 nm ZnSe-CdS NR, $\Delta I_{R/B}$ reduces by 66% (for a blue-shifting orientation) and increases by 259% (for a red-shifting orientation) for same voltage sweep (Fig. 5 D).

Figure 5.

(A) A scatter plot of normalized spectral widths ${\gamma }_{\text{FWHM}}$ as function of Stark shifts $\Delta \lambda$ for 275 ZnSe-CdS NRs. (B) The ratiometric observable $I_{R/B}$ as function of the Stark shift $\Delta \lambda$. (Inset) Lorentzian fits to average spectrum (blue) and red-shifted spectrum (red). (C and D) $\Delta I_{R/B}$ as function of NRs’ length and $V_m$ (referenced to $V_m=0$) for CdSe NRs (C) and ZnSe-CdS NRs (D). To see this figure in color, go online.

Discussion

The most convenient method for visualizing APs is by monitoring the intensity changes $\Delta I/I$ of the sensors in an acquired wide-field movie. While best-performing voltage-sensitive dyes exhibit $\Delta I/I\propto 20\%/100\text{mV}$, 4 nm type-II QDs are predicted to exhibit $\Delta I/I\approx 30\%/100\text{mV}$ (13). Our calculations suggest that 12-nm-long type-I CdSe NRs could potentially exhibit $\Delta I/I\approx 42\%/100\text{mV}$ (Fig. 4 C) and 12-nm-long type-II ZnSe-CdS heterostructure NRs could potentially exhibit $\Delta I/I>190\%/100\text{mV}$ (Fig. 4, D–F). Degree of nonradiative transition has a large influence on sensitivity of intensity measurement (Fig. 4). For the single exciton (α = 1) with high QY sample (QY ≈ 1), $\Delta QY$ has weak dependency on $\Delta V$:

$$\Delta Q{Y}^X=\frac{k_r\times \Delta k_r/k_r\Delta k_r+k_t}{k_r/k_r+k_t}\approx \frac{1}{1}=1,$$

where $\Delta k_r$ is the ratio between before and after $\Delta V=100\text{mV}$ is applied. In this case, intensity change is hardly detectable. However, the low $Q{Y}^X\left(k_r\ll k_t\right)$ sample at single exciton, $Q{Y}^X$, becomes $\approx kr/kt$. $\Delta Q{Y}^X$ approaches $\Delta k_r$, which will serve the maximum sensitivity of intensity detection:

$$\Delta Q{Y}^X=\frac{k_r\times \Delta k_r/k_r\Delta k_r+k_t}{k_r/k_r+k_t}\approx \frac{k_r\times \Delta k_r/k_t}{k_r/k_t}=\Delta k_r=\frac{1}{\Delta {\tau }_r}.$$

This result suggests the fundamental tradeoff between brightness and sensitivity of sensors, providing nonlinear dependence of sensitivity on nonradiative transition. For the trion state, an additional nonradiative transition (Auger recombination) was taken into account for assessing QY. When potential changes from −70 to 30 mV, both f and $k_A$ increase, which are destructively added, cancelling the intensity change for the ZnSe-CdS type-II NR (Figs. 2 and 4, D–I). However, it is not significant for the type-I NR (Fig. 4, A–C).

The ratiometric observable $\Delta I_{R/B}$ (based on $\Delta \lambda$ spectral shift) provides a more robust (and less noisy) measurement as compared to the intensity-based $\Delta I/I$ measurement, especially for short, weakly excited NRs (when most of the emission is from the X state). While $\Delta I/I$ of a 4 nm type-I CdSe NR in the X state is hardly $\Delta I/I\approx 2\%$, the ratiometric measurement provides $\Delta I_{R/B}\approx 3\%$ (Fig. 5 C) without sacrificing the QY. The largest $\Delta I/I$ signal for this particle (12 nm) approaches ≈40% but at the expense of reduced brightness (Fig. 4 C). The ratiometric measurement provides $\Delta I_{R/B}\approx 11\%$ (Fig. 5 C), which is smaller than $\Delta I/I$ of a low QY NR (Fig. 4 C), but larger than a high QY NR (Fig. 4, A and B). While NRs’ length plays an important role in $\Delta I/I$ measurements (Fig. 4), ratiometric $\Delta I_{R/B}$ measurements exhibit very sensitive detection even for short type-II NRs. For example, $\Delta I_{R/B}$ is decreased (red shift) by ≈62% (−70 to +30 mV) for a 4 nm type-II NR and is increased (blue shift) by ≈217% for the same particle in the opposite orientation. Ratiometric $\Delta I_{R/B}$ measurements are therefore the method of choice for shorter particles, which are more easily inserted into the membrane (K.P., Y. Kuo, V. Shvadchak, A. Ingargiola, X. Dai, L. Hsiung, W. Kim, Z. Hong Zhou, P. Zou, A. J. Levine, and S.W., unpublished data).

Our calculations also show that the sensors’ fluorescence lifetime is strongly modulated by the membrane voltage and therefore a lifetime measurement by time-correlated single photon counting (36) could also serve as a noise-robust voltage-sensing observable with an improved signal-to-noise ratio.

Table 1 summarizes the calculated voltage sensitivity results for the $\Delta \lambda$, $\Delta \tau {}_r/{\tau }_r$, $\Delta I/I$, and $\Delta I_{R/B}$, observables, for type-I and type-II NRs, with lengths ranging from 4 to 12 nm. The table clearly shows that longer NRs exhibit larger voltage sensitivities (for all observables) as compared to short NRs. However, the stable insertion of long NRs into the membrane, with both ends symmetrically extruding the membrane on both sides, is a very challenging task (see Fig. 1 B versus Fig. S4). It requires anisotropic (facet-selective) functionalization that imparts membrane proteinlike properties to the NRs such that NRs’ side walls are lipophilic and the NRs tips are hydrophilic. Several recent works report on the intimate association of QDs with cell membranes (37) and liposomes (38). Possible pathways of NRs’ membrane insertion include 1) surface modification of NRs’ side walls with amphiphilic peptides or polymers, and 2) facet-selective surfactants exchange (based on different surface energies for the different facets). We recently succeeded in inserting NRs into membranes using peptides (K.P., Y. Kuo, V. Shvadchak, A. Ingargiola, X. Dai, L. Hsiung, W. Kim, Z. Hong Zhou, P. Zou, A. J. Levine, and S.W., unpublished data).

Table 1.

QCSE Observable Changes in AP ($V_m$ = −70→+30 mV)

	CdSe		ZnSe-CdS
	4 nm	12 nm	4 nm	12 nm
$\Delta {\tau }_r/{\tau }_r$ (%)	−1.5	−31.5	31.2 (−24.0)	204 (−70.2)
$\Delta I/I$ (QY = 0.5) (%)	1	22	15 (−12)	98 (−40)
$\Delta \lambda$ (nm)	−0.3	−1.3	12.8 (−12.5)	14.5 (−13.8)
$\Delta I_{R/B}$ (%)	−3	−10	217 (−62)	259 (−66)

To record APs using the QCSE, the NRs need to be inserted in the correct orientation into the cell membrane (Fig. 1). We also calculated electrostatic potential for nonideal cases, where NRs are partially embedded into the membrane (Fig. S4). These calculations suggest that $F_{\mathrm{int}}$ is concentrated in the membrane-embedded part of the NR when it asymmetrically extrudes out of the membrane. In this case, most of the membrane potential drops outside of the NR and the linear approximation $F_{\mathrm{int}}=\Delta V/l-V_m/l$ is no longer valid.

For a given $V_m$, QCSE will be maximized when both ends of the NR symmetrically extrude the membrane on both sides (see Fig. S4). We admit that our linear approximation is only valid when NRs inserted symmetrically and vertically. Our calculation serves as a guideline of maximum voltage sensitivity of different observables. Other geometries’ voltage sensitivities such as in Fig. S4 or a NR’s insertion with canting angle (θ > 0) to membrane normal direction (θ = 0) can be estimated if internal electric field is known (Fig. 2 shows voltage sensitivity at different internal electric field). The internal electric field will be reduced by $1-\text{cos}\left(\theta \right)$ when NRs inserted with an angle (θ). Accordingly, NRs’ voltage sensitivity $\Delta \lambda \left(F\right)$ becomes $\Delta \lambda \left(F^{\prime }\right)$, where $F^{\prime }=F\left(1-\text{cos}\left(\theta \right)\right)$. The degree of insertion has a major impact on the voltage sensitivity. As shown in Fig. S4, C and D, there is little or no internal electric field inside the NRs. On the other hand, potential drop (= internal electric field is generated) is found when the end of the NR’s tip reaches to the membrane-water interface as in Fig. S4, A and B, for which a sizeable QCSE could still be expected.

To calculate this configuration, the potential distribution shown in Fig. 1 C or Fig. S4 should be used. However, due to computational cost (and computational resources available to us), it was unrealistic to calculate this expanded geometry (Fig. 1 C or Fig. S4), as it requires >4 times more memory (see also Materials and Methods). We therefore mimicked the potential distribution (red in Fig. 1 D) with a sigmoid curve (SI-5) to increase the accuracy. Compared to the more realistic sigmoid curve model, the linear approximation underestimates the field by ∼10–15%, i.e., the actual voltage sensitivity will be ∼>10% higher in terms of $\Delta \lambda$.

Among the considered observables, the highly sensitive spectrally separated intensity ratio measurement $\Delta I_{R/B}$ (Fig. 5) is influenced by NRs’ size (and spectral) heterogeneity the most. Fig. S6 shows the error in reporting Stark red and blue shifts via the ΔI_R/B observable for NRs with peak emission wavelengths that are different from the nominal (averaged) ensemble peak (due to heterogeneity). The results show that spectral heterogeneity impacts the reporting of a Stark red shift much more than the reporting of a Stark blue shift. For example, a +5 nm Stark red shift will be reported by a smaller seed NR having a spectral peak of 590 nm (as compared to a nominal, 600 nm ensemble spectra) with an error of +28%. The same +5 nm Stark red shift will be reported by a larger seed NR having a spectral peak of 610 nm (as compared to a nominal, 600 nm ensemble spectra) with an error of −8.7%. This calculation shows that recording with heterogenous particles is possible, but voltage calibration and accuracy of exact voltage determination suffers from heterogeneity. Moreover, depending on insertion orientation of type-II NRs, some NRs will exhibit a larger error in $\Delta I_{R/B}$ in the depolarization segment of the AP while others will exhibit a larger error in $\Delta I_{R/B}$ in the polarization segment of the AP. We conclude that recording with single (heterogenous) particles is possible, but voltage calibration and accuracy of exact voltage determination will suffer from heterogeneity.

In 2014, ensemble linewidths <30 nm were reported (39). With this degree of size uniformity, heterogeneity will not pose a serious limitation on using the spectrally separated intensity ratio as an observable. More importantly, single particle measurements are less affected by the NRs’ heterogeneity in terms of reporting on dynamical voltage changes (but are more difficult to calibrate). In addition, we succeeded in inserting 10-nm-length NRs into the membrane in the desired orientation. These membrane-inserted NRs, tested under patch-clamping using a 400 Hz voltage modulation, successfully reported the modulated membrane potential via correlated fluorescence changes (K.P., Y. Kuo, V. Shvadchak, A. Ingargiola, X. Dai, L. Hsiung, W. Kim, Z. Hong Zhou, P. Zou, A. J. Levine, and S.W., unpublished data).

Lastly, random orientation of membrane-inserted asymmetric (type II) sensors could result in the cancelation of the (ensemble level) voltage signal due to opposite sign spectral shifts (or intensity changes). Methods for directional insertions that ensure same orientation for all sensors will need to be developed. Note that if such sensors are bright enough to operate on the single particle level (dilute limit), this problem is alleviated as there is no cancelation of the signal.

Conclusions

Self-consistent Schrödinger-Poisson calculations were used to assess the voltage-sensing performance of type-I CdSe NRs and type-II ZnSe-CdS heterostructure NRs, embedded in a membrane. The calculations show that type-I CdSe NRs could exhibit a sizeable $\Delta I/I$ (due to a voltage-dependent decrease in $Q{Y}^X$ and $Q{Y}^{X+}$). The calculations also show that type-II ZnSe-CdS heterostructure NRs exhibit sizeable $\Delta \lambda$, $\Delta I/I$, and $\Delta I_{R/B}$ with even higher voltage sensitivities. Lastly, the calculations show that a fluorescence lifetime measurement ($\Delta {\tau }_r/{\tau }_r$) could also be a sensitive reporter of voltage (due to large voltage-dependent changes in $k_r$ and $k_A$ for both types of NRs).

When compared with conventional VSDs and VSPs, voltage-sensing NRs are brighter, they exhibit higher voltage sensitivity and faster temporal response, they hardly photobleach, and they afford noise-robust ratiometric analysis. On the other hand, they suffer from heterogeneity in size and spectral properties. Our calculations suggest that these sensors could possibly be used on the single molecule level and provide design rules for their further development and optimization. Approaches for functionalization and stable membrane insertion of these sensors are currently being developed.

Author Contributions

K.P. designed and carried out the simulation; S.W. conceived and managed the project; and K.P. and S.W. wrote the article.

Editor: Brian Salzberg.

Supporting Citations

References (40, 41, 42, 43, 44) appear in the Supporting Material.