Multiple Ligand Unbinding Pathways and Ligand-Induced Destabilization Revealed by WExplore

Abstract

We report simulations of full ligand exit pathways for the trypsin-benzamidine system, generated using the sampling technique WExplore. WExplore is able to observe millisecond-scale unbinding events using many nanosecond-scale trajectories that are run without introducing biasing forces. The algorithm generates rare events by dividing the coordinate space into regions, on-the-fly, and balancing computational effort between regions through cloning and merging steps, as in the weighted ensemble method. The averaged exit flux yields a ligand exit rate of 180 μs, which is within an order of magnitude of the experimental value. We obtain broad sampling of ligand exit pathways, and visualize our findings using conformation space networks. The analysis shows three distinct exit channels, two of which are formed through large, rare motions of the loop regions in trypsin. This broad set of ligand-bound poses is then used to investigate general properties of ligand binding: we observe both a direct stabilizing effect of ligand-protein interactions and an indirect destabilizing effect on intraprotein interactions that is induced by the ligand. Significantly, the crystallographic binding poses are distinguished not only because their ligands induce large stabilizing effects, but also because they induce relatively low indirect destabilizations.

Introduction

The pathways traveled by ligands as they bind to their molecular receptors are important to drug design. Although the binding thermodynamics is purely determined by the endpoints of these pathways, analysis of the entire paths can reveal binding transition states that govern the kinetics of the binding process. Underappreciated until recently, long residence times have been shown in a handful of systems to be more predictive of in vivo efficacy than the thermodynamics alone (1, 2). Conversely, fast binding and release could also be preferable in some applications, including enzyme inhibition (3), and for systems where fast clearance of the drug is essential. Robust methods that can predict structure-kinetics relationships would thus be of tremendous value to drug design efforts. Unfortunately, structural details of ligand-binding transition states are difficult to capture experimentally, and ligand binding and release typically occur on timescales that are inaccessible to conventional molecular simulation.

Recently, a handful of cutting-edge applications of molecular dynamics, using either specialized hardware (4, 5), large parallel sampling efforts synthesized with Markov state models (6, 7, 8), or customized enhanced sampling algorithms (9, 10, 11, 12), have been applied to study full ligand binding or unbinding pathways. These have revealed an intricate interplay between the conformations of the ligand and receptor, and are beginning to reveal how biological molecules are controlled by exogenous factors, which is important both for our understanding of biology, and for our ability to design drugs that elicit a desired biomolecular response. Despite some progress, the principles that govern the general relationship between ligand binding and protein stability or protein activity remain elusive. General biophysical properties of protein-ligand interactions are needed to elucidate and predict phenomena such as allosteric signaling networks (13), and ligand-induced stability changes (14). This necessitates a general knowledge of how ligand binding is coupled with conformational change in the binding site.

The binding of the ligand benzamidine to trypsin has in recent years served as the system of choice to demonstrate emerging enhanced sampling approaches to study ligand binding (6, 8, 9, 11, 12, 15, 16). Long simulations of ligand binding synthesized with Markov state models obtained binding rates that showed good agreement with experiment (6, 8, 15), but the unbinding rates were consistently overpredicted, owing to the steep free energy barrier of ligand unbinding. Particularly, Plattner and Noé (8) used hundreds of microseconds of simulation to show a dynamic picture of trypsin with two main binding channels and multiple long-lived trypsin conformations. Approaches using metadynamics with path-based order parameters have also obtained unbinding rates (11), but these were significantly underpredicted, although again the binding rates showed excellent agreement. Teo et al. (12) used the adaptive multilevel splitting method to obtain excellent agreement with the experimental rate with modest computational cost, but did not observe some of the long timescale conformational transitions seen by previous investigations.

Here we use our own technique, WExplore (17), to investigate a broad set of ligand release pathways in the trypsin-benzamidine system. This and related methods have been used to study protein unfolding, hydration changes near a fluorophore (18), long timescale conformational transitions in a RNA helix-helix junction (19), and to generate the ensemble of unbinding pathways of small ligands from the protein FKBP (20). Like MSM approaches, it uses trajectories that are run with the unbiased Hamiltonian and are suitable for a network-based conformation analysis (21, 22, 23), but it is based on a weighted ensemble of trajectories, and obtains unbinding rates by a different mechanism that does not rely on a Markovian assumption of transitions between regions. A set of trajectories are run in parallel, each with a statistical weight, and these are actively managed on the picosecond timescale using cloning and merging steps that maximize the heterogeneity of the trajectory set. As in the original weighted ensemble algorithm (24), during cloning the weights are split, and during merging, the weights are added. Observables can then be computed using weighted averages. One such observable is the flux of trajectories that cross into the unbound state, which in the nonequilibrium unbinding ensemble is equal to the unbinding rate (25, 26, 27).

In the next section, we discuss the methodology used for the simulations, the WExplore sampling and the clustering that serves as the basis for conformation space network analysis. The results are presented in Results and Discussion, including the calculation of the residence time, exit pathway characterization, and a survey of the energetic properties of representative structures. We then summarize our findings and present an outlook for the future of the field.

Materials and Methods

Molecular dynamics simulations

Dynamics are run in CHARMM (28) on graphics processing units using the program OpenMM, version 6.3 (https://simtk.org/projects/openmm). The system is constructed using the coordinates from Protein Data Bank (PDB): 3PTB, preserving the crystallographic calcium ion and the 62 crystallographic water molecules. The system is then solvated with a 12 Å cutoff surrounding the protein and the ligand, resulting in 12,592 waters. Nine chlorine ions are added to neutralize the system, resulting in 41,006 atoms total. Cubic periodic boundary conditions with a box-size of 74.3 Å are used. The ligand is parameterized using the CHARMM Generalized Force Field (29).

For dynamics, we use a 2 fs timestep. Dynamics are performed in the constant pressure, constant temperature ensemble, coupled to a Langevin heatbath with temperature 300 K and friction coefficient of 1 ps⁻¹, and a Monte Carlo barostat with a reference temperature of 1 atm, and volume moves attempted every 50 timesteps. We compute nonbonded interactions using particle mesh Ewald, with a switching function that scales the nonbonded interactions to zero at 10 Å, starting at 8.5 Å.

The solvent is first minimized using 500 steps of steepest decent followed by 500 steps of the adopted basis Newton-Raphson method, and the entire system is then minimized in the same way. After minimization, we gradually heat the system from 50 to 300 K in 10 steps of 10 ps each, followed by equilibration at 300 K for 500 ps. the resulting structure is then used as the initial conformation for all walkers in the WExplore sampling method.

WExplore sampling

The WExplore methodology has been described in detail in previous work (17, 19), including its application to ligand unbinding simulations (20). Here we review the principal aspects of this methodology, which is built on the weighted ensemble algorithm (24). Many copies of the simulation (here, 48), called “walkers”, are run in parallel and each of these carries with it a statistical weight. Every 20 ps, these walkers are cloned and/or merged to increase the heterogeneity of the trajectory set, by merging walkers in overrepresented regions and cloning them in underrepresented regions. The regions are dynamically defined Voronoi polyhedra: each is defined by a single point, called an “image”, and a polyhedron is defined as containing the set of points that are closer to its image than to any of the other images. Each image is a protein-ligand conformation, and the distance from a point to an image is calculated as the root mean squared distance (RMSD) between the two conformations of the ligand after alignment to the protein.

WExplore simulations are started with a single image near the crystallographic bound state, and more images are defined as the simulation progresses. No starting path is necessary, and sampling proceeds outward from this initial point in an undirected way. This is an important feature, as the exit paths obtained are not influenced by prior assumptions. Additional images are defined when a structure is found that is greater than a certain cutoff (d) from all other images that have been defined so far, resulting in a set of images that are all far from each other. This is akin to an on-the-fly clustering method. An important aspect of the WExplore method is the use of a hierarchy, with a small set of large images that tile the entire space (with large d), each of which is broken up by smaller images (with smaller d), which are themselves broken up by smaller images, and so on. Here we use a four-level hierarchy with d = 10, 5, 3, and 1.7 Å.

As in previous work (20), we institute a maximum and a minimum weight that the walkers can have. This prevents wasting computational resources on walkers that will not contribute meaningfully to observables, and prevents all of the weight from coalescing into a single walker. We use a minimum weight of 10⁻¹² and a maximum weight of 0.1, which are enforced by preventing cloning and merging operations that would violate these rules.

Clustering

To visualize the results of our sampling in a conformation space network, we jointly cluster the conformations observed in all five WExplore simulations. This is done in MSMBuilder (30), using a set of ligand-protein distances. The set of distances is constructed using the 50 closest heavy atoms in the protein to the ligand in its crystallographic conformation (set A), and the nine heavy atoms in the ligand (set B). We use every possible connection between sets A and B for clustering: a set of 450 distances. These are clustered using the KCenters algorithm and the Canberra distance metric, which highlights differences between quantities that are small. This is ideal for our purposes, as it helps avoid overclustering poses in the unbound state, which have large distances between the ligand and receptor.

Results and Discussion

Ligand residence time

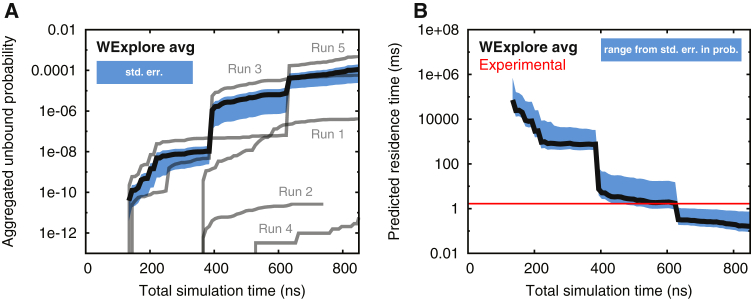
Each run uses 48 trajectories total that are cloned and merged repeatedly throughout the simulation, and these operations affect the weights that are attached to each walker. These simulations are run in the unbinding ensemble, where trajectories are initiated in the bound state and are terminated when they enter the unbound state, defined here as having a minimum ligand-protein interatomic distance >10 Å. Using a well-established technique (25, 26, 27, 31), we can determine the unbinding rate by measuring the flux of trajectories into the unbound ensemble, that is, the sum of the weights of the exited walkers divided by the elapsed time. Fig. 1 A shows the aggregated probability that has entered the unbound state as a function of time for the five independent WExplore runs conducted here. All curves are monotonically increasing, and large jumps are created by exiting walkers that have a higher weight than those that were previously recorded. The average curve between the three runs is shown and is heavily dominated by the highest probability runs. The probabilities from different runs differ over eight orders of magnitude, owing to large differences in the weight of the trajectories that break out of the binding pocket, which can be as low as 10⁻¹². One important aspect of the WExplore algorithm is that once the first trajectory has broken out of the pocket, it is cloned many times to explore new parts of conformation space. Computational effort is then focused on exploring new areas, and as such it becomes less likely that new walkers with higher weights will also emerge from the binding pocket. However, we note that multiple breakout events are still possible, and are clearly observed in runs 3 and 5. With this in mind, we expect that extensions of runs 2 and 4 would eventually converge toward the mean, although we have found that multiple shorter runs are more efficient than single long ones, as the weight distributions within a run are much more highly correlated than those between the runs.

Figure 1.

Calculating the MFPT of ligand unbinding. (A) A running total of the weight of exited walkers is shown for all five runs as a function of simulation time (grey lines). The average probability is shown as a thick black line, and the standard error of this quantity is shown as a filled area surrounding the curve. (B) The predicted residence time computed using the average probability flux across all WExplore simulations is shown as a thick black line, and shows reasonable agreement with the experimentally determined residence time (39), shown as a thin horizontal line. The standard error of the probability flux is used to estimate the uncertainty in the predicted mean first passage time by calculating minimum and maximum values at each time point using the mean flux plus or minus the standard error, respectively. These minimum and maximum values bound the filled area surrounding the curve. To see this figure in color, go online.

By dividing this probability by the elapsed time, we obtain the probability flux into the unbound state, which is equal to k_off. We can then predict the mean first passage time (MFPT = 1/k_off) as a function of simulation time for five independent WExplore runs (Fig. 1 B). A total of 4.1 μs of simulation time is used to generate the average curve (thick black line) that obtains a final prediction of 180 μs, using the last 10% of the data. Despite the run-to-run variability, the averaged trajectory flux gives a MFPT that is within an order of magnitude of the experimental value of 1700 μs (Table S1 in the Supporting Material). It is important to note that directly averaging the MFPT from each run would result in a very different prediction that is heavily dominated by runs 2 and 4, in the neighborhood of 10⁷ ms. This would not be appropriate, as the probability of exited trajectories is an extensive quantity that can be averaged across simulations, while the MFPT is not.

The error bars in each panel are calculated using the standard error (SE) of the average probability flux calculated over the five simulations. In the case of the MFPT curve, a minimum and a maximum MFPT is calculated using the mean flux plus or minus the SE, respectively. We note that this error measurement can only predict the uncertainty given the data at hand, and cannot take into account the possibility that a new unbinding event could occur in the future that carries significantly higher probability than that which has been observed here. Another means of analyzing the error is to calculate averages using subsamples of the five runs, and examine how the variation in the averages decreases as more runs are added. Fig. S1 shows the mean k_off value and the SD of the subsampled averages for groups of runs ranging from 1 to 4. As a fraction of the mean, the deviation decreases steadily as a function of the number of runs: 1.95, 1.12, 0.75, and 0.49 for groups of 1, 2, 3, and 4 runs, respectively.

To help illustrate the performance of the WExplore algorithm, we plot the number of exit points observed as a function of time across the five sampling runs (Fig. S2). There is considerable variability in the total number of exit points observed, ranging from 115 for run 3 down to only nine points for run 4. Run 4 recorded its first exit point after 546 ns of total simulation, which is much longer than the average of 315 ns. As expected, the total number of exit points observed is much less than previous applications of WExplore on a system with unbinding times in the nanosecond range (20). In WExplore runs observing three small ligands dissociate from the protein FKBP, we previously obtained an average of 602 unbinding events per microsecond of simulation. Here we obtain an average of 82 unbinding events per microsecond for the trypsin-benzamidine system, which is reduced by only about a factor of seven. This is remarkable, as the trypsin-benzamidine unbinding timescale is ∼18,000 times longer than that of the FKBP ligands.

In Fig. S3 we compare the number of sampling regions created in each of the five runs. Only regions that are at the bottom of the hierarchy are counted (i.e., those with d = 1.7 Å). This is mostly consistent with the recording of exit points shown in Fig. S2: runs with the largest number of sampling regions also recorded the largest number of exit points. The curves for all runs except run 4 have a similar shape, with a lag phase of variable length followed by a rapid growth in sampling regions that coincides with the recording of the first exit points (as seen in Fig. S2). Run 4 is significantly different in this regard, as region creation occurs at a slow but steady pace. The difference can be explained by the unique unbinding pathway sampled by run 4, which is described below.

Ligand unbinding pathways

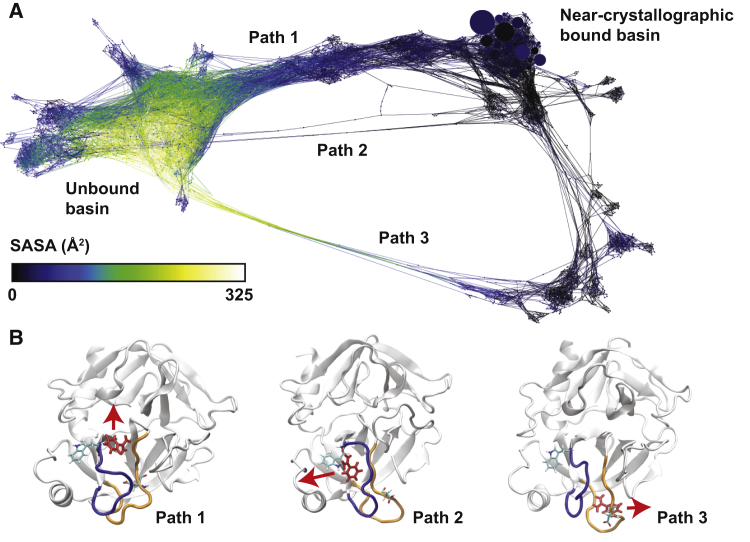
These simulations can be reduced to a large set of trajectory segments, of length 20 ps, conducted using an unbiased Hamiltonian. We cluster the data from all simulations into 4000 states using a set of 450 ligand-protein distances, construct a transition probability matrix, and use conformation space networks to synthesize our findings (21, 22, 23). Each node in the network represents a state in the transition probability matrix, and each nonzero off-diagonal element corresponds to an edge in the network (19,039 total). The network graph is created using the ForceAtlas 2 algorithm in Gephi (32) using edge weights between 1 and 1000 as described in previous work (23). Fig. 2 A shows the complete network of states visited by all five simulations. Generally, nodes that are close together in this figure can interconvert quickly, and those that are far apart interconvert slowly. Node sizes show the state probabilities, as determined by summing the weights of all walker conformations that have visited that state, and normalizing such that the sum of all probabilities is 1. The biggest nodes in the top right are the bound states closest to the crystal structure used to initialize the simulations (PDB: 3PTB). Nodes are colored here by solvent-accessible surface area (SASA), which reveals a large number of states that are kinetically far from the crystal state, but are still completely buried inside the protein.

Figure 2.

Trypsin-benzamidine unbinding network shows three exit pathways. (A) The conformation space network of the trypsin-benzamidine system is shown. The size of the nodes corresponds to the weight of the states, and the node color shows the SASA of a representative structure from that region. The bound and unbound basins are connected by three discrete transition paths, which are labeled. (B) Representative structures are shown that characterize the mechanism of the three transition paths. Benzamidine is shown in red licorice representation (dark color), and the general direction of exit is shown with an arrow for each pathway. Residues TRP208 and ASP186 are shown in licorice representation (light color), and the loop regions 179-190 and 209-218 are shown in orange (right) and blue (left), respectively. To see this figure in color, go online.

We find three transition paths that connect the bound and unbound basins (Fig. 2 B). These transition paths are completely discrete, as they involve topologically distinct exit routes with respect to the backbone of the trypsin protein. Path 1 is the direct exit pathway that has been found by all previous investigations, where benzamidine exits through the space between the blue (residues 209–218) and orange (residues 179–190) loops. This channel is open in the crystal structure (PDB: 3PTB). In Path 2, the blue loop undergoes a conformational change, which closes the first exit channel and creates an alternative pathway for benzamidine release. This path was previously observed by Plattner and Noé (8), and significant loop motions in this region were also observed using metadynamics (11). Path 3 involves a similar conformational change in the orange loop that closes the original channel and opens a third distinct exit pathway. This path has not been observed by previous investigations, and as shown in Fig. 2 A, it creates a large set of bound states that are distinct from the crystal structure, but are still completely buried in the protein.

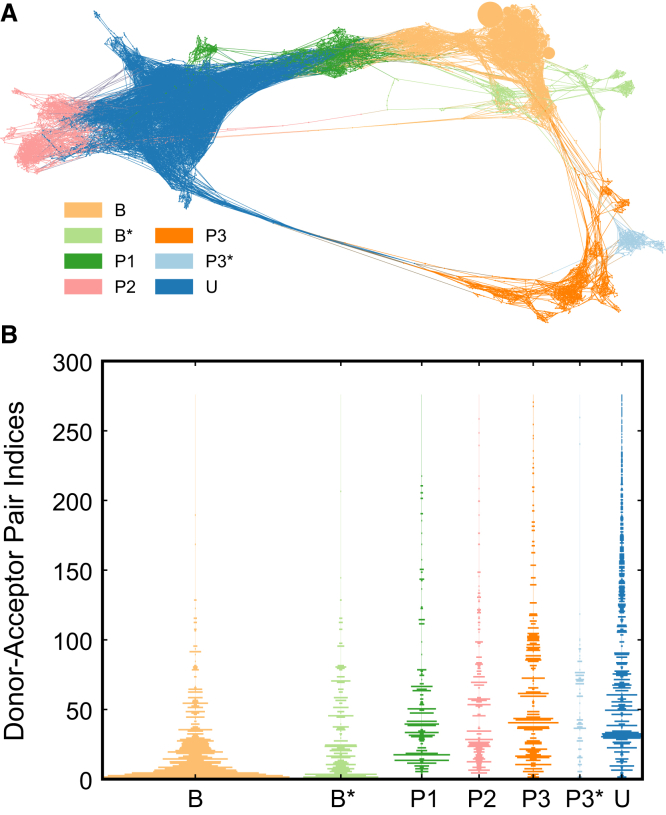
To facilitate further analysis, we break up our network into communities using a fast stochastic modularity-based community detection algorithm (33) (Fig. 3 A). We obtain seven communities: two of each representing the bound (B,B^∗), and path 3 (P3,P3^∗) states, and one of each representing unbound (U), path 1 (P1), and path 2 (P2). To study these communities, we first profile the entire set of ligand-protein hydrogen bonds (H-bonds) in the network. For this purpose, we have developed the software Mastic (which is provisionally available at https://github.com/salotz/mast, and will be officially released in the near future when it is feature-complete) (34). Hydrogen bonds are detected as having an acceptor-donor distance of <4.1 Å and a donor-hydrogen-acceptor angle between 100 and 180°. For each H-bond that we observe in our simulations, Fig. 3 B shows the frequency with which it is observed in each of the seven communities. Two-hundred-and-seventy-six unique acceptor-donor pairs are found with 8621 H-bonding instances total. The B and B^∗ distributions are dominated by the same high frequency pairs, while U has many low to moderate frequency pairs, as expected. The remaining unbinding pathway communities (P1, P2, P3, and P3^∗) have somewhat heterogeneous distributions but feature some high frequency interaction pairs that are mostly nonoverlapping between pathways. This suggests that each pathway may be characterized uniquely by a small set of specific interactions. In Fig. S4 we show the number of interactions per node in each community, and find that B and B^∗ have a high average number of interactions per node, but also the largest ranges. P3 stands out from P1, P2, and P3^∗ in having a fairly high average number of interactions per node, which is consistent with the high number of completely buried states.

Figure 3.

Community detection and hydrogen bonding frequencies. (A) Network plot showing communities of the network. The labels B and B^∗ correspond to the two bound state communities and U corresponds to the unbound states. P3^∗ is classified as a distinct component of the P3 pathway. (B) Violin barplots of hydrogen bond frequencies. (Vertical axis) Donor-acceptor pairs sorted by their frequency in the whole network. Each violin shows the frequencies with which the H-bonds are observed within each community.

Using these results we, for each community, identify the highest frequency interaction, find the set of all structures exhibiting this interaction, and then assign the highest weighted of these structures to be a “representative structure” for this community. These structures are shown in Fig. S5, where the highest frequency hydrogen bond is indicated and the residue Asp¹⁸⁹ is shown as a point of reference. The representative structure for B happens to be from the highest weighted node in the network and is similar to the crystal structure. For P1 (the highest weighted unbinding pathway), the representative structure shows the ligand simply backing out of the pocket and the highest frequency hydrogen bond occurs with the adjacent Ser¹⁹⁰ side chain. The U community is not well represented by a single high-frequency interaction, but the representative structure is, unsurprisingly, related in position to the P1 unbinding pathway, which is the highest probability pathway. Benzamidine hydrogen bonding in B^∗ also involves Asp¹⁸⁹, but there is a conformational change of the blue loop that opens the P2 exit pathway. The B^∗ structure appears to be a precursor to P2 as Asp¹⁸⁹ is flipped out of the pocket, allowing hydrogen bond formation with a backbone oxygen on Trp²¹⁵ (and likely π-π stacking against the indole ring) guiding the ligand away from the binding pocket. P3 and P3^∗ are related both in their localization in the network pathways as well as in the conformational changes in the blue and orange loops. In both, there is a closing of the binding site by the blue loop and the opening of gaps in the orange loop. It also appears that P3^∗ is a precursor to P3, as the ligand is much closer to the original B position and orientation in P3^∗. However, the P3 community is very diverse compared with P1 and P2, and this relationship is likely to be more complex. The identification of B^∗ and P3^∗ indicate that the use of graph theoretic methods will likely continue to be useful in identifying and refining unique states along complex unbinding pathways and ultimately identifying the salient intermolecular interactions useful for developing drug targets.

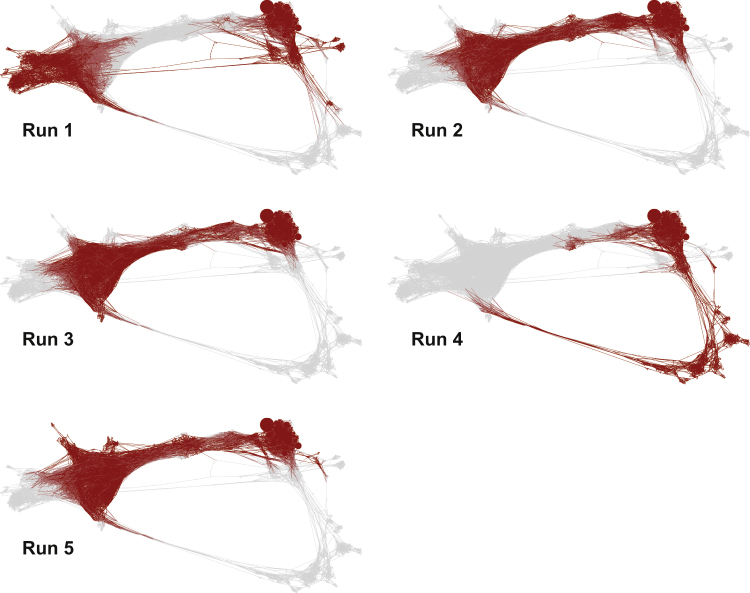
Each of the three pathways is not observed by every WExplore simulation (Fig. 4). Path 1 is observed in runs 2, 3 and 5, Path 2 is observed only in run 1, and Path 3 is observed only in run 4. Fig. 5 shows the free energy of each state, which shows Path 1 to be by far the most probable, Path 2 to be the next most probable, and Path 3 to be the least probable, consistent with Fig. 1. This also allows us to estimate pathway-specific residence times (T_r), by separately determining the unbinding flux for each run, combining fluxes for runs 2, 3, and 5 in the case of path 1, and inverting this quantity to get the residence times. In this way, Path 1 has a reactive flux of 6.3 × 10³ s⁻¹, and a T_r of 160 μs, which is very close to the overall residence time. Path 2 has a reactive flux of 4.7 s⁻¹, and T_r = 200 ms, ∼1400 times slower than Path 1. Path 3 has a reactive flux of 5.7 × 10⁻⁴ s⁻¹, and T_r = 1700 s, or ∼30 min. It is important to emphasize that the residence time estimates for Paths 2 and 3 are crude estimates at this point, as each has only been observed in a single WExplore simulation, and as shown in the T_r variation in runs 2, 3, and 5, results from single simulations can vary significantly. Nonetheless, these results underscore the ability of WExplore to discover alternative bound conformations, even those that are separated by large free energy barriers, requiring significant rearrangement of local protein structure.

Figure 4.

Conformation space networks colored by the contribution from the five WExplore runs. (In each figure, a node is colored in red (dark color) if it is sampled in that run, and in light gray if it is not.) To see this figure in color, go online.

Figure 5.

Conformation space network colored by free energy. The free energy is shown in units of kT.

General properties of ligand-protein interactions

The large set of bound but buried states generated here presents a unique opportunity to examine general properties of ligand-protein interactions across many heterogeneous ligand-protein conformations. Specifically, we examine the relationship between ligand-protein interactions and protein-protein interactions by examining the set of protein atoms that are close enough to directly interact with the ligand. To this end, we identify a set of protein atoms that are within 4 Å of any atom in the ligand; we call this set of atoms “D₄” (Fig. 6 C). This selection is unique for each of the 4000 nodes in the network, as the ligand takes on a wide range of conformations in different regions of the protein and the local protein structure also varies significantly. We examine the interaction energies of this selection with its surroundings and compare it to the interaction energy of the same selection in a set of 10 apo structures. The apo structures chosen are the 10 highest probability states that have a minimum protein-ligand distance >5 Å (Fig. S6). These differences in interaction energies reveal the direct and indirect impacts of ligand binding on protein stability.

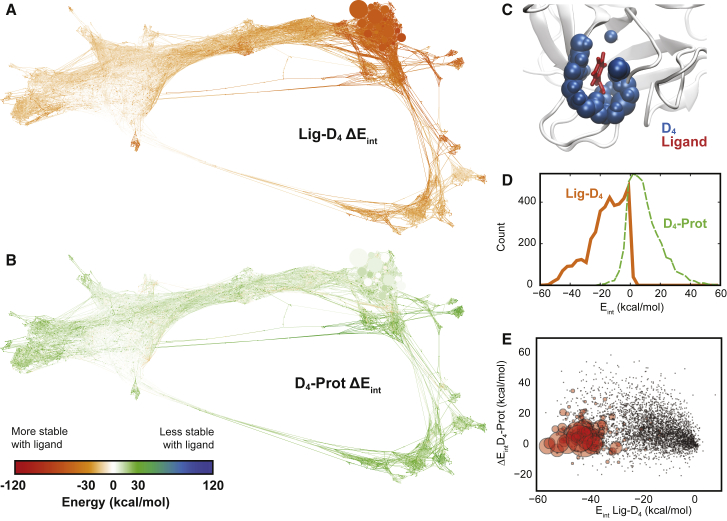
Figure 6.

Protein-ligand contacts disrupt protein-protein interactions. (A) Conformation space network (CSN) of trypsin-benzamidine colored by the interaction energy between the ligand and a selection of protein atoms that are within 4 Å of the ligand (D₄). (Bottom left) Color scale: (red and orange) stabilizing interactions; (white) no interaction; (green and blue) destabilizing interactions. (B) A CSN colored by the difference in the D₄-protein interaction energy, comparing each node to an ensemble of apo structures. (Green nodes) Corresponding D₄ atoms have a lower energy in the apo structures. (C) A visualization of the ligand (in red licorice representation), and the D₄ selection for that pose. (D) Probability distributions for Ligand-D₄ interaction energies (solid orange) and D₄-Protein interaction energies (dashed green). (E) Scatter plot of Ligand-D₄ interaction energies versus D₄-Protein interaction energies. The size of the circles is proportional to the statistical weight of each state.

Fig. 6 A shows the interaction energy of D₄ with the ligand, and as expected it is favorable, ranging from ≈−55 kcal/mol in the highest probability bound states, to approximately zero for the unbound states. Fig. 6 B shows the difference in D₄-protein interaction energies from the set of apo states, for each state in the network, where “protein” is defined as protein atoms that are not in the D₄ set. Orange and red colors indicate that the D₄-protein interactions are more stable in the presence of the ligand, while green and blue colors indicate that they are less stable in the presence of the ligand. As shown in Fig. 6 B and summarized in Fig. 6 D, the presence of the ligand is destabilizing for most of the ligand poses in the network. A handful of states exist with more stable D₄-protein interactions when the ligand is bound (orange), up to 20 kcal/mol, although the majority show a small destabilization (green). We thus observe that the presence of a ligand is generally indirectly destabilizing to protein-protein interactions.

Fig. 6 E shows a scatter plot comparing the ligand-D₄ interaction energy and the difference in D₄-protein interaction energies for all of the nodes in the network. The size of each circle corresponds to the weight of that node in the network. While there is little correlation between the two quantities (see Fig. S7 for correlation analysis, as well as analysis of D₄-D₄ and D₄-solvent interactions), it is significant that the highest probability nodes in the network are distinguished by both favorable ligand-D₄ interaction energies as well as low D₄-protein destabilizations. For the network as a whole, the mean D₄-ligand interaction energy is −16.2 ± 0.2 kcal/mol, where the uncertainty is the SE. For the set of nodes with probability >0.01, the mean D₄-ligand interaction energy is −43.9 ± 1.5 kcal/mol, which is significantly more favorable. Similarly, the mean difference in D₄-protein interaction energies is 9.6 ± 0.2 and 3.9 ± 1.0 kcal/mol for the entire network and top-weighted nodes, respectively. This indicates that the indirect destabilization of protein-protein interactions can be a useful quantity for the prediction of high-probability ligand binding poses.

Comparison to previous simulations

Table S1 compares the residence times obtained in this work and those from previous simulations of ligand (un)binding in the trypsin-benzamidine system. This is a useful measure of efficiency, but it is important to take them in context, as the sampling methods differ in the quantities they can predict (i.e., k_on, k_off, ΔG_bind) and in the range of sampling for motions in both the ligand and the protein. The simulations here are performed strictly in the nonequilibrium unbinding ensemble, and offer predictions of k_off, but not k_on, which would allow us to calculate the free energy of binding, ΔG_bind. The nonequilibrium unbinding ensemble can be rigorously defined using a previous framework (25, 26) with two basins, B and U, that define the bound and unbound ensembles. Here, B can be defined as the set of conformers where the ligand is within a certain root mean squared distance (say, 3 Å) away from its crystallographic pose, and U is defined as the set of conformers where the minimum protein-ligand distance is farther than 10 Å. Our sampling is composed of two types of paths: B → B paths, and B → U paths. By the microscopic reversibility principle, the B → U ensemble and the U → B ensemble are identical under equilibrium conditions, however, our simulations will differ from those conducted in the nonequilibrium binding ensemble, which would include U → U pathways, and neglect B → B pathways.

In Fig. S8 we identify nodes in our network that correspond to states previously observed by Buch et al. (6) in simulations that mostly approximate the binding ensemble (S1, S2, and S3). The S1 state was characterized to involve interactions with the residues 55, 87, and 91 (shown in blue), the S2 state involved interactions with residues 37, 38, and 146 (shown in red), and the S3 state involved interactions with residues 95, 96, 170, 172, and 175 (shown in green). To determine whether one of our structures is in these three states, we calculate the minimum distance between atoms in the ligand and atoms in these sets of residues, and if the largest such minimum distance is <4 Å, we consider that state to be in that pocket. We observe many nodes in the U community that are determined to be in the S2 and S3 states, although we observe none in state S1, indicating that S1 states are not observed in this ensemble of unbinding trajectories. This implies that S1 is not in the U → B ensemble, instead lying in the U → U ensemble.

Teo et al. (12) recently reported simulations in the nonequilibrium unbinding ensemble using the adaptive multilevel splitting algorithm. This method efficiently determined the off-rate to excellent agreement with the experimental value. In adaptive multilevel splitting, a progress coordinate (z) is defined, and an ensemble of trajectory loops that begin and end in the bound state are sampled until the unbound state (characterized by z_max) is reached. Loops with the lowest maximum distance from the bound state are terminated, and are respawned from intermediate points of old loops, guaranteeing that they reach a distance of z_min from the bound state, a threshold that progressively increases over the course of the simulation. Although there is nothing in the algorithm that restricts the sampling to a single exit channel, the progressive respawning from intermediate points should cause the sampling to coalesce along a single pathway. WExplore, in contrast, encourages diversity not only along a given progress coordinate, but orthogonal to it as well. To compare with our results, we computed the same z coordinate value for each state in the network (Fig. S9). To appreciate the breadth of our sampling of the degrees of freedom that are orthogonal to the z coordinate, we have placed asterisks next to regions with z ∼ 5 Å, which is an arbitrarily chosen intermediate value. These regions involve structures on all three transition paths, as well as off-pathway intermediates, illustrating broad sampling along variables that are orthogonal to z. This breadth of sampling with WExplore is a distinguishing feature of the algorithm that enables a deeper analysis of ligand bound ensembles, such as that presented above.

Plattner and Noé (8) extensively sampled the trypsin-benzamidine system, which enabled a thorough analysis not only of benzamidine binding, but of multiple long-lived trypsin conformational states. This study identified two unbinding pathways for trypsin (8), in one of which the ligand exits through the 209–218 loop, as in our Path 2. This alternative binding pathway was shown to be preferred for alternative trypsin conformations, the highest probability of which was called the “red state”. We obtained three representative structures of the red state, and calculate the RMSD to the red-state residues 209–218 for each node in the network, averaged over the three conformations. We find some clusters show good local alignment to the red-state loop structures, although the global alignments are poor (Fig. S10, B and C). Fig. S10 A shows a visualization of the RMSD to the red-state structures on the network. Interestingly, a large cluster of states showing good local alignment lies at the foot of Path 2 in our conformation space network.

Conclusions

The solid agreement with experimental rates, the broad sampling of pathways and poses, and the relative efficiency of our technique bode well for future applications of WExplore to ligand-release processes. Druglike ligands can have residence times approaching minutes or hours, which will be prohibitive to straightforward molecular dynamics for the foreseeable future, but is comparable to the residence time that we predict for benzamidine dissociating via Path 3, which involves substantial rearrangements of the protein that occur on extremely long timescales. Further testing is needed on ligand dissociation events that occur on longer timescales, which could reveal important information about the optimization of kinetic properties for drugs under development. (Un)binding pathways can also reveal important molecular motions in the receptor that can be used to design new ligands that stabilize alternative receptor conformations. As an example, many states are identified here where the ligand is still deeply buried (SASA ≈ 0), which is kinetically far from the crystallographic starting structure. It is easy to imagine this approach being used to identify such states, which can serve as templates for the design of new ligands that bind via an induced-fit mechanism.

An important difference between WExplore and other enhanced sampling methods that rely on the identification of one or two order parameters to describe a transition, such as umbrella sampling (35) or metadynamics (9, 36), is that WExplore uses a distance metric to define its sampling regions that can be defined in a many-dimensional space. Here, this distance is calculated as the RMSD in ligand position after aligning to the protein binding site, and new sampling regions are defined as the ligand translates and rotates away from its starting pose. It is important to emphasize that two new poses, say i and j, that are both an RMSD of 5.0 Å from the initial pose, are not in the same sampling region unless the RMSD between states i and j is small. The sampling regions in WExplore are best thought of as the results of an on-the-fly clustering procedure, where the distance between all pairs of regions is taken into account. This results in an ensemble of states that is not only far from the initial structure, but far from each other, which is ideal for determining broad ensembles of possible bound states.

It is important to note that our trajectory segments are short compared to those used by Plattner and Noé (8), and we use much less aggregate simulation time (Table S1). We are able to observe much variation in the degrees of freedom that are encompassed in our distance metric (i.e., the ligand and the set of residues close to the crystallographic binding site), which is manifested in a broad ensemble of ligand-bound poses and exit pathways. However, as the distance metric does not include many other protein degrees of freedom, there is nothing to encourage long timescale protein motions that are uncoupled with ligand binding. Therefore, to observe these motions with the strategy employed here, either the trajectory segments would need to be long enough that these motions are spontaneously observed, or the motions would need to be incorporated into the distance metric. An alternative strategy would be to generate a more diverse ensemble of starting positions using a method such as temperature-accelerated molecular dynamics (37) or self-guided Langevin dynamics (38), and use these to investigate the impact of protein motions on ligand release. This could be particularly useful if long timescale protein motions are a prerequisite for substantial ligand motion along ligand release pathways.

As more protein-ligand pathway studies are conducted, we will learn more about the biophysical principles that govern ligand binding. Here we have found that the presence of the ligand indirectly introduces a ∼10 kcal/mol destabilization to protein-protein interactions, and that this is ∼6 kcal/mol lower for high-probability binding modes. As benzamidine is relatively small, it will be interesting to see how this destabilization strength changes for larger, more druglike ligands. Although it is natural to assume that large ligands will induce larger indirect destabilizations, it remains to be seen to what extent the high probability states will find ways to mitigate this destabilization, and whether the gap between high probability states and the bulk will be larger than the 6 kcal/mol gap observed here.

Author Contributions

A.D. designed and performed research; S.D.L. contributed analytic tools; and A.D. and S.D.L. both analyzed data and wrote the article.

Editor: Amedeo Caflisch.