Examining the Assumptions Underlying Continuum-Solvent Models

Abstract

Continuum-solvent models (CSMs) have successfully predicted many quantities, including the solvation-free energies (ΔG) of small molecules, but they have not consistently succeeded at reproducing experimental binding free energies (ΔΔG), especially for protein–protein complexes. Several CSMs break ΔG into the free energy (ΔG_vdw) of inserting an uncharged molecule into solution and the free energy (ΔG_el) gained from charging. Some further divide ΔG_vdw into the free energy (ΔG_rep) of inserting a nearly hard cavity into solution and the free energy (ΔG_att) gained from turning on dispersive interactions between the solute and solvent. We show that for 9 protein–protein complexes neither ΔG_rep nor ΔG_vdw was linear in the solvent-accessible area A, as assumed in many CSMs, and the corresponding components of ΔΔG were not linear in changes in A. We show that linear response theory (LRT) yielded good estimates of ΔG_att and ΔΔG_att, but estimates of ΔΔG_att obtained from either the initial or final configurations of the solvent were not consistent with those from LRT. The LRT estimates of ΔG_el differed by more than 100 kcal/mol from the explicit solvent model’s (ESM’s) predictions, and its estimates of the corresponding component (ΔΔG_el) of ΔΔG differed by more than 10 kcal/mol. Finally, the Poisson–Boltzmann equation produced estimates of ΔG_el that were correlated with those from the ESM, but its estimates of ΔΔG_el were much less so. These findings may help explain why many CSMs have not been consistently successful at predicting ΔΔG for many complexes, including protein–protein complexes.

Graphical Abstract

1. INTRODUCTION

Implicit solvent models, such as the Poisson–Boltzmann equation¹ (PBE), generalized Born (GB) models,² proximal distribution approaches,^3–5 and integral equation methods,^6,7 provide estimates of the solvation energies (ΔG) of biomolecules more quickly than explicit solvent models (ESMs). Implicit solvent models are faster than ESMs because they approximately integrate over the degrees of freedom of the aqueous solvent in the partition function. Once estimates of ΔG have been obtained, they can be used to obtain estimates of other free energies, such as binding (ΔΔG) and mutation free energies.^8,9 Implicit solvent models may be divided into two classes, continuum solvent models (CSMs),^1,2 such as the PBE and GB models that model water as a high-dielectric continuum, and those that approximate the distribution of the solvent,^3–7 such as integral equations, density functional theories, and other structured approaches. CSMs have been fairly successful at predicting many quantities, such as ΔG, and the salt dependencies of various free energies,^10–14 but they have not been uniformly successful at predicting some other quantities, such as ΔΔG.^15–21

Typically, CSMs break ΔG into the free energy (ΔG_vdw) required to insert an uncharged molecule into solution and the free energy (ΔG_el) gained by turning on the partial atomic charges.^22–24 Some researchers have then further divided ΔG_vdw into the free energy (ΔG_rep) required to insert a nearly hard cavity into solution and the free energy (ΔG_att) gained from turning on the dispersive interactions between the solute and solvent.^25–33 The Methods contains formal definitions of these and related quantities.

In previous work, we demonstrated that the methods used to compute ΔG_rep, ΔG_att, and ΔG_vdw in some CSMs were unsatisfactory for alanine and glycine peptides.^24,34 In this work, we extend this analysis to nine protein–protein complexes covering wide ranges of sizes, biological functions, and equilibrium binding constants. By doing so, we try to ensure that our results are generally applicable to protein–protein complexes and not artifacts of our choice of examples. The complexes with their PDB codes are bovine α-chymotrypsin with eglin c complex (1ACB),³⁵ porcine pancreatic trypsin with soybean trypsin inhibitor complex (1AVX),³⁶ bovine β-lactoglobulin, which is a homodimer (1BEB),³⁷ barnase–barstar complex (1BRS),³⁸ colicin E9 dnase domain with IM9 (1EMV),³⁹ Pseudomonas aeruginosa exos toxin with human rac (1HE1),⁴⁰ bovine β-trypsin with CMTI-I (1PPE),⁴¹ and uracil-dna glycosylase with uracil glycosylase inhibitor (1UDI).⁴² In the following sections, we present the theoretical framework followed by the computational methods. We then present our results and discuss their implications for CSMs.

2. THEORY

In principle, ΔG_rep, ΔG_att, ΔG_vdw, and ΔG_el could be computed with thermodynamic integration by integrating over λ the derivatives (〈∂U_rep(λ)/∂λ〉_λ, 〈∂U_att(λ)/∂λ 〉_λ, 〈∂U_vdw(λ)/∂λ〉_λ, and 〈∂U_el(λ)/∂λ〉_λ) of λ-dependent potentials.^43,44 Plots of 〈∂U_att(λ)/∂λ〉_λ and 〈∂U_el(λ)/∂λ〉_λ for one of the complexes in the present study (1BRS) are shown in the Supporting Information. If these curves represented purely linear functions of λ, then ΔG_att and ΔG_el could be computed from linear response theory (LRT)

$$\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}=1/2({\langle U_{\text{att}}\rangle }_0+{\langle U_{\text{att}}\rangle }_1)$$ (1)

$$\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt}}=1/2({\langle U_{\text{el}}\rangle }_0+{\langle U_{\text{el}}\rangle }_1)$$ (2)

where U_att and U_el are attractive and electrostatic potential energies between the solute and solvent, respectively, as defined in the Methods, and 〈…〉₀ and 〈…〉₁ indicate that expectation values were computed in ensembles where λ = 0 and λ = 1. Some work has then gone farther by assuming that ΔG_att can be computed by averaging U_att over an approximate solvent distribution.^29,30,33 Natural choices for such a solvent distribution would be either the initial or final solvent configurations leading to single-step perturbation (SSP) estimates

$$\mathrm{\Delta }{G}_{\text{att}}^{\text{ssp,0}}={\langle U_{\text{att}}\rangle }_0$$ (3)

$$\mathrm{\Delta }{G}_{\text{att}}^{\text{ssp,1}}={\langle U_{\text{att}}\rangle }_1$$ (4)

of ΔG_att. Similarly, most CSMs assume that 〈U_el〉₀ = 0,^5,45 yielding a SSP approximation

$$\mathrm{\Delta }{G}_{\text{el}}^{\text{ssp}}=1/2{\langle U_{\text{el}}\rangle }_0$$ (5)

In contrast, the LRT cannot be used to compute either ΔG_rep or ΔG_vdw because 〈∂U_rep/∂λ〉_λ and 〈∂U_vdw/∂λ〉_λ typically contain large peaks or even poles.^24,46 Instead, CSMs typically use formulas taken from macroscopic liquid theory, such as

$$\mathrm{\Delta }{G}_{\text{vdw}}={\gamma }_{\text{vdw}}A+b$$ (6)

$$\mathrm{\Delta }{G}_{\text{rep}}={\gamma }_{\text{rep}}A+b$$ (7)

where A is the solvent-accessible surface area of the molecule, and γ_vdw and γ_rep are positive constants analogous to the surface tension of macroscopic liquid interfaces.^9,47–51

Alternatively, some studies have claimed that ΔG_rep should increase linearly with the solvent-accessible volume (V) rather than A for sufficiently small cavities and that for larger cavities it should approach eq 7.^52–55 In the present study, all of our proteins are large enough that this model would predict that ΔG_rep should approximately obey eq 7. The interested reader is referred to ref 24 and its supporting information for the volume correlations.

For an equilibrium binding process between proteins A and B, given that estimates of ΔG of the components and the complex have been obtained, the desolvation energy (ΔΔG^desol = ΔG^c − ΔG^a − ΔG^b, where ΔG^a, ΔG^b, and ΔG^c are the ΔG’s of the first component of the complex, the second component, and the complex, respectively) can be defined. In turn, ΔΔG^desol can be broken into repulsive $(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}})$, attractive $(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}})$, total van der Waals cavity insertion $(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}})$, and electrostatic $(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}})$ components, as described in the Methods.

Combining the definitions of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}$ with eqs 6 and 7, we can write

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}={\gamma }_{\text{vdw}}\mathrm{\Delta }A$$ (8)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}={\gamma }_{\text{rep}}\mathrm{\Delta }A$$ (9)

where ΔA = A^c − A^b − A^a, where A^c, A^a, and A^b are the areas of the complex and its two components.

Given ΔΔG^desol, estimates of ΔΔG can be obtained by adding the binding free energy (ΔG^vac) of the complex in vacuum. In turn, ΔΔG can be broken into repulsive (ΔΔG_rep), attractive (ΔΔG_att), total van der Waals cavity insertion (ΔΔG_vdw), and electrostatic (ΔΔG_el) components, as described in the Methods.

Many of these assumptions underlying CSMs can be called into question for biomolecules with rough surfaces and charge distributions varying over lengths comparable to the size of a water molecule. We recently found that none of ΔG_rep, ΔG_att, or ΔG_vdw are simple functions of A for alkanes and short peptides, indicating that eqs 6 and 7 are not strictly valid, and that eqs 3 and 4 were not consistent with ESMs.^{24,34,46,56,57} Some other studies have examined the validity of eqs 2 and 5.^5,45 Also, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$ are typically positive because they account for the loss of favorable solute–solvent interactions upon binding. In contrast, $\mathrm{\Delta }{G}_{\text{att}}^{\text{vac}}$ and $\mathrm{\Delta }{G}_{\text{el}}^{\text{vac}}$ are typically negative because $U_{\text{att}}^{\mathit{\text{ij}}}<0$ and because binding partners usually have complementary charges at the binding interface. Therefore, ΔΔG_att and ΔΔG_el can be much smaller than the ΔG_att and ΔG_el of the complex and its components. Because of this cancellation of free energies, theories that generate estimates of ΔG that are correlated with experimental data are not guaranteed to produce similarly accurate estimates of ΔΔG.⁵⁸

In the present study, we test the validity of eqs 1–9 for 9 protein–protein complexes^35–42,59 and also whether the PBE¹ produces estimates of ΔG_el, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$, and ΔΔG_el consistent with those obtained from ESMs for these complexes.

3. METHODS

All MD simulations were run with a modified version of NAMD 2.9.⁶⁰ SHAKE was used to constrain the hydrogens. All simulations used the TIP3P water model⁶¹ modified for use with the CHARMM force field,⁶² a constant temperature of 300 K, a constant pressure of 1 atm, periodic boundary conditions, particle mesh Ewald for the electrostatics, and a 2 fs time step. In all simulations, all protein atoms were fixed. All A, V, and their derivatives with respect to the atomic coordinates were computed with the DAlphaBall program.⁶³ The solvent-accessible surface was used⁶⁴ with the van der Waals radii taken from the CHARMM36 force field.^62,65,66 A probe radius of 1.7682 Å was used rather than the normal choice of 1.4 Å because it corresponds to the vdW radius of the oxygen atom in the water model, which for a chargeless protein is the only interaction with solvent via the Lennard-Jones force. This choice has been used in previous works.^24,34

All PBE calculations were run with the Adaptive Poisson– Boltzmann Solver (APBS)⁶⁷ with a temperature of 300 K, an interior dielectric constant of 1 (because the CHARMM36 force field is not polarizable), an exterior dielectric constant of 96.7 (to match the dielectric constant of TIP3P water⁶⁸), the solvent-excluded surface defined with a probe radius of 1.4 Å, no salt, autofocusing with a fine grid 20 Å larger than the molecule in each dimension, a coarse grid 1.7 times the size of the molecule in each dimension, and a fine-grid spacing of either 0.5 or 0.55 Å (to check convergence with respect to grid spacing).

3.1. Structure Preparation

The coordinates of the 9 protein–protein complexes^35–42,59 were taken from the RCSB protein databank⁶⁹ with no minimization or equilibration of these initial structures. These atomic coordinates remained fixed through all of the remaining calculations. All crystal waters and nonprotein atoms were removed. The chains from these structure files used in each calculation are shown in Table 1.

Table 1.

Chains from the Structure Files Used in Each Calculation^a

	molecule first chain second chain	1ACB E I	1AVX A B	1BEB A B	1BRS A D	1EAW A B	1EMV A B	1HE1 A C	1PPE E I	1UDI E I
protein A	A	48978	44830	35787	24965	48348	20160	29952	44429	50395
	γrep	0.017	0.020	0.017	0.023	0.012	0.024	0.019	0.017	0.017
	R2	0.51	0.55	0.46	0.61	0.40	0.64	0.53	0.49	0.47
	γvdw	0.040	0.042	0.034	0.051	0.027	0.048	0.040	0.041	0.039
	R2	0.15	0.14	0.12	0.20	0.08	0.21	0.15	0.14	0.13
protein B	A	15699	39342	35458	20705	14221	30953	39824	8048	20087
	γrep	0.025	0.019	0.020	0.024	0.027	0.019	0.018	0.032	0.022
	R2	0.64	0.54	0.54	0.64	0.66	0.55	0.50	0.73	0.55
	γvdw	0.051	0.041	0.043	0.051	0.051	0.038	0.035	0.062	0.042
	R2	0.19	0.15	0.16	0.19	0.22	0.13	0.10	0.34	0.15
complex	A	62232	81657	69623	43280	60246	48726	66480	49854	67477
	γrep	0.016	0.012	0.015	0.013	0.012	0.016	0.012	0.018	0.013
	R2	0.49	0.38	0.40	0.39	0.37	0.49	0.36	0.49	0.38
	γvdw	0.042	0.029	0.030	0.026	0.025	0.037	0.028	0.045	0.030
	R2	0.15	0.08	0.09	0.07	0.06	0.13	0.09	0.16	0.08
binding	γrep	0.017	0.014	0.017	0.017	0.014	0.019	0.015	0.019	0.016
	R2	0.50	0.40	0.47	0.47	0.40	0.52	0.42	0.50	0.44
	γvdw	0.041	0.031	0.034	0.037	0.028	0.039	0.033	0.044	0.036
	R2	0.15	0.09	0.12	0.14	0.09	0.14	0.12	0.16	0.12

^aHorizontal sections labeled protein A, protein B, and complex give estimates of γ_rep and γ_vdw obtained by fitting ∂ΔG_rep/∂x_i and ∂ΔG_vdw/∂x_i versus ∂A/∂x_i and the squares (R²) of the Pearson’s correlation coefficients of these plots. The horizontal section labeled binding contains estimates of γ_rep and γ_vdw obtained by fitting ∂ΔΔG_rep/∂x_i and ∂ΔΔG_vdw/∂x_i versus ∂ΔA/∂x_i and the squares (R²) of the Pearson’s correlation coefficients of these plots. The plots are in the Supporting Information. All A are in units of Ų, and all γ_vdw and γ_rep are in units of kcal mol⁻¹ Å⁻².

3.2. Potential and Free Energy Components

We defined ΔG_vdw to be the free energy required to move from an ensemble where the solute and solvent did not interact to one where the interaction potential between an atom i in the solute and an atom j in the solvent was given by the Lennard-Jones potential

$$U_{\text{vdw}}^{\mathit{\text{ij}}}={\epsilon }_{\mathit{\text{ij}}}[{\left(\frac{r_{\mathit{\text{ij}}}^{\text{min}}}{r_{\mathit{\text{ij}}}}\right)}^{12}-2{\left(\frac{r_{\mathit{\text{ij}}}^{\text{min}}}{r_{\mathit{\text{ij}}}}\right)}^6]$$ (10)

where ε_ij is the well depth, and $r_{\mathit{\text{ij}}}^{\text{min}}$ is the location of the minimum of $U_{\text{vdw}}^{\mathit{\text{ij}}}$. Our definitions of ΔG_rep and ΔG_att followed the Weeks–Chandler–Andersen breakdown,^25,26 where ΔG_rep was the free energy required to move from an ensemble where the solute and solvent did not interact to one where the interaction potential between an atom i in the solute and an atom j in the solvent was given by

$$U_{\text{rep}}^{\mathit{\text{ij}}}=\{\begin{array}{cc}{\epsilon }_{\mathit{\text{ij}}}[{\left(\frac{r_{\mathit{\text{ij}}}^{\text{min}}}{r_{\mathit{\text{ij}}}}\right)}^{12}-2{\left(\frac{r_{\mathit{\text{ij}}}^{\text{min}}}{r_{\mathit{\text{ij}}}}\right)}^6+1]\hfill & \text{if }{r}_{\mathit{\text{ij}}}<r_{\mathit{\text{ij}}}^{\text{min}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (11)

Next, we defined ΔG_att to be the free energy gained by moving from an ensemble where the solute–solvent potential was given by $U_{\text{rep}}^{\mathit{\text{ij}}}$ to one where it was given by $U_{\text{vdw}}^{\mathit{\text{ij}}}$. This process could also be described as turning on the attractive part of $U_{\text{vdw}}^{\mathit{\text{ij}}}$

$$U_{\text{att}}^{\mathit{\text{ij}}}=\{\begin{array}{cc}-{\epsilon }_{\mathit{\text{ij}}}\hfill & \text{if }{r}_{\mathit{\text{ij}}}<r_{\mathit{\text{ij}}}^{\text{min}}\hfill \\ {\epsilon }_{\mathit{\text{ij}}}[{\left(\frac{r_{\mathit{\text{ij}}}^{\text{min}}}{r_{\mathit{\text{ij}}}}\right)}^{12}-2{\left(\frac{r_{\mathit{\text{ij}}}^{\text{min}}}{r_{\mathit{\text{ij}}}}\right)}^6]\hfill & \text{otherwise}\hfill \end{array}$$ (12)

Finally, we defined ΔG_el to be the free energy gained by moving from an ensemble where the solute–solvent potential was given by $U_{\text{vdw}}^{\mathit{\text{ij}}}$ to one where it was given by

$$U^{\mathit{\text{ij}}}=U_{\text{vdw}}^{\mathit{\text{ij}}}+U_{\text{el}}^{\mathit{\text{ij}}}$$

$$=U_{\text{vdw}}^{\mathit{\text{ij}}}+q_i{q}_j/4\pi {\epsilon }_0{r}_{\mathit{\text{ij}}}$$ (13)

where q_i and q_j are the charges on atoms i and j, respectively, and ε₀ is the permittivity of free space.

We then defined $U_{\text{rep}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{rep}}^{\mathit{\text{ij}}},U_{\text{att}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{att}}^{\mathit{\text{ij}}},U_{\text{vdw}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{vdw}}^{\mathit{\text{ij}}}$, and $U_{\text{el}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{el}}^{\mathit{\text{ij}}}$, where the summations were taken over all solute–solvent atom pairs.

Similarly to the definition of ΔΔG^desol in the Introduction, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$, and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$ can be defined by

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}=\mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{c}}-\mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{b}}-\mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{a}}$$ (14)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}=\mathrm{\Delta }{G}_{\text{att}}^{\mathrm{c}}-\mathrm{\Delta }{G}_{\text{att}}^{\mathrm{b}}-\mathrm{\Delta }{G}_{\text{att}}^{\mathrm{a}}$$ (15)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}=\mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{c}}-\mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{b}}-\mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{a}},\text{and}$$ (16)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}=\mathrm{\Delta }{G}_{\text{el}}^{\mathrm{c}}-\mathrm{\Delta }{G}_{\text{el}}^{\mathrm{b}}-\mathrm{\Delta }{G}_{\text{el}}^{\mathrm{a}}$$ (17)

where $\mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{c}},\mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{a}}$, and$\mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{b}}$ are the ΔG_rep of the complex and its first and second components, $\mathrm{\Delta }{G}_{\text{att}}^{\mathrm{c}},\mathrm{\Delta }{G}_{\text{att}}^{\mathrm{a}}$, and $\mathrm{\Delta }{G}_{\text{att}}^{\mathrm{b}}$ are the ΔG_att of the complex and its first and second components, $\mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{c}},\mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{a}}$, and $\mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{b}}$ are the ΔG_vdw of the complex and its first and second components, and $\mathrm{\Delta }{G}_{\text{el}}^{\mathrm{c}},\mathrm{\Delta }{G}_{\text{el}}^{\mathrm{a}}$, and $\mathrm{\Delta }{G}_{\text{el}}^{\mathrm{b}}$ are the ΔG_el of the complex and its first and second components, respectively.

ΔΔG and its components were defined as follows

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }\mathrm{\Delta }{G}^{\text{desol}}+\mathrm{\Delta }{G}^{\text{vac}}$$ (18)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}+\mathrm{\Delta }{G}_{\text{rep}}^{\text{vac}}$$ (19)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}+\mathrm{\Delta }{G}_{\text{att}}^{\text{vac}}$$ (20)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}+\mathrm{\Delta }{G}_{\text{vdw}}^{\text{vac}}$$ (21)

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}+\mathrm{\Delta }{G}_{\text{el}}^{\text{vac}}$$ (22)

where $\mathrm{\Delta }{G}_{\text{vac}}={\sum }_{\mathit{\text{ij}}}{U}^{\mathit{\text{ij}}},\mathrm{\Delta }{G}_{\text{rep}}^{\text{vac}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{rep}}^{\mathit{\text{ij}}},\mathrm{\Delta }{G}_{\text{att}}^{\text{vac}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{att}}^{\mathit{\text{ij}}},\mathrm{\Delta }{G}_{\text{vdw}}^{\text{vac}}={\sum }_{\mathit{\text{ij}}}{U}_{\text{vdw}}^{\mathit{\text{ij}}}$ and $\mathrm{\Delta }{G}_{\text{el}}^{\text{vac}}={\sum }_{\mathit{\text{ij}}}{U}_{\mathrm{e}l}^{i\mathrm{j}}$, where these summations were taken over atom pairs with one atom in each component of the complex.

3.3. Free Energy Calculations

For the 1BRS complex, we computed ΔG_att and ΔG_el by backward and forward free energy perturbation (FEP) and thermodynamic integration (TI).^43,44 To do so, we defined the λ-dependent potentials

$$U_{\text{att}}^{\mathit{\text{ij}}}(\lambda )=U_{\text{rep}}^{\mathit{\text{ij}}}+\lambda U_{\text{att}}^{\mathit{\text{ij}}}$$ (23)

$$U_{\text{el}}^{\mathit{\text{ij}}}(\lambda )=U_{\text{vdw}}^{\mathit{\text{ij}}}+\lambda U_{\text{el}}^{\mathit{\text{ij}}}$$ (24)

To compute ΔG_att for each component and the complex, 11 1 ns simulations were run at λ values ranging from 0 to 1 in intervals of 0.1. To compute ΔG_el for the components of the complex, 21 1 ns simulations were run at λ values ranging from 0 to 1 in intervals of 0.05. To compute ΔG_el for the complex 1 ns simulations were run at the following λ values: 0, 0.025, 0.05, 0.075, 0.1, 0.125, 0.15, 0.175, 0.2, 0.225, 0.25, 0.275, 0.3, 0.325, 0.35, 0.375, 0.4, 0.425, 0.45, 0.475, 0.5, 0.525, 0.55, 0.575, 0.6, 0.625, 0.65, 0.675, 0.7, 0.725, 0.75, 0.775, 0.8, 0.825, 0.85, 0.8625, 0.875, 0.8875, 0.9, 0.9125, 0.925, 0.9375, 0.95, 0.9625, 0.975, 0.9875, and 1.

For the other 8 complexes, $\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$ and $\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt}}$ were computed using eqs 1 and 2 for both the components and the complexes by running 1 ns simulations where the interaction potential between the solute and solvent was $U_{\text{rep}}^{\mathit{\text{ij}}},U_{\text{att}}^{\mathit{\text{ij}}}$, and U^ij. Estimates of $\mathrm{\Delta }{G}_{\text{att}}^{\text{ssp,0}},\mathrm{\Delta }{G}_{\text{att}}^{\text{ssp,1}}$, and $\mathrm{\Delta }{G}_{\text{el}}^{\text{ssp}}$ were extracted from these same simulations.

Initial structures for all of these simulations were obtained by immersing the structure in a water box that was 20 Å longer in each dimension than the molecule and adding either Na⁺ or Cl⁻ ions to neutralize the system. The structures were then minimized for 500 steps with the solute–solvent potential set as U^ij. Copies of these minimized structure then underwent equilibration at each value of λ. The temperature of each of these systems was increased from 0 to 300 K in units of 25 K with 1000 steps of simulation time at each temperature.

3.4. Free Energy Derivatives

Computing ΔG_rep and ΔG_vdw for systems as large as these protein–protein complexes would require a great deal of computational time due to the drying of the molecular interior, so we instead adopted a procedure used in our previous publications,^24,34 computing the derivatives of ΔG_rep and ΔG_vdw with respect to the coordinates (x_i) of the centers of the fixed protein atoms

$$\partial \mathrm{\Delta }{G}_{\text{rep}}/\partial x_i={\langle \partial U_{\text{rep}}/\partial x_i\rangle }_{\text{rep}}$$ (25)

where this average was taken in the ensemble defined by U_rep, and

$$\partial \mathrm{\Delta }{G}_{\text{vdw}}/\partial x_i={\langle \partial U_{\text{att}}(1)/\partial x_i\rangle }_1$$ (26)

where these derivatives were computed from the same simulations used to compute the LRT and SSP estimates of ΔG_att. These derivatives were computed for each Cartesian coordinate of each protein atom with the rest of the coordinates held fixed.

If ΔG_rep and ΔG_vdw were linear functions of either A or V, as expected from eqs 6 and 7, then the slopes of plots of these quantities versus A would be γ_rep and γ_vdw, respectively. Similarly, if $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}$ were linear in ΔA, then plots of

$$\partial \mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}/\partial x_i=\partial \mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{c}}/\partial x_i-\partial \mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{b}}/\partial x_i-\partial \mathrm{\Delta }{G}_{\text{rep}}^{\mathrm{a}}/\partial x_i$$ (27)

$$\partial \mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}/\partial x_i=\partial \mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{c}}/\partial x_i-\partial \mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{b}}/\partial x_i-\partial \mathrm{\Delta }{G}_{\text{vdw}}^{\mathrm{a}}/\partial x_i$$ (28)

versus ΔA would have slopes of γ_rep and γ_vdw, respectively. Estimates of γ_rep and γ_vdw obtained from such plots are shown in Table 1.

4. RESULTS

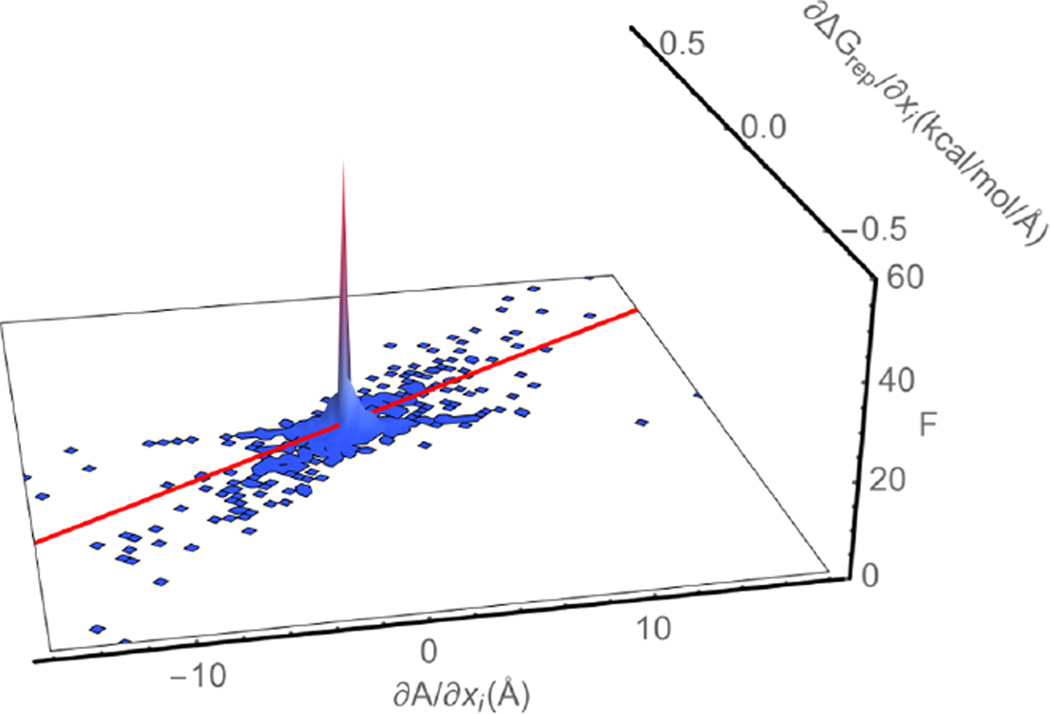
Table 1 gives estimates of γ_rep and γ_vdw obtained by fitting least-squares lines to plots of ∂ΔG_rep/∂x_i and ∂ΔG_vdw/∂x_i versus ∂A/∂x_i and $\partial \mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}/\partial x_i$ and $\partial \mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}/\partial x_i$ versus ∂ΔA/∂x_i. The Supporting Information contains these plots and analyses of the precision of the underlying quantities. If eqs 6–9 were valid, then the squares of the Pearson’s correlation coefficients (R²) would be close to 1, and the estimates of γ_rep and γ_vdw would be consistent from molecule to molecule as well as between estimates obtained from solvation free energies and those obtained from binding free energies. Instead, plots of ∂ΔG_rep/∂x_i and ∂ΔΔG_rep/∂x_i versus ∂A/∂x_i and ∂ΔA/∂x_i revealed very weak correlations between these quantities. Figure 1 shows a typical example of a plot of ∂ΔG_rep/∂x_i versus ∂A/∂x_i for one protein molecule. These findings are in agreement with our previous findings that the geometry and chemical environment of an atom’s surroundings affects how changes in that atom’s position change ΔG_rep.^24,34

Figure 1.

A plot of the probability density (F) of a given combination of the derivative (∂ΔG_rep/∂x_i) of the repulsive component (ΔG_rep) of the free energy required to insert an uncharged molecule into solution with respect to the atomic coordinates (x_i) and the derivative (∂A/∂x_i) of the solvent-accessible surface area (A) with respect to x_i for the second chain of the 1UDI complex. The red line is a least-squares line drawn through all of the points. Its slope provides an estimate of γ_rep for this protein, and it is equal to 0.022 kcal mol⁻¹ Å⁻². Those atoms for which both ∂ΔG_rep/∂x_i and ∂A/∂x_i were equal to 0 were not included when computing F. If they had been included, the peak in F would have been significantly larger.

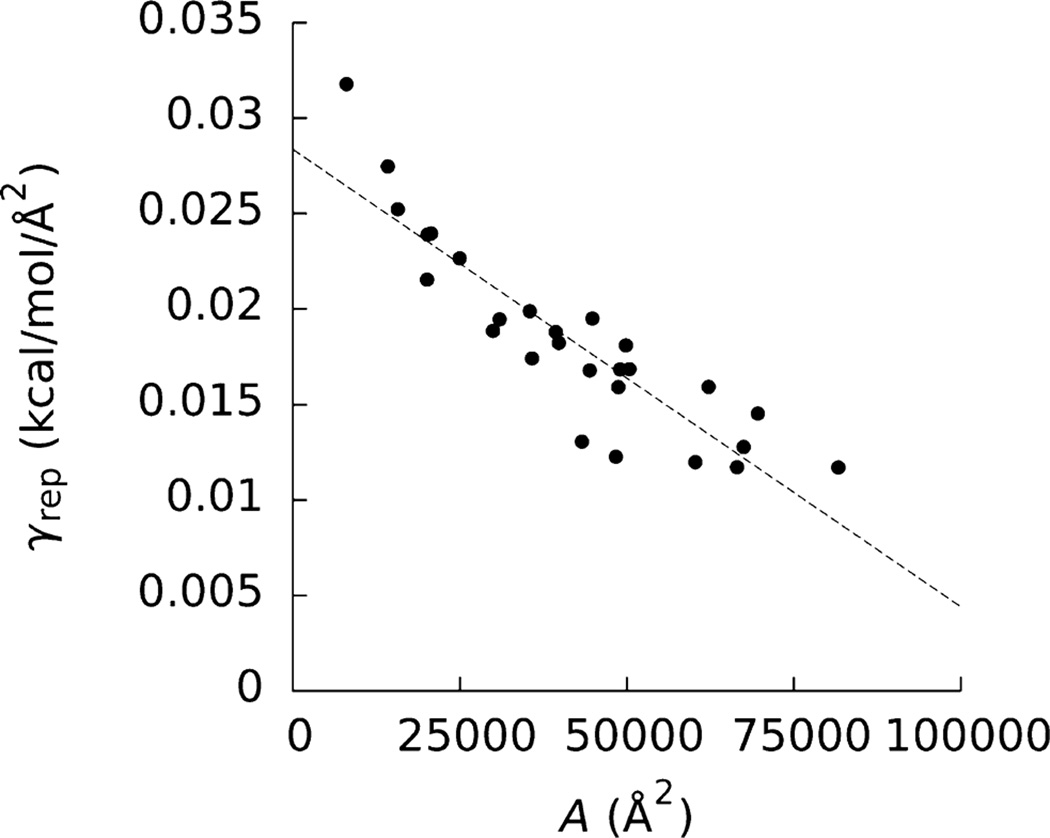
The estimates of γ_rep obtained from plots of ∂ΔG_rep/∂x_i versus ∂A/∂x_i not only differed between molecules but decreased with increasing A (Table 1 and Figure 2). These estimates of γ_rep ranged from 0.012 to 0.032 kcal mol⁻¹ Å⁻², and these values were generally smaller than those we found previously for decaalanine, decaglycine, and alkanes, which generally had smaller A than the proteins examined here.^24,34 This observation appears to contradict the notion that a critical A exists for which molecules with larger A have ΔG_rep that are linear in A and below which ΔG_rep is linear in V. This finding may indicate that the vicinity of the biomolecule becomes progressively “dryer” as the size of the cavity increases. Eq 7 is not consistent with these findings.

Figure 2.

Slopes (γ_rep) of the least-squares fit of the derivatives (∂G_rep/∂x_i) of the repulsive (ΔG_rep) component of the cavity-insertion energy (ΔG_vdw) with respect to the coordinates (x_i) of the atomic centers versus derivatives (∂A/∂x_i) of the solvent-accessible surface areas (A) with respect to x_i versus A for all complexes and components in this study.

Table 2 shows estimates of ΔG_att and ΔG_el for one of the complexes (1BRS) and its components and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}$, and ΔΔG_el for this complex given by FEP, TI, LRT, and SSP. These data show that the LRT gives good estimates of $\mathrm{\Delta }{G}_{\text{att}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$, and ΔΔG_att for this complex, confirming the validity of eq 1 for this complex. However, SSP gave estimates of $\mathrm{\Delta }{G}_{\text{att}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$, and ΔΔG_att that differed significantly from those given by FEP, indicating that eqs 3 and 4 were not valid for this system.

Table 2.

Attractive (ΔG_att) and Electrostatic Components (ΔG_el) of the Solvation Energy of the 1BRS Complex and Its Two Components and the Attractive ($\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ and ΔΔG_att) and Electrostatic ($\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$ and ΔΔG_el) Components of the Desolvation and Binding Free Energies^a

	$\mathrm{\Delta }{G}_{\text{att}}^a$	$\mathrm{\Delta }{G}_{\text{att}}^b$	$\mathrm{\Delta }{G}_{\text{att}}^c$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$	ΔΔGatt
forward FEP	−315	−259	−458	116	2
backward FEP	−312	−259	−458	113	−1
TI	−311	−260	−457	114	−1
LRT	−325	−267	−480	112	−2
SSP λ = 0	−165	−143	−218	89	−25
SSP λ = 1	−485	−392	−742	135	21
	$\mathrm{\Delta }{G}_{\text{el}}^a$	$\mathrm{\Delta }{G}_{\text{el}}^b$	$\mathrm{\Delta }{G}_{\text{el}}^c$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$	ΔΔGel
forward FEP	−1385	−1556	−2449	492	−17
backward FEP	−1387	−1558	−2443	501	−9
TI	−1388	−1562	−2448	501	−9
LRT	−1517	−1694	−2691	520	10
SSP λ = 1	−1528	−1670	−2678	520	10

^aThese energies were obtained by forward and backward free energy perturbation (FEP), thermodynamic integration (TI), linear response theory (LRT), and single-step perturbation (SSP) from either the beginning (λ = 0) or ends (λ = 1) of the integration. All energies are in units of kcal/mol.

The data in Table 2 show that the LRT yielded estimates of ΔG_el that were more than 100 kcal/mol different from those obtained with FEP, indicating that eq 2 is poor for this system. FEP estimates of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$ and ΔΔG_el also differed significantly from those given by LRT.

Table 3 shows the R², slopes, and y-intercepts of least-squares lines comparing various computed quantities for the 9 protein–protein complexes. All of these plots and analyses of the precisions of the resulting quantities are in the Supporting Information. These data show that the estimates of ΔG_att obtained from the LRT were highly correlated with A, but its estimates of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ and ΔΔG_att were not strongly correlated with ΔA, demonstrating that two theories can yield similar results for ΔG and very different results for ΔΔG.

Table 3.

Slopes (m), y-Intercepts (b), and the Squares of Pearson’s Correlation Factors (R²) of Least-Squares Lines of the Quantities Listed in the y-Column versus Those in the x-Column^a

x	y	R2	m	b
A	$\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$	0.992	−0.050	−19
ΔA	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt,desol}}$	0.64	−0.077	−33
ΔA	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$	0.25	−0.040	−77
$\mathrm{\Delta }{G}_{\text{att}}^{\text{SSP,0}}$	$\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$	0.97	3.4	203
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{SSP,0,desol}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt,desol}}$	0.64	1.60	−37
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{SSP,0}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$	0.38	0.89	19
$\mathrm{\Delta }{G}_{\text{att}}^{\text{SSP,1}}$	$\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$	0.9991	0.58	−38
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{SSP,1,desol}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt,desol}}$	0.97	0.60	35
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{SSP,1}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{lrt}}$	0.89	0.57	−10.5
$\mathrm{\Delta }{G}_{\text{el}}^{\text{SSP}}$	$\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt}}$	0.9997	1.01	16
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{SSP,desol}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt,desol}}$	0.99997	1.0007	2.0
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{SSP}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt}}$	0.9999	1	1.6
$\mathrm{\Delta }{G}_{\text{el}}^{\text{APBS}}$	$\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt}}$	0.96	1.03	−138
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{APBS,desol}}$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt,desol}}$	0.92	0.40	125
$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{APBS}}$	$\mathrm{\Delta }{G}_{\text{el}}^{\text{lrt}}$	0.42	−7.57	510

^aThe corresponding plots are in Supporting Information. All energies are in kcal/mol. All areas and changes in area are in units of Ų. All m and b are in the corresponding units.

Additionally, the data in Table 3 show that both eqs 3 and 4 produced estimates of ΔG_att that were highly correlated with those obtained from the LRT (R² > 0.97), but eq 3 systematically underestimated ΔG_att whereas eq 4 overestimated it. Table 3 also shows that the estimates of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ obtained from eq 3 were not highly correlated with those obtained from LRT. Conversely, the predictions of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ and ΔΔG_att obtained from eq 4 were reasonably well-correlated with those obtained from LRT, but these estimates were significantly larger than those obtained from LRT, indicating that combining these energy terms with the other components of ΔΔG could lead to unexpected results.

The data in Table 3 also show that the computations of $\mathrm{\Delta }{G}_{\text{el}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$, and ΔΔG_el given by SSP are very highly correlated (R² > 0.999) with those obtained from LRT. Therefore, if the LRT is sufficient to predict these quantities, then the SSP would be sufficient as well. Unfortunately, the results in Table 2 indicate that the LRT may not be sufficient for computing these quantities.

Table 3 also shows that the PBE yielded predictions ($\mathrm{\Delta }{G}_{\text{el}}^{\text{APBS}}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{APBS,desol}}$) of ΔG_el and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$ that were highly correlated with those obtained from the LRT, but its estimates $(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{APBS}})$ of ΔΔG_el were not correlated with those obtained from LRT (R² = 0.43). Once again, this finding shows that strong correlations between the predictions of ΔG given by two theories do not guarantee that the theories will produce highly correlated estimates of ΔΔG.

5. CONCLUSIONS

The calculations on protein–protein complexes presented in this paper allow us to draw some conclusions about the assumptions underlying CSMs. As in our previous work, eqs 6 and 7 were not consistent with the results. Neither ΔG_rep nor ΔG_vdw was proportional to A. Eqs 8 and 9 were inconsistent with our calculations. Neither $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}}$ nor $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}$ was proportional to ΔA. Apparently, the idea that either ΔG_vdw or ΔG_rep is linear in A and that the resulting ΔG_vdw can be combined with the ΔG_el obtained from CSMs to obtain good estimates of ΔG is not valid for protein–protein complexes.

Additionally, although these results show that none of ΔG_rep, ΔG_vdw, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rep}}^{\text{desol}},\text{ or }\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{vdw}}^{\text{desol}}$ are truly linear in A or ΔA, if we extract estimates of apparent γ_rep from the derivative plots described above, we find our estimates of γ_rep decrease with A. This finding contradicts the hypothesis that there is a well-defined A above which ΔG_rep is linear in A and below which ΔG_rep is linear in V for realistic biomolecular solutes.

We found that LRT was sufficient for estimating $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$, and ΔΔG_att. However, although the SSP using either eq 3 or 4 yielded estimates of ΔG_att that were correlated with those given by the LRT, and the predictions of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ and ΔΔG_att given by eq 4 were also correlated to those given by LRT, the magnitudes of these quantities were significantly different from those given by LRT. Whether such estimates would be sufficient for in turn estimating ΔΔG is therefore much less clear. Additionally, whereas ΔG_att was correlated with A, neither $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{att}}^{\text{desol}}$ nor ΔΔG_att was correlated with ΔA, highlighting the observation that two theories could produce correlated estimates of solvation free energies while producing uncorrelated estimates of binding free energies.

For the one protein in the data set where ΔG_el was obtained with FEP, this estimate differed by more than 100 kcal/mol from those given by SSP and LRT, and the corresponding estimate of ΔΔG_el obtained from FEP differed by more than 10 kcal/mol from those obtained from the LRT and SSP, implying that the LRT and SSP approximations may be problematic in some situations. However, for all of the complexes in the data set, the SSP gave estimates of $\mathrm{\Delta }{G}_{\text{el}},\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{el}}^{\text{desol}}$, and ΔΔG_el that were highly correlated with those given by the LRT. Therefore, if the LRT is a reasonable approximation for a system, the SSP is probably reasonable as well. These calculations will have to be repeated for other systems to determine how general are these conclusions.

In summary, many of the assumptions underlying common CSMs are brought into question by this work. The predictions yielded by often-used hydrophobic models disagreed with the results from FEP. LRT did not yield estimates of electrostatic energies that were consistent with those obtained with FEP. Furthermore, although the PBE yielded estimates of ΔG_el that were highly correlated with those obtained from FEP, its estimates of ΔΔG_el were not in good agreement with those obtained by FEP. In combination with our observation that ΔG_att was correlated with A but that ΔΔG_att was not, we can see that we cannot conclude that a theory will give good estimates of ΔΔG simply because its estimates of ΔG have some agreement with experimental data. Attempting to improve the estimates of ΔΔG given by CSMs by comparing their predictions of ΔG to experimental measurements may therefore not be productive.