OPERATOR NORM INEQUALITIES BETWEEN TENSOR UNFOLDINGS ON THE PARTITION LATTICE

Abstract

Interest in higher-order tensors has recently surged in data-intensive fields, with a wide range of applications including image processing, blind source separation, community detection, and feature extraction. A common paradigm in tensor-related algorithms advocates unfolding (or flattening) the tensor into a matrix and applying classical methods developed for matrices. Despite the popularity of such techniques, how the functional properties of a tensor changes upon unfolding is currently not well understood. In contrast to the body of existing work which has focused almost exclusively on matricizations, we here consider all possible unfoldings of an order-k tensor, which are in one-to-one correspondence with the set of partitions of {1, …, k}. We derive general inequalities between the l^p-norms of arbitrary unfoldings defined on the partition lattice. In particular, we demonstrate how the spectral norm (p = 2) of a tensor is bounded by that of its unfoldings, and obtain an improved upper bound on the ratio of the Frobenius norm to the spectral norm of an arbitrary tensor. For specially-structured tensors satisfying a generalized definition of orthogonal decomposability, we prove that the spectral norm remains invariant under specific subsets of unfolding operations.

1. Introduction

Tensors of order 3 or greater, known as higher-order tensors, have recently attracted increased attention in many fields across science and engineering. Methods built on tensors provide powerful tools to capture complex structures in data that lower-order methods may fail to exploit. Among numerous examples, tensors have been used to detect patterns in time-course data [7, 17, 22, 29] and to model higher-order cumulants [1, 2, 14]. However, tensor-based methods are fraught with challenges. Tensors are not simply matrices with more indices; rather, they are mathematical objects possessing multilinear algebraic properties. Indeed, extending familiar matrix concepts such as norms to tensors is non-trivial [12, 18], and computing these quantities has proven to be NP-hard [4–6].

The spectral relations between a general tensor and its lower-order counterparts have yet to be studied. There are generally two types of approaches underlying many existing tensor-based methods. The first approach flattens the tensor into a matrix and applies matrix-based techniques in downstream analyses, notably higher-order SVD [3, 10] and TensorFace [25]. Flattening is computationally convenient because of the ubiquity of well-established matrix-based methods, as well as the connection between tensor contraction and block matrix multiplication [19]. However, matricization leads to a potential loss of the structure found in the original tensor. This motivates the key question of how much information a flattening retains from its parent tensor.

The second approach either handles the tensor directly or unfolds it into objects of order-3 or higher. Recent work on bounding the spectral norm of sub-Gaussian tensors reveals that solving for the convex relaxation of tensor rank by unfolding is suboptimal [24]. Interestingly, in the context of tensor completion, unfolding a higher-order tensor into a nearly cubic tensor requires smaller sample sizes than matricization [28]. These results are probabilistic in nature and merely focus on a particular class of tensors. Assessing the general impact of unfolding operations on an arbitrary tensor and the role of the tensor’s intrinsic structure remains challenging.

The primary goal of this paper is to study the effect of unfolding operations on functional properties of tensors, where an unfolding is any lower-order representation of a tensor. We study the operator norm of a tensor viewed as a multilinear functional because this quantity is commonly used in both theory and applications, especially in tensor completion [15,28] and low-rank approximation problems [23, 27]. Given an order-k tensor, we represent each possible unfolding operation using a partition π of [k] = {1, …, k}, where a block in π corresponds to the set of modes that should be combined into a single mode. Each unfolding is a rearrangement of the elements of the original tensor into a tensor of lower order. Here we study the l^p operator norms of all possible tensor unfoldings, which together define what we coin a “norm landscape” on the partition lattice. A partial order relation between partitions enables us to find a path between an arbitrary pair of unfoldings and establish our main inequalities relating their operator norms. For specially-structured tensors satisfying a generalized definition of orthogonal decomposability, we show that the spectral norm (p = 2) remains invariant under unfolding operations corresponding to a specific subset of partitions. To our knowledge, our results represent the first attempt to provide a full picture of the norm landscape over all possible tensor unfoldings.

The remainder of this paper is organized as follows. In Section 2, we introduce some notation, and relate the spectral norm and the general l^p-norm of a tensor. We then describe in Section 3 general tensor unfoldings defined on the partition lattice. In Section 4, we present our main results on the inequalities between the operator norms of any two tensor unfoldings and describe how the norm landscape changes over the partition lattice. In Section 5, we generalize the notion of orthogonal decomposable tensors and prove that the spectral norm is invariant within a specific set of tensor unfoldings. We conclude in Section 6 with discussions about our findings and avenues of future work.

2. Higher-order tensors and their operator norms

An order-k tensor 𝒜 = 〚a_{i1 … ik}〛 ∈ 𝔽^{d₁×⋯×d_k} over a field 𝔽 is a hypermatrix with dimensions (d₁, …, d_k) and entries a_i1…ik ∈ 𝔽, for 1 ≤ i_n ≤ d_n, n = 1, …, k. In this paper, we focus on real tensors, 𝔽 = ℝ. The total dimension of 𝒜 is denoted by $\text{dim}(𝒜)={\prod }_{n=1}^k{d}_n$.

The vectorization of 𝒜, denoted Vec(𝒜), is defined as the operation rearranging all elements of 𝒜 into a column vector. For ease of notation, we use the shorthand [n] to denote the n-set {1, …, n} for n ∈ ℕ₊, and sometimes write ${\otimes }_{n=1}^k{\mathit{x}}_n={\mathit{x}}_1\otimes \cdots \otimes {\mathit{x}}_k$ when space is limited. We use S^d−1 = {x ∈ ℝ^d : ‖x‖₂ = 1} to denote the (d − 1)-dimensional unit sphere, and I_d to denote the d × d identity matrix.

For any two tensors 𝒜 = 〚a_{i1 … ik}〛, ℬ = 〚b_{i1 … ik}〛 ∈ ℝ^{d₁×⋯×d_k} of identical order and dimensions, their inner product is defined as

$$\langle 𝒜,ℬ\rangle =\sum _{i_1,\dots ,i_k}{a}_{i_1\dots i_k}{b}_{i_1\dots i_k},$$

while the tensor Frobenius norm of 𝒜 is defined as

$${\Vert 𝒜\Vert }_F=\sqrt{\langle 𝒜,𝒜\rangle }=\sqrt{\sum _{i_1,\dots ,i_k}{|a_{i_1\dots i_k}|}^2},$$

both of which are analogues of standard definitions for vectors and matrices.

Following [12], we define the covariant multilinear matrix multiplication of a tensor 𝒜 ∈ ℝ^{d₁×⋯×d_k} by matrices ${\mathit{M}}_1=(m_{i_1{j}_1}^{(1)})\in {ℝ}^{d_1\times s_1},\dots ,{\mathit{M}}_k=(m_{i_k{j}_k}^{(k)})\in {ℝ}^{d_k\times s_k}$ as

$$𝒜(M_1,\dots ,M_k)=〚\sum _{i_1=1}^{d_1}\cdots \sum _{i_k=1}^{d_k}{a}_{i_1\dots i_k}{m}_{i_1{j}_1}^{(1)}\cdots m_{i_k{j}_k}^{(k)}〛,$$

which results in an order-k tensor in ℝ^{s₁×⋯×s_k}. This operation multiplies the n^th mode of 𝒜 by the matrix M_n for all n ∈ [k]. Just as a matrix may be multiplied in up to two modes by matrices of consistent dimensions, an order-k tensor can be multiplied by up to k matrices in k modes. In the case of k = 2, 𝒜 is a matrix and $𝒜({\mathit{M}}_1,{\mathit{M}}_2)={\mathit{M}}_1^T𝒜{\mathit{M}}_2$. Sometimes we are interested in multiplying by vectors rather than matrices, in which case we obtain the k-multilinear functional 𝒜: ℝ^d₁×⋯× ℝ^d_k → ℝ given by

$$𝒜({\mathit{x}}_1,\dots ,{\mathit{x}}_k)=\sum _{i_1=1}^{d_1}\cdots \sum _{i_k=1}^{d_k}{a}_{i_1\dots i_k}{x}_{i_1}^{(1)}\cdots x_{i_k}^{(k)}=\langle 𝒜,{\mathit{x}}_1\otimes \cdots \otimes {\mathit{x}}_k\rangle ,$$ (1)

where ${\mathit{x}}_n={(x_1^{(n)},\dots ,x_{d_n}^{(n)})}^T\in {ℝ}^{d_n}$, n ∈ [k]. Note that multiplying by a vector in r modes in the manner defined in (1) reduces the order of the output tensor to k − r, whereas multiplying by matrices leaves the order unchanged. Although the coordinate representation of a tensor as a hypermatrix provides a concrete description, viewing it instead as a multilinear functional provides a coordinate-free, basis-independent perspective which allows us to better characterize the spectral relations among different tensor unfoldings.

We define the operator norm, or induced norm, of a tensor 𝒜 using the associated k-multilinear functional (1).

Definition 2.1 (Lim [12])

Let 𝒜 ∈ ℝ^{d₁×⋯×d_k} be an order-k tensor. For any 1 ≤ p ≤ ∞, the l^p-norm of the multilinear functional associated with 𝒜 is defined as

$${\Vert 𝒜\Vert }_p=\text{sup }\{\frac{𝒜({\mathit{x}}_1,\dots ,{\mathit{x}}_k)}{{\Vert {\mathit{x}}_1\Vert }_p\cdots {\Vert {\mathit{x}}_k\Vert }_p}:{\mathit{x}}_n\ne 0,{\mathit{x}}_n\in {ℝ}^{d_n},n\in [k]\}=\text{sup }\{𝒜({\mathit{x}}_1,\dots ,{\mathit{x}}_k):{\Vert {\mathit{x}}_n\Vert }_p=1,{\mathit{x}}_n\in {ℝ}^{d_n},n\in [k]\},$$ (2)

where ‖x_n‖_p denotes the vector l^p-norm of x_n.

Remark 2.2

The special case of p = 2 is called the spectral norm, frequently denoted ‖𝒜‖_σ. By (2), ‖𝒜‖_σ is the maximum value obtained as the inner product of the tensor 𝒜 with a rank-1 tensor, x₁ ⊗ ⋯ ⊗ x_n, of Frobenius norm 1 and of the same dimensions. This point of view provides an equivalent definition of ‖𝒜‖_σ as determining the best rank-1 tensor approximation to 𝒜, and we note that the rank-1 constraint becomes weaker as more unfolding is applied. See Section 4 for further details.

Because we restrict all entries of 𝒜 and ${\{{\mathit{x}}_n\}}_{n=1}^k$ to be real, we need not take the absolute value of 𝒜(x₁, …, x_k) as in [12]. It is worth mentioning that the notion of tensor l^p-norms defined by (2) are not extensions of the classical matrix l^p-norms when p ≠ 2. To see this, recall that for an m × n matrix A, one usually defines the l^p operator norm as

$${\Vert \mathit{A}\Vert }_p=\text{sup }\{\frac{{\Vert \mathit{A}\mathit{x}\Vert }_p}{{\Vert \mathit{x}\Vert }_p}:\mathit{x}\ne \mathbf{0},\mathit{x}\in {ℝ}^n\}.$$ (3)

In general (2) and (3) are not equal even for matrices, illustrated by the following example:

Example 2.3

Let A = 〚a_ij〛 be the 2 × 2 matrix $\mathit{A}=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 4\hfill \end{array}\right]$ and consider p = 1. Solving (3), we have

$${\Vert \mathit{A}\Vert }_1=\text{sup }\{\frac{{\Vert \mathit{A}\mathit{x}\Vert }_1}{{\Vert \mathit{x}\Vert }_1}:\mathit{x}\ne \mathbf{0},\mathit{x}\in {ℝ}^2\}=\underset{j}{\text{sup}}\sum _i|a_{ij}|=5.$$

However, instead using (2) gives

$${\Vert \mathit{A}\Vert }_1=\text{sup }\{\frac{{\mathit{x}}_1^T\mathit{A}{\mathit{x}}_2}{{\Vert {\mathit{x}}_1\Vert }_1{\Vert {\mathit{x}}_2\Vert }_1}:{\mathit{x}}_n\in {ℝ}^2,{\mathit{x}}_n\ne \mathbf{0},n\in [2]\}=\text{sup }\{{\mathit{x}}_1^T\mathit{A}{\mathit{x}}_2:{\mathit{x}}_n\in {ℝ}^2,{\Vert {\mathit{x}}_n\Vert }_1=1,n\in [2]\}=4,$$

which is neither the classical matrix l¹-norm (equal to 5), nor the entry-wise l¹-norm (equal to ∑_i,j |a_ij | = 6).

Throughout this paper, we adopt Definition 2.1 and always use ‖·‖_p to denote the l^p-norm defined therein, even for matrices. In fact, (3) defines an operator norm by viewing the matrix as a linear operator from ℝ^d₂ to ℝ^d₁, whereas (2) defines an operator norm in which the matrix defines a bilinear functional from ℝ^d₁ × ℝ^d₂ to ℝ. These two definitions are equivalent when p = 2, but otherwise represent two different operators and result in two distinct operator norms. To be consistent with our treatment of tensors as k-multilinear functionals, we formulate matrices as bilinear functionals.

For a given tensor, its l^p-norm and l^q-norm mutually control each other, and the comparison bound is polynomial in the total dimension of the tensor, $\text{dim}(𝒜)={\prod }_{n=1}^k{d}_n$.

Proposition 2.4 (l^p-norm vs. l^q-norm)

Let 𝒜 ∈ ℝ^{d₁× ⋯ ×d_k} be an order-k tensor. Suppose ‖·‖_p and ‖·‖_q are two norms defined in (2) with q ≥ p ≥ 1. Then,

$${\Vert 𝒜\Vert }_p\le {\Vert 𝒜\Vert }_q\le \text{dim}{(𝒜)}^{\frac{1}{p}-\frac{1}{q}}{\Vert 𝒜\Vert }_p.$$

Proof

Starting from Definition 2.1, we have

$${\Vert 𝒜\Vert }_q=\text{sup }\{\frac{𝒜({\mathit{x}}_1,\dots ,{\mathit{x}}_k)}{{\Vert {\mathit{x}}_1\Vert }_q\cdots {\Vert {\mathit{x}}_k\Vert }_q}:{\mathit{x}}_n\ne \mathbf{0},{\mathit{x}}_n\in {ℝ}^{d_n},n\in [k]\}=\text{sup }\{\frac{𝒜({\mathit{x}}_1,\dots ,{\mathit{x}}_k)}{{\Vert {\mathit{x}}_1\Vert }_p\cdots {\Vert {\mathit{x}}_k\Vert }_p}\times \frac{{\Vert {\mathit{x}}_1\Vert }_p\cdots {\Vert {\mathit{x}}_k\Vert }_p}{{\Vert {\mathit{x}}_1\Vert }_q\cdots {\Vert {\mathit{x}}_k\Vert }_q}:{\mathit{x}}_n\ne \mathbf{0},{\mathit{x}}_n\in {ℝ}^{d_n},n\in [k]\}.$$ (4)

For any q ≥ p ≥ 1, the equivalence of vector norms tells us

$${\Vert \mathit{x}\Vert }_q\le {\Vert \mathit{x}\Vert }_p\le d^{\frac{1}{p}-\frac{1}{q}}{\Vert \mathit{x}\Vert }_q,\text{ for all }\mathit{x}\in {ℝ}^d.$$ (5)

Applying (5) to x_n, for n ∈ [k], gives

$$1\le \prod _{n=1}^k\frac{{\Vert {\mathit{x}}_n\Vert }_p}{{\Vert {\mathit{x}}_n\Vert }_q}\le {\left(\prod _{n=1}^k{d}_n\right)}^{\frac{1}{p}-\frac{1}{q}}.$$ (6)

Inserting (6) into (4) and noting $\text{dim}(𝒜)={\prod }_{n=1}^k{d}_n$, we find

$${\Vert 𝒜\Vert }_p\le {\Vert 𝒜\Vert }_q\le \text{dim}{(𝒜)}^{\frac{1}{p}-\frac{1}{q}}{\Vert 𝒜\Vert }_p,$$

which completes the proof.

3. Partitions and general tensor unfoldings

Any higher-order tensor can be transformed into different lower-order tensors by modifying its indices in various ways. The most common transformations are n-mode flattenings, or matricizations, which rearrange the elements of an order-k tensor into a d_n × ∏_i≠n d_i matrix. For example, the n-mode matricization of a tensor 𝒜 ∈ ℝ^{d₁×⋯×d_k} is obtained by mapping the fixed tensor index (i₁, …, i_k) to the matrix index (i_n, m), where

$$m=1+\prod _{a\in [k],a\ne n}(i_a-1)J_a,\text{ where }{J}_a=\prod _{l\in [a-1],l\ne n}{d}_l.$$ (7)

Recently there has been much interest in studying the relationship between tensors and their matrix flattenings [9]. We present here a more general analysis by considering all possible lower-order tensor unfoldings rather than just matricizations. Using the blocks of a partition of [k] to specify which modes are combined into a single mode of the new tensor, we establish a one-to-one correspondence between the set of all partitions of [k] and the set of lower-order tensor unfoldings. The partition lattice then describes the underlying relationship between possible tensor unfoldings of a tensor 𝒜.

For any k ∈ ℕ₊, a partition π of [k] is a collection $\{B_1^{\pi },B_2^{\pi },\dots ,B_{\ell }^{\pi }\}$ of disjoint, nonempty subsets (or blocks) $B_i^{\pi }$ satisfying ${\cup }_{i=1}^{\ell }{B}_i^{\pi }=[k]$. The set of all partitions of [k] is denoted 𝒫_[k]. We use |π| to denote the number of blocks in π, and $|B_i^{\pi }|$ to denote the number of elements in $B_i^{\pi }$. We say that a partition π is a level-ℓ partition if |π| = ℓ. The set of all level-ℓ partitions of [k] is denoted by ${𝒫}_{[k]}^{\ell }$, which is a set of S(k, ℓ) elements, where S(k, ℓ) is the Stirling number of the second kind.

The following partial order naturally relates partitions satisfying a basic compatibility constraint and the resulting structure plays a key role in our work.

Definition 3.1 (Partition Lattice)

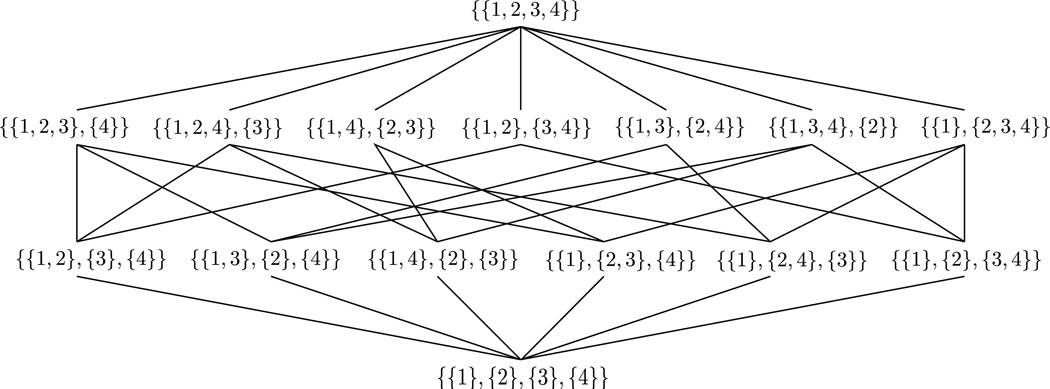
A partition π₁ ∈ 𝒫_[k] is called a refinement of π₂ ∈ 𝒫_[k] if each block of π₁ is a subset of some block of π₂; conversely, π₂ is said to be a coarsening of π₁. This relationship defines a partial order, expressed as π₁ ≤ π₂, and we say that π₁ is finer than π₂ while π₂ is coarser than π₁. If either π₁ ≤ π₂ or π₂ ≤ π₁, then π₁ and π₂ are comparable. According to this partial order, the least element of 𝒫_[k] is 0_[k] ≔ {{1}, …, {k}}, while the greatest element is 1_[k] ≔ {{1, …, k}}. Equipped with this notion, 𝒫_[k] generates a partition lattice by connecting any two comparable partitions that differ by exactly one level. An example is illustrated in Figure 1. Henceforth, 𝒫_[k] may represent either the set of all partitions of [k] or the partition lattice it generates depending on context.

Figure 1.

The partition lattice 𝒫_[4].

It is clear that many partitions are not comparable, including every pair of distinct partitions at the same level. To consider arbitrary partitions in tandem, we require an extension of this partial order. In general, for any two partitions π₁, π₂ ∈ 𝒫_[k], we define their greatest lower bound π₁ ∧ π₂ as

$${\pi }_1\wedge {\pi }_2≔\text{sup}\{\pi \in {𝒫}_{[k]}:\pi \le {\pi }_1,\pi \le {\pi }_2\}.$$

More concretely, π₁ ∧ π₂ consists of the collection of all nonempty intersections of blocks in π₁ and π₂ and is unique for a given pair (π₁, π₂).

Example 3.2

Figure 1 illustrates 𝒫_[4] in lattice form. Recall that an edge connects two partitions if and only if they are comparable and their levels differ by exactly one. Partitions are comparable if and only if there exists a non-reversing path between them. To clarify the components of Definition 3.1, take π₁ = {{1, 4}, {2, 3}} and π₂ = {{1, 3, 4}, {2}}. Then π₁ ∧ π₂ = {{1, 4}, {2}, {3}}, 0_[4] = {{1}, {2}, {3}, {4}}, and 1_[4] = {{1, 2, 3, 4}}.

The following definition generalizes the concept of n-mode flattenings defined in (7) to general unfoldings induced by arbitrary partitions π ∈ 𝒫_[k].

Definition 3.3 (General Tensor Unfolding)

Let 𝒜 ∈ ℝ^{d₁×⋯×d_k} be an order-k tensor and $\pi =\{B_1^{\pi },\dots ,B_{\ell }^{\pi }\}\in {𝒫}_{[k]}$. The partition π defines a mapping ${\varphi }_{\pi }:[d_1]\times \cdots \times [d_k]\to [{\prod }_{j\in B_1^{\pi }}{d}_j]\times \cdots \times [{\prod }_{j\in B_{\ell }^{\pi }}{d}_j]$ such that

$${\varphi }_{\pi }(i_1,\dots ,i_k)=(m_1,\dots ,m_{\ell }),$$ (8)

where

$$m_j=1+\prod _{r\in B_j^{\pi }}(i_r-1)J_r,\text{ where }{J}_r=\prod _{l\in B_j^{\pi },l<r}{d}_l,\text{ for all }j\in [\ell ].$$

Clearly, ϕ_π is a one-to-one mapping, so its inverse ${\varphi }_{\pi }^{-1}$ is well defined. Thus ϕ_π induces an unfolding action 𝒜 ↦ Unfold_π(𝒜) such that

$${({\text{Unfold}}_{\pi }(𝒜))}_{(m_1,\dots ,m_{\ell })}={(𝒜)}_{{\varphi }_{\pi }^{-1}(m_1,\dots ,m_{\ell })},$$

for all $(m_1,\dots ,m_{\ell })\in [{\prod }_{j\in B_1^{\pi }}{d}_j]\times \cdots \times [{\prod }_{j\in B_{\ell }^{\pi }}{d}_j]$ or, equivalently,

$${({\text{Unfold}}_{\pi }(𝒜))}_{{\varphi }_{\pi }(i_1,\dots ,i_k)}={(𝒜)}_{(i_1,\dots ,i_k)},$$

for all (i₁, …, i_k) ∈ [d₁]×⋯× [d_k]. Thus Unfold_π(𝒜) is an order-ℓ tensor of dimensions $({\prod }_{i\in B_1^{\pi }}{d}_i,\dots ,{\prod }_{i\in B_{\ell }^{\pi }}{d}_i)$, and we call it the tensor unfolding of 𝒜 induced by π.

Remark 3.4

By the definition of ϕ_π in (8), Unfold_0[k](𝒜) = 𝒜 and Unfold_1[k](𝒜) = Vec(𝒜).

Example 3.5

Consider an order-4 tensor 𝒜 = 〚a_ijkl〛 ∈ ℝ^2×2×2×2. We provide a subset of the possible tensor unfoldings to elucidate both the manner in which the operation works and the natural association with partitions.

• For π = {{1, 2}, {3}, {4}}, Unfold_π(𝒜) is an order-3 tensor of dimensions (4, 2, 2) with entries given by

  $${({\text{Unfold}}_{\pi }(𝒜))}_{1kl}=a_{11kl},{({\text{Unfold}}_{\pi }(𝒜))}_{2kl}=a_{12kl},$$

  $${({\text{Unfold}}_{\pi }(𝒜))}_{3kl}=a_{21kl},{({\text{Unfold}}_{\pi }(𝒜))}_{4kl}=a_{22kl},$$

  for all (k, l) ∈ [2] × [2].
• For π = {{1, 2}, {3, 4}}, Unfold_π(𝒜) is a 4 × 4 matrix

  $${\text{Unfold}}_{\pi }(𝒜)=\left(\begin{array}{cccc}\hfill a_{1111}\hfill & \hfill a_{1112}\hfill & \hfill a_{1121}\hfill & \hfill a_{1122}\hfill \\ \hfill a_{1211}\hfill & \hfill a_{1212}\hfill & \hfill a_{1221}\hfill & \hfill a_{1222}\hfill \\ \hfill a_{2111}\hfill & \hfill a_{2112}\hfill & \hfill a_{2121}\hfill & \hfill a_{2122}\hfill \\ \hfill a_{2211}\hfill & \hfill a_{2212}\hfill & \hfill a_{2221}\hfill & \hfill a_{2222}\hfill \end{array}\right).$$
• For π = {{1, 2, 3}, {4}}, Unfold_π(𝒜) is a 8 × 2 matrix

  $${\text{Unfold}}_{\pi }(𝒜)=\left(\begin{array}{cc}\hfill a_{1111}\hfill & \hfill a_{1112}\hfill \\ \hfill a_{1121}\hfill & \hfill a_{1122}\hfill \\ \hfill a_{1211}\hfill & \hfill a_{1212}\hfill \\ \hfill a_{1221}\hfill & \hfill a_{1222}\hfill \\ \hfill a_{2111}\hfill & \hfill a_{2112}\hfill \\ \hfill a_{2121}\hfill & \hfill a_{2122}\hfill \\ \hfill a_{2211}\hfill & \hfill a_{2212}\hfill \\ \hfill a_{2221}\hfill & \hfill a_{2222}\hfill \end{array}\right).$$

Remark 3.6

There are different conventions to order the elements within each transformed mode. In principle, the ordering of elements within each transformed mode is irrelevant, so we do not explicitly spell out their orderings hereafter.

Remark 3.7

The unfolding operation leaves the Frobenius norm unchanged; that is, ‖𝒜‖_F = ‖Unfold_π(𝒜)‖_F for all π ∈ 𝒫_[k]. More generally, the inner product remains invariant under all unfoldings: 〈𝒜, ℬ〉 = 〈Unfold_π(𝒜), Unfold_π(ℬ)〉 for all π ∈ 𝒫_[k], where 𝒜, ℬ ∈ ℝ^{d₁×⋯×d_k} are two order-k tensors of the same dimensions.

4. Operator norm inequalities on the partition lattice

In this section, we compare the operator norms of different unfoldings of a tensor, in particular relative to that of the original tensor. We first focus on the spectral norm (p = 2) and then discuss extensions to general l^p-norms.

Recall that for an order-k tensor 𝒜 ∈ ℝ^{d₁×⋯×d_k}, its spectral norm is defined as

$${\Vert 𝒜\Vert }_{\sigma }=\text{sup }\{𝒜({\mathit{x}}_1,\dots ,{\mathit{x}}_k):{\Vert {\mathit{x}}_n\Vert }_2=1,{\mathit{x}}_n\in {ℝ}^{d_n},n\in [k]\}.$$ (9)

The maximization of the polynomial form 𝒜(x₁, …, x_k) on the unit sphere is closely related to the best, in the least-square sense, rank-1 tensor approximation. Specifically, for an order-k tensor 𝒜 ∈ ℝ^{d₁×⋯×d_k}, the problem of determining the spectral norm is equivalent to finding a scalar λ and a rank-1 norm-1 tensor x₁ ⊗⋯⊗ x_k that minimize the function

$$f({\mathit{x}}_1,\dots ,{\mathit{x}}_k)={\Vert 𝒜-\lambda {\mathit{x}}_1\otimes \cdots \otimes {\mathit{x}}_k\Vert }_F.$$

The corresponding value of λ is equal to ‖𝒜‖_σ. Since x₁ ⊗⋯⊗ x_k must have the same order and dimensions as 𝒜, the rank-1 condition becomes less strict the more unfolded the tensor. In particular, for the vectorized unfolding, Vec(𝒜), the best rank-1 tensor approximation is simply Vec(𝒜) itself. For unfoldings into a matrix, Mat(𝒜), the best rank-1 approximation is the outer product of the leading left and the right singular vectors of Mat(𝒜). For higher-order unfoldings, the closed form of the best rank-1 approximation is not known in general. Nevertheless, the set of the rank-1 tensors over which the supremum is taken in (9) becomes more restricted. This observation implies that the spectral norm of a tensor unfolding decreases as the order of the unfolded tensor increases; that is, the spectral norm preserves the partial order on partitions.

Proposition 4.1 (Monotonicity)

For all partitions π₁, π₂ ∈ 𝒫_[k] satisfying π₁ ≤ π₂,

$${\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }.$$

In particular, we have the global extrema

$${\Vert 𝒜\Vert }_{\sigma }={\Vert {\text{Unfold}}_{0_{[k]}}(𝒜)\Vert }_{\sigma }=\underset{\pi \in {𝒫}_{[k]}}{\text{min}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma },$$

$${\Vert 𝒜\Vert }_F={\Vert {\text{Unfold}}_{1_{[k]}}(𝒜)\Vert }_{\sigma }=\underset{\pi \in {𝒫}_{[k]}}{\text{max}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }.$$

Proof

Suppose π₁, π₂ ∈ 𝒫_[k], and π₁ is a one-step refinement of π₂. Without loss of generality, assume π₂ is obtained by merging two blocks B₁, B₂ ∈ π₁ into a single block B ∈ π₂. Let Unfold_π1(𝒜) ∈ ℝ^{d₁×⋯×d_ℓ} denote the tensor unfolding induced by π₁ = {B₁, …, B_ℓ}. Then, Unfold_π2(𝒜) is a (d₁ · d₂, d₃, …, d_ℓ)-dimensional tensor. By definition of the spectral norm,

$${\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }=\text{sup }\{\langle {\text{Unfold}}_{{\pi }_1}(𝒜),{\mathit{x}}_1\otimes \cdots \otimes {\mathit{x}}_{\ell }\rangle :{\mathit{x}}_n\in S^{d_n-1},n\in [\ell ]\}=\text{sup }\{\langle {\text{Unfold}}_{{\pi }_2}(𝒜),\text{Vec}({\mathit{x}}_1\otimes {\mathit{x}}_2)\otimes {\mathit{x}}_3\otimes \cdots \otimes {\mathit{x}}_{\ell }\rangle :{\mathit{x}}_n\in S^{d_n-1},n\in [\ell ]\}\le \text{sup }\{\langle {\text{Unfold}}_{{\pi }_2}(𝒜),\mathit{y}\otimes {\mathit{x}}_3\cdots \otimes {\mathit{x}}_{\ell }\rangle :\mathit{y}\in S^{d_1·d_2-1},{\mathit{x}}_n\in S^{d_n-1},n=3,\dots ,\ell \}={\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma },$$

where the third line comes from the fact that the set {Vec(x₁ ⊗ x₁) : (x₁, x₂) ∈ S^d₁−1 × S^d₂−1} is contained in the set {y : y ∈ S^{d₁·d₂−1}}.

In general, if π₁ ≤ π₂, we can obtain Unfold_π2(𝒜) from Unfold_π1(𝒜) by a series of single unfoldings. Hence, applying the above arguments to these successive unfoldings gives the desired result.

The following lemma will play a key role in proving our main results:

Lemma 4.2 (One-Step Inequality)

For 1 < ℓ ≤ k, let ℬ ∈ ℝ^{d₁×⋯×d_ℓ} be an order-ℓ tensor unfolding of an order-k tensor 𝒜 induced by the partition {B₁, …, B_ℓ} ∈ 𝒫_[k], and let 𝒞 be an order-(ℓ − 1) tensor unfolding of ℬ induced by merging blocks B_i and B_j for some i, j ∈ [ℓ]. Then,

$$\text{min }{(d_i,d_j)}^{-1/2}{\Vert 𝒞\Vert }_{\sigma }\le {\Vert ℬ\Vert }_{\sigma }\le {\Vert 𝒞\Vert }_{\sigma }.$$ (10)

Proof

The upper bound follows readily from Proposition 4.1. To prove the lower bound, without loss of generality, assume 𝒞 corresponds to the merging of blocks B_ℓ−1 and B_ℓ so that 𝒞 is a (d₁, …, d_ℓ−2, d_ℓ−1·d_ℓ)-dimensional tensor. Note that S^d₁−1 ×⋯× S^{d_ℓ−2−1} × S^{d_ℓ−1d_ℓ−1} is a compact set, so the supremum (9) is attained in that set for 𝒞. Then, there exists $({\mathit{x}}_1^{*},\dots ,{\mathit{x}}_{\ell -2}^{*},{\mathit{y}}^{*})\in S^{d_1-1}\times \cdots \times S^{d_{\ell -2}-1}\times S^{d_{\ell -1}{d}_{\ell }-1}$ such that

$${\Vert 𝒞\Vert }_{\sigma }=\langle 𝒞,{\mathit{x}}_1^{*}\otimes \cdots \otimes {\mathit{x}}_{\ell -2}^{*}\otimes {\mathit{y}}^{*}\rangle .$$ (11)

Define ${𝒞}^{*}=𝒞({\mathit{x}}_1^{*},\dots ,{\mathit{x}}_{\ell -2}^{*},{\mathit{I}}_{d_{\ell -1}{d}_{\ell }})\in {ℝ}^{d_{\ell -1}{d}_{\ell }}$. By the self duality of the Frobenius norm in ℝ^{d_ℓ−1d_ℓ}, we can rewrite (11) as

$${\Vert 𝒞\Vert }_{\sigma }=\text{sup }\{\langle {𝒞}^{*},\mathit{y}\rangle :\mathit{y}\in S^{d_{\ell -1}{d}_{\ell }-1}\}={\Vert {𝒞}^{*}\Vert }_F.$$ (12)

On the other hand, if we define $\text{Mat}({𝒞}^{*})≔ℬ({\mathit{x}}_1^{*},\dots ,{\mathit{x}}_{\ell -2}^{*},{\mathit{I}}_{\ell -1},{\mathit{I}}_{\ell })\in {ℝ}^{d_{\ell -1}\times d_{\ell }}$, then 𝒞* is simply the vectorization of Mat(𝒞*). Hence, by Remark 3.7, we obtain

$${\Vert {𝒞}^{*}\Vert }_F={\Vert \text{Mat}({𝒞}^{*})\Vert }_F.$$ (13)

Using the definition of Mat(𝒞*), we can write

$${\Vert ℬ\Vert }_{\sigma }\ge \text{sup }\{\langle ℬ,{\mathit{x}}_1^{*}\otimes {\mathit{x}}_2^{*}\otimes \cdots \otimes {\mathit{x}}_{\ell -2}^{*}\otimes {\mathit{x}}_{\ell -1}\otimes {\mathit{x}}_{\ell }\rangle :({\mathit{x}}_{\ell -1},{\mathit{x}}_{\ell })\in S^{d_{\ell -1}-1}\times S^{d_{\ell }-1}\}=\text{sup }\{\langle \text{Mat}({𝒞}^{*}),{\mathit{x}}_{\ell -1}\otimes {\mathit{x}}_{\ell }\rangle :({\mathit{x}}_{\ell -1},{\mathit{x}}_{\ell })\in S^{d_{\ell -1}-1}\times S^{d_{\ell }-1}\}={\Vert \text{Mat}({𝒞}^{*})\Vert }_{\sigma }.$$ (14)

Recall that Mat(𝒞*) is a matrix of size d_ℓ−1 × d_ℓ, meaning [8]

$${\Vert \text{Mat}({𝒞}^{*})\Vert }_{\sigma }\ge \text{min }{(d_{\ell -1},d_{\ell })}^{-1/2}{\Vert \text{Mat}({𝒞}^{*})\Vert }_F.$$ (15)

Using (14) in conjunction with (15), (13), and (12), we then obtain

$${\Vert ℬ\Vert }_{\sigma }\ge \text{min }{(d_{\ell -1},d_{\ell })}^{-1/2}{\Vert \text{Mat}({𝒞}^{*})\Vert }_F=\text{min }{(d_{\ell -1},d_{\ell })}^{-1/2}{\Vert {𝒞}^{*}\Vert }_F=\text{min }{(d_{\ell -1},d_{\ell })}^{-1/2}{\Vert 𝒞\Vert }_{\sigma },$$

which proves the lower bound.

Remark 4.3

Both bounds in the one-step inequality (10) are sharp. The sharpness of the upper bound will be discussed in Section 5. For the lower bound, consider an order-ℓ tensor unfolding $ℬ=({\sum }_{i=1}^{d_1}{\mathit{e}}_{1,i}\otimes {\mathit{e}}_{2,i})\otimes 𝒟\in {ℝ}^{d_1\times d_2\times \cdots \times d_{\ell }}$, where {e_1,i : i ∈ [d₁]} is the standard orthonormal basis of ℝ^d₁, {e_2,i : i ∈ [d₁]} is a set of d₁ standard basis vectors in ℝ^d₂, and 𝒟 is an arbitrary (d₃, …, d_ℓ)-dimensional tensor. Assume d₁ ≤ d₂ and consider the two blocks B₁ = {1}, B₂ = {2}. By the unfolding operation specified in Lemma 4.2 with B₁ and B₂, $𝒞=({\sum }_{i=1}^{d_1}\text{Vec}({\mathit{e}}_{1,i}\otimes {\mathit{e}}_{2,i}))\otimes 𝒟\in {ℝ}^{d_1·d_2\times d_3\times \cdots \times d_{\ell }}$, which is an order-(ℓ − 1) tensor unfolding by merging the first two modes of ℬ into a single mode. It follows that ‖ℬ‖_σ = ‖𝒟‖_σ and ${\Vert 𝒞\Vert }_{\sigma }=\sqrt{d_1}{\Vert 𝒟\Vert }_{\sigma }$, and therefore the left-hand-side inequality in (10) is saturated.

More generally, we can establish inequalities relating the spectral norms of two tensor unfoldings corresponding to two arbitrary partitions π₁, π₂ ∈ 𝒫_[k] that are not necessarily comparable. To do so, we must first introduce the following definition.

Definition 4.4

Given an order-k tensor 𝒜 ∈ ℝ^{d₁×⋯×d_k}, we define the map dim_𝒜 : 𝒫_[k] ×𝒫_[k] → ℕ₊ as

$${\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)=\prod _{B\in {\pi }_1}\underset{B\prime \in {\pi }_2}{\text{max}}{D}_{𝒜}(B,B\prime ),\text{ where }{D}_{𝒜}(B,B\prime )=\prod _{n\in B\cap B\prime }{d}_n,$$

where π₁, π₂ ∈ 𝒫_[k].

We label this quantity as dim_𝒜(·, ·) because it involves a product of a subset of the dimensions of 𝒜, and dim_𝒜(π₁, π₂) ≤ dim(𝒜) with equality only when π₁ = π₁ ∧ π₂. Intuitively, dim_𝒜(π₁, π₂) reflects the overlap between the unfoldings induced by π₁ and π₁ ∧ π₂. Example 4.6 presents a concrete illustration.

Remark 4.5

We set D_𝒜(B, B′) = 0 when B ∩ B′ = ∅. This does not affect the multiplication in Definition 4.4 because a block of π₁ cannot be disjoint from every block of π₂. Note that D_𝒜(B, B′) = D_𝒜(B′, B), but in general dim_𝒜(π₁, π₂) ≠ dim_𝒜(π₂, π₁).

Example 4.6

To illustrate the above map, let 𝒜 ∈ ℝ^{d₁×d₂×d₃×d₄} and consider the partitions π₁ = {{1, 2}, {3, 4}} and π₂ = {{1, 2, 3}, {4}}, for which π₁∧π₂ = {{1, 2}, {3}, {4}}. From Definition 4.4,

$$D_{𝒜}(\{1,2\},\{1,2,3\})=d_1{d}_2$$

$$D_{𝒜}(\{3,4\},\{1,2,3\})=d_3$$

$$D_{𝒜}(\{1,2\},\{4\})=0$$

$$D_{𝒜}(\{3,4\},\{4\})=d_4.$$

Then,

$${\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)=\text{max }\{D_{𝒜}(\{1,2\},\{1,2,3\}),D_{𝒜}(\{1,2\},\{4\})\}\times \text{max }\{D_{𝒜}(\{3,4\},\{1,2,3\}),D_{𝒜}(\{3,4\},\{4\})\}=d_1{d}_2\text{max}\{d_3,d_4\}.$$

Exchanging arguments, we find

$${\text{dim}}_{𝒜}({\pi }_2,{\pi }_1)=\text{max }\{D_{𝒜}(\{1,2,3\},\{1,2\}),D_{𝒜}(\{1,2,3\},\{3,4\})\}\times \text{max }\{D_{𝒜}(\{4\},\{1,2\}),D_{𝒜}(\{4\},\{3,4\})\}=d_4\text{ max}\{d_1{d}_2,d_3\}.$$

Remark 4.7

As in Lemma 4.2, if π₂ is a one-step coarsening of π₁ obtained by merging two blocks $B_i^{{\pi }_1}$ and $B_j^{{\pi }_1}$ of dimensions d_i and d_j into a single block $B_1^{{\pi }_2}$, then

$$D_{𝒜}(B_i^{{\pi }_1},B_1^{{\pi }_2})=d_i,$$

$$D_{𝒜}(B_j^{{\pi }_1},B_1^{{\pi }_2})=d_j.$$

Hence, Lemma 4.2 can be written as

$$\text{min }{\{D_{𝒜}(B_i^{{\pi }_1},B_1^{{\pi }_2}),D_{𝒜}(B_j^{{\pi }_1},B_1^{{\pi }_2})\}}^{-1/2}{\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }.$$

Having introduced Definition 4.4, we can now state our main result on how the spectral norms of two arbitrary unfoldings of a tensor are related:

Theorem 4.8 (Spectral norm inequalities)

Let 𝒜 ∈ ℝ^{d₁×⋯×d_k} be an arbitrary order-k tensor, and π₁, π₂ any two partitions in 𝒫_[k]. Then,

$${\left[\frac{\text{dim}(𝒜)}{{\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)}\right]}^{-1/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }\le {\left[\frac{\text{dim}(𝒜)}{{\text{dim}}_{𝒜}({\pi }_2,{\pi }_1)}\right]}^{1/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }.$$

Remark 4.9

1. Note that π₁ and π₂ need not be comparable.

2. If d_n = d for all n ∈ [k], then the result reduces to

   $$d^{-c_1/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }\le d^{c_2/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma },$$

   where c₁ = (k − ∑_B∈π1 max_B′∈π2 |B ∩ B′|) and c₂ = (k − ∑_B∈π2 max_B′∈π1 |B ∩ B′|).

3. For k = 4, the above inequalities in (b) are sharp. For example, consider the tensor 𝒜 = I_d ⊗ I_d, and partitions π = {{1, 2}, {3, 4}} and π′ = {{1}, {2}, {3}, {4}}, for which we have ‖Unfold_π(𝒜)‖_σ = d and ‖Unfold_π′(𝒜)‖_σ = 1. If π₁ = π and π₂ = π′, then c₁ = 2 and d^−c₁/2 ‖Unfold_π1(𝒜)‖_σ = ‖Unfold_π2(𝒜)‖_σ. On the other hand, if π₁ = π′ and π₂ = π, then we have c₂ = 2 and ‖Unfold_π2(𝒜)‖_σ = d^c₂/2 ‖Unfold_π1(𝒜)‖_σ. This particular tensor is further discussed later in Example 4.15.

Proof of Theorem 4.8

The main idea is to apply Lemma 4.2 to some appropriate sequence of partitions connecting π₁ and π₂ in the partition lattice. To do so, we consider Unfold_π1∧π2(𝒜) and compare its spectral norm to that of Unfold_π1(𝒜). Since π₁ ∧ π₂ ≤ π₁, from Proposition 4.1 we have

$${\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }.$$ (16)

Let ${\pi }_1=\{B_i^{{\pi }_1}:i\in [{\ell }_1]\}$ and ${\pi }_2=\{B_j^{{\pi }_2}:j\in [{\ell }_2]\}$, and note that ${\pi }_1\wedge {\pi }_2=\{B_i^{{\pi }_1}\cap B_j^{{\pi }_2}:i\in [{\ell }_1],j\in [{\ell }_2]\}$. Now, order the blocks in π₂ such that

$$D_{𝒜}(B_1^{{\pi }_1},B_{m_1}^{{\pi }_2})\ge D_{𝒜}(B_1^{{\pi }_1},B_{m_2}^{{\pi }_2})\ge \cdots \ge D_{𝒜}(B_1^{{\pi }_1},B_{m_{{\ell }_2}}^{{\pi }_2}),$$ (17)

and define $B_{1j}=B_1^{{\pi }_1}\cap B_{m_j}^{{\pi }_2}$. Consider a sequence (𝒯₁, 𝒯₂, …, 𝒯_ℓ2−1) of unfoldings of 𝒜 where 𝒯_j, for 1 ≤ j ≤ ℓ₂ − 1, is obtained from the tensor Unfold_π1∧π2(𝒜) by an unfolding operation corresponding to merging the blocks B_1,1, …, B_1,j+1 into a single block. Using Lemma 4.2 and (17), we obtain

$${\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }\ge \text{min}{\{D_{𝒜}(B_1^{{\pi }_1},B_{m_1}^{{\pi }_2}),D_{𝒜}(B_1^{{\pi }_1},B_{m_2}^{{\pi }_2})\}}^{-1/2}{\Vert {𝒯}_1\Vert }_{\sigma }={[D_{𝒜}(B_1^{{\pi }_1},B_{m_2}^{{\pi }_2})]}^{-1/2}{\Vert {𝒯}_1\Vert }_{\sigma }.$$

Similarly for all i ∈ [ℓ₂ − 2],

$${\Vert {𝒯}_i\Vert }_{\sigma }\ge \text{min }{\{D_{𝒜}(B_1^{{\pi }_1},B_{m_{i+2}}^{{\pi }_2}),\prod _{j=1}^{i+1}{D}_{𝒜}(B_1^{{\pi }_1},B_{m_j}^{{\pi }_2})\}}^{-1/2}{\Vert {𝒯}_{i+1}\Vert }_{\sigma }={[D_{𝒜}(B_1^{{\pi }_1},B_{m_{i+2}}^{{\pi }_2})]}^{-1/2}{\Vert {𝒯}_{i+1}\Vert }_{\sigma }.$$

Combining these inequalities gives

$${\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }\ge {[\prod _{j=2}^{{\ell }_2}{D}_{𝒜}(B_1^{{\pi }_1},B_{m_j}^{{\pi }_2})]}^{-1/2}{\Vert {𝒯}_{{\ell }_2-1}\Vert }_{\sigma }={\left[\frac{\prod _{j=1}^{{\ell }_2}{D}_{𝒜}(B_1^{{\pi }_1},B_j^{{\pi }_2})}{\underset{j\in [{\ell }_2]}{\text{max}}\{D_{𝒜}(B_1^{{\pi }_1},B_j^{{\pi }_2})\}}\right]}^{-1/2}{\Vert {𝒯}_{{\ell }_2-1}\Vert }_{\sigma }.$$

We can iterate the same line of argument with $\{B_i^{{\pi }_1}\cap B_{m_j}^{{\pi }_2}:j\in [{\ell }_2]\}$ for i = 2, …, ℓ₁ to obtain

$${\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }\ge \prod _{i=1}^{{\ell }_1}{\left[\frac{\prod _{j=1}^{{\ell }_2}{D}_{𝒜}(B_i^{{\pi }_1},B_j^{{\pi }_2})}{\underset{j\in [{\ell }_2]}{\text{max}}\{D_{𝒜}(B_i^{{\pi }_1},B_j^{{\pi }_2})\}}\right]}^{-1/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }={\left[\frac{\prod _{i=1}^{{\ell }_1}\prod _{j=1}^{{\ell }_2}{D}_{𝒜}(B_i^{{\pi }_1},B_j^{{\pi }_2})}{\prod _{i=1}^{{\ell }_1}\underset{j\in [{\ell }_2]}{\text{max}}\{D_{𝒜}(B_i^{{\pi }_1},B_j^{{\pi }_2})\}}\right]}^{-1/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }={\left[\frac{{\prod }_{n\in [k]}{d}_n}{{\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)}\right]}^{-1/2}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }.$$

Together with (16), this last inequality means

$${\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }\le {\left[\frac{{\prod }_{n\in [k]}{d}_n}{{\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)}\right]}^{1/2}{\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }.$$ (18)

By symmetry,

$${\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }\le {\left[\frac{{\prod }_{n\in [k]}{d}_n}{{\text{dim}}_{𝒜}({\pi }_2,{\pi }_1)}\right]}^{1/2}{\Vert {\text{Unfold}}_{{\pi }_1\wedge {\pi }_2}(𝒜)\Vert }_{\sigma }.$$ (19)

Finally, combining (18) and (19) completes the proof.

We may immediately establish several corollaries of Theorem 4.8.

Corollary 4.10

All order-k tensors 𝒜 ∈ ℝ^{d₁×⋯×d_k} satisfy

$${\Vert 𝒜\Vert }_F\le {\left[\frac{\text{dim}(𝒜)}{{\text{max}}_{n\in [k]}{d}_n}\right]}^{1/2}{\Vert 𝒜\Vert }_{\sigma }.$$

Proof

Taking π₁ = 0_[k] and π₂ = 1_[k] in Theorem 4.8 yields the result.

Corollary 4.10 gives the worst-case ratio of the Frobenius norm to the spectral norm for an arbitrary tensor. This ratio is sharper than the bound recently found by Friedland and Lim [5, Lemma 5.1], namely ‖𝒜‖_F ≤ dim(𝒜)^1/2 ‖𝒜‖_σ.

We now give a set of inequalities comparing the spectral norms of unfoldings at level ℓ to that at either level k or level 1. For ease of exposition, we assume d_n = d for all n ∈ [k].

Corollary 4.11 (Bottom-Up Inequality)

Let 𝒜 ∈ ℝ^d×⋯×d be an order-k tensor with the same dimension d in all modes. For all levels 1 ≤ ℓ ≤ k and partitions $\pi \in {𝒫}_{[k]}^{\ell }$,

$$d^{-(k-\ell )/2}\underset{\pi \in {𝒫}_{[k]}^{\ell }}{\text{max}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }\le {\Vert 𝒜\Vert }_{\sigma }\le \underset{\pi \in {𝒫}_{[k]}^{\ell }}{\text{min}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }.$$ (20)

Proof

Take π₂ = 0_[k] in Theorem 4.8.

Remark 4.12

The existing work that is most closely related to our own is that of Hu’s [9], in which the author bounds the nuclear norm of a tensor by that of its matricization. Since the nuclear norm and spectral norm are dual to each other in tensor space, many of our results apply to the nuclear norm as well. Particularly, letting ℓ = 2 in the bottom-up inequality (20) reproduces Hu’s results.

Corollary 4.13 (Top-Down Inequality)

Let 𝒜 ∈ ℝ^d×⋯×d be an order-k tensor with the same dimension d in all modes. For all levels 1 ≤ ℓ ≤ k and partitions $\pi \in {𝒫}_{[k]}^{\ell }$,

$$d^{-(k-{\text{max}}_{i\in [\ell ]}|B_i^{\pi }|)/2}{\Vert 𝒜\Vert }_F\le {\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }\le {\Vert 𝒜\Vert }_F.$$

Proof

Take π₁ = 1_[k] in Theorem 4.8.

Corollary 4.14

Let 𝒜 ∈ ℝ^d×⋯×d be an order-k tensor with the same dimension d in all modes. For all levels 1 ≤ ℓ ≤ k,

$$d^{-(k-\lceil k/\ell \rceil )/2}{\Vert 𝒜\Vert }_F\le \underset{\pi \in {𝒫}_{[k]}^{\ell }}{\text{min}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }.$$

Proof

Note that the minimum of the maximal block sizes across all level-ℓ partitions of [k] is $\underset{\pi \in {𝒫}_{[k]}^{\ell }}{\text{min}}\underset{B\in \pi }{\text{max}}|B|=\lceil k/\ell \rceil$, and apply Corollary 4.13.

The above corollaries bound the amount by which norms can vary over a specific level ℓ. They imply that the ratios ‖Unfold_π(𝒜)‖_σ/‖𝒜‖_σ and ‖Unfold_π(𝒜)‖_σ/‖𝒜‖_F fall in the intervals [1, d^(k−ℓ)/2] and [d^{−(k− ⌈k/ℓ⌉)/2}, 1], respectively. Therefore, in the worst case, ‖Unfold_π(𝒜)‖_σ only recovers ‖𝒜‖_σ or ‖𝒜‖_F at poly(d) precision. Note that the factor d^(k−ℓ)/2 has an exponent linear in the difference between the orders of the original tensor and its flattening. This means that the potential deviation between their spectral norms depends only on the difference in their orders rather than the actual orders themselves, and that the deviation accumulates in multiplicative fashion with a loss of $\sqrt{d}$ in precision at each level. In contrast, the factor d^{−(k−⌈k/ℓ⌉)/2} depends on more than just the gap between k and ℓ, with a larger impact for unfoldings with orders close to k.

We provide a low-order example that reaches the poly(d) scaling factor in Corollary 4.11.

Example 4.15

Consider the order-4 tensor 𝒜 = I_d ⊗ I_d. Straightforward calculation shows that ‖𝒜‖_σ = 1. Furthermore, by symmetry, the spectral norm of an unfolding induced by any partition in ${𝒫}_{[4]}^2$ or ${𝒫}_{[4]}^3$ must fall into one of the following five representative cases:

• For ${\pi }_1=\{\{1\},\{2\},\{3,4\}\}\in {𝒫}_{[4]}^3,{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }=\sqrt{d}$.

• For ${\pi }_2=\{\{1\},\{3\},\{2,4\}\}\in {𝒫}_{[4]}^3,{\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }=1$.

• For ${\pi }_3=\{\{1,2\},\{3,4\}\}\in {𝒫}_{[4]}^2,{\Vert {\text{Unfold}}_{{\pi }_3}(𝒜)\Vert }_{\sigma }=d$.

• For ${\pi }_4=\{\{1\},\{2,3,4\}\}\in {𝒫}_{[4]}^2,{\Vert {\text{Unfold}}_{{\pi }_4}(𝒜)\Vert }_{\sigma }=\sqrt{d}$.

• For ${\pi }_5=\{\{1,3\},\{2,4\}\}\in {𝒫}_{[4]}^2,{\Vert {\text{Unfold}}_{{\pi }_5}(𝒜)\Vert }_{\sigma }=1$.

Therefore

$$\underset{\pi \in {𝒫}_{[4]}^3}{\text{max}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }=d^{(4-3)/2}{\Vert 𝒜\Vert }_{\sigma }\text{ and }\underset{\pi \in {𝒫}_{[4]}^3}{\text{min}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }={\Vert 𝒜\Vert }_{\sigma }.$$

$$\underset{\pi \in {𝒫}_{[4]}^2}{\text{max}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }=d^{(4-2)/2}{\Vert 𝒜\Vert }_{\sigma }\text{ and }\underset{\pi \in {𝒫}_{[4]}^2}{\text{min}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }={\Vert 𝒜\Vert }_{\sigma }.$$

We conclude this section by generalizing Theorem 4.8 to l^p-norms.

Theorem 4.16 (^lp-norm inequalities)

Let 𝒜 ∈ ℝ^{d₁×⋯×d_k} be an arbitrary order-k tensor, and π₁, π₂ any two partitions in 𝒫_[k]. Then,

1. For any 1 ≤ p ≤ 2,

   $$\frac{{[\text{dim}(𝒜)]}^{-1/p}}{{[{\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)]}^{-1/2}}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_p\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_p\le \frac{{[\text{dim}(𝒜)]}^{1/p}}{{[{\text{dim}}_{𝒜}({\pi }_2,{\pi }_1)]}^{1/2}}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_p.$$
2. For any 2 ≤ p ≤ ∞,

   $$\frac{{[\text{dim}(𝒜)]}^{\frac{1}{p}-1}}{{[{\text{dim}}_{𝒜}({\pi }_1,{\pi }_2)]}^{-1/2}}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_p\le {\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_p\le \frac{{[\text{dim}(𝒜)]}^{1-\frac{1}{p}}}{{[{\text{dim}}_{𝒜}({\pi }_2,{\pi }_1)]}^{1/2}}{\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_p.$$

Proof

We only prove (a) since (b) follows similarly. For any given 1 ≤ p ≤ 2, taking q = 2 in Proposition 2.4 implies that the bound between the l^p-norm and spectral norm depends only on the total dimension of the tensor, dim(𝒜) = ∏_n∈[k] d_n. Because the total dimension is invariant under any unfolding operation, we have

$$\text{dim}{(𝒜)}^{\frac{1}{2}-\frac{1}{p}}{\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_p\le {\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma },$$ (21)

for all π ∈ 𝒫_[k]. Combining (21) with Theorem 4.8 gives the desired results.

5. Orthogonal decomposability and norm equality on upper cones

We have seen that the unfolding operation may change the spectral norm by up to a poly(d) factor for an arbitrary 𝒜. This is undesirable in many flattening-based algorithms, such as [3, 25]. However, for some specially-structured tensors, the operator norm on the partition lattice may not change much either globally or locally. We demonstrate such a behavior for the following class of tensors:

Definition 5.1 (π-orthogonal decomposable)

Let 𝒜 ∈ ℝ^{d₁×⋯×d_k} be an order-k tensor and consider any partition π ∈ 𝒫_[k]. Then 𝒜 is called π-orthogonal decomposable, or π-OD, over ℝ if it admits the decomposition

$$𝒜=\sum _{n=1}^r{\lambda }_n{\mathit{a}}_1^{(n)}\otimes \cdots \otimes {\mathit{a}}_k^{(n)},$$ (22)

where λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_r ≥ 0, and the set of vectors $\{{\mathit{a}}_i^{(n)}\in {ℝ}^{d_i}:i\in [k],n\in [r]\}$ satisfies

$$\langle {\otimes }_{i\in B}{\mathit{a}}_i^{(n)},{\otimes }_{i\in B}{\mathit{a}}_i^{(m)}\rangle ={\delta }_{nm},$$

for all B ∈ π and all n, m ∈ [r].

A concept similar to π-OD, referred to as biorthogonal eigentensor decomposition [28], is introduced in the tensor completion literature when k = 3 and π = {{1}, {2, 3}}. Informally speaking, π-OD imposes an orthogonality constraint on every block of singular vectors.

Remark 5.2 (0_[k]-OD)

When π = 0_[k] in Definition 5.1, we obtain the special case of 0_[k]-OD tensors, which admit the decomposition (22) while satisfying

$$\langle {\mathit{a}}_i^{(n)},{\mathit{a}}_i^{(m)}\rangle ={\delta }_{nm},$$

for all i ∈ [k] and all n, m ∈ [r].

The definition of 0_[k]-OD tensors generalizes the definition of orthogonal decomposable tensors presented in [21], as we require neither symmetry nor equality of dimension across modes. In fact, a 0_[k]-OD tensor 𝒜 is a diagonalizable tensor [3], meaning that the core tensor output from higher-order SVD is superdiagonal (i.e., entries are zero unless i₁ = ⋯ = i_k).

Lemma 5.3

Consider an order-k tensor 𝒜 ∈ ℝ^{d₁×⋯×d_k}.

1. Let π₁, π₂ ∈ 𝒫_[k] and π₁ ≤ π₂. If 𝒜 is π₁-OD, then 𝒜 is π₂-OD.

2. Let π ∈ 𝒫_[k] and π ≠ 1_[k]. If 𝒜 is π-OD, then

   $${\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }={\lambda }_1.$$ (23)

Proof

Part (a): For any two finite sets of vectors {x_i} and {y_i} for which x_i, y_i ∈ ℝ^d_i, we have

$$\langle {\otimes }_{i\in B}{\mathit{x}}_i,{\otimes }_{j\in B}{\mathit{y}}_j\rangle =\prod _{i\in B}\langle {\mathit{x}}_i,{\mathit{y}}_i\rangle ,$$ (24)

for all B ⊂ [k]. Suppose B ∈ π₂. If π₁ ≤ π₂, then there exist subsets C₁, …, C_m ∈ π₁ such that C₁ ∪ ⋯ ∪ C_m = B. So,

$$\langle {\otimes }_{i\in B}{\mathit{x}}_i,{\otimes }_{j\in B}{\mathit{y}}_j\rangle =\prod _{i\in B}\langle {\mathit{x}}_i,{\mathit{y}}_i\rangle =\prod _{a=1}^m\prod _{i\in C_a}\langle {\mathit{x}}_i,{\mathit{y}}_i\rangle =\prod _{a=1}^m\langle {\otimes }_{i\in C_a}{\mathit{x}}_i,{\otimes }_{j\in C_a}{\mathit{y}}_j\rangle ,$$

which implies that 𝒜 is π₂-OD if 𝒜 is π₁-OD.

Part (b): Suppose $\pi \in {𝒫}_{[k]}^{\ell }$ is of the form $\pi =\{B_i^{\pi }:i\in [\ell ]\}$. Note that π ≠ 1_[k] implies ℓ ≥ 2. Letting $\tau =\{B_1^{\pi },{(B_1^{\pi })}^c\}$ where ${(B_1^{\pi })}^c$ denotes the complement of $B_1^{\pi }$ with respect to [k], we have $\tau \in {𝒫}_{[k]}^2$ and π ≤ τ. By Lemma 5.3(a), 𝒜 is τ-OD, so 𝒜 admits a decomposition of the form

$$𝒜=\sum _{n=1}^r{\lambda }_n{\mathit{a}}_1^{(n)}\otimes \cdots \otimes {\mathit{a}}_k^{(n)},$$ (25)

where

$$\langle {\otimes }_{i\in B_1}{\mathit{a}}_i^{(n)},{\otimes }_{j\in B_1}{\mathit{a}}_j^{(m)}\rangle ={\delta }_{nm}\text{ and }\langle {\otimes }_{i\in {(B_1^{\pi })}^c}{\mathit{a}}_i^{(n)},{\otimes }_{j\in {(B_1^{\pi })}^c}{\mathit{a}}_j^{(m)}\rangle ={\delta }_{nm}$$ (26)

for all n, m ∈ [r].

Now define ${\mathit{x}}_n=\text{Vec}({\otimes }_{i\in B_1^{\pi }}{\mathit{a}}_i^{(n)})$ and ${\mathit{y}}_n=\text{Vec}({\otimes }_{i\in {(B_1^{\pi })}^c}{\mathit{a}}_i^{(n)})$ for all n ∈ [r]. By (26), both {x_n} and {y_n} are sets of orthonormal vectors. By the definition of Unfold_τ (𝒜), (25) implies

$${\text{Unfold}}_{\tau }(𝒜)=\sum _{n=1}^r{\lambda }_n{\mathit{x}}_n{\mathit{y}}_n^T,$$

which is simply the matrix SVD of Unfold_τ (𝒜). Hence ‖Unfold_τ (𝒜)‖_σ = λ₁. Using monotonicity (c.f., Proposition 4.1), we have

$${\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }\le {\Vert {\text{Unfold}}_{\tau }(𝒜)\Vert }_{\sigma }={\lambda }_1.$$ (27)

Conversely, by the definition of the spectral norm, we have

$$\begin{gathered} {\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }\ge \langle {\text{Unfold}}_{\pi }(𝒜),\text{Vec }\left({\otimes }_{i\in B_1^{\pi }}{\mathit{a}}_i^{(1)}\right)\otimes \cdots \otimes \text{Vec }\left({\otimes }_{i\in B_{\ell }^{\pi }}{\mathit{a}}_i^{(1)}\right)\rangle \\ =\sum _{n=1}^r{\lambda }_n\langle \text{Vec }\left({\otimes }_{i\in B_1^{\pi }}{\mathit{a}}_i^{(n)}\right)\otimes \cdots \otimes \text{Vec }\left({\otimes }_{i\in B_{\ell }^{\pi }}{\mathit{a}}_i^{(n)}\right), \\ \text{Vec }\left({\otimes }_{i\in B_{\ell }^{\pi }}{\mathit{a}}_i^{(1)}\right)\otimes \cdots \otimes \text{Vec }\left({\otimes }_{i\in B_{\ell }^{\pi }}{\mathit{a}}_i^{(1)}\right)\rangle \\ =\sum _{n=1}^r{\lambda }_n\prod _{j\in [\ell ]}\langle \text{Vec }\left({\otimes }_{i\in B_j^{\pi }}{\mathit{a}}_i^{(n)}\right),\text{Vec }\left({\otimes }_{i\in B_j^{\pi }}{\mathit{a}}_i^{(1)}\right)\rangle \\ =\sum _{n=1}^r{\lambda }_n{\delta }_{n,1}={\lambda }_1 \end{gathered}$$ (28)

where the third line comes from (24) and the last line follows from the fact that 𝒜 is π-OD. Combining (27) and (28), we conclude ‖Unfold_π(𝒜)‖_σ = λ₁.

Remark 5.4

The condition π ≠ 1_[k] in Lemma 5.3 is needed for (23) to hold. In fact, consider a 2 × 2 matrix A = 2e₁ ⊗ e₁ + e₁ ⊗ e₂, where {e_i, i ∈ [2]} is the canonical basis of ℝ². Then, A is 1_[k]-OD with λ₁ = 2, but ${\Vert {\text{Unfold}}_{{\mathbf{1}}_{[k]}}(𝒜)\Vert }_{\sigma }={\Vert 𝒜\Vert }_F=\sqrt{5}\ne 2$.

Theorem 5.5 (Norm equality on upper cones)

If 𝒜 is π-OD, then for any partition in the upper cone U_π = {τ ∈ 𝒫_[k] : π ≤ τ < 1_[k]} of π, we have

$${\Vert {\text{Unfold}}_{\tau }(𝒜)\Vert }_{\sigma }={\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }.$$

Proof

If 𝒜 is π-OD, then by Lemma 5.3(b), we have ‖Unfold_π(𝒜)‖_σ = λ₁. Given any τ ≥ π, by Lemma 5.3(a), 𝒜 is also τ-OD. Again, using Lemma 5.3(b), we have ‖Unfold_τ (𝒜)‖_σ = λ₁. Therefore, ‖Unfold_τ (𝒜)‖_σ = ‖Unfold_π(𝒜)‖_σ.

Theorem 5.5 states that the spectral norm is invariant for π-OD 𝒜 under any unfolding induced by the partitions in the upper cone U_π of π. This lies in contrast with the poly(d) factor we have seen for unstructured tensors.

Corollary 5.6

If 𝒜 is 0_[k]-OD, then for all partitions π ≠ 1_[k], we have

$${\Vert {\text{Unfold}}_{\pi }(𝒜)\Vert }_{\sigma }={\Vert 𝒜\Vert }_{\sigma }.$$

Corollary 5.6 implies that for 0_[k]-OD tensors, the operator norm is invariant under any unfolding operations except vectorization. Lastly, π₁, π₂ ∈ U_π1∧π2 implies the following corollary:

Corollary 5.7

Let π₁, π₂ ∈ 𝒫_[k]. If 𝒜 is (π₁ ∧ π₂)-OD, then

$${\Vert {\text{Unfold}}_{{\pi }_1}(𝒜)\Vert }_{\sigma }={\Vert {\text{Unfold}}_{{\pi }_2}(𝒜)\Vert }_{\sigma }.$$

6. Discussion

In this paper, we presented a new framework representing all possible tensor unfoldings by the partition lattice and established a set of general inequalities quantifying the impact of tensor unfoldings on the operator norms of the resulting tensors. We showed that the comparison bounds scale polynomially in the dimensions {d_n} of the tensor, with powers depending on the corresponding partition and block sizes for any pair of tensor unfoldings being compared. As a direct consequence, we demonstrated how the operator norm of a general tensor is lower and upper bounded by that of its unfoldings.

In general, an unfolding operation may inflate the operator norm by up to a poly(d) factor, as seen in Corollary 4.11. Note that the quantity dim(𝒜) plays a key role in the worst-case inflation factor and is a manifestation of the curse of dimensionality. Specifically, dim(𝒜) can be quite large as the mode dimensions and tensor order increase, with particular sensitivity to the latter. In such settings, our main result seems to bode poorly for flattening-based algorithms; however, we believe that it should be interpreted with caution because our comparison bounds deal with arbitrary tensors rather than those often sought in applications. In fact, π-OD tensors permit much tighter bounds in which some unfoldings, including certain matricizations, leave the operator norm relatively unaffected. In practice, π-OD tensors, or those within a small neighborhood around π-OD tensors, arise widely in statistical and machine learning applications [1, 11, 16, 26].

Additionally, our work enables us to compare different unfoldings at the same level ℓ. Recent work on problems featuring nuclear-norm regularization has shown that not all n-mode flattenings are equally preferable [13]. Indeed, as illustrated in Example 4.15, the operator norm of level-2 unfoldings (i.e. matricizations) can be quite different. Recently, several algorithms have been proposed to account for this behavior. For example, Tomioka et al. [23] consider a weighted sum of the norms of all single-mode matricizations. Other techniques include two-mode matricization [26] and square matricization [15, 20], in which the original tensor is reshaped into a matrix by flattening along multiple modes. Our work provides general bounds to evaluate the effectiveness of such schemes. In particular, the results presented here are used in the theoretical analysis of a two-mode higher-order SVD algorithm proposed recently [26].

We have not attempted to characterize the degree to which operator norm relations on the partition lattice restrict the original tensor. Essentially, this is a converse problem asking whether π-OD is a necessary condition for Theorem 5.5 and Corollary 5.6 in addition to being sufficient. If not, it would be useful to determine the extent to which such equalities inform us about the intrinsic structure of the original tensor. From a practical standpoint, norm comparisons between different matricizations are relatively simple, but the optimal manner in which to use this information to learn about the original tensor remains unknown.

In closing, we emphasize that while this work focuses on theory rather than computational tractability, it possesses practical implications as well. Because direct calculation of the operator norm of a level-ℓ tensor is generally computationally prohibitive for ℓ ≥ 3, exploiting level-2 unfoldings may be attractive when the unfolding effect is small enough. Alternatively, for more precise calculations, a number of approximation algorithms exist for higher-order tensor problems [23, 27] at the cost of increased computation. Given that the trade-off between accuracy and computation is often unavoidable, our work may be of help in finding an appropriate application-specific balance when working with higher-order tensors.