Response to “Gaussian or Poisson noise?”

Abstract

In this response we underscore that the instrumentation described in the original publication (Liu et al., 2012) was based on pulse-sampling technique, while the comment by Zhang et al is based on the assumption that a time-correlated single photon counting (TCSPC) instrumentation was used. Therefore the arguments made in the comment are not applicable to the noise model reported by Liu et al. As reported in the literature (Lakowicz, 2006), while in the TCSPC the experimental noise can be estimated from Poisson statistics, such assumption is not valid for pulse-sampling (transient recording) techniques. To further clarify this aspect, we present here a comprehensive noise model describing the signal and noise propagation of the pulse sampling time-resolved fluorescence detection. Experimental data recorded in various conditions are analyzed as a case study to demonstrate the noise model of our instrumental system.

In addition, regarding the statement of correcting Eq. 3 in (Liu et al., 2012), the notation of discrete time Laguerre function in the original publication was clear and consistent with literature conventions (Marmarelis, 1993; Westwick and Kearney, 2003). Thus, it does not require revision.

A. Noise model of multi-spectral time-resolved fluorescence spectroscopy

The time-resolved fluorescence detection method that was discussed in (Liu et al., 2012) and commonly used by our group is pulse sampling technique. The description of the instrumentation in the original publication and its references (Sun et al., 2009; Sun et al., 2011) clearly referred to the use of analog mode of the MCP-PMT and digital oscilloscope. See also (Sun et al., 2008; Yankelevich et al., 2014). White Gaussian noise was used in the simulation as an approximation to the realistic noise. Below we present a more comprehensive noise model for the pulse sampling technique, which can be simplified to white Gaussian noise in certain instrumental configurations. A case study was used to demonstrate the noise model’s capacity of explaining the variance of experimental data. Instrumental configurations leading to the approximation of white Gaussian noise was discussed.

Noise model based on signal/noise propagation

The fluorescence impulse response function (fIRF) is the spontaneous emission intensity of all fluorophores interrogated by the excitation beam, which is conventionally modeled as multi-exponential functions, as shown in Eq. 1.

$$fIRF\left(t\right)=\sum _{i=1}^N{a}_i\ast \text{exp}\left(-\frac{t}{{\tau }_i}\right)$$ (1)

where a_i and τ_i are the amplitude and lifetime for the ith exponential component, and N is the total number of fluorophores. The detected fluorescence signal by the MCP-PMT can be modeled as a Poisson random process S₁(t). The photon counts at ith time bin t_i with bin width δt of S₁(t) can be modeled as independently distributed Poisson random variables,

$$S_1\left(t\right)~Poisson\left(fIRF\left(t_i\right)\delta t\right)$$ (2)

for all time bins, such that, for constant bin width δt as usually used in practice,

$$\begin{array}{cc}\hfill E\left[S_1\left(t_i\right)\right]& =fIRF\left(t_i\right)\delta t\hfill \\ \hfill Var\left[S_1\left(t_i\right)\right]& =fIRF\left(t_i\right)\delta t\hfill \end{array}$$ (3)

To simplify notation, we dropped the time bin index in following discussion.

The magnification of the MCP-PMT (η) can be multiplied to the Poisson process as a constant, since the noise introduced in the early stages dominates the overall detector noise. (Donati, 2001) The effects of the other electronic devices, which include the amplifier and the digitizer/oscilloscope, can be summarized by a band-pass filter and additive white Gaussian noise. Thus, the final data S₂(t) can be modeled as a filtered Poisson process with additive white Gaussian noise,

$$S_2\left(t\right)=\eta \cdot S_1\left(t\right)\otimes iIRF\left(t\right)+n\left(t\right)$$ (4)

where the instrument impulse response function (iIRF) describes the overall pulse broadening effect of all devices and the additive white Gaussian noise n(t) with mean zero and variance σ₀ accounts for the thermal noise of the amplifier and the front end of digitizer, as well as the digitizing error. Here, ⊗ is the convolution operator. The mean and variance of the measured signal are

$$\{\begin{array}{c}E\left[S_2\left(t\right)\right]=\eta \cdot fIRF\left(t\right)\otimes iIRF\left(t\right)\cdot \delta t\hfill \\ Var\left[S_2\left(t\right)\right]={\eta }^2\cdot fIRF\left(t\right)\otimes {\mid iIRF\left(t\right)\mid }^2\cdot \delta t+{\sigma }_0^2\hfill \end{array}\phantom{\}}$$ (5)

In this model, if the variance of the filtered Poisson process is small compared to the white Gaussian noise, the model can be well-approximated by additive white Gaussian noise model. In current instrumental configuration, shot noise limited detection (Poisson noise) is difficult to achieve, for the reasons that 1) the bandwidths of the devices are not large enough to ignore the filtering effect; and 2) the front-end thermal noise and digitizing error of the digitizer are not negligible.

Case study of experimental data

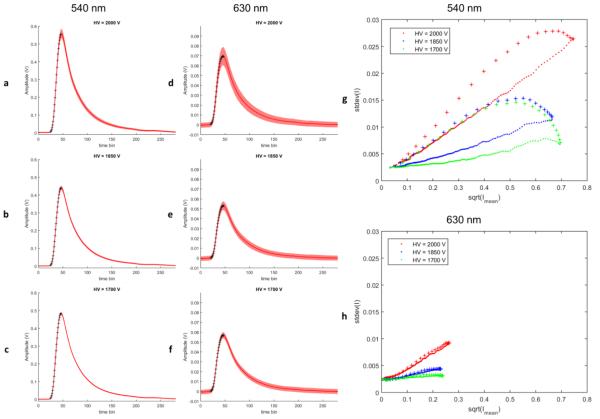
A time-resolved fluorescence measurement using the pulse-sampling technique was conducted in Rhodamine 6G (Exciton, Rhodamine 590, ethanol solution). The fluorescence was excited by a Q-switched laser (Teem, 355 nm, 700 ps, 1 μJ) and detected by MCP-PMT (Hamamatsu, R3809U-50, 45 ps, FWHM of IRF). The electrical signal from the MCP-PMT is passed through a broad-band amplifier (MITEQ, AM-1607-3000, 10 kHz – 3 GHz, 40 dB) and digitized by a high speed digitizer (National Instruments, NI-5185, 12.5 GS/s, 3 GHz, 8-bits). Number of collected photons was varied by changing the excitation-collection geometry, which required changing the high voltage (HV) on the MCP for different magnification to match the signal to the range of the digitizer. In the three sets of data containing each 5000 repeated measurements, HV of 1700V, 1850V and 2000V were used, respectively, where a higher HV value corresponds to a lower number of photons and vice versa. For each data set, the wavelength selection module of the instrument acquired fluorescence signals of Rhodamine 6G in two wavelength bands centered at 540 nm and 630 nm, respectively.

In Figure 2 a-f, the sample means and standard deviations (SD) over the 5000 fluorescence measurement waveforms were presented in time-domain, where the solid line delineated the mean and the shaded area delineated the SD. Data in Figure 2 a-c and d-f were acquired in the wavelength bands centered at 540 nm and 630 nm, respectively. Scatter plots in Figure 1 g-h were generated by mapping the square-root of the mean versus SD for each time bin in Figure 1 a-c and d-f.

Figure 1.

Experimental data acquired from Rhodamine B. For easier differentiation, data points on the rising edge of the waveforms are identified by cross markers.

Assuming solely Poisson noise model, I^0.5 versus SD plot should be a straight line through the origin with a slope of 1 (i.e. SD = I^0.5). However, assuming only white Gaussian noise model, the plot will be a flat line with non-zero Y intercept and a slope of 0 (SD = σ₀, σ₀ > 0 for any I). Note that for the experimental data under various conditions, the Y intercepts were all non-zero and the SD showed certain extent of dependence on the intensity. Applying the noise model described in the previous section, the additive white Gaussian noise is responsible for the constant variance that offset the entire curve by the constant Y intercept value. As shown in Figure 1 g-h, the slopes of the quasilinear part of the curves increased as the HV increased (thus the magnification increased). This can be explained by the noise model, in which the Poisson processes S₁(t) scaled by the MCP magnification η presents a linear relationship between I^0.5 and SD with a slope proportional to η^0.5. This is simply because: $\frac{Var[\eta \cdot S_1\left(t\right)]}{E[\eta \cdot S_1\left(t\right)]}=\frac{{\eta }^2\cdot Var\left[S_1\left(t\right)\right]}{\eta \cdot E\left[S_1\left(t\right)\right]}=\eta$. It is interesting to see that the mean and variance relationship exhibits a hysteretic behavior, which was partly due to the temporal filtering in Eq. (3). Another possible reason for the data on the rising edge to have higher variance is that samples on the rising edge are more sensitive to the time jitter of the digitizer.

In (Liu et al., 2012) paper, the data were acquired with the high-energy laser pulses (>2 μJ) (more total fluorescence photons) and longer time bins of the digitizer (more equivalent photon counts per time bin). Thus, the noise can be approximated by white Gaussian noise. Furthermore, as demonstrated in Figure 5 and 7 of (Liu et al., 2012), the experimental data sets acquired at the time by a different instrumentation presented good agreement of the residual statistics with the normality test hypothesis, indicating that Gaussian noise could be the main source of error. In fact, the least-squared method is based on the assumption of homoscedasticity (homogeneity of variance), which makes it ideal in case of pure white Gaussian noise. For data with significant Poisson-like noise, weighted least-squares or other approaches should be used instead.

Conclusion

Here we recapitulated that the instrumentation employed in the (Liu et al., 2012) publication was based on pulse sampling method, which is different from TCSPC. Therefore, although the comment “Gaussian or Poisson noise?” made a good point under the assumption of TCSPC instrumentation, the same arguments cannot be simply applied to pulse sampling instrumentation. We provided a comprehensive noise model of the signal/noise propagation process for instrumentation systems using pulse sampling method in general. A case study of experimental data was presented to demonstrate applicability of the noise model. The behaviors of experimental measurement variability were explained by different aspects of the noise model. The noise model can be approximated by white Gaussian noise under certain conditions. The instrumental configuration and the statistical tests of residuals presented in the original publication suggested using Gaussian noise in the simulation was a sound approximation to the original data.

B. Notation of discrete time Laguerre function

Eq. 3 in (Liu et al., 2012) is the full form definition of discrete time Laguerre functions, instead of the recursive form. An exact same definition of the functions can be found in (Marmarelis, 1993) (Equation 11) or many other textbooks on system identifications (Westwick and Kearney, 2003) (Equation 7.26). Mathematically, the term (k,i) in Eq. 3, is the binomial coefficient, which is only nonzero for i<=k by definition. The equation used in the paper is in standard form, and it is completely redundant to add the term claimed in the comment.