Marginal Structural Models for Skewed Outcomes: Identifying Causal Relationships in Health Care Utilization

Abstract

Evaluating the impacts of clinical or policy interventions on health care utilization requires addressing methodological challenges for causal inference while also analyzing highly skewed data. We examine the impact of registering with a Family Medicine Group (FMG), an integrated primary care model in Quebec, on hospitalization and emergency department visits using propensity scores to adjust for baseline characteristics and marginal structural models to account for time-varying exposure. We also evaluate the performance of different marginal structural GLMs in the presence of highly skewed data and conduct a simulation study to determine the robustness of different GLMs to distributional model mis-specification. Although the simulations found that the zero-inflated Poisson likelihood performed the best overall, the negative binomial likelihood gave the best fit for both outcomes in the real dataset. Our results suggest that registration to a FMG for all three years caused a small reduction in the number of emergency room visits, and no significant change in the number of hospitalizations in the final year.

1. Introduction

Health care utilization data is useful to characterize the health care system and to investigate the answers to a wide array of policy questions. It is defined as the number of services used by a patient over a period of time, such as the number of hospitalizations or the number of visits to a physician over a period of one year for example. The data are usually characterized by a highly right-skewed distribution with an inflated number of zeros, reflecting the fact that a majority of people are in relatively good health, and a minority of them are very sick.

Longitudinal datasets where the exposure may vary over time pose further obstacles in estimating the average causal effect of an intervention or policy. It is not unusual in such observational datasets to encounter situations where covariates are simultaneously confounders and intermediate steps in the pathway between the exposure and the outcome. Typical data analysis methods will produce biased estimates in such cases [1]. The International Society for Pharmacoeconomics and Outcomes Research (ISPOR) Good Research Practices for Retrospective Database Analysis Task Force Report suggests using alternative methods such as marginal structural models (MSMs) to investigate such datasets [2].

Marginal structural models typically produce estimates using inverse probability of treatment weighting (IPTW). MSMs have been shown to successfully estimate the total causal effect of exposure on outcome in observational studies where the exposure varies with time, and where some time-varying confounders are affected by previous exposure [3, 4]. In this manuscript, we focus on the impact patient registration in an integrated primary care delivery model (Family Medicine Groups or FMGs) on the utilization of services in the province of Québec, Canada. Utilization will be measured by two different outcomes, the number of emergency room visits per year and the number of hospitalizations per year. In this paper, we will attempt to identify the causal effect of the FMG model on the utilization of health care services, and to characterize the performance of different marginal structural GLMs in the presence of highly skewed data. This paper is organized as follows: in Section 2, we review current practices in the analysis of health care utilization data and introduce marginal structural models. Section 3 presents an analysis of the health care utilization data, considering patient membership in a FMG over time as the key exposure of interest. This is followed by a simulation study designed to determine the robustness of different GLMs to distributional model mis-specification in Section 4. We conclude in Section 5.

2. Background

2.1 Modelling health utilization data

It is not uncommon to see health care utilization data analysed using ordinary least-squares (OLS) regression. However, this practice often violates the normality assumption of the OLS model since the data typically do not follow a normal distribution. In particular, it may violate the assumption of homoscedasticity since utilization data variability tends to increase with the mean [5]. Thus alternative analysis methods are recommended. Transformations are commonly used to make the data more symmetrically distributed, shortening the long right tail. The log transformation is usually preferred since it is easier to interpret its coefficients [5]. It also lessens homoscedasticity and may decrease the influence of outliers. Provided that the sample size is large enough, the estimates will be unbiased [5]. Transformed outcomes can then be analysed with either an OLS regression model, or a general linear model (GLM). However, inference must then be done on the log scale, which is not always ideal. If the inference must be done in the original scale, these transformations cannot be used since the un-transformed estimates will then be biased toward the mean [6].

Because the data typically consist of counts, another common analysis method is to use a Poisson GLM. The assumption of this model that the mean is equal to the variance must first be verified, and may not always hold since the counts are typically not independent. In fact, the Poisson procedure will often reveal over-dispersion in the data [7]. The negative binomial model may be preferred over the Poisson since it allows a more flexible mean-variance assumption that can naturally incorporate over-dispersion. However, both models’ predicted number of zero outcomes often fail to reach the quantity that is actually found in the data [7].

Alternatively, a two-part model can be used where the probability that a person has a positive utilization of services is modelled in a first step, and the amount of services used in a second step [8, 9]. Zero-inflated Poisson (ZIP) or the zero-inflated negative binomial (ZINB) likelihoods are typically used [10]. They are based on a mixture probability distribution (binomial-Poisson and binomial-negative binomial respectively). For example, the ZIP model will first estimate the probability p to observe an excess zero count, and then with probability (1-p), estimate a Poisson distribution with mean λ. These models are easy to interpret and allow for a more appropriate analysis, particularly when this two-part model intuitively fits the substantive knowledge of the outcome [10].

2.2 Causal inference in longitudinal observational studies

In investigating a typical public policy intervention such as the implementation of FMGs in Québec, one will compare the observed outcomes between patients who received the intervention and those who did not. Since the intervention is not assigned at random and in fact, patients and physicians joined on a voluntary basis, selection bias will likely occur. In order to measure the average causal effect, appropriate statistical methods must be used to balance the data in such a way to emulate a randomized control trial and ensure that the exchangeability criterion holds. One such method is the use of marginal structural models (MSMs).

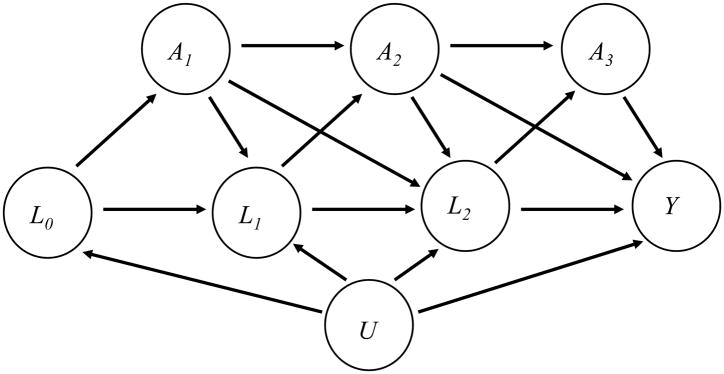
Let A_k denote a binary exposure during the k^th interval, for k=1,…,K, and Y an end-of-study measured at the end of the K^th interval. Denote baseline confounding variables by L₀, and denote by L_k (k=1,…,K) time-varying confounders which causally affect exposure A_k+1 and the outcome Y; these variables may also be affected by prior exposures. Further, there may be unmeasured variables, U, such as an underlying health status that affect the covariates L_k (k=0,…,K) and the outcome Y. An example of such a set-up for K=3 is given by the directed acyclic graph (DAG) in Figure 1.

Figure 1.

A counterfactual, or potential outcome, is the outcome that would be observed if a particular exposure pattern were “forced” on an individual; the exposure pattern under consideration is indicated by parentheses, so that, for example, Y(1,1,1) indicates the outcome that would be observed in an individual who was exposed in intervals 1, 2, and 3. Marginal structural models are used to estimate the expected counterfactual outcome (or contrasts of these), permitting the analyst to examine questions such as what is the expected difference in outcome if the entire population were always exposed, versus had the population never been exposed?

In our context, MSMs permit estimation of the population average effect of following a particular FMG exposure history. The approach has grown in popularity, in part because it is simple to implement: it involves fitting the observed data as a function of exposure (and perhaps also baseline covariates) while weighting each uncensored patient by the inverse of the probability of receiving the treatment actually received. For example, in the absence of censoring, each observation is weighted by the probability of having received the exposure pattern that was observed, i.e. for K=3 by

$$s{w}_i=\frac{\begin{array}{c}P(A_1=a_{1i}\mid L_0=l_{0i})\times P(A_2=a_{2i}\mid A_1=a_{1i},L_0=l_{0i})\times \\ P(A_3=a_{3i}\mid A_1=a_{1i},A_2=a_{2i},L_0=l_{0i})\end{array}}{\begin{array}{c}P(A_1=a_{1i}\mid L_0=l_{0i})\times P(A_2=a_{2i}\mid A_1=a_{1i},L_0=l_{0i},L_1=l_{1i})\times \\ P(A_3=a_{3i}\mid A_1=a_{1i},A_2=a_{2i},L_0=l_{0i},L_1=l_{1i},L_2=l_{2i})\end{array}}.$$

The weighting creates a pseudopopulation where the variables we have identified as confounders are no longer related to the exposure. In doing so, the outcome may be modelled as a function of exposures and baseline covariates only, avoiding conditioning on the time-varying covariates L_k and thereby avoiding blocking exposure effects that are mediated through these covariates as well as introducing collider-stratification bias through the unmeasured variables U.

For MSMs to provide unbiased estimates of the population average exposure effects, we must assume that there are no unmeasured confounders of exposure and outcome at each interval, the both the exposure models and the outcome model are correctly specified, and that positivity holds, i.e. there are no combinations of covariates for which either exposure level is not permitted. In the presence of censoring, the weights must additionally incorporate a model for continued observation in the study, and the assumptions must be expanded to include that all covariates that influence the outcome and loss of follow-up have been measured, and that the censoring mechanism model is correctly specified.

3. Identifying the impact of FMG enrolment on healthcare utilization

3.1 Context and data source

In Québec, Canada, all medically necessary services provided by a general practitioner, family doctor, medical specialist, or in a hospital are covered by the Régie d’assurance maladie du Québec (RAMQ) Health Insurance Plan. Thus the RAMQ database forms a rich source of information on all health services utilization by residents, along with physician information, and whether or not they are part of a FMG.

The Family Medicine Group model was introduced in Québec in 2002 as a way to improve the organization of the primary healthcare system. A FMG is a group of family doctors who work closely with clinical and administrative staff in order to provide primary care to a group of registered patients.[11] The Population Health and Health Services Group at the Montreal Public Health Department and Agency for Health and Social Services has developed a database encompassing all vulnerable individuals in Québec who were identified as such in the RAMQ database between November 1^st 2002 and January 31^st, 2005. A vulnerable patient is defined as a person who is either 70 years old or above, or has at least one of the following conditions: psychosis, chronic obstructive pulmonary disease (COPD), moderate to severe asthma, pneumonia, cardiovascular disease, cancer associated with past, present or future chemotherapy or radiotherapy treatments, cancer in a terminal phase, diabetes, alcohol or hard drug withdrawal, drug addiction treated with methadone, HIV/AIDS, or a degenerative disease of the nervous system [12]. The database is comprised of 797,826 patients who were enrolled as vulnerable by a physician between November 1^st 2002 and January 31^st, 2005. It contains two years before their enrolment (time zero), and three years subsequent. Roughly 15% of the patients (122,724) were enrolled at time zero by a physician in a FMG, and the remaining 675,102 were not. Only the FMGs that had been open for four months and had at least 300 vulnerable patients registered by January 2005 were included [13]. This amounted to 79 practices in total (8 FMGs were excluded).

3.2 Selection of the analytic sub-sample

Neither the patients nor the physicians in the dataset were randomized to a FMG or a non-FMG practice. There are undoubtedly underlying characteristics that made them more likely to join one or the other initially. Using pre-enrolment data, Coyle (2011) [14] showed that living outside a university/urban region, being in the highest material deprivation group, having diabetes, having visited the ER for ambulatory care sensitive conditions or being hospitalized for any cause were all risk factors that increased the chance of a patient joining a FMG, while having hypertension, more outpatient clinic visits, and having a usual provider of care decreased it. Propensity scores [15] were proposed in order to address this selection bias and to achieve balance on observable characteristics at baseline amongst those patients enrolled in a FMG at time zero and those who were not.

Coyle and colleagues (2011) [14] generated propensity scores for this dataset from the patient data at the year prior to enrolment (year -1); a thorough literature review was conducted and used in conjunction with a stepwise procedure to determine which covariates were predictors of joining the FMG cohort. These covariates included demographics (age, socio-demographic status, geography, gender), chronic illness and burden, health services utilization, ambulatory care use, and whether the patient had a usual provider of care. The final model selected by Coyle (2011) [14] was used to generate the propensity scores for the dataset used in the present analysis. We employed 1:1 matching without replacement using the psmatch2 Stata module [16] to obtain a sub-sample of the dataset in which patients who were, and were not, enrolled in a FMG were comparable at baseline (year 0). In doing so, we can then compare our longitudinal results to the cross-sectional results of Coyle and colleagues [14]. Furthermore, by employing matching at baseline, we take advantage of maximal bias reduction, as it has been established (see, for example, [17, 18]) that propensity score matching is better able to reduce systematic differences in baseline characteristics between the exposed and unexposed members of the sample than stratification. Of course, matching also results in a smaller analytic sample, however we retain 231,938 for our analysis and hence are reassured that power will not be adversely affected.

Table 1 describes the dataset before and after the propensity score match. Standardized differences are used to compare the different covariates (dividing the difference in means by the pooled standard deviation). The standardized difference is a measure that is not influenced by sample size and is appropriate in this instance since the unmatched data has a number of controls that is far larger than the number of exposed [19]. Most covariates are well balanced in the final dataset which is made up of 231,938 vulnerable patients, half of whom joined a FMG at time zero. The largest standardized difference in the unmatched population is −0.3307 for the university/urban region, and the largest one in the matched population is 0.069 for the number of emergency room visits. D’Agostino (1998) [20] suggests that standardized differences of less than 0.10 are sufficiently balanced and this is the case for all our covariates. Thus remaining differences are unlikely to be clinically relevant.

Table 1.

Baseline distributions of patients’ characteristics before and after the (baseline) propensity score matching

		Unmatched (n=797,826)			PS Matched (n=231,938)
		Non-FMG (n=675,102)	FMG (n=122,724)	Standardized difference	Non-FMG (n=115,969)	FMG (n=115,969)	Standardized difference
		Proportion
Age	< 1	0.0002	0.0004	-0.0526	0.0002	0.0003	−0.0244
	1–4	0.0012	0.0011		0.0011	0.0011
	5–9	0.0018	0.0017		0.0017	0.0018
	10–14	0.0017	0.0019		0.0015	0.0019
	15–19	0.0026	0.0030		0.0027	0.0030
	20–24	0.0043	0.0051		0.0047	0.0049
	25–29	0.0056	0.0065		0.0061	0.0063
	30–34	0.0078	0.0086		0.0083	0.0083
	35–39	0.0141	0.0151		0.0148	0.0148
	40–44	0.0232	0.0250		0.0250	0.0248
	45–49	0.0349	0.0379		0.0363	0.0373
	50–54	0.0498	0.0527		0.0526	0.0523
	55–59	0.0685	0.0707		0.0705	0.0708
	60–64	0.0758	0.0777		0.0771	0.0784
	65–69	0.1346	0.1393		0.1372	0.1412
	70–74	0.2293	0.2223		0.2264	0.2249
	75–79	0.1731	0.1707		0.1721	0.1713
	80–84	0.1061	0.1023		0.1021	0.1009
	>= 85	0.0654	0.0580		0.0596	0.0556
Sex	(male)	0.4392	0.4432	0.0081	0.4418	0.4436	0.0035
Region residing	University region	0.3933	0.2414	−0.3307	0.2341	0.2367	0.0061
	Peripheral region	0.3750	0.4416	0.1359	0.4578	0.4487	−0.0184
	Intermediate region	0.1887	0.2658	0.1848	0.2591	0.2620	0.0066
	Remote region	0.0429	0.0510	0.0383	0.0490	0.0526	0.0167
	Nordic region	0.0001	0.0001	−0.0019	0.0000	0.0001	0.0069
Material Deprivation Index	1. Most privileged	0.1758	0.1318	−0.1222	0.1319	0.1321	0.0005
	2.	0.1825	0.1797	−0.0073	0.1800	0.1797	−0.0010
	3.	0.2051	0.2332	0.0680	0.2341	0.2332	−0.0023
	4.	0.2188	0.2378	0.0453	0.2374	0.2375	0.0002
	5. Most deprived	0.2178	0.2175	−0.0007	0.2165	0.2176	0.0026
Hypertension		0.3547	0.2492	−0.2313	0.2603	0.2517	−0.0198
Diabetes		0.1633	0.1762	0.0344	0.1658	0.1785	0.0336
COPD		0.0653	0.0734	0.0319	0.0637	0.0735	0.0388

3.3 Key variables

3.3.1 Exposure measure

The propensity score matching was done using the FMG variable defined when the patients were enrolled as vulnerable by a physician at time zero. However, patients did not necessarily remain in a FMG for the remaining three years, or even for the remaining days of the first year. Thus a second exposure variable was generated for the purpose of the subsequent analyses. A patient was defined to be in the FMG group during that year if affiliated in a FMG for at least 75% of that year; that is, A₁=1 for an individual provided if he was enrolled in a FMG for at least 75% of the first year of follow-up, and similarly for A₂ and A₃. Otherwise, the patient was in the non-FMG group. (The distribution of patients according to FMG affiliation over the three years of follow-up does not vary much when the FMG definition cut-off ranges from 75% to 100%.)

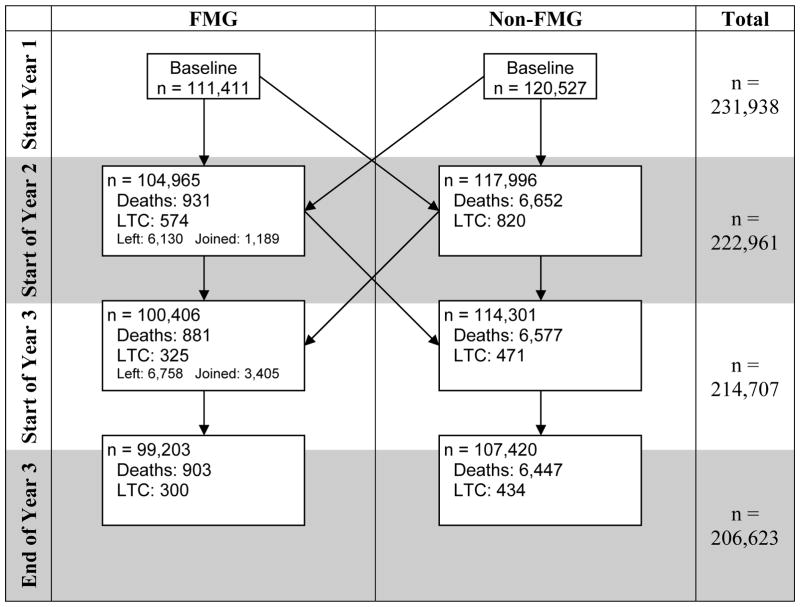
Over time, some patients moved from one group to the other, and the resulting net movement is described in Figure 2. For example, at the start of Year 2, a total of 6,130 individuals had left their FMG since time zero and moved to the non-FMG group, and 1,189 individuals joined a FMG and moved to the FMG group, resulting in a net movement of 4,941 in the non-FMG group. Because of the administrative nature of the database, patients could only be lost to follow up for two reasons: death or moving into a long term care facility.

Figure 2.

LTC is the number of patients who transitioned to a long-term care facility. “Net movement” represents the net number of individuals incoming from the other cohort.

Table 2 describes the movement of uncensored individual patients in and out of a FMG over the three years of the cohort follow-up. While 95% of patients either remain in the FMG or outside any FMG for the entire duration as per our definition of FMG, the remaining 5% joined an FMG later on, left a FMG, or moved in and out of a FMG sporadically. Most of these “movers” also move between geographic regions during the three years.

Table 2.

FMG exposure patterns

	code	FMG in Year			Proportion (n=206,623)
		1	2	3
Never FMG	000	n	n	n	0.4906
Always FMG	111	y	y	y	0.4586
Joined FMG Later	011	n	y	y	0.0103
	001	n	n	y	0.0052
Dropped out of FMG	110	y	y	n	0.0195
	100	y	n	n	0.0095
Other FMG movement	010	n	y	n	0.0003
	101	y	n	y	0.0061

3.3.2 Outcome measures

The utilization of health services, Y, is measured by the number of ER visits and the number of hospitalizations in Year 3. These variables are characterized by highly skewed distributions. Most individuals do not visit the ER (67%) and are not hospitalized (86%) during the year. However, a few individuals, arguably much sicker, make use of the health services quite disproportionally (maximum of 39 visits to the ER, and of 21 hospitalizations).

3.3.3 Confounding variables

Available confounding variables include demographic variables (location, material deprivation [21], gender, age), health resources utilization (past number of ER visits, past number of hospitalizations) and chronic illnesses. The latter are a surrogate for the patients’ general health, as we cannot measure level of exercise, smoking status, and diet directly.

3.4 Analysis via marginal structural models

With respect to the DAG in Figure 1, let A_k be the exposure of interest (FMG membership) at the start of the k^th year in the database, k ∈ {1,2,3}. Let Y be the outcome, which is a count representing health care utilization in the final year (k = 3). Furthermore, let L₀ denote a vector of baseline confounders that may influence the outcome as well as the exposure A₁ (specifically, age, gender, geographical location, diabetes, COPD, hypertension, material deprivation index, number of ER visits and hospitalizations); baseline confounders were measured in year -1, that is, before any patient joined a FMG. The exposure in the second and third years (A₂ and A₃) may also be associated with the time-dependent confounders geographical location, diabetes, COPD, hypertension, material deprivation index, number of ER visits and number of ER hospitalizations measured at the end of Years 1 and 2 (denoted L₁ and L₂).

Identify the histories of exposure and of confounders as Ā = (A₁, A₂, A₃) and L̄ = (L₀, L₁, L₂, L₃) respectively. Let ᾱ = (α₁, α₂, α₃) denote exposure histories for a given patient. Thus there are 2³ = 8 different possible values of ᾱ. For a given patient with a history ᾱ, we will observe the outcome Y_ᾱ. The probability of observing an outcome of γ emergency room visits, given that our entire population experienced the same history ᾱ of FMG is denoted P(Y_ᾱ = γ).

3.4.1 MSM weight models

Stabilized weights were used; these are commonly used to reduce the variability of the MSM estimators [3]. The denominator of the weights for the FMG data was obtained by multiplying the predicted probabilities of a patient belonging to a FMG (the treatment history weight) by that of being uncensored in the database (the censoring history weight), where these models are conditional on the history of covariates and past history. The numerator of the stabilized weights is constructed by multiplying treatment and censoring predicted probabilities that are conditional only on baseline covariates and FMG exposure history. Letting C_t be an indicator of censoring by visit t, the weights are computed as a product of treatment and censoring weights (sw_i and sw_i*, respectively) where

$$s{w}_i=\frac{\begin{array}{c}P(A_1=a_{1i}\mid L_0=l_{0i},C_1=0)\times P(A_2=a_{2i}\mid A_1=a_{1i},L_0=l_{0i},C_1=0,C_2=0)\times \\ P(A_3=a_{3i}\mid A_1=a_{1i},A_2=a_{2i},L_0=l_{0i},C_1=0,C_2=0,C_3=0)\end{array}}{\begin{array}{c}P(A_1=a_{1i}\mid L_0=l_{0i},C_1=0)\times P(A_2=a_{2i}\mid A_1=a_{1i},L_0=l_{0i},L_1=l_{1i},C_1=0,C_2=0)\times \\ P(A_3=a_{3i}\mid A_1=a_{1i},A_2=a_{2i},L_0=l_{0i},L_1=l_{1i},L_2=l_{2i},C_1=0,C_2=0,C_3=0)\end{array}}$$

and

$$s{w}_i\ast =\frac{\begin{array}{c}P(C_1=0\mid L_0=l_{0i})\times P(C_2=0\mid A_1=a_{1i},L_0=l_{0i},C_1=0)\times \\ P(C_3=0\mid A_1=a_{1i},A_2=a_{2i},L_0=l_{0i},C_1=0,C_2=0)\end{array}}{\begin{array}{c}P(C_1=0\mid L_0=l_{0i},)\times P(C_2=0\mid A_1=a_{1i},L_0=l_{0i},L_1=l_{1i},C_1=0)\times \\ P(C_3=0\mid A_1=a_{1i},A_2=a_{2i},L_0=l_{0i},L_1=l_{1i},L_2=l_{2i},C_1=0,C_2=0)\end{array}}.$$

The weights were calculated via the above equation using the confounders described in Section 3.3.3, using logistic regression to estimate each of the probabilities required for the calculations. The resulting summaries (mean, maximum) for the estimated treatment, censoring and final weights respectively are (1.00, 3.01), (1.37, 262.67) and (1.38, 260.27). The final weights are highly right skewed with 75% of patients having a weight less than 1.52. Due to the presence of large weights, a sensitivity analyses was also conducted in which weights are truncated at the 95^th percentile of the estimated weights distribution.

3.4.2 Outcome models

Three models were considered for the analysis of health services utilization by patients in year 3. First, a Poisson likelihood was used since the outcomes of interest are counts (Model 1). However, the overall mean and variance of the outcomes are not very close (mean (variance) ER visits: 0.65 (1.88); hospitalizations: 0.21 (0.37)), suggesting that the Poisson likelihood may not be the best modelling choice, particularly for ER visits; FMG pattern specific means are also typically exceeded by their variances. The second likelihood considered was a negative binomial (Model 2), a popular parametric choice for over-dispersion. As well as exhibiting over-dispersion, the outcome data contains an excess number of zeros. The final likelihood considered is a zero-inflated Poisson (Model 3), which will enable explicit modelling of the excess zeros. We use a standard ZIP model that is a mixture of a point-mass at 0 and a Poisson distribution, with both the mixing probability and the Poisson mean modelled using the same covariates (described below) used in the Poisson and negative binomial outcome models.

Both outcomes were first modelled as a function of FMG history in the three years observed, and second, adjusting for some baseline covariates measured before the patients joined the cohort. The baseline covariates are age, gender, location, diabetes, hypertension (HTN), chronic obstructive pulmonary disease (COPD), socio-economic status, number of ER visits and number of hospitalizations. All models also adjusted for the propensity scores as a covariate. While matching controls for most of the variation in the baseline covariates, some residual imbalance may remain. By conditioning on the propensity score, we achieve conditional independence of individuals in the matched pairs and provide additional control over potential confounding at “low price” of estimating one additional parameter as the matching did not provide exact balance.

Robust standard errors were used to adjust for heterogeneity in the model and estimation of the weights used for the MSM. Since the outcome is not observed in the dataset unless the patient survived and did not transfer to long term care for all three years, the outcome models are restricted to uncensored patients only, though all subjects contribute data as available to the treatment and censoring models.

3.5 Health care utlization results

Tables 3 and 4 report the results of three marginal structural models for the number of emergency room visits and the number of hospitalizations in the final year, respectively. The results are presented in terms of incidence risk ratios relative to ā = (0,0,0), i.e. the case where a person never joins a FMG. Evidence of over-dispersion indicate that the Poisson model in Table 3 (Model 1) is not a good fit for the number of emergency room visits (dispersion/degrees of freedom = 2.43). The negative binomial model (Model 2) estimates a statistically significant dispersion parameter (95% CI) of 2.34 (2.27, 2.41), suggesting that it provides a better fit to the data than the first model, while the zero-inflated Poisson model (Model 3) does not provide a good fit to the data. The negative binomial model yielded the smallest Quasi-Akaike Information Criteria (QIC), however this may not be a reliable measure with which to compare model fits when contrasting across different likelihoods or non-nested models. Vuong’s likelihood ratio test for non-nested likelihoods [22], however its performance for weighted likelihoods in the semi-parametric setting of marginal structural models has not been investigated.

Table 3.

MSMs of the number of ER visits

	M1 Poisson			M2 Negative Binomial			M3 Zero-Inflated Poisson
	RR	[95% CI]		RR	[95% CI]		RR	[95% CI]
ᾱ = (0, 0, 1)	2.107	0.923	4.809	2.099	0.924	4.767	2.218	0.986	4.990
ᾱ = (0, 1, 0)	2.173**	1.236	3.820	2.194**	1.241	3.879	1.670	0.854	3.265
ᾱ = (0, 1, 1)	1.116	0.965	1.292	1.115	0.963	1.291	1.134	0.966	1.332
ᾱ = (1, 0, 0)	1.146**	1.037	1.267	1.151**	1.040	1.272	0.984	0.873	1.109
ᾱ = (1, 0, 1)	1.206**	1.064	1.368	1.209**	1.066	1.372	1.025	0.882	1.191
ᾱ = (1, 1, 0)	1.265**	1.172	1.364	1.266**	1.174	1.366	1.078	0.987	1.177
ᾱ = (1, 1, 1)	0.984	0.956	1.013	0.984	0.956	1.013	0.983	0.948	1.019
ᾱ = (0, 0, 1)							1.090	0.967	1.229
ᾱ = (0, 1, 0)							0.603	0.220	1.658
ᾱ = (0, 1, 1)							1.028	0.829	1.276
ᾱ = (1, 0, 0)							0.757**	0.639	0.896
ᾱ = (1, 0, 1)							0.741**	0.595	0.924
ᾱ = (1, 1, 0)							0.748**	0.660	0.846
ᾱ = (1, 1, 1)							0.997	0.958	1.038
No. Obs.	199,682			199,682			199,682
QIC	3.518			2.953			3.107
BIC	−1.952e+06			−1.85E+06			−1.82E+06
log-likelihood	−351214			−294827			−310192
p	<0.001			<0.001			0.0563
Expected no. of zeros+	108,800			139,686			139,167

All regressions adjust for propensity score and marginal structural weights. For the ZIP, the top panel indicates the Poisson model for the counts, while the bottom panel indicates the parameters for the any/no outcome component of the model using a logistic function.

⁺Actual number of zeros is 138,901.

^*p<.01,

^**p<.001 based on Wald tests

Table 4.

MSMs of the number of hospitalizations

	M1 Poisson			M2 Negative Binomial			M3 - Zero-Inflated Poisson
	RR	[95% CI]		RR	[95% CI]		RR	[95% CI]
ᾱ = (0, 0, 1)	1.660	0.725	3.802	1.657	0.725	3.788	2.184	0.846	5.636
ᾱ = (0, 1, 0)	2.165*	1.201	3.901	2.177**	1.209	3.921	0.645	0.357	1.166
ᾱ = (0, 1, 1)	1.030	0.784	1.352	1.029	0.784	1.351	1.178	0.780	1.777
ᾱ = (1, 0, 0)	1.217**	1.056	1.404	1.218**	1.056	1.405	0.980	0.756	1.272
ᾱ = (1, 0, 1)	1.492**	1.268	1.755	1.493**	1.269	1.757	1.215	0.944	1.565
ᾱ = (1, 1, 0)	1.360**	1.211	1.528	1.361**	1.212	1.529	1.181	0.939	1.485
ᾱ = (1, 1, 1)	1.024	0.988	1.062	1.024	0.988	1.062	1.016	0.952	1.084
ᾱ = (0, 0, 1)							1.455**	1.132	1.870
ᾱ = (0, 1, 0)							7.50e–8**	5.69e-9	9.89e-7
ᾱ = (0, 1, 1)							1.206	0.763	1.906
ᾱ = (1, 0, 0)							0.722	0.491	1.061
ᾱ = (1, 0, 1)							0.735	0.498	1.087
ᾱ = (1, 1, 0)							0.811	0.613	1.073
ᾱ = (1, 1, 1)							0.988	0.907	1.076
No. Obs.	199,682			199,682			199,682
QIC	1.478			1.389			1.399
BIC	−2.224e+06			−2.16E+06			−2.16E+06
log-likelihood	−147552			−138717			−139683
p	<0.001			<0.001			0.108
Expected no. of zeros+	171,823			178,243			178,195

All regressions adjust for propensity score and marginal structural weights. For the ZIP, the top panel indicates the Poisson model for the counts, while the bottom panel indicates the parameters for the any/no outcome component of the model using a logistic function

⁺Actual number of zeros is 177,762.

^*p<.01,

^**p<.001 based on Wald tests

One the other hand, Table 4 shows that the number of hospitalizations exhibits less overdispersion and is well-fitted using the Poisson model (Model 1) (dispersion/degrees of freedom = 1.06). The negative binomial model (Model 2) is also a good fit and estimates a statistically significant dispersion parameter (95% CI) of 2.89 (2.74, 3.04). The negative binomial QAIC is smaller than the Poisson model’s (1.389 and 1.478 respectively), and it estimates a number of zero counts that is much closer to the actual one (178,243 vs. 171,823 respectively, actual is 177,762).

We conclude from Tables 3 and 4 that the zero-inflated Poisson models (Model 3) are not a good fit for either outcome, and that the Poisson model (Model 1) is not a good fit for the number of ER visits since it does not model the over-dispersion in the data. Although Model 1 performs well for the number of hospitalizations, it does not when modelling the number of zero counts. Thus the negative binomial (Model 2) is the best fit for both investigated outcomes. According to Model 2, the rate ratio (RR) of emergency room visits and of hospitalizations for a vulnerable patient in the matched dataset who is in a FMG for all three years compared to none (95% CI) is not significant at 0.984 (0.965, 1.013) and 1.024 (0.988, 1.062) respectively. However, patients with unstable FMG patterns all have an RR that is greater than one for both outcomes, and it is highly significant when the patients are not joining the FMG until the second or third year (ᾱ = (0,0,1) or (0,1,1)). While this is consistent with the descriptive analysis of this small subset of patients, the reason for their high service utilization is not clear. It is plausible that the larger RRs associated with these patterns of FMG membership are a consequence of the smaller numbers of individuals on which the estimates are based.

Table 5 compares four different negative binomial models of the number of emergency room visits to compare different ways in which the analysis might be done. All models adjusted for the propensity score, and all showed a significant likelihood ratio test statistic (p<0.001), suggesting that they are better fits than a model with just the intercept (a null model). A crude model is first estimated (Model 2a), adjusting only for baseline covariates. Model 2b adjusted for baseline covariates and for all time-varying covariates. We expect these two models to be confounded since the first does not account for the time-varying covariates that confound the relationship between the FMG status at the mid-time points and the outcome, and the second adjusts for these variables that are on the causal pathway between the exposure and the outcome. Model 2c is a reproduction of the negative binomial model weighed by MSMw_i described in Table 3. The last model (Model 2d) adjusts for baseline covariates and is weighted by MSMw_i, adjusting for time-varying covariates. As noted in Section 2.2, Models 2c and 2d are expected to provide unbiased estimates, Model 2d being most accurate and producing tighter confidence intervals.

Table 5.

A comparison of MSM and standard regression model estimates (number of ER visits)

Negative Binomial Regressions Modelling the Number of ER Visits
	2a. Crude Model			2b. Adjusted Model			2c. MSM			2d. Adjusted MSM
	RR	[95% CI]		RR	[95% CI]		RR	[95% CI]		RR	[95% CI]
gmf001	1.138**	1.052	1.231	1.085*	1.005	1.170	2.099	0.924	4.767	1.522	0.999	2.320
gmf010	2.018**	1.355	3.003	1.311	0.869	1.978	2.194**	1.241	3.879	1.745*	1.091	2.792
gmf011	1.133*	1.016	1.264	1.065	0.957	1.185	1.115	0.963	1.291	1.034	0.892	1.198
gmf100	1.059	0.975	1.150	1.035	0.955	1.120	1.151**	1.040	1.272	1.034	0.935	1.143
gmf101	1.142*	1.032	1.264	1.056	0.957	1.166	1.209**	1.066	1.372	1.087	0.960	1.231
gmf110	1.197**	1.131	1.267	1.195**	1.132	1.263	1.266**	1.174	1.366	1.171**	1.090	1.258
gmf111	0.961**	0.945	0.977	0.979*	0.963	0.995	0.984	0.956	1.013	0.933**	0.909	0.958
alpha	1.81	1.78	1.84	1.4	1.38	1.43	2.34	2.27	2.41	1.81	1.76	1.86
No. Obs.	206,623			202,678			199,682			199,682
QIC	2.087			2.024			2.953			2.859
BIC	−2.10E+06			−2.07E+06			−1.85E+06			−1.87E+06
loglikelihood	−215581			−205000			−294827			−285420
p	<0.001			<0.001			<0.001			<0.001
Expected no. of zeros+	138,860			135,872			139,686			140,069

All regressions adjust for the propensity score.

Crude model adjusted for baseline covariates; Adjusted model adjusted for baseline and time-varying covariates MSM model using marginal structural weight; Adjusted MSM also adjusted for baseline covariates

⁺Actual number of zeros is 138,901.

^*p<.01,

^**p<.001 based on Wald tests

All four models show that belonging to a FMG for all three years reduces the expected number of visits to the ER for patients in the matched dataset, although the estimated coefficient in Model 2c is not significant and we expect the estimates from 2a and 2b to be biased. Since the MSM adjusting for baseline covariates (Model 2d) may be a better specified model (see Section 3.4.2), our best estimate of the RR of the number of ER visits (95% CI) in this vulnerable population is 0.933 (0.909, 0.958).

For hospitalizations, all four models show no significant effect of belonging to a FMG for all three years compared to none for patients in the matched dataset, with most RR point estimates very close to 1 (results not shown).

3.6 Discussion of findings

One of the key assumptions required in order for marginal structural models to produce unbiased estimates of the causal relationship between exposure and outcome is that there are no unobserved confounders, an assumption that is not testable with the observed data but which may be plausible given good substantive knowledge. In the analysis of the FMG data, it would be desirable to have more detailed information on individual-level socio-economic status and health status, and on the FMG’s modes of practice (CLSC, family medicine unit (Unité de medicine familiale or UMF), private practice, etc.), none of which are available in the dataset.

Some individuals were missing geographic location of residence (1.9%) and some were missing the material deprivation index (1.7%). Although this represents a very small proportion of the population of interest, it appears that the information was not missing completely at random. Overall, 47% of the patients who were dropped from the analysis because of missing values were in the FMG group in the final year. The patients dropping out who were in a FMG in the final year are characterized in that year by a slightly younger age, fewer ER visits, and less diagnoses of hypertension or diabetes compared to patients in a FMG in the final year who did not drop out. In the patients who were not in a FMG in the final year, those who were lost to follow-up were characterized by a geographic location that is closer to university centers, younger age, slightly more advantaged, more likely to be female and fewer diagnoses of hypertension, diabetes and COPD.

A sensitivity analysis assessed the impact of the patients with the 95% highest marginal structural weights in the dataset. The weights of those 6,943 individuals, 49% of which were in a FMG in the final year, were truncated at the 95^th percentile value of 135. The results did not vary greatly from the ones reported previously. The revised baseline adjusted negative binomial MSM (Model 2d) for the number of ER visits estimated an RR (95% CI) of 1.010 (0.939, 1.087) compared to 0.933 (0.909, 0.958) previously reported, no longer showing a significant effect of being in a FMG all three years (but showing very close confidence intervals). Similarly, the same model estimating the number of hospitalizations reported an RR (95% CI) of 1.126 (0.994, 1.276) compared to 0.991 (0.957, 1.026). Thus the individuals with the highest weights seem to slightly pull the estimate away from the null, but they do not seem to skew the reported estimates.

4. Simulation study

In order to assess the ability of the marginal structural model to identify a possible causal relationship between FMG and the health services utilization, synthetic datasets were generated and analysed using different models. First, data with time-varying confounding and mediation over three time intervals were generated using Poisson, log-normal and mixture of a Poisson distribution and a point-mass at 0. The synthetic datasets were generated by approximately copying the relationship between the time-varying number of emergency visits and the FMG exposure in the real dataset. Details of the simulation settings and Stata code used to generate the data are provided in Appendices I and II. Additional simulation results based on smaller sample sizes are provided in Appendix III.

We considered three data-generating scenarios, and for each, the data were analysed using the same models as are considered for the FMG data analysis: regression using a Poisson model, a negative binomial model and a zero-inflated Poisson model. Each regression adjusted for the time-varying exposure variables A₁, A₂ and A₃. Model 1 also adjusted for the baseline covariate L₁, Model 2 adjusted for L₁, L₂ and L₃, and inverse weights were added to (marginal) Models 3 and 4, the latter also adjusting for L₁, consistent with models 2a–2d in Section 3.5

Table 6 describes the results of the Monte Carlo simulations over 500 runs, each time generating a dataset of 100,000 observations. True parameter values were obtained by randomly assigning exposure in a dataset of 1,000,000 observations run 50 times, as described by Xiao and colleagues [23]. Over all simulations, Model 1 estimates the effect of A₁ with little bias since it adjusts only for baseline confounder L₁ and does not adjust for covariates L₂ and L₃ that would be on this causal pathway. However, it poorly estimates A₂ since it fails to account for the effect of L₂ and L₃. On the other hand, Model 2 adjusts for all confounders and does not yield unbiased estimates of the effects of either A₁ or A₂ because the effects of these variables which are mediated through the time-dependent covariates are blocked by the conditioning. Models 3 and 4 consistently have smaller percent biases in their estimates of A₁ and A₂, Model 3 having an average percent bias reduction of 94% compared to Model 2.

Table 6.

Simulation results: Marginal structural GLMs for skewed outcome data

A. Poisson Outcome
1) Poisson Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0653	0.5%	22.8%	1.5%	2.9%	0.029	0.029	0.029	0.028	0.028	0.028	0.028	0.028	0.029	0.033	0.029	0.028	95.0%	92.2%	95.0%	95.4%
A2	−0.0315	7.8%	42.2%	2.8%	8.8%	0.03	0.03	0.03	0.031	0.031	0.031	0.031	0.031	0.03	0.033	0.030	0.031	96.0%	94.0%	95.8%	94.2%
A3	−0.0097	19.1%	5.7%	5.2%	1.2%	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	94.0%	94.2%	94.2%	95.0%

2) Negative Binomial Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0653	1.2%	21.0%	0.2%	0.8%	0.029	0.029	0.029	0.028	0.028	0.028	0.028	0.028	0.029	0.032	0.029	0.028	94.2%	90.4%	94.0%	95.8%
A2	−0.0315	7.0%	41.2%	1.8%	4.8%	0.031	0.031	0.031	0.03	0.031	0.031	0.031	0.031	0.031	0.033	0.031	0.03	94.0%	93.2%	93.8%	95.2%
A3	−0.0097	24.4%	0.8%	0.4%	2.8%	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	0.022	95.0%	95.0%	95.2%	95.0%

3) Zero-Inflated Poisson Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0652	6.2%	18.3%	6.2%	5.6%	0.033	0.033	0.034	0.035	0.034	0.034	0.033	0.035	0.034	0.035	0.034	0.035	92.4%	89.0%	92.2%	91.0%
A2	−0.0332	13.9%	37.6%	8.2%	7.0%	0.036	0.035	0.037	0.035	0.037	0.036	0.037	0.038	0.036	0.037	0.037	0.035	93.2%	90.8%	92.8%	93.4%
A3	−0.0092	15.1%	13.8%	14.8%	2.7%	0.027	0.025	0.027	0.029	0.027	0.025	0.027	0.029	0.028	0.026	0.027	0.029	92.4%	92.2%	92.0%	93.6%

B. Log-Normal Outcome
1) Poisson Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0883	1.8%	25.3%	1.1%	1.1%	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.032	0.023	0.023	93.6%	84.8%	93.6%	93.6%
A2	−0.0445	2.4%	44.9%	1.6%	1.4%	0.025	0.025	0.025	0.025	0.026	0.026	0.026	0.026	0.025	0.032	0.025	0.025	95.4%	90.0%	95.2%	95.2%
A3	−0.0119	24.1%	2.5%	2.8%	3.0%	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	93.6%	95.0%	94.8%	94.8%

2) Negative Binomial Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0883	1.8%	25.2%	1.1%	1.0%	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.032	0.023	0.023	93.8%	84.2%	93.4%	93.6%
A2	−0.0445	2.7%	45.4%	1.4%	1.2%	0.025	0.025	0.025	0.025	0.026	0.026	0.026	0.026	0.025	0.032	0.025	0.025	96.0%	90.0%	95.6%	95.6%
A3	−0.0119	24.9%	3.9%	3.3%	3.5%	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.019	0.018	0.018	0.018	93.0%	94.0%	94.8%	95.0%

3) Zero-Inflated Poisson Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0883	0.3%	26.6%	0.5%	0.6%	0.024	0.024	0.024	0.024	0.023	0.023	0.023	0.023	0.024	0.034	0.024	0.024	92.6%	82.6%	92.6%	92.4%
A2	−0.0445	7.1%	49.3%	3.3%	3.5%	0.026	0.026	0.026	0.026	0.026	0.026	0.026	0.026	0.026	0.034	0.026	0.026	95.4%	85.8%	95.4%	95.4%
A3	−0.0119	27.1%	5.7%	6.1%	6.3%	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	94.8%	95.4%	95.6%	95.6%

C. Mixture Outcome (Zero-Inflated Poisson)
1) Poisson Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0376	1.2%	232.0%	3.8%	13.8%	0.035	0.039	0.034	0.032	0.038	0.038	0.039	0.038	0.035	0.095	0.034	0.033	96.2%	35.8%	96.8%	97.2%
A2	−0.0072	224.0%	1098.0%	37.8%	83.2%	0.04	0.043	0.039	0.037	0.042	0.041	0.043	0.042	0.043	0.09	0.039	0.038	95.2%	52.4%	97.4%	96.8%
A3	−0.0473	40.9%	7.8%	3.3%	7.3%	0.029	0.028	0.025	0.024	0.029	0.029	0.03	0.029	0.035	0.029	0.025	0.024	90.4%	94.4%	98.8%	99.4%

2) Negative Binomial Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0376	5.5%	278.0%	9.6%	21.2%	0.039	0.04	0.036	0.036	0.04	0.039	0.039	0.04	0.039	0.112	0.037	0.037	95.0%	23.2%	96.6%	96.0%
A2	−0.0071	285.0%	1428.0%	37.7%	143.0%	0.042	0.044	0.04	0.039	0.044	0.043	0.043	0.044	0.047	0.111	0.040	0.040	94.4%	34.6%	96.4%	97.4%
A3	−0.0473	52.4%	47.5%	6.7%	16.3%	0.032	0.03	0.026	0.025	0.031	0.03	0.03	0.031	0.04	0.038	0.026	0.026	87.2%	89.4%	97.8%	97.6%

3) Zero-Inflated Poisson Regression
Variable	True Value	% Bias				Monte Carlo SE				Model-based SE				rMSE				Coverage
		M1	M2	M3	M4	M1	Value	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4	M1	M2	M3	M4
A1	0.0890	2.0%	45.5%	0.1%	0.2%	0.03	0.026	0.031	0.03	0.031	0.027	0.031	0.031	0.03	0.048	0.031	0.03	95.0%	67.8%	94.4%	95.6%
A2	−0.0543	9.8%	69.2%	0.5%	0.8%	0.034	0.03	0.035	0.034	0.034	0.03	0.035	0.034	0.034	0.048	0.035	0.034	95.2%	78.8%	95.2%	95.6%
A3	−0.0041	228.0%	160.0%	30.6%	49.9%	0.025	0.023	0.025	0.025	0.024	0.021	0.024	0.024	0.027	0.024	0.025	0.025	91.6%	91.4%	94.2%	94.6%

Model 1: Regression adjusting for time-varying treatment (A₁–A₃) and baseline covariate only (L₁).

Model 2: Regression adjusting for time-varying treatment (A₁–A₃) and all time-varying covariates (L₁–L₃).

Model 3: Marginal structural model weights added in the regression adjusting for time-varying treatment only (A₁–A₃).

Model 4: Marginal structural model weights added in the regression adjusting for time-varying treatment and baseline covariates (A₁–A₃ and L₁).

Regardless of the model used, the simulation results clearly highlight the fact that using a likelihood that properly fits the dataset is of great importance in producing unbiased results. Although MSMs produce estimates that are unbiased, they are not useful when attempting to model data from a binomial-Poisson mixture distribution with a Poisson or a negative binomial likelihood. For example, Model 4 in Table 6 shows a percent bias on the estimate of A₁ of 13.8% and 21.2% when using a Poisson and a negative binomial respectively when the data is generated from a binomial-Poisson mixture. However, when using a zero-inflated Poisson likelihood which models the excess zeros using a binomial distribution, only 0.2% bias remains.

Over all three data-generating models, the adjusted ZIP model performs quite well, though rMSE and coverage are often similar across the models considered. The percent bias, MSE and coverage of the ZIP are not uniformly best, but are typically competitive with the best model. However, we note that these results are limited to a scenario designed to mimic the effect sizes observed in the FMG analysis. We then attempted to implement the simulations in smaller samples and found that we simply had too few events with the parameter settings used; we therefore increased the strength of the relationships throughout the simulations (see Appendices I–II), and conducted further simulations in sample of size 100 and 500. In these much smaller samples, the ZIP model tended to perform less well, and the negative binomial model generally performed well (results shown in Appendix III). Thus we urge caution and recommend careful assessment of model fit in any application: as we saw in the FMG data, the negative binomial model appeared to fit the data significantly better than the Poisson and ZIP models, though coefficient estimates were quite similar to those yielded by the Poisson model.

5. Discussion and conclusion

In this paper, we sought to estimate the causal effect of vulnerable patients being registered to a Family Medicine Group in Québec for three consecutive years on their utilization of health services. To model time-varying confounders and exposure over the three years of observed data, marginal structural models were used, estimated via IPTW. Weighting the regression models allowed the removal of any measured confounding bias based on observed factors at each time period (essentially removing all arrows in the DAG pointing to the exposure). Since the outcomes of interest were counts, generalized linear models with different likelihoods were assessed for best fit. Synthetic datasets were also generated and analysed using the same methods in order to assess the overall performance of these marginal structural models.

Our results suggest that registration to a FMG for all three years caused a slight reduction in the number of emergency room visits, and no significant change in the number of hospitalizations in the final year. These findings are consistent with Strumpf et al. (2011) [24], who analyzed the same dataset using propensity score weighting and FMG status at time zero to investigate patients’ emergency department and hospital utilization. Although they did not adjust for time-varying FMG status and confounding, their results are very similar to ours, finding very small differences in utilization of FMG patients compared to non-FMG patients. Our results rely on the assumption that all confounding variables have been measured. Although physician-level variables were not explicitly included in the exposure models, many of the physician characteristics that are related to FMG status are also patient-level characteristics, e.g. region in which the practice is located is the same as the region in which the patient is treated. Thus, while it may not be exactly true that we have captured all confounding variables, we believe that the assumptions holds at least approximately, as major predictors of health care services utilization and FMG status such as age, diabetes, hypertension, chronic obstructive pulmonary disease, socio-economic status, number of ER visits and hospitalizations prior to the study period were all captured in our data.

The negative binomial likelihood gave the best fit for both outcomes in the real dataset. Simulations displayed the importance of correctly specifying the likelihood when modelling these types of skewed zero-inflated outcome data. Although the simulations found that the zero-inflated Poisson likelihood performed the best overall in simulations designed to mimic the FMG data, models with this likelihood did not produce the best fits when modelling the real data. In this dataset, the negative binomial likelihood was able to best capture the variations in the health services utilization. A variety of plausible likelihoods should be compared when modelling these types of outcomes.

The simulations also highlighted the need for larger samples, as models that perform well in larger samples may not fare as well in settings where information is more limited. Even when sample sizes are large, if outcomes are rare, there may be exposure patterns whose effects estimates are unstable. But note that there were few patients in those unstable FMG groups. For example, we found that patients with some unstable FMG patterns such as belonging only during the second year of the study (the 0,1,0 pattern) had a significantly higher rate of ER visits and hospitalizations than individuals who never belonged to an FMG under most of the models considered, however this was the smallest exposure pattern group, containing fewer than 65 of the more than 206,000 patients in the total sample.

Care must be taken when analysing the causal effect of the introduction of a policy such as FMGs on health care utilization outcomes in an observational study. Propensity scores and marginal structural models are statistical tools that should be used in order to properly adjust for selection bias based on observed factors, time-varying covariates and to model the time-varying exposure. Proper specification of the likelihood function modelling the zero-inflated, right-skewed utilization count data is also essential in order to produce unbiased estimates of the impact of the introduction of the policy.