Rare Variant Association Test with Multiple Phenotypes

Abstract

Although genome-wide association studies (GWAS) have now discovered thousands of genetic variants associated with common traits, such variants cannot explain the large degree of “missing heritability,” likely due to rare variants. The advent of next generation sequencing technology has allowed rare variant detection and association with common traits, often by investigating specific genomic regions for rare variant effects on a trait. Although multiply correlated phenotypes are often concurrently observed in GWAS, most studies analyze only single phenotypes, which may lessen statistical power. To increase power, multivariate analyses, which consider correlations between multiple phenotypes, can be used. However, few existing multi-variant analyses can identify rare variants for assessing multiple phenotypes. Here, we propose Multivariate Association Analysis using Score Statistics (MAAUSS), to identify rare variants associated with multiple phenotypes, based on the widely used Sequence Kernel Association Test (SKAT) for a single phenotype. We applied MAAUSS to Whole Exome Sequencing (WES) data from a Korean population of 1,058 subjects, to discover genes associated with multiple traits of liver function. We then assessed validation of those genes by a replication study, using an independent dataset of 3,445 individuals. Notably, we detected the gene ZNF620 among five significant genes. We then performed a simulation study to compare MAAUSS's performance with existing methods. Overall, MAAUSS successfully conserved type 1 error rates and in many cases, had a higher power than the existing methods. This study illustrates a feasible and straightforward approach for identifying rare variants correlated with multiple phenotypes, with likely relevance to missing heritability.

Introduction

Genome-wide association studies (GWAS) have been commonly used to find genetic variants such as single nucleotide polymorphisms (SNPs) associated with common traits. Early GWAS focused on the analysis of common variants. Although GWAS have identified many variants associated with common traits such as diabetes, heart disease, and schizophrenia [hindorff et al., 2009; Zuk et al., 2014], such common variants could explain only small degrees of the heritability of those phenotypes, a phenomenon known as the missing heritability problem [Zuk et al., 2014; Manolio et al., 2009; Visscher et al., 2008]. For example, human height is known to be a complex trait with an estimated heritability of about 80%, and although at least 40 loci have been associated with the trait, the discovered variants could explain only about 5% of the phenotypic variance [Visscher et al., 2008].

Many researchers have endeavored to identify the primary causes of missing heritability, including gene-gene interactions [Zuk et al., 2012] and rare variants. Gene-gene interaction represents the effect of one gene on traits that are co-affected by other genes. With the development of next-generation sequencing (NGS) technology [Mardis et al., 2008], it is now possible to study rare variants at low cost and high throughput. Many statistical methods have now been developed to study rare variants, including the cohort allelic sums test (CAST) [Morgenthaler et al., 2007], combined multivariate and collapsing (CMC) [Li et al., 2008], weighted sum test (WST) [Madsen et al., 2009], and variable threshold (VT) [Price et al., 2010]. These methods are burden type tests in the sense that they test the association between a summary variable aggregating information on rare variants within a specific genomic region associated with a specific trait. All these burden type tests make some strong assumptions such as causality of all variants, identical effect sizes, and the same directions of effects. However, these assumptions may not be satisfied in biological systems. So, if one performs burden type tests to discover genetic variants associated with traits, statistical power could be lost. To address this problem, several non-burden type tests have been developed. The C-alpha test uses a sum of differences between the expected and actual variances of the distribution of an allele frequency [Neale et al., 2011]. Under certain conditions, the C-alpha test is equivalent to the sequence kernel association test (SKAT), an approach that aggregates individual score test statistics of SNPs in specific genomic regions to efficiently compute region level p-values, while also adjusting for covariates [Wu et al., 2011].

Another effort to reduce missing heritability is to identify additional causal variants associated with a phenotype by increasing statistical power (e.g., larger sample sizes). In GWAS, the phenotype of interest is often derived from multiple variables. For example, diabetes is diagnosed from four phenotypes: two hours after plasma glucose level (≥200mg/dl), fasting glucose (≥126mg/dl), random plasma glucose (≥200mg/dl), and HbA1c (≥6.5%), according to the American Diabetes Association [American diabetes association, 2010]. In addition, GWAS often collect multiple correlated phenotypes simultaneously, such as blood test measures, body size, or multiple answers to a questionnaire [Yang et al., 2012]. Most GWAS have focused on analyses of single phenotypes individually, followed by assembling the results for each single phenotype analysis to simultaneously identify genetic variants associated with multiple phenotypes [Yang et al., 2012]. It has been hypothesized that GWAS may be underpowered to discern genetic variants having only moderate-to-small effects [Yang et al., 2012]. It is possible, however, to increase power by appraising their correlation to identify additional genetic variants with small effects associated with multiple phenotypes. Such joint analyses could also avoid multiple testing penalties caused by analyzing a single phenotype separately [Yang et al., 2012].

In GWAS, several methods have been developed for multivariate analysis [Yang et al., 2012] to consider multiple phenotypes simultaneously. Current multivariate methods can be classified into three categories: regression analysis, variable reduction analysis, and combining approach [Yang et al., 2012]. First, regression analysis is a common statistical method that has been used in many GWAS, and includes multivariate analysis of variance (MANOVA), linear mixed effect models (LMM) [Laird et al., 1982], and generalized estimating equations (GEE) [Liang et al., 1986] analysis. MultiPhen uses a proportional odds logistic model that considers the number of minor alleles in a SNP as a response variable and multiple phenotypes as independent variables [O'reilly et al., 2012]. Secondly, variable reduction methods such as principal components analysis (PCA) [Ott et al., 1999] and canonical correlation analysis (CCA) have also been widely used for multivariate analysis. Finally, combining the test statistics or p-values of univariate analysis is another popular approach [O'Brien, 1984 ; Xu et al., 2003 ; Wei et al., 1985]. The Trait-based Association Test that uses Extended Simes (TATES) procedure combines p-values obtained from standard univariate GWAS to one p-value, while correcting for correlations between p-values that are approximated by correlations between phenotypes [Sluis et al., 2013].

However, many of these existing methods for multivariate analysis cannot be applied to rare variant analyses directly. Rare variants are not appropriate for these analyses, due to their large numbers causing multiple comparison problems and their low frequency. Moreover, sparsity of data could cause problems in fitting regression models and applying variable reduction methods.

Rare variant and multivariate analysis could help reduce the missing heritability problem by detecting novel causal variants. In the current study, we propose the Multivariate Association Analysis Using Score Statistic (MAAUSS) method, an extension of the sequence kernel association test (SKAT), to identify genetic variants associated with multiple phenotypes. SKAT has been widely used in rare variant analysis because it is computationally efficient and uses a regression approach while adjusting for covariates [Wu et al., 2011]. However, since SKAT assumes that response variables are independent, one needs to estimate a variance-covariance matrix between phenotypes and extend statistics by considering the variance-covariance matrix. The variance-covariance matrix is estimated using a restricted maximum likelihood (REML) approach under the null hypothesis that genetic variants have no effects on the phenotypes of interest. Then, the MAAUSS method is developed for the following two cases: (1) homogeneous effects of SNPs (homo-MAAUSS); and (2) heterogeneous effects of SNPs (hetero-MAAUSS) on multiple phenotypes.

Here, we demonstrate that our proposed method is more powerful than TATES and a univariate analysis using SKAT. Furthermore, MAAUSS was applied to Whole Exome Sequencing (WES) data from a Korean population to successfully discover genetic variants associated with levels of the liver enzymes alanine aminotransferase (ALT) and aspartate aminotransferase (AST). We successfully identified 5 significant genes from analysis of the discovery dataset. Also, we validated the significant genes from real data analysis in a replication study using an independent Korean dataset. We detected the ZNF620 gene among 5 significant genes from real data analysis. Consequently, MAAUSS could likely address the missing heritability problem, with applications to “personalized medicine” (based on a specific patient's genome) and the discovery of “targeted therapies” designed to affect the activity of distinct gene products involved in important signal pathways.

Materials and Methods

Data

We used Whole Exome Sequencing (WES) data obtained from a discovery study of Type 2 Diabetes Genetic Exploration by next-generation sequencing in Ethnic Samples (T2D-GENES). Next-generation sequencing (NGS) was performed at the Broad Institute (Cambridge, MA, USA) with Agilent (Santa Clara, CA, USA) v2 capture reagents on a HiSeq platform (Illumina, San Diego, CA) from about 10,000 subjects from 5 different ancestry groups: African Americans, Hispanics, Eastern Asians, Southern Asians, and Europeans. We used subjects included in the Korean Association REsource (KARE) [Cho et al., 2009] study who were also included in Eastern Asians ancestry of T2D-GENES. The KARE study was initiated in 2007 to conduct a large-scale GWA analysis among 10,038 participants from rural Ansung (n = 5,018) and urban Ansan (n = 5,020) cohorts to discover variants associated with numerous complex traits. The KARE dataset was produced from the Korean Genome Analysis Project (4845-301), the Korean Genome and Epidemiology Study (4851-302), and Korea Biobank Project (4851-307, KBP-2013-000) that were supported by the Korea Center for Disease Control and Prevention, Republic of Korea. The data was obtained by sending a request to the Distribution desk of Korea Biobank Network, National Institute of Health, Korea. The selected phenotypes were alanine aminotransferase (ALT) and aspartate aminotransferase (AST), traits both known to relate to liver function. The number of samples was 1,058, excluding subjects who took medication, and the samples used in the analysis were not related. For the analysis, we adjusted for covariates such as age, sex, and area (Ansung or Ansan).

To validate the identified genes from our discovery analysis, we applied MAAUSS to other independent datasets from the Korean population, namely the Health Examinee (HEXA) cohort shared control study [Kim et al., 2011], for a replication study. The HEXA-shared control is part of the Korean Genome and Epidemiology Study (KoGES) population-based cohorts that were initiated in 2001. To build a shared control group for the Korean cancer and coronary artery disease (CAD) GWA studies, 3,445 subjects were randomly selected from the HEXA cohort (aged 40-69) and were genotyped using a HumanExome BeadChip v1.1 (Illumina, Inc., San Diego, CA) containing approximately 240,000 variants. The dataset was comprised of 3,445 individuals with ALT and AST data. The phenotypes were also adjusted for covariates such as age and sex.

Multivariate Association Analysis Using Score Statistic (MAAUSS)

The proposed Multivariate Association Analysis Using Score Statistic (MAAUSS) is a SKAT-based method for analyzing associations between single nucleotide polymorphisms (SNPs) in a specific genomic region of interest and multiple phenotypes. SKAT is an association test for the joint effects of multiple genetic variants in a region of interest on a single phenotype. Such a region could be a known genetic region or a user-defined region. SKAT obtains a p-value for each region while also adjusting for covariate effects, based on a linear mixed effect model for a continuous phenotype, with the assumption of random effects of SNPs [Wu et al., 2011]. Also, adjustment for multiple testing such as family-wise error rate (FWER) or false discovery rate (FDR) controls is necessary, based on the large number of genes in a whole genome.

In this approach, we assume phenotypes to be continuous variables. Assuming that n subjects are sequenced with p SNPs in a region of interest, several variables such as age and sex might be considered for adjustment. For the i-th subject, y_ik denotes the k-th continuous response variable, X_i = (X_i1,X_i2, ..., X_iq) is the vector of q covariates, and G_i = (G_i1,G_i2, ..., G_ip) is the vector of genotypes corresponding to p variants within the region. Assuming an additive genetic model, G_ij = 0, 1, or 2 represents the number of copies of the minor allele in the j-th SNP.

MAAUSS uses the same procedure as the SKAT method but extends the dimension of the covariate matrix, genotype matrix, and corresponding vectors of coefficients to handle multiple phenotypes. Also, it is assumed that multiple phenotypes correlate with each other. However, because we actually do not know the covariance between phenotypes, it is necessary to estimate the variance-covariance matrix. For the i-th subject, yi = (y_i1, ..., y_im)′ is the vector of m multiple phenotypes, Z_i = diag(X_i, ..., X_i), α₀ = (α₀₁, ..., α_0m)′, and $\tilde{\alpha }={({\alpha }_1^{\prime },\dots ,{\alpha }_m^{\prime })}^{\prime }$ are an m × (mq) extended covariate matrix and vectors of corresponding coefficients, respectively. ε_i is an error term following a multivariate normal distribution, with a mean of a zero vector and a variance-covariance matrix of V. Also, and a B_i and $\tilde{\beta }$ are genotype matrix and a vector of random effects of SNPs on multiple phenotypes, respectively. Then, we can consider the multivariate linear model:

$${\mathbf{y}}_{\mathbf{i}}={\alpha }_0+{\mathit{Z}}_{\mathbf{i}}\tilde{\alpha }+{\mathbf{B}}_{\mathbf{i}}\tilde{\beta }+{\epsilon }_{\mathbf{i}}.$$ (1)

This model considers the heterogeneous effects of covariates on multiple phenotypes. Here, we consider the case when the random effects of a SNP are identical for all phenotypes and the case when they are different on each phenotype. For these two cases, a genotype matrix B_i and a corresponding vector $\tilde{\beta }$ would be different.

Homogeneous Effects of SNPs on Multiple Phenotypes

Assuming that SNPs have homogeneous or heterogeneous effects on phenotypes, the homogeneous case (homo-MAAUSS) supposes that the effects of a SNP on multiple phenotypes are identical. With an assumption of homogeneous effects, ${\mathbf{B}}_{\mathbf{i}}={({\mathbf{G}}_{\mathbf{i}}^{\prime },\dots ,{\mathbf{G}}_{\mathbf{i}}^{\prime })}^{\prime }$ and $\tilde{\beta }={({\beta }_1,\dots ,{\beta }_p)}^{\prime }$ are an m × p genotype matrix of the i-th subject and a corresponding coefficient vector with length p, respectively. Evaluating whether the genetic variants have effects on the phenotypes in the model coincides with testing the null hypothesis $H_0:\tilde{\beta }=0$, that is, β₁ = ··· = β_p = 0. MAAUSS assumes that each β_j follows an arbitrary distribution with a mean of zero and a variance of τw_j², where τ is a variance component and w_j is a prespecified weight for the j-th SNP. W = diag(w₁, ..., w_p) is a diagonal matrix with elements of the weights of p variants. A commonly used weight is the value of a density function of beta distribution with 1 and 25 degrees of freedom for a given minor allele frequency (MAF) of the SNP, which means assigning greater weights to rarer SNPs. Then, testing the null hypothesis $H_0:\tilde{\beta }=0$ is equivalent to testing H₀ : τ = 0 using a variance component score test in the corresponding linear mixed effect model. The score statistic is then:

$$\mathbf{Q}={(\mathbf{y}-\widehat{\mu })}^{\prime }{\widehat{\Omega }}^{-1}\mathbf{K}{\widehat{\Omega }}^{-1}(\mathbf{y}-\widehat{\mu }),$$ (2)

where $\widehat{\mu }=\widehat{{\alpha }_0}+\mathbf{Z}\widehat{\tilde{\alpha }}$ is an estimated mean of y under the null hypothesis, using general linear regression on the (nm) × (mq) extended covariate matrix Z = (Z₁′, ..., Z_n′)′. Here, y = y₁′, ..., y_n′)′ is a vector of multiple response variables of length nm, K = BWWB′ where B = (B₁′, ..., B_n′)′ is a (nm) × p genotype matrix (W is described above), V̂ is an estimated m × m variance-covariance matrix between m phenotypes under the null hypothesis, using a Restricted Maximum Likelihood (REML) approach, and $\widehat{\Omega }={\mathit{I}}_{\mathit{n}}\otimes \widehat{\mathbf{V}}$ is an estimated (nm) × (nm) variance-covariance matrix. K is an (nm) × matrix with the (i, i′)-th element equal to $K({\mathbf{G}}_{\mathbf{i}},{\mathbf{G}}_{{\mathbf{i}}^{\prime }})={\sum }_{j=1}^p{w_j}^2{G}_{ij}{G}_{i\prime j}.K(\cdot ,\cdot )$ is the “kernel function” and K(G_i, G_i′) measures the genetic similarity between i and i′-th response variables in the genomic region through p markers [Wu et al., 2011]. It means that when i and i′-th response variables are from different subjects, K(G_i, G_i′) presents the genetic similarity between the subjects. Consequently, the score statistic Q follows a mixture of chi-square distributions ${\sum }_{l=1}^{nm}{\lambda }_l{{\chi }_{1,l}}^2$ where χ_1,λ² is an independent chisquare distribution with 1 degree of freedom, and λ_l is the l-th eigenvalue of ${{\mathbf{P}}_0}^{1∕2}{{\mathbf{KP}}_0}^{1∕2},{\mathbf{P}}_0={\widehat{\Omega }}^{-1}-{\widehat{\Omega }}^{-1}\tilde{\mathbf{Z}}{\left({\tilde{\mathbf{Z}}}^{\prime }{\widehat{\Omega }}^{-1}\tilde{\mathbf{Z}}\right)}^{-1}{\tilde{\mathbf{Z}}}^{\prime }{\widehat{\Omega }}^{-1}$ and Z̃ = [1,Z].

Heterogeneous Effects of SNPs on Multiple Phenotypes

In the case of the heterogeneous assumption (hetero-MAAUSS), ${\mathbf{B}}_{\mathbf{i}}=I_{\mathit{m}}\otimes {\mathbf{G}}_{\mathbf{i}}$ is an m × (mp) genotype matrix and $\tilde{\beta }$ is a corresponding coefficient vector of length mp. The test statistic and its distribution take the same form shown in equation (2) for the homogeneous effects case, but uses different B_is. The assumption of homogeneous effects of SNPs on multiple phenotypes could increase statistical power, because it tests for a smaller number of parameters. Therefore, an assumption of homogeneous effects could bring better results if the assumption is satisfied.

In univariate cases, when the number of phenotypes m is one, hetero-MAAUSS is equivalent to homo-MAAUSS and SKAT. Under the same score statistic as MAAUSS, K = GWWG′, and $\widehat{\mu }={\widehat{\alpha }}_0+\mathbf{X}\widehat{\alpha }$ is the predicted mean of y under H₀, where ${\widehat{\alpha }}_0$ and $\widehat{\alpha }$ are the estimated coefficients under the null model using multiple linear regression, i.e., ${[{\widehat{\alpha }}_0,\widehat{\alpha }]}^{\prime }={\left({\tilde{\mathbf{X}}}^{\prime }{\widehat{\mathbf{V}}}^{-1}\tilde{\mathbf{X}}\right)}^{-1}{\tilde{\mathbf{X}}}^{\prime }{\widehat{\mathbf{V}}}^{-1}\mathbf{y}$ where $\tilde{\mathbf{X}}=[1,\mathbf{X}]$ We assume that the variance of y_i is σ², such that $\widehat{\Omega }$ is an n × n diagonal matrix with the elementis $\widehat{{\sigma }^2}$. Here, G is an n × p matrix with the (i, j)-th element being the genotype of the j-th SNP of the i-th subject, and W = diag(w₁, ..., w_p) is a diagonal matrix with elements of pre-specified weights of p variants. The score statistic Q follows a mixture of chi-square distributions ${\sum }_{l=1}^n{\lambda }_l{{\chi }_{1,l}}^2$, where χ_1,l² is an independent chi-square distribution with 1 degree of freedom, λ_l is the l-th eigenvalue of ${{\mathbf{P}}_0}^{1∕2}{{\mathbf{KP}}_0}^{1∕2}$, and ${\mathbf{P}}_0={\widehat{\mathbf{V}}}^{-1}-{\widehat{\mathbf{V}}}^{-1}\tilde{\mathbf{X}}{\left({\tilde{\mathbf{X}}}^{\prime }{\widehat{\mathbf{V}}}^{-1}\tilde{\mathbf{X}}\right)}^{-1}{\tilde{\mathbf{X}}}^{\prime }{\widehat{\mathbf{V}}}^{-1}$.

Numerical Experiments and Simulations

We next performed simulation studies to investigate whether or not MAAUSS preserved type 1 error rates, and to evaluate its power compared to univariate SKAT and TATES. For univariate SKAT, we obtained the results of each phenotype from SKAT, and then performed multiple comparisons via Bonferroni's correction. TATES also used the test results of SKAT to combine p-values from each phenotype.

Simulation for Type 1 Error

Simulation studies were used to evaluate whether MAAUSS preserved the desired type 1 error rate at a significant level, such as α = 10⁻⁶, which is smaller than Bonferroni corrected significance level when we performed gene level tests with all genes (2 × 10⁻⁶ = 0.05/25,000). To obtain the expected type 1 error rate at this significance level, at least 1 million simulation datasets were needed. However, generating genotypes was too time-consuming, due to computational burden. Therefore, we generated 10,000 genotype datasets with lengths of 30kb, using SimRare, a program that generates variant data for a specific genomic region using forward-time simulations that incorporate realistic population demographic and evolutionary scenarios [Li et al., 2012]. We also made 100 sets of continuous phenotypes to obtain 10⁶ combinations of simulation datasets, using the model:

$$y_{ik}=0.5X_{i1}+0.5X_{i2}+{\epsilon }_{ik},k=1,2$$

where X_i1 is a continuous covariate following a standard normal distribution, and X_i2 is a binary covariate following a Bernoulli distribution with a probability of 0.5. For simplicity, we performed the simulation study for the bivariate case. ε_i = (ε_i1,ε_i2)′ is an error vector following the bivaiate normal distribution with a mean of (0,0)′ and a variance-covariance of $\mathrm{V}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill 1\hfill \end{array}\right)$, where ρ is set to be one of (0.25, 0.5, 0.75). Note that the response variable, y_ik, was not affected by any of the genotype information to calculate type 1 error under the null hypothesis. The simulation study was performed on sample sizes of 500 and 1,000. To apply MAAUSS, and compare it to other methods for rare variant analysis, we considered only rare variants having MAF ≤ 1%. We also filtered variants found in only one or two individuals. The average numbers of variants in a gene after filtering were 280 and 813, corresponding to sample sizes of 500 and 1,000, respectively.

Simulation of Empirical Power

We used similar approaches as above for type 1 error simulations, but also added genotype information to the phenotypes. Let t be the number of causal variants in a 10% subset randomly selected from the simulated rare variants passing the previous filtering criteria. We made 100 continuous phenotypes with a sample size of 1,000, according to 100 genotype datasets randomly selected from the 10,000 genotype datasets generated for estimating type 1 error, using the model:

$$y_{ik}=0.5X_{i1}+0.5X_{i2}+{\beta }_{1k}{g}_{i1}+{\beta }_{2k}{g}_{i2}+\cdots +{\beta }_{pk}{g}_{it}+{\epsilon }_{ik},k=1,2$$

where X_i1, X_i2, and ε_ik are defined the same as for the type 1 error rate simulations described above. β_jk is the effect size of the j-th causal rare variant on the k-th phenotype. We set the value of β_jk to c_k|log₁₀MAF_j|, where MAF_j is the minor allele frequency of the j-th variant, meaning that rarer variants would affect more phenotypes. We next considered the ratio Δ (±2, ±1, ±0.75, ±0.5, ±0.25, ±0.1, 0) of c₂ to c₁; in other words, c₂ = Δ × c₁. Here, we set c₁ to 0.05 and 0.2. We also took into account the directions of on βs a phenotype by randomly selecting a subset of βs in the opposite direction. We assumed that η% of the causal variants had effects in the opposite direction, where η = 0, 20, and 50. For example, when the value of η is 20, in the case of c₁ = 0.2 and c₂ = −0.1 (Δ = −0.5), 80% of causal SNP effects on the first and second phenotypes are 0.2|log₁₀MAF_j| and −0.1|log₁₀MAF_j|, respectively.

The remaining 20% of effects are −0.2|log₁₀MAF_j| and 0.1|log₁₀MAF_j| on the first and second phenotypes, respectively.

Results

Simulation of the Type 1 Error

Table I shows the empirical type 1 error rates for univariate SKAT (after multiplying two p-values, obtained from each phenotype using SKAT, by 2, if at least one of them was smaller than α, it was counted as a significant result), TATES, and MAAUSS for each significance level α = 10⁻³, 10⁻⁴, and 10⁻⁵ for a sample size of 500. These results suggest that the type 1 error rate is protected for all methods and the empirical type 1 error rates are similar. However, at the significance level of α = 10⁻⁵, MAAUSS (both homogeneous and heterogeneous cases) was less conservative than the other two methods. That is, there were more cases when MAAUSS had p-values smaller than the other two methods. For the sample size of 1,000, the empirical type 1 error rates are presented in Table II. While the type 1 error rate was slightly higher than that in the sample size of 500, the type 1 error rate was still preserved.

Table I.

Estimated type 1 errors of SKAT, TATES, and MAAUSS for a sample size of 500.

ρ	α	Univariate SKAT	TATES	Homo-MAAUSS	Hetero-MAAUSS
0.25	10−3	6.51E-04	6.63E-04	7.08E-04	6.66E-04
	10−4	4.90E-05	5.00E-05	5.20E-05	4.70E-05
	10−5	2.00E-06	2.00E-06	3.00E-06	4.00E-06
0.5	10−3	6.36E-04	7.00E-04	6.46E-04	6.40E-04
	10−4	5.90E-05	6.70E-05	6.00E-05	5.70E-05
	10−5	2.00E-06	2.00E-06	8.00E-06	6.00E-06
0.75	10−3	6.13E-04	7.95E-04	6.63E-04	6.54E-04
	10−4	5.20E-05	6.60E-05	6.30E-05	5.40E-05
	10−5	3.00E-06	4.00E-06	7.00E-06	5.00E-06

The values in each cell represent the proportion of p-values under each significance level α for the results of 10⁶ simulated phenotypes.

Table II.

Estimated type 1 errors of SKAT, TATES, and MAAUSS for a sample size of 1,000.

ρ	α	Univariate SKAT	TATES	Homo-MAAUSS	Hetero-MAAUSS
0.25	10−3	7.45E-04	7.60E-04	7.50E-04	7.82E-04
	10−4	7.10E-05	7.10E-05	7.10E-05	7.50E-05
	10−5	2.00E-06	2.00E-06	7.00E-06	7.00E-06
0.5	10−3	7.32E-04	8.00E-04	7.73E-04	7.40E-04
	10−4	7.50E-05	8.40E-05	8.40E-05	6.20E-05
	10−5	5.00E-06	6.00E-06	5.00E-06	8.00E-06
0.75	10−3	6.68E-04	8.42E-04	7.48E-04	7.42E-04
	10−4	6.40E-05	7.60E-05	6.40E-05	6.30E-05
	10−5	5.00E-06	7.00E-06	5.00E-06	6.00E-06

The values in each cell represent the proportion of p-values under each significance level α for the results of 10⁶ simulated phenotypes.

Statistical Power of MAAUSS and Other Methods

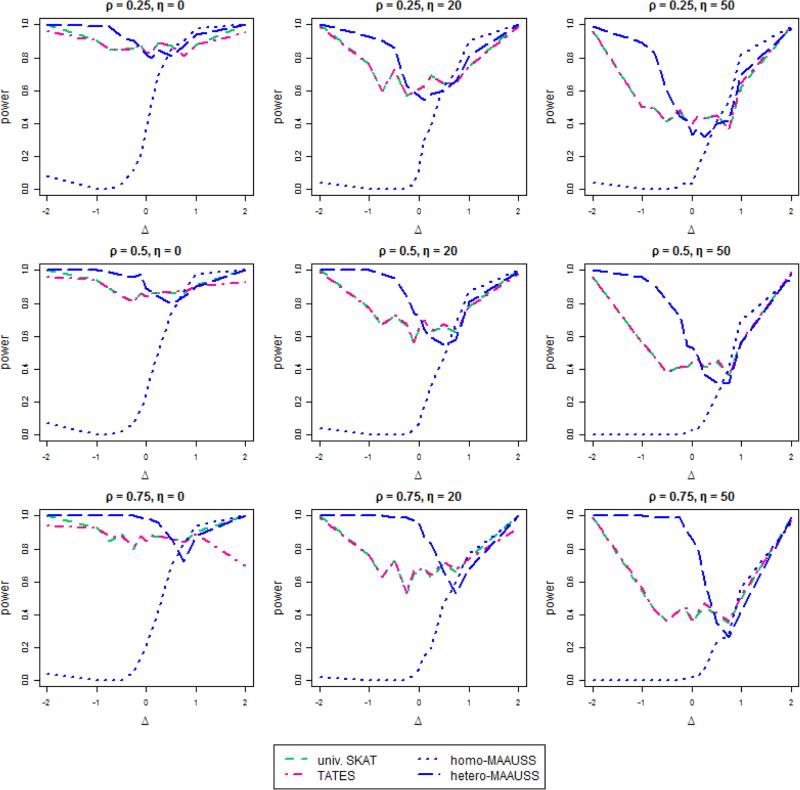
We compared the power of MAAUSS with two other methods, using 100 simulated datasets for several cases. We set the effects of the j-th SNP on the first phenotype to be 0.2|log₁₀MAF_j| (c₁ = 0.2) and 0.05|log₁₀MAF_j| (c₁ = 0.05). The effect on the second phenotype was assumed to be prorportional to the effects on the first phenotype (β_j2 = Δ × β_j1). The proportionality parameter Δ, ranging from −2 to 2, represents the difference of SNP effects on each phenotype. The results for c₁ = 0.2 are whon in Figure 1. The nine graphs present the statistical power of MAAUSS compared to univariate SKAT and TATES in different scenarios of the direction of effects on a phenotype η, and the correlations between phenotypes ρ. The x-axis presents Δ, and the y-axis represents the statistical power estimates, i.e., the proportion of significant results among 100 tests at the significance level α=10⁻⁶. Three plots in each row show the different settings of η (0, 20, and 50 from left to right) and three plots in each column represent the different correlation ρ between phenotypes (0.25, 0.5, and 0.75 from top to bottom). The statistical power increased when the directions of the SNP effects on a phenotype became similar.

Figure 1. The power of MAAUSS compared with univariate SKAT and TATES when c₁ = 0.2.

The effect of the j-th SNP on the first phenotype β_j1 is 0.2|log₁₀MAF_j| and the effect on the second phenotype is Δ × β_i1. The x-axis presents Δ and the y-axis represents the statistical power, i.e., the proportion of significant results among 100 tests at a significance level of α = 10⁻⁶. The three plots in each row show the different settings of η. that are the proportions of different directions of effects on a phenotype. The three plots in each column represent the different correlations between phenotypes, ρ.

When Δ has negative values, hetero-MAAUSS has similar or greater power than univariate SKAT and TATES, while the power of homo-MAAUSS is close to zero in all settings, due to assuming the effects of SNPs on phenotypes are all the same. The average MAF was 0.004189 for a sample size of 1,000, and the average effect size on the first phenotype was 0.4756. When Δ was equal to −1, the average effect size on the second phenotype was −0.4756. The large difference between the two effects, and the opposite directions, offset the effects of SNPs on phenotypes under the assumption of homogeneity. As the correlation increases, the power of hetero-MAAUSS also increases. As η increases (i.e., the directions of effects on a phenotype become more different), the difference of the power between hetero-MAAUSS and univariate SKAT or TATES increases. Specifically, when ρ and η are 0.75 and 50, respectively, hetero-MAAUSS far surpasses the performances of univariate SKAT and TATES.

As Δ changes from a negative to a positive value, the power of homo-MAAUSS rapidly increases. Furthermore, when the value of Δ is close to 1, homo-MAAUSS has greater power than univariate SKAT and TATES. When the correlation between phenotypes is low (ρ = 0.25), the power of hetero-MAAUSS is also higher than the other two methods. When the correlation is high (ρ = 0.75), the power of hetero-MAAUSS is slightly lower than univariate SKAT and TATES. There are some cases when the power of univariate SKAT and TATES are similar or greater than both homo- and hetero-MAAUSS. However, as ρ increases and β decreases, the power of MAAUSS exceeds that of univariate SKAT and TATES, under more cases of Δ.

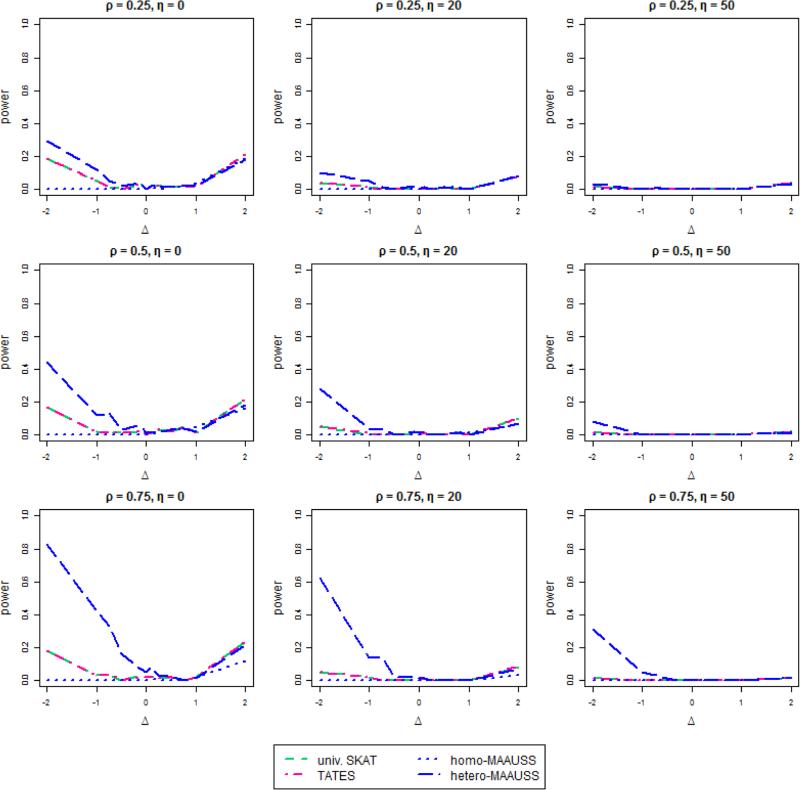
The results for c₁ = 0.05 are shown in Figure 2. The power is much lower than that in the case of c₁ = 0.2, because of the small effect sizes. In all settings, univariate SKAT, TATES, and MAAUSS had similar power when the value of Δ was positive. However, when Δ has negative values, the power of hetero-MAAUSS is much greater than the other methods. Furthermore, as the correlation between phenotypes increases, the power of hetero-MAAUSS also increases, especially when (ρ,η,Δ) are (0.75,0,-2), the power of hetero-MAAUSS is 0.83, while the power of both univariate SKAT and TATES is 0.18.

Figure 2. The power of MAAUSS compared with univariate SKAT and TATES when c₁ = 0.05.

The effect of j-th SNP on the first phenotype β_j1 is 0.05|log₁₀MAF_j|, and the effect on the second phenotype is Δ × β_j1.

In summary, if the directions of effects of SNPs are different on phenotypes, hetero-MAAUSS has better power than other methods, especially when the correlation between phenotypes is high. Furthermore, when the effects become similar (i.e., in the same direction), homo-MAAUSS tends to have the largest power.

Application to Korean Exome data

We next analyzed Whole Exome Sequencing (WES) data from the Korean population using the proposed method MAAUSS, in comparison to univariate SKAT and TATES. The estimated correlation between ALT and AST was 0.7255, as estimated using an REML approach with covariate adjustment, and the correlation was 0.7129, without covariate adjustment. We analyzed the data with several filtering option of rare variants. We used two types of filtering conditions: minor allele frequency (MAF) and minor allele count (MAC). We perform the analysis using the SNPs having MAF less than 1% or 5%, and having MAC greater or equal than from 2 to 4. Table III present the five genes significant at the 5% significance level after the Bonferroni correction by any of four methods (univariate SKAT, TATES, homo-MAAUSS, and hetero-MAAUSS). Table III shows the number of SNPs in each gene, and the p-values that have at least one significant result from the analyses based on several filtering options. The result of univariate SKAT was obtained by calculating the minimum p-value between two phenotypes and comparing it to 2.5% for Bonferroni correction. There are several genes that have only one variant. For these cases, the univariate SKAT analysis provided similar results to those of standard single variant analysis. Slight differences were caused by using the fixed effects or random effects. MAAUSS can also handle the genes with single variants and provided similar results to those from the standard analysis.

Table III.

Analysis results for testing rare variant effects on ALT and AST using univariate SKAT, TATES and MAASS for rare variants with different filtering options.

				GPT	PCDHGB1	ZNF620
MAF ≤1%	MAC ≥2	Discovery for 13,317 genes (cut off : 3.75E-06)	# of SNPs	3	3	4
			ALT	5.51E-03	3.17E-02	3.52E-01
			AST	4.70E-01	8.32E-05	3.98E-06
			TATES	8.88E-03	1.34E-04	6.42E-06
			Homo-M	7.59E-01	1.77E-04	8.02E-05
			Hetero-M	2.84E-06	4.90E-04	9.80E-08
		replication	# of SNPs	2	14	-
			Homo-M	1.00E+00	9.47E-01	-
			Hetero-M	9.96E-01	7.97E-01	-
	MAC ≥3	Discovery for 11,348 genes (cut off : 4.41E-06)	# of SNPs	-	2	4
			ALT	-	3.30E-02	3.52E-01
			AST	-	8.45E-05	3.98E-06
			TATES	-	1.36E-04	6.42E-06
			Homo-M	-	2.55E-04	8.02E-05
			Hetero-M	-	5.99E-04	9.80E-08
		replication	# of SNPs	-	14	-
			Homo-M	-	9.47E-01	-
			Hetero-M	-	7.97E-01	-
	MAC ≥4	Discovery for 9,818 genes (cut off : 5.09E-06)	# of SNPs	-	2	-
			ALT	-	3.30E-02	-
			AST	-	8.45E-05	-
			TATES	-	1.36E-04	-
			Homo-M	-	2.55E-04	-
			Hetero-M	-	5.99E-04	-
		replication	# of SNPs	-	14	-
			Homo-M	-	9.47E-01	-
			Hetero-M	-	7.97E-01	-
MAF ≤5%	MAC ≥2	Discovery for 13,731 genes (cut off : 3.64E-06)	# of SNPs	3	6	4
			ALT	5.51E-03	1.44E-03	3.52E-01
			AST	4.70E-01	3.62E-06	3.98E-06
			TATES	8.88E-03	5.83E-06	6.42E-06
			Homo-M	7.59E-01	4.00E-06	8.02E-05
			Hetero-M	2.84E-06	2.06E-05	9.80E-08
		replication	# of SNPs	2	25	-
			Homo-M	1.00E+00	4.12E-01	-
			Hetero-M	9.96E-01	9.50E-02	-
	MAC ≥3	Discovery for 12,139 genes (cut off : 4.12E-06)	# of SNPs	-	5	4
			ALT	-	1.48E-03	3.52E-01
			AST	-	4.01E-06	3.98E-06
			TATES	-	6.46E-06	6.42E-06
			Homo-M	-	4.26E-06	8.02E-05
			Hetero-M	-	1.77E-05	9.80E-08
		replication	# of SNPs	-	25	-
			Homo-M	-	4.12E-01	-
			Hetero-M	-	9.50E-02	-
	MAC ≥4	Discovery for 10,954 genes (cut off : 4.56E-06)	# of SNPs	-	5	-
			ALT	-	1.48E-03	-
			AST	-	4.01E-06	-
			TATES	-	6.46E-06	-
			Homo-M	-	4.26E-06	-
			Hetero-M	-	1.77E-05	-
		replication	# of SNPs	-	25	-
			Homo-M	-	4.12E-01	-
			Hetero-M	-	9.50E-02	-

Five genes had at least one significant result using the four methods at the Bonferroni significance level. The significant results are shown in bold for each Bonferroni cutoff.

The GPT gene was detected only by hetero-MAAUSS when selecting the SNPs with MAF≤1% or 5% and MAC≥ 2 (p-value=2.84 × 10⁻⁶) whose significance was caused by three SNPs (var_8_145729713, var_8_145730446, and var_8_145731280). For the SNPs with MAC≥3, there was only one SNP (var_8_145730446) left. The p-value of hetero-MAAUSS increased slightly, but remained very small. The other methods, univariate SKAT, TATES, and homo-MAAUSS, did not provide any significant results. The GPT gene is known to encode cytosolic alanine aminotransaminase 1 (ALT 1), and also be associated with fatty liver disease and liver cirrhosis [Safran et al., 2010].

The PCDHGB1 gene was found by homo-MAAUSS only when selecting the SNPs with MAF≤5% and MAC≥ 4 (p-value=4.26 × 10⁻⁶). The PCDHGB1 gene is known to be related to operational tolerance in liver transplantation [Martinez-Llordella et al., 2007]. This gene is included in a functional category of cadherins, which significantly differ between operationally tolerant recipients of deceased adult donor liver transplants and liver recipients in whom drug weaning was attempted but led to acute rejection requiring reintroduction of immunosuppressors.

The ZNF620 gene was identified by hetero-MAAUSS when selecting SNPs with MAF≤1% or 5% and MAC≥2 or 3 (p-value=9.80 × 10⁻⁸) whose significance was caused by four SNPs. We could locate no literature reports on the ZNF620 gene or its effect on liver function.

Replication Study

We next performed a validation study for the three genes identified from the analysis of the discovery data of Korean population. The replication dataset was the HEXA-shared control dataset. The replication analysis found one significant gene, ZNF620, among the three remaining genes at a significance level of α=0.05, using both homo- and hetero-MAAUSS with SNPs having MAF≤5% and MAC≥2 to 4 (p-value=4.66 ×10–2 and 3.66 × 10⁻², respectively). Especially, the ZNF620 gene was significant at the Bonferroni's significant level in discovery study by only hetero-MAAUSS not univariate SKAT or TATES. The ZNF620 gene is unknown to associate with certain diseases or traits. Thus, ZNF620 is a good candidate gene associated with liver function or a disease that requires further study.

Discussion

Several methods have been proposed for identifying rare variants within specific genomic regions. Although multivariate analyses of common variants are available, there are few methods for multivariate analysis of rare variants within a distinct region. Here, we proposed a new approach, MAAUSS, an extended method of SKAT for multiply correlated phenotypes. MAAUSS is a statistical method for performing association tests between SNPs in a region of interest and multiple phenotypes. We demonstrated that MAAUSS successfully conserved type 1 error rates and in many cases, had a higher power than the univariate SKAT and TATES methods. Homo-MAAUSS yielded more significant results when the effects of SNPs on phenotypes tended to be similar. Also, Hetero-MAAUSS, in particular, detected many significant results when the difference between effects on phenotypes was large and especially, when the directions of effects were different across phenotypes.

Moreover, MAAUSS can be applied to multiply correlated binary phenotypes, handled by a working correlation matrix, using the generalized estimating equation (GEE) approach [Lian et al., 1986]. This quasi-score type of statistics can be easily constructed for association tests [Godambe et al., 1989], and MAAUSS could also handle correlated binary and continuous phenotypes in a similar manner, using the GEE framework.

MAAUSS can be used under the assumption of homogeneous effects of a SNP on phenotypes or with no such assumption. If users have some information about the homogeneity of SNP effects in advance of the analysis, a more reasonable choice could be selected. However, that information is usually not known. Hetero-MAAUSS allows different effects of a SNP on phenotypes, although the dimension of the genotype matrix is larger than that in the homogeneous case, resulting in a lower speed of computation. The homogeneity of effects on phenotypes could be tested using statistical methods such as likelihood ratio tests. If the hypothesis of homogeneity is rejected, then hetero-MAAUSS should be used to analyze association.

Furthermore, our proposed MAAUSS method uses the same variance component τ for all phenotypes, meaning that MAAUSS assumes the same variance of SNP effects of on all phenotypes, even in the heterogeneous case. If the ranges of phenotypes are different, or the magnitudes of effects are distinct, assuming the same variance may not be appropriate. It would also be possible to put a different variance component on each phenotype and then derive a statistic along with its distribution.

Computational time might be a weakness of MAAUSS. Since MAAUSS is an extended method of SKAT that expands a dimension of phenotypes and design matrices, analyzing a large number of phenotypes and a large sample size could become a computational burden. For example, if the number of phenotypes of interest is 10, then the length of a phenotype vector, the number of columns and rows of a covariate matrix would be 10 times larger (i.e., a 100 times larger covariate matrix), and also the genotype matrix would be 10 and 100 times larger in the homogeneous and heterogeneous cases, respectively. We measured the computation times for the analysis of various number of phenotypes for sample sizes of 1,000 and 5,000, and the results are presented in Table IV. The number of genes and covariates were 15,866 and 12 (age, sex, and top 10 principal components of genetic variation [Price et al., 2006]), respectively. For reducing the computation time and using software available, the covariates under the null were estimated first by the generalized least squares method. After estimating the covariates, the residuals from the null model were decomposed orthogonally. Finally, the meta-SKAT method applied to the decomposed residuals for estimating the score-type statistics. Although our effort for reducing the computation time, the computational time taken for analysis naturally increases as the number of phenotypes or samples increases. Such an increase of computational time might be caused by calculating score statistics. However, the computational time is smaller than m times of a univariate case, except for the sample size of 5,000 and the number of phenotypes of 10. So, the computational time of MAAUSS would not be a big hurdle.

Table IV.

Computation time taken to analyze real data using SKAT and MAAUSS.

Time (min.)	Univariate (SKAT)	2 phenotypes		3 phenotypes		5 phenotypes		10 phenotypes
		Homo-	Hetero-	Homo-	Hetero-	Homo-	Hetero-	Homo-	Hetero-
1,000 samples	6.46	6.59	6.65	8.87	9.04	14.60	14.72	49.30	50.45
5,000 samples	14.76	21.81	22.15	33.27	33.92	59.59	61.88	301.69	315.67

In summary, we have introduced MAAUSS as a statistical method for genomic regionally-based multivariate analysis that retains the beneficial features of SKAT, and considers either homogeneous or heterogeneous effects of a SNP on a phenotypes. We demonstrated MAAUSS to achieve increased power through a large number of simulations over a wide range of scenarios. Consequently, we propose the use of MAAUSS for rare variant analysis of multiply correlated phenotypes. Such knowledge could increase the efficacy of genotyping for phenotype prediction, including the recent adoption of genomic “personalized medicine.”