Non-Linear Bayesian Framework to Determine the Transcriptional Effects of Cancer-Associated Genomic Aberrations

Abstract

While the tumorigenic effects of specific recurrent mutations in known cancer driver-genes is well-characterized, not much is known about the functional relevance of the vast majority of recurrent mutations observed across cancers. Prior studies have attempted to identify functional genomic aberrations by integrating multi-omics measurements in cancer samples with community-curated biological pathway networks. However, the majority of these approaches overlook the following biological considerations: i) signaling pathway networks are highly tissue-specific and their regulatory interactions differ across tissue types; ii) regulatory factors exhibit heterogeneous influence on downstream gene transcription; iii) epigenetic and genomic alterations exhibit nonlinear impact on gene transcription.

In order to accommodate these biological effects, we propose a hybrid Bayesian method to learn tissue-specific pairwise influence models amongst genes and to predict a gene's expression level as a nonlinear-function of its epigenetic and regulatory influences. We employ a novel tree-based depth-penalization mechanism in order to capture the higher regulatory impact of closer neighbors in the regulatory network. Using a breast cancer multi-omics dataset (N=1190), we show that our proposed method has superior prediction power over optimization-based regression models, with the additional advantage of revealing gene deregulations potentially driven by somatic mutations.

I. Introduction

Large-scale profiling studies of multiple cancers have revealed a plethora of genomic aberrations whose functional significance in driving the respective cancers remains largely unknown. This has resulted in the need for biologically savvy computational approaches [1] that can integrate multiple genomic measurements of cancer tissues to identify functional genomic aberrations that underlie cancer development and progression.

One computational approach involves assessment of an enrichment score that captures the deviation from random representation of a predefined set of genes within a ranked gene list associated with the cancer phenotype [2]. While this approach identifies functional genomic alterations, it does not explicitly incorporate regulatory relationships amongst genes. Subsequent approaches [3-5] also incorporated these regulatory networks to capture signaling programs that may be driving cancer progression. These methods integrate well-curated biological pathway databases with genomic measurements into a unified modeling framework to estimate activity levels of network nodes associated with tissue-level phenotypes. Such network-based inference of pathway-level activities has also been used to evaluate if specific mutations are functionally deregulating pathways [6]. These approaches mainly rely on the following assumptions: a) the pathway networks accurately and fully capture the cellular mechanisms across tissue types, b) that the influence of regulatory parents nodes on the downstream gene expression is equal and c) the relation between the gene expression and epigenetic information is linear. These assumptions underestimate the complexities and heterogeneity inherent in the biology of cancer.

We develop an integrative model that incorporates multi-omics measurements, including RNAseq-based gene expression, array-based DNA methylation (epigenetic) and SNP-array based somatic copy-number alterations (sCNA), and biological pathway network information to build a gene-gene regulatory influence network. Briefly, a non-linear Bayesian model is learned to predict the expression level of any given gene using its own sCNA and methylation data along with upstream regulatory influences inferred from biological pathway networks. The learned model is then used to identify genes whose measured expression levels show significant and abnormal deviations from the predictions, thus allowing for the discovery of somatic mutations that functionally alter gene regulation.

II. Method Overview

The proposed algorithm consists of several sequential steps to identify and report potential somatic aberrations driving deregulated genes. The first step is to build a tree for each gene that captures the relationship of the gene's expression levels with its own genomic (e..g. copy-number) and epigenetic (e.g. DNA methylation) status as well as its upstream transcriptional regulators (e.g. gene families and protein complexes). The gene of interest resides in the root node and the leaves of the tree represent all of the genes that potentially regulate its transcription either directly or indirectly through intermediate signaling partners. In the second step, we train a non-linear function to predict the gene expression level of the gene of interest by incorporating the molecular measurements associated with the leaves. The parameters of the non-linear function are estimated using a Bayesian inference method incorporating a novel depth penalization mechanism to capture the potentially stronger regulatory impact of nodes closer to the root node in the tree. The third and final step calculates relative inconsistency scores between the predicted and observed expression levels for each gene and reports deregulated genes. A subsequent analysis identifies the potential drivers of the gene deregulations arising from somatic mutations targeting the gene or its upstream transcriptional regulators.

Regulatory Tree Construction

In order to identify the genes that regulate the target gene expression level, we build a tree for each target gene by integrating information from well-curated pathway databases including NCI-PID, Biocarta, and Reactome similar to the PARADIGM framework [3].

The network consists of multiple node types and regulatory interactions (Fig. 1). In order to develop the regulatory tree for each gene we start with a specific target gene and traverse upstream along the pathway networks and capture the regulatory genes (referred to as regulators hereafter for brevity) along with their depth (defined as the number of links to the root node) to the root node (Fig. 1), using a depth-first traversal algorithm, collecting all nodes based on the following rules:

• i)At depth = 1, we exclude the post-transcriptional modifiers of the root node.
• ii)When we include a gene as a regulator and passing to the next level of regulators, we exclude transcriptional regulators of that gene since their effects are already captured by the gene's expression level.
• iii)We terminate traversing a branch once we reach a predefined maximum depth level d_max or we reach an abstract process node, since the nodes connected via abstract nodes may not have real pairwise causal impacts.
• iv)If we meet a leaf node via multiple disjoint paths, the shortest path is considered.
• v)We also include the gene of interest's epigenetic (DNA methylation) and somatic copy-number measurements as two additional nodes directly connected to the root node.

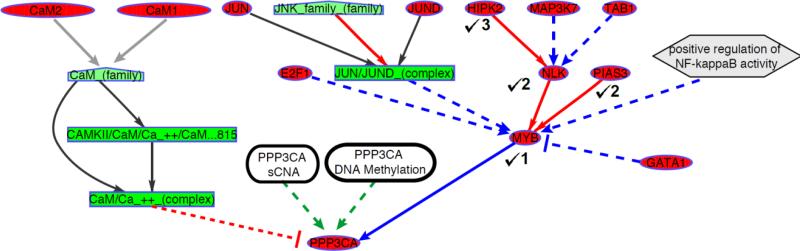
Fig. 1.

An example of a tree (d_max = 3) generated using the regulatory interactions derived from pathway databases for a sample gene PPP3CA. Node types are denoted as Genes (ovals), Protein complexes (rectangles), gene families (pentagon), abstract concepts (hexagon). The edges are colored according to their regulatory function with protein activation (red), transcriptional regulation (blue), component of protein complex (black) and gene family member (grey). The root node's epigenetic and sCNA measurements (rounded rectangles), considered as additional regulatory parents, are connected by green arrows. The nodes chosen as regulators are marked () along with their depths.

Thus, the tree construction algorithm reports the genes whose expression levels regulate the root gene's expression along with their corresponding depth parameters.

A. Learning Gene Regulatory Functions

Here we train a function that predicts the target gene expression level based on measurements of the nodes in the regulatory network. We use the following regression model for gene g using a training set of n normal and cancer samples:

$${\mathbf{y}}_{\mathrm{g}}={\mu }_{\mathrm{g}}{1}_{\mathrm{n}}+{\mathrm{X}}_{\mathrm{g}}{\beta }_{\mathrm{g}}+ϵ,ϵ\sim N(0,{\sigma }_{\mathrm{g}}^2{\mathrm{I}}_{n_g})$$ (1)

where $X_g=[X_g^S,X_g^P]$ is a n × p data matrix composed of two parts including $X_g^S$ (the target gene's DNA methylation and sCNA measurements) and $X_g^P$ the expression levels of the P regulators identified in Step 1. 1_n is a one column vector of size n, β_g is the regression coefficients of size p × 1 and ϵ is the Gaussian distributed model noise with zero-mean and identity covariance matrix. y_g represents values of the target gene expression levels across the n training samples. Finally, μ_g is the expected value of target gene's expression level. We omit subscript g hereafter for notation convenience.

Considering the fact that the pathway networks are not tissue specific and may involve pathway links that are absent or loosely connected in a specific tissue type, the model parameters β_i are expected to be sparse. The second consideration is possibly non-linear relationships between the measurements. Therefore, we apply non-linear transformation to the data prior to developing our regression model. We used a centered sigmoid function $f_1(x,c)=e^{-\frac{x}{c}}∕(1+e^{-\frac{x}{c}})$ to capture the sensitivity around the mean value and a soft-thresholding function $f_2(x,c)=\mathrm{sign}\left(x\right)(\sqrt{x^2+c^2}-c)$ to account for the impact of extreme values. We have applied the element-wise non-linear extension $X\to \Psi \left(X\right)=[X^S,f_1\left(X^S\right),f_2\left(X^S\right),X^P]$ only to X^s, hence increasing the number of predictors compared to the number of regulators. It is notable, that if the actual underlying function is linear, the coefficients of the nonlinear terms tend to zero in the proposed model.

Thirdly, to account for closer regulators having a greater impact on the target gene expression, we therefore extended the Bayesian lasso scheme to include a depth penalization mechanism in addition to the non-linear terms.

We used the following prior construction:

$$\begin{array}{cc}\hfill & X\to \Psi \left(X\right)\hfill \\ \hfill & \mathit{y}\mid X,K,\beta ,{\sigma }^2\sim N(\Psi \left(X\right)\beta ,{\sigma }^2{\mathit{I}}_n),K=\mathrm{diag}\left([k_1^2,\dots ,k_p^2]\right)\hfill \\ \hfill & \beta \mid {\sigma }^2,{\tau }_1^2,\dots ,{\tau }_p^2\sim N_p(0_p,{\sigma }^2{D}_{\tau }{K}^{-1}),D_{\tau }=\mathrm{diag}\left([{\tau }_1^2,\dots ,{\tau }_p^2]\right)\hfill \\ \hfill & k_1^2,k_2^2,\dots ,k_p^2\sim \prod _{j=1}^p\frac{{(a_k∕d_j^2)}^{a_k}}{\Gamma \left(a_k\right)}{k}_j^{2(a_k-1)}{e}^{-\frac{a_k{k}_j^2}{d_j^2}},j=1,2,3,\dots \hfill \\ \hfill & {\tau }_1^2,\dots ,{\tau }_p^2\sim {\prod }_{j=1}^p\frac{{\lambda }^2}{2}{e}^{-\frac{{\lambda }^2{\tau }_j^2}{2}}\hfill \\ \hfill & \pi \left({\sigma }^2\right)=\frac{b^a{\sigma }^2}{\Gamma \left(a_{{\sigma }^2}\right)}{\left({\sigma }^2\right)}^{-a_{{\sigma }^{2-1}}}{e}^{-\frac{b_{{\sigma }^2}}{{\sigma }^2}}\hfill \end{array}$$ (2)

The proposed Bayesian hierarchical generative model is desired over optimization-based sparse regression models such as LASSO, RIDGE and ELASTIC NET, since it provides a full posterior distribution of the model parameters. Moreover, we can easily incorporate any prior knowledge such as depth information to the model. While this leads to additional computation costs for sampling, it occurs only once during the training phase.

In the above formulations, the model parameters β are conditionally normal distributed around zero with variances that are controlled by three sets of hyper-parameters $({\beta }_i=\frac{{\sigma }^2{\tau }_i^2}{k_i^2})$, where σ² controls the global shrinkage, ${\tau }_i^2$ accounts for the local shrinkage using the exponential prior and k_i enforces the link depth impact. To provide more flexibility and a closed-form posterior, we assign a Gamma prior distribution for $k_i^2\sim \text{Gamma}(a_{k_i},b_{k_i})$ such that the standard deviation of β_i is inversely proportional to the corresponding link depth d_i (i.e. $E\left[k_i^2\right]=a_{k_i}∕b_{k_i}=d_i^{2}c$, where c is a normalizing term to ensure $\frac{1}{p}{\mid K\mid }_1=1$, which is obtained by setting $c=p∕{\sum }_{i=1}^p{d}_i^2$). Therefore, we only have one free hyper-parameter a_ki for _ki prior distribution and the second parameter b_ki is automatically obtained from $b_{k_i}=a_{k_i}∕c{d}_i^2$. We note that $\mathrm{var}\left(k_i\right)=\frac{a_{k_i}}{b_{k_i}^2}=c^2{d}_i^4∕a_{k_i}$. Setting a_ki to small values provides higher variance for _ki and hence is less formative, while large values of a_ki provides low variance reflecting a high certainty about the network topology and the fact that node pairs with shorter paths are associated with higher influences to one another. In this case, the gamma distribution approaches a Gaussian distribution concentrated around _di. We choose the large value of a_ki = 10 to highlight on the significance of the underlying biological network.

Using the conjugate priors in (2) and applying Bayes rule results in the following closed form conditional distribution for the model parameters as in [7], where the details of derivations are omitted for brevity.

$$\begin{array}{cc}\hfill & \beta \mid S\backslash \beta \sim N(A^{-1}\Psi {\left(X\right)}^T\mathit{y},{\sigma }^2{A}^{-1}),A=\Psi {\left(X\right)}^T\Psi \left(X\right)+K{D}_{\tau }^{-1}\hfill \\ \hfill & {\gamma }_i=1∕{\tau }_{\mathrm{i}}^2\mid S\backslash D_{\tau }\sim N^{-1}\left(\frac{\lambda \sigma }{\mid {\beta }_i\mid },{\lambda }^2\right)I({\gamma }_i>0)\hfill \\ \hfill & k_i^2\mid S\backslash K\sim GA\left(a_k+\frac{1}{2},\frac{a_k}{d_i^2}+\frac{{\beta }_i^2}{2{\sigma }^2{\tau }_i^2}\right)\hfill \\ \hfill & {\sigma }^2\mid S\backslash {\sigma }^2\sim G{A}^{-1}(a+\frac{n+p}{2},b+\frac{1}{2}{(\mathit{y}-\Psi \left(X\right)\beta )}^T(\mathit{y}-\Psi \left(X\right)\beta )+\frac{1}{2}{\beta }^T{D}_{\tau }^{-1}K\beta )\hfill \end{array}$$ (3)

where $S=\{\mu ,\beta ,\Psi \left(X\right),y,{\sigma }^2,{\tau }_1^2,\dots ,{\tau }_p^2\}$ is the set of all variables and ‘\’ is exclusion operator. N(.), N⁻¹(.), GA(.), GA⁻¹(.) denote the Gaussian, inverse Gaussian, Gamma and inverse Gamma distributions.

There are several ways to set the regularization parameter λ including cross validation or expectation maximization. In this work, we used a gamma prior for λ ~ GA(a_λ, b_λ) and included it as an additional step in the Gibbs sampler.

B. Inconsistency Analysis

Comparison of the observed gene expression measurement $y_g^o$ with the predicted value, $y_g^p$ (the maximum a posteriori MAP estimate) for a given cancer sample determines the level inconsistency for gene g.

We note that the predictive distribution for the RNA expression of gene g for each new test sample $y_g^{new}$ is obtained by marginalizing out the model parameters from the conditional posterior distribution for given input ${\mathit{x}}_g^{new}$:

$$\begin{array}{cc}\hfill & f(y_g^{new}\mid {\mathit{x}}_g^{new})=\int f(y^{new}\mid {\mathit{x}}^{new},\beta ,{\sigma }^2)f(\beta ,{\sigma }^2\mid y,X)d\beta d{\sigma }^2\approx \frac{1}{N}{\sum }_{i=1}^{N}f(y_g^{new}\mid {\mathit{x}}_g^{new},{\beta }_g^{\left(i\right)},{\sigma }_g^{\left(i\right)})\hfill \\ \hfill & y_g^p=\underset{y_g^{new}}{\mathrm{argmax}}f(y_g^{new}\mid {\mathit{x}}_g^{new})\hfill \end{array}$$ (4)

where ${\beta }_g^{\left(i\right)}$, ${\sigma }_g^{\left(i\right)}$ are the samples of the model parameters for gene g obtained from the N iterations of Gibbs sampling.

Consequently, the Z-score and the equivalent Log Likelihood of the consistency level of gene g in the new sample is obtained using the following equations:

$$\begin{array}{cc}\hfill z_g^{new}& =\frac{y_g^o-y_g^p}{{\sigma }_{y_g^{new}\mid {\mathit{x}}_g^{new}}}\hfill \\ \hfill L_c^{new}& =\log f(y_g^{new}\mid {\mathit{x}}_g^{new})\hfill \\ \hfill & =cnst-\log \left({\sigma }_{y_g^{new}\mid {\mathit{x}}_g^{new}}^2\right)-\frac{{\left(z_g^{new}\right)}^2}{2}\hfill \end{array}$$

where the mean ${\mu }_{y_g^{new}\mid {\mathit{x}}_g^{new}}$ and variance ${\sigma }_{y_g^{new}\mid {\mathit{x}}_g^{new}}^2$ are provided by the Gibbs sampler.

III. Results

In this section, we first provide prediction results for sample genes that have valid regulatory connections in the pathway network and are known to be highly associated with cancer. RNA-seq based gene expression, DNA Methylation using the Illumina Infinium Methylation assays and sCNA profiles using Affymetrix SNP arrays were obtained using The Cancer Genome Atlas portal for a breast cancer dataset, containing 111 normal and 1079 cancer samples.

We compared the results of our proposed Bayesian method with state-of-the-art optimization-based sparse regression models including LASSO, RIDGE and Elastic-Net Regressions with solutions based on Coordinate Descent [8]. The Minimum Square Error (MSE) ratio $\frac{{(y^o-y^p)}^2}{{\left(y^p\right)}^2}$ and, State Error Rate (SER) obtained by mapping the observed and predicted values to three (low, neutral and overexpressed) states, are presented across frameworks in Table 1. The results for all models are derived from a test dataset independent of the training set.

Table I.

Prediction accuracy for the proposed method in comparison with the benchmark optimization-based sparse regression models

Method	Test on Normal Samples		Test on Cancer Samples
	MSE	SER	MSE	SER
LSE	0.4028	0.1156	0.6102	0.2774
Lasso	0.332	0.0638	0.4867	0.1481
Ridge	0.3987	0.0848	0.5415	0.1997
Elastic-NET (0.5)	0.3469	0.0758	0.493	0.1667
PROPOSED	0.2797	0.0534	0.4688	0.1406

From Table 1, we see that the proposed method outperforms the state of the art sparse regression models with the additional advantage of providing full posterior distribution for the gene expression level required for subsequent inconsistency analysis. Another observation from Table 1 is that all models show higher predictability on the test set of normal samples despite the fact that the number of cancer samples used for model training is larger than the normal samples. This reveals that the functional states of gene expression in normal tissues are more consistent with their upstream regulatory networks than in cancer tissues. We further highlight the utility of our proposed method using two genes (ERBB2 and PTEN) of high import in breast cancer.

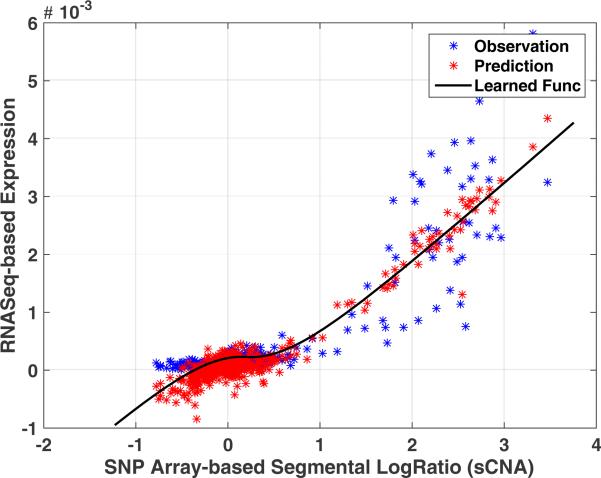
ERBB2 is highly expressed in a subset of breast cancers due to sCNAs. Our model appropriately captures this non-linear effect (Fig. 2), by automatically assigning high values for the coefficient associated with the soft-thresholding function of sCNA, reflecting the fact that variations around zero in sCNA values correspond to measurement noise.

Fig. 2.

The observed and predicted relationship between sCNA and gene expression for ERBB2 in normal and cancer samples. The coefficient corresponding to f₂(sCNA) dominates the other predictors of the model for ERBB2, with ${\beta }_2∕{\sum }_{j=1}^p\mid B_j\mid \approx 0.82$.

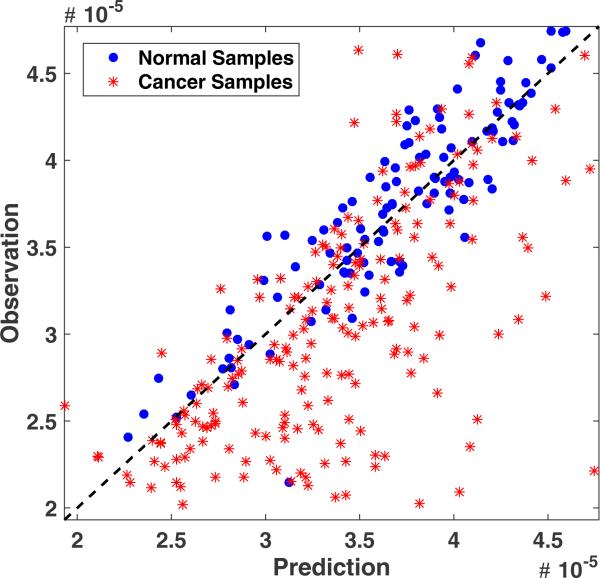
On the other hand, inactivation of the gene PTEN is functionally important in breast cancer due to its essential role in down-regulation the PI3K pathway, a key mechanism of resistance to anti-HER2 therapy. Fig. 3 shows that a subset of breast cancers with significantly lower observed gene expression levels of PTEN as predicted by our model's integration of sCNA and regulatory networks. It is also notable that some cancer samples show significant inconsistency with the predictions. We hypothesize that these inconsistencies are likely associated with somatic mutations affecting either PTEN or its regulatory network. We therefore count all non-silent mutations affecting either PTEN or its regulators for each of the cancer samples scaled by their absolute inconsistency levels. In order to apply the same concept of depth-penalization, we penalize the count of mutations with (α)^d_i,g, where (0 < α < 1) is an arbitrary penalization factor and d_i,g, is the depth of the regulatory gene i to the target gene g = PTEN. In general, the functional impact of mutations in gene h on the expression of gene g, denoted by f_g(h) is calculated as:

$$f_g\left(h\right)=\frac{{\sum }_{j=1}^{n}1(h\in M_j\cap P_g){\left(\alpha \right)}^{d_{h,g}}\mid z_g^i\mid )}{{\sum }_{l\in P_g}{\sum }_{j=1}^{n}1(l\in M_j\cap P_g){\left(\alpha \right)}^{d_{l,g}}\mid z_g^i\mid )}$$

where P_g is the set of regulatory ancestor genes of gene g, M_j is the set of genes mutated in sample j, $z_g^j$ is the inconsistency score of gene g at sample j and 1(.) is the indicator function. The role of denominator is to $\text{normalize}{\sum }_{h\in P_g}{f}_{g\left(h\right)}=1$.

Fig. 3.

Predicted versus observed expression levels of PTEN. Cancer samples () show widespread inconsistency as compared to normal samples ().

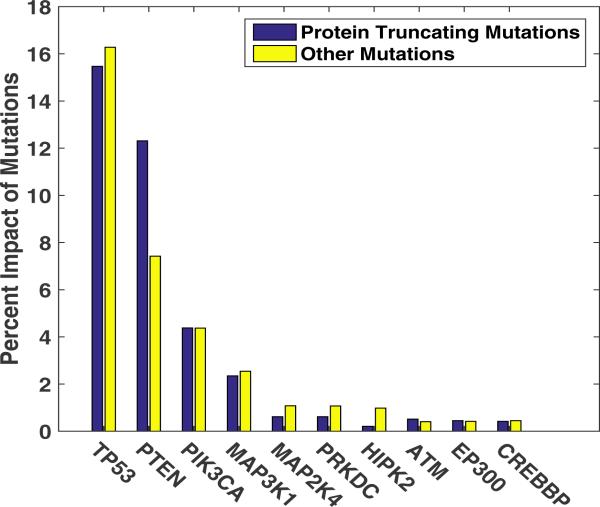
The functional impact of somatic mutations on the deregulation of gene PTEN is depicted in Fig. 4, revealing that the inconsistencies in PTEN expression are highly associated with mutations in TP53, PTEN, PIK3CA, MAP3K1 and MAP2K4. The higher impact of TP53 mutations versus PIK3CA is particularly interesting given that PIK3CA is mutated more often than TP53 (387 samples versus 333 samples respectively). We observe that MAP3K1 and MAP2K4 mutations, previously shown to be associated with luminal breast cancers [9], impact PTEN inactivation, thus providing an intriguing nexus between these genes in driving a key subtype of breast cancers. We also calculate the relative impact of protein-truncating and other non-synonymous mutations after normalizing to their absolute counts on the inconsistency score for PTEN. The model determines that the two kinds of mutations have similar impact when they affect any of the regulatory genes of PTEN while the protein-truncating mutations in PTEN have an outsize impact on its deregulation, consistent with nonsense-mediated decay of PTEN mRNA. These findings highlight the capability of our modeling framework to capture the expected impact of somatic mutations in a gene on its own expression level, while also enabling the discovery of the functional effects of mutations in upstream regulatory genes.

Fig. 4.

The Impact of somatic mutations in the upstream regulatory subnetwork of PTEN on its gene expression inconsistency. Depth penalization parameter is set to α = ½. The bars show the relative degree of association of mutations in genes (horizontal-axis) on the level of inconsistency between the observed PTEN gene expression level and its predicted value. The impact is divided between protein truncating mutations (blue) and other missense mutations (yellow) normalized by their counts in the respective genes.

IV. Conclusions

We have developed a novel Bayesian approach that integrates multi-omics data with prior biological knowledge derived from pathway annotation databases. Our approach captures the non-linear and heterogeneous influence of both upstream regulatory genes as well as epigenetic alterations on target gene expression levels. Furthermore, the inconsistency score estimated by our model quantifies the impact of somatic mutations potentially driving deregulation of gene expression in cancer samples. Our framework provides a new toolkit for cancer biologists to identify novel driver mutations in cancer through the integrative analysis of multi-omics cancer profiles.