Changes in shape and cross‐sectional geometry in the tibia of mice selectively bred for increases in relative bone length

Abstract

Limb bone size and shape in terrestrial mammals scales predictably with body mass. Weight‐bearing limb bones in these species have geometries that enable them to withstand deformations due to loading, both within and between species. Departures from the expected scaling of bone size and shape to body mass occur in mammals that have become specialized for different types of locomotion. For example, mammals adapted for frequent running and jumping behaviors have hind limb bones that are long in relation to body mass, but with narrower cross‐sections than predicted for their length. The Longshanks mouse was recently established, a selectively bred line of mice with ~12–13% longer tibiae relative to body mass. This increased limb length resembles superficially the derived limb proportions of rodents adapted for hopping and jumping. Here, 3D geometric morphometrics and analyses of bone cross‐sectional geometry were combined to determine whether selection for increased relative tibia length in Longshanks mice has altered the scaling relationship of size and shape, and/or bone robusticity, relative to the tibiae of random‐bred control mice from the same genetic background. The results suggest that the Longshanks tibia is not a geometrically scaled version of the control tibiae. Instead, the Longshanks tibia has become narrower in cross‐section in relation to its increased length, leading to a decrease in overall bending strength when compared with control tibiae. These changes in bone shape and robusticity resemble the derived morphology of mammals adapted for running and jumping, with important implications for the material properties and strength of bone in these mammals.

Introduction

The limb skeleton of terrestrial mammals plays a vital role in ensuring their survival, enabling them, for example, to acquire resources and mates, capture prey or escape predators. The limb skeleton is comprised of an articulated series of bones with a characteristic shape and size. Over ontogenetic timescales, bone is a plastic tissue, capable of growing and remodeling in response to the loads an individual experiences throughout life (Barak et al. 2011; Krause et al. 2013; Wallace et al. 2013). Over evolutionary timescales, bones as organs are also capable of responding to selection, evolving different sizes, shapes and cross‐sectional properties adapted to the functional demands placed upon them, especially in the context of locomotion (Van Valkenburgh, 1987; Bou et al. 1990; Biknevicius, 1993; Polk et al. 2000; Samuels & Van Valkenburgh, 2008; Samuels et al. 2013).

At both timescales, limb bones must have geometries and structural properties that enable them to withstand deformations due to gravitational and locomotor loads (Biewener, 1983; Bertram & Biewener, 1990). One of the most important determinants of bone and joint loading is an animal's body mass. Hence, in general, limb bone geometry tends to scale predictably with body mass across multiple orders of magnitude in terrestrial mammals. The nature of the scaling relationships of skeletal size and shape to body mass, but also of skeletal dimensions to each other and to a bone's cross‐sectional geometry (e.g. to cross‐sectional bone area), has been the focus of much research, beginning with Galileo in the 17th century (Schmidt‐Nielsen, 1984).

The scaling of skeletal size, shape and cross‐sectional geometry to body mass between species, both extinct and extant, is a topic of particular interest among comparative biologists and biomechanists (McMahon, 1973, 1975; Alexander et al. 1979; Bou et al. 1987; Bertram & Biewener, 1990; Casinos et al. 1993; Christiansen, 1999a, 2002; Elissamburu & Vizcaino, 2004; Maidment et al. 2012). By studying how a long bone's length, cross‐sectional area (CSA) or mass scales across several orders of magnitude (e.g. from mouse to elephant), a number of important, and sometimes conflicting, scaling ‘power law’ relationships have been proposed. These relationships take the following form:

$$\mathrm{Y}=a{\mathrm{X}}^b$$ (1)

where Y is a skeletal property (e.g. long bone length or CSA), X is body mass or some other skeletal dimension (e.g. long bone diameter), a is a constant, and b is the exponent that characterizes the power law relationship between the variables. Many of these scaling laws have been derived by matching empirical observations to theoretical relationships. For example, McMahon (1973, 1975) found that long bone lengths in ungulates tend to scale with bone diameters to the power b = 0.67. McMahon used this empirical observation to propose that long bones in terrestrial mammals, or at least in ungulates, scale in such a way as to preserve elastic similarity. Bone is an elastic tissue (Reilly & Burstein, 1975), and is prone to failure by elastic buckling when exposed to bending forces (McMahon, 1975; Schmidt‐Nielsen, 1984; Kokshenev et al. 2003; Biewener, 2005). McMahon argued from engineering principles that the exponent b = 0.67 characterizing the relationship of length to transverse diameter in ungulates maintains similar elastic deformations under equal loading conditions across animal size (McMahon, 1973, 1975; Biewener, 2005).

Although subsequent studies provided some support for McMahon's theory (Alexander, 1977), others have since found that the elastic similarity model does not fit empirical observations outside of Bovidae, and may not hold across a broad range of body sizes. Instead, the long bones of terrestrial mammals as a group tend to scale closer to geometric similarity, in which skeletal dimensions at small sizes are multiplied by some common factor at larger sizes, i.e. where the exponent b is closer to 1 (Eq.(1); Alexander et al. 1979; Biewener, 1983; Bou et al. 1987; Bertram & Biewener, 1990; Christiansen, 1999b). Others have also shown that the scaling laws are different at large and small body sizes. Specifically, length to diameter relationships in long bones in large animals tend to scale with significant negative allometry (b ≈ 0.75–0.85), and increase towards isometry as mammals get smaller (Bertram & Biewener, 1990; Christiansen 1999a,b). This difference may exist because deformations under static and dynamic loads are likely to be a more important factor in bone design and safety in larger animals (Economos, 1983; Bou et al. 1987).

Intra‐specific scaling relationships in the limb skeleton have received comparatively less attention. Evolutionary biologist Stephen J. Gould argued that, within species or populations, biological structures should scale isometrically (Gould, 1971). With regards to the skeleton, this could be because the range of body sizes over which the skeletal measures are collected are much smaller, and thus the range of static or dynamic stresses experienced by long bones across individuals is relatively narrow as well. It may also be due to shared genetic mechanisms that maintain shape as a function of size within a population or species (Gould, 1971; McMahon, 1975). Empirical evidence, primarily from primates, provides ambivalent support for this hypothesis, with some species (e.g. orangutans and gorillas; Steudel, 1982; Ruff, 1988) showing significant departures from isometry in the relationship of limb bone cross‐sectional properties, and others scaling isometrically (e.g. humans, macaques; Ruff, 1984, 2002).

At the inter‐specific level, there are notable deviations from the relationship of limb bone length to cross‐sectional geometries. Not surprisingly, these deviations are found in terrestrial quadrupedal mammals that have become functionally specialized, whether for locomotion or other functions such as digging (Bou et al. 1987; Christiansen, 1999a; Elissamburu & Vizcaino, 2004; Janis et al. 2014). Among rodents, for example, the relatively thickest humeri are found in subterranean burrowing species such as the European mole (Talpa europea) and golden moles (Family Chrysochloridae), while species that frequently engage in long‐distance running, sprinting or bounding behaviors, such as the Patagonian mara (Dolochotis patagonum) and chinchillas (Chinchilla sp.), have relatively long and slender hind limb bones (Bou et al. 1987; Casinos et al. 1993; Elissamburu & Vizcaino, 2004).

Selection for functional specializations can thus lead to marked departures from the predicted relationship between limb bone lengths and cross‐sectional geometry. These changes may in turn have important implications for organismal design, especially with respect to the structural properties and strength of long bones. For example, at the inter‐specific level, a recent study found that lagomorphs that frequently engage in running (jackrabbits) have relatively longer distal limb bones than related species that do not run as often (Young et al. 2014). Their limb bones are also less robust, indicating that, in theory, they are less able to withstand bending loads. These observations suggest that anatomical specializations for running or jumping may involve trade‐offs between increased whole organism performance (e.g. improved running economy) and reduced bone safety factors (Young et al. 2014). Intra‐specifically, a study by Kemp et al. (2005) found that selective breeding for relatively longer and more gracile limb bones in the context of racing performance in greyhounds caused a decrease in the bending strength of their proximal limb bones relative to pit bull terriers, a breed that has been selectively bred for fighting.

Recently, the Longshanks mouse was established, a line of mice selectively bred from an outbred stock (CD1) for increases in tibia length relative to body mass (Marchini et al. 2014). The artificial selection experiment is similar in design, and uses the same mouse stock, as a previously established long‐term selection experiment targeting increased voluntary wheel‐running behavior (Swallow et al. 1998a,b; Garland, 2003). The goals of these two long‐term studies are largely complementary.

Garland's selection experiment targets a performance trait based on a complex ‘behavior’, providing important insights into its genetic basis (Kelly et al. 2014a), as well as its downstream impacts on physiology (Swallow et al. 1998b; Houle‐Leroy et al. 2000; Meek et al. 2009; Kelly et al. 2014b) and musculoskeletal morphology (Zhan et al. 1999; Houle‐Leroy et al. 2003; Garland & Freeman, 2005; Young et al. 2009; Wallace et al. 2012). In contrast, the Longshanks experiment targets a complex ‘musculoskeletal trait’ in order to study the genetic and developmental basis of phenotypic variation in this trait, and to examine how phenotypic variation in the trait in turn affects physiology, function and performance, for example during locomotion. By generation F14, mean tibia length in the Longshanks mouse had increased by 12–13% relative to a random‐bred cohort (hereafter Controls), but body masses remained identical (Marchini et al. 2014). The resultant increased bone length superficially resembles the changes in relative hind limb length observed in mammals that frequently hop, bound and/or run.

In this study, it is asked whether tibia shape in the Longshanks mouse has changed in response to intensive selection for an increase in length relative to body mass and whether the size and/or shape change has altered the bone's robusticity and inferred bending strength. The null hypothesis that the increase in tibia length in the Longshanks mouse has been accompanied by isometric changes in its overall shape and cross‐sectional properties is tested. In other words, the prediction that in all respects the Longshanks tibia is a geometrically scaled larger ‘version’ of its random‐bred Control counterpart is tested, under the assumption that the two groups are part of the same population with a greater range of variation in relative tibia length.

The current study consists of two complementary analyses. First, overall shape changes between the two groups are focused on using 3D geometric morphometrics. If the Longshanks and Control tibiae are geometrically similar, then a 3D geometric morphometric analysis is predicted to show a complete overlap in the multivariate shape spaces of the bones in the two groups (Zelditch et al. 2004). Second, the cross‐sectional geometry of the tibia mid‐shaft is examined to determine whether there has been a change in the bone's inferred strength in relation to increased bone length, as observed in lagomorphs (Young et al. 2014) and certain dog breeds (Kemp et al. 2005).

Materials and methods

Samples

All procedures for the use of live animals were approved by the Health Sciences Animal Care Committee at the University of Calgary (protocol AC13‐0077). Bones for the analysis came from sex‐balanced samples of mice from generation F10 of the Longshanks selection experiment. In this ongoing artificial selection experiment, originally three closed lines of mice (16 breeding pairs each) were set up, two lines selectively bred for increases in tibia length relative to body mass (hereafter Longshanks), and one random‐bred control line (hereafter Control). Each generation, 8‐week‐old mice were anesthetized, weighed to the nearest 0.01 g and digitally radiographed to obtain tibia length. In the Longshanks lines, an index of tibia length relative to body mass was calculated for each member of a litter, and males and females were ranked separately. The top ranked male and female are selected as breeders for the following generation, and are mated at random with breeders from other litters within a line, to avoid sibling pairings. Control mice are measured but not ranked, and are randomly paired in a similar fashion. For further details on the breeding protocol, see Marchini et al. (2014). In this study, tibiae were taken from one of the two Longshanks lines (Line 1, n = 105) and the Control line (n = 111, hereafter Control). At generation F10, Longshanks Line 1 mice had tibiae that were on average 9.9% longer than Control mice (sexes pooled, 19.49 ± 0.56 vs. 17.56 ± 0.54 mm ± SD), while the cube root of body mass was ~0.3% lower (3.30 ± 0.17 vs. 3.31 ± 0.16 g^1/3 ± SD), after controlling for co‐variation with litter size and age at measurement (see table S1 in Marchini et al. 2014).

Mice that were not selected as breeders for generation F11 were killed by CO₂ inhalation at 56–58 days as part of the selection experiment protocol, while breeders were killed from 83 to 160 days, after successful pairing and weaning. Mice were weighed and packed into Styrofoam tubes, and a Skyscan 1173 µCT scanner (Bruker, Kontich, Belgium) was used to perform full body scans at a resolution of 45 μm (70 kV voltage, 114 µA current). Scans were reconstructed into a series of .JPEG images using nrecon v1.6.9 (Bruker, Kontich, Belgium). JPEG stacks were imported into amira v.5.4.2 (Visage Imaging, Berlin, Germany) for 3D landmarking, or into image j v.1.49g (Rasband, 2014) to measure cross‐sectional geometric properties.

3D landmarks and shape data

A series of 12 3D landmarks was placed on homologous anatomical structures in the scans of the right tibia from each mouse. No landmarks were placed on the fibula. The landmarks captured the overall shape of the tibia, focusing on the cross‐sectional shape at the proximal epiphysis, as well as the point of fusion between the tibia and fibula (Fig. 1; Table 1).

Figure 1.

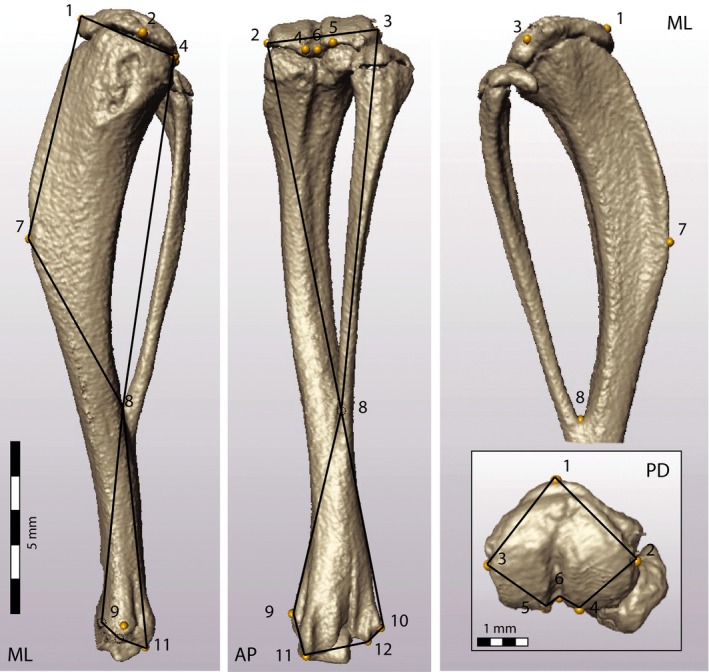
Representative μCT scan of the right tibia, showing the location of the 16 landmarks for 3D geometric morphometric analyses (Table 1). The medio‐lateral (ML, left), antero‐posterior (AP, center) and proximo‐distal (PD, lower right inset) views also show the wireframes (black outlines) used to assess the shape deformations associated with the principal component scores in Figs 2 and 4.

Table 1.

Anatomical location of landmarks on the tibia

LM #	Anatomical location (right tibia)	ME (mm)
1	Cranial tip of the proximal epiphysis	0.054
2	Most medial point of the medial condyle of the proximal epiphysis	0.075
3	Most lateral point of the lateral condyle of the proximal epiphysis	0.035
4	Caudal tip of the medial condyle of the proximal epiphysis	0.049
5	Caudal tip of the lateral condyle of the proximal epiphysis	0.052
6	Deepest point of the caudal inter‐condylar notch on the proximal epiphysis	0.033
7	Cranial point of inflection on the tibial tuberosity	0.085
8	Proximal aspect of the fusion between tibia and fibula	0.050
9	Most medial point of the medial flange of the medial malleolus	0.074
10	Most lateral point of the lateral flange at the lateral malleolus	0.052
11	Caudal distal tip of the medial malleolus	0.051
12	Caudal distal tip of the lateral malleolus	0.046

The right column shows the average absolute measurement error (ME) in mm, as explained in the text.

LM, landmark.

Measurement error (ME) and reliability

To assess intra‐observer ME and repeatability of landmark placement, MNC placed landmarks on the scans of 10 individuals (five Longshanks, five Control) five times each, with each session separated by at least 24 h. Absolute ME was determined by calculating the distance in mm between homologous landmarks in the five trials for an individual, and averaging these distances over all individuals (Richtsmeier et al. 1995). ME values for each landmark are reported in Table 1. The mean ME was 0.055 mm across all landmarks. The landmark on the cranial inflection of the tibial tuberosity (LM7) had the highest ME (0.085 mm; Table 1), which is less than 2 pixels in any direction at the scan resolution, or approximately 0.5% of mean tibia length (18.41 mm, n = 216) and 0.3% of mean centroid size (CS) across groups (28.53 mm, n = 216).

To assess the reliability of landmark placement and its impact on discriminating tibia shape between groups, first the inter‐landmark distance between all pairs of landmarks (66 linear distances) for each of the 50 landmark datasets was calculated (10 individuals × 5 trials each; Richtsmeier et al. 1995). Next, a one‐way anova was used, with individuals as a random categorical factor and the linear distances as dependent variables, in order to obtain the intra‐class correlation (ICC) for each distance, i.e. the proportion of variance due to differences among individuals to the total variance in that linear distance (Weinberg et al. 2009). The average ICC across all 66 linear distances was 0.97. A single ICC was below 0.8 (for the distance between landmarks four and six). The ICC data thus indicate a high reliability in landmark placement, further suggesting that any existing tibia shape differences among individuals and groups are significantly greater than ME in the current sample.

Cross‐sectional properties

The following procedure was used to obtain cross‐sectional geometry at the mid‐shaft of the tibial CT scans in Longshanks and Control mice. Because full body scans were acquired, the mice were not always positioned with their tibiae in the same orientation. Thus, first the tilt was removed from the CT images of the tibia using the imagej plugin ‘Untilt Stack’ (http://rsbweb.nih.gov/ij/plugins/untilt-stack/index.html). This plugin realigns and reconstructs the image stack so that the long axis of the scanned object (the tibia) is parallel to the long axis of the scanning tube, and hence transverse CT images taken anywhere along the tibia's proximo‐distal axis are truly orthogonal to it. Then, the mid‐shaft location was identified as the slice that was exactly halfway between the slice where the proximal tibial epiphysis first appears, and the slice where the medial malleolus can last be seen, in other words, at 50% total bone length (Ruff, 2003).

The bonej plugin was used in imagej (Doube et al. 2010) to measure CSA (mm²) and the polar section modulus (i.e. Z _P, in mm³) at the mid‐shaft. Z _P is the ratio of the polar moment of area J (a measure of the mean distribution of bone in relation to the central axis of the bone's cross‐section) to the maximum radius of the cross‐section, and is frequently used as a measure of long bone bending strength (see also Ruff, 2003; Young et al. 2010,2014).

Analyses

Geometric morphometric analysis

The 12‐variable 3D landmark dataset was first subjected to a general least‐squares Procrustes superimposition to: (i) remove the effects of size by scaling each specimen to unit CS; and (ii) remove differences between specimens in position and orientation (Dryden & Mardia, 1998; Slice, 2005). A multivariate regression of the Procrustes shape coordinates on litter size and age at measurement, pooled within group, revealed that these co‐variates accounted for small but significant portions of the total shape variation (0.99% and 2.67%, respectively). Accordingly, their effects on the Procrustes shape variables were removed by using the residuals of the multivariate regression of shape on litter size and age at measurement in all subsequent analyses (Drake & Klingenberg, 2008). These Procrustes shape residuals were then used in two geometric morphometric analyses that considered the effect of tibia size on shape variation separately.

In the first analysis, shape differences between the groups were explored by means of principal components analysis (PCA) directly on residual Procrustes shape variables adjusted only for litter size and measurement age. In the second analysis, the allometric effect of tibia size on shape variation was evaluated by means of a PCA on the residuals of a pooled within‐group regression of the Procrustes shape variables on litter size, measurement age and CS. Procrustes superimposition removes the effect of scale but not the allometric shape variation associated with size (Hallgrimsson et al. 2007). Comparing the results of the first and second PCAs thus allowed to evaluate shape differences between Longshanks and Control that remain after removing any allometric shape variation associated with size variation.

In both geometric morphometric shape analyses, shape changes along principal components were visualized by means of deformations of wireframes that described shape in the medio‐lateral, antero‐posterior and proximo‐distal epiphyseal profiles of the tibia (Fig. 1). Differences between the groups were also examined by means of discriminant function analysis (DFA), based on a permutation analysis (10 000 permutations) of the mean Procrustes distance between the Longshanks and Control groups, as implemented in morphoj v1.04a.

Analysis of cross‐sectional properties

Mechanical loading of long bones is typically greatest in bending (Rubin & Lanyon, 1982; Polk et al. 2000). Bending moments will vary as a function of bone length (which is proportional to the load arm at the mid‐shaft) and body mass (which is proportional to the load itself). Accordingly, the tibia's bending strength was assessed, measured here by the polar section modulus Z _p, in relation to its length and the mass of the animal. An index of robusticity (IR) was calculated by taking the ratio of Z _p (in mm³) to the product of bone length (in mm) and body mass (in mg^2/3, to ensure lack of dimensionality; Polk et al. 2000; Ruff, 2000, 2003; Young et al. 2010, 2014). Then, one‐way anovas were used to determine whether intensive selection for increases in bone length caused changes in the mean cross‐sectional properties (CSA, Z _p) and scaled bending strength (IR) of the Longshanks and Control tibiae.

Results

Size‐dependent shape changes

In this sample, Longshanks mice had tibiae that were, on average, 11.2% longer than their Control counterparts (19.42 ± 0.51 vs. 17.46 ± 0.51 mm, observed means ± SD, anova, F _1,214 = 594, P < 0.001), as measured by taking the distance between landmarks one and 12 (Table 1). Similarly, the observed mean of CS in Longshanks group was 11.2% greater than in Control tibiae (30.1 ± 1.2 vs. 27.1 ± 0.7 mm, observed means ± SD, anova, F _1,214 = 524, P < 0.001). PCA on the residuals of the regression of Procrustes scores on age and litter size is presented in Fig. 2. Together, the first five PCs account for 68.8% of the total shape variance in the sample. The plots of the PCs reveal that the two groups can be distinguished along PC2 and PC3, but not PC1. This distinction is further confirmed by the DFA (Procrustes distance between group means, 0.0193, permutation P‐value < 0.0001). Cross‐validation scores from the DFA indicate that five out of 104 Control individuals were incorrectly assigned to the Longshanks group, while three out of 110 Longshanks tibiae were incorrectly classified as Controls.

Figure 2.

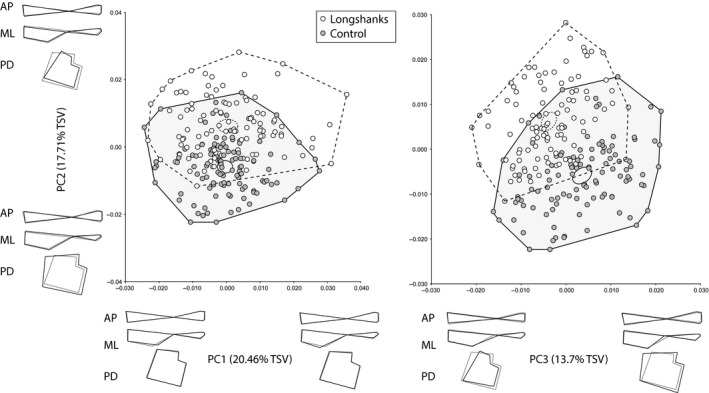
Scatterplots of the first three principal components (PCs) of the residuals of the regression of Procrustes shape coordinates on age and litter size only. Ellipses represent the 95% confidence intervals of the mean PC scores of each group. Black wireframes along each axis illustrate the shape deformations in relation to the mean shape (dashed wireframes) associated with moving from one extreme PC score to another in the medio‐lateral (ML), antero‐posterior (AP) and proximo‐distal (PD) profiles of the tibia (see Fig. 1). %TSV = percentage of total shape variance accounted for by given PC.

Shape changes along PC1 are primarily related to changes in the proximo‐distal position of the inflection point of the tibial tuberosity (LM7; Fig. 2). The fact that both groups overlap completely along this axis, however, indicates that this shape change is not unique to either group. Rather, the overlap in shape of the two groups along this PC may capture ‘isometric’ shape changes, or the overall size range, associated with the increase in tibia length in Longshanks. In contrast, PC2 and PC3 indicate important differences in the proximo‐distal, medio‐lateral and antero‐posterior profiles between Longshanks and Control. Shape changes on PC2 from negative to positive scores, which correspond to a shift from Longshanks to Control mean scores, include a reduction of the CSA of the proximal epiphysis, a thinning of the proximal shaft in the antero‐posterior direction, and a reduction in medio‐lateral width of the distal shaft. The shape change along this PC also shows a proximal shift in the location of the point of fusion between the tibia and fibula (Fig. 2). Shape changes along PC3 are similar, with positive scores (Control‐like) having larger epiphyseal cross‐sections, antero‐posteriorly wider proximal shafts and medio‐laterally broader distal shafts. Along this PC the relative position of the tibia–fibula junction is reversed, with positive scores associated with a proximal shift. Overall, PCA on the Procrustes shape residuals controlling only for age and litter size indicate that the Longshanks tibiae are smaller in cross‐section, with generally thinner shafts both proximally and distally.

Allometric shape changes

A multivariate regression of the Procrustes shape variables on CS (pooled within group) shows a positive relationship between shape and CS in both groups (Fig. 3), indicating that size has an allometric effect on tibia shape (Drake & Klingenberg, 2008). Importantly, there is also a shift in this relationship in Longshanks relative to Control (Fig. 3). In other words, size not only has an allometric effect on tibia shape in both groups, but the increased size due to selection on tibia length has caused a further allometric shift in Longshanks. The PCA on the residuals of the regression of Procrustes shape variables on age, litter size and CS are shown in Fig. 4. The first five principal components account for ~71.5% of the total shape variance. Here, the two groups can be readily distinguished along PC1 and PC2. This is confirmed by DFA (Procrustes distance between group means, 0.0181, permutation P‐value < 0.001). Cross‐validation scores for this analysis show that only two individuals in each group were incorrectly assigned to the other group.

Figure 3.

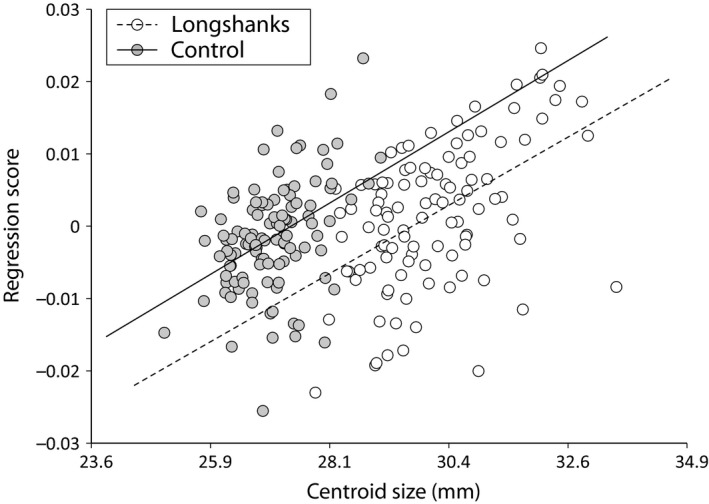
Scatterplot of the multivariate regression of Procrustes coordinates on CS in Longshanks and Control, pooled within group. The non‐overlapping regression lines indicate a different relationship between CS and shape in the two groups, implying a change in the allometric effect of size in the Longshanks relative to the Control tibia.

Figure 4.

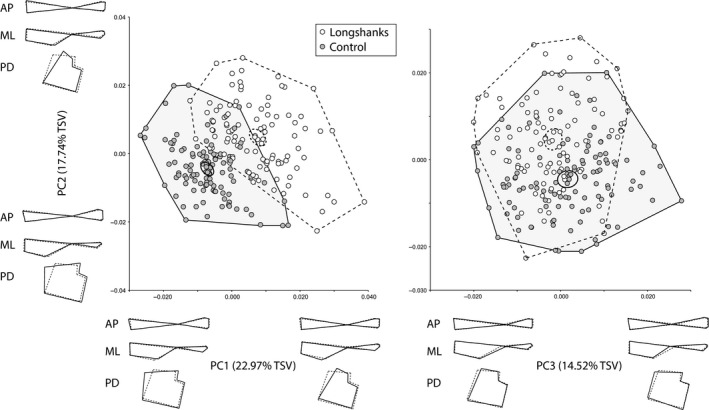
Scatterplots of the first three principal components (PCs) of the residuals of the regression of Procrustes shape coordinates on age, litter size and CS. Details are as in Fig. 2.

Positive increases in PC1, corresponding to a shift towards mean Longshanks shape, are associated with a reduction in the CSA of the epiphysis, reduction of the medio‐lateral width of the distal shaft, and proximal shift in the location of the distal lip of the tibia tuberosity. Positive shifts in PC2, also corresponding to the shift from Control to Longshanks mean shape, are associated with a reduction in the CSA of the proximal epiphysis, in addition to an antero‐posterior thinning of the proximal shaft, and increased medio‐lateral breadth of the distal shaft (Fig. 4). In sum, as in the previous PCA, shape differences between the two groups relate primarily to the Longshanks tibia being relatively more gracile, i.e. thinner in relation to its length, throughout the bone.

Cross‐sectional changes

Cross‐sectional area and the polar section modulus do not differ between the two groups (Table 2). When the section modulus, which reflects bending strength, is standardized to body mass and bone length, however, the resulting IR is significantly lower in Longshanks tibiae (6.48 × 10⁻⁴ vs. 7.22 × 10⁻⁴ mm² g⁻¹, anova, F _1,214 = 15.6, P < 0.001). Although the mean section modulus is ~5% greater in Longshanks, these mice are also on average ~4.5% heavier, and have tibiae that are on average 11.2% longer (observed means). Accordingly, their IR is ~10% lower when compared with Control tibiae, reflecting a bone that should be weaker in resisting bending loads.

Table 2.

Observed means and standard deviations for body mass, tibia length and mid‐shaft cross‐sectional geometry in Longshanks and Control tibiae

	Body mass (g)	Tibia length (mm)	CSA (mm2)	Polar section modulus (mm3)	IR (mm2 mg−2/3)
Longshanks (n = 105)	37.91 (0.56)	19.42 (0.07)	1.32 (0.02)	0.48 (0.01)	2.17 × 10 −5
Control
(n = 111)	36.28 (0.58)	17.46 (0.04)	1.29 (0.02)	0.45 (0.01)	2.37 × 10 −5
% Change	+4.5%	+11.2%	+2.1%	+5.1%	−8.6%

Values in bold are significantly different between the two groups at P = 0.05, as determined using one‐way anova.

CSA, cross‐sectional area; IR, index of robusticity.

Discussion

Mechanically appropriate scaling of skeletal dimensions of the limb bones in terrestrial quadrupedal mammals is an important determinant of an organism's ability to function and survive (Schmidt‐Nielsen, 1984). Much of the comparative research into the scaling of skeletal traits has revealed the existence of power law‐based relationships that describe how a bone's length scales, or should scale, to its diameter and cross‐sectional properties across several orders of magnitude in body mass (McMahon, 1975; Alexander et al. 1979; Bou et al. 1987; Bertram & Biewener, 1990; Christiansen, 1999a, 2002; Ruff, 2000, 2003). Studies of skeletal scaling are less common within species or populations (Steudel, 1982; Ruff, 1984, 2002), but it is thought that at that level, biological dimensions will tend to scale isometrically (Gould, 1971). Geometric similarity within populations may be attributable to genetic mechanisms or to the smaller range of body or skeletal sizes over which the limb bone measurements are collected, and their inferred deformations under broadly similar loads.

At the inter‐specific level, deviations from these scaling laws tend to be associated with limb functional specializations. For example, rodents specialized for hopping have longer limb bones than predicted for their cross‐sectional dimensions, while conversely rodents adapted for digging tend to have forelimb bones that are relatively wider compared with species of comparable size and limb bone length (Bou et al. 1987; Elissamburu & Vizcaino, 2004). Similarly, lagomorphs that frequently engage in running have relatively longer limb bones that lead to altered cross‐sectional geometries relative to non‐running lagomorphs (e.g. mass‐specific polar section moduli; Young et al. 2014). These patterns suggest that selective forces related to functional specializations in terrestrial quadrupedal mammals can alter the relationship between a limb bone's length and its cross‐sectional properties.

In this study, shape and cross‐sectional changes were examined in the Longshanks mouse, a unique line of mice selectively bred for increases in tibia length relative to body mass (Marchini et al. 2014). The general hypothesis that selection for an increase in tibia length would cause an isometric change in its shape and cross‐sectional geometry was tested. Specifically, it was hypothesized that, because they are derived from the same genetic stock, and their original skeletal sizes were comparable, the Longshanks tibia would be a geometrically scaled ‘version’ of the Control tibia.

The current results suggest that the shape of the tibia in Longshanks has been significantly altered as a result of an intensive selection regime for increased length. The 3D geometric morphometric analysis reveals that the Longshanks tibia has become more gracile, being relatively smaller in epiphyseal cross‐section than its Control counterpart. The Longshanks tibia also has a thinner AP and ML profile at both the proximal and distal shaft (Figs 2 and 4). The PC analyses with and without the effects of co‐variation with CS further indicate that these shape differences remain after removing the allometric effects of CS. The shape changes observed in Longshanks are thus not simply due to an increase in length, but represent genuine differences that distinguish the two groups, and which were presumably introduced as a result of selection for increased tibia length independent of a constant body size.

The results of the cross‐sectional geometry analyses indicate that, while the mid‐shaft CSA and the polar section modulus increased slightly in Longshanks, neither increased in geometric proportion to its increased tibia length. The relatively unchanged CSA suggests that the Longshanks tibia should be equally strong in resisting compressive (axial) loads as in Control mice. In contrast, the unchanged section modulus coupled with an increased bone length in Longshanks produces an IR that is significantly lower than the Control tibia (Table 2). Put differently, for a given load applied at the proximal epiphysis (the stifle), the longer moment arm of the Longshanks tibia increases the bending moment that the bone will experience at the mid‐shaft.

Study limitations

It is important to discuss two limitations of the current study. The first is the lack of a replicate Longshanks sample in both analyses. While the selection experiment includes two independently selected lines (Marchini et al. 2014), owing to time and cost constraints it was elected to include a larger sample from only one Longshanks line, in order to be able to detect evidently subtle changes in shape and cross‐sectional geometry. As a result of choosing only one line, the possibility cannot be ruled out that the changes observed in Line 1 are idiosyncratic, for example being influenced by founder effects or genetic drift (although the cumulative response to selection in the experiment suggests the latter is not the case; Henderson, 1997; Marchini et al. 2014, fig. 5).

Second, a bone's bending strength is not only proportional to its cross‐sectional geometry (e.g. Z _p, CSA, IR), length and the organism's body mass, but is also a function of its tissue mineral density (TMD), with higher mineral content associated with increased bone strength (Ferretti et al. 1996; Ominsky et al. 2010). One limitation of this study is that the relatively low CT scan resolution (45 μm) and absence of a density phantom during the scans prevented the estimation of TMD in Longshanks and Control tibiae. If TMD in the two groups remains similar, which may be expected given their shared genetic background (Jepsen et al. 2001), then the relatively lower standardized bending strength at the mid‐shaft of the Longshanks tibia predicts that it will fail (i.e. fracture) at a lower applied load in three‐point bending. The authors are currently investigating the consequences of altered length and cross‐sectional geometry properties on the comparative strength of Longshanks and Control bones.

Evolutionary implications

The current results indicate that under strong selection pressures, the scaling relationships of skeletal size, shape and cross‐sectional geometry in terrestrial quadrupedal mammals is altered. Admittedly, these changes may be extreme, associated with intensive artificial selection for changes in bone length relative to body mass, as observed in the differences in relative bending strength of greyhounds vs. pit bulls (Kemp et al. 2005). Nonetheless, these types of selection pressures likely still occur naturally in the context of locomotor or habitat specializations in mammals, as demonstrated by the relative length, gracility and decreased bending strength of lagomorphs adapted for running performance (Young et al. 2014), the decreased limb bone robusticity of bounding rodents (Bou et al. 1987), and bovids adapted to life in open grasslands and arid areas (Scott, 1985). The ongoing selection experiment has already changed the relationship of tibia length to body mass (Marchini et al. 2014). The authors showed that, in fewer than 15 generations of selective breeding, they were able to produce relative tibia lengths in the Longshanks mouse that were similar to those of the northern viscacha (Lagidium peruanum), a rodent that is known to hop among the rocky outcrops of its natural Andean habitat (Galende & Raffaele, 2008).

The present study further demonstrates that, within the tibia, strong selection for increased length leads to a shift in the relationship of bone cross‐sectional properties to bone length similar to the evolutionary morphology and shape relationships of rodent, insectivore and lagomorph species adapted for bounding, hopping and/or running (Bou et al. 1987; Young et al. 2014) In essence, through ‘forward engineering’, artificial selection is recapitulating the presumably adaptive changes in tibia length relative to body mass and cross‐sectional dimensions associated with specialized forms of locomotion in smaller mammals. It will be interesting to determine whether these artificially produced body and skeletal shape changes have also impacted locomotor performance in the Longshanks mouse, for example with respect to locomotor economy (Taylor et al. 1974).

The substantial change in the shape of the Longshanks tibia does raise the question of why this bone is not simply a geometrically scaled up version of the Control bone, and why the relationship between bone cross‐sectional geometries and length actually changed in relation to the length differences between the groups. There are at least two possible explanations for this pattern. The first is that mid‐shaft properties were not the targets of the selection protocol. If, as the data suggest, the phenotypic (and perhaps underlying genetic) correlation between the diameters and length is weak, then selection on tibia length should not be expected to produce correlated changes in widths and other mid‐shaft parameters such as CSAs (Lande, 1979). If true, then these parameters could simply be ‘free’ to change because of random genetic processes (e.g. drift). Related to this, limb bones grow in length and diameter through two complementary developmental mechanisms: interstitial growth mediated via the epiphyseal growth plate; and appositional growth mediated via the perichondrium/periosteum, respectively (Olsen et al. 2000). The extent to which these two mechanisms are genetically and developmentally coupled is poorly known (Rauch, 2005), but it is possible that selection for increased tibia length in Longshanks targeted developmental mechanisms of interstitial bone growth independent of those that govern appositional growth.

Second, there may be a form of developmental constraint at work in the Longshanks mouse. The aim of this artificial selection program is to select for increases in tibia length independent of body mass. At generation F10, when these mice were scanned, body masses between Longshanks and Control were similar. Thus, the F10 Longshanks mice have nearly identical net weight but a significantly longer tibia than Controls, along with more modest size increases in other bones (Rolian, unpublished data). In other words, Longshanks mice are skeletally larger, but with the same body mass. If the portion of somatic growth invested in building skeletal mass is the same in Longshanks and Control, then the increase in length of the postcranial bones in Longshanks may have necessitated a trade‐off with other bone properties, including cross‐sectional dimensions, bone mineral density and/or trabecular volume. In future studies, this unique mouse will be used to quantify total bone volume, skeletal mass and BMD. This will enable the determination of whether intensive selection for increased bone length has been offset by other skeletal changes that maintain total bone mass, or whether it has perhaps led to trade‐offs with other somatic tissues in order to maintain the same average body mass between Longshanks and Control.

Author Contributions

MNC and CR designed the experiment; MNC and LMS collected the data; MNC and CR analyzed the data and wrote the manuscript.