Doctor AI: Predicting Clinical Events via Recurrent Neural Networks

Abstract

Leveraging large historical data in electronic health record (EHR), we developed Doctor AI, a generic predictive model that covers observed medical conditions and medication uses. Doctor AI is a temporal model using recurrent neural networks (RNN) and was developed and applied to longitudinal time stamped EHR data from 260K patients over 8 years. Encounter records (e.g. diagnosis codes, medication codes or procedure codes) were input to RNN to predict (all) the diagnosis and medication categories for a subsequent visit. Doctor AI assesses the history of patients to make multilabel predictions (one label for each diagnosis or medication category). Based on separate blind test set evaluation, Doctor AI can perform differential diagnosis with up to 79% recall@30, significantly higher than several baselines. Moreover, we demonstrate great generalizability of Doctor AI by adapting the resulting models from one institution to another without losing substantial accuracy.

1. Introduction

A common challenge in healthcare today is that physicians have access to massive amounts of data on patients, but little time nor tools. Intelligent clinical decision support anticipates the information at the point of care that is specific to the patient and provider needs. Electronic health records (EHR), now commonplace in U.S. healthcare, represent the longitudinal experience of both patients and doctors. These data are being used with increasing frequency to predict future events. While predictive models have been developed to anticipate needs, most existing work has focused on specialized predictive models that predict a limited set of outcomes. However, day-to-day clinical practice involves an unscheduled and heterogeneous mix of scenarios and needs different prediction models in the hundreds to thousands. It is impractical to develop and deploy specialized models one by one.

Leveraging large historical data in EHR, we developed Doctor AI, a generic predictive model that covers observed medical conditions and medication uses. Doctor AI is a temporal model using recurrent neural networks (RNN) and was developed and applied to longitudinal time stamped EHR data. In this work, we are particularly interested in whether historical EHR data may be used to predict future physician diagnoses and medication orders. Applications that accurately forecast could have many uses such as anticipating the patient status at the time of visit and presenting data a physician would want to see at the moment. The primary goal of this study was to use longitudinal patient visit records to predict the physician diagnosis and medication order of the next visit. As a secondary goal we predicted the time to the patients next visit. Predicting the visit time facilitates guidance of whether a patient may be delayed in seeking care.

The two tasks addressed in this work are different from sequence labeling tasks often seen in natural language processing applications, e.g., part-of-speech tagging. Our proposed model, Doctor AI, performs multilabel prediction (one for each disease or medication category) over time while sequence labeling task predicts a single label at each step. The key challenge was finding a flexible model that is capable of performing the multilabel prediction problem. The two main classes of techniques have been proposed in dealing with temporal sequences: 1) continuous-time Markov chain based models (Nodelman et al., 2002; Lange et al., 2015; Johnson and Willsky, 2013), and 2) intensity based point process modeling techniques such as Hawkes processes (Liniger, 2009; Zhu, 2013; Choi et al., 2015). However, both classes are expensive to compute, especially for nonlinear settings. Furthermore, they often make strong assumptions about the data generation process which might not be valid for EHR data. Our modeling strategy was to develop a generalized approach to representing patient temporal healthcare experience to predict all the diagnoses, medication categories and visit time. We used recurrent neural network (RNN), considering that RNNs have been particularly successful for representation learning in sequential data, e.g. Graves (2013); Graves and Jaitly (2014); Sutskever et al. (2014); Kiros et al. (2014); Zaremba and Sutskever (2014). In particular, we make the following main contributions in this paper:

• We demonstrate how RNNs can be used to represent the patient status and predict diagnosis, medication order and visit time. The trained RNN is able to achieve above 64% recall@10 and 79% recall@30 for diagnosis prediction, showing potential to serve as a differential diagnosis assistance.

• We propose an initialization scheme for RNNs using Skip-gram embeddings (Mikolov et al., 2013) and show that it improves the performance of the RNN in both accuracy and speed.

• We empirically confirm that RNN models possess great potential for transfer learning across different medical institutions. This suggests that health systems with insufficient patient data can adopt models learned from larger datasets of other health systems to improve prediction accuracy on their smaller population.

2. Related Work

In this section, we briefly review the common approaches to modeling multilabel event sequences with special focus on the models that have been applied to medical data. There are two main approaches to modeling multilabel event sequences: with or without discretization (binning) of time.

Discretization

When the time axis is discretized, the point process data can be converted to binary time series (or time series of count data if binning is coarse) and analyzed via time series analysis techniques (Truccolo et al., 2005; Bahadori et al., 2013; Ranganath et al., 2015). However, this approach is inefficient as it produces long time series whose elements are mostly zero. Furthermore, discretization of time introduces noise in the time stamps of visits. Finally, these approaches are often not able to model the duration until next event. Thus, it is advantageous not to discretize the data both in terms of modeling and computation.

Continuous-time models

Among the continuous-time models, there are two main techniques: continuous-time Markov chain based models (Foucher et al., 2007; Johnson and Willsky, 2013; Lange, 2014; Liu et al., 2013) and their extension using Baysian networks (Nodelman et al., 2002; Weiss et al., 2012) and intensity function modeling techniques such as Cox and Hawkes processes (Liniger, 2009; Zhou et al., 2013; Linderman and Adams, 2014; Choi et al., 2015).

Intensity function modeling techniques have been shown to have computational advantages over the continuous-time Markov chain based models. Moreover, modeling multilabel marked point processes with continuous-time Markov chains expands their state-space and make them even more expensive. However, Hawkes processes only depend linearly on the past observation times; while there are limited classes of non-linear Hawkes process (Zhu, 2013), the temporal dynamics can be more complex. Finally, Hawkes processes are known to have a flat loss function near optimal value of the parameters which renders the gradient-based learning algorithms inefficient (Veen and Schoenberg, 2008). In this paper we address these challenges by designing a recurrent neural network which has been shown to be successful in learning complex sequential patterns.

Disease progression models

There have been active research in modeling the temporal progression of diseases (Mould, 2012). Generally, most works can be divided into two groups: works that focus on a specific disease and works that focus on a broader range of diseases.

Specific-purpose progression modeling

There have been many studies that focus on modeling the temporal progression of a specific disease based on either intensive use of domain-specific knowledge (De Winter et al., 2006; Ito et al., 2010; Tangri et al., 2011) or taking advantage of advanced statistical methods (Liu et al., 2013; Jackson et al., 2003; Sukkar et al., 2012; Zhou et al., 2012). Specifically, studies have been conducted on Alzheimer’s disease (Ito et al., 2010; Zhou et al., 2012; Sukkar et al., 2012), glaucoma (Liu et al., 2013), chronic kidney disease (Tangri et al., 2011), diabetes mellitus (De Winter et al., 2006), and abdominal aortic aneurysm (Jackson et al., 2003)

General-purpose progression modeling

Recently, Wang et al. (2014); Choi et al. (2015); Ranganath et al. (2015) proposed more general approaches to modeling the progression of wider range of diseases. As discussed earlier, Choi et al. (2015) used Hawkes process, and Ranganath et al. (2015) discretized time in order to model multiple patients and multiple diseases. Wang et al. (2014) proposed a graphical model based on Markov Jump Process to predict the stage progression of chronic obstructive pulmonary disease (COPD) and its co-morbid diseases.

One of the main challenges in using these algorithms is scalability. The datasets used in previous works typically contain up to a few thousands of patients and a few hundreds of codes. Even the largest dataset used by Ranganath et al. (2015) contains 13,180 patients and 8,722 codes, which is significantly smaller than our dataset described in Table 1. Need for domain-specific knowledge is also a big challenge. For example, Wang et al. (2014) not only used a smaller dataset (3,705 patients and 264 codes) but also used co-morbidity information to improve the performance of their algorithm. Such expert knowledge is difficult to obtain from typical EHR data.

Table 1.

Basic statistics of the the clinical records dataset.

# of patients	263,706	Total # of codes	38,594
Avg. # of visits	54.61	Total # of 3-digit D× codes	1,183
Avg. # of codes per visit	3.22	# of top level R× codes	595
Max # of codes per visit	62	Avg. duration between visits	76.12 days

Deep learning models for EHR

Researchers have recently begun attempting to apply neural network based methods (or deep learning) to EHR to utilize its ability to learn complex patterns from data. Previous studies such as phenotype learning (Lasko et al., 2013; Che et al., 2015; Hammerla et al., 2015) or representation learning (Choi et al., 2016b,a; Miotto et al., 2016), however, have not fully addressed the sequential nature of EHR. Lipton et al. (2016) is especially related to our work in that both studies use RNN for sequence prediction. However, while Lipton et al. (2016) uses regular times series of real-valued variables collected from ICU patients to predict diagnosis codes, we use discrete medical codes (e.g. diagnosis, medication, procedure) extracted from longitudinal patient visit records. Also, in each visit we make a prediction about predict diagnosis, medication order in the next visit and and the time to next visit.

3. Cohort

Population and source of data

The source population for this study was primary care patients from Sutter Health Palo Alto Medical Foundation. Sutter Health is a large primary care and multispecialty group practice that has used an Epic Systems Corporation EHR for more than a decade. The dataset was extracted from a density sampled case-control study for heart failure. The dataset consists of de-identified encounter orders, medication orders, problem list records and procedure orders.

Data processing

As inputs, we use ICD-9 codes, medication codes, and procedure codes. We extracted ICD-9 codes from encounter records, medication orders, problem list records and procedure orders. Generic Product Identifier (GPI) medication codes and CPT procedure codes were extracted from medication orders and procedure orders respectively. All codes were timestamped with the patients visit time. If a patient received multiple codes in a single visit, those codes were given the same timestamp. We excluded patients that made less than two visits. The resulting dataset consists of 263,706 patients who made on average 54.61 visits per person.

Grouping medical codes

There are more about 11,000 unique ICD-9 codes and 18,000 GPI medication codes in the dataset, many of which are very granular. For example, pulmonary tuberculosis (ICD-9 code 011) is divided into 70 subcategories (ICD-9 code 011.01, 011.02, …, 011.95, 011.96). Simply knowing that a patient is likely to have pulmonary tuberculosis is enough to increase the doctor’s awareness of the severity of the clinical situation. Therefore, to predict diagnosis and medication order, we grouped codes into higher-order categories to reduce the feature set and information overload. For the diagnosis codes, we use the 3-digit ICD-9 codes, yielding 1183 unique codes. For the medication codes, we use the Generic Product Identifier Drug Class, which groups the medication codes into 595 unique groups. The label y_i we use in the following sections represents the 1,778-dimensional vector (i.e., 1183 + 595) for the grouped diagnosis codes and medication codes.

4. Methods

This section describes the RNN model for multilabel point processes. We will also describe how we predict diagnosis, medication order and visit time using the RNN model.

Problem setting

For each patient, the observations are drawn from a multilabel point process in the form of (t_i, x_i) for i = 1, …, n. Each pair represents an event, such as an ambulatory care visit, during which multiple medical codes such as ICD-9 diagnosis codes, procedure codes, or medication codes are documented in the patient record. The multi-hot label vector x_i ∈ {0, 1}^p represents the medical codes assigned at time t_i, where p denotes the number of unique medical codes. At each timestamp, we may extract higher-level codes for prediction purposes and denote it by y_i, see the details in Section 3. The number of events for each patient may differ.

Gated Recurrent Units Preliminaries

Specifically, we implemented our RNN with Gated Recurrent Units (GRU). Although Long Short Term Memory (LSTM) (Hochreiter and Schmidhuber, 1997; Graves et al., 2009) has drawn much attention from many researchers, GRU has recently shown to have similar performance as LSTM, while employing a simpler architecture (Chung et al., 2014). In order to precisely describe the network used in this work, we reiterate the mathematical formulation of GRU as follows:

$$\begin{array}{cc}\hfill {\mathit{z}}_i& =\sigma \left({\mathit{W}}_z{\mathit{x}}_i+{\mathit{U}}_z{\mathit{h}}_{i-1}+{\mathit{b}}_z\right)\hfill \\ \hfill {\mathit{r}}_i& =\sigma \left({\mathit{W}}_r{\mathit{x}}_i+{\mathit{U}}_r{\mathit{h}}_{i-1}+{\mathit{b}}_r\right)\hfill \\ \hfill {\tilde{\mathit{h}}}_i& =\text{tanh}\left({\mathit{W}}_h{\mathit{x}}_i+{\mathit{r}}_{i}o{\mathit{U}}_h{\mathit{h}}_{i-1}+{\mathit{b}}_h\right)\hfill \\ \hfill {\mathit{h}}_i& ={\mathit{z}}_{i}o{\mathit{h}}_{i-1}+(1-{\mathit{z}}_i)o{\tilde{\mathit{h}}}_i\hfill \end{array}$$

where z_i and r_i respectively represent the update gate and the reset gate, ${\tilde{\mathit{h}}}_i$ the intermediate memory unit, h_i the hidden layer, all at timestep t_i. A detailed description of GRU is provided in Appendix A.

Description of neural network architecture

Our goal is to learn an effective vector representation for the patient status at each timestamp t_i. Using effective patient representations, we are interested in predicting diagnosis and medication categories in the next visit y_i+1 and the time duration until the next visit d_i+1 = t_i+1 − t_i. Finally, we would like to perform all these steps jointly in a single supervised learning scheme. We use RNN to learn such patient representations, treating the hidden layer as the representation for the patient status and use it for the prediction tasks.

The proposed neural network architecture (Figure 1) receives input at each timestamp t_i as the concatenation of the multi-hot input vector x_i of the multilabel categories and the duration d_i since the last event. In our datasets, the input dimension is as large as 40, 000. Thus, the next layer projects the input to a lower dimensional space. Then, we pass the lower dimensional vector through RNN (implemented with GRU in our study). We can also stack multiple layers of RNN to increase the representative power of the network. Finally, we use a Softmax layer to predict the diagnosis codes and the medication codes, and a rectified linear unit (ReLU) to predict the time duration until next visit.

Figure 1.

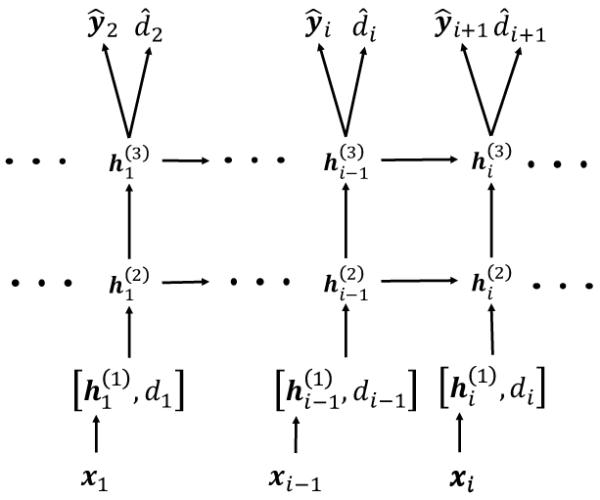
This diagram shows how we have applied RNNs to solve the problem of forecasting of next visits’ time and the codes assigned during each visit. The first layer simply embeds the high-dimensional input vectors in a lower dimensional space. The next layers are the recurrent units (here two layers), which learn the status of the patient at each timestamp as a real-valued vector. Given the status vector, we use two dense layers to generate the codes observed in the next timestamp and the duration until next visit.

For predicting the diagnosis codes and the medication codes at each timestep t_i, a Softmax layer is stacked on top of the GRU, using the hidden layer h_i as the input: ${\widehat{\mathit{y}}}_{i+1}=\text{softmax}\left({{\mathit{W}}_{\mathit{code}}}^{\top }{\mathit{h}}_i+{\mathit{b}}_{\mathit{code}}\right)$. For predicting the time duration until the next visit, a rectified linear unit (ReLU) is placed on top of the GRU, again using the hidden layer h_i as the input: ${\widehat{d}}_{i+1}=\text{max}\left({w_{\mathit{time}}}^{\top }{\mathit{h}}_i+{\mathit{b}}_{\mathit{time}},0\right)$. The objective of training our model is to learn the weights W_{z,r,h,code}, U_{z,r,h}, b_{z,r,h,code}, w_time and b_time. The values of all W’s and U’s were initialized to orthonormal matrices using singular value decomposition of matrices generated from the normal distribution (Saxe et al., 2013). The initial value of w_time was chosen from the uniform distribution between −0.1 and 0.1. All b’s and b_time were initialized to zeros. The joint loss function consists of the cross entropy for the code prediction and the squared loss for the time duration prediction, as described below for a single patient:

$$\mathcal{L}\left(\mathit{W},\mathit{U},\mathit{b},w_{\mathit{time}},b_{\mathit{time}}\right)=\sum _{i=1}^{n-1}\left\{\left({\mathit{y}}_{i+1}\log ({\widehat{\mathit{y}}}_{i+1})+(1-{\mathit{y}}_{i+1})\log (1-{\widehat{\mathit{y}}}_{i+1})\right)+\frac{1}{2}{\Vert d_{i+1}-{\widehat{d}}_{i+1}\Vert }_2^2\right\}$$

As mentioned above, the multi-hot vectors x_i of almost 40,000 dimensions are first projected to a lower dimensional space, then put into the GRU. We employed two different approaches for this: (1) We put an extra layer of a certain size between the multi-hot input x_i and the GRU, and call it the embedding layer. We denote the weight matrix between the multi-hot input vector and the embedding layer as W_emb. Then we learn the weight W_emb as we train the entire model. (2) We initialize the weight W_emb with a matrix generated by Skip-gram algorithm (Mikolov et al., 2013), then refine the weight W_emb as we train the entire model. This can be seen as using the pre-trained Skip-gram vectors as the input to the RNN and fine-tuning them with the joint prediction task. The brief description of learning the Skip-gram vectors from the EHR is provided in Appendix B. The first and second approach can be formulated as follows:

$${\mathit{h}}_i^{(1)}=\left[\text{tanh}({{\mathit{x}}_i}^{\top }{\mathit{W}}_{\mathit{emb}}+{\mathit{b}}_{\mathit{emb}}),d_i\right]$$ (1)

$${\mathit{h}}_i^{(1)}=\left[{{\mathit{x}}_i}^{\top }{\mathit{W}}_{\mathit{emb}},d_i\right]$$ (2)

where [·, ·] is the concatenation operation used for appending the time duration to the multi-hot vector ${\mathit{h}}_i^{(1)}$ to make it an input vector to the GRU.

5. Results

We now describe the details of our experiments in the proposed RNN approach to forecasting the future clinical events. The source code of Doctor AI is publicly available at https://github.com/mp2893/doctorai.

5.1 Experiment Setup

For training all models including the baselines, we used 85% of the patients as the training set and 15% as the test set. We trained the RNN models for 20 epochs (i.e., 20 iterations over the entire training data) and then evaluated the final performance against the test set. To avoid overfitting, we used dropout between the GRU layer and the prediction layer (i.e. code prediction and time duration prediction). Dropout was also used between GRU layers if we were using a multilayer GRU. We also applied norm-2 regularization on both W_code and w_time. Both regularization coefficients were set to 0.001. The size of the hidden layer h_i of the GRU was set to 2000 to guarantee a sufficient expressive power. After running sets of preliminary experiments where we tried the size from 100 to 2000, we noticed that the code prediction performance started to saturate around 1600~1800. All models were implemented with Theano (Bastien et al., 2012) and trained on a machine equipped with two Nvidia Tesla K80 GPUs.

We train total four different variation of Doctor AI as follows,

• RNN-1: RNN with a single hidden layer initialized with a random orthogonal matrix for W_emb.

• RNN-2: RNN with two hidden layers initialized with a random orthogonal matrix for W_emb.

• RNN-1-IR: RNN using a single hidden layer initialized embedding matrix W_emb with the Skip-gram vectors trained on the entire dataset.

• RNN-2-IR: RNN with two hidden layers initialized embedding matrix W_emb with the Skip-gram vectors trained on the entire dataset. dataset.

5.2 Evaluation metrics

The performance of algorithms in predicting diagnoses and medication codes was evaluated using the Top-k recall defined as:

$$\text{top}-k\text{recall}=\frac{\#\text{of true positives in the top}k\text{predictions}}{\#\text{of true positives}}$$

Top-k recall mimics the behavior of doctors conducting differential diagnosis, where doctors list most probable diagnoses and treat patients accordingly to identify the patient status. Therefore, a machine with a high Top-k recall translates to a doctor with an effective diagnostic skill. This makes Top-k recall an attractive performance metric for our problem.

We select the maximum k to be 30 to evaluate the performance of the models not only for simple cases but also for complex cases. Near 50.7% of the patients have been assigned with more than 10 diagnosis and medication codes at least once. Since it is those complex cases that are of interest to predict and analyze, we choose k to be large enough (i.e., 3 times of the mean).

Coefficient of determination

(R²) was used to evaluate the predictive performance of regression and forecasting algorithms. It compares the accuracy of the prediction with respect to the simple prediction by mean of the target variable.

$$R^2=1-\frac{\sum _i{(y_i-{\widehat{y}}_i)}^2}{\sum _i{(y_i-\overline{y_i})}^2}$$

Because time to the next visit can be highly skewed, we measure the R² performance of the algorithms in predicting log(d_i) to lower the impact of anomalous long durations in the performance metric. In the same spirit, we train all models to predict the logarithm of the time duration between visits.

5.3 Baselines

We compare our model against several baselines as described below. Some of the existing techniques based on continuous-time Markov chain and latent space models were not scalable enough to be trained using the entire dataset in a reasonable amount of time; thus comparison is not feasible.

Frequency baselines

We compare our algorithms against simple baselines that are based on experts’ intuition about the dynamics of events in clinical settings. The first baseline uses a patient’s medical codes in the last visit as the prediction for the current visit. This baseline is competitive when the status of a patient with a chronic condition stabilizes over time. We enhanced this baseline using the top-k most frequent labels observed in visits prior to the current visits. In the experiments we observe that the baseline of top-k most frequent labels is quite competitive.

Logistic and Neural Network time series models

A common way to perform prediction task is to use x_i−1 to predict the codes in the next visit x_i using logistic regression or multilayer perceptron (MLP). To enhance the baseline further, we can use the data from L time lags before and aggregate them x_i−1 + x_i−2 + , +x_i−L for some duration L to create the features for prediction of x_i. Similarly, we can have a model that predicts the time until next visit using rectified linear units (ReLU) as the output activation. We set the lag L = 5 so that the logistic regression and MLP can use information from maximum five past visits. The details of MLP design are described in Appendix C.

5.4 Prediction performance

Table 2 compares the results of different algorithms with RNN based Doctor AI. We report the results in three settings: when we are interested in (1) predicting only diagnosis codes (Dx), (2) predicting only medication codes (Rx), and (3) jointly predicting Dx codes, Rx codes, and the time duration to next visit. The results confirm that the proposed approach is able to outperform the baseline algorithms by a large margin. Note that the recall values for the joint task are lower than those for Dx code prediction or Rx code prediction because the hypothesis space is larger for the joint prediction task.

Table 2.

Accuracy of algorithms in forecasting future medical activities. Embedding matrices W_emb of both RNN-1 (using one hidden layer) and RNN-2 (using two hidden layers) are initialized with random orthogonal vectors. Embedding matrices W_emb of both RNN-1-IR (using one hidden layer) and RNN-2-IR (using two hidden layers) are initialized with Skip-gram vectors trained on the entire dataset.

	D× Only Recall @k			R× Only Recall @k			D×,R×,Time Recall @k
Algorithms	k = 10	k = 20	k = 30	k = 10	k = 20	k = 30	k = 10	k = 20	k = 30	R 2
Last visit	29.17			13.81			26.25			—
Most freq.	56.63	67.39	71.68	62.99	69.02	70.07	48.11	60.23	66.00	—
Logistic	43.24	54.04	60.76	45.80	60.02	68.93	36.04	46.32	52.53	0.0726
MLP	46.66	57.38	64.03	47.62	61.72	70.92	38.82	49.09	55.74	0.1221
RNN-1	63.12	73.11	78.49	67.99	79.55	85.53	53.86	65.10	71.24	0.2519
RNN-2	63.32	73.32	78.71	67.87	79.47	85.43	53.61	64.93	71.14	0.2528
RNN-1-IR	63.24	73.33	78.73	68.31	79.77	85.52	54.37	65.68	71.85	0.2492
RNN-2-IR	64.30	74.31	79.58	68.16	79.74	85.48	54.96	66.31	72.48	0.2534

The superior performance of RNN based approaches can be attributed to the efficient representation that they learn for patients at each visit (Bengio et al., 2013; Schmidhuber, 2015). RNNs are able to learn succinct feature representations of patients by accumulating the relevant information from their history and the current set of codes, which outperformed hand-picked features of frequency baselines.

Table 2 confirms that learning patient representation with RNN is easier with the input vectors that are already efficient representations of the medical codes. The RNN trained with the Skip-gram vectors (denoted by RNN-IR) consistently outperforms the RNN that learns the weight matrix W_emb directly from the data, with only one exception, the medication prediction Recall@30, although the differences are insignificant. The results also confirm that having multiple layers when using RNN improves its ability to learn more efficient representations. The results also indicate that a single layer RNN might have enough representative power to capture the dynamics of medications, and adding more layers may not improve the performance.

The results also indicate that our approach significantly improves the accuracy of predicting the time duration until the next visit compared to the baselines. However, the absolute value of R² metric shows that accurate prediction of time intervals remains as a challenge. We believe achieving significantly better time prediction without extra features should be difficult because the timing of a clinical visit can be a ected by many personal factors such as financial status, location of residence, means of transportation, and life style, to name a few. Thus, without such sensitive personal information, which is rarely included in the EHR, accurate prediction of time intervals should be unlikely.

5.5 Understanding the behavior of the network

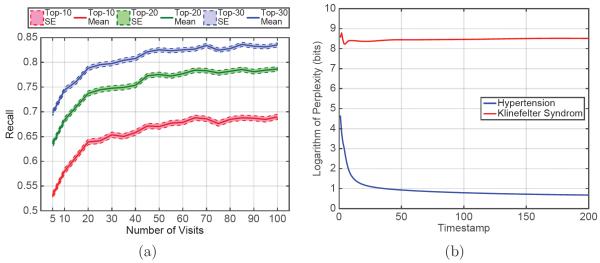
To study the applicability of our model in a real-world setting where patients have varying length of medical records, we conducted an additional experiment to study the relationship between the length of the patient medical history and the prediction performance. To this end, we selected 5,800 patients from the test set who had more than 100 visits. We used the best performing model to predict the diagnosis codes at visits at different times and found the mean and standard error of recall across the selected patients. Figure 2a shows the result of the experiment. We believe that the increase in performance can be due to two reasons: (1) RNN is able to learn a better estimate of the patient status as it sees longer patient records and (2) Visits are correlated with poor health. Those with high visit count are more likely to be severely ill, and therefore their future is easier to predict.

Figure 2.

Characterizing behavior of the trained network: (a) Prediction performance of Doctor AI as it sees a longer history of the patients. (b) Change in the perplexity of response to a frequent code (hypertension) and an infrequent code (Klinefelter’s syndrome).

Another experiment was conducted to understand the behavior of the network by giving synthetic inputs. We chose hypertension (ICD-9 code 401.9) as an example of a frequently observed diagnosis, and Klinefelter’s syndrome (ICD-9 code 758.7) as an example of an infrequent diagnosis. We created two synthetic patients who respectively have 200 visits of 401.9 and 758.7. Then we used the best performing model to predict the diagnosis codes for the next visits. Figure 2b shows contrasting patterns: when the input is one of the frequent codes such as hypertension, the network quickly learns a more specific set of output codes as next disease. When we select an infrequent code like Klinefelter’s syndrome as the input, the network’s output is more diverse and mostly the frequently observed codes. The top 30 codes after convergence shown in Table 4 in Appendix D confirm the disparity of the diversity of the predicted codes for the two cases.

5.6 Knowledge transfer across hospitals

As we observed from the previous experiments, the dynamics of clinical events are complex, which requires models with a high representative power. However, many institutions have not yet collected large scale datasets, and training such models could easily lead to overfitting. To address this challenge, we resort to the recent advances in domain adaptation techniques for deep neural networks (Mesnil et al., 2012; Bengio, 2012; Yosinski et al., 2014; Hoffman et al., 2014).

A different dataset, MIMIC II, which is a publicly available clinical dataset collected from ICU patients over 7 years of observation, was chosen to conduct the experiment. This dataset differs from the Sutter dataset in that it consists of demographically and diagnostically different patients. The number of patients who made at least two visits is 2,695, and the number of unique diagnosis code (3-digit ICD-9 code) is 767, which is a subset of the Sutter dataset. From the dataset, we extracted sequences of 3-digit ICD-9 codes. We chose 2,290 patients for training, 405 for testing. We chose the 2-layer RNN with 1000 dimensional hidden layer, and performed two experiments: 1) We trained the model only on the MIMIC II dataset. 2) We initialized the coefficients of the model with the values learned from the 3-digit ICD-9 sequences of the Sutter data, then we refined the coefficients with the MIMIC II dataset. Figure 3 shows the vast improvement of the prediction performance induced by the knowledge transfer from the Sutter data.

Figure 3.

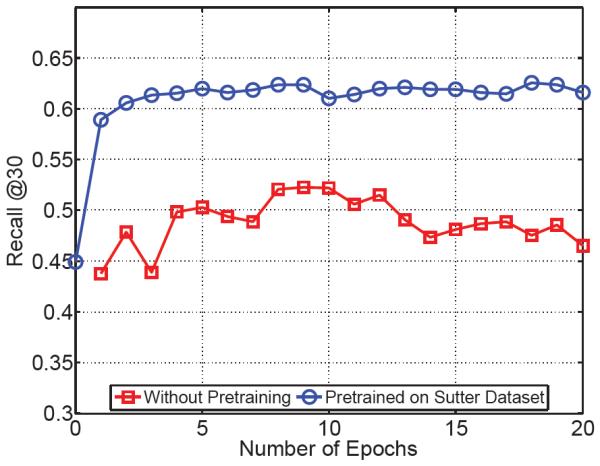
The impact of pre-training on improving the performance on smaller datasets. In the first experiment, we first train the model on a small dataset (red curve). In the second experiment, we pre-train the model on our large dataset and use it for initializing the training of the smaller dataset. This procedure results in more than 10% improvement in the performance.

6. Conclusion

In this work, we proposed Doctor AI system, which is a RNN-based model that can learn efficient patient representation from a large amount of longitidinal patient records and predict future events of patients. We tested Doctor AI on a large real-world EHR datasets, which achieved 79.58% recall@30 and significantly outperformed many baselines. We have also shown that the patient’s visit count and the rarity of medical codes highly influence the performance. We have also demonstrated that knowledge learned from one hospital could be adapted to another hospital. The empirical analysis by a medical expert confirmed that Doctor AI not only mimics the predictive power of human doctors, but also provides diagnostic results that are clinically meaningful.

One limitation of Doctor AI is that, in medical practice, incorrect predictions can sometimes be more important than correct predictions as they can degrade patient health. Also, although Doctor AI has shown that it can mimic physicians’ average behavior, it would be more useful to learn to perform better than average. We set as our future work to address these issues so that Doctor AI can provide practical help to physicians in the future.

Appendix A. Description of Gated Recurrent Units

Figure 4.

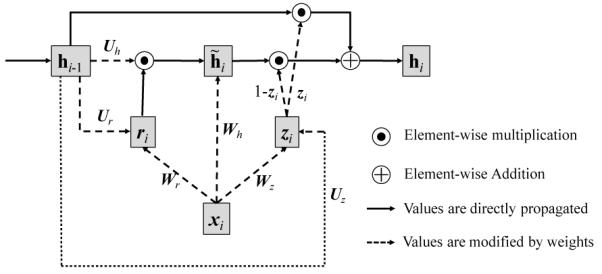
Architecture of GRU

We first reiterate the mathematical formulation of GRU so that the reader can see Figure 4 and the formulations together.

$$\begin{array}{cc}\hfill {\mathit{z}}_i& =\sigma \left({\mathit{W}}_z{\mathit{x}}_i+{\mathit{U}}_z{\mathit{h}}_{i-1}+{\mathit{b}}_z\right)\hfill \\ \hfill {\mathit{r}}_i& =\sigma \left({\mathit{W}}_r{\mathit{x}}_i+{\mathit{U}}_r{\mathit{h}}_{i-1}+{\mathit{b}}_r\right)\hfill \\ \hfill {\tilde{\mathit{h}}}_i& =\text{tanh}\left({\mathit{W}}_h{\mathit{x}}_i+{\mathit{r}}_{i}o{\mathit{U}}_h{\mathit{h}}_{i-1}+{\mathit{b}}_h\right)\hfill \\ \hfill {\mathit{h}}_i& ={\mathit{z}}_{i}o{\mathit{h}}_{i-1}+(1-{\mathit{z}}_i)o{\tilde{\mathit{h}}}_i\hfill \end{array}$$

Figure 4 depicts the architecture of the GRU, where x_i, z_i and r_i respectively represent the input, update gate and the reset gate, ${\tilde{\mathit{h}}}_i$ the intermediate memory unit, h_i the hidden layer, all at timestep t_i. W_h, W_z, W_r, U_h, U_z, U_r are the weight matrices to be learned. Note that the bias vectors b_h, b_z, b_r are omitted in Figure 4.

The outstanding difference between the classical RNN (Elman Network) and GRU is that the previous hidden layer h_i−1 and the current input x_i do not directly change the value of the current hidden layer h_i. Instead, they change the values of both gates z_i, r_i and the intermediate memory unit ${\tilde{\mathit{h}}}_i$. Then the current hidden layer h_i is updated by ${\tilde{\mathit{h}}}_i$ and z_i. Due to the σ function, both gates z_i and r_i have values between 0 and 1. Therefore if the reset gate r_i is close to zero, the intermediate memory unit ${\tilde{\mathit{h}}}_i$ will disregard the past values of the hidden layer h_i−1. If the update gate z_i is close to one, the current hidden layer h_i will disregard the current input x_i, and retain the value from the previous timestep h_i−1.

Simply put, the reset gate allows the hidden layer to drop any information that is not useful in making a prediction, and the updated gate controls how much information from the previous hidden layer should be propagated to the current hidden layer. This characteristic of GRU is especially useful as it is not easy to identify information essential to predicting the future diagnosis, medication or the time duration until the next visit.

Appendix B. Learning the Skip-gram vectors from the EHR

Learning efficient representations of medical codes (e.g. diagnosis codes, medication codes, and procedure codes) may lead to improved performance of many clinical applications. We specifically used Skip-gram Mikolov et al. (2013) to learn real-valued multidimensional vectors to capture the latent representation of medical codes from the EHR.

We processed the private dataset so that diagnosis codes, medication codes, procedure codes are laid out in a temporal order. If there are multiple codes at a single visit, they were laid out in a random order. Then using the context window size of 5 to the left and 5 to the right, and applying Skip-gram, we were able to project diagnosis codes, medication codes and procedure codes into the same lower dimensional space, where similar or related codes are embedded close to one another. For example, hypertension, obesity, hyperlipidemia all share similar values compared to pneumonia or bronchitis. The trained Skip-gram vectors are then plugged into RNN so that a multi-hot vector can be converted to vector representations of medical codes.

Appendix C. Details of the training procedure of multilayer perceptron

We use a multilayer perceptron with a hidden layer of width 2,000. We apply L₂ regularization to all of the weight matrices. The activation functions in the first and output layers are selected to be tanh and softmax functions respectively. For prediction of time intervals, we used rectified linear units.

Appendix D. Case study

The detailed results are shown in Table 3. To take a closer look at the performance of Doctor AI, in Table 3 (in Appendix D) we list the predicted, true, and historical diagnosis codes for five visits of different patients. The blue items represent the correct predictions. The results are promising and show that, given the history of the patient, the Doctor AI can predict the true diagnostic codes. The results highly mimic the way a human doctor will interpret the disease predictions from the history. For all five of the cases shown in Table 3, the set of predicted diseases contain most, if not all of the true diseases. For example, in the first case, the top 3 predicted diseases match the true diseases. A human doctor would likely predict similar diseases to the ones predicted with Doctor AI, since old myocardial infarction and chronic ischemic heart disease can be associated with infections and diabetes (Stevens et al., 1978).

In the fourth case, visual disturbances can be associated with migraines and essential hypertension (Keith et al., 1939). Further, essential hypertension may be linked to cognitive function (Kuusisto et al., 1993), which plays a role in anxiety disorders and dissociative and somatoform disorders. Regarding codes that are guessed incorrectly with the fourth case, they can still be plausible given the history. For example, cataracts, and disorders of refraction and accommodation could have been guessed based on a history of visual disturbances, as well as strabismus and disorders of binocular eye movements. Allergic rhinitis could have been guessed, because there was a history of allergic rhinitis. In summary, Doctor AI is able to very accurately predict the true diagnoses in the sample patients. The results are promising and should motivate future studies involving the application of Doctor AI on different datasets exhibiting other populations of patients.

Table 3.

Comparison of the diagnoses by Doctor AI and the true future diagnoses.

Predicted		True		History
ICD9	Description	ICD9	Description	ICD9	Description
412 V58 414 272 250 585 428 285 V04 V76	Old myocardial infarction Encounter for other and unspecified procedures Other forms of chronic ischemic heart disease Disorders of lipoid metabolism Diabetes mellitus Chronic kidney disease (CKD) Heart failure Other and unspecified anemias Need for prophylactic vaccin. and inocul. against certain diseases Special screening for malignant neoplasms	414 412 V58	Other forms of chronic ischemic heart disease Old myocardial infarction Encounter for other and unspecified procedures	465 250 366 V58 362	Acute upper respiratory infec. of multiple or unspec. sites Diabetes mellitus Cataract Encounter for other and unspecified procedures Other retinal disorders
V07 477 780 401 786 493 300 461 530 719	Need for isolation and other prophylactic measures Allergic rhinitis General symptoms Essential hypertension Symptoms involving respiratory system Asthma Anxiety, dissociative and somatoform disorders Acute sinusitis Diseases of esophagus Other and unspecified disorders of joint	V07 401 786 782	Need for isolation and other prophylactic measures Essential hypertension Symptoms involving respiratory system Symptoms involving skin and other integumentary tissue	782 477 V07 564 401	Symptoms involving skin and other integumentary tissue Allergic rhinitis Need for isolation and other prophylactic measures Functional digestive disorders, not elsewhere classified Essential hypertension
453 V58 719 V12 V43 729 715 733 726 451	Other venous embolism and thrombosis Encounter for other and unspecified procedures Other and unspecified disorders of joint Personal history of certain other diseases Organ or tissue replaced by other means Other disorders of soft tissues Osteoarthrosis and allied disorders Other disorders of bone and cartilage Peripheral enthesopathies and allied syndromes Phlebitis and thrombophlebitis	715 V12 719 V58	Osteoarthrosis and allied disorders Personal history of certain other diseases Other and unspecified disorders of joint Encounter for other and unspecified procedures	453 956 V43	Other venous embolism and thrombosis Injury to peripheral nerve(s) of pelvic girdle and lower limb Organ or tissue replaced by other means
477 780 300 401 346 366 V43 367 368 272	Allergic rhinitis General symptoms Anxiety, dissociative and somatoform disorders Essential hypertension Migraine Cataract Organ or tissue replaced by other means Disorders of refraction and accommodation Visual disturbances Disorders of lipoid metabolism	401 780 346 300	Essential hypertension General symptoms Migraine Anxiety, dissociative and somatoform disorders	782 477 692 368 378	Symptoms involving skin and other integumentary tissue Allergic rhinitis Contact dermatitis and other eczema Visual disturbances Strabismus and other disorders of binocular eye movements
428 427 272 401 786 185 250 414 788 424	Heart failure Cardiac dysrhythmias Disorders of lipoid metabolism Essential hypertension Symptoms involving respiratory system Malignant neoplasm of prostate Diabetes mellitus Other forms of chronic ischemic heart disease Symptoms involving urinary system Other diseases of endocardium	250 402 428 272 427	Diabetes mellitus Hypertensive heart disease Heart failure Disorders of lipoid metabolism Cardiac dysrhythmias	466 428 786 785 250	Acute bronchitis and bronchiolitis Heart failure Symptoms involving respiratory system Symptoms involving cardiovascular system Diabetes mellitus

Table 4.

Comparison of the diagnoses by Doctor AI for a frequent and an infrequent disease code after 200 time step.

Hypertension		Klinefelter’s syndrome
ICD9	Description	ICD9	Description
401	Essential hypertension	272	Disorders of lipoid metabolism
272	Disorders of lipoid metabolism	V70	General medical examination
786	Symptoms involving respiratory system and other chest symptoms	V04	Need for prophylactic vaccination and inoculation against certain diseases
V06	Need for prophylactic vaccination and inoculation against combinations of diseases	730	Osteomyelitis, periostitis, and other infections involving bone
790	Nonspecific findings on examination of blood	780	General symptoms
V76	Special screening for malignant neoplasms	783	Symptoms concerning nutrition, metabolism, and development
V04	Need for prophylactic vaccination and inoculation against certain diseases	295	Schizophrenic disorders
V70	General medical examination	V76	Special screening for malignant neoplasms
780	General symptoms	141	Malignant neoplasm of tongue
276	Disorders of fluid, electrolyte, and acid-base balance	V06	Need for prophylactic vaccination and inoculation against combinations of diseases
782	Symptoms involving skin and other integumentary tissue	250	Diabetes mellitus
268	Vitamin D deficiency	782	Symptoms involving skin and other integumentary tissue
719	Other and unspecified disorders of joint	786	Symptoms involving respiratory system and other chest symptoms
427	Cardiac dysrhythmias	208	Leukemia of unspecified cell type
380	Disorders of external ear	401	Essential hypertension
250	Diabetes mellitus	790	Nonspecific findings on examination of blood
599	Other disorders of urethra and urinary tract	280	Iron deficiency anemias
V72	Special investigations and examinations	607	Disorders of penis
789	Other symptoms involving abdomen and pelvis	281	Other deficiency anemias
729	Other disorders of soft tissues	V03	Need for prophylactic vaccination and inoculation against bacterial diseases
682	Other cellulitis and abscess	332	Parkinson’s disease
V03	Need for prophylactic vaccination and inoculation against bacterial diseases	255	Disorders of adrenal glands
724	Other and unspecified disorders of back	799	Other ill-defined and unknown causes of morbidity and mortality
V58	Encounter for other and unspecified procedures and aftercare	244	Acquired hypothyroidism
278	Overweight, obesity and other hyperalimentation	V58	Encounter for other and unspecified procedures and aftercare
V82	Special screening for other conditions	151	Malignant neoplasm of stomach
V65	Other persons seeking consultation	294	Persistent mental disorders due to conditions classified elsewhere
585	Chronic kidney disease (CKD)	V72	Special investigations and examinations
274	Gout	344	Other paralytic syndromes
V49	Other conditions inuencing health status	146	Malignant neoplasm of oropharynx