Computational models of atrial cellular electrophysiology and calcium handling, and their role in atrial fibrillation

Abstract

The complexity of the heart makes an intuitive understanding of the relative contribution of ion channels, transporters and signalling pathways to cardiac electrophysiology challenging. Computational modelling of cardiac cellular electrophysiology has proven useful to integrate experimental findings, extrapolate results obtained in expression systems or animal models to other systems, test quantitatively ideas based on experimental data and provide novel hypotheses that are experimentally testable. While the bulk of computational modelling has traditionally been directed towards ventricular bioelectricity, increasing recognition of the clinical importance of atrial arrhythmias, particularly atrial fibrillation, has led to widespread efforts to apply computational approaches to understanding atrial electrical function. The increasing availability of detailed, atrial‐specific experimental data has stimulated the development of novel computational models of atrial‐cellular electrophysiology and Ca²⁺ handling. To date, more than 300 studies have employed mathematical simulations to enhance our understanding of atrial electrophysiology, arrhythmogenesis and therapeutic responses. Future modelling studies are likely to move beyond current whole‐cell models by incorporating new data on subcellular architecture, macromolecular protein complexes, and localized ion‐channel regulation by signalling pathways. At the same time, more integrative multicellular models that take into account regional electrophysiological and Ca²⁺ handling properties, mechano‐electrical feedback and/or autonomic regulation will be needed to investigate the mechanisms governing atrial arrhythmias. A combined experimental and computational approach is expected to provide the more comprehensive understanding of atrial arrhythmogenesis that is required to develop improved diagnostic and therapeutic options. Here, we review this rapidly expanding area, with a particular focus on Ca²⁺ handling, and provide ideas about potential future directions.

Abbreviations

AF

atrial fibrillation

AP

action potential

APD

action potential duration

cAF

long‐standing persistent (chronic) atrial fibrillation

EAD

early afterdepolarizations

DAD

delayed afterdepolarization

NCX

Na⁺/Ca²⁺ exchanger

pAF

paroxysmal AF

PV

pulmonary vein

RyR2

ryanodine receptor type‐2

SAN

sinoatrial node

SERCA

sarcoplasmic/endoplasmic reticulum Ca²⁺‐ATPase

SR

sarcoplasmic reticulum

Introduction

The electrical activity of the heart is controlled by an intricate system of ion channels, transporters, intracellular organelles and signalling pathways. The complexity of this regulation makes it challenging to obtain an intuitive understanding of the role of individual components in the integrated system. Computational modelling was developed to complement experimental approaches to improve understanding of cardiac electrophysiology and arrhythmogenesis (Rudy & Silva, 2006; Bers & Grandi, 2011; Trayanova, 2014). Although computational work initially focused predominantly on ventricular electrophysiology, the interest in atrial‐specific computational models has increased rapidly in recent years. A better integrative understanding of atrial arrhythmias is critical given the clinical importance of the atria. Atrial fibrillation (AF) is presently the most common sustained arrhythmia, is expected to increase in prevalence with the ageing of the population, and has an important impact on morbidity and mortality (Andrade et al. 2014). During the last decades, a central role for Ca²⁺ handling abnormalities has been identified in promoting ectopic activity and re‐entry, the two major mechanisms underlying AF (Nattel & Dobrev, 2012; Greiser & Schotten, 2013; Heijman et al. 2014). However, translating these findings into improved patient care has proven challenging (Heijman et al. 2015). A critical requirement for therapeutic advances is to identify key nodal points amenable to pharmacological therapy to improve treatment options for AF patients. Computational atrial Ca²⁺ handling models may play a key role in identifying such nodal points by determining the hierarchy of individual contributors to AF mechanisms. In this review, we summarize key aspects of atrial cellular Ca²⁺ handling in the larger context of atrial cardiomyocyte electrophysiology and discuss the methodology and application of computational modelling, aiming to enable both experimental and computational cardiovascular scientists to understand the main properties of atrial cardiomyocyte models, their uses and the gaps in current knowledge.

Cardiac cellular electrophysiology and Ca²⁺ handling

General components of subcellular Ca²⁺ handling in cardiomyocytes

In both atrial and ventricular cardiomyocytes, depolarization of the membrane potential (V _M) during the action potential (AP) activates voltage‐dependent L‐type Ca²⁺‐channels, resulting in increased subsarcolemmal [Ca²⁺]. Consequent activation of ryanodine receptor type‐2 (RyR2) channels on the sarcoplasmic reticulum (SR) results in a much larger SR Ca²⁺ release, producing the systolic Ca²⁺ transient required to cause effective cardiomyocyte contraction (Fig. 1 A). Relaxation is mediated by a decrease in intracellular Ca²⁺ through reuptake into the SR by the SR Ca²⁺‐ATPase type‐2a (SERCA2a), and extrusion from the cell via the electrogenic Na⁺/Ca²⁺ exchanger type‐1 (NCX1) or the plasmalemmal Ca²⁺‐ATPase (PMCA). SERCA2a function is modulated via the inhibitory SERCA‐binding proteins phospholamban or sarcolipin (Fig. 1 A). All Ca²⁺‐transport mechanisms are regulated by a wide range of signalling pathways that fine‐tune cardiac contractility (Bers, 2008; Heijman et al. 2014; Kohler et al. 2014).

Figure 1. Cardiac Ca²⁺ handling .

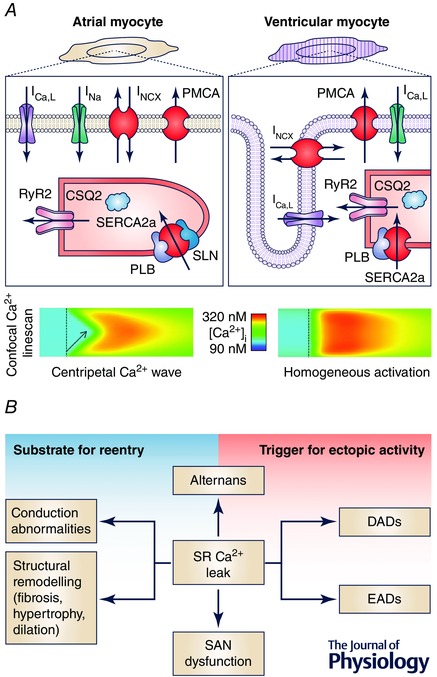
A, schematic representation of proteins involved in cardiac excitation–contraction coupling (top) and the consequences for Ca²⁺ transients (bottom) of differences in subcellular structure between atrial cardiomyocytes lacking an extensive t‐tubular network (left), and ventricular cardiomyocytes with a t‐tubular network (right). B, multiple roles through which SR Ca²⁺ leak can promote the trigger and substrate for atrial fibrillation. Abbreviations: CSQ2, calsequestrin‐2; DAD, delayed afterdepolarization; EAD, early afterdepolarization; I _Ca,L, L‐type Ca²⁺ current; I _Na, Na⁺ current; I _NCX, Na⁺–Ca²⁺‐exchange current; PMCA, plasmalemmal Ca²⁺‐ATPase; PLB, phospholamban; RyR2, ryanodine receptor channel type‐2; SERCA2a, SR Ca²⁺‐ATPase; SLN, sarcolipin; SR, sarcoplasmic reticulum.

Differences between atrial, ventricular and sinoatrial node cardiomyocytes

Despite their overall similarity, there are important quantitative and qualitative electrophysiological differences between atrial, ventricular and sinoatrial node (SAN) cardiomyocytes (Schram et al. 2002; Gaborit et al. 2007). These include differences in the expression and function of ion channels, with atrial cardiomyocytes possessing a number of ion currents that are largely absent in the ventricle (e.g. ultra‐rapid delayed‐rectifier K⁺ current I _Kur, or acetylcholine‐activated inward‐rectifying K⁺ current I _K,ACh). SAN cardiomyocytes additionally express more hyperpolarization‐activated cyclic nucleotide‐gated (HCN) channels but have relatively few Na⁺ channels. The T‐type Ca²⁺ current is largest in the SAN and smallest in the ventricles. On the other hand, ventricular cardiomyocytes have a larger basal inward‐rectifying K⁺ current (I_K1). These differences result in markedly different APs, including a less pronounced plateau in atrial cardiomyocytes, a more negative resting membrane potential in ventricular cardiomyocytes and spontaneous diastolic depolarization in SAN cardiomyocytes (Schram et al. 2002; Gaborit et al. 2007).

In addition, there are intrinsic differences in Ca²⁺ handling between cell types (Bootman et al. 2006; Dobrev et al. 2009). Atrial cardiomyocytes express more SERCA2a and less phospholamban than ventricular (Luss et al. 1999; Gaborit et al. 2007; Walden et al. 2009). In addition, sarcolipin is predominantly expressed in the atria (Ellinghaus et al. 2005; Babu et al. 2007). Human atrial tissue samples also have weaker expression of RyR2 and the SR Ca²⁺ buffer calsequestrin than ventricular samples (Gaborit et al. 2007). Together, these changes contribute to atrial‐specific Ca²⁺ handling properties (Luss et al. 1999; Walden et al. 2009). There are also important structural differences between atrial and ventricular cardiomyocytes (Fig. 1 A, bottom), with ventricular myocytes having a well‐developed system of membrane invaginations (t‐tubules), bringing sarcolemmal components deep into the cell interior, which are largely lacking in atrial cardiomyocytes. In several species, including humans, a partial atrial t‐tubular structure may exist (Richards et al. 2011). The relative absence of t‐tubules in atrial cardiomyocytes results in a centripetal Ca²⁺ wave whereby RyR2s close to the sarcolemma get activated first and sequentially activate neighbouring RyR2s towards the cell centre (Greiser et al. 2014). In contrast, ventricular cardiomyocytes show a uniform SR Ca²⁺ release throughout the cell.

Role of Ca²⁺ handling abnormalities in atrial arrhythmias

Ca²⁺ handling abnormalities play numerous roles in atrial arrhythmogenesis (Fig. 1 B). In particular, increased SR Ca²⁺ leak resulting from RyR2‐dysfunction or SR Ca²⁺ overload can activate NCX, resulting in a transient‐inward current that promotes early or delayed afterdepolarizations (EADs and DADs, respectively) that induce cardiac alternans. In parallel, Ca²⁺‐dependent signalling pathways contribute to the vulnerable substrate for re‐entry through ion‐channel remodelling, structural remodelling (including atrial fibrosis, hypertrophy and dilatation) and direct modulation of conduction velocity (Fig. 1 B), as detailed in recent reviews (Nattel & Dobrev, 2012; Greiser & Schotten, 2013; Heijman et al. 2014). SR Ca²⁺ releases also contribute to pacemaker activity in the SAN and disturbed SAN Ca²⁺ handling can produce SAN dysfunction, which is associated with an increased risk for AF (Fig. 1 B), as recently reviewed (Monfredi & Boyett, 2015). While SAN abnormalities are important for some of the consequences of AF (e.g. ‘tachy‐brady syndrome’) and sinus bradycardia may be associated with increased AF risk, the SAN shows high‐grade entrance block during AF so that it does not participate in maintaining the arrhythmia (Kirchhof & Allessie, 1992). The major differences in ion‐channel and Ca²⁺ handling properties between atrial, ventricular and SAN cardiomyocytes highlight the need for atrial‐specific cardiomyocyte models to better understand AF mechanisms.

Computational modelling of atrial cellular electrophysiology and Ca²⁺ handling

Simulation of atrial cellular electrophysiology and Ca²⁺ handling is an iterative process. Each model employs a ‘state vector’ reflecting dynamic quantities (V _M, intracellular Ca²⁺, gating variables of individual ion channels, etc.; Fig. 2 A). The changing state properties over time are mathematically represented by a system of non‐linear ordinary differential equations (Rudy & Silva, 2006). At each time point in a simulation, the change in the virtual cardiomyocyte state is calculated and is used to update the current state, so that the dynamic evolution of the overall state is determined by integrating instantaneous changes. The update cycle contains two major components. First, individual ion currents and intracellular ion fluxes are determined based on the current state vector. Subsequently, the ion currents/fluxes are combined based on the (sub)cellular geometry, diffusion and ionic buffers to calculate the changes in intracellular ion concentrations and V _M. Together, these steps allow calculation of the updated state vector (Fig. 2 A). Distinctions between atrial cardiomyocyte models therefore include differences in formulations of ion channels and/or transporters, as well as differences in the representation of subcellular structure.

Figure 2. General approach to simulate atrial cellular electrophysiology and Ca²⁺ handling .

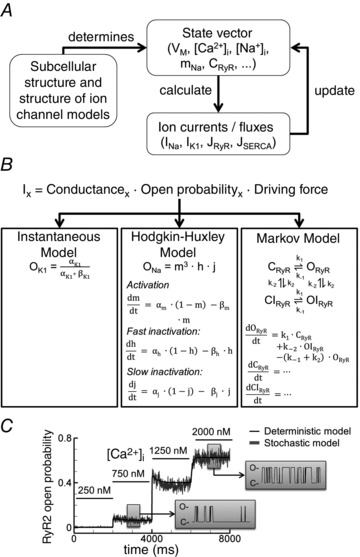
A, the state vector is determined by the subcellular structure and the structure of individual ion channel formulations. Each simulation is an iterative process involving the calculation of individual ion currents based on the current state vector, and updating of the state vector, including intracellular concentrations based on current flow/ion transport and the new membrane potential (V _M). B, types of ion‐channel formulations. Instantaneous, time‐independent currents such as the inward‐rectifier K⁺ current (I _K1); Hodgkin–Huxley‐type formulations such as the Na⁺ current (I _Na) with three time‐dependent gating variables operating independently (m, j and h); and Markov models, for example for the type‐2 ryanodine receptor channel (RyR2)‐mediated Ca²⁺ release (J _RyR), with individual channel states (closed, open, inactivated) and rate constants controlling state transitions. C, simulations using a deterministic (black line) and stochastic (grey line) implementation of the RyR2 Markov model from panel B show the same average whole‐cell open probability, but stochastic simulations enable investigation of the impact of single‐channel gating (grey boxes; C denotes closed, O open).

Types of ion‐channel models

Currents through specific types of ion channels are determined by three elements (Fig. 2 B): a fixed total conductance, the dynamic open probability, and the driving force (the difference between V _M and the equilibrium potential of permeant ions) (Dössel et al. 2012). There are three common approaches to simulate ion‐channel open probability (Fig. 2 B). Several ion currents, such as I _K1, have such rapid kinetics that their open probabilities are generally represented as instantaneous, time‐independent functions of V _M or other state variables (Lindblad et al. 1996). For other currents, physiologically relevant kinetic properties like activation and inactivation can be represented as Hodgkin–Huxley functions, based on the seminal AP model of the squid giant axon (Hodgkin & Huxley, 1952), or using Markov models. In Hodgkin–Huxley representations, each kinetic process is represented with a single state variable varying dynamically based on ‘on’ and ‘off’ rates, which depend on V _M and/or other components of the state vector. For example, in Fig. 2 B, middle, the open probability of the Na⁺ channel is represented by channel activation (m) and two inactivation processes (fast and slow, represented by h and j), each with distinct V _M‐dependent rates α and β. All kinetic processes take place independently and the open probability is obtained by multiplying the individual processes (Rudy & Silva, 2006). In a Markov model (Fig. 2 B, right), ion channels are represented by a number of states (open, closed, inactivated, etc.), with a value reflecting the fraction of ion channels currently residing in each state. Rates are defined for each state transition and can depend on any state variable. Each Hodgkin–Huxley model has an equivalent Markov model, but Markov models can additionally capture dependent state transitions (Rudy & Silva, 2006). For example, in a Markov model it is possible for inactivation only to take place from the open state. Finally, recent work has highlighted the importance of considering the stochastic nature of individual ion channels for repolarization dynamics and spontaneous SR Ca²⁺‐release events (Heijman et al. 2013; Voigt et al. 2014). Markov models can be adapted to simulate the stochastic nature of ion channel gating (Fig. 2 C), and validated using single‐channel recordings, while retaining the macroscopic behaviour of deterministic Markov models (Heijman et al. 2013).

Atrial cardiomyocyte models and their principal findings

An overview of commonly used atrial cardiomyocyte models and their main properties is given in Table 1 and briefly summarized below. The evolution of these models is illustrated in Fig. 3.

Table 1.

Overview of atrial cardiomyocyte models

Reference	Species (types)	Structure (compartments)	Ion currents/fluxes
Schmidt et al. (2015)	Human (Ctl/cAF)	Common pool (cytosol, SR, dyadic space, subsarcolemma)	HH: I Na, I to, I Kur, I Kr, I Ks, I Ca,L, J RyR, I K2P
			Inst: I K,ACh, I K1, I Kp, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, I Cl,Ca, I Cl,b, J SERCA, J leak, J tr, J diff,ss, J diff,j
Davies et al. (2014)	Mouse	Common pool (cytosol, network SR, junctional SR, dyadic space)	Markov: I Na, I Ca,L, I Kr
			HH: I Kur, I Ks, I Kto,s, I Kto,f, I Kss
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Cl,Ca,, J up, J leak, J tr, J xfer
Voigt et al. (2014)	Human (Ctl, pAF)	Spatial (50× longitudinal, 18× transverse; cytosol, SR, subsarcolemmal space, SR release space)	Markov: I Ca,L, J RyR (stochastic)
			HH: I Na, I to, I Kur, I Kr, I Ks
			Inst: I K,ACh, I K1, I Kp, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, I Cl,Ca, I Cl,b, J SERCA, J diff,ss, J diff,j
		SR, subsarcolemmal space, SR release space)
Colman et al. (2013)	Human (Ctl/cAF; regions: AS, AVR, BB, CT, LA, LAA, PM, PV, RAA)	Common pool (subsarcolemmal space, non‐junctional cytosol, network SR, junctional SR)	HH: I Na, I to, I Kur, I Kr, I Ks, I Ca,L, J RyR
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, J SERCA, J leak, J tr
Li et al. (2012)	Generic	Spatial (subsarcolemmal space and 13× transverse cytosol/SR)	HH: I Ca,L
			Inst: I NCX, I p,Ca, J RyR, J SERCA
Thul et al. (2012); Thul et al. (2015)	Generic	Spatial (3‐dimensional)	Implicit: J RyR, J SERCA, I Ca,L, I NCX
Grandi et al. (2011); Voigt et al. (2013)	Human (Ctl/cAF; RA/LA; 2 AP morphologies; adrenergic stimulation)	Common pool (cytosol, SR, dyadic space, subsarcolemma)	HH: I Na, I to, I Kur, I Kr, I Ks, I Ca,L, J RyR
			Inst: I K,ACh, I K1, I Kp, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, I Cl,Ca, I Cl,b, J SERCA, J leak, J diff,ss, J diff,j
Koivumaki et al. (2011); Koivumaki et al. (2014)	Human (Ctl/cAF)	Spatial (dyadic subspace and 8× transverse cytosol/SR)	HH: I Na, I to, I sus, I Kr, I Ks, I Ca,L, I f, J RyR
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, J SERCA, J leak, J tr, J diff
Maleckar et al. (2009)	Human (Ctl/cAF)	Common pool (cytosol, network SR, junctional SR, cleft, dyadic space)	HH: I Na, I to, I Kur, I Kr, I Ks, I Ca,L, J RyR
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, J SERCA, J leak, J tr, J diff
Ramirez et al. (2000); Kneller et al. (2002)	Dog (Ctl/ATR; regions: AVR, CT, PM, RAA)	Common pool (cytosol, network SR, junctional SR)	HH: I Na, I to, I Kur,d, I Kr, I Ks, I Ca,L, J RyR
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, I Cl,Ca, J SERCA, J leak, J tr
Nygren et al. (1998)	Human	Common pool (cytosol, network SR, junctional SR, cleft, dyadic space)	HH: I Na, I to, I sus, I Kr, I Ks, I Ca,L, J RyR
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b,
Courtemanche et al. (1998)	Human (3 AP morphologies)	Common pool (cytosol, network SR, junctional SR)	HH: I Na, I to, I Kur, I Kr, I Ks, I Ca,L, J RyR
			Inst: I K1, I NaK, I NCX, I p,Ca, I Na,b, I Ca,b, J SERCA, J leak, J tr
Lindblad et al. (1996)	Rabbit	Common pool (cytosol, network SR, junctional SR)	HH: I Na, I Ca,L, I Ca,T, I to, I Kr, I Ks, J RyR
			Inst: I NaK, I NCX, I p,Ca, I Ca,b, I Na,b, I Cl,b, I K1, J SERCA, J tr
Rasmusson et al. (1990)	Bullfrog	Common pool (cytosol, cleft)	HH: I Na, I Ca, I K
			Inst: I K1, I B, I NaK, I NCX, I p,Ca
Hilgemann & Noble (1987)	Rabbit	Common pool (cytosol, network SR, junctional SR, cleft)	HH: I Na, I Ca,L, J RyR
			Inst: I K, I K2, I NaK, I NCX, I Ca,b, I Na,b, J p,Ca, J SERCA, J tr

AP, action potential; ATR, atrial tachycardia‐induced remodelling; AS, atrial septum; AVR, atrio‐ventricular ring; BB, Bachmann's bundle; cAF, chronic atrial fibrillation; CT, crista terminalis; Ctl, control model; HH, Hodgkin–Huxley formulations of ion channels; Inst, instantaneous, time‐independent formulations of ion channels; LA, left atrium; LAA, left atrial appendage; Markov, Markov models of ion channels; pAF, paroxysmal atrial fibrillation; PM, pectinate muscle; PV, pulmonary vein; RA, right atrium; RAA, right atrial appendage; SR, sarcoplasmic reticulum. For definition of individual model currents, the reader is referred to the respective reference.

Figure 3. Evolution of the development of atrial cardiomyocyte models and their interdependencies .

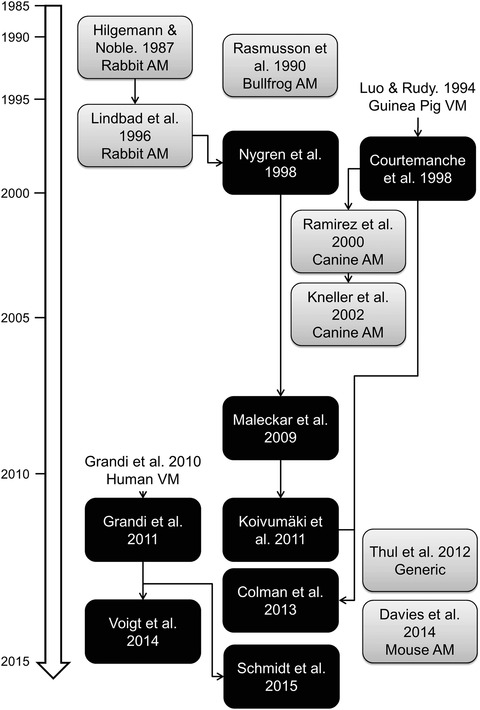
Human atrial cardiomyocyte models are shown in black boxes; other species are shown in grey. Abbreviations: AM, atrial cardiomyocyte; VM, ventricular cardiomyocyte.

Computational models based on experimental data from animals

Even in the first atrial cardiomyocyte model developed in 1987, Ca²⁺ handling plays a major role (Hilgemann & Noble, 1987). The model simulates Ca²⁺ influx through Ca²⁺ channels, SR Ca²⁺ release, Ca²⁺‐dependent activation of NCX1 and Ca²⁺‐dependent inactivation of I _Ca,L to integrate various findings on Ca²⁺‐transport processes in rabbit atrial muscle and their dynamics in the presence of premature stimulations. A computational model of the bullfrog atrial cardiomyocyte (Rasmusson et al. 1990), containing three Hodgkin–Huxley‐based ion currents (I _Na, I _Ca, I _K), six instantaneous currents and variable intracellular and cleft Na⁺, K⁺ and Ca²⁺ concentrations, was the first to provide insights into the contribution of individual ion currents to atrial AP initiation, repolarization and resting membrane potential. Like the Hilgemann and Noble model, this model incorporated dynamic changes in intracellular Ca²⁺, albeit in the absence of a functional SR, based on experimental data. The model highlights a role for Ca²⁺ buffers in the positive force–frequency relationship (Rasmusson et al. 1990). Later, the Ca²⁺ handling of the Hilgemann and Noble model was combined with newer ion current data obtained in rabbit atrial cardiomyocytes (Lindblad et al. 1996). The subcellular structure of this model (with uptake and release compartments within the SR, a cytosolic space, Ca²⁺ buffers, and a non‐permeable space representing nucleus and mitochondria) and Hodgkin–Huxley ion channel formulations, represents the standard that was employed in most subsequent common‐pool atrial cardiomyocyte models (Table 1).

The dog is a commonly used large‐animal model to study arrhythmia mechanisms, including the AF‐promoting effects of various cardiovascular diseases and the atrial tachycardia‐related remodelling mechanisms that promote AF maintenance (Nishida et al. 2010). Ramirez et al. developed a model with Hodgkin–Huxley‐based formulations of the major ion currents in the canine atrial cardiomyocyte and common‐pool Ca²⁺ handling (Ramirez et al. 2000). The model reproduced regional heterogeneities in AP properties by taking into account the heterogeneous expression of different ion currents. Moreover, incorporation of atrial tachycardia‐dependent ion channel remodelling allowed reproduction of major experimentally observed AP features, notably AP shortening and loss of rate adaptation. Improved formulations to simulate atrial Ca²⁺ handling, including the effects of atrial tachycardia, were incorporated in a follow‐up study (Kneller et al. 2002). In addition to ion channel remodelling, atrial tachycardia‐dependent Ca²⁺ handling remodelling importantly contributes to the loss of AP rate adaptation.

Despite the extensive use of genetically engineered mouse models to study AF‐promoting molecular mechanisms (Nishida et al. 2010), there is a relative paucity of computational murine atrial cardiomyocyte models. One notable exception is a recent study showing how the electrotonic interactions between a mouse atrial AP model and a model of an atrial (myo)fibroblast decrease atrial‐cardiomyocyte AP amplitude and upstroke velocity, prolong action potential duration (APD) and depolarize resting membrane potential (Davies et al. 2014). In multicellular simulations, increased cardiomyocyte–(myo)fibroblast coupling might decrease conduction velocity and promote re‐entry (Ashihara et al. 2012; Aguilar et al. 2014; Davies et al. 2014), but it remains highly controversial whether these mechanisms take place in vivo. Although Ca²⁺ handling abnormalities (e.g. mutations in RyR2 or loss of the RyR2‐stabilizing subunit FKBP12.6) can increase the susceptibility to pacing‐induced AF in mice (Chelu et al. 2009), there are, as far as we know, no computational models of mouse atrial cardiomyocytes that simulate subcellular Ca²⁺ handling abnormalities.

Computational models of human atrial cardiomyocytes

Information obtained from human atrial samples provides the most directly relevant insights into clinical AF mechanisms (Heijman et al. 2014). Human samples capture the full complexity of the disease and provide the most clinically relevant cellular model to study the underlying mechanisms, with caveats because of varying ages, and variability in diseases and therapeutic regimens of the patients. The availability of human cellular electrophysiology data led to the first two computational models of the human atrial cardiomyocyte (Courtemanche et al. 1998; Nygren et al. 1998). Both are common‐pool models, approximating the cytosol as a homogeneous compartment without considering local changes in intracellular ion concentrations (Fig. 4 A). Hodgkin–Huxley ion‐channel formulations are used, and both models included for the first time the atrial‐predominant current I _Kur. The long‐term stability of the Nygren model was improved by incorporating charge conservation for the stimulus current (Jacquemet, 2007), and formulations of several K⁺ currents were subsequently updated to improve AP rate dependence, without significant changes in model structure or Ca²⁺ handling (Maleckar et al. 2009). These models have provided substantial insights into the dynamics of atrial cellular electrophysiology and are widely used for single‐cell and multicellular simulation studies.

Figure 4. Schematic representation of common subcellular spatial representations employed in human atrial cardiomyocyte models .

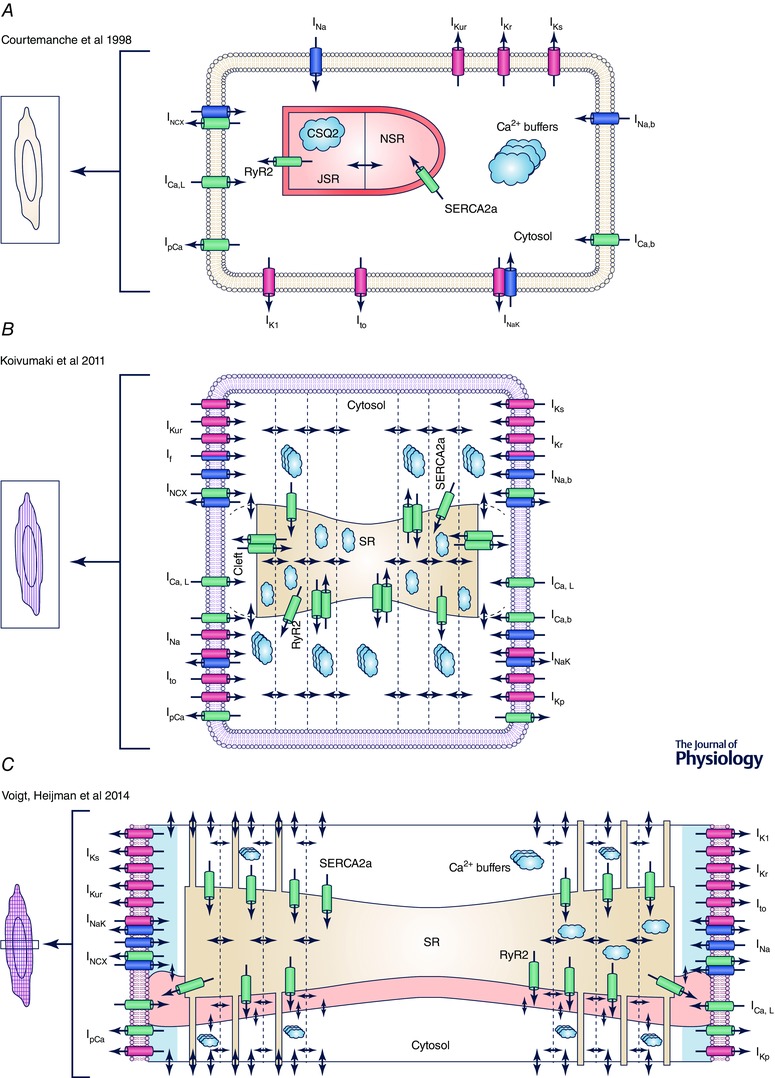
A, example of a common‐pool model without spatial representation of intracellular Ca²⁺ (Courtemanche et al. 1998). B, example of a model with transverse compartments to simulate centripetal Ca²⁺ diffusion (Koivumaki et al. 2011). C, model with transverse and longitudinal compartments allowing simulation of centripetal Ca²⁺ waves and spontaneous SR Ca²⁺‐release events (Voigt et al. 2014). Abbreviations: JSR, junctional SR; NSR, network SR; SR, sarcoplasmic reticulum; SRS, SR Ca²⁺‐release space. For more information about individual ion currents, see Table 1.

Despite the similarities in subcellular structure and the substantial overlap in experimental data used to create them, the Courtemanche and Nygren models show important differences in AP morphology and rate dependence, resulting in distinct properties of re‐entrant waves in multicellular simulations (Nygren et al. 2001; Cherry & Evans, 2008; Cherry et al. 2008). These differences can partly be reconciled by scaling a number of currents. However, more recent analyses incorporating the ion‐channel formulations of one model into the subcellular structure and Ca²⁺ handling of the other (and vice versa) have indicated that differences in Ca²⁺ handling dynamics also contribute (Cherry et al. 2008). The Courtemanche, Nygren and Maleckar models were developed largely in the absence of detailed information on human atrial cardiomyocyte Ca²⁺ handling specifics. Formulations for Ca²⁺ fluxes were taken from previously developed ventricular cardiomyocyte models, resulting in simulated Ca²⁺ transients with peak values exceeding 700 nmol L⁻¹ under basal conditions and a very fast time‐to‐peak (Wilhelms et al. 2012), results that are inconsistent with more recent experimental data (Neef et al. 2010; Voigt et al. 2012).

Newer human atrial cardiomyocyte models have focused in greater detail on the simulation of atrial Ca²⁺ handling (Grandi et al. 2011; Koivumaki et al. 2011). Grandi et al. developed a common‐pool model of the atrial cardiomyocyte with detailed validation of rate‐dependent Ca²⁺ handling, based on experimental data obtained in isolated human atrial cardiomyocytes at physiological temperature (Grandi et al. 2011). This model makes it possible to simulate the electrophysiological consequences of β‐adrenoceptor and muscarinic receptor stimulation and to assess differences between left and right atrial cardiomyocytes. The Grandi et al. model highlighted the important bi‐directional interactions between intracellular ion concentrations (notably Na⁺ and Ca²⁺) and cellular electrophysiology. For example, blocking I _Kur to mimic loss‐of‐function Kv1.5 mutations increases intracellular Ca²⁺ and can cause arrhythmogenic EADs during adrenergic stress, as observed experimentally (Grandi et al. 2011). Koivumäki et al. extended the Nygren model by dividing the cytosol and SR into several transverse components with centripetal Ca²⁺ diffusion between them (Fig. 4 B), thereby providing the first model with a partial spatial representation of the atrial cardiomyocyte (Koivumaki et al. 2011). Along with the Grandi model, this model increased awareness of the important interactions between Ca²⁺ and Na⁺ and their role in rate‐dependent APD changes (Grandi et al. 2011; Koivumaki et al. 2011). The major electrophysiological properties of these human atrial cardiomyocyte models have been compared in detail (Wilhelms et al. 2012). These analyses highlight, for example, rate‐dependent differences in APD and AP upstroke velocity between the models that affect alternans and re‐entry behaviours in simulations. Furthermore, these models also show distinct responses to varying experimental conditions, such as changing electrolyte concentrations during haemodialysis (Passini et al. 2014). Finally, several adaptations of these models, like including Na⁺‐dependent regulation of I _K1 and I _K,ACh (Voigt et al. 2013) or incorporation of the two‐pore K⁺ current and its regulation in AF (Schmidt et al. 2015), have recently been published based on new experimental data.

Spatial models of atrial Ca²⁺ handling

The transverse segmentation in the Koivumäki et al. model (Fig. 3 B) allows simulation of the centripetal Ca²⁺ wave that occurs in the absence of a well‐developed t‐tubular network (Koivumaki et al. 2011). This model indicates that subsarcolemmal SR Ca²⁺‐release sites influence AP shape, whereas the central release sites control centripetal Ca²⁺ wave propagation, thereby influencing morphology and amplitude of the whole‐cell Ca²⁺ transient. A similar one‐dimensional subcellular structure, but without species‐specific validation or additional ion channels that shape the atrial AP, was employed to further investigate the mechanisms that influence centripetal Ca²⁺ wave propagation and Ca²⁺ transient alternans (Li et al. 2012). This model showed that local regeneration of Ca²⁺ propagation through sequential activation of RyR2s creates a steep relationship between SR Ca²⁺‐content and cytoplasmic Ca²⁺ transients, playing a critical role in the development of Ca²⁺ alternans. Of note, although the subcellular structure can modulate Ca²⁺ alternans, common‐pool models also show alternans, as recently demonstrated for the Grandi model (Chang et al. 2014). This type of alternans critically depends on intrinsic RyR2 properties.

However, a transverse division of the cardiomyocyte does not provide the full spatial information needed to study the dynamics of spontaneous Ca²⁺ waves, which result from localized spontaneous SR Ca²⁺‐release events. We recently developed the first human atrial cardiomyocyte model with both transverse and longitudinal compartmentation of Ca²⁺ handling (Fig. 4 C), along with stochastic gating of RyR2s using a Markov‐model approach (Voigt et al. 2014). Figure 5 shows simulations with this model of the changes in atrial‐cardiomyocyte APs and [Ca²⁺]_i predicted to result from the RyR2 dysregulation (increased channel expression and open probability) and SERCA dysfunction (increased activity) seen in paroxysmal AF (pAF) patients. The model indicates that RyR2 dysregulation alone produces membrane oscillations but not spontaneous APs, whereas SERCA dysregulation causes larger spontaneous Ca²⁺ releases and triggered activity. The combination of changes produces sustained triggered activity. To our knowledge, this is the first model to reproduce the observed triggered‐AP generation resulting from spontaneous Ca²⁺ releases in human atrial cells from patients with pAF and long‐standing persistent (chronic) AF (cAF; Neef et al. 2010; Voigt et al. 2012, 2014).

Figure 5. Simulation of spontaneous Ca²⁺‐release events, delayed afterdepolarizations and triggered action potentials .

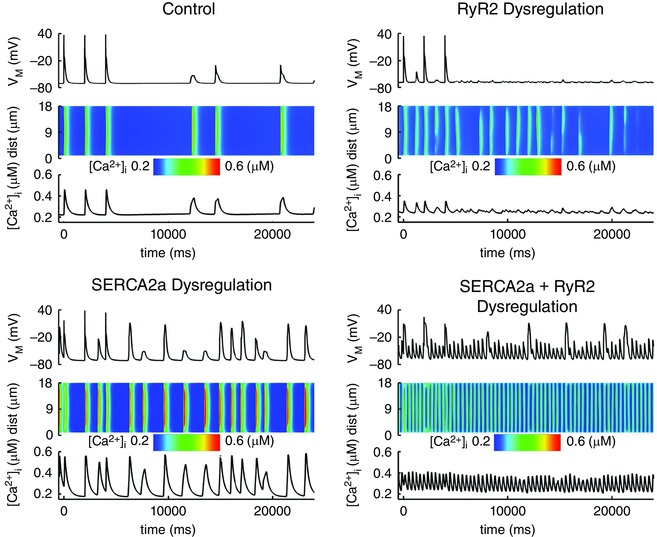
A representation of simulations for the present paper with the model described in (Voigt et al. 2014). Membrane potential (V _M) and intracellular [Ca²⁺] are simulated using the human atrial cardiomyocyte model with localized Ca²⁺ handling and stochastic RyR2 gating under control conditions (top left), with RyR2 dysregulation as observed in paroxysmal AF (Voigt et al. 2014) (top right), with increased SERCA2a function (25% increase in Ca²⁺ affinity; bottom left) or combined SERCA2a and RyR2 dysregulation (bottom right). Insets show local [Ca²⁺]_i from a transverse line‐scan, showing [Ca²⁺]_i (on a colour scale with blue indicating lowest values and red highest values) across the width of a cardiomyocyte (vertical axis) as a function of time (horizontal axis).

The only full three‐dimensional representation of Ca²⁺ in an atrial cardiomyocyte devoid of t‐tubules was developed by Thul et al. (2012) using a set of stacked disks, each with concentric circles of RyR2s. In line with the work by Li et al. (2012), this generic model without other Na⁺ or K⁺ channels highlights a critical role for SR Ca²⁺‐release strength and RyR2 activation threshold in determining successful propagation of the centripetal Ca²⁺ wave (Thul et al. 2012). In addition, this model proposes ‘ping waves’, consisting of rotating waves of partial SR Ca²⁺ releases within a single disk that emit Ca²⁺ waves to neighbouring planes, as a novel mechanism for repeated spontaneous SR Ca²⁺‐release events. Of note, such mechanisms can only be discovered in two‐dimensional or three‐dimensional representations of subcellular structure. The likelihood of spontaneous Ca²⁺ waves is further increased by spatially heterogeneous fluctuations in SR Ca²⁺‐release parameters (Thul et al. 2012) and even small variations in randomly positioned Ca²⁺‐release sites causes highly heterogeneous cellular responses (Thul et al. 2015), further highlighting the importance of the atrial‐specific subcellular structure in modulating Ca²⁺ handling abnormalities.

The role of computational modelling in AF research and future directions

Applications of computational modelling in AF research

The number of publications incorporating computational modelling has increased significantly over the last few years (Fig. 6 A). Computational modelling offers a framework with complete control over all parameters that can be employed to generate or verify hypotheses about AF mechanisms. A complete overview of insights obtained from computational modelling is beyond the scope of this review. Instead, we will highlight a few examples of applications exploiting the advantages of computational modelling.

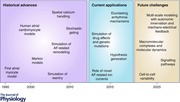
Figure 6. Historical application of computational AF research and future challenges .

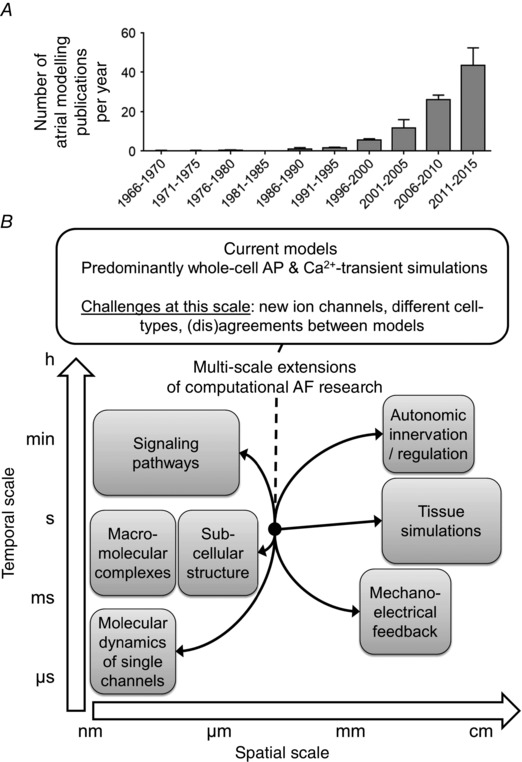
A, number of publications (mean ± SD) concerning computational analysis of atrial fibrillation (AF) per year (identified by the Pubmed query: ‘atrial fibrillation’ AND (‘computational model’ OR ‘theoretical model’ OR ‘simulation’ OR ‘simulations’ OR ‘computational modelling’)) in 5‐year intervals. B, current models incorporate an intermediate level of spatial and temporal complexity with whole‐cell action potential (AP) and Ca²⁺ transient simulations. There are several challenges at this level and future research is likely to extend computational models in both directions of the spatial and temporal scales.

Different forms of human AF are associated with remodelling of a wide range of ion channels and Ca²⁺ handling proteins (Dobrev & Ravens, 2003; Heijman et al. 2014), each of which can contribute to changes in AP properties and Ca²⁺ handling abnormalities. It is not experimentally possible to modulate the function of a single channel or transporter in human atrial cardiomyocytes with high specificity. Complete control over individual parameters makes computational models suitable to study the relative contribution of individual processes to the macroscopic phenotype. We employed our spatial Ca²⁺ handling model of the human atrial cardiomyocyte to assess the relative contribution of the experimentally observed increased SERCA2a function and RyR2 dysregulation to spontaneous SR Ca²⁺‐release events in pAF patients (Voigt et al. 2014). The results indicate that both increased SR Ca²⁺ load due to enhanced SERCA2a function and RyR2 dysregulation can increase the incidence of spontaneous SR Ca²⁺‐release events, but that the increased SR Ca²⁺ load is more critical for the generation of large, propagating Ca²⁺ waves and triggered APs (Fig. 5). Combined, both components showed synergistic effects on Ca²⁺ handling abnormalities. Similarly, the relative contribution of distinct ion channel and Ca²⁺ handling remodelling processes in cAF patients has recently been investigated, showing that remodelling of Ca²⁺ handling occurs predominantly via changes in L‐type Ca²⁺ channels, RyR2 and atrial cardiomyocyte size, and this strongly impacts repolarization and cellular excitability (Koivumaki et al. 2014). These findings also indicate that rescue of a single remodelled component is insufficient to restore the normal phenotype (Koivumaki et al. 2014). Prospective experimental validation is now needed to confirm these predictions.

Another application of computational modelling is assessment of potential mechanisms of atrial arrhythmogenesis in relation to experimental findings about changes in ion‐channel function. Several mutations in cardiac ion channels have been associated with familial AF. Hancox et al. employed computational modelling to analyse experimental findings on S140G‐mutation‐induced changes in I _Ks current obtained in heterologous expression systems (Hancox et al. 2014). Their simulations, based on the Courtemanche et al. model of the human atrial cardiomyocyte, predict that the mutation would cause a pronounced decrease in APD, resulting in re‐entrant activity in multicellular simulations. Computational models can also facilitate comparisons of arrhythmogenic effects of different mutations, as shown for two gain‐of‐function mutations in I _Kr predisposing to AF (Loewe et al. 2014 b), providing a first step towards genotype‐guided therapy. Simulations also permit analysis of the predicted effects of ion‐channel modulation under a wide range of conditions. For example, the combined concentration‐dependent and rate‐dependent effects of amiodarone and dronedarone on APD, effective refractory period, conduction velocity and other parameters have recently been evaluated in the sinus rhythm and cAF versions of the Courtemanche et al. model (Loewe et al. 2014 a), highlighting important rate‐dependent differences between the two antiarrhythmic drugs which might contribute to their distinct clinical efficacy.

The cellular models described in this review have been used as a basis for simulation in multicellular systems that mimic part or all of the atria to analyse the basis of arrhythmias in intact atria. A detailed discussion is beyond the scope of the present paper, but several recent articles have dealt with this subject (Dössel et al. 2012; Colman et al. 2013; Trayanova, 2014)

The advances and applications of atrial cardiomyocyte models have been paralleled by advances in the development of models for other cell types. There are numerous ventricular cardiomyocyte models available for a wide variety of species (Roberts et al. 2012). Similar to atrial models, these ventricular models can be divided into common‐pool and spatial ‘local‐control’ models, although because of the presence of a t‐tubular structure there is no centripetal Ca²⁺ wave in spatial ventricular models (Fig. 1 A). Ventricular models have been employed for a wide range of purposes, including analysing the effects of ion‐channel mutations, studying arrhythmogenic mechanisms and facilitating pharmacological screening, (Roberts et al. 2012). Similarly, computational models of the SAN cardiomyocyte have advanced to include detailed representations of both the membrane clock and the Ca²⁺ clock and have recently also started to simulate local Ca²⁺‐release events (Maltsev et al. 2014). Advances in ventricular and SAN models are likely to contribute indirectly to the further development of atrial cardiomyocyte models through application of methods in other systems.

Gaps in knowledge and future directions

Despite the significant progress that has been made in the development of computational atrial cardiomyocyte models and their application to study AF mechanisms, numerous challenges remain. The present modelling approach reflects a ‘middle‐out approach’ (Noble, 2006), in which most models have an intermediate level of complexity (i.e. deterministic common‐pool models to simulate APs and whole‐cell Ca²⁺ transients), corresponding to the amount of available experimental data (Fig. 6 B). However, even at the comparatively well‐characterized cellular level many questions remain. For example, recently identified AF‐dependent regulation of several ion currents (e.g. small‐conductance Ca²⁺‐activated K⁺ currents (Zhou et al. 2012) or Kv1.1 currents (Glasscock et al. 2015)), has not yet been incorporated in computational models.

Furthermore, atrial APs show pronounced inter‐patient and regional variation (Ravens et al. 2015). The muscle sleeves surrounding the pulmonary veins (PVs) have specific electrophysiological and Ca²⁺ handling properties, making them more likely to produce ectopic activity (Heijman et al. 2014). Due to the limited availability of experimental data, most human cardiomyocyte models represent characteristics of right‐atrial appendages only. A few region‐specific human atrial cardiomyocyte models have recently been developed (Colman et al. 2013), and a multicellular simulation of the canine PVs showed that besides electrophysiological differences, discontinuous fibre arrangements make the PVs susceptible to wave breaks and re‐entry (Colman et al. 2014). However, regional Ca²⁺ handling differences have not yet been taken into account. Even when regional variations in ion channel expression have been considered, computational analyses of atrial cardiomyocyte function have so far considered a single ‘representative’ cardiomyocyte for a given region. However cell‐to‐cell and intersubject variability in electrophysiological and Ca²⁺ handling properties can produce heterogeneous responses to varying conditions (e.g. application of antiarrhythmic drugs), with potentially important clinical implications. Computational studies of ventricular cardiomyocytes and cardiac Purkinje cells have started to take into account cell‐to‐cell variability by investigating populations of virtual cells created by small variations in model parameters (Britton et al. 2013; Heijman et al. 2013). These studies have shown that such model populations can predict the range of variability in response to pharmacological interventions. A similar approach could be employed for atrial cardiomyocyte models to investigate intersubject differences in AF mechanisms and therapeutic options.

The significant differences between fundamental properties of existing human models for the same cell type (Wilhelms et al. 2012) indicate that further model development and validation are necessary and that individual models may be more appropriate to address specific research questions. For example, the more recent human atrial cardiomyocyte models (Grandi et al. 2011; Koivumaki et al. 2011; Voigt et al. 2014) are better suited to investigate atrial Ca²⁺ handling than earlier models. Of these, our recent model is the only human atrial cardiomyocyte model suitable to investigate determinants of spontaneous Ca²⁺‐release events (Voigt et al. 2014). On the other hand, their computational tractability and repolarization dynamics make the Courtemanche et al. and Maleckar et al. models more suitable for the larger multicellular substrates needed to investigate rotor dynamics and re‐entrant arrhythmia mechanisms (Courtemanche et al. 1998; Maleckar et al. 2009).

To create the hierarchical, multiscale understanding of AF that is needed to optimally develop novel antiarrhythmic therapies, models will also have to be extended from this cellular level in both subcellular and multicellular directions (Noble, 2006), and will have to cover a larger range of time scales (Fig. 6 B). At the subcellular level, several gaps in computational modelling knowledge can be identified. The exact localization of ion channels influences their functional properties and regulation, but this level of spatial detail is not included in any currently available cardiomyocyte model. Similarly, although detailed molecular representations of a single ion channel based on protein structure exist, only millisecond molecular dynamic simulations are computationally feasible, precluding direct predictions of the electrophysiological effects of novel pharmacological compounds or genetic mutations at the whole‐cell level. Moreover, these models do not take into account the fact that cardiac ion channels are generally organized in macromolecular multiprotein complexes that produce dynamic regulation by localized signalling pathways (Balycheva et al. 2015). Although aspects of localized cyclic AMP/protein kinase‐A and CaMKII signalling have been incorporated in some ventricular cardiomyocyte models (Heijman et al. 2011), this has not yet been done for atrial cardiomyocytes, and regulation by other signalling pathways remains largely unexplored. Finally, long‐term regulation of ion channels, for example through pathways controlling their transcription, translation, trafficking, membrane targeting, endocytosis or degradation, has not been incorporated in any atrial cardiomyocyte model, although these aspects are likely to play a key role in AF‐promoting remodelling.

The gap between current computational models and the details available from experimental knowledge is illustrated using the RyR2 channel as an exemplar in Fig. 7. Most whole‐cell models represent the entire population of RyR2s by one compound flux regulated by cytosolic and luminal Ca²⁺. While recent stochastic models have added some detail by considering the individual, localized behaviour of single RyR2s (Greiser et al. 2014; Voigt et al. 2014), this is still far removed from the reality within a cardiomyocyte (Fig. 7). The RyR2 is situated within a large macromolecular complex of various regulatory proteins that modulate RyR2 function through direct binding, oxidation and phosphorylation of multiple sites in response to numerous signalling pathways (Bers, 2004; Heijman et al. 2014). RyR2 expression in the SR is increased in pAF (Voigt et al. 2014), by reduced post‐translational repression by microRNAs (Chiang et al. 2014). Finally, the exact organization of RyR2s within clusters in specific subcellular locations strongly influences their function, with ‘orphaned’ RyR2s providing potential foci for spontaneous SR Ca²⁺‐release events (Bers, 2004). Although the detail needed for accurate simulation depends on the question under consideration, the aforementioned processes are likely to influence the antiarrhythmic properties of RyR2‐targeting drugs currently under investigation (Heijman et al. 2015). The appropriate computational models may help to better understand the properties required for optimal antiarrhythmic effectiveness in a variety of conditions.

Figure 7. The ryanodine receptor channel type‐2 (RyR2) as an exemplar for the gap between current computational models and the detail available from experimental knowledge .

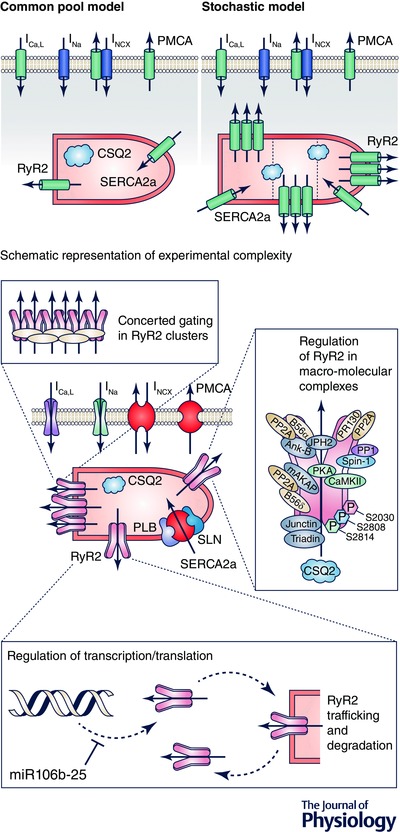
Level of detail in RyR2 formulations in current common‐pool models (top left), stochastic models that incorporate single‐channel gating and subcellular distribution (top right), and the experimental complexity of the regulation of RyR2 function involving concerted gating in clusters, channel regulation within a macromolecular multiprotein complex, as well as regulation of RyR2 amounts through transcription, translation, trafficking, membrane targeting, endocytosis and degradation (bottom). The (abbreviations of the) proteins in the RyR2 macromolecular complex are defined in Dobrev & Wehrens (2014).

Despite the increasing prevalence of tissue simulations (Trayanova, 2014), many challenges remain at the multicellular level. In particular, multicellular simulations are computationally demanding, particularly when using realistic geometries. Technological limitations have thus far prevented the use of models with detailed subcellular Ca²⁺ handling in multicellular simulations. Advances in computer hardware and simulation tools will likely make this possible, and enabling such applications as the computational analysis of the role of spontaneous SR Ca²⁺‐release events in AF initiation in situ. Of note, single cell models have generally been developed using data obtained from isolated cardiomyocytes. These models are appropriate to investigate phenomena observed under similar conditions, but may not be able to reproduce the complex environment present in vivo. For example, the extracellular environment and electrolyte composition, notably extracellular Ca²⁺, is different in vivo and in vitro, with potentially relevant consequences for Ca²⁺ handling and arrhythmogenesis (Severi et al. 2009). Other macroscopic components such as contractile remodelling, stretch, mechano‐electrical feedback and heterogeneous autonomic innervation are likely also to play a major role in the initiation, maintenance and progression of AF (Heijman et al. 2014) and present interesting long‐term goals for computational analyses (Trayanova, 2014).

Conclusion

Substantial progress has been made in the development of atrial cardiomyocyte computer models. Simulation of atrial‐specific Ca²⁺ handling has received increasing attention during the last 5 years, but much work is still needed. Computational models have helped to identify the mechanisms controlling centripetal Ca²⁺ wave propagation, spontaneous SR Ca²⁺‐release events, and the impact of Ca²⁺ on repolarization. Furthermore, models have helped to determine the relative contribution of individual AF‐related remodelling processes to atrial electrophysiology. More advanced computational approaches will be critical to tackle the complexity of atrial arrhythmogenesis and facilitate the future development of improved therapeutic options.

Additional information

Competing interests

None (all authors).

Author contributions

All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

The authors’ work is supported by the European Network for Translational Research in Atrial Fibrillation (EUTRAF, No. 261057, to D.D.), the DZHK (German Centre for Cardiovascular Research, to D.D.), the Canadian Institutes of Health Research (6957 and 44365, to S.N.) and the Heart and Stroke Foundation of Canada (to S.N.).

Biography

Jordi Heijman (far left) is a former postdoctoral fellow at the Institute of Pharmacology, West‐German Heart and Vascular Center, University Duisburg‐Essen, Germany and is currently assistant professor at the Department Cardiology, Cardiovascular Research Institute Maastricht, Maastricht University, The Netherlands. Dobromir Dobrev (far right) is professor and director of the Institute of Pharmacology and Pegah Erfanian Abdoust and Niels Voigt work at his institute as a PhD student and a postdoctoral fellow, respectively. Stanley Nattel is a professor at the Research Centre of the Montreal Heart Institute, Canada. The authors have a long‐standing research interest in atrial fibrillation and have collaborated in various studies to employ experimental and computational methodologies to elucidate the basic mechanisms of atrial fibrillation. The present review deals with a particular group interest: the development of computational models of atrial cellular electrophysiology and calcium handling, and the use of these models in atrial fibrillation research.