Relationship between retinal blood flow and arterial oxygen

Abstract

Key points

• Vascular reactivity, the response of the vessels to a vasoactive stimulus such as hypoxia and hyperoxia, can be used to assess the vascular range of adjustment in which the vessels are able to compensate for changes in $P_{{\mathrm{O}}_2}$.

• Previous studies in the retina have not accurately quantified retinal vascular responses and precisely targeted multiple $P_{\mathrm{a}{\mathrm{O}}_2}$ stimuli at the same time as controlling the level of carbon dioxide, thus precluding them from modelling the relationship between retinal blood flow and oxygen.

• The present study modelled the relationship between retinal blood flow and $P_{\mathrm{a}{\mathrm{O}}_2}$, showing them to be a combined linear and hyperbolic function.

• This model demonstrates that the resting tonus of the vessels is at the mid‐point and that they have great vascular range of adjustment, compensating for decreases in oxygen above a $P_{\mathrm{ETC}{\mathrm{O}}_2}$ of 32–37 mmHg but being limited below this threshold.

Abstract

Retinal blood flow (RBF) increases in response to a reduction in oxygen (hypoxia) but decreases in response to increased oxygen (hyperoxia). However, the relationship between blood flow and the arterial partial pressure of oxygen has not been quantified and modelled in the retina, particularly in the vascular reserve and resting tonus of the vessels. The present study aimed to determine the limitations of the retinal vasculature by modelling the relationship between RBF and oxygen. Retinal vascular responses were measured in 13 subjects for eight different blood gas conditions, with the end‐tidal partial pressure of oxygen ($P_{\mathrm{ETC}{\mathrm{O}}_2}$) ranging from 40–500 mmHg. Retinal vascular response measurements were repeated twice; using the Canon laser blood flowmeter (Canon Inc., Tokyo, Japan) during the first visit and using Doppler spectral domain optical coherence tomography during the second visit. We determined that the relationship between RBF and $P_{\mathrm{a}{\mathrm{O}}_2}$ can be modelled as a combination of hyperbolic and linear functions. We concluded that RBF compensated for decreases in arterial oxygen content for all stages of hypoxia used in the present study but can no longer compensate below a $P_{\mathrm{ETC}{\mathrm{O}}_2}$ of 32–37 mmHg. These vessels have a great vascular range of adjustment, increasing diameter (8.5% arteriolar and 21% total venous area) with hypoxia (40 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$; P < 0.001) and decreasing diameter (6.9% arteriolar and 23% total venous area) with hyperoxia (500 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$; P < 0.001) to the same extent. This indicates that the resting tonus is near the mid‐point of the adjustment ranges at resting $P_{\mathrm{a}{\mathrm{O}}_2}$ where sensitivity is maximum.

Key points

• Vascular reactivity, the response of the vessels to a vasoactive stimulus such as hypoxia and hyperoxia, can be used to assess the vascular range of adjustment in which the vessels are able to compensate for changes in $P_{{\mathrm{O}}_2}$.

• Previous studies in the retina have not accurately quantified retinal vascular responses and precisely targeted multiple $P_{\mathrm{a}{\mathrm{O}}_2}$ stimuli at the same time as controlling the level of carbon dioxide, thus precluding them from modelling the relationship between retinal blood flow and oxygen.

• The present study modelled the relationship between retinal blood flow and $P_{\mathrm{a}{\mathrm{O}}_2}$, showing them to be a combined linear and hyperbolic function.

• This model demonstrates that the resting tonus of the vessels is at the mid‐point and that they have great vascular range of adjustment, compensating for decreases in oxygen above a $P_{\mathrm{ETC}{\mathrm{O}}_2}$ of 32–37 mmHg but being limited below this threshold.

Abbreviations

CLBF

Canon laser blood flowmeter

MAP

mean arterial pressure

$P_{\mathrm{a}{\mathrm{O}}_2}$

arterial oxygen tension

$P_{\mathrm{aC}{\mathrm{O}}_2}$

arterial partial pressure of carbon dioxide

$P_{\mathrm{ET}{\mathrm{O}}_2}$

end‐tidal oxygen

$P_{\mathrm{ETC}{\mathrm{O}}_2}$

end‐tidal carbon dioxide

$P_{{\mathrm{O}}_2}$

partial pressure of oxygen

RBF

retinal blood flow

SaO₂

oxygen saturation

Introduction

The retinal circulation forms a closed circuit such that the central retinal artery, which penetrates the optic nerve, passes blood through the arterioles and into the superior capillary plexus or deep capillary plexus, eventually draining into the venules surrounding the optic nerve head. The inner retinal vasculature is uniquely situated in that imaging through the eye permits non‐invasive investigation of vascular reactivity, comprising the response of these vessels to a vasoactive stimulus. By examining total flow through all the venules surrounding the optic nerve head or by investigating flow through a specific arteriole, and assuming the arterioles all respond similarly, we can evaluate the response of the retinal vasculature to a stimulus. The retinal vessels, much like the rest of the brain vasculature, respond to increases in oxygen (hyperoxia) by constricting the vessels to decrease blood flow (Eperon et al. 1975; Kiss et al. 2002; Wimpissinger et al. 2005; Sehi et al. 2012; Werkmeister et al. 2012; Tsui et al. 2013) and respond to reductions in oxygen (hypoxia) by dilating the vessels to increase blood flow (Hickam & Frayser, 1966; Frayser et al. 1971; Fallon et al. 1985). Measurements of retinal vascular reactivity may be used to investigate vascular dysregulation in ocular diseases such as diabetic retinopathy (Gilmore et al. 2007) and primary open angle glaucoma (Venkataraman et al. 2010). Indeed, using vascular reactivity assessment to determine retinal vasculature dysfunction will enhance the comprehension of pathophysiology. However, first, the retinal vascular reactivity in healthy young individuals must be characterized.

The relationship between retinal blood flow and oxygen for healthy participants has been only loosely defined in previous studies. When examining the acute effects of hypoxia, Hickam & Frayser (1966) and Fallon et al. (1985) demonstrated that retinal vessels in healthy individuals dilate by 10% and increase blood flow by 16–38% for an arterial oxygen saturation (SaO₂) of 70–80%. However, studies at altitude (Frayser et al. 1971; Rennie & Morrissey, 1975; Bosch et al. 2009) appear to indicate that the vessels can dilate by as much as 20–40%. Vascular reactivity to hyperoxia (100% oxygen) has generally shown that retinal vessels constrict by 10–15%, whereas flow decreases by as much as 40–50% (Eperon et al. 1975; Kiss et al. 2002; Wimpissinger et al. 2005; Sehi et al. 2012; Werkmeister et al. 2012; Tsui et al. 2013). These previous studies (Hickam & Frayser, 1966; Frayser et al. 1971; Fallon et al. 1985; Brinchmann‐Hansen & Myhre, 1990; Wimpissinger et al. 2005; Sehi et al. 2012; Werkmeister et al. 2012; Tsui et al. 2013) have generally investigated only one hypoxic or hyperoxic stimulus, which precludes modelling the entire relationship between retinal blood flow and oxygen, as well as determining the vascular reserve and resting tonus of the retinal vessels. The methodologies employed probably resulted in large inter‐individual variability not only because of instrument inaccuracies, but also as a result of the imprecision of the gas provocation method used to target a given arterial partial pressure of oxygen ($P_{\mathrm{a}{\mathrm{O}}_2}$). Breath to breath fluctuations in end‐tidal partial pressures of oxygen ($P_{\mathrm{ETC}{\mathrm{O}}_2}$) and an inability to maintain isocapnia have therefore limited previous investigations (Hickam & Frayser, 1966; Frayser et al. 1971; Fallon et al. 1985; Brinchmann‐Hansen et al. 1989).

The retinal vascular responses to oxygen can also be used to determine the vascular adjustment reserve of the vessels, which is the maximal amount by which the vessels can dilate and constrict, as well as the resting tonus, which is the tone of the vessels at resting $P_{\mathrm{a}{\mathrm{O}}_2}$. Measurements of the vascular reserve and resting tonus of the retinal vessels will demonstrate the extent of the ability of the vasculature to compensate for changes in oxygen. Studies in monkeys report conflicting results, with one study (Tsacopoulos & David, 1973) finding the resting tonus at the mid‐point of the adjustment range, and another (Eperon et al. 1975) showing that it is closer to the vasoconstrictive limit. In humans, the resting tonus of the vessels remains to be determined (Hickam & Frayser, 1966; Eperon et al. 1975; Fallon et al. 1985; Gilmore et al. 2005).

In the brain, the relationship between blood flow and hypoxia was previously shown to be modelled as a rectangular hyperbolic function (Mardimae et al. 2012). However, its relationship in the retina has not been accurately characterized (Hickam & Frayser, 1966; Frayser et al. 1971; Eperon et al. 1975; Rennie & Morrissey, 1975; Fallon et al. 1985; Brinchmann‐Hansen & Myhre, 1990; Gilmore et al. 2005). The present study used innovative instrumentation that allowed us not only to accurately quantify retinal vascular responses, but also to precisely target the $P_{\mathrm{a}{\mathrm{O}}_2}$ stimulus at the same time as controlling the level of carbon dioxide. We aimed to characterize the limitations of the retinal vasculature by modelling the relationship between retinal blood flow and oxygen, thereby simultaneously defining the vascular reserve and resting tonus of the vessels.

Methods

Ethical approval and subjects

Thirteen healthy non‐smoking individuals (age 26.4 ± 4.5 years) participated in the present study. Informed consent was obtained for all thirteen participants. There was no history of ocular, cardiovascular or respiratory disorders for any participant. The study was approved by the Research Ethics Board of the University Health Network, University of Toronto and followed the recent guidelines set by the Declaration of Helsinki. All participants had a logMAR visual acuity of 0.0 or better and a refractive error of <±6.00 diopter spheres and/or <±2.5 diopter cylinders. Participants were asked to refrain from heavy exercise and caffeine 24 h prior to the study.

Gas delivery system

The mask of a sequential gas delivery circuit (Hi‐Ox80; Viasys Healthcare, Yorba Linda, CA, USA) covered each participant's mouth and nose with an airtight seal using adhesive tape (Tegaderm; 3M Healthcare, St Paul, Minnesota, USA). The sequential gas delivery circuit was connected to a prospective gas targeting system, Respiract™ (Thornhill Research Inc., Toronto, Canada), which has been detailed elsewhere (Slessarev et al. 2007; Ito et al. 2008). In brief, the Respiract™ is an automated gas flow controller that provides low gas flow of specific gas compositions to the inspiratory bag of the sequential delivery circuit, with inspired concentrations of gas individually titrated to independently target P_ETO₂ and end‐tidal partial pressures of carbon dioxide ($P_{\mathrm{ETC}{\mathrm{O}}_2}$) independent of minute ventilation. Previous studies (Ito et al. 2008; Willie et al. 2012) have shown that $P_{\mathrm{ETC}{\mathrm{O}}_2}$ and $P_{\mathrm{ET}{\mathrm{O}}_2}$ are statistically identical to arterial partial pressures of carbon dioxide ($P_{\mathrm{aC}{\mathrm{O}}_2}$) and oxygen ($P_{\mathrm{a}{\mathrm{O}}_2}$), respectively. $P_{\mathrm{ET}{\mathrm{O}}_2}$ and $P_{\mathrm{a}{\mathrm{O}}_2}$ are approximately equivalent because, when alveolar ventilation is equal or greater than the inspiratory gas flow of the sequential delivery circuit, further inspired gas into the anatomical dead space comes from the expiratory bag, which is considered ‘neutral’ with respect to alveolar ventilation. ‘Neutral’ gas has a concentration equal to that of mixed alveolar gas and hence the only gas exchange that occurs comes from the inspiratory gas flow of the sequential delivery circuit. Mixed alveolar gas is equilibrated with pulmonary capillary blood and should also reflect arterial partial pressures and end‐tidal partial pressures if there are minimal effects from alveolar dead space ventilation and shunt (Slessarev et al. 2007).

Canon laser blood flowmeter (CLBF‐100)

The CLBF‐100 (Canon Inc., Tokyo, Japan) calculates the blood flow through a small cross‐section of a straight‐line vessel. For ease of imaging purposes, blood flow measurements were made in the superior temporal arteriole of each participant. The CLBF‐100 uses a red diode laser (675 nm) to measure the centerline velocity over a 2 s window margin using bi‐directional technology that has been described elsewhere (Riva et al. 1979; Guan et al. 2003). Briefly, the maximum velocity over the two second period is summated and averaged by the CLBF to give the average maximum velocity over two cardiac cycles. The CLBF then uses the formula F = V _max S/2 to calculate flow, where S is the cross‐sectional area of the vessel at the measurement site. A second HeNe green rectangular laser (543 nm) simultaneously uses densitometry to measure the diameter of the vessel every 4 ms in the first and last 60 ms of the 2 s acquisition period. Assuming Poiseuille's principles, velocity and diameter are used to calculate flow in absolute units. A minimum of four separate measurements was taken for each gas condition.

Doppler spectral domain optical coherence tomography (RTVue)

The RTVue (Optovue Inc., Fremont, CA, USA) is a morphometric Doppler spectral‐domain optical coherence tomography instrument, which, in prototype form, measures total retinal blood flow by summing flows through all the veins and venules surrounding the optic nerve head. The prototype instrument has been described in detail elsewhere (Wang et al., 2007, 2009; Tan et al. 2012). In brief, the instrument operates at a wavelength of 841 nm with a power of 750 μW and has an axial resolution of 5 μm and a transverse resolution of 20 μm. As a result of the movement of blood through the vessels, there is an inherent Doppler shift that is detected from the phase shift of the spectral interference pattern acquired by the line camera. This phase shift is proportional to the velocity and is used to calculate flow with information obtained from circum‐papillary double circular scans that are 3.40 mm and 3.75 mm in diameter surrounding the optic nerve head. The distribution of the flow speed, which is based on the velocity vectors of each voxel of the cross‐sectional area, is used to calculate volumetric flow of each vessel. The venous area of each vessel is therefore given by the distribution of the Doppler signal. The reported venous area is the summation of the cross‐sectional area of all venules surrounding the optic nerve head. The velocity reported is the average venous velocity of all vessels given by the summation of volumetric flow from all venous vessels divided by the total cross‐sectional area of all venous vessels. The RTVue allows for post hoc correction of each vessel diameter, which can be assessed from the shadow left by each vessel in the optical coherence tomography scan. The quality of the scan is assessed in two ways: the instrument allows for the strength of the Doppler signal to be visualized during the scan by a green bar signal and the distribution of the Doppler signal in each vessel, as well as its strength, can be visualized and graded post hoc to determine the confidence of the vessel. For each measurement, four pairs of circular scans were taken over two cardiac cycles and a minimum of six measurements was achieved for each gas condition.

Critical care gas analyser

Heart rate and SaO₂ were continuously monitored with a pulse oximeter, and blood pressure was measured every 2.5 min with an automated sphygmomanometer (mean blood pressure) connected to a critical care gas analyser (Cardiocap 5; Datex‐Ohmeda, Helsinki, Finland). All data outputs were downloaded to an electronic acquisition system (S5 Collect; Datex‐Ohmeda).

Experimental protocol

Participants attended on two separate occasions. A test eye was randomly selected at the first visit and this eye was dilated with one drop of tropicamide 1% ophthalmic solution (Alcon, Mississauga, Canada) 20 minutes prior to connecting the participant to the sequential gas delivery mask. The gas conditions used during each visit are shown in Fig. 1. Participants experienced eight different gas conditions for each instrument measurement, with the CLBF‐100 utilized on the first visit and the RTVue on the second. There were seven isocapnic $P_{{\mathrm{O}}_2}$ stages (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$), including four stages of hypoxia (40, 50, 60, 80 $P_{\mathrm{ET}{\mathrm{O}}_2}$), normoxia (100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$) and two conditions of hyperoxia (300 and 500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$). An additional hypocapnic hyperoxic condition (30 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$, 500 mmHg P_ETO₂) was administered to determine whether the vessels had fully constricted. Retinal haemodynamic measurements began after a minimum of 4 min of stable $P_{\mathrm{ETC}{\mathrm{O}}_2}$ and $P_{\mathrm{ET}{\mathrm{O}}_2}$ targeting, and each stage lasted ∼10–15 min.

Figure 1. Protocol for eight blood gas conditions repeated for two visits .

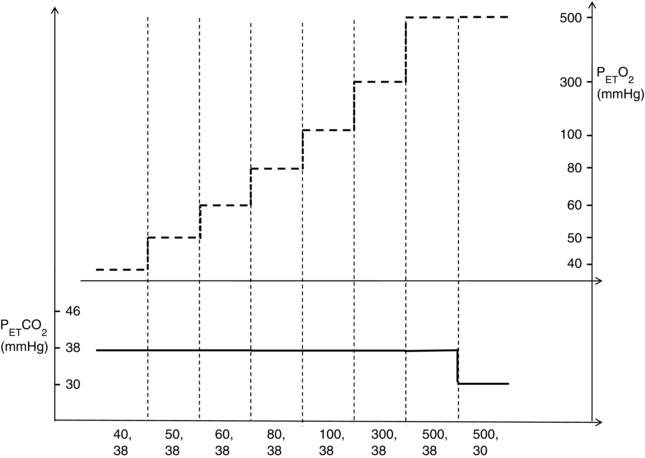
Participants experienced seven isocapnic (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) changes in oxygen (40–500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$) and additional hypocapnic hyperoxic conditions (30 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$, 500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$).

Statistical analysis

Retinal vascular responses and cardiorespiratory variables were averaged over the last 5 min of each blood gas condition. Retinal responses were normalized using the relative percent change from a standardized baseline (100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 38 $P_{\mathrm{ETC}{\mathrm{O}}_2}$). Sigmaplot, version 12 (Systat Software Inc., San Jose, CA, USA) was used to apply a one‐way repeated‐measures ANOVA (rmANOVA) on both absolute and relative retinal response parameters, as well as cardiorespiratory parameters. The variables examined were arteriolar diameter, total venous area, arteriolar velocity, venous velocity, retinal blood flow (RBF), total RBF, systolic blood pressure, diastolic blood pressure, mean arterial pressure (MAP), SaO₂ and heart rate. The within subject factors were the different blood gas conditions. Holm–Sidak post hoc tests were used to determine level of significance of the different blood gas stages relative to the standardized baseline.

Results

Participants

Ten of the thirteen healthy volunteers completed the entire protocol. The hypoxic stimulus was not easily tolerated, partly as a result of the lengthy nature of each condition, so that three subjects did not complete the 40 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ stage and two participants did not complete the 50 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ stage during the CLBF imaging. For the RTVue imaging, two participants did not complete the 40 and 50 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ stages. Furthermore, one participant decided not to participate in the second visit, whereas the results for another subject had the 60 and 80 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ stages discarded as a result of poor quality scans.

Measured variables

Tables 1 and 2 show the cardiorespiratory and retinal haemodynamic variables for all eight provocation stages for the CLBF and RTVue, respectively. Figure 2 shows that hypoxia significantly increased both retinal arteriolar diameter (Fig. 2 A) and total venous area (Fig. 2 B) respectively, relative to the standardized baseline (100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$). At 50 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, arteriolar diameter increased by 5.98 ± 7.21% (P = 0.004) and total venous area increased by 14.72 ± 12.91% (P = 0.003). Hyperoxia at 300 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ significantly decreased retinal arteriolar diameter (P = 0.027) but not total venous area (P = 0.085).

Table 1.

Retinal haemodynamic and cardiovascular variables (CLBF)

Gas provocation stages
($P_{\mathrm{ET}{\mathrm{O}}_2}$, $P_{\mathrm{ETC}{\mathrm{O}}_2}$)	40, 38	50, 38	60, 38	80, 38	100, 38	300, 38	500, 38	500, 30	P value
SBP (mmHg)	119.21 (8.06)	117.45 (9.57)	117.57 (10.81)	116.86 (9.83)	115.93 (8.76)	118.41 (9.13)	119.06 (8.97)	119.02 (8.60)	<0.001
DBP (mmHg)	71.80 (6.04)	71.23 (5.23)*	75.24 (6.15)	75.84 (7.17)	75.93 (6.55)	76.18 (6.10)	77.35 (5.83)	77.54 (5.60)	0.001
HR (beats min−1)	86.41 (10.33)***	78.59 (10.70)***	77.22 (11.03)*	73.09 (9.02)	72.82 (10.75)	68.48 (8.34)*	69.64 (8.25)	69.6 (9.22)	<0.001
SaO2 (%)	74.18 (2.54)***	82.90 (2.24)***	90.93 (2.30)***	96.53 (1.53)*	98.30 (0.95)	99.29 (0.39)	99.37 (0.45)	99.43 (0.41)	<0.001
MAP (mmHg)	87.60 (5.43)	86.64 (5.80)	89.35 (6.84)	89.52 (7.15)	89.26 (6.32)	90.26 (6.09)	91.26 (5.97)	91.36 (5.45)	<0.001
$P_{\mathrm{ETC}{\mathrm{O}}_2}$ (mmHg)	38.34 (0.38)	38.12 (0.64)	38.44 (0.60)	38.31 (0.48)	38.12 (0.86)	38.02 (0.33)	37.92 (0.65)	29.31 (0.76)***	<0.001
$P_{\mathrm{ET}{\mathrm{O}}_2}$ (mmHg)	41.14 (1.40)***	49.75 (1.82)***	59.39 (1.34)***	79.76 (1.86)***	101.65 (3.28)	299.56 (6.05)***	494.51 (9.14)***	493.54 (19.81)***	<0.001
Sample size	10	11	13	13	13	13	13	13
Arteriolar diameter (uM)	110.64 (15.38)***	109.59 (14.56)**	107.25 (12.98)	105.76 (12.88)	104.63 (11.49)	100.44 (13.86)*	97.52 (13.27)***	96.30 (12.53)***	<0.001
∆ % Diameter	8.53 (7.19)***	5.98 (7.21)**	2.45 (3.24)	0.97 (2.19)	0.0 (0.00)	−4.23 (3.94)*	−6.94 (5.23)***	−8.04 (4.96)***	<0.001
Arteriolar velocity (mm s−1)	35.79 (8.14)**	30.92 (6.87)	31.62 (9.32)	31.25 (9.83)	30.28 (7.66)	26.42 (9.71)	20.74 (7.39)***	20.38 (6.42)***	<0.001
∆ % Velocity	26.92 (18.85)***	4.72 (10.10)	4.43 (15.62)	2.83 (18.21)	0.00 (0.00)	−13.91 (14.76)*	−31.37 (16.29)***	−34.11 (14.70)***	<0.001
RBF (μl min−1)	10.76 (4.41)***	9.19 (3.78)	9.07 (4.34)	8.65 (4.17)	8.16 (3.46)	6.87 (4.27)	4.93 (2.70)***	4.73 (2.43)***	<0.001
∆ % Flow	48.66 (19.02)***	17.88 (16.63)*	9.53 (16.95)	5.04 (19.82)	0.00 (0.00)	−20.25 (18.71)**	−40.45 (16.31)***	−41.71 (15.03)***	<0.001

SBP, systolic blood pressure; DBP, diastolic blood pressure; HR, heart rate; ∆, change. *P < 0.05; **P < 0.01; ***P < 0.001 vs. standardized baseline (100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 38 $P_{\mathrm{ETC}{\mathrm{O}}_2}$).

Table 2.

Retinal haemodynamic and cardiovascular variables (RTVue)

Gas provocation stages
($P_{\mathrm{ET}{\mathrm{O}}_2}$, $P_{\mathrm{ETC}{\mathrm{O}}_2}$)	40, 38	50, 38	60, 38	80, 38	100, 38	300, 38	500, 38	500, 30	P value
SBP (mmHg)	119.32 (9.12)	116.20 (6.56)	116.07 (5.02)	114.36 (8.72)	115.58 (7.62)	114.65 (8.46)	116.47 (9.51)	116.48 (8.38)	0.001
DBP (mmHg)	75.94 (4.45)	74.11 (6.46)	76.50 (5.28)	75.29 (6.84)	77.60 (6.87)	77.24 (5.14)	78.43 (7.00)	77.13 (5.28)	0.044
HR (beats min−1)	86.34 (12.19)***	77.45 (8.82)	76.87 (8.13)	73.26 (7.83)	71.22 (9.81)	68.26 (7.72)	68.54 (8.26)	69.01 (8.40)	<0.001
SaO2 (%)	74.46 (2.61)***	84.08 (1.29)***	90.47 (1.82)***	96.41 (1.63)*	98.34 (0.70)	99.36 (0.40)	99.51 (0.41)	99.52 (0.45)	<0.001
MAP (mmHg)	90.40 (5.42)	88.14 (6.00)	89.69 (4.12)	88.31 (6.43)	90.26 (6.51)	89.71 (5.61)	91.11 (7.27)	90.24 (5.50)	0.005
$P_{\mathrm{ETC}{\mathrm{O}}_2}$ (mmHg)	38.21 (0.45)	37.90 (0.58)	38.00 (0.56)	38.56 (1.09)	38.02 (0.85)	38.25 (0.68)	38.46 (0.94)	29.90 (0.62)***	<0.001
$P_{\mathrm{ET}{\mathrm{O}}_2}$ (mmHg)	40.81 (1.20)***	50.03 (0.81)***	60.03 (1.21)***	77.91 (2.90)***	100.10 (3.84)	298.562 (8.31)***	494.48 (10.66)***	496.52 (12.08)***	<0.001
Sample size	10	10	11	11	12	12	12	12	–
Venous area (x 102 mm2)	6.16 (0.83)***	5.85 (0.97)**	5.58 (0.98)	5.25 (0.88)	5.12 (0.82)	4.69 (0.82)	3.96 (0.78)***	3.90 (0.82)***	<0.001
∆ Area (%)	21.38 (15.84)***	14.72 (12.91)**	9.06 (12.39)	2.80 (8.20)	0.00 (0.00)	−8.50 (6.25)	−22.55 (8.64)***	−23.68 (11.75)***	<0.001
Venous velocity (mm s−1)	16.75 (3.10)	17.90 (3.94)*	14.74 (2.83)	16.29 (3.84)	15.07 (2.93)	13.62 (2.33)	12.73 (2.71)*	12.64 (3.05)*	<0.001
∆ Velocity (%)	11.61 (24.74)	18.33 (24.42)*	1.74 (12.02)	12.51 (19.46)	0.00 (0.00)	−8.14 (14.94)	−14.17 (17.52)	−15.60 (14.55)	<0.001
Total RBF (μl min−1)	60.00 (13.99)***	60.49 (14.05)***	48.75 (9.52)	50.99 (12.72)	45.88 (9.34)	37.89 (7.05)*	30.14 (8.11)***	28.98 (6.78)***	<0.001
∆ RBF (%)	33.35 (23.19)***	34.73 (25.57)***	10.18 (11.13)	14.94 (17.19)	0.00 (0.00)	−15.88 (15.51)*	−32.86 (18.66)***	−35.05 (17.73)***	<0.001

SBP, systolic blood pressure; DBP, diastolic blood pressure; HR, heart rate; ∆, change. *P < 0.05; **P < 0.01; ***P < 0.001 vs. standardized baseline (100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 38 $P_{\mathrm{ETC}{\mathrm{O}}_2}$).

Figure 2. Change in arteriolar diameter and venous area .

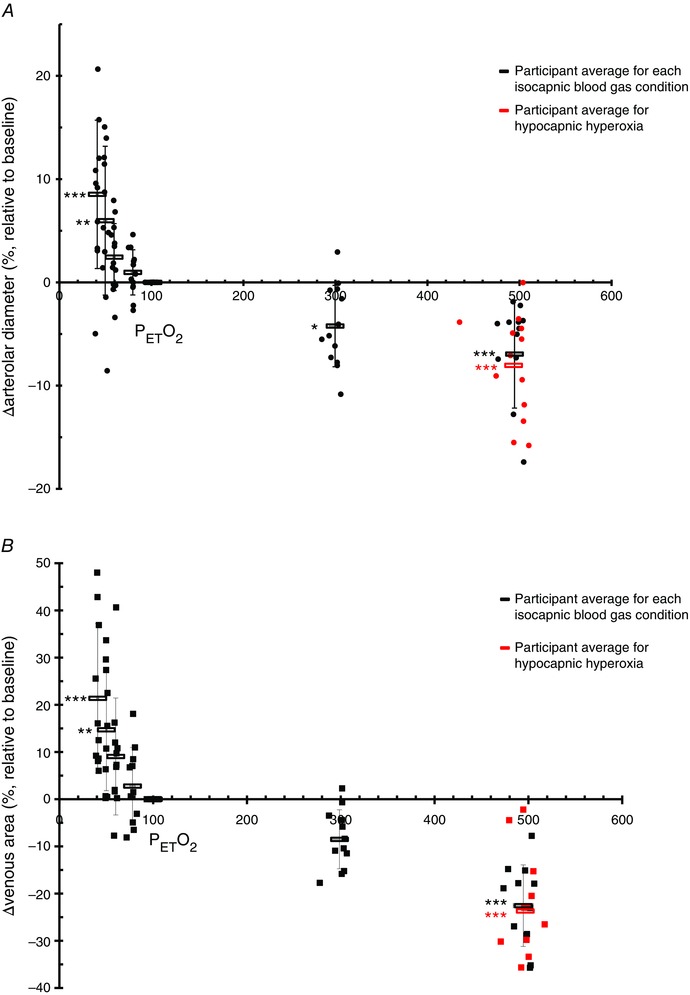
Change in arteriolar diameter (A) and venous area (B) measured with the CLBF and RTVue, respectively, as a percentage relative to standardized baseline (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$, 100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$) over seven isocapnic (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) changes in oxygen (40–500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$). Each black circle (A, CLBF) and square (B, RTVue) represents a participant for a single blood gas condition. The average of each isocapnic stage is shown as a black rectangle. The additional hypocapnic hyperoxic stages are delineated by red circles (A) or red squares (B), with each point representing a single participant; the red rectangle displays the average of this stage. *P < 0.05, **P < 0.01, ***P < 0.001.

Figure 2 also shows that severe hypoxia (40 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$) increased arteriolar diameter (Fig. 2 A) and venous area (Fig. 2 B) as much as it was reduced by severe hyperoxia. In severe hypoxia, arteriolar diameter increased by as much as 8.53 ± 7.19% (P < 0.001) and total venous area by as much as 21.38 ± 15.84% (P < 0.001). In severe hyperoxia (500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$), arteriolar diameter and total venous area eventually decreased by 6.94 ± 5.23% (P < 0.001) and 22.55 ± 8.64% (P < 0.001), respectively.

Figure 3 A shows that hypoxia increased retinal blood flow relative to baseline, becoming significantly elevated at 50 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ (P = 0.018) and increasing by as much as 48.66 ± 19.02% (P < 0.001) at 40 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ as measured with the CLBF. Figure 3 B shows that retinal blood flow measured by the RTVue was significantly augmented at both 40 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ and 50 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$ by 33.35 ± 23.19 % (P < 0.001) and 34.73 ± 25.57 (P < 0.001), respectively. Hyperoxia decreased retinal blood flow (Fig. 3), becoming significantly lower than baseline at 300 mmHg for both CLBF (P = 0.003) (Fig. 3 A) and RTVue (P = 0.048) (Fig. 3 B) measurements. In severe hyperoxia at 500 mmHg, $P_{\mathrm{ET}{\mathrm{O}}_2}$ retinal blood flow decreased to an even greater degree as measured with both the CLBF (40.45 ± 16.31%, P < 0.001) and RTVue (32.86 ± 18.66%, P < 0.001).

Figure 3. Change in retinal blood flow and total retinal blood flow .

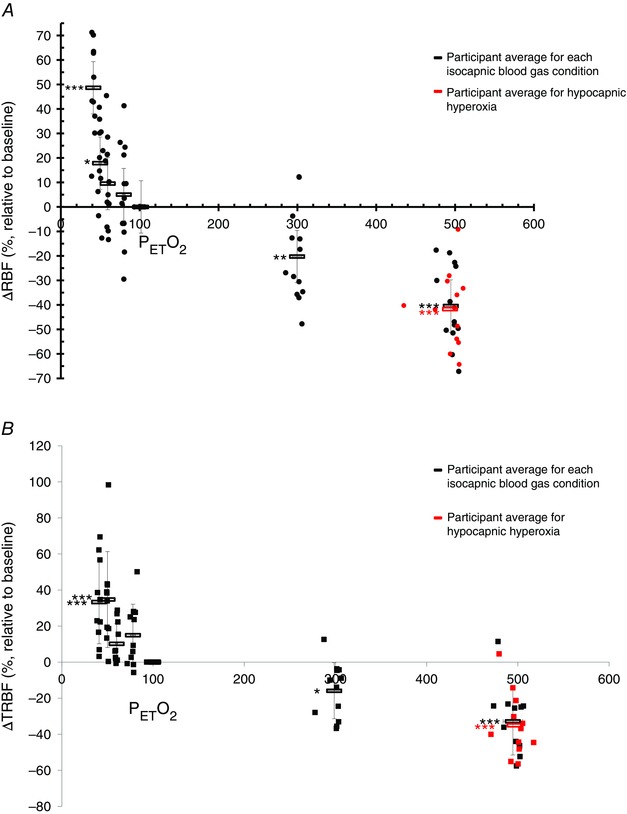
Change in retinal blood flow (RBF) measured with CLBF (A) and total retinal blood flow (TRBF) measured with the RTVue (B) as a percentage relative to standardized baseline (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$, 100 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$) over seven isocapnic (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) changes in oxygen (40–500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$). Each black circle (A, CLBF) and square (B, RTVue) represents a participant for a single blood gas condition. The average of each isocapnic stage is shown as a black rectangle. The additional hypocapnic hyperoxic stages are delineated by red circles (A) or red squares (B), with each point representing a single participant; the red rectangle displays the average of this stage. *P < 0.05, **P < 0.01, ***P < 0.001.

The responses to combined hypocapnic hyperoxia (500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 30 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) were similar to those to severe hyperoxia (500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) (Figs 2 and 3). Combined hypocapnic hyperoxia significantly decreased arteriolar diameter (Fig. 2 A) and venous area (Fig. 2 B) by 8.04 ± 4.96% (P < 0.001) and 23.68 ± 11.75% (P < 0.001), respectively. Retinal blood flow diminished by by 41.71 ± 15.03% (P < 0.001) as measured with the CLBF (Fig. 3 A) and by 35.05 ± 17.73% (P < 0.001) as measured with the RTVue (Fig. 2 B). Retinal blood flow was plotted against SaO₂ for the normoxic and hypoxic stages in all participants for both the CLBF (Fig. 4 A) and the RTVue (Fig. 4 B). The relationship was linear, with retinal blood flow increasing as saturation decreased. The slopes of the linear functions were −1.83 (r ² = 0.91) and −1.34 (r ² = 0.75) for the CLBF and RTVue, respectively.

Figure 4. Retinal blood flow .

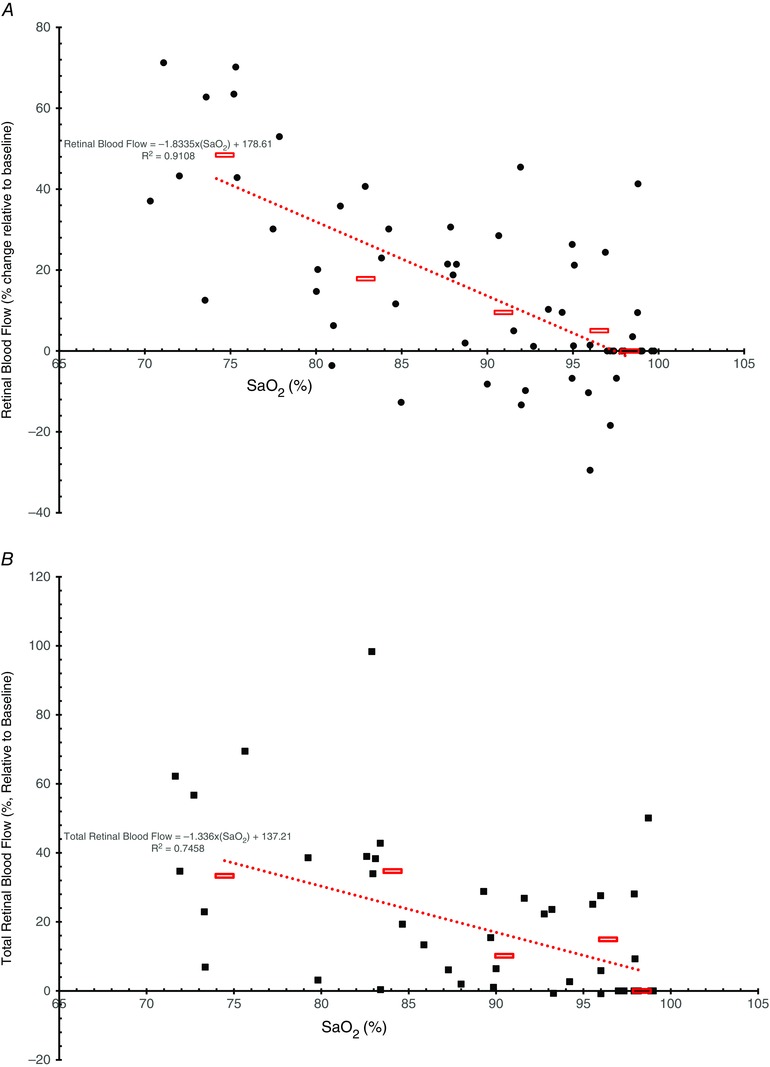
Retinal blood flow measured with the CLBF (visit 1, A) and total retinal blood flow measured with the RTVue (visit 2, B) as a percentage change relative to standardized baseline (SaO₂ = 98%) vs. arterial oxygen saturation (SaO₂) over four hypoxic stages (SaO₂ = 74–96%). Each black circle (A, CLBF) and square (B, RTVue) represents a participant during one blood gas condition. Average blood flow changes for all participants in a given hypoxic stage are shown as red rectangles. The red dotted line shows the line of best fit for the average retinal blood flow change with an r ² value of 0.9108 for CLBF (A) and 0.7458 for RTvue (B).

Figure 5 shows the relationship between the two measurement systems in terms of the relative blood flow measurements. The Pearson correlation coefficient was 0.716 with P < 0.001.

Figure 5. Total retinal blood flow and percent changes in retinal blood flow .

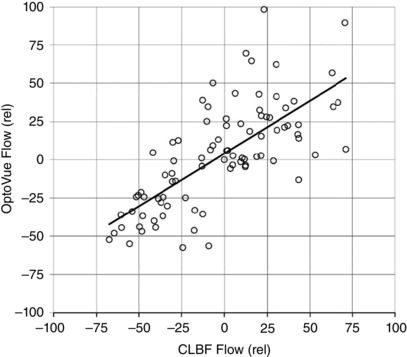
Correlation between percentage changes in total retinal blood flow measured with the Optovue and percent changes in retinal blood flow measured with the CLBF. The Pearson correlation coefficient was 0.716 with P < 0.001.

A model of retinal responses

A model of the relationship between retinal blood flow and $P_{\mathrm{a}{\mathrm{O}}_2}$ was developed based on a combination of hyperbolic and linear functions (see Appendix). The model shown in Fig. 6 is based on the raw average data collected from the CLBF in visit 1 (Fig. 6 A) and the RTVue instrument in visit 2 (Fig. 6 B). The $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote of the model for the CLBF (Fig. 6 A) is 36.8 mmHg, whereas that of RTVue (Fig. 6 B) is 32.7 mmHg.

Figure 6. Combined hyperbolic and linear function for retinal blood flow and total retinal blood flow .

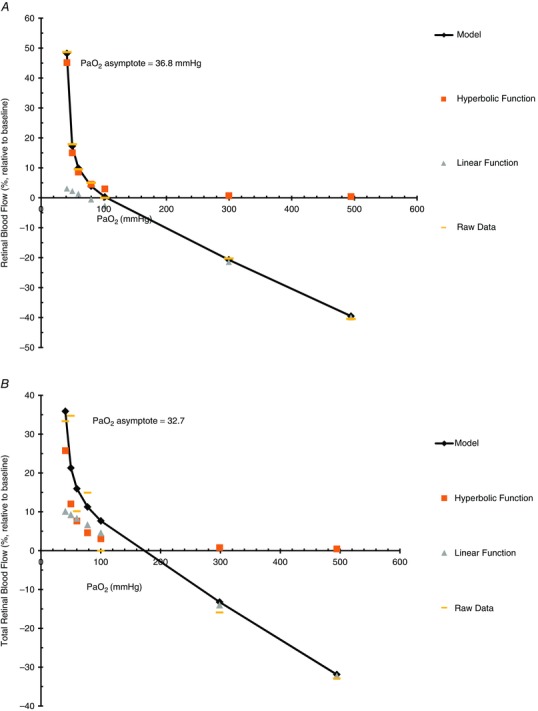
Model delineating a combined hyperbolic and linear function for retinal blood flow measured with CLBF (A) and total retinal blood flow measured with the RTVue (B) during seven isocapnic (38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) stages of $P_{\mathrm{ET}{\mathrm{O}}_2}$ (40, 50, 60, 80, 100, 300, 500 mmHg). The addition of series 2, the hyperbolic function, and series 3, the linear fit, gives the model, series 1. Series 4 shows the mean raw data.

Discussion

The results of the present study demonstrate that the retinal vasculature compensates for hypoxia above a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 32–37 mmHg but is unable to do so below this value. Additionally, they show that the retinal vessels have large vasodilatory and vasoconstrictive reserves, allowing them to compensate for a wide range of $P_{\mathrm{a}{\mathrm{O}}_2}$, and that the resting tonus of the retinal vasculature in normoxia is near the mid‐point of the adjustment range where sensitivity is maximum.

To our knowledge, no previous studies have used multiple stages of hypoxia and hyperoxia to determine the relationship between retinal blood flow and oxygen in humans. One previous study in monkeys examined retinal vascular reactivity with multiple stages of hypoxia and hyperoxia and, similar to our findings, it was reported that retinal blood flow compensates for hypoxia by increasing blood flow by as much as 98% at a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 27–47 mmHg (Eperon et al. 1975). The same study also found a 20% and 34% increase in arteriolar and venous diameter during severe hypoxia, which is greater than the increases that we observed (Eperon et al. 1975). With a hyperoxic stimulus of 315–470 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$, the study in monkeys by Eperon et al. (1975) reported results similar to ours, as well as those of other studies (Kiss et al. 2002; Gilmore et al. 2005; Wimpissinger et al. 2005; Sehi et al. 2012; Werkmeister et al. 2012; Tsui et al. 2013), showing an ∼7% decrease in both arteriolar and venous diameter (Eperon et al. 1975). However, the gas provocation method used in that study was of limited precision; the $P_{\mathrm{a}{\mathrm{O}}_2}$ stimulus was not consistent between subjects, resulting in a large retinal measurement variability. This high variability precluded an accurate depiction of the blood flow vs. oxygen relationship in the retina to discern the limitations of the retinal vasculature.

Other previous studies examining the retinal blood flow response to acute hypoxia used inhalation of 10% oxygen, with findings similar to that of our severe hypoxic stage (40 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$). For a hypoxic stimulus of 40–50 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$, several studies (Brinchmann‐Hansen et al. 1989; Brinchmann‐Hansen & Myhre, 1990) noted increases in retinal arteriolar diameter of 8.1–9.4%, 8.2% and 10.0%, respectively, whereas retinal venous diameter increased by 8.0–9.0%, 7.4% and 10.0%, respectively. By contrast, studies at altitude demonstrated that the retinal vessels can dilate to an even greater degree. At an altitude of 19,300 feet and 17,500 feet, arteriolar diameter increase by 24% and 18% and venous diameter by 23% and 21% (Frayser et al. 1971; Rennie & Morrissey, 1975). At an altitude of 6865 m (22,523 feet), a recent study (Bosch et al. 2009) showed as much as a 45% increase in arteriolar diameter and a 43% augmentation in venous diameter. These altitude study findings are comparable to our measurements with respect to venous area. However, these comparisons must be interpreted with caution given the differences between these previous studies and our own. Differences in species, instrumentation (i.e. fundus photography vs. densitometry), time spent under hypoxia and a more severe hypoxic stimulus may explain why some previous studies found a greater arteriolar dilatation.

With respect to hyperoxia, the present study, similar to other previous studies (Kiss et al. 2002; Gilmore et al. 2005; Wimpissinger et al. 2005; Sehi et al. 2012; Werkmeister et al. 2012; Tsui et al. 2013), found that retinal blood flow decreases more than necessary, although these findings are in contrast to those of Eperon et al. (1975) who reported that retinal blood flow was reduced in monkeys by as much as 12–13%, in compensation for the ∼10% increase in oxygen content during hyperoxia. Nevertheless, it is widely accepted (Kiss et al. 2002; Gilmore et al. 2005; Wimpissinger et al. 2005; Sehi et al. 2012; Werkmeister et al. 2012; Tsui et al. 2013) that retinal blood flow overcompensates during hyperoxia (500 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$), decreasing by as much as 35–50%. This overcompensation may not affect oxygen supply to the retina because of its dual‐circulatory supply; the decrease in oxygen delivery from the inner retinal vasculature may be compensated for by the relatively unreactive choroid (Kergoat & Faucher, 1999; Tonini et al. 2010), which greatly increases oxygen flux (Yu et al. 2005) during hyperoxia.

Previous studies (Hickam & Frayser, 1966; Frayser et al. 1971; Fallon et al. 1985; Brinchmann‐Hansen et al. 1989; Kiss et al. 2002; Gilmore et al. 2005; Bosch et al. 2009; Sehi et al. 2012) have failed to directly investigate the resting tonus of the retinal vessels. We found that retinal vessels dilated from baseline as much as they constricted. Our vasoconstrictive stimulus was supermaximal because hyperoxia (500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 38 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$) and the even greater vasoconstrictive stimulus, combined hypocapnic hyperoxia (500 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$, 30 mmHg $P_{\mathrm{ETC}{\mathrm{O}}_2}$), constricted the vessels to the same degree. However, our most severe hypoxic stimulus (40 mmHg $P_{\mathrm{ET}{\mathrm{O}}_2}$) may not have been supermaximal because we did not reach the model hypoxic asymptote (33–36 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$). Indeed, it may be that the retinal vessels can dilate more than they can constrict, based on the findings in monkeys by Eperon et al. (1975), although an in vitro study (Delaey et al. 2000) observing bovine retinal arteries using hypoxia and hyperoxia indicated that the resting tonus of the vessels is at the mid‐point of the adjustment range. The latter study (Delaey et al. 2000) showed that, relative to baseline (20% oxygen), a 95% O₂ mixture constricted the vessels to the same degree as they dilated with 0% O₂. In light of these findings, we suggest that the resting tonus of the retinal vessels in humans is at or below the mid‐point, supporting the idea that the retinal vessels have a high vasodilatory reserve, allowing them to compensate for decreases in oxygen.

The relationship between retinal blood flow and $P_{{\mathrm{O}}_2}$

The mechanism between oxygen sensing in the retina and increases in retinal blood flow is not completely understood. Oxygen sensing in the retina may be carried out via oxygen sensitive ion channels that respond directly to changes in oxygen or indirectly via metabolites such as adenosine. Given the slow response time to hypoxia in the retina, we suggest that a metabolic pathway is probable. The terminal arterioles and the retinal capillaries are considered to operate as one functional unit with the retinal capillaries containing ATP sensitive potassium channels, whereas the voltage‐dependent calcium channels are primarily located on tertiary arterioles (Lange & Bainbridge, 2012). The capillaries may hyperpolarize as a result of low levels of ATP and/or adenosine metabolites and this information is transduced via gap junction pathways into a vasomotor response by the terminal arterioles through voltage‐dependent calcium channels causing vasodilatation. The upstream arterioles near the optic nerve head, which were examined in the present study and contain the greatest vascular smooth muscle, may then dilate, perhaps via a flow‐mediated mechanism (Nagaoka et al. 2002). Other metabolic factors, such as retinal relaxing factor, which is released by the retinal tissue and causes vasodilatation in retinal bovine arterioles (Delaey et al. 2000), as well as lactate (Yamanishi et al. 2006), may be responsible for retinal vasodilatation during hypoxia. However, it is important to note that the mechanism between the response to hyperoxia and hypoxia may be different; the linear function in the model mainly describes the response to hyperoxia and the hyperbolic function primarily describes the response to hypoxia. Furthermore, the response times of the vessels to hyperoxia (2–5 min) (Grunwald et al. 1984; Kiss et al. 2002; Luksch et al. 2002; Gilmore et al. 2005; Jean‐Louis et al. 2005) and hypoxia (6–10 min) (Gidday & Park, 1993; Nagaoka et al. 2002) differ. It is possible that, at high oxygen tension values, other mechanisms cause the endothelium to release endothelin‐1, a well‐known factor involved in hyperoxic vasoconstriction (Takagi et al. 1996).

The relationship between the response of the venules and the arterioles is not well understood in the retina. In other vascular beds, the venules may communicate with the arteries and arterioles via flow‐mediated dilatations (Koller et al. 1994), conducted vasodilatation (Duling & Berne, 1970) and myogenic vasodilatation (Meininger et al. 1987). The venules can modulate arteriolar diameter via the release of endothelial‐derived factors during muscle stimulation (Hester & Hammer, 2002). Whether this control occurs in the retinal vessels is unknown. A pertinent question, however, is whether the venules are responding passively or actively to changes in $P_{{\mathrm{O}}_2}$. Given the idea that the venules, similar to the arterioles, have an endothelium and vascular smooth muscles, metabolites may act at both sites of the arterioles and venules to induce vasodilatation. Downstream dilatation from the arterioles at the site of the venules surrounding the optic nerve head may explain why arteriolar velocity increases significantly at a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 40 mmHg. Similarly, venular constriction may explain significant decreases in arteriolar velocity during hyperoxia. However, caution must be taken in this interpretation because other sites downstream of the secondary arterioles may have also dilated, including the terminal arterioles. Although we consider that the increase in total venous area of the venules surrounding the optic nerve head indicates a vasodilatory response during hypoxia, it is also plausible that the veins may also respond passively. The venules have high capacitance and may passively distend as a result of an increased volume from the high flow rate causing increases in total venous area during hypoxia.

Our model of the relationship between retinal blood flow and $P_{{\mathrm{O}}_2}$ allowed us to make several observations with respect to the regulation of retinal blood flow in hypoxia. Part of the model describing the relationship between retinal blood flow and hypoxia was a hyperbolic function showing that retinal blood flow is maximal at the $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote (36.8 mmHg, CLBF or 32.7 mmHg, RTVue), a value similar to that for the brain (Mardimae et al. 2012). We suggest that retinal blood flow is able to compensate for decreases in oxygen to the right of the asymptote, and we note that the top portion of the oxygen haemoglobin dissociation curve and the hypoxic portion of the hyperbolic function are similarly shaped. We therefore only begin to see a significant rise in retinal blood flow, arteriolar diameter and venous area above a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 60 mmHg because that is the approximate shoulder of the oxygen haemoglobin saturation curve, where oxygen saturation and content begin to decrease in a steep and linear manner.

Transforming the hyperbolic function of the oxygen haemoglobin dissociation curve demonstrated that the relationship between retinal blood flow and SaO₂ is linear. The hyperbolic function of the model relating retinal blood flow and hypoxia therefore shows that oxygen delivery may be maintained relatively constant in the face of $P_{{\mathrm{O}}_2}$ changes to the right of the asymptote. For example, a stimulus of 50 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$ would decrease arterial oxygen content by ∼16%, which would require a 19% increase in retinal blood flow to maintain oxygen delivery. The model prediction from the CLBF data is an increase in blood flow of ∼18% for a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 50 mmHg (83% SaO₂). Thus, to the left of the $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote, blood flow may not be able to compensate for hypoxia, causing oxygen delivery to decrease.

We suggest that the oxygen gradient between the photoreceptors and the retinal arterioles determines the $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote; retinal tissue $P_{{\mathrm{O}}_2}$ decreases markedly to the left of the asymptote. This idea is supported by experiments in cats where pre‐retinal $P_{{\mathrm{O}}_2}$ in the vitreous, which can be considered as an indicator for inner retinal $P_{{\mathrm{O}}_2}$, changes by as little as 0.14‐0.20 mmHg mmHg⁻¹ $P_{\mathrm{a}{\mathrm{O}}_2}$ above a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 35 mmHg, but changes by as much as 0.62 mmHg mmHg⁻¹ $P_{\mathrm{a}{\mathrm{O}}_2}$ below 35 mmHg (Enroth‐Cugell et al. 1980). This notion has shown to be true in rats, where oxygen consumption decreases at a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 31 mmHg but remains constant at a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 46 mmHg (Wanek et al. 2013). The $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote has also shown to have this functional significance by other studies, where a $P_{\mathrm{a}{\mathrm{O}}_2}$ of <35–40 mmHg causes cat ganglion cell contrast sensitivity (Enroth‐Cugell et al. 1980) and relative b‐wave amplitude to decrease (Linsenmeier, 1990). We therefore concluded that the asymptote describes the $P_{{\mathrm{O}}_2}$ at which oxygen delivery cannot be sustained causing functional hypoxia and decreases in oxygen consumption to occur when the vasodilatory reserve is exhausted.

Limitations

Several limitations of the present study deserve consideration. First, the sympathetic nervous system may have been stimulated during our most severe stage of hypoxia, although we were unable to directly observe its effects on the retinal vasculature. Although it is true that the inner retina is devoid of autonomic innervation (Pournaras et al. 2008), its effects may still have indirectly contributed to changes within the inner retinal vessels. The hypoxic stimulus may have stimulated the sympathetic nervous system via carotid body afferent signals to cause the small and non‐significant rise in MAP. For most participants, this rise appears to be insignificant but, for a few individuals, the arteriolar vessels appeared to constrict during severe hypoxia (40 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$). Thus, for some individuals, we are unable to distinguish between the retinal vessels response to hypoxia and the autoregulation of the vasculature. Moreover, the retinal vasculature has α₁ and α₂ adrenergic receptors (Yu et al. 2003) that may be influenced by circulatory hormones and neurotransmitters, as caused by sympathetic nervous system activation, resulting in attenuation of the hypoxic dilated retinal vessels. We were also unable to observe whether the vessels had maximally dilated with our severe hypoxic stimulus but, based on our model of the response, we were very close to the $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote where blood flow is maximal.

Another limitation of the present study was that we were unable to see how much blood flow actually increased during severe hypoxia with the RTVue instrument. The limited measurement of high flows with the RTVue is probbaly a result of signal loss from fringe washout at higher velocities, or restrictions in the instrument's ability to detect frequency shifts that are above 13.6 kHz. We also note that we did not measure oxygen delivery during the different blood gas conditions to demonstrate that it was constant during our stages of hypoxia. However, in our estimation, blood flow does indeed compensate for decreases in oxygen content. Finally, the limited number of subjects in the present study should be taken into consideration when applying the findings to the general population. However, the statistical power of the study was calculated to be 77.5% based on the 40 mmHg stage of hypoxia and the 100 mmHg stage of normoxia.

Conclusions

In the present study, we have established and modelled the relationship between retinal blood flow and oxygen as a combined linear and hyperbolic function. Furthermore, we measured the vascular reserves of the retinal vessels, both vasodilatory and vasoconstrictive, and showed that the resting tonus is near the mid‐point. We conclude that retinal blood flow compensates for hypoxia by increasing blood flow such that oxygen delivery is maintained relatively constant above a $P_{\mathrm{a}{\mathrm{O}}_2}$ of 32–37 mmHg.

This work, which was undertaken in vivo on human volunteers, is not relevant just to ocular physiology. Because the eye is an extension of the brain and also because the internal carotid artery gives rise to the ophthalmic artery from which the central retinal artery branches, the results are clearly relevant to cortical and general vascular physiology and the present study is unique because the data were gathered non‐invasively from humans. Future advances in ocular imaging technology may well make the eye a useful site of investigation for the general physiologist.

We suggest that future studies should quantify the retinal blood flow and oxygen relationship in patients with ocular disease as we have done in the present study for healthy individuals. Such information will indicate how much vascular reserve is present and where retinal vessels are limited in their ability to compensate for hypoxia. For example, the flow–hypoxia relationship and limits may be different in those with ocular diseases, particularly where there is a known compromised vascular component such as diabetic retinopathy, age‐related macular degeneration, glaucoma and central retinal vein occlusion. Knowledge of the relationship between retinal blood flow and oxygen will provide information relevant to the pathophysiology of the disease, thus enabling better treatment.

Additional information

Competing interests

JAF is Chief Scientist and JD is Senior Scientist at Thornhill Research Inc. (TRI), a spin‐off company from the University Health Network that developed the RespirAct™. RespirAct™ is currently a non‐commercial research tool assembled, and made available by TRI to research institutions to enable CVR studies. Furthermore, JGF and CH have shares in TRI.

Author contributions

CH, JAF, JD and JGF were responsible for conception and design of experiments, analysis and interpretation of data, and revising the manuscript critically for important intellectual content. MJ, FY and ET were responsible for collection of data and revision of manuscript critically for important intellectual content. RWC was responsible for the conception and design of experiment as well as collection, analysis and interpretation of data, and drafting the article. All authors approved the final version of the manuscript, all persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by grants from the Ontario Research Fund (ORF).

The model of retinal blood flow and $P_{\mathrm{a}{\mathrm{O}}_2}$ is based on previous studies that have demonstrated a rectangular hyperbolic relationship between cerebral blood flow and hypoxia (Mardimae et al. 2012). We also noted that the relationship between retinal blood flow and hyperoxia is linear. This led to a model that demonstrates an overall combined linear and rectangular hyperbolic function to describe the relationship between retinal blood flow and $P_{\mathrm{a}{\mathrm{O}}_2}$.

The equation for the relationship is:

$$y=a/\left(x-b\right)+\mathrm{c}\times \left(500-x\right)+y_{500}$$

a/(x – b) represents the rectangular hyperbolic function where a is the area constant (mmHg %), b is the $P_{\mathrm{a}{\mathrm{O}}_2}$ asymptote (mmHg) and x is the input $P_{\mathrm{a}{\mathrm{O}}_2}$ (mmHg). The linear function is c × (500 – x) + y ₅₀₀ where c represents the linear slope (% mmHg^–1), x is again the input $P_{\mathrm{a}{\mathrm{O}}_2}$ (mmHg) and y ₅₀₀ (%) represents the minimum haemodynamic parameter at 500 mmHg $P_{\mathrm{a}{\mathrm{O}}_2}$. The retinal haemodynamic value is represented by y (%).

The parameters describing the relationship between blood flow measured with the CLBF were obtained using the Levenburg Marquardt algorithm to determine the least squares set of equation coefficients that best fit the data (r ² = 0.99). They are:

• a = 193.987

• b = 36.8419

• c = 0.0948409

• y ₅₀₀ = −40.454

The parameters describing the relationship between blood flow measured with the RTVue were obtained using the Levenburg Marquardt algorithm to determine the least squares set of equation coefficients that best fit the data (r ² = 0.96). They are:

• a = 208.805

• b = 32.7099

• c = 0.0936079

• y ₅₀₀ = –32.859