Abstract
Mathematical modeling has been instrumental in identifying common principles of cell polarity across diverse systems. These principles include positive feedback loops that are required to destabilize a spatially uniform state of the cell. The conserved small G-protein Cdc42 is a master regulator of eukaryotic cellular polarization. Here we discuss recent developments in studies of Cdc42 polarization in budding and fission yeasts and demonstrate that models describing symmetry-breaking polarization can be classified into six minimal classes based on the structure of positive feedback loops that activate and localize Cdc42. Owing to their generic system-independent nature, these model classes are also likely to be relevant for the G-protein–based symmetry-breaking systems of higher eukaryotes. We review experimental evidence pro et contra different theoretically plausible models and conclude that several parallel and non–mutually exclusive mechanisms are likely involved in cellular polarization of yeasts. This potential redundancy needs to be taken into consideration when interpreting the results of recent cell-rewiring studies.
INTRODUCTION
Eukaryotic cell polarization is a fundamental process that involves formation of a persistent morphological axis akin to a compass needle (Bourne and Weiner, 2002). The transition from an unpolarized state with all spatial directions potentially equal to a state with one specific direction chosen, or symmetry breaking, continues to puzzle and fascinate researchers across many disciplines. The intellectual appeal of cell polarization, as well as its biological importance, has driven significant experimental and theoretical effort in understanding the basic mechanisms of cell polarity. This work established the existence of evolutionarily conserved polarity proteins and common biophysical principles but also revealed staggering diversity, redundancy, and mutability of polarity mechanisms (Drubin and Nelson, 1996; Martin-Belmonte and Mostov, 2008; McCaffrey and Macara, 2012).
Here we focus on the molecular mechanisms and theoretical models of cell polarity establishment in budding and fission yeasts. Based on decades of genetic studies, we now have an almost complete list of “players”—yeast proteins involved in the polarity mechanisms (Drees et al., 2001). Although we do not yet fully understand how these players act together, in yeasts, we are perhaps the closest to the dream of mechanistic modeling—to be able to match any model variable to a specific protein and every arrow to a particular biochemical reaction. In addition to classical genetic methods, “cell-rewiring” approaches have become increasingly popular. These studies deployed synthetic proteins to purposefully change the layout of molecular networks, for example, by altering cellular localization of specific players. These efforts, frequently initiated to test the validity of preexisting conceptual models, generated alternative models of their own. The resulting proliferation of the rewired mutants, new mathematical models, and unfamiliar jargon borrowed from physical and mathematical sciences make it difficult to follow progress in the field. Here we review these recent developments and show that the existing models fall within a few well-delimited conceptual classes. Surprisingly, we conclude that, beyond the already proposed models, additional model classes are theoretically possible and, at least in part, are supported by experimental data. We argue that, simple as they may appear in comparison with higher eukaryotes, yeasts likely possess multiple redundant mechanisms of symmetry breaking. This conclusion calls for a caution in interpreting the results of recent studies directed at identifying “the correct” model of yeast cell polarity.
SYMMETRY BREAKING: FROM PHYSICS TO BIOLOGY
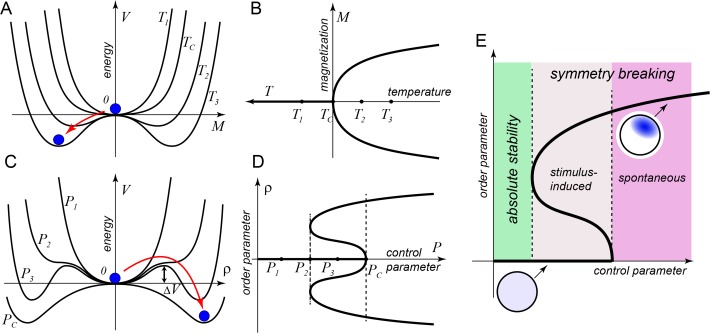
The notion of spontaneous symmetry breaking (Baker and Glashow, 1962) originated in particle physics, rapidly spread across all of physics, and gained prominence as one of its central unifying concepts (Bijker, 2009). A classical example of spontaneous symmetry breaking is the ferromagnetic phase transition that occurs at the Curie temperature, Tc (Figure 1, A and B). When temperature (the control parameter) is above critical, T > Tc, the matter is in the paramagnetic phase, which is symmetric, in the sense that all directions of atomic magnetic dipoles are equally probable, and the average value of magnetization, M (the order parameter), is 0. For T ≤ Tc, the paramagnetic state, M = 0, is no longer the minimum of potential energy but, instead, its local maximum. This means that the symmetric state, M = 0, becomes absolutely unstable, and the system randomly selects a new energy minimum out of infinitely many equienergetic ferromagnetic states with a nonzero average magnetization and, therefore, broken rotational symmetry.
FIGURE 1:
Symmetry breaking in physics and biology. (A, B) Transition of paramagnetic to ferromagnetic state as a prototypical example of symmetry breaking. (A) Symmetric state M = 0 changes from the energy minimum to a local maximum at the Curie temperature. (B) At the transition point, the system selects one of two equivalent branches. (C, D) A system in which the symmetric state ρ = 0 remains locally stable after asymmetric states are born. (C) The system can be forced out of the symmetric state if the energy barrier is exceeded. (D) Multistable parameter region corresponds to an energy function with three minima. (E) Symmetry breaking in a biological system far from thermodynamic equilibrium. Nonzero order parameter corresponds to the emergence of spatial structure. Spatially homogeneous and polarized states of the system are shown schematically as uniform and patterned spherical cells, respectively.
Consider now a different example of symmetry breaking with a more complex shape of energy function, V(ρ) (Figure 1, C and D). Here there is a range of control parameter values, P2 < P < Pc, within which energy has three minima. If the control parameter is increased from, say, P1 to P3 , the system that at P1 was in the symmetric state, ρ = 0, will remain there at P3, even though the asymmetric states have lower energy. The state of the system will remain unchanged until a sufficiently large perturbation throws it over the energy barrier, ∆V, that separates the states. If the control parameter continues to increase, the symmetric state, ρ = 0, becomes absolutely unstable at P = Pc, just as in the ferromagnetic example. However, in the second example, before this spontaneous transition, the system can be forced to undergo symmetry breaking. This requires an external stimulus with amplitude larger than a certain threshold.
Prigogine and colleagues proposed that the Turing mechanism for the spontaneous emergence of spatial organization via the diffusion-driven instability of a spatially homogeneous state (Turing, 1952), or Turing instability, can be considered a spontaneous symmetry-breaking transition (Prigogine and Nicolis, 1967; Prigogine et al., 1969). They foresaw that this type of symmetry breaking plays an important role in biology and demonstrated that it can happen only in systems far from thermodynamic equilibrium. Although the useful concept of potential energy is no longer well defined in these systems, they behave surprisingly similarly to equilibrium systems (Figure 1E). Just as in equilibrium phase transitions, there exists a critical parameter value beyond which the spatially homogeneous state is unstable to any perturbation, including thermal molecular noise. Between the domains of absolute stability and instability of the “symmetric” state lies an area where symmetry can be broken by a superthreshold stimulus.
By now the concept of symmetry breaking has firmly established itself in biology (Kirschner et al., 2000; Atkins et al., 2008; Li and Bowerman, 2010). Whereas the original idea of Turing was based on the interplay of chemical reactions and diffusion, the “multiphysics” nature of biological systems calls for a much broader exploration for causes of symmetry breaking. Indeed, hydrodynamic (Gowrishankar et al., 2012; Tjhung et al., 2012), mechanical (Howard et al., 2011; Maiuri et al., 2015), and electrical (Homble and Leonetti, 2007; Chang and Minc, 2014) forces can also drive symmetry breaking when coupled with nonlinear chemical reactions, with each other, or even on their own.
Physiologically, symmetry breaking in biological systems is guided by certain “cues,” stimuli that are either intrinsic, also known as “landmarks,” or extrinsic, such as gradients of signaling molecules detected by sensors. Stimulus-induced transitions provide the ability to sense and amplify environmental cues that exceed the level of background noise. Thus it appears that, under normal physiological conditions, biological systems are maintained within the region of parameters corresponding to the bistable state, posed for the stimulus-induced symmetry breaking (Figure 1E). Accordingly, much effort has been put into the characterization of cues that initiate the symmetry-breaking transition. Nonetheless, it was the experimental decoupling of inputs from landmarks and sensors that permitted discovery of the existence of spontaneous cell-intrinsic symmetry-breaking mechanisms in various organisms.
CELL POLARIZATION IN YEAST AND ITS RELATION TO SYMMETRY BREAKING
In the budding yeast Saccharomyces cerevisiae, cell polarization has been historically associated with polarized cell growth during vegetative budding and formation of a mating protrusion, also known as a shmoo (Drubin, 1991; Pruyne and Bretscher, 2000; Bi and Park, 2012). The fission yeast Schizosaccharomyces pombe also forms polarized mating protrusions, but, instead of budding, it exhibits polarized vegetative growth localized to one or both tips of its cylindrical cell. Polarized growth in yeasts is attributed to the localized insertion of secretory vesicles that stream along the actin cables directed toward the sites of polarized growth. Polarization of actin cytoskeleton, revealed by both the organization of actin cables and localization of endocytic actin patches, together with polarization of membrane insertion and cell wall remodeling have been frequently used as distinctive signs of yeast cell polarity (Drubin, 1991).
Already early genetic analyses identified the small Rho GTPase Cdc42 as an essential regulator of cell polarization (Adams et al., 1990; Johnson and Pringle, 1990). A breakthrough in understanding the role of Cdc42 in yeast polarity was made possible by the introduction of Cdc42 activity reporters (Nalbant et al., 2004; Ozbudak et al., 2005; Tong et al., 2007). These probes are fusions of fluorescent proteins with the Cdc42-binding (or CRIB) domains of Cdc42 effectors, proteins that interact preferentially with the GTP-bound, or active, form of Cdc42 (Burbelo et al., 1995). Live-cell imaging studies with CRIB reporters demonstrated that, in budding yeast, an approximately round cluster of Cdc42-GTP emerges at the presumptive bud site (PBS) well in advance of the beginning of bud protrusion (Ozbudak et al., 2005; Tong et al., 2007; Okada et al., 2013). Formation of this cluster of Cdc42-GTP, as reported by the CRIB activity probe, and local enrichment in total Cdc42, as reported by direct labeling of the GTPase with fluorescent proteins, is frequently referred to as Cdc42 polarization. Similar clusters of Cdc42-GTP are routinely observed at the growing tips of fission yeast cells, as well as in germinating spores and at the mating protrusions in both yeasts (Bonazzi et al., 2014; Martin, 2015).
Treatment of budding yeast with latrunculin A (Lat A) depolymerizes both cables and endocytic patches (Ayscough et al., 1997) but does not prevent either emergence or maintenance of clusters of Cdc42-GTP (Ayscough et al., 1997; Irazoqui et al., 2003; Okada et al., 2013). Furthermore, application of Lat A to cells deleted for one or more Cdc42 inactivators, GTPase-activating proteins (GAPs), demonstrated that in these cells, overactive Cdc42-GTP clusters can drive pronounced polarized cell growth in the absence of cables (Okada et al., 2013). However, in fission yeast, Lat A disperses Cdc42-GTP clusters from the cell tips (Bendezu and Martin, 2011; Bendezu et al., 2015). On the surface, this result could have been considered as supporting the notion that Cdc42 polarization depends on actin cytoskeleton, at least in S. pombe. However, it should be kept in mind that, in addition to depolymerizing F-actin, Lat A also induces a cell stress response via the stress-activated mitogen-activated protein kinases (MAPKs; McMillan et al., 1998; Harrison et al., 2004). A recent study in S. pombe unequivocally demonstrates that Lat A induces stress-activated MAPK Sty1 and inhibition of Sty1 activation prevents Cdc42 depolarization despite the complete depolymerization of the actin cytoskeleton (Mutavchiev et al., 2016). Thus, in both yeasts, actin cytoskeleton per se is not required for Cdc42 polarization. A more complex subject—the requirement for polarized secretion in Cdc42 polarization—remains a matter of controversy. Regardless of the relationships between various constituents of polarized growth, emergence of the Cdc42-GTP cluster has become the de facto criterion for judging whether a given set of experimental conditions permits or prevents cellular polarization. Therefore in the following we focus on the molecular mechanisms and theoretical models of Cdc42 polarization.
Does symmetry breaking play any role in Cdc42 polarization? In budding yeast, Cdc42 polarization is directed by the budding landmarks and signaling of G-proteins that are activated downstream of mating pheromones (Butty et al., 1998; Park and Bi, 2007; Bi and Park, 2012). Landmarks ensure that, in haploid yeasts, a new bud forms right next to the budding scar from the previous cell cycle (axial pattern), whereas in diploid cells, buds form in the alternating bipolar pattern. Multiple landmark systems engage the Cdc42 polarity module via a single common element, a Ras-like GTPase Rsr1/Bud1 (Bender and Pringle, 1989). In rsr1Δ cells, spatially uniform activity of CDK1 increases the control parameter (in this case, the cytoplasmic concentration of the Cdc42 activator) until Cdc42 polarization emerges at a random cortical location, apparently via spontaneous symmetry breaking (Irazoqui et al., 2003). However, even in the presence of landmarks, polarization can satisfy the criteria for symmetry breaking. Indeed, the landmarks are physically positioned in a circle surrounding the birth scar, that is, with circular symmetry, 0 < ϕ < 2π, whereas the bud forms at a particular location, ϕ = ϕ0, just outside of this circle. Thus a random noise–driven choice breaks the circular symmetry of landmark distribution (Wu et al., 2013). Unfortunately, Rsr1 is not conserved in fission yeast, and the exact relationship between the fission yeast landmarks and the Cdc42 module is not well understood. In all fungi, spore germination is possibly the most biologically relevant scenario in which polarization of Cdc42 occurs via symmetry breaking naturally, without experimental intervention (Bonazzi et al., 2014; Lichius et al., 2014; Bendezu et al., 2015).
Mathematical models that attempt to explain spontaneous Cdc42 polarization should be able to describe spontaneous symmetry breaking. This means that within a reasonably broad domain of parameters, their spatially uniform steady state should be unstable to infinitesimally small perturbations, that is, exhibit Turing instability. Landmarks and sensory inputs can be readily added to such models by, for example, spatially dependent initial conditions. A less constrained and therefore much larger set of models can describe amplification of Cdc42 activity or enrichment in response to a spatially dependent template of activation or transport. However, the majority of these models will lose Cdc42 polarization as soon as this input is withdrawn. Thus, for a model that attempts to explain spontaneous Cdc42 polarization in yeast, the ability to sustain polarization in the steady state, long after the initial perturbation that biased the symmetry breaking has vanished, is the necessary condition of applicability. A number of models assumed a preexisting polarization of actin cables (Wedlich-Soldner et al., 2003; Marco et al., 2007; Slaughter et al., 2009, 2013; Das et al., 2012). In these models, spatial symmetry is broken from the outset by the model design, and the authors instead focus their attention on how the spatial distribution of Cdc42 might follow that of the actin cables. In the following discussion, we restrict our attention to models that can describe spontaneous symmetry breaking.
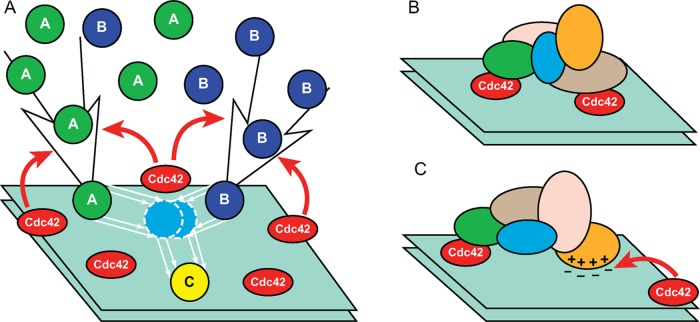
The processes that enable Cdc42 polarization include translocation to and away from the site of polarization, local cycles of activation/inactivation, and, finally, diffusion on the plasma membrane, all of which depend on interactions with other cellular proteins and membrane lipids (Park and Bi, 2007; Ridley, 2015). The nucleotide state of Cdc42 is controlled by activating nucleotide exchange factors (GEFs), which catalyze the exchange of Cdc42-bound GDP to GTP, and inactivating GAPs, which accelerate the hydrolysis of GTP by Cdc42. The GTP-bound, or active, form of Cdc42 (denoted RT in the formulas and diagrams) has a conformation distinct from that of the GDP-bound form (RD). Proteins capable of detecting this conformation difference, for example, effectors, interact differentially with active and inactive forms. This makes RT and RD effectively distinct chemical species that are interconverted by the cycles of activation/inactivation. In the language of chemical kinetics, the rate of change of the local concentration of Cdc42-GTP can be expressed formally as
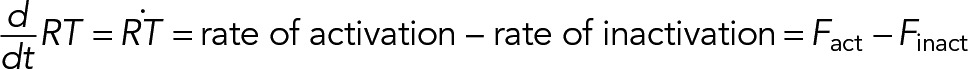 (1) (1)
|
and the rate of change of RD by an expression in which the signs of the rates of activation and inactivation are reversed. Because both processes are enzymatic reactions, their rates are generally described by the familiar Michaelis–Menten formula. However, if GEFs and GAPs function far from saturation, the rates of activation and inactivation become simply the rates of two bimolecular reactions:
|
|
Assuming for now that the system is spatially homogeneous, we find that Eq. 2 has a simple steady-state solution. Because in the steady state RT = 0, we get RT/RD = E/A. This steady state is, in fact, stable. Intuitively, this can be seen directly from Eq. 2. If we try to perturb the steady state by activating Cdc42, that is, converting some RD into RT, the rate of activation will drop while the rate of inactivation will increase, and the system will return back.
HOW MUCH POSITIVE FEEDBACK IS NEEDED FOR SYMMETRY BREAKING?
Because symmetry breaking is associated with instability of the preexisting steady state, to achieve Cdc42 polarization, it is necessary that the rate of activation grows faster with the increase in RT than the rate of inactivation. Here we also assume that the total cellular amount of the GTPase is conserved during the transition. Then, if Fact ~ RTn and Finact ~ RTm, for the symmetry breaking to occur, it is required that n > m. This condition can be satisfied only in the presence of feedback, that is, when the local rates of Cdc42 activation, inactivation, or both depend on the activity of Cdc42 itself.
The crucial role of feedback in the emergence of complex behavior, such as bistability, oscillations, and spatial structures, has been well understood mathematically and is by now firmly established in biology (Novak and Tyson, 2008; Ferrell, 2013). In Cdc42 polarization, positive feedback can emerge via a number of nonexclusive scenarios—for example, if Cdc42 activity is involved in the recruitment to the site of polarization of GEFs or Cdc42 itself. A double-negative loop in which Cdc42 activity causes reduction in the activity of a GAP will also generate a cumulative positive feedback loop. Of interest, theorists noticed that a single positive feedback loop does not provide symmetry breaking in the models of cell polarization (Lo et al., 2014). A notable exception was reported in a stochastic model of budding yeast cell polarity (Altschuler et al., 2008). That a single positive feedback loop is not sufficient to break symmetry, at least within the deterministic approach, can be illustrated using Eqs. 1 and 2. For example, if either a GEF or inactive Cdc42 can be recruited to the site of polarization by the activity of Cdc42, the rate of activation will be proportional to RT, and thus n = 1. However, Eq. 2 shows that Finact ~ RT, and therefore n = m = 1, and the condition n > m is not satisfied.
Multiple feedback loops are commonly found in biological molecular networks. However, the presence of several feedback loops by itself does not yet guarantee symmetry breaking. In a hypothetical cell in which Cdc42 is activated by two distinct GEFs both recruited to the membrane by the Cdc42 activity, the rate of Cdc42 activation is a sum of two functions, Fact(GEF1) + Fact(GEF2), each proportional to RT, and the outcome does not differ from that in the case of a single feedback loop. This is a typical example of parallel feedback loops. To achieve symmetry breaking, feedback loops must be converging, or cooperating (Lo et al., 2014). Convergence of feedback loops (Figure 2A) can be exemplified by a hypothetical scenario in which both a GEF and RD are recruited to the membrane by the activity of Cdc42. Because the activation of Cdc42 by its GEF is a bimolecular reaction, according to the mass-action rate law of chemical kinetics, its rate is proportional to the product of the local concentrations of the two molecules:
|
|
FIGURE 2:
Sources of nonlinearity in the Cdc42 polarity module. (A) If reaction A + B → C takes place on the membrane and both A and B are recruited downstream of Cdc42 activity, the rate of production of C is proportional to the square of Cdc42-GTP concentration. (B) The membrane concentration of a protein complex that interacts with the membrane via two independent Cdc42 effectors (or one bivalent effector) is proportional to the square of Cdc42-GTP concentration. (C) Similar to B, but in this case, one of the complex subunits interacts with negatively charged phospholipids whose accumulation is downstream of Cdc42 activity.
This makes n = 2, and, if m = 1 as in Eq. 2, the condition for symmetry breaking is satisfied.
Positive feedback loops are sufficient to enable symmetry-breaking polarization. Addition of negative feedback dramatically increases the range of spatiotemporal patterns that can be observed in biological systems. In models of yeast polarity, additional negative feedback produces Cdc42-GTP clusters that move, oscillate in place, or jump between different locations on the cell cortex (Ozbudak et al., 2005; Howell et al., 2012; Dyer et al., 2013; Okada et al., 2013; Wu and Lew, 2013; McClure et al., 2015).
SIX MECHANISTIC METAMODELS OF CDC42 POLARIZATION
We can modify Eq. 2 by introducing an arbitrary number of converging positive feedback loops that affect concentrations of GEFs and GAPs and inactive Cdc42:
|
|
In Eq. 4, we explicitly distinguish k feedback loops converging on the recruitment of a GEF from l converging feedback loops that control the concentration of inactive Cdc42. The condition for symmetry breaking then becomes
|
|
Inequality 5 can be satisfied by a great many potential models. However, if we request that the models must have minimal complexity, that is, that the total number of all feedback loops is kept to a minimum and k + l – m = 1, we find that all minimal models with symmetry breaking fall within six classes. These classes can be mathematically represented by distinct combinations of small integer numbers k, l, and m that satisfy inequality 5.
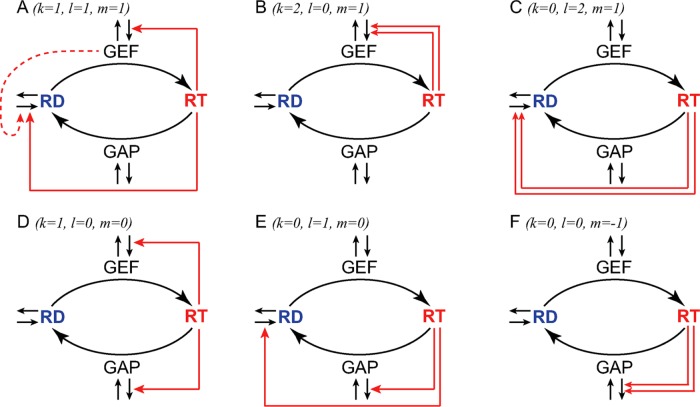
Model A. Converging linear feedback via GEF and RD (k = 1, l = 1, m = 1)
In budding yeast, Cdc42 effector Bem1 forms a stable complex with the only Cdc42 GEF, Cdc24. Recruitment of Cdc24 by Cdc42-GTP via Bem1 constitutes a Cdc42 autoactivation loop that has been shown to be necessary for Cdc42 polarization (Gulli et al., 2000; Bose et al., 2001; Butty et al., 2002; Irazoqui et al., 2003). The feedback complex also includes another Cdc42 effector, Pak kinase Cla4 (Kozubowski et al., 2008). Bem1 is conserved among fungi, and its fission yeast homologue, Scd2, plays a similar role in recruiting GEF Scd1 (Chang et al., 1994). Consequently a number of yeast polarity models, in addition to unaided membrane-cytoplasmic shuttling of GEF, rely on the existence of a positive feedback loop in which a cytosolic GEF is recruited by active Cdc42 via an effector:
|
|
where EC and EM are the cytoplasmic and membrane-bound GEF–effector complexes, respectively. We consider RT to be membrane bound and omit the subscript M as redundant.
Because a single linear positive feedback loop is insufficient to provide symmetry breaking, the necessary additional feedback loop can come from the recruitment of Cdc42 itself (Figure 3A). Several mutually nonexclusive mechanisms can be proposed here. Yeast Cdc42 in its inactive form can be delivered to the plasma membrane by secretory vesicles (Watson et al., 2014; Bendezu et al., 2015). Secretion in yeasts is positively regulated by Cdc42-GTP via at least two parallel pathways: tethering of vesicles to the plasma membrane and, independently, regulation of actin cable polymerization (Bendezu and Martin, 2011). In the former pathway, the effector in question is the exocyst, a multiprotein complex several subunits of which have been shown to interact with Cdc42-GTP (Adamo et al., 2001; Zhang et al., 2001, 2008; Wu et al., 2010a). In the latter pathway, formins that synthesize the cables (Bni1 and Bnr1 in budding and For3 in fission yeast) are believed to interact with Cdc42-GTP either directly (Martin et al., 2007) or via other effectors (Chen et al., 2012). Cdc42 can also travel through the cytoplasm diffusively either in a complex with GDP dissociation inhibitors (GDIs) or on its own (Johnson et al., 2009; Zhang et al., 2014). In both budding and fission yeast, Cdc42 attaches to membranes by the C-terminal prenyl (geranylgeranyl) moiety and a short polybasic cluster of four lysine residues (+4). Cdc42-induced local increase in the membrane negative charge due, for example, to the flippase-mediated enrichment of phosphatidylserine (Das et al., 2012; Bruurs et al., 2015) could provide a positive feedback loop that would work for both GDI-dependent (Ugolev et al., 2006, 2008) and GDI-independent routes of Cdc42 diffusive transport. Other lipid-mediated mechanisms of positive feedback are also possible because negatively charged phosphoinositides phosphatidylinositol-4,5-bisphosphate and phosphatidylinositol-4-phosphate have also been shown to be enriched at the sites of cellular polarization (Garrenton et al., 2010; Ghugtyal et al., 2015). An additional potential GDI-dependent feedback mechanism involves the Cdc42 effector kinase Cla4, which was reported to reduce the interaction between budding yeast GDI Rdi1 and Cdc42 and increase deposition of the GTPase on the membrane (Tiedje et al., 2008). Similar to reaction 6, each of the foregoing molecular mechanisms in aggregate can be represented by cumulative expressions:
|
|
FIGURE 3:
Six classes of Cdc42 polarization models with spontaneous symmetry breaking. Feedback loops connecting the active form of Cdc42 (RT) to its regulators and the recruitment of inactive Cdc42 (RD) are shown by red arrows. Double red arrows indicate nonlinear positive feedback. See text for detailed discussion.
Together reactions 6 and 7 ensure that the concentrations of both membrane-bound GEF and RD depend on RT and satisfy the symmetry-breaking condition.
Of importance, the two feedback loops in this model class need not be independent. Wedlich-Söldner, Frey, and colleagues proposed a model (Freisinger et al., 2013; Klunder et al., 2013) in which Cdc42-GTP recruits Cdc24 via Bem1, whereas Cdc24, in turn, recruits cytoplasmic Cdc42-GDP (dashed arrow in Figure 3A) and simultaneously activates it:
|
|
It is easy to show that the net effect of reactions 6 and 8 is the same as that of reactions 6 and 7. Notice, however, that if cytoplasmic Cdc42-GDP is bound to a GDI, reaction 8 implicitly assumes formation of a heterotrimeric complex GEF-RD-GDI, which is believed to be prohibited by a significant overlap of the binding sites for GEF and GDI on the GTPase (Hoffman et al., 2000; Rossman et al., 2005). If GDI is taken into the consideration explicitly and reaction 8 is split into two consecutive steps that no longer require the existence of the heterotrimeric GEF-RD-GDI complex (Robbe et al., 2003),
|
|
the Wedlich-Söldner–Frey model can no longer explain symmetry breaking. This caveat does not apply, however, to class A models that do not require direct recruitment of RD by a GEF. The model by Ozbudak et al. (2005) without additional actin-mediated negative feedback can be also assigned to class A even though the authors did not suggest any explicit molecular mechanism.
Model B. Nonlinear feedback via recruitment of GEF (k = 2, l = 0, m = 1)
Another way to achieve dependence of the Cdc42 activation rate on RT2 is to propose that the feedback loop that recruits GEF is nonlinear (Figure 3B; Liu and Barabasi, 2016). For example, this would be the case if the effector or the effector complex (Figure 2B) that recruits a GEF can simultaneously bind to two molecules of Cdc42-GTP (Khan and Menetrey, 2013; Rai et al., 2016). Of interest, Scd2 has been reported to bind two Cdc42-GTP molecules via its two adjacent SH3 domains (Endo et al., 2003; Wheatley and Rittinger, 2005), but this 1:2 binding stoichiometry has not been seen for Bem1. The Bem1-Cla4 effector complex (Kozubowski et al., 2008), in principle, could bind two active molecules of Cdc42 via effector domains of Bem1 and Cla4 (Bose et al., 2001; Takaku et al., 2010). However, this hypothetical bivalent interaction appears to be nonessential because BEM1 deletion mutant was rescued by a GEF-effector chimera containing only a single effector domain of Bem1 (Kozubowski et al., 2008).
Goryachev and Pokhilko (2008) provided the first detailed mathematical analysis of the biochemical mechanism of symmetry-breaking Cdc42 polarization. They assumed that diffusive transport of Cdc42-GDP in complex with GDI follows mechanism 9. In this scenario, delivery of Cdc42-GDP to the site of polarization is governed by the competition between GEF and GDI for inactive GTPase (Robbe et al., 2003; Schoebel et al., 2009; Wu et al., 2010b; Freisinger et al., 2013) but does not involve direct recruitment of RD via either RT (reaction 7) or GEF (reaction 8). Further, they suggested that interaction 6 between the cytosolic Bem1 (or Bem1-Cdc24 complex) and membrane-bound Cdc42-GTP should also occur on the membrane (Goryachev and Pokhilko, 2006), that is,
|
|
From relation 6, it follows that the concentration of membrane-bound GEF is proportional to the local concentration of Cdc42-GTP (EM ~ RT). The mass-action rate law applied to reaction 10 then gives us that the concentration of the RT-E complex at the polarization site is proportional to EM(RT)·RT ~ RT2, and thus the feedback via Bem1-Cdc24 recruitment is nonlinear. Only a fraction of the GEF-effector complex is required to be in the complex with Cdc42-GTP at any time for the symmetry breaking to occur in the model. In theory, if Cdc42-GTP formed RT-E only with the cytoplasmic Bem1-Cdc24 and, for some unknown reason, could not interact with the membrane-bound GEF, the model would lose its symmetry-breaking property. In practice, this is hardly a limitation of the model because it provides robust symmetry breaking even if the on rate of the reaction between EM and RT is <1/30,000 of that for the reaction between EC and RT.
The Goryachev–Pokhilko model has been tested experimentally and, with minor modifications and additions, has been extensively used in the literature (Howell et al., 2009; Layton et al., 2011; Savage et al., 2012; Jose et al., 2013; Okada et al., 2013; Wu et al., 2013, 2015; Woods et al., 2015, 2016). A very similar model of this class with Bem1-mediated nonlinear feedback [GEF] ~ RT2 has been proposed by Park, Chou, and colleagues (Lo et al., 2013; Lee et al., 2015). Freisinger et al. (2013) questioned the existence of the complex RT-E predicted by the Goryachev–Pokhilko model. They reasoned that because Cdc24 is in complex with Cdc42-GTP, the membrane–cytoplasmic shuttling of Cdc24 should depend on Cdc42 activity. Indeed, with the originally published set of model parameters (Goryachev and Pokhilko, 2008), nearly all of the Cdc24 on the membrane was within the RT-E complex. Freisinger et al. (2013) measured Cdc24 fluorescence recovery after photobleaching (FRAP) recovery time in Δbem2 cells, which exhibit heightened Cdc42 activity because they lack Cdc42 GAP Bem2, and found no difference in comparison with control cells. This observation per se does not invalidate the model because, with a different set of reaction rate parameters, the model enables symmetry breaking with <10% of Cdc24 within the RT-E complex. Such low relative abundance of the complex would make it hard to detect the dependence of Cdc24 FRAP on Cdc42 activity.
Model C. Nonlinear feedback via recruitment of RD (k = 0, l = 2, m = 1)
Could symmetry breaking occur if Cdc42-GTP did not recruit its GEF? Mathematically, this is possible, for example, if the feedback loop that recruits Cdc42-GDP to the site of polarization is nonlinear, that is, if RD ~ RT2 (Figure 3C). Li, Rubinstein, and colleagues proposed a model of this class (Smith et al., 2013). They postulated that the relationship RD ~ RT2 represents the Cdc42-GTP–dependent release of Cdc42-GDP from the complex with Rdi1; however no specific molecular mechanism providing the required quadratic dependence on RT was suggested. Of interest, their model could be potentially explained by the vesicle-based transport of Cdc42. Indeed, two subunits of budding yeast exocyst, Sec3 and Exo70, have been reported as the interactors of Cdc42-GTP and phosphoinisotide lipids (Zhang et al., 2008; Wu et al., 2010a). Bivalent binding of the single exocyst complex to two molecules of RT would provide the required quadratic dependence RD ~ RT2 (Figure 2B). Even if only one of the two exocyst subunits interacts with Cdc42-GTP directly but the binding of the other to the membrane requires negatively charged lipids and their enrichment at the polarization site is downstream of Cdc42 activity (Figure 2C), the required quadratic relationship still stands. A model of Cdc42 polarization during mating (Hegemann et al., 2015) can be also allocated to this model class. Although this model did not explicitly consider Cdc42 nucleotide cycling, it proposed that polarization is achieved by a nonlinear feedback via Cdc42 recruitment.
Model D. Converging linear feedback via GEF and GAP (k = 1, l = 0, m = 0)
Symmetry breaking can arise not only from feedback regulation of Cdc42 activators but also from that of its inactivators, GAPs. One class of models of this type requires a linear feedback loop (6) that provides recruitment of a GEF and another linear feedback loop that involves negative regulation of the localization or activity of a GAP (Figure 3D). For example, if only the membrane-bound fraction of a GAP can inactivate Cdc42-GTP and local activity of Cdc42 increases the rate of GAP dissociation from the membrane, for example, via phosphorylation of GAP by an effector kinase,
|
|
we find that the rate of Cdc42 inactivation can be expressed as
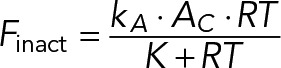 (12) (12)
|
This relationship means that at the site of polarization, where the concentration of RT is high, the rate of Cdc42 inactivation saturates and, at this location, is no longer dependent on RT (m = 0), so only a simple linear feedback via GEF recruitment would suffice to overcome RT inactivation and enable symmetry breaking. Remarkably, expression 12 has a familiar Michaelis–Menten form, which implies that the requirement for negative regulation of a GAP can be replaced by the requirement that the GAP at the site of polarization is saturated by its substrate, RT. Both mechanistic assumptions produce mathematical expressions of exactly the same form as expression 12.
To the best of our knowledge, models of this type have not yet been proposed in the literature, possibly because exclusion of Cdc42 GAPs from the site of polarization has not been seen in budding yeast. On the contrary, several of these GAPs have been reported to localize to the site of Cdc42 polarization at various stages of bud morphogenesis (Caviston et al., 2003; Knaus et al., 2007; Tong et al., 2007). However, in fission yeast, both known Rho GAPs with activity toward Cdc42-GTP, Rga4 and Rga6, localize in a pattern complementary to that of Cdc42-GTP (Das et al., 2007; Tatebe et al., 2008; Revilla-Guarinos et al., 2016). Although the exclusion of Rga4 relies, at least in part, on the activity of the fission yeast polarity landmark pathway (Kokkoris et al., 2014), it remains to be seen whether activity of Cdc42 is directly or indirectly involved in excluding the GAPs from the site of polarization.
E. Converging linear feedback via RD and GAP (k = 0, l = 1, m = 0)
This model class attributes symmetry breaking to the convergence of the two already discussed feedback loops: via recruitment of inactive form of Cdc42 and exclusion of inactivating GAP (Figure 3E). Again, the two feedback loops need not be mechanistically independent. For example, polarized insertion of secretory vesicles guided by Cdc42 activity could potentially deliver inactive Cdc42 and, at the same time, dilute the local concentration of membrane-bound GAPs. For the dilution mechanism to be effective, GAPs need to diffuse on the membrane very slowly, for example, due to association with polymeric cytoskeletal structures. The dilution effect due to Cdc42-driven polarized exocytosis is essential for the formation of the nascent septin ring (Okada et al., 2013). Okada et al. (2013) identified a pool of GAP Bem2, which was associated with septin polymer and was no longer detectable in the temperature-sensitive septin mutant cdc12-6 at a nonpermissive temperature. Failure to maintain a sufficiently high rate of exocytosis resulted in the coalescence of the nascent septin ring into a continuous cap and abrogation of Cdc42 activity at the polarity site. Of interest, Revilla-Guarinos et al. (2016) reported that reduction of Rga6 density at the tips of growing fission yeast cells depended on the presence of actin cables. Because actin cables dramatically accelerate polarized exocytosis, it is tempting to speculate that Rga6 exclusion is associated with localized insertion of membrane.
F. Nonlinear feedback via GAP exclusion (k = 0, l = 0, m = –1)
Is it possible to have cell polarization without local recruitment of both GEF and the GTPase? Although experimental evidence for this type of model is lacking, a theoretical possibility exists if we assume that exclusion of GAPs from the site of polarization depends on the square of the local concentration of Cdc42-GTP (Figure 3F). Following the same line of reasoning as in Eqs. 11 and 12, we arrive at
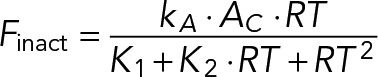 (13) (13)
|
which states that, due to the nonlinear exclusion of GAPs, the rate of Cdc42 inactivation decreases rather than increases with Cdc42-GTP concentration. This instability ensures spontaneous polarization of Cdc42 activity. As before, the nonlinearity may arise due to, for example, the existence of a molecular complex that incorporates several Cdc42 effectors and provides local exclusion or inhibition of GAPs.
HOW MODELING HELPS IN UNDERSTANDING CELLULAR POLARIZATION
Mathematical modeling has been instrumental in revealing common principles underpinning cellular polarization in various systems (Iglesias and Devreotes, 2008; Jilkine and Edelstein-Keshet, 2011; Mogilner et al., 2012). Many models describing cellular polarization rely on the reaction-diffusion mechanisms and are both dependent on and independent of the activity of small GTPases (Levchenko and Iglesias, 2002; Dawes and Munro, 2011; Griffin et al., 2011; Lin et al., 2012; Semplice et al., 2012). A rapidly growing cohort of studies also has begun to address the mechanochemical mechanisms of cell polarization (Tostevin and Howard, 2008; Goehring et al., 2011; Lomakin et al., 2015; Maiuri et al., 2015).
Studying GTPase-based polarization of motile cells, Edelstein-Keshet and colleagues focused their attention on “wave pinning,” a stimulus-induced symmetry-breaking behavior that they studied in models that can exhibit bistability of the reaction mechanism (Mori et al., 2008, 2011; Holmes and Edelstein-Keshet, 2016). This type of bistability can occur in spatially homogeneous systems and should be distinguished from the type of bistability shown in Figure 1E, where the two states of the system, polarized and unpolarized, can be exhibited only by spatially extended systems with diffusion. Nevertheless, there is no qualitative divide between these models and the models exhibiting spontaneous symmetry breaking (Trong et al., 2014; Holmes and Edelstein-Keshet, 2016; Nirody and Rangamani, 2016). In fact, all wave-pinning models published so far, under variation of parameters, can also exhibit absolute loss of stability, or Turing instability. Conversely, all models that originally focused on Turing-type behavior can also exhibit wave pinning. In general, if a model can support symmetry breaking (Figure 1E), stimulus-induced and spontaneous symmetry breaking are found within adjacent domains of parameters, so that the wave-pinning structure transforms smoothly into the Turing structure as the parameters vary. Similarly, bistability of the reaction mechanism is neither necessary nor sufficient for polarization. Instead, reaction bistability and formation of a spatial structure are two types of symmetry-breaking behavior that commonly arise in nonlinear systems with positive feedback. Therefore they often co-occur in the same polarity models within overlapping but not coinciding parameter domains.
What have we learned from the mechanistic models of Cdc42 polarization? Here we demonstrated that layout of the biochemical network that controls the dynamics of Cdc42 readily supports symmetry-breaking behavior, such as bistability and polarization. This behavior occurs when the regulators of GTPase activity are wired into converging positive feedback loops. Native or synthetic GTPase effectors can provide this wiring by connecting active form of the GTPase to its regulators. A minimum network layout that permits symmetry breaking consists of either two converging linear feedback loops or a single nonlinear feedback (Figure 3). All combinations of such feedback loops based on the recruitment of the GTPase itself and its GEF and exclusion of GAPs generate six distinct model classes. Within each class, multiple model flavors can be proposed on the basis of specific assumptions on the molecular mechanisms that implement the feedback loops.
It is not uncommon that theory offers more possibilities than are actually implemented in the real world. Which of the considered model classes are better supported by the existing experimental evidence? A positive feedback loop based on the recruitment of a GEF is possibly the best-studied element of the symmetry-breaking mechanism (Gulli et al., 2000; Bose et al., 2001; Butty et al., 2002; Irazoqui et al., 2003; Kozubowski et al., 2008). Scaffold-effector Bem1 (Scd2 in fission yeast) was found to be a critical element of this feedback as the molecular link between the GEF and the GTPase. Deletion of BEM1 causes a pronounced phenotype but is not lethal as far as cells express Ras-like GTPase Rsr1/Bud1 (Irazoqui et al., 2003). Despite an impressive body of evidence that supports Bem1-mediated feedback, its existence was challenged, chiefly on the basis of claim that, contrary to the previous data, double-knockout Δrsr1Δbem1 is viable (Smith et al., 2013). The following study that used the same strain, however, did not confirm this claim (Woods et al., 2015). Another strong argument in support of the crucial role of Bem1 in symmetry breaking was provided in a recent study that used an optogenetic technique to rapidly and reversibly recruit Bem1 to mitochondria (Jost and Weiner, 2015). This study demonstrated that 80% of cells that were unpolarized before Bem1 sequestration completely failed to polarize in the presence of light, even with intact RSR1. Regardless of the specific molecular roles of Bem1 and Scd2, recruitment of GEFs Cdc24 and Scd1 into the respective polarity clusters is firmly established. Taken together, these facts strongly argue in favor of models A, B, and D, which rely on feedback via GEF recruitment (Figure 3).
Is the Bem1 (Scd2)-dependent pathway the only mechanism that provides recruitment of GEF Cdc24 (Scd1)? Fission yeast cells deleted for scd2 no longer localize Scd1 to the tips but continue to exhibit tip-localized Cdc42-GTP clusters, albeit with reduced activity (Kelly and Nurse, 2011). In budding yeast, it has been long known that BEM1 genetically interacts with RSR1 (Chant and Herskowitz, 1991). Furthermore, the Δrsr1Δbem1 mutant is synthetic lethal (Irazoqui et al., 2003). If Rsr1 was merely transmitting the spatial information encoded by the nonessential budding landmarks, genetic interaction of BEM1 and RSR1 would be difficult to interpret (Wu et al., 2013). Of interest, two studies found that Bud5, an Rsr1 GEF, rapidly relocates during Cdc42 polarization from the landmark-determined ring that surrounds the bud scar into the Cdc42-GTP cluster itself (Kang et al., 2001; Marston et al., 2001). This result suggests a molecular mechanism that recruits Bud5 to Cdc42-GTP. Together with the well-characterized interaction between Cdc24 and Rsr1-GTP (Park et al., 1997; Shimada et al., 2004), this hypothetical mechanism would form a positive feedback loop in which Cdc42 and Rsr1 mutually activate each other by recruiting their respective GEFs. If proven correct, this attractive hypothesis would mean the existence of two parallel feedback loops that recruit Cdc24 to Cdc42-GTP.
Is the GEF-mediated positive feedback loop sufficient to enable symmetry breaking? Indeed, model B suggests this by pointing out that the biochemical mechanism of this feedback is nonlinear. Although model B is consistent with the experimental data, it may not be all-inclusive. Because multiple mechanisms have been proposed to increase membrane deposition of Cdc42 downstream of Cdc42 activity via both diffusive and vesicle-mediated transport, it is highly likely that model A is also involved in yeast cellular polarization. In fact, the two model classes need not be mutually exclusive but instead could operate in parallel. Indeed, models A and B share the same feedback loop via recruitment of a GEF. In addition, model A incorporates parallel feedback loops based on Cdc42 transport, which may increase the robustness of polarization. Model D, introduced here, also deserves attention. Although it may not be relevant to Cdc42 polarization in budding yeast, it may operate, for example, in fission yeast, either on its own or in parallel with model A. The latter, judging by its robust generic layout, could be a recipe for Cdc42 polarization across multiple species, beyond yeasts. A recent report of tight spatiotemporal correlation between Cdc42 activation and its release from the complex with a GDI in motile mammalian cells suggests a possibility of feedback loops based on GTPase diffusive transport also in higher eukaryotes (Hodgson et al., 2016).
CONCLUSION
Summing up the discussion, we conclude that the existing experimental data do not unequivocally select a single model class. Instead, in its present state, our knowledge suggests the possibility that several parallel and mutually nonexclusive polarization mechanisms are encoded by the genomes of eukaryotes, even as “simple” as yeasts. These mechanisms are likely not deployed equally within and between different species, with one of them gaining dominance while others are “down-regulated” in the course of evolution. Genetic deletions can result in compensatory changes in the expression of other pathway components (Cerikan et al., 2016). This could explain, for example, why acute optogenetic sequestration of Bem1 produces a much stronger phenotype than its genetic deletion (Jost and Weiner, 2015). Compared to traditional knockouts, synthetic proteins bring both a higher level of system control and as-yet-underappreciated potential increase in the system’s complexity. By disrupting one polarization mechanism, a synthetic molecule could potentially enable a bypass mechanism that was either disabled or nonexistent in the native organism. These potential synthetic effects should be carefully considered when planning and interpreting the results of cell-rewiring experiments.
ACKNOWLEDGMENTS
We thank Roger Goody, Kent Rossman, Erfei Bi, Ken Sawin, and Ann Miller for stimulating discussions and helpful feedback on the manuscript. This work was supported by the Biotechnology and Biological Sciences Research Council of the United Kingdom (BB/K021699/1).
Abbreviations used:
- FRAP
fluorescence recovery after photobleaching
- GAP
GTPase-activating protein
- GDP
guanosine diphosphate
- GEF
guanine-nucleotide exchange factor
- GTP
guanosine triphosphate
- MAPK
mitogen-activated protein kinase.
Footnotes
REFERENCES
- Adamo JE, Moskow JJ, Gladfelter AS, Viterbo D, Lew DJ, Brennwald PJ. Yeast Cdc42 functions at a late step in exocytosis, specifically during polarized growth of the emerging bud. J Cell Biol. 2001;155:581–592. doi: 10.1083/jcb.200106065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams AE, Johnson DI, Longnecker RM, Sloat BF, Pringle JR. CDC42 and CDC43, two additional genes involved in budding and the establishment of cell polarity in the yeast Saccharomyces cerevisiae. J Cell Biol. 1990;111:131–142. doi: 10.1083/jcb.111.1.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschuler SJ, Angenent SB, Wang Y, Wu LF. On the spontaneous emergence of cell polarity. Nature. 2008;454:886–889. doi: 10.1038/nature07119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkins BD, Yoshida S, Pellman D. Symmetry breaking: scaffold plays matchmaker for polarity signaling proteins. Curr Biol. 2008;18:R1130–R1132. doi: 10.1016/j.cub.2008.11.005. [DOI] [PubMed] [Google Scholar]
- Ayscough KR, Stryker J, Pokala N, Sanders M, Crews P, Drubin DG. High rates of actin filament turnover in budding yeast and roles for actin in establishment and maintenance of cell polarity revealed using the actin inhibitor latrunculin-A. J Cell Biol. 1997;137:399–416. doi: 10.1083/jcb.137.2.399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker M, Glashow SL. Spontaneous breakdown of elementary particle symmetries. Phys Rev. 1962;128:2462–2471. [Google Scholar]
- Bender A, Pringle JR. Multicopy suppression of the cdc24 budding defect in yeast by CDC42 and three newly identified genes including the ras-related gene RSR1. Proc Natl Acad Sci USA. 1989;86:9976–9980. doi: 10.1073/pnas.86.24.9976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendezu FO, Martin SG. Actin cables and the exocyst form two independent morphogenesis pathways in the fission yeast. Mol Biol Cell. 2011;22:44–53. doi: 10.1091/mbc.E10-08-0720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendezu FO, Vincenzetti V, Vavylonis D, Wyss R, Vogel H, Martin SG. Spontaneous Cdc42 polarization independent of GDI-mediated extraction and actin-based trafficking. PLoS Biol. 2015;13:e1002097. doi: 10.1371/journal.pbio.1002097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi E, Park HO. Cell polarization and cytokinesis in budding yeast. Genetics. 2012;191:347–387. doi: 10.1534/genetics.111.132886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijker R. Phase transitions and spontaneously broken symmetries. In: Moran-Lopez JL, editor. Fundamentals of Physics. Vol. 3. Oxford, UK: Eolss Publishers; 2009. pp. 51–60. [Google Scholar]
- Bonazzi D, Julien JD, Romao M, Seddiki R, Piel M, Boudaoud A, Minc N. Symmetry breaking in spore germination relies on an interplay between polar cap stability and spore wall mechanics. Dev Cell. 2014;28:534–546. doi: 10.1016/j.devcel.2014.01.023. [DOI] [PubMed] [Google Scholar]
- Bose I, Irazoqui JE, Moskow JJ, Bardes ES, Zyla TR, Lew DJ. Assembly of scaffold-mediated complexes containing Cdc42p, the exchange factor Cdc24p, and the effector Cla4p required for cell cycle-regulated phosphorylation of Cdc24p. J Biol Chem. 2001;276:7176–7186. doi: 10.1074/jbc.M010546200. [DOI] [PubMed] [Google Scholar]
- Bourne HR, Weiner O. A chemical compass. Nature. 2002;419:21. doi: 10.1038/419021a. [DOI] [PubMed] [Google Scholar]
- Bruurs LJ, Donker L, Zwakenberg S, Zwartkruis FJ, Begthel H, Knisely AS, Posthuma G, van de Graaf SF, Paulusma CC, Bos JL. ATP8B1-mediated spatial organization of Cdc42 signaling maintains singularity during enterocyte polarization. J Cell Biol. 2015;210:1055–1063. doi: 10.1083/jcb.201505118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burbelo PD, Drechsel D, Hall A. A conserved binding motif defines numerous candidate target proteins for both Cdc42 and Rac GTPases. J Biol Chem. 1995;270:29071–29074. doi: 10.1074/jbc.270.49.29071. [DOI] [PubMed] [Google Scholar]
- Butty AC, Perrinjaquet N, Petit A, Jaquenoud M, Segall JE, Hofmann K, Zwahlen C, Peter M. A positive feedback loop stabilizes the guanine-nucleotide exchange factor Cdc24 at sites of polarization. EMBO J. 2002;21:1565–1576. doi: 10.1093/emboj/21.7.1565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butty AC, Pryciak PM, Huang LS, Herskowitz I, Peter M. The role of Far1p in linking the heterotrimeric G protein to polarity establishment proteins during yeast mating. Science. 1998;282:1511–1516. doi: 10.1126/science.282.5393.1511. [DOI] [PubMed] [Google Scholar]
- Caviston JP, Longtine M, Pringle JR, Bi E. The role of Cdc42p GTPase-activating proteins in assembly of the septin ring in yeast. Mol Biol Cell. 2003;14:4051–4066. doi: 10.1091/mbc.E03-04-0247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerikan B, Shaheen R, Colo GP, Glasser C, Hata S, Knobeloch KP, Alkuraya FS, Fassler R, Schiebel E. Cell-Intrinsic adaptation arising from chronic ablation of a key Rho GTPase regulator. Dev Cell. 2016;39:28–43. doi: 10.1016/j.devcel.2016.08.020. [DOI] [PubMed] [Google Scholar]
- Chang EC, Barr M, Wang Y, Jung V, Xu HP, Wigler MH. Cooperative interaction of S. pombe proteins required for mating and morphogenesis. Cell. 1994;79:131–141. doi: 10.1016/0092-8674(94)90406-5. [DOI] [PubMed] [Google Scholar]
- Chang F, Minc N. Electrochemical control of cell and tissue polarity. Annu Rev Cell Dev Biol. 2014;30:317–336. doi: 10.1146/annurev-cellbio-100913-013357. [DOI] [PubMed] [Google Scholar]
- Chant J, Herskowitz I. Genetic control of bud site selection in yeast by a set of gene products that constitute a morphogenetic pathway. Cell. 1991;65:1203–1212. doi: 10.1016/0092-8674(91)90015-q. [DOI] [PubMed] [Google Scholar]
- Chen H, Kuo CC, Kang H, Howell AS, Zyla TR, Jin M, Lew DJ. Cdc42p regulation of the yeast formin Bni1p mediated by the effector Gic2p. Mol Biol Cell. 2012;23:3814–3826. doi: 10.1091/mbc.E12-05-0400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A, Slaughter BD, Unruh JR, Bradford WD, Alexander R, Rubinstein B, Li R. Flippase-mediated phospholipid asymmetry promotes fast Cdc42 recycling in dynamic maintenance of cell polarity. Nat Cell Biol. 2012;14:304–310. doi: 10.1038/ncb2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das M, Wiley DJ, Medina S, Vincent HA, Larrea M, Oriolo A, Verde F. Regulation of cell diameter, For3p localization, and cell symmetry by fission yeast Rho-GAP Rga4p. Mol Biol Cell. 2007;18:2090–2101. doi: 10.1091/mbc.E06-09-0883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawes AT, Munro EM. PAR-3 oligomerization may provide an actin-independent mechanism to maintain distinct par protein domains in the early Caenorhabditis elegans embryo. Biophys J. 2011;101:1412–1422. doi: 10.1016/j.bpj.2011.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drees BL, Sundin B, Brazeau E, Caviston JP, Chen GC, Guo W, Kozminski KG, Lau MW, Moskow JJ, Tong A, et al. A protein interaction map for cell polarity development. J Cell Biol. 2001;154:549–571. doi: 10.1083/jcb.200104057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drubin DG. Development of cell polarity in budding yeast. Cell. 1991;65:1093–1096. doi: 10.1016/0092-8674(91)90001-f. [DOI] [PubMed] [Google Scholar]
- Drubin DG, Nelson WJ. Origins of cell polarity. Cell. 1996;84:335–344. doi: 10.1016/s0092-8674(00)81278-7. [DOI] [PubMed] [Google Scholar]
- Dyer JM, Savage NS, Jin M, Zyla TR, Elston TC, Lew DJ. Tracking shallow chemical gradients by actin-driven wandering of the polarization site. Curr Biol. 2013;23:32–41. doi: 10.1016/j.cub.2012.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endo M, Shirouzu M, Yokoyama S. The Cdc42 binding and scaffolding activities of the fission yeast adaptor protein Scd2. J Biol Chem. 2003;278:843–852. doi: 10.1074/jbc.M209714200. [DOI] [PubMed] [Google Scholar]
- Ferrell JE Jr. Feedback loops and reciprocal regulation: recurring motifs in the systems biology of the cell cycle. Curr Opin Cell Biol. 2013;25:676–686. doi: 10.1016/j.ceb.2013.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freisinger T, Klunder B, Johnson J, Muller N, Pichler G, Beck G, Costanzo M, Boone C, Cerione RA, Frey E, Wedlich-Soldner R. Establishment of a robust single axis of cell polarity by coupling multiple positive feedback loops. Nat Commun. 2013;4:1807. doi: 10.1038/ncomms2795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrenton LS, Stefan CJ, McMurray MA, Emr SD, Thorner J. Pheromone-induced anisotropy in yeast plasma membrane phosphatidylinositol-4,5-bisphosphate distribution is required for MAPK signaling. Proc Natl Acad Sci USA. 2010;107:11805–11810. doi: 10.1073/pnas.1005817107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghugtyal V, Garcia-Rodas R, Seminara A, Schaub S, Bassilana M, Arkowitz RA. Phosphatidylinositol-4-phosphate-dependent membrane traffic is critical for fungal filamentous growth. Proc Natl Acad Sci USA. 2015;112:8644–8649. doi: 10.1073/pnas.1504259112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goehring NW, Trong PK, Bois JS, Chowdhury D, Nicola EM, Hyman AA, Grill SW. Polarization of PAR proteins by advective triggering of a pattern-forming system. Science. 2011;334:1137–1141. doi: 10.1126/science.1208619. [DOI] [PubMed] [Google Scholar]
- Goryachev AB, Pokhilko AV. Computational model explains high activity and rapid cycling of Rho GTPases within protein complexes. PLoS Comput Biol. 2006;2:e172. doi: 10.1371/journal.pcbi.0020172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goryachev AB, Pokhilko AV. Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett. 2008;582:1437–1443. doi: 10.1016/j.febslet.2008.03.029. [DOI] [PubMed] [Google Scholar]
- Gowrishankar K, Ghosh S, Saha S, C R, Mayor S, Rao M. Active remodeling of cortical actin regulates spatiotemporal organization of cell surface molecules. Cell. 2012;149:1353–1367. doi: 10.1016/j.cell.2012.05.008. [DOI] [PubMed] [Google Scholar]
- Griffin EE, Odde DJ, Seydoux G. Regulation of the MEX-5 gradient by a spatially segregated kinase/phosphatase cycle. Cell. 2011;146:955–968. doi: 10.1016/j.cell.2011.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulli MP, Jaquenoud M, Shimada Y, Niederhauser G, Wiget P, Peter M. Phosphorylation of the Cdc42 exchange factor Cdc24 by the PAK-like kinase Cla4 may regulate polarized growth in yeast. Mol Cell. 2000;6:1155–1167. doi: 10.1016/s1097-2765(00)00113-1. [DOI] [PubMed] [Google Scholar]
- Harrison JC, Zyla TR, Bardes ES, Lew DJ. Stress-specific activation mechanisms for the “cell integrity” MAPK pathway. J Biol Chem. 2004;279:2616–2622. doi: 10.1074/jbc.M306110200. [DOI] [PubMed] [Google Scholar]
- Hegemann B, Unger M, Lee SS, Stoffel-Studer I, van den Heuvel J, Pelet S, Koeppl H, Peter M. A cellular system for spatial signal decoding in chemical gradients. Dev Cell. 2015;35:458–470. doi: 10.1016/j.devcel.2015.10.013. [DOI] [PubMed] [Google Scholar]
- Hodgson L, Spiering D, Sabouri-Ghomi M, Dagliyan O, DerMardirossian C, Danuser G, Hahn KM. FRET binding antenna reports spatiotemporal dynamics of GDI-Cdc42 GTPase interactions. Nat Chem Biol. 2016;12:802–809. doi: 10.1038/nchembio.2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman GR, Nassar N, Cerione RA. Structure of the Rho family GTP-binding protein Cdc42 in complex with the multifunctional regulator RhoGDI. Cell. 2000;100:345–356. doi: 10.1016/s0092-8674(00)80670-4. [DOI] [PubMed] [Google Scholar]
- Holmes WR, Edelstein-Keshet L. Analysis of a minimal Rho-GTPase circuit regulating cell shape. Phys Biol. 2016;13:046001. doi: 10.1088/1478-3975/13/4/046001. [DOI] [PubMed] [Google Scholar]
- Homble F, Leonetti M. Emergence of symmetry breaking in fucoid zygotes. Trends Plant Sci. 2007;12:253–259. doi: 10.1016/j.tplants.2007.04.007. [DOI] [PubMed] [Google Scholar]
- Howard J, Grill SW, Bois JS. Turing’s next steps: the mechanochemical basis of morphogenesis. Nat Rev Mol Cell Biol. 2011;12:392–398. doi: 10.1038/nrm3120. [DOI] [PubMed] [Google Scholar]
- Howell AS, Jin M, Wu CF, Zyla TR, Elston TC, Lew DJ. Negative feedback enhances robustness in the yeast polarity establishment circuit. Cell. 2012;149:322–333. doi: 10.1016/j.cell.2012.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell AS, Savage NS, Johnson SA, Bose I, Wagner AW, Zyla TR, Nijhout HF, Reed MC, Goryachev AB, Lew DJ. Singularity in polarization: rewiring yeast cells to make two buds. Cell. 2009;139:731–743. doi: 10.1016/j.cell.2009.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iglesias PA, Devreotes PN. Navigating through models of chemotaxis. Curr Opin Cell Biol. 2008;20:35–40. doi: 10.1016/j.ceb.2007.11.011. [DOI] [PubMed] [Google Scholar]
- Irazoqui JE, Gladfelter AS, Lew DJ. Scaffold-mediated symmetry breaking by Cdc42p. Nat Cell Biol. 2003;5:1062–1070. doi: 10.1038/ncb1068. [DOI] [PubMed] [Google Scholar]
- Jilkine A, Edelstein-Keshet L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput Biol. 2011;7:e1001121. doi: 10.1371/journal.pcbi.1001121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DI, Pringle JR. Molecular characterization of CDC42, a Saccharomyces cerevisiae gene involved in the development of cell polarity. J Cell Biol. 1990;111:143–152. doi: 10.1083/jcb.111.1.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JL, Erickson JW, Cerione RA. New insights into how the Rho guanine nucleotide dissociation inhibitor regulates the interaction of Cdc42 with membranes. J Biol Chem. 2009;284:23860–23871. doi: 10.1074/jbc.M109.031815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jose M, Tollis S, Nair D, Sibarita JB, McCusker D. Robust polarity establishment occurs via an endocytosis-based cortical corralling mechanism. J Cell Biol. 2013;200:407–418. doi: 10.1083/jcb.201206081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jost AP, Weiner OD. Probing yeast polarity with acute, reversible, optogenetic inhibition of protein function. ACS Synth Biol. 2015;4:1077–1085. doi: 10.1021/acssynbio.5b00053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang PJ, Sanson A, Lee B, Park HO. A GDP/GTP exchange factor involved in linking a spatial landmark to cell polarity. Science. 2001;292:1376–1378. doi: 10.1126/science.1060360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly FD, Nurse P. Spatial control of Cdc42 activation determines cell width in fission yeast. Mol Biol Cell. 2011;22:3801–3811. doi: 10.1091/mbc.E11-01-0057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan AR, Menetrey J. Structural biology of Arf and Rab GTPases’ effector recruitment and specificity. Structure. 2013;21:1284–1297. doi: 10.1016/j.str.2013.06.016. [DOI] [PubMed] [Google Scholar]
- Kirschner M, Gerhart J, Mitchison T. Molecular “vitalism.”. Cell. 2000;100:79–88. doi: 10.1016/s0092-8674(00)81685-2. [DOI] [PubMed] [Google Scholar]
- Klunder B, Freisinger T, Wedlich-Soldner R, Frey E. GDI-mediated cell polarization in yeast provides precise spatial and temporal control of Cdc42 signaling. PLoS Comput Biol. 2013;9:e1003396. doi: 10.1371/journal.pcbi.1003396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knaus M, Pelli-Gulli MP, van Drogen F, Springer S, Jaquenoud M, Peter M. Phosphorylation of Bem2p and Bem3p may contribute to local activation of Cdc42p at bud emergence. EMBO J. 2007;26:4501–4513. doi: 10.1038/sj.emboj.7601873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kokkoris K, Gallo Castro D, Martin SG. The Tea4-PP1 landmark promotes local growth by dual Cdc42 GEF recruitment and GAP exclusion. J Cell Sci. 2014;127:2005–2016. doi: 10.1242/jcs.142174. [DOI] [PubMed] [Google Scholar]
- Kozubowski L, Saito K, Johnson JM, Howell AS, Zyla TR, Lew DJ. Symmetry-breaking polarization driven by a Cdc42p GEF-PAK complex. Curr Biol. 2008;18:1719–1726. doi: 10.1016/j.cub.2008.09.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton AT, Savage NS, Howell AS, Carroll SY, Drubin DG, Lew DJ. Modeling vesicle traffic reveals unexpected consequences for Cdc42p-mediated polarity establishment. Curr Biol. 2011;21:184–194. doi: 10.1016/j.cub.2011.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee ME, Lo WC, Miller KE, Chou CS, Park HO. Regulation of Cdc42 polarization by the Rsr1 GTPase and Rga1, a Cdc42 GTPase-activating protein, in budding yeast. J Cell Sci. 2015;128:2106–2117. doi: 10.1242/jcs.166538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levchenko A, Iglesias PA. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys J. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Bowerman B. Symmetry breaking in biology. Cold Spring Harb Perspect Biol. 2010;2:a003475. doi: 10.1101/cshperspect.a003475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichius A, Goryachev AB, Fricker MD, Obara B, Castro-Longoria E, Read ND. CDC-42 and RAC-1 regulate opposite chemotropisms in Neurospora crassa. J Cell Sci. 2014;127:1953–1965. doi: 10.1242/jcs.141630. [DOI] [PubMed] [Google Scholar]
- Lin B, Holmes WR, Wang CJ, Ueno T, Harwell A, Edelstein-Keshet L, Inoue T, Levchenko A. Synthetic spatially graded Rac activation drives cell polarization and movement. Proc Natl Acad Sci USA. 2012;109:E3668–E3677. doi: 10.1073/pnas.1210295109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y-Y, Barabasi A-L. Control principles of complex systems. Rev Mod Phys. 2016;88:035006. [Google Scholar]
- Lo WC, Lee ME, Narayan M, Chou CS, Park HO. Polarization of diploid daughter cells directed by spatial cues and GTP hydrolysis of Cdc42 budding yeast. PLoS One. 2013;8:e56665. doi: 10.1371/journal.pone.0056665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo WC, Park HO, Chou CS. Mathematical analysis of spontaneous emergence of cell polarity. Bull Math Biol. 2014;76:1835–1865. doi: 10.1007/s11538-014-9982-2. [DOI] [PubMed] [Google Scholar]
- Lomakin AJ, Lee KC, Han SJ, Bui DA, Davidson M, Mogilner A, Danuser G. Competition for actin between two distinct F-actin networks defines a bistable switch for cell polarization. Nat Cell Biol. 2015;17:1435–1445. doi: 10.1038/ncb3246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maiuri P, Rupprecht JF, Wieser S, Ruprecht V, Benichou O, Carpi N, Coppey M, De Beco S, Gov N, Heisenberg CP, et al. Actin flows mediate a universal coupling between cell speed and cell persistence. Cell. 2015;161:374–386. doi: 10.1016/j.cell.2015.01.056. [DOI] [PubMed] [Google Scholar]
- Marco E, Wedlich-Soldner R, Li R, Altschuler SJ, Wu LF. Endocytosis optimizes the dynamic localization of membrane proteins that regulate cortical polarity. Cell. 2007;129:411–422. doi: 10.1016/j.cell.2007.02.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marston AL, Chen T, Yang MC, Belhumeur P, Chant J. A localized GTPase exchange factor, Bud5, determines the orientation of division axes in yeast. Curr Biol. 2001;11:803–807. doi: 10.1016/s0960-9822(01)00230-5. [DOI] [PubMed] [Google Scholar]
- Martin SG. Spontaneous cell polarization: Feedback control of Cdc42 GTPase breaks cellular symmetry. Bioessays. 2015;37:1193–1201. doi: 10.1002/bies.201500077. [DOI] [PubMed] [Google Scholar]
- Martin SG, Rincon SA, Basu R, Perez P, Chang F. Regulation of the formin for3p by cdc42p and bud6p. Mol Biol Cell. 2007;18:4155–4167. doi: 10.1091/mbc.E07-02-0094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin-Belmonte F, Mostov K. Regulation of cell polarity during epithelial morphogenesis. Curr Opin Cell Biol. 2008;20:227–234. doi: 10.1016/j.ceb.2008.01.001. [DOI] [PubMed] [Google Scholar]
- McCaffrey LM, Macara IG. Signaling pathways in cell polarity. Cold Spring Harb Perspect Biol. 2012;4:a009654. doi: 10.1101/cshperspect.a009654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure AW, Minakova M, Dyer JM, Zyla TR, Elston TC, Lew DJ. Role of polarized G protein signaling in tracking pheromone gradients. Dev Cell. 2015;35:471–482. doi: 10.1016/j.devcel.2015.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillan JN, Sia RA, Lew DJ. A morphogenesis checkpoint monitors the actin cytoskeleton in yeast. J Cell Biol. 1998;142:1487–1499. doi: 10.1083/jcb.142.6.1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Allard J, Wollman R. Cell polarity: quantitative modeling as a tool in cell biology. Science. 2012;336:175–179. doi: 10.1126/science.1216380. [DOI] [PubMed] [Google Scholar]
- Mori Y, Jilkine A, Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys J. 2008;94:3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori Y, Jilkine A, Edelstein-Keshet L. Asymptotic and bifurcation analysis of wave-pinning in a reaction-diffusion model for cell polarization. SIAM J Appl Math. 2011;71:1401–1427. doi: 10.1137/10079118X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutavchiev DR, Leda M, Sawin KE. Remodeling of the fission yeast Cdc42 cell-polarity module via the Sty1 p38 stress-activated protein kinase pathway. Curr Biol. 2016;26:2921–2928. doi: 10.1016/j.cub.2016.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nalbant P, Hodgson L, Kraynov V, Toutchkine A, Hahn KM. Activation of endogenous Cdc42 visualized in living cells. Science. 2004;305:1615–1619. doi: 10.1126/science.1100367. [DOI] [PubMed] [Google Scholar]
- Nirody JA, Rangamani P. An introduction to linear stability analysis for deciphering spatial patterns in signaling networks. arXiv. 2016 1501.06640v2 [q-bio.SC] [Google Scholar]
- Novak B, Tyson JJ. Design principles of biochemical oscillators. Nat Rev Mol Cell Biol. 2008;9:981–991. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada S, Leda M, Hanna J, Savage NS, Bi E, Goryachev AB. Daughter cell identity emerges from the interplay of Cdc42, septins, and exocytosis. Dev Cell. 2013;26:148–161. doi: 10.1016/j.devcel.2013.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozbudak EM, Becskei A, van Oudenaarden A. A system of counteracting feedback loops regulates Cdc42p activity during spontaneous cell polarization. Dev Cell. 2005;9:565–571. doi: 10.1016/j.devcel.2005.08.014. [DOI] [PubMed] [Google Scholar]
- Park HO, Bi E. Central roles of small GTPases in the development of cell polarity in yeast and beyond. Microbiol Mol Biol Rev. 2007;71:48–96. doi: 10.1128/MMBR.00028-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park HO, Bi E, Pringle JR, Herskowitz I. Two active states of the Ras-related Bud1/Rsr1 protein bind to different effectors to determine yeast cell polarity. Proc Natl Acad Sci USA. 1997;94:4463–4468. doi: 10.1073/pnas.94.9.4463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prigogine I, Lefever R, Goldbeter A, Herschkowitz-Kaufman M. Symmetry breaking instabilities in biological systems. Nature. 1969;223:913–916. doi: 10.1038/223913a0. [DOI] [PubMed] [Google Scholar]
- Prigogine I, Nicolis G. On symmetry-breaking instabilities in dissipative systems. J Chem Phys. 1967;46:3542–3550. [Google Scholar]
- Pruyne D, Bretscher A. Polarization of cell growth in yeast. I. Establishment and maintenance of polarity states. J Cell Sci. 2000;113:365–375. doi: 10.1242/jcs.113.3.365. [DOI] [PubMed] [Google Scholar]
- Rai A, Oprisko A, Campos J, Fu Y, Friese T, Itzen A, Goody RS, Gazdag EM, Muller MP. bMERB domains are bivalent Rab8 family effectors evolved by gene duplication. Elife. 2016;5:e18675. doi: 10.7554/eLife.18675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revilla-Guarinos MT, Martin-Garcia R, Villar-Tajadura MA, Estravis M, Coll PM, Perez P. Rga6 is a fission yeast Rho GAP involved in Cdc42 regulation of polarized growth. Mol Biol Cell. 2016;27:1524–1535. doi: 10.1091/mbc.E15-12-0818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridley AJ. Rho GTPase signalling in cell migration. Curr Opin Cell Biol. 2015;36:103–112. doi: 10.1016/j.ceb.2015.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robbe K, Otto-Bruc A, Chardin P, Antonny B. Dissociation of GDP dissociation inhibitor and membrane translocation are required for efficient activation of Rac by the Dbl homology-pleckstrin homology region of Tiam. J Biol Chem. 2003;278:4756–4762. doi: 10.1074/jbc.M210412200. [DOI] [PubMed] [Google Scholar]
- Rossman KL, Der CJ, Sondek J. GEF means go: turning on RHO GTPases with guanine nucleotide-exchange factors. Nat Rev Mol Cell Biol. 2005;6:167–180. doi: 10.1038/nrm1587. [DOI] [PubMed] [Google Scholar]
- Savage NS, Layton AT, Lew DJ. Mechanistic mathematical model of polarity in yeast. Mol Biol Cell. 2012;23:1998–2013. doi: 10.1091/mbc.E11-10-0837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoebel S, Oesterlin LK, Blankenfeldt W, Goody RS, Itzen A. RabGDI displacement by DrrA from Legionella is a consequence of its guanine nucleotide exchange activity. Mol Cell. 2009;36:1060–1072. doi: 10.1016/j.molcel.2009.11.014. [DOI] [PubMed] [Google Scholar]
- Semplice M, Veglio A, Naldi G, Serini G, Gamba A. A bistable model of cell polarity. PLoS One. 2012;7:e30977. doi: 10.1371/journal.pone.0030977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimada Y, Wiget P, Gulli MP, Bi E, Peter M. The nucleotide exchange factor Cdc24p may be regulated by auto-inhibition. EMBO J. 2004;23:1051–1062. doi: 10.1038/sj.emboj.7600124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slaughter BD, Das A, Schwartz JW, Rubinstein B, Li R. Dual modes of cdc42 recycling fine-tune polarized morphogenesis. Dev Cell. 2009;17:823–835. doi: 10.1016/j.devcel.2009.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slaughter BD, Unruh JR, Das A, Smith SE, Rubinstein B, Li R. Non-uniform membrane diffusion enables steady-state cell polarization via vesicular trafficking. Nat Commun. 2013;4:1380. doi: 10.1038/ncomms2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SE, Rubinstein B, Mendes Pinto I, Slaughter BD, Unruh JR, Li R. Independence of symmetry breaking on Bem1-mediated autocatalytic activation of Cdc42. J Cell Biol. 2013;202:1091–1106. doi: 10.1083/jcb.201304180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takaku T, Ogura K, Kumeta H, Yoshida N, Inagaki F. Solution structure of a novel Cdc42 binding module of Bem1 and its interaction with Ste20 and Cdc42. J Biol Chem. 2010;285:19346–19353. doi: 10.1074/jbc.M110.116749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatebe H, Nakano K, Maximo R, Shiozaki K. Pom1 DYRK regulates localization of the Rga4 GAP to ensure bipolar activation of Cdc42 in fission yeast. Curr Biol. 2008;18:322–330. doi: 10.1016/j.cub.2008.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiedje C, Sakwa I, Just U, Hofken T. The Rho GDI Rdi1 regulates Rho GTPases by distinct mechanisms. Mol Biol Cell. 2008;19:2885–2896. doi: 10.1091/mbc.E07-11-1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjhung E, Marenduzzo D, Cates ME. Spontaneous symmetry breaking in active droplets provides a generic route to motility. Proc Natl Acad Sci USA. 2012;109:12381–12386. doi: 10.1073/pnas.1200843109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Z, Gao XD, Howell AS, Bose I, Lew DJ, Bi E. Adjacent positioning of cellular structures enabled by a Cdc42 GTPase-activating protein-mediated zone of inhibition. J Cell Biol. 2007;179:1375–1384. doi: 10.1083/jcb.200705160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tostevin F, Howard M. Modeling the establishment of PAR protein polarity in the one-cell C. elegans embryo. Biophys J. 2008;95:4512–4522. doi: 10.1529/biophysj.108.136416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trong PK, Nicola EM, Goehring NW, Kumar KV, Grill SW. Parameter-space topology of models for cell polarity. New J Phys. 2014;16:065009. [Google Scholar]
- Turing AM. The chemical basis of morphogenesis. Phil Trans R Soc B Biol Sci. 1952;237:37–72. [Google Scholar]
- Ugolev Y, Berdichevsky Y, Weinbaum C, Pick E. Dissociation of Rac1(GDP).RhoGDI complexes by the cooperative action of anionic liposomes containing phosphatidylinositol 3,4,5-trisphosphate, Rac guanine nucleotide exchange factor, and GTP. J Biol Chem. 2008;283:22257–22271. doi: 10.1074/jbc.M800734200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ugolev Y, Molshanski-Mor S, Weinbaum C, Pick E. Liposomes comprising anionic but not neutral phospholipids cause dissociation of Rac(1 or 2) x RhoGDI complexes and support amphiphile-independent NADPH oxidase activation by such complexes. J Biol Chem. 2006;281:19204–19219. doi: 10.1074/jbc.M600042200. [DOI] [PubMed] [Google Scholar]
- Watson LJ, Rossi G, Brennwald P. Quantitative analysis of membrane trafficking in regulation of Cdc42 polarity. Traffic. 2014;15:1330–1343. doi: 10.1111/tra.12211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedlich-Soldner R, Altschuler S, Wu L, Li R. Spontaneous cell polarization through actomyosin-based delivery of the Cdc42 GTPase. Science. 2003;299:1231–1235. doi: 10.1126/science.1080944. [DOI] [PubMed] [Google Scholar]
- Wheatley E, Rittinger K. Interactions between Cdc42 and the scaffold protein Scd2: requirement of SH3 domains for GTPase binding. Biochem J. 2005;388:177–184. doi: 10.1042/BJ20041838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods B, Kuo CC, Wu CF, Zyla TR, Lew DJ. Polarity establishment requires localized activation of Cdc42. J Cell Biol. 2015;211:19–26. doi: 10.1083/jcb.201506108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods B, Lai H, Wu CF, Zyla TR, Savage NS, Lew DJ. Parallel actin-independent recycling pathways polarize Cdc42 in budding yeast. Curr Biol. 2016;26:2114–2126. doi: 10.1016/j.cub.2016.06.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu CF, Chiou JG, Minakova M, Woods B, Tsygankov D, Zyla TR, Savage NS, Elston TC, Lew DJ. Role of competition between polarity sites in establishing a unique front. Elife. 2015;4:e11611. doi: 10.7554/eLife.11611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu CF, Lew DJ. Beyond symmetry-breaking: competition and negative feedback in GTPase regulation. Trends Cell Biol. 2013;23:476–483. doi: 10.1016/j.tcb.2013.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu CF, Savage NS, Lew DJ. Interaction between bud-site selection and polarity-establishment machineries in budding yeast. Philos Trans R Soc Lond B Biol Sci. 2013;368:20130006. doi: 10.1098/rstb.2013.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, Turner C, Gardner J, Temple B, Brennwald P. The Exo70 subunit of the exocyst is an effector for both Cdc42 and Rho3 function in polarized exocytosis. Mol Biol Cell. 2010a;21:430–442. doi: 10.1091/mbc.E09-06-0501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu YW, Oesterlin LK, Tan KT, Waldmann H, Alexandrov K, Goody RS. Membrane targeting mechanism of Rab GTPases elucidated by semisynthetic protein probes. Nat Chem Biol. 2010b;6:534–540. doi: 10.1038/nchembio.386. [DOI] [PubMed] [Google Scholar]
- Zhang SC, Gremer L, Heise H, Janning P, Shymanets A, Cirstea IC, Krause E, Nurnberg B, Ahmadian MR. Liposome reconstitution and modulation of recombinant prenylated human Rac1 by GEFs, GDI1 and Pak1. PLoS One. 2014;9:e102425. doi: 10.1371/journal.pone.0102425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Bi E, Novick P, Du L, Kozminski KG, Lipschutz JH, Guo W. Cdc42 interacts with the exocyst and regulates polarized secretion. J Biol Chem. 2001;276:46745–46750. doi: 10.1074/jbc.M107464200. [DOI] [PubMed] [Google Scholar]
- Zhang X, Orlando K, He B, Xi F, Zhang J, Zajac A, Guo W. Membrane association and functional regulation of Sec 3 by phospholipids and Cdc42. J Cell Biol. 2008;180:145–158. doi: 10.1083/jcb.200704128. [DOI] [PMC free article] [PubMed] [Google Scholar]