Feature-based three-dimensional registration for repetitive geometry in machine vision

Abstract

As an important step in three-dimensional (3D) machine vision, 3D registration is a process of aligning two or multiple 3D point clouds that are collected from different perspectives together into a complete one. The most popular approach to register point clouds is to minimize the difference between these point clouds iteratively by Iterative Closest Point (ICP) algorithm. However, ICP does not work well for repetitive geometries. To solve this problem, a feature-based 3D registration algorithm is proposed to align the point clouds that are generated by vision-based 3D reconstruction. By utilizing texture information of the object and the robustness of image features, 3D correspondences can be retrieved so that the 3D registration of two point clouds is to solve a rigid transformation. The comparison of our method and different ICP algorithms demonstrates that our proposed algorithm is more accurate, efficient and robust for repetitive geometry registration. Moreover, this method can also be used to solve high depth uncertainty problem caused by little camera baseline in vision-based 3D reconstruction.

1. Introduction

3D machine vision has been widely used in fields of industrial design, reverse engineering, surface defect inspection, manufacturing, virtual reality and even homeland security by its capability of reconstructing 3D surface. There are various optical 3D surface reconstruction methods have been developed, such as time-of-flight [1], structured-light [2], laser scanning [3], structure-from-motion (SfM) [4], multiview stereo vision [5] and etc. These 3D reconstruction methods create different 3D point clouds of various density, efficiency and accuracy. A common attribute is the generation of partial surface of the scanned object or scene in general cases due to the limited field of view of the camera/sensor. To build a complete surface, the 3D surface acquisition system needs to be moved around to capture all the parts of the object/scene from different perspectives. 3D geometrical registration of all of these point clouds, that are created from different perspectives, into the same coordinate system is one of the most important and critical steps in 3D reconstruction. The most widely used method for registering 3D point clouds is called ICP [6].

With a proper initial rough alignment and sufficient overlapping 3D points, ICP algorithm obtains an optimal registration solution by minimizing the distance between point-to-point correspondences, known as closest point, in an iterative way [6]. The output of ICP algorithm is a 3D rigid transformation matrix (combination of rotation and translation) from source point cloud to reference cloud such that the root mean square (RMS) between correspondences is minimal. Many improved ICP algorithms have been proposed and studied since introduction of ICP [7]. Different with point-to-point approach, point-to-plane ICP minimizes the sum of the squared distance between a point in the source data and the tangent plane at its correspondence point [8]. Both of the point-to-point and point-to-plane ICP approaches require a good initial coarse alignment, which may be performed manually. Mian et al. developed an automatic pairwise registration of 3D point clouds by a novel tensor representation, which represents semi-local geometric structure patches of the point clouds [9]. Although ICP has become the most popular method for 3D registration, there remains a fundamental problem of ICP-based methods. They do not work well for the 3D registration of plane, cylinder and other objects with repetitive geometric structures. One solution to this problem is by attaching reference marks (RM) on the object [10]. However, the RM methods require preparation work before 3D scanning, and also they are very limited to complex and rough surfaces.

To solve this repetitive geometry issue, a feature-based 3D registration algorithm is proposed in this study to align two point clouds that are generated by vision-based 3D reconstruction, such as SfM, multiview stereo and structured-light scanning. To take advantage of the two-dimensional (2D) texture image of the object, features are detected from the texture images and matched to find the 3D correspondences between the two point clouds, with what 3D registration is much simplified. In this study, a test is performed with multiview stereo vision data. Performance evaluation of our proposed method and ICP-based ones (point-to-point, point-to-plane and Mian's) is performed. The comparison result demonstrates that the proposed method works for the alignment of repetitive geometries and performs more accurate, efficient and robust than ICP-based methods for this example case.

2. Methodology and experiment

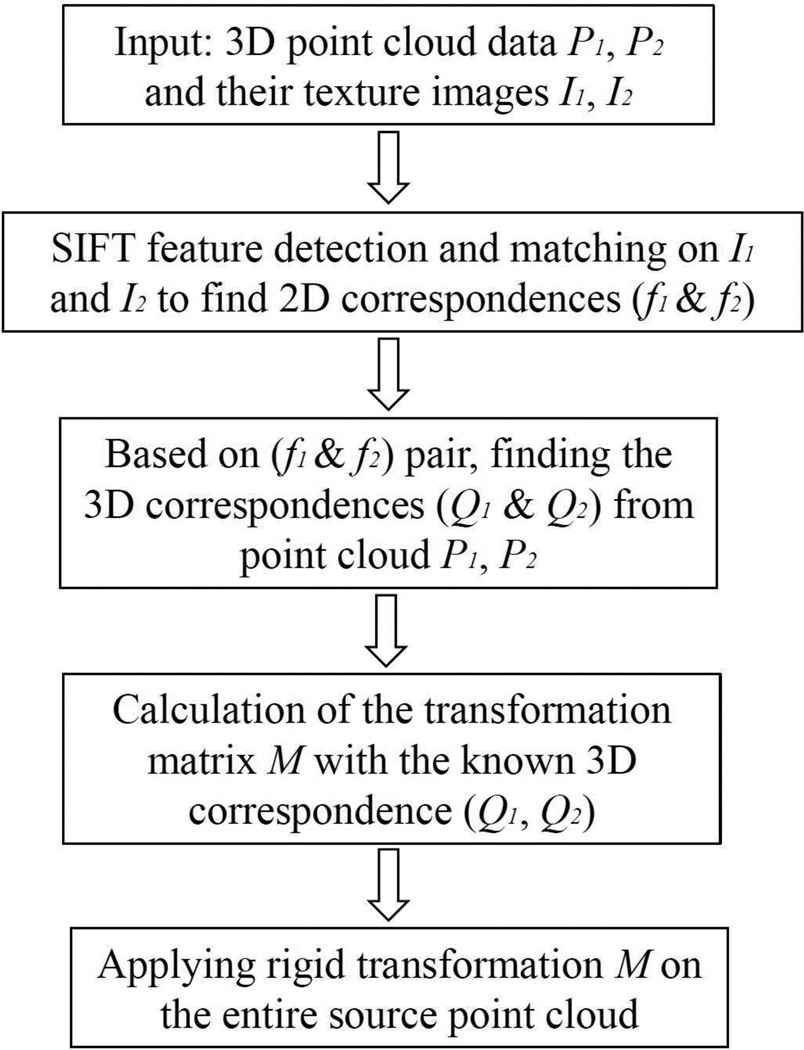
Figure 1 shows the flow chart of the proposed feature-based 3D registration algorithm, which follows a similar principle as the RM method, but with the ability to automate and generalize using computer vision. Instead of manually attaching physical reference markers on the object surface in RM, our approach detects the unique ``markers'' (features) from the 2D texture images. By using advanced computer vision algorithms of feature detection and matching, pairs of corresponding feature points are collected. In this study, scale-invariant feature transform (SIFT) [11] detection algorithm was applied to find the unique ``markers'' from each texture image; Random Sample Consensus (RANSAC) was used to select the robust matching feature pairs by calculating the Euclidean distance in SIFT descriptor space. The 3D coordinates of these correspondences can be easily retrieved from the 3D point clouds. 3D registration problem is then much simplified by only calculating the rigid-body transformation matrix between these 3D correspondences. Unlike the RM method, our approach does not require any preparation work before scanning and is not limited to complex surface or working space.

Figure 1.

The flow chart of the proposed feature-based 3D registration algorithm.

Internally threaded hole is chosen in this study as the scanning object. Internal threads have repetitive geometry in both axial and angular directions, see Fig. 2(c); and this application has great industrial value. The rapid 3D optical measurement of the internal threads becomes more important nowadays especially in the transportation (automobile) industry since the internally threaded holes in engine are crucial to the safety, longevity and efficiency of modern engines [12]. Our previous work demonstrated that a vision-based 3D reconstruction technique, called axial-stereo vision, could be used for the measurement of small internally threaded holes [13]. However, it only recovered very limited internal profile at the opening of the hole. To generate complete 3D model of threaded hole, 3D registration of such vision-based reconstructed point clouds is mandatory.

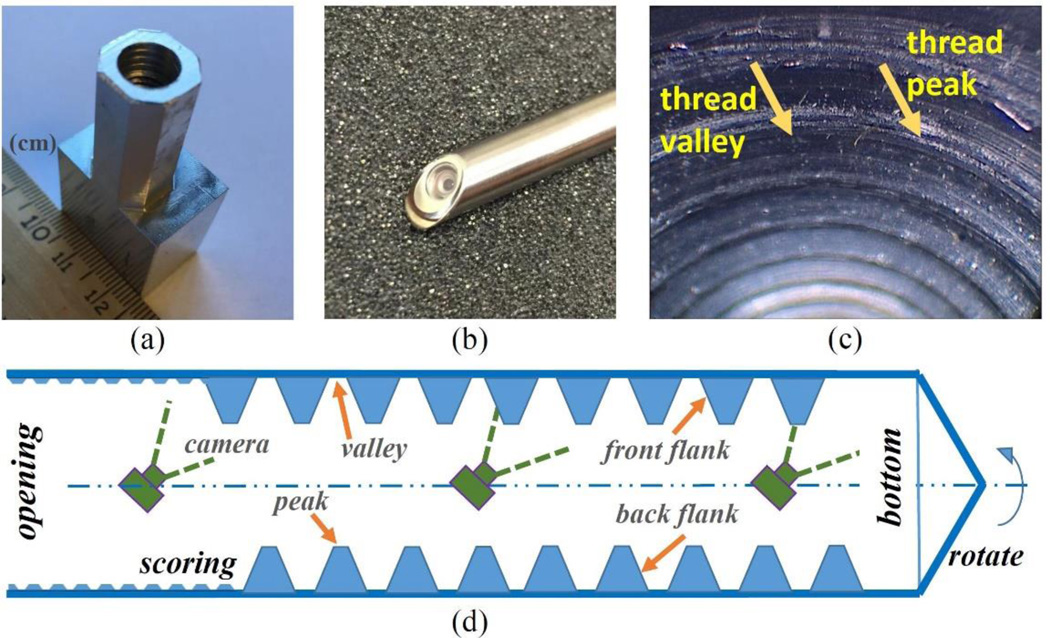
Figure 2.

Data collection. (a) shows the aluminum object of coarse M8 internal threads; (b) shows angled tip of the commercial 45° side-viewing Stryker™ scope; (c) shows an image of M8 internal threads captured by the scope. The thread peak and valley shown as bright belt and dark area, respectively; (d) shows the diagram of a full axial scan of an internally threaded blind hole with 45° side-view camera.

In this study, a coarse M8 internal thread was used as the sample. To capture its high topographic relief of internal thread profile, such as the peaks and valleys, a commercial side-view camera (Stryker™ scope #502--503--045) is used in this study, see Fig. 2(b). This commercial camera provides 45° side-viewing vision of the inner surface of the hole, see Fig. 2(c), which ensures good and consistent image quality with 1280 × 1024 pixels.

The procedure of generating two point clouds having repetitive profile can be laid out as four steps, see Fig. 2(d): step 1) placing the camera (center) along the axis of the threaded hole, facing to the side wall; step 2) with the same camera orientation, taking a series of images (the first data set) as the camera moves inwards from the opening to the bottom with constant step distance. We call such sequential images as a “quadrant”; step 3) repositioning the camera at the hole opening and rotating it along the hole axis at a proper rotation degree to ensure image overlapped with the previously captured quadrant; step 4) repeating the step 2) and collecting the second data set. For 3D reconstruction and registration purposes, the step distance and rotation angle are set as 0.1 mm and 30° respectively in this study to ensure more than 50% image overlap within neighbor images, which are realized by micro-positioning and rotation stages. In this study, the neighbor images that are collected with pure camera linear motion called an “axial neighbor”, and the ones that are captured with pure camera rotation are called an “angular neighbor”.

Due to the use of micro-positioning and rotation stages, the camera position and orientation data can be collected accurately and slowly. By taking advantage of the known camera pose information, the 3D reconstruction of the threads is accurate and efficient since it only needs to triangulate the 3D point cloud representing the internal surface, called multiview stereo [14]. However, processing all the images at once with state-of-art software VisualSfM [15], OpenMVG [16] or even the customized MATLAB code [17] does not result in a satisfying 3D reconstruction. The reason is that these quadrants are captured with pure camera rotation (the baseline is zero) if the camera center is aligned with the rotation axis, Fig. 2(d). For this scenario, the complete 3D model can be reconstructed by stacking all the quadrants together with known rotation angles. However, we have to consider the real cases of axes misalignment in the practical applications.

There are three axes in the procedure: hole axis, camera center axis and rotation axis. The misalignment of hole axis with the other two does not affect the reconstruction result. However, the misalignment of camera center line and rotation axis could generate geometrical discontinuity once stacking quadrants together directly. In the practical cases, such misalignment is small and also unknown. Both scenarios of well-alignment and misalignment would generate significant error when triangulating the depth [18], resulting gross reconstruction error. To avoid this, we propose to use axial sequence images to reconstruct the 3D point cloud of each quadrant with a multiview stereo algorithm, and the angular neighboring frames for the 3D registration of neighbor quadrant point clouds. This is one significance of this proposed feature-based 3D registration algorithm that it can solve high depth uncertainty problem caused by little camera baseline in vision-based 3D reconstruction.

Given a set of n axial images for the ith quadrant $I_i=\{I_i^1,I_i^2,\dots ,I_i^n\}$ that are captured with linear motion of camera in one quadrant, feature detection and matching algorithms are applied to find the corresponding points in the image set. Let k_i represent all the features that are detected from I_i and g_i for the features used in the 3D reconstruction. g_i is a subset of k_i, g_i ∈ k_i, since not every feature in an image has correspondences in its axial neighbors. With a priori knowledge of camera extrinsic parameters, two 3D point clouds representing these two quadrants can be generated independently by the multiview stereo vision technique, see the details in [14].

In this experiment, 155 axial images were captured for each quadrant covering the range from the opening through the bottom. Here, we utilized state-of-art software VisualSfM [15] for the processing and visualization for each quadrant, shown in Fig. 3, with label of the opening of threaded hole, and the start and end of the threads. The colorful straight line in Fig. 3 is the series of camera positions of the line of these axial images as the micro-positioning stage moved inwards.

Figure 3.

The 3D reconstruction of one quadrant of the recessed internally threaded hole from a sequence of axial images with known camera position and orientation.

To register these two generated point clouds, the same feature matching algorithm is applied on the angular neighbor images to find the corresponding features between these two quadrants. Here, f_i is used to represent all the features in k_i that have correspondences in the other data set, so f_i ∈ k_i. For the common features that are used in both 3D reconstruction and 3D registration (g_i ∩ f_i), their 3D coordinates in their own local coordinate systems are represented by Q_i, which can be retrieved from the reconstructed 3D models. The size of Q is 3 × m where m is the total number of 3D correspondences. To register the first quadrant data (source) to the second one (reference), we have

$$R{Q}_1^j-t=Q_2^j$$ (1)

for jth pair of 3D correspondence, j=1,2,…,m. In Eq. (1), Q₁ and Q₂ are known; R is a 3 × 3 rotation matrix from the coordinate system of the first quadrant to the second one. Strictly speaking, det(R)=1. t=[t_x, t_y, t_z]^T is the translation vector. By subtracting off the respective mean Q̅_i from data Q_i, the effect of the translation vector t is eliminated. Considering this is an over-determined problem, rotation R can be solved by:

$$\text{min }\parallel R{Y}_1-Y_2\parallel$$ (2)

where Y_i=Q_i−Q̅_i. R can be obtained by taking the singular value decomposition of the covariance matrix Y₂Y₁^T and t can be calculated by t=RQ̅₁ -Q̅₂. So far, the registration of these two point clouds is achieved by applying rotation R and translation t on the entire source point cloud.

3. Results

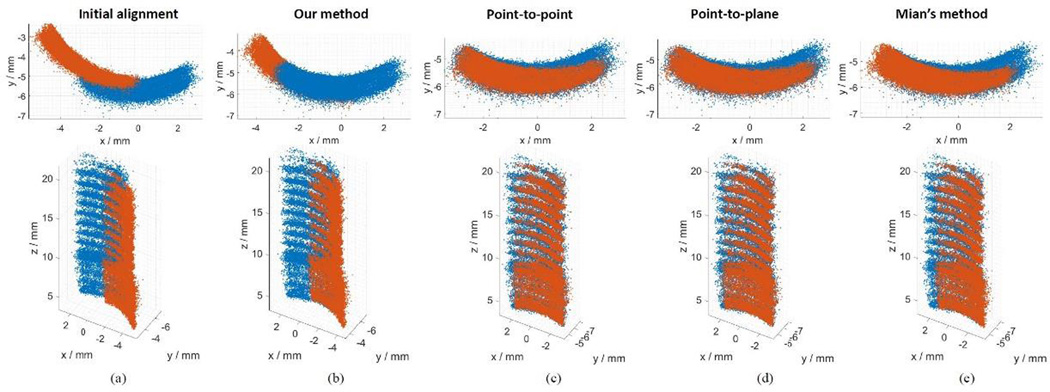
To evaluate our proposed feature-based 3D registration algorithm, performances of our method and standard ICP-based (point-to-point, point-to-plane and Mian's) methods are compared. The visualization of the registration results is shown in Fig. 4. The initial alignment is shown in Fig. 4(a) by stacking two quadrants together directly. The obvious “discontinuity” of the two point clouds is caused by misalignment between camera center and hole axis in the practical setup. Since these two point clouds were nearly identical and repetitive in geometry, all the ICP-based methods result in a complete overlapping model, see Fig. 4(c–e). In contrast, the proposed feature-based 3D registration algorithm produced a qualitatively better result, see Fig. 4(b), with a rough 30° rotation angle and geometrical continuity.

Figure 4.

The comparison of 3D registration results by our proposed feature-based method and popular ICP approaches. (a) shows the top and side views of the initial alignment of two differently colored neighbor quadrants with known 30° rotation angle; (b) shows the top and side views of the result of our proposed feature-based 3D registration method, good alignment shows smooth connection between these two data sets; (c) shows the top and side views of the result of the point-to-point ICP method; (d) shows the top and side views of the result of the point-to-plane ICP; (e) shows the top and side views of the result of the Mian's method. ICP-based methods (c)-(e) generated incorrect 3D registration of quadrant views of a threaded hole.

To better understand the significance of the proposed feature-based 3D registration algorithm, two tables were created with more details of the performance comparison of our method and ICP-based approaches. Table 1 shows that our method generated 2.4° error (8%) for the estimation of rotation angle (we consider 30° is the ground truth). All three ICP-based methods generated more than 22°error (>74%) for the rotation angle estimation. These results of ICP-based methods are completely wrong even with root mean square (RMS) error of only about 0.088 mm that is much smaller than the one of our method (0138 mm), see Table 1. Among ICP-based methods, Mian’s performs slightly better than the other two. The performance of point-to-point and point-to-plane methods are very close, except computation time. Moreover, our method is much faster than ICPs, allowing over 50,000× improvement by only calculating a rigid transformation with known 3D correspondences.

Table 1.

The comparison of our method and ICP approaches

method	error of rotation angle (°)	computation time (sec)	RMS of registration (mm)
our method	2.4	0.001	0.138
point-to-point ICP	26.7	1574	0.088
point-to-plane ICP	26	1186	0.088
Mian’s method	22.2	78	0.087

Table 2 shows the comparison of the robustness of our method and standard ICP-based methods. Five independent tests were performed, following by the same flow chart but with different quadrants data of the internal threads. The comparison result shows that our method keeps a very low estimation error of the rotation angle within a threaded hole.

Table 2.

The rotation angle evaluation of our method and ICP-based approaches with multiple tests (°)

	our method	point-to-point ICP	point-to- plane ICP	Mian’s method
test 1	5.51	28.69	27.98	22.46
test 2	2.44	26.7	26.02	22.16
test 3	4.05	30.27	30.53	18.71
test 4	3.24	27.45	27.45	24.09
test 5	3.1	26.18	26.39	23.29
avg.	3.67	27.86	27.67	22.14
std.	1.18	1.64	1.78	2.06

All the algorithms were implemented in MATLAB, running on a Dell Precision 5510 with 2.8 GHz Intel E3-1505M CPUs, 32.0 GB memory in a 64-bit Window operating system.

4. Discussion and conclusion

In this study, a feature-based 3D registration algorithm is proposed to solve the repetitive geometry issue for the point clouds that are generated by vision-based 3D reconstruction techniques. The standard ICP-based algorithms do not work well for the geometry with repetitive profiles. By taking advantage of the texture images and the robustness of the SIFT feature, 3D correspondences between these two point clouds can be collected by finding the matching features in the texture images. In this study, two point clouds of the internally threaded hole were generated independently based on multiview stereo. The internally threaded hole in metal is considered as a good test sample since its profile comes with repetitive shape in both axial and angular directions, and has wide-spread industrial applicability. The comparison among our method and ICP-based (point-to-point, point-to-plane, Mian's) methods demonstrated that our approach works much better (less registration error) for this case in a more efficient and robust way.

This proposed feature-based 3D registration method can be used for the registration of point clouds that are not just generated by multiview stereo 3D reconstruction, but also for other vision-based 3D reconstruction techniques, such as structured-light scanning. The texture images of the object or scene from different perspectives can be generated by three-step phase-shifting algorithm [19]. The same as our proposed approach, feature detection and matching are performed to find the 2D matching features, based on which 3D correspondences are retrieved from individual 3D model at each view. Moreover, this proposed method can be also used to improve the SfM 3D reconstruction. Different with multiview stereo, SfM doesn't require camera information. It estimates all the camera parameters and 3D scene simultaneously by solving a non-linear, non-convex optimization problem [20]. With little camera baseline and therefore high depth uncertainty, the non-convexity of SfM may generate a completely unacceptable 3D model. The strategy proposed here of classifying images as two categories, one for 3D reconstruction and the other for 3D registration, can be used to eliminate the effect of little camera baseline issue.