Mechanistically Inspired Route toward Hexahydro-2H-chromenes via Consecutive [4 + 2] Cycloadditions

Abstract

Utilizing two robust C–C bond-forming reactions, the Baylis–Hillman reaction and the Diels–Alder reaction, we report a highly enantio-, regio-, and diastereoselective synthesis of hexahydro-2H-chromenes via two sequential [4 + 2] cycloadditions. These tandem and formal cycloadditions have also been performed as a “one-pot” sequence to access the corresponding heterocycles constituting up to five contiguous stereocenters in excellent yields and stereoselectivity.

Graphical abstract

Although the synthesis of hexahydro-2H-chromenes (4) can be achieved through a number of strategic disconnections,¹ we sought to explore a rapid assembly, as depicted retrosynthetically in Scheme 1. The enantioenriched precursor diene (3), required for the concomitant Diels–Alder reaction, would be obtained via a chiral amine catalyzed modified Baylis–Hillman reactionof allenoate 2 with chalcone 1 that precedes a formal [4+ 2] cycloaddition. The latter strategy provides an expedient route toward substituted hexahydro-2H-chromenes with high stereo-selectivity via two consecutive [4 + 2] cycloaddition reactions.

Scheme 1. (Top) Retrosynthetic Strategy for the Synthesis of Hexahydro-2H-chromenes. (Bottom) Paths A and B Represent a Simplified Mechanistic Picture of the Canonical vs the Modified Baylis–Hillman Pathway^a.

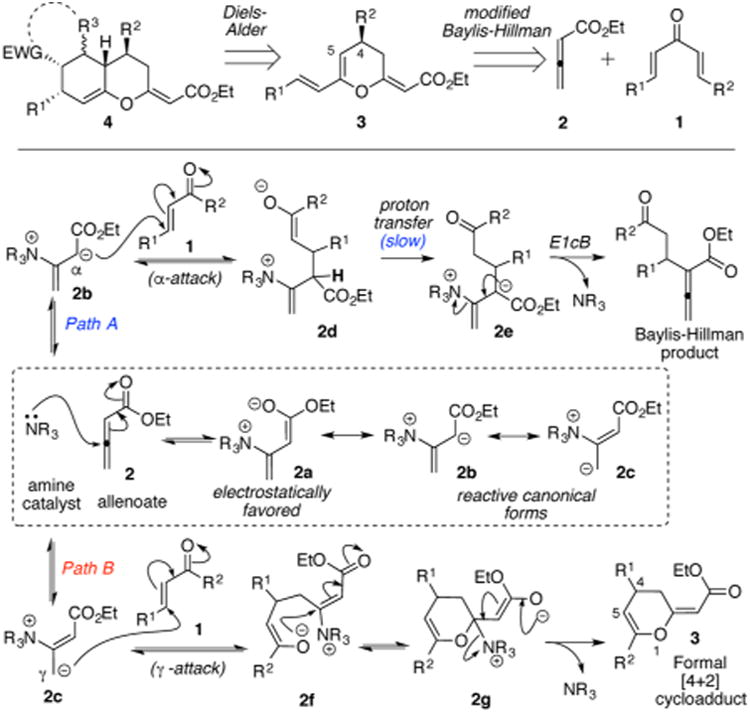
^aPossible resonance structures of the amine–allenoate adduct are shown in the dashed box with 2a being the major contributor.

The approach described above requires a facile strategy for the synthesis of dihydropyrans with the general structure depicted in 3 in high enantioselectivity. A number of groups, including ours, have addressed this requirement.² Our endeavor in this field commenced with the early discovery for the mechanistically guided synthesis of substituted dihydropyrans.^2e As shown in Scheme 1, we circumvent the rate-limiting proton transfer associated with the Baylis–Hillman reaction of enones and allenoates (path A, 2d → 2e),³ by utilizing acyclic enones (1) as secondary electrophiles. The relatively fast intramolecular trapping of the oxyanion 2f siphons the reaction toward formation of the corresponding dihydropyran 3 in high yields and enantioselectivity via path B (modified Baylis–Hillman route⁴). We predicted that a similar transformation initiated with a symmetric chalcone (such as 1, Scheme 1) would yield the required diene 3 for the proposed Diels–Alder reaction. Furthermore, we surmised that the enantioenriched C4 substituent in 3 would serve as a stereochemical driver in the concomitant [4 + 2] cycloaddition. The conjugated diene motif in 3 displays a unique integration of two key features: (a) the extended cross-conjugation of the pyranyl oxygen atom (O1) results in an electronic bias that may allow regioselective trapping of a unsymmetrically substituted dienophile and (b) the nucleophilic carbon (C5) and the stereochemical driver (C4 substituent), both being part of a conformationally rigid cyclic framework, may allow an easy access to diastereoselective [4 + 2] cycloadditions. The latter hypotheses were readily examined by subjecting a model substrate, dibenzalacetone 1a, to the catalytic asymmetric formal [4 + 2] cycloaddition under an optimized set of conditions (Scheme 2). Initial screening with several chiral amines revealed A and B as optimum catalysts for the synthesis of oxatriene 3a-(S) and 3a-(R), respectively. Using catalyst A under solvent-free conditions, oxatriene 3a-(S) was obtained in 98% yield and 98% ee. Subsequent treatment of this oxatriene with maleic anhydride 4a furnished the stereopentad 5aa as a single diastereomer in 78% yield. This offers an alternate approach to previous explorations⁵ directed toward controlling stereoselectivity in cycloadditions of dienes bearing an allylic chiral center.⁶

Scheme 2. Preliminary Results for Consecutive [4 + 2] Cycloadditions under Optimized Conditions Using Dibenzalacetone (1a) as a Test Substrate^a–c.

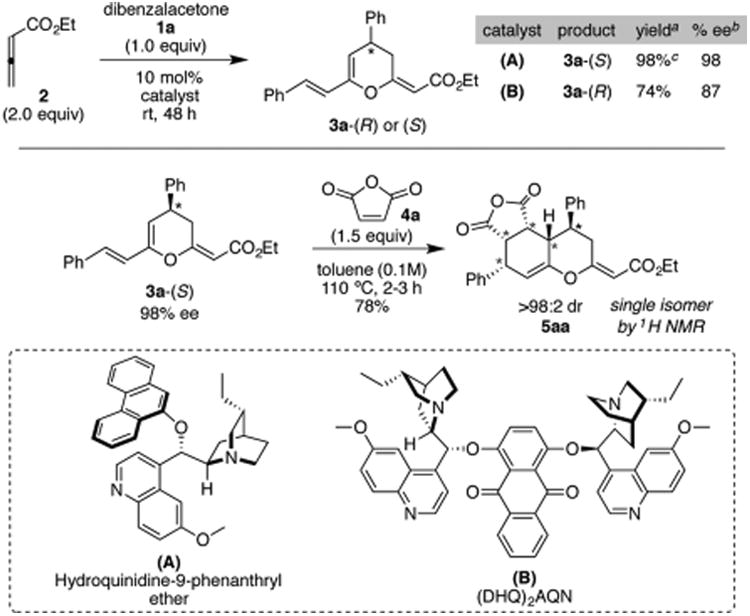
^aIsolated yields. ^bRatios were determined by HPLC analysis. ^cReaction was performed using 1 g (4.3 mmol) of 1a.

Intrigued by the levels of stereoinduction, especially in the latter cycloaddition, we decided to probe the origins of stereoselectivity by employing quantum chemical computational analysis of the transition states (TS) at the B3LYP/6-31G*/SM8 (toluene) level of theory.⁷ Hydroquinidine (instead of catalyst A) was employed to reduce the computational expense. In accordance with the previous findings,^2e the diastereomeric transition state TS-1 (Figure 1a), which provides the product 3a-(S), was favored by 2.7 kcal/mol (corresponding to er = 99:1). The steric congestion (gauche interactions highlighted by bonds in red color) and the diminished electrostatic stabilization (as determined by the C=O^δ−…^δ++NR₄ distance) in TS-2 make it energetically less favorable than TS-1. The computational analysis corroborates the experimental observation in the initial [4 + 2] cycloaddition (98% ee using the hydroquinidine based catalyst-A, see the SI for details). We next examined the stereoinduction associated with the Diels–Alder reaction of 3a-(S) with maleic anhydride 4a. In agreement with the experimentally observed endo-selectivity,^5e,8 TS-3_endo was found to be more favored over TS-4_exo by 2.8 kcal/mol (Figure 1b). TS-4_exo also suffers from the electrostatic repulsion between the π-cloud of the C4 phenyl substituent in 3a-(S) and the electron density on the proximal carbonyl of 4a (see the SI for details). Furthermore, the corresponding TS-5_endo that involves the approach of dienophile 4a from the sterically hindered face of the diene is disfavored over TS-3_endo by 1.8 kcal/mol (see dashed box in Figure 1b). Although the B3LYP/6-31G* level of theory underestimates the energetics of secondary interactions in the Diels–Alder reaction,⁹ it clearly depicts the correct energetic trend as observed experimentally.¹⁰ Overall, the stereochemistry at C4, obtained from the Baylis–Hillman reaction, governs the stereospecificity in the concomitant Diels–Alder reaction.

Figure 1.

(a) Two diastereomeric transition states TS-1 and TS-2 calculated at the B3LYP/6-31G*/SM8(toluene) level of theory. The bonds highlighted in red color depict the unfavorable gauche interactions in TS-2. (b) Three possible transition states associated with the [4 + 2] cycloaddition of 3a-(S) and 4a. TS-3_(endo) is favored by 2.8 kcal/mol over TS-4_(exo) and by 1.8 kcal/mol over TS-5_(endo). The fourth possible TS involving an exo approach of 4a from the same face as the C4-Ph substituent cannot be calculated due to severe steric clash between the approach dienophile and the aromatic ring.

The mechanistic nuances underlying the modified Baylis–Hillman reaction of allenoates (primary electrophile) with dibenzalacetone (secondary electrophile) are more complex than the simplified picture depicted in Scheme 1, leading to the following central question. Despite the possibility for the formation of several theoretical adducts (based on the relative reactivity of the primary and secondary electrophile), which factor governs the formation of 3 as the predominant product? To address this question, the identity of stable intermediates that arise during the reaction of 1a with 2, catalyzed by quinuclidine C (an achiral surrogate of catalysts A and B), were investigated by ESI-MS (Figure 2). A nucleophilic attack of the Lewis base catalyst C on allenoate 2 generates the zwitterionic intermediate 2/C. The resulting enolate can attack another molecule of 2 to furnish the intermediate 2²/C. Sequential additions of 2 will yield the trimeric adduct 2³/C and higher oligomers that constitute several polymeric adducts in equilibrium. This is indeed supported by ESI-MS analysis of a preincubated mixture of C and 2 (Figure 2b). When this mixture was treated with the secondary electrophile 1a, intermediates 1a-2/C en route to product 3a and higher order adduct 1a-2²/C were observed (Figure 2c).¹¹ This study suggests that the reaction of 1a, 2, and C indeed yields a mixture of several adducts in equilibrium; however, the irreversibility associated with the ring-closure step (see dashed box, Figure 2a) adventitiously siphons the equilibrium mixture to the desired cycloadduct 3a.

Figure 2.

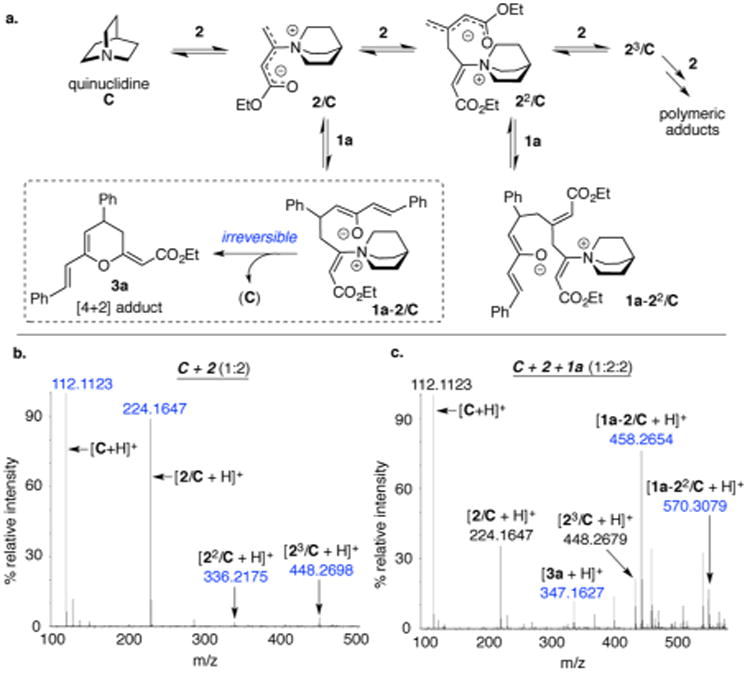
(a) Equilibrium mixture of putative intermediates in the Baylis–Hillman reaction of 1a and 2. For simplicity, intermediates arising only from the γ-attack of the enolate are shown. (b) ESI-MS spectrum of a reaction mixture (preincubated for 30 min) constituting of a 1:2 ratio of C and allenoate 2. (c) ESI-MS spectrum obtained after 1 h upon addition of 1a to the mixture of C and 2.

To explore the scope of this reaction, a series of substituted dibenzalacetones (1a–p) were reacted with allenoate 2 under solvent-free conditions (see Table 1). Catalysts A and B (see Scheme 2) were employed to access either enantiomer of the corresponding oxatrienes 3a–p. Overall, catalyst A displayed better efficiency and stereoinduction over catalyst B. Regardless of the electronics of the substituents attached; i.e., electron-donating aryl (entries 2–6 and 13), electron-withdrawing aryl (entries 7–12), and even aliphatic substituents (entries 14–16), excellent enantioinduction was observed with catalyst A.¹² The X-ray crystal structures of derivatives of 3b-(S) and 3j-(S) provided unequivocal evidence for the absolute stereochemistry of the products obtained using catalyst A (see Scheme 3, dashed box). These results also corroborated the quantum chemical computational analysis (Figure 1a) that revealed the absence of a gauche interaction (sterics) in TS-1 is responsible for favoring the (S)-enantiomer.

Table 1. Substrate Scope for Enantioselective Synthesis of Substituted Oxatrienes.

entry	R	cat.	product	time (h)	yielda (%)	eeb (%)
1	Ph	A	3a-S	40	98c	98
		B	3a-R	8	74	87
2	o-OMeC6H4	A	3b-S	60	60d	90
		B	3b-R	60	65d	82
3	m-OMeC6H4	A	3c-S	12	98	96
		B	3c-R	12	87	88
4	p-OMeC6H4	A	3d-S	60	25d	94
		B	3d-R	60	20d	76
5	o-MeC6H4	A	3e-S	40	75	88
		B	3e-R	10	68	82
6	p-MeC6H4	A	3f-S	60	43d	94
		B	3f-R	60	57d	72
7	o-FC6H4	A	3g-S	48	78	92
		B	3g-R	48	71	88
8	o-BrC6H4	A	3h-S	30	95	88
		B	3h-R	30	95	78
9	p-BrC6H4	A	3i-S	40	66	94
		B	3i-R	40	32	72
10	o-ClC6H4	A	3j-S	25	99e	90
		B	3j-R	25	89	84
11	p-ClC6H4	A	3k-S	48	58	91
		B	3k-R	48	36	88
12	2-furyl	A	3l-S	48	27	95
		B	3l-R	48	32	78
13	1-naphthyl	A	3m-S	40	76	92
		B	3m-R	40	69	72
14	n-propyl	A	3n-S	72	28 (52)d,f	90
		B	3n-R	72	24 (50)d,f	67
15	isopropyl	A	3o-S	72	29 (87)d,f	94
		B	3o-R	72	23 (80)d,f	58
16	Me	A	3p-S	36	48	90
		B	3p-R	36	26	72

^aIsolated yields.

^bRatios were determined by HPLC analysis using chiral stationary phase columns.

^cReaction was performed on a 1 g scale of 1a.

^dLonger reaction times led to degradation of allenoate 2, and incomplete conversion of dienones was observed.

^eReaction was performed on a 0.5 g scale of 1j.

^fNumbers in parentheses refer to yield based on recovered starting material.

Scheme 3. Diels–Alder Reaction of Substituted Oxatrienes 3a–c,j with Illustrative Dienophiles 4a–d^a–e.

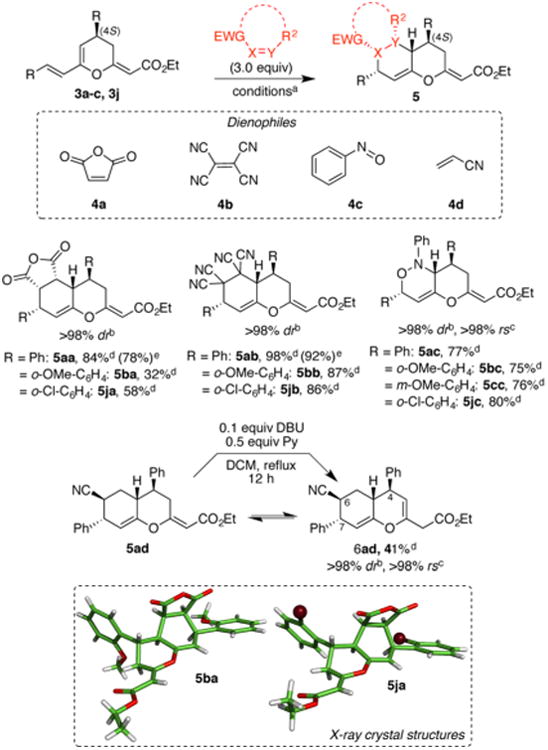
^aDiels–Alder reaction conditions for each dienophile are as follows: dienophile 4a, 0.1 M toluene, reflux, 2–16 h; dienophile 4b, 0.1 M toluene, reflux, 2 h; dienophile 4c, 0.1 M EtOH/DCM (1:1), 0 °C → rt, 12 h; dienophile 4d, 0.1 M in toluene, reflux, 12 h. ^bDiastereomeric ratios (dr) were determined by ¹H NMR analysis of the crude reaction mixture. ^cRegioselectivity (rs) and relative stereochemistry were determined via NMR analysis of the purified product. ^dIsolated yields. ^eIsolated yields for “one pot” consecutive transformations from 1a as a starting material.

As a proof of principle, we briefly explored the ability of these oxatrienes to govern regio- and stereoinduction in the Diels–Alder reaction. Scheme 3 summarizes the results of 11 cycloaddition reactions of dienes 3a-(S), 3b-(S), 3c-(S), and 3j-(S) with an illustrative set of dienophiles 4a-d. Dienophiles 4a and 4b exhibited exclusive diastereoselective addition, whereas 4c and 4d displayed excellent regioselection. Furthermore, these sequential transformations (Baylis–Hillman reaction followed by a concomitant Diels–Alder reaction) were also performed efficiently as a “one-pot” domino reaction (see Scheme 3 for products 5aa and 5ab). As anticipated, the cross-conjugation of the endocyclic oxygen (O1) not only enhances the HOMO energy of the diene motif in 3 but also generates an electronic bias that allows regiospecific trapping of the dienophiles 4c and 4d, thus validating the initial hypothesis. Of interest is the reaction of 3a with 4d, which led to an isomeric mixture of products 5ad and 6ad in nearly equimolar ratios. Fortuitously, upon treatment with DBU in refluxing DCM, the mixture was cleanly converted to yield the endocyclic product 6ad in high diastereo- and regioselectivity. Unlike the products of other Diels–Alder reactions depicted in Scheme 3, 6ad (and for that matter 5ad) is the result of an exo [4 + 2] cycloaddition (see SI for stereochemical assignment based on NMR studies). Although we see no evidence of the endo product during the course of the reaction, we cannot exclude the possibility of either epimerization at C6 or a reversible Diels–Alder process that ultimately settles for the thermodynamic product.

In summary, a two-step process is reported for the synthesis of hexahydro-2H-chromenes. The asymmetric Baylis–Hillman reaction provides the dihydropyrans in high stereoselectivity. The ensuing Diels–Alder reaction is also under strict regio- and stereochemical control. The C4 stereocenter, established during the initial [4 + 2] cycloaddition, is the stereochemical driver, whereas the cross-conjugation of pyranyl oxygen (O1) aids to generate an electronic bias for the observed regioselectivity in the Diels–Alder reaction. This methodology provides a complementary approach to control the stereochemistry in Diels–Alder reactions of chiral dienes:^5b,f,h,i unlocking opportunities toward expanding the repertoire of stereo- and regioselective reactions of chiral dienes.

Supplementary Material

Supplementary Data

Experimental and DFT computational data (PDF)

X-ray crystallographic data for 5ba (CIF)

X-ray crystallographic data for 5ja (CIF)