Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Mar 9;7:44255. doi: 10.1038/srep44255

Calcium isotope fractionation between aqueous compounds relevant to low-temperature geochemistry, biology and medicine

Frédéric Moynier 1,2,a, Toshiyuki Fujii 3
PMCID: PMC5343585  PMID: 28276502

Abstract

Stable Ca isotopes are fractionated between bones, urine and blood of animals and between soils, roots and leaves of plants by >1000 ppm for the 44Ca/40Ca ratio. These isotopic variations have important implications to understand Ca transport and fluxes in living organisms; however, the mechanisms of isotopic fractionation are unclear. Here we present ab initio calculations for the isotopic fractionation between various aqueous species of Ca and show that this fractionation can be up to 3000 ppm. We show that the Ca isotopic fractionation between soil solutions and plant roots can be explained by the difference of isotopic fractionation between the different first shell hydration degree of Ca2+ and that the isotopic fractionation between roots and leaves is controlled by the precipitation of Ca-oxalates. The isotopic fractionation between blood and urine is due to the complexation of heavy Ca with citrate and oxalates in urine. Calculations are presented for additional Ca species that may be useful to interpret future Ca isotopic measurements.

Calcium is the fifth most abundant element in the Earth and meteorites1. It plays a central role in cosmochemical, geochemical and biological processes. It is the most refractory major element (temperature of 50% condensation of 1505 K, ref. 2) and it is therefore one of the main constituents of the first solids formed in the solar system, the so called calcium-aluminium rich inclusions. Because of its refractory behavior, calcium is generally supposed not to be lost by evaporation during planetary formation and therefore its isotopic composition has been used as a tracer of the materials that have accreted to form the Earth2,3. In surfaces environments, Ca is ubiquitous in living organisms and many minerals (e.g. calcite), and it plays a central role in the regulation of the carbon cycle and climate evolution4.

Calcium has 6 stable isotopes (40Ca, 42Ca, 43Ca, 44Ca, 46Ca, and 48Ca). The isotopic composition of Ca is usually reported as the δ notation as:

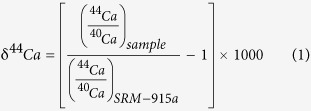graphic file with name srep44255-m1.jpg

with the data reported relative to the standard NIST SRM915a5. SRM915a is now unavailable and has been replaced in some studies by SRM915b which is offset by ~+0.7 permil for δ44Ca2,6. In addition, Ca isotopic data are sometimes reported as δ44/42Ca, and because all the isotopic fractionation measured so far in terrestrial samples are mass dependent, δ44/42Ca is simply δ44Ca/2. For the sake of consistency, we will only refer to δ44Ca normalized to SRM915a in the rest of the manuscript.

Calcium isotopes have been widely used to study the paleo-variation of Ca abundance in the hydrosphere4,7,8,9 and the uptake and transport of Ca in biological materials, including plants10 and animals11. In addition, Ca isotopes have been utilized as biotracers for bone mineral balances12. This medical application of Ca isotopes is based on the fact that Ca isotopes are naturally fractionated between different organs and body fluids11,12,13,14. The bones are enriched in the lighter isotopes of Ca by ~1 permil compare to the blood in horses and mice11,15 and the urine is enriched in the heavy isotopes compare to the blood by ~2.4 permil as estimated from human patients14. Because of these isotopic variations between bones and body fluids, Ca isotopes have been used as biomarkers of change in bone mineral balances12. However, the origin of this isotopic fractionation between blood/urine and blood/bones is presently not understood.

Calcium isotopic variations are also a common feature in the plant kingdom. The roots are generally enriched in the lighter isotopes of Ca and the shoots are enriched in the heavier isotopes of Ca compare to the roots10,16,17,18. Again, the origin of the isotopic fractionation between the different plant components and between the roots and the source of Ca is not well understood.

It is known that large isotope fractionation during exchange reactions reflects isotopic differences between the equilibrium constants of Ca isotopologues. This comes from the fact that the partitioning isotopes of a particular element among coexisting species depend on the vibrational frequency of the bond19,20. For example, isotopic fractionation of ~1‰ was observed following cation-exchange chromatography of Ca with low (50–80%) elution yield21. It is therefore possible that the Ca isotopic fractionations that occur among ligands relevant to Ca species in plants, animals, water or soils may be controlled by the difference of equilibrium constants between the isotopologues. Similar mechanisms have been proposed for the origin of Zn22,23,24,25,26,27 Cu28,29, Ni30, Si31,32 or Fe33,34,35,36 isotope fractionations.

Here, we calculate the molecular orbitals of a large variety of Ca species to obtain the reduced partition function ratio (RPFR) of isotopologues. The ab initio calculations were then extended to hydrated Ca(II) complexes, chlorides, hydroxide, sulfate, carbonate, phosphates, citrates, malates, and oxalate. The choice of oxalate was motivated by evidence of isotopic fractionation of Ca between urine and blood of human patients14 and its importance as Ca carrier in plants37. Applications of our calculations to the understanding of Ca isotope variability into biological samples are briefly outlined.

Results and Discussion

All the data are reported in Table 1 and Figs 1 and 2 for some of the most relevant molecules discussed. The geometry of each molecules are reported in Supplementary Information.

Table 1. Logarithm of the reduced partition function, 1000 ln β, for the pair 44Ca-40Ca of Ca(II) complexes.

Species Coordination number Temperature (K) ln β vs Td
273 298 310 323 373 473 573 A B
Ca(H2O)62+ 6 17.483 14.802 13.727 12.687 9.611 6.049 4.148 1.2867 0.2939
Ca(H2O)72+ 7 16.431 13.903 12.890 11.911 9.017 5.670 3.886 1.2112 0.2565
Ca(H2O)82+ 8 15.273 12.918 11.975 11.064 8.372 5.261 3.606 1.1264 0.2272
CaF(H2O)5+a 6 19.444 16.506 15.324 14.180 10.779 6.813 4.685 1.4257 0.4410
CaF2(H2O)4a 6 19.003 16.139 14.987 13.871 10.553 6.681 4.598 1.3914 0.4604
CaCl(H2O)5+a 6 17.679 14.970 13.883 12.832 9.723 6.120 4.198 1.3018 0.3022
CaCl2(H2O)4a 6 16.802 14.221 13.187 12.187 9.230 5.808 3.983 1.2377 0.2760
CaSO4(H2O)5a 6 19.784 16.795 15.593 14.429 10.971 6.939 4.774 1.4498 0.4582
CaHS(H2O)5+a 6 17.181 14.544 13.487 12.465 9.442 5.942 4.076 1.2654 0.2868
Ca(HS)2(H2O)4a 6 15.108 12.785 11.854 10.955 8.296 5.219 3.579 1.1131 0.2441
CaOH(H2O)5+a 6 18.982 16.111 14.956 13.839 10.518 6.649 4.572 1.3918 0.4273
Ca(OH)2(H2O)4a 6 17.630 14.976 13.908 12.873 9.798 6.207 4.275 1.2900 0.4399
CaHCO3(H2O)5+a 6 19.334 16.383 15.198 14.052 10.658 6.718 4.612 1.4217 0.3637
CaHCO3(H2O)4+b 6 19.339 16.379 15.192 14.044 10.646 6.706 4.603 1.4230 0.3465
CaCO3(H2O)4b 6 19.070 16.182 15.022 13.898 10.565 6.682 4.598 1.3976 0.4338
CaH2PO4(H2O)5+a 6 18.953 16.057 14.894 13.771 10.442 6.581 4.518 1.3939 0.3507
CaH2PO4(H2O)6+a 7 18.075 15.307 14.197 13.124 9.947 6.265 4.299 1.3302 0.3196
CaHPO4(H2O)5a 6 19.583 16.626 15.436 14.285 10.862 6.871 4.727 1.4349 0.4564
CaH3SiO4(H2O)5+a 6 19.334 16.387 15.204 14.059 10.667 6.727 4.620 1.4210 0.3759
CaH2SiO4(H2O)5a 6 18.824 15.970 14.823 13.713 10.420 6.586 4.530 1.3805 0.4150
CaNO3(H2O)5+a 6 19.263 16.319 15.137 13.994 10.611 6.686 4.590 1.4169 0.3533
CaH(ox)(H2O)4+b 6 19.440 16.463 15.269 14.115 10.699 6.739 4.624 1.4306 0.3446
CaH(ox)(H2O)5+b 7 18.383 15.559 14.428 13.334 10.100 6.356 4.359 1.3540 0.3041
Ca(ox)(H2O)4b 6 20.012 16.975 15.755 14.574 11.071 6.994 4.808 1.4683 0.4302
CaH(cit)(H2O)3c 6 18.697 15.833 14.685 13.575 10.290 6.484 4.451 1.3755 0.3355
Ca(cit)(H2O)3−c 6 19.860 16.830 15.614 14.438 10.955 6.912 4.749 1.4591 0.3894
Ca(cit)(H2O)4−c 7 18.721 15.863 14.717 13.608 10.325 6.514 4.476 1.3755 0.3655
CaH(mal)(H2O)4+b 6 18.617 15.766 14.622 13.517 10.244 6.452 4.428 1.3701 0.3284
Ca(mal)(H2O)4b 6 19.139 16.217 15.044 13.910 10.552 6.655 4.571 1.4067 0.3670
Open in a new tab

aCounter anions are treated as monodentate ligands.

bCounter anions are treated as bidentate ligands.

cCounter anions are treated as tridentate ligands.

dTemperature dependence was analyzed by regression approximation, 103 ln β = 106 A T−2 + B.

Figure 1. ln β of hydrated Ca2+ ion.

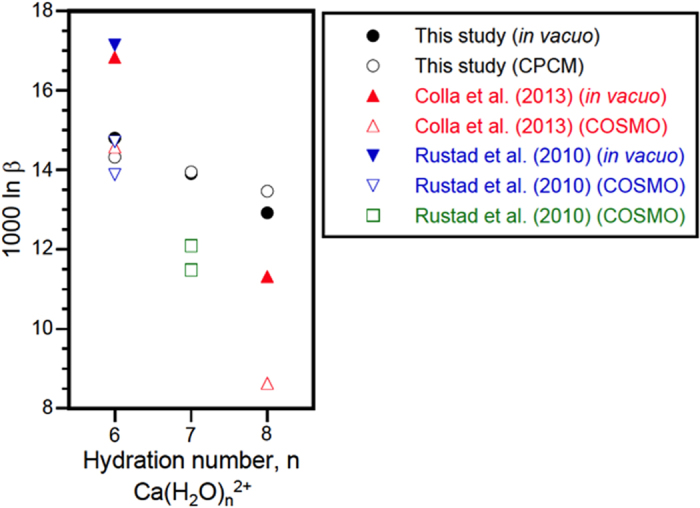
Figure 1

Open in a new tab

The ln β values of Ca(H2O)n2+ (n: 6, 7, or 8) are shown together with the literature values42,44 obtained for [Ca(H2O)n](H2O)m2+ (n: 6 or 8, m: 12, 14, or 16) with or without the solvation model (COSMO: conductor like screening model). Solid marks (in vacuo), open marks (CPCM or COSMO)42.

Figure 2. Temperature dependence of ln β.

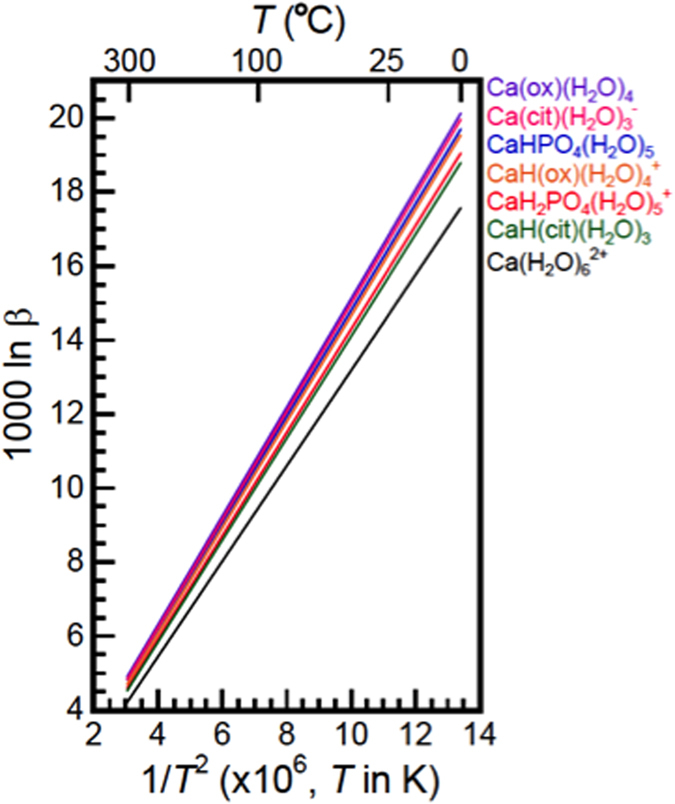
Figure 2

Open in a new tab

The ln β values of hydrated Ca2+, Ca-oxalates, Ca-citrates, and Ca-apatites are shown as linear functions of T−2.

Hydrated Ca(II) ions

The hydrated form of the Ca(II) ion is still the subject of debate and it is usually represented on the form [Ca(H2O)n]2+ with n = 6, 7 or 8 (refs 38, 39, 40). The atomic distances between Ca and O of hydration waters in the first coordination sphere modeled as octahedral Ca(H2O)62+ were analyzed to be 2.40–2.44 Å by x-ray diffraction41. In the present study, the Ca-O distance of Ca(H2O)62+ was calculated to be 2.405 Å (in vacuo) and 2.413 Å (CPCM). This agrees with the literature data obtained both experimentally (2.41–2.45 Å)41 and theoretically (2.380 Å (in vacuo) and 2.4034 Å (COSMO) for Ca(H2O)6•12H2O)42.

The absolute values of ln β estimated with the large cluster model (considering first and far coordination spheres) should be more accurate than estimates based on the small cluster model (considering first coordination sphere), if the modeled complex is stereochemically correct. Introducing the solvation model (setting the dielectrics around the molecule) may improve the calculation, but its effect in the β estimation looks to be insignificant29. The treatment of the second coordination sphere was performed for hydrated complexes of a congener Mg43. Arranging water molecules in the second coordination sphere shifts 1/100 of ln β, which is much smaller than the absolute ln β value.

The computational results of hydrated Ca ion are shown in Fig. 1 together with the theoretically obtained data42,44. Our results of ln β for the sixfold coordination Ca(H2O)62+ agree well with those of Colla et al.42 and Rustad et al.44. We also find that ln β decreases with increasing hydration number of the first coordination sphere from 6 to 8 (Fig. 1). On the other hand, we find that the magnitude of the isotopic fractionation between 6 and 8 is ~twice smaller than in the study of Colla et al.42. The origin of this discrepancy is unclear at the moment.

To further test the effect we have computed the ln β for seven-fold coordination of a phosphate (CaH2PO4(H2O)6+), a citrate (Ca(cit)(H2O)4−), and an oxalate (CaH(ox)(H2O)5+) (Table 1). At 310 K, their ln β values are systematically shifted by 0.7–0.9 permil compare to the six-fold coordination species similarly to what is observed for hydrated Ca molecules. Since the shift between 6- and 7-fold coordination is systematically in the same direction and magnitude, we adopt the small cluster model of six-fold coordination (in vacuo) for inter-molecule comparisons in the following sections.

Application to biological activity

The application of Ca isotopes as biomarkers is based on the fact that Ca is enriched in the heavier isotopes in the order: bones, blood and urine11,14,45,46. Since >99% of the Ca budget of the human body is located in the bones, small degree of bone loss releases detectable amount of Ca in the blood stream, with Ca being isotopically lighter compared to blood background (e.g. refs 12,14,45). It is therefore possible to monitor the Ca flux out and in the bones through Ca isotopic measurements, which is relevant to bone loss conditions associated with prolonged bed rests (e.g. refs 12,14) and potentially osteoporosis. However, the origin of this isotopic fractionation has been puzzling.

In the bones, Ca is under the form of hydroxyapatite, Ca5(PO4)3(OH). Hydroxyapatite precipitates and mineralizes in cells called osteoblasts47,48. On the other hand, osteoclasts are the cells responsible of the bone resorption that return Ca to the blood stream47,48. The speciation of Ca in the blood is more diverse. Depending on the methods, forty five to seventy percent of the total Ca are estimated to be free (Ca2+) and in the biologically active form, thirty-fifty percent are bound to proteins (principally albumins and globulins) and the remaining (~10%) is complexed (e.g citrate)49,50,51,52,53,54.

For the urine, Ca is first extracted from the blood and filtrated through the glomeruli and then a major fraction (>98%) of calcium is re-adsorbed through the renal tube and the loop of Henle54,55. Part of this re-adsorption occurs through active Na+/Ca2+ exchanger selecting free Ca2+ and therefore leaves the excreted urine enriched in complexed Ca (Ca citrate, Ca oxalate)54.

From our ab initio calculations we can infer some of the directions of the isotopic fractionations observed between bones, blood and urine. The enrichment of ~2.4‰ of the excreted urine compare to the whole blood14 is consistent with the difference of speciation of Ca as the urine is enriched in citrate and oxalate Ca complexes, both species having among the highest ln β (14.685 up to 15.755 at 310 K. Table 1 and Fig. 2) compared to free Ca (l nβ up to 13.727 at 310 K) which is the dominant specie in the blood. The difference in the l nβ(citrate/oxalate) and free Ca reproduce the right order of magnitude for the difference of isotopic composition between blood and urine (~2‰).

14On the other hand the enrichment in the lightest isotopes of Ca in the hydroxyapatite compared to the blood is not easily explained by equilibrium between free Ca2+ and phosphates, which should be enriched in the heavier isotopes, as previously noted by Albarede et al. (ref. 56). The most straightforward explanation is that most of the (light) Ca is transferred from the free Ca specie of the blood to the osteoblasts and that reaction of apatite precipitation is quantitative and therefore not associated with further isotopic fractionation. This would leave an isotopically light bone compared to the blood.

Calcium is up taken by the plants through Ca-specific ion channels57. The lighter isotope enrichment of plant roots compared to the soil solutions (~1‰) has been suggested to be due to kinetic isotopic fractionation during the uptake of Ca from the soil to the roots58. While possible, there is however no evidence that this uptake produces kinetic isotopic fractionation. In aqueous solution, the solvation number of Ca is one of the most complex. It has a hydrated structure that have water molecules in the first coordination shell between 6 to 8 (ref. 39) while other elements like Mg has a stable 6-fold coordination59. Our calculations show that the l nβ of the different coordinations change by ~1‰ between 6 and 7 and by ~1‰ between 7 and 8. Calcium enters the plant cell through Ca2+-permeable ion channels in their plasma membranes. The ion channels are size specifics and therefore select preferentially Ca with a specific coordination. While the hydration coordination of Ca selected by ion pump is an active subject of research60,61, recent work points toward hydrated Ca2+ to be favored61. This suggests that Ca pump would preferentially select isotopically lighter Ca2+ and would produce isotopic fractionation between soil solutions and roots with the right order of magnitude (1–2‰), which would explain the isotopically light roots without calling for un-observed kinetic isotopic fractionations.

The enrichment in the heavier isotopes of Ca in the stems and leaves of higher plants could also be explained by a difference of coordination of Ca between the roots and the shoots. In particular, the leaves are the isotopically heavier part of a plant at >1‰ heavier than the roots10,16,58,62,63,64. Calcium-oxalates are found in the stems and leaves of all photosynthesis plants37. In particular, Ca-oxalates are produced in order to regulate the concentration of free Ca2+ in leaves following water loss by evaporation37,65. Calcium oxalates have among the highest l nβ of the Ca species (Table 1) and therefore concentrate the heavier isotopes following oxalate precipitation in the upper parts of the plants.

Isotopic fractionation of Ca at equilibrium between several species (hydrated Cu ions, hydroxides, chlorides, sulfides, sulfate, and carbonates) and organic ligands (oxalate, citrates, and malates) was demonstrated theoretically. We found that speciations of Ca can lead to large (>3‰) isotopic fractionation at 298 K. The theoretical estimation of δ44Ca in ligand exchange between inorganic ligands is useful to understand the natural isotopic variations in nature like the distribution of Ca within plants or animal bodies.

Methods

Orbital geometries and vibrational frequencies of aqueous Ca(II) species were computed using the density functional theory (DFT) as implemented by the Gaussian09 code66. The DFT method employed here is a hybrid density functional consisting of Becke’s three-parameter non-local hybrid exchange potential (B3)67 with Lee-Yang-and Parr (LYP)68 non-local functionals. Using the 6–311 + G(d, p) basis set or higher is recommended for calculating the Mg (homologous element of Ca) complexes43,44. For Ca aquo ion, the 6–311 + G(2d, 2p) basis set was reported to be used for H and O, while the 6–311 G basis set for Ca42,44. Hence, in the present study, the 6–311 + G(d, p) basis set, which is an all-electron basis set, was chosen for H, C, N, O, F, P, S, Cl, and Ca in this study. Molecules were modeled without any forced symmetry. An “ultrafine” numerical integration grid was used and the SCF (self-consistent field) convergence criterion was set to 10−8. The conductor-like polarizable continuum model (CPCM) was tested to model Ca2+ solvation in water. All the geometry of the molecules are reported in the Supplementary Information.

The isotope enrichment factor due to intramolecular vibrations can then be evaluated from the reduced partition function ratio (s/s’)f19, also noted β,

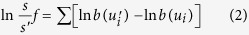graphic file with name srep44255-m2.jpg

where

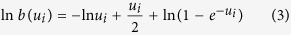graphic file with name srep44255-m3.jpg

and

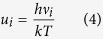graphic file with name srep44255-m4.jpg

in which ν stands for vibrational frequency, s for the symmetry number of the Ca compound, h the Plank constant, k the Boltzmann constant, and T the absolute temperature. The subscript i denotes the ith mode of molecular vibration, and primed variables refer to the light isotopologue. The isotope enrichment factor due to molecular vibrations can be evaluated from the frequencies (ν) summed over all the different modes. The isotopic difference in the stability constant of chemical reactions is identical to the difference of ln β between related species. For example, a chemical exchange reaction,

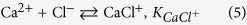graphic file with name srep44255-m5.jpg

with stability constant 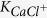Inline graphic, the isotope fractionation between the hydrated Ca2+ and CaCl+ is,

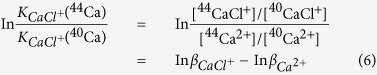graphic file with name srep44255-m7.jpg

Additional Information

How to cite this article: Moynier, F. and Fujii, T. Calcium isotope fractionation between aqueous compounds relevant to low-temperature geochemistry, biology and medicine. Sci. Rep. 7, 44255; doi: 10.1038/srep44255 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep44255-s1.pdf (137.2KB, pdf)

Acknowledgments

FM acknowledges funding from the European Research Council under the H2020 framework program/ERC grant agreement #637503 (Pristine), as well as the financial support of the UnivEarthS Labex program at Sorbonne Paris Cité (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02), and the ANR through a chaire d’excellence Sorbonne Paris Cité.

Footnotes

The authors declare no competing financial interests.

Author Contributions F.M. and T.F. designed the project. T.F. performed the calculations. F.M. wrote the manuscript.

References

  1. Palme H. & O’Neill H. In Treatise on Geochemistry Vol. 2 (eds Holland H. D. & Turekian K. K.) 1–38 (2003). [Google Scholar]
  2. Valdes M., Moreira M., Foriel J. & Moynier F. The nature of Earth’s building blocks as revealed by calcium isotopes. Earth Planet. Sci. Lett. 394, 135–145 (2014). [Google Scholar]
  3. Simon J. I. & DePaolo D. J. Stable calcium isotopic composition of meteorites and rocky planets. Earth Planet. Sci. Lett. 289, 457–466 (2010). [Google Scholar]
  4. Fantle M. S. & Tipper E. T. Calcium isotopes in the global biogeochemical Ca cycle: Implications for development of a Ca isotope proxy. Earth-Science Reviews 129, 148–177 (2014). [Google Scholar]
  5. Halicz L., Galy A., Belshaw N. S. & O’Nions R. K. High-precision measurement of calcium isotopes in carbonates and related materials by multiple collector inductively coupled plasma mass spectrometry (MC-ICP-MS). J. Anal. Atom. Spec. 14, 1835–1838 (1999). [Google Scholar]
  6. Heuser A. & Eisenhauer A. The calcium isotope composition (delta Ca-44/40) of NIST SRM 915b and NIST SRM 1486. Geostand. Geoanal. Res. 32, 311–315 (2008). [Google Scholar]
  7. De La Rocha C. L. & DePaolo D. J. Isotopic evidence for variations in the marine calcium cycle over the cenozoic. Science 289, 1176–1178 (2000). [DOI] [PubMed] [Google Scholar]
  8. Kasemann S. A. et al. Continental weathering following a Cryogenian glaciation: Evidence from calcium and magnesium isotopes. Earth Planet. Sci. Lett. 396, 66–77 (2014). [Google Scholar]
  9. Farkas J. et al. Calcium isotope record of Phanerozoic oceans: Implications for chemical evolution of seawater and its causative mechanisms. Geochim. Cosmochim. Acta 71, 5117–5134 (2007). [Google Scholar]
  10. Schmitt A. D. et al. Processes controlling the stable isotope compositions of Li, B, Mg and Ca in plants, soils and waters: A review. Comptes Rendus Geoscience 344, 704–722 (2012). [Google Scholar]
  11. Skulan J. & DePaolo D. J. Calcium isotope fractionation between soft and mineralized tissues as a monitor of calcium use in vertebrates. Proc. Nat. Acad. Sci. 96, 13709–13713 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Morgan J. L. L. et al. Rapidly assessing changes in bone mineral balance using natural stable calcium isotopes. Proceedings of the National Academy of Sciences of the United States of America 109, 9989–9994 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. DePaolo D. J. In Rev Mineral Geochem Vol. 55 Reviews in Mineralogy & Geochemistry (eds Johnson C. M., Beard B. L., & Albarede F.) 255–288 (2004). [Google Scholar]
  14. Channon M. B. et al. Using natural, stable calcium isotopes of human blood to detect and monitor changes in bone mineral balance. Bone 77, 69–74 (2015). [DOI] [PubMed] [Google Scholar]
  15. Hirata T. et al. Isotopic Analysis of Calcium in Blood Plasma and Bone from Mouse Samples by Multiple Collector-ICP-Mass Spectrometry. Anal Sci 24, 1501–1507 (2008). [DOI] [PubMed] [Google Scholar]
  16. Hindshaw R. S. et al. Calcium isotope fractionation in alpine plants. Biogeochemistry 112, 373–388 (2013). [Google Scholar]
  17. Farkas J., Dejeant A., Novak M. & Jacobsen S. B. Calcium isotope constraints on the uptake and sources of Ca2+ in a base-poor forest: A new concept of combining stable (delta Ca-44/42) and radiogenic (epsilon(Ca)) signals. Geochim. Cosmochim. Acta 75, 7031–7046 (2011). [Google Scholar]
  18. Cobert F. et al. Experimental identification of Ca isotopic fractionations in higher plants. Geochim. Cosmochim. Acta 75, 5467–5482, 2 (2011). [Google Scholar]
  19. Bigeleisen J. & Mayer M. G. Calculation of equilibrium constants for isotopic exchange reactions. J. Chem. Phys. 15, 261–267 (1947). [Google Scholar]
  20. Schauble E. A. In Reviews in Mineralogy & Geochemistry Vol. 55 (ed. Beard B. L., Johnson C. M. & Albarede F.) 65–111 (2004). [Google Scholar]
  21. Russell W. A. & Papanastassiou D. A. Calcium isotope fractionation in ion-exchange chromatography. Anal. Chem. 50, 1151–1154 (1978). [Google Scholar]
  22. Balter V. et al. Contrasting Cu, Fe, and Zn isotopic patterns in organs and body fluids of mice and sheep, with emphasis on cellular fractionation. Metallomics 5, 1470–1482 (2013). [DOI] [PubMed] [Google Scholar]
  23. Fujii T. & Albarede F. Ab Initio Calculation of the Zn Isotope Effect in Phosphates, Citrates, and Malates and Applications to Plants and Soil. Plos One 7, doi: 10.1371/journal.pone.0030726 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fujii T., Moynier F., Pons M. L. & Albarede F. The origin of Zn isotope fractionation in sulfides. Geochim. Cosmochim. Acta 75, 7632–7643 (2011). [Google Scholar]
  25. Fujii T. et al. Mass-Dependent and Mass-Independent Isotope Effects of Zinc in a Redox Reaction. J. Phys. Chem. A 113, 12225–12232 (2009). [DOI] [PubMed] [Google Scholar]
  26. Black J., Kavner A. & Schauble E. Calculation of equilibrium stable isotope partition function ratios for aqueous zinc complexes and metallic zinc. Geochim Cosmochim Acta 75, 769–783 (2011). [Google Scholar]
  27. Moynier F., Fujii T., Shaw A. & Le Borgne M. Heterogeneous distribution of natural zinc isotopes in mice. Metallomics 5, 693–699 (2013). [DOI] [PubMed] [Google Scholar]
  28. Fujii T., Moynier F., Abe M., Nemoto K. & Albarede F. Copper isotope fractionation between aqueous compounds relevant to low temperature geochemistry and biology. Geochim. Cosmochim. Acta 110, 29–44 (2013). [Google Scholar]
  29. Fujii T., Moynier F., Blichert-Toft J. & Albarede F. Density functional theory estimation of isotope fractionation of Fe, Ni, Cu, and Zn among species relevant to geochemical and biological environments. Geochim. Cosmochim. Acta 140, 553–576 (2014). [Google Scholar]
  30. Fujii T., Moynier F., Dauphas N. & Abe M. Theoretical and experimental investigation of nickel isotopic fractionation in species relevant to modern and ancient oceans. Geochim. Cosmochim. Acta 75, 469–482 (2011). [Google Scholar]
  31. Dupuis R., Benoit M., Nardin E. & Meheut M. Fractionation of silicon isotopes in liquids: The importance of configurational disorder. Chem. Geol. 396, 239–254 (2015). [Google Scholar]
  32. Fujii T., Pringle E. A., Chaussidon M. & Moynier F. Isotope fractionation of Si in protonation/deprotonation reaction of silicic acid: A new pH proxy. Geochim. Cosmochim. Acta 168, 193–205 (2015). [Google Scholar]
  33. Hill P. S. & Schauble E. A. Modeling the effects of bond environment on equilibrium iron isotope fractionation in ferric aquo-chloro complexes. Geochim. Cosmochim. Acta 72, 1939–1958 (2008). [Google Scholar]
  34. Rustad J. R. & Yin Q.-Z. Iron isotope fractionation in the Earth’s lower mantle. Nature Geoscience 2, 514–518 (2009). [Google Scholar]
  35. Fujii T., Moynier F., Telouk P. & Albarede F. Isotope fractionation of iron(III) in chemical exchange reactions using solvent extraction with crown ether. J. Phys. Chem. A 110, 11108–11112 (2006). [DOI] [PubMed] [Google Scholar]
  36. Moynier F., Fujii T., Wang K. & Foriel J. Ab initio calculations of the Fe(II) and Fe(III) isotopic effects in citrates, nicotianamine, and phytosiderophore, and new Fe isotopic measurements in higher plants. Comptes Rendus Geoscience 345, 230–240 (2013). [Google Scholar]
  37. Franceschi V. R. & Nakata P. A. In Annual Review of Plant Biology Vol. 56 Annual Review of Plant Biology 41–71 (2005). [DOI] [PubMed] [Google Scholar]
  38. Hewish N. A., Neilson G. W. & Enderby J. E. Environment of Ca2+ ions in aqueous solvent. Nature 297, 138–139 (1982). [Google Scholar]
  39. Katz A. K., Glusker J. P., Beebe S. A. & Bock C. W. Calcium ion coordination: A comparison with that of beryllium, magnesium, and zinc. J Am Chem Soc 118, 5752–5763 (1996). [Google Scholar]
  40. Jalilehvand F. et al. Hydration of the calcium ion. An EXAFS, large-angle X-ray scattering, and molecular dynamics simulation study. J Am Chem Soc 123, 431–441 (2001). [DOI] [PubMed] [Google Scholar]
  41. Magini M. X-Ray Diffraction of Ions in Aqueous Solutions: Hydration and Complexation Formation (CRC Press, 1988). [Google Scholar]
  42. Colla C. A., Wimpenny J., Yin Q. Z., Rustad J. R. & Casey W. H. Calcium-isotope fractionation between solution and solids with six, seven or eight oxygens bound to Ca(II). Geochim. Cosmochim. Acta 121, 363–373 (2013). [Google Scholar]
  43. Schott J., V. M., Fujii T., Pearce C. R. & Oelkers E. The Control of Magnesium Aqueous Speciation on Mg Isotope Composition in Carbonate Minerals: Theoretical and Experimental Modeling. Chem. Geol. 445, 120–134 (2016). [Google Scholar]
  44. Rustad J. R. et al. Isotopic fractionation of Mg2+(aq), Ca2+(aq), and Fe2+(aq) with carbonate minerals. Geochim. Cosmochim. Acta 74, 6301–6323, 8 (2010). [Google Scholar]
  45. Heuser A. & Eisenhauer A. A pilot study on the use of natural calcium isotope ((44)ca/Ca-40) fractionation in urine as a proxy for the human body calcium balance. Bone 46, 889–896 (2010). [DOI] [PubMed] [Google Scholar]
  46. Heuser A., Eisenhauer A., Scholz-Ahrens K. E. & Schrezenmeir J. Biological fractionation of stable Ca isotopes in Gottingen minipigs as a physiological model for Ca homeostasis in humans. Isotopes in Environmental and Health Studies 52, 633–648 (2016). [DOI] [PubMed] [Google Scholar]
  47. Beck G. R. Inorganic phosphate as a signaling molecule in osteoblast differentiation. Journal of Cellular Biochemistry 90, 234–243 (2003). [DOI] [PubMed] [Google Scholar]
  48. Heinegard D. & Oldberg A. Structure and biology of cartilage and bone-matrix noncollagenous macromolecules. Faseb J 3, 2042–2051 (1989). [DOI] [PubMed] [Google Scholar]
  49. Baird G. S. Ionized calcium. Clin Chim Acta 412, 696–701 (2011). [DOI] [PubMed] [Google Scholar]
  50. Copp D. H. Endocrine control of calcium homeostatis Journal of Endocrinology 43, 137–140 (1969). [DOI] [PubMed] [Google Scholar]
  51. Kallner A. Preanalytical procedures in the measurement of ionized calcium in serum and plasma. Europ. J. Clin. Chem. Clin. Bioch. 34, 53–58 (1996). [DOI] [PubMed] [Google Scholar]
  52. Robertson W. G. & Marshall R. W. Calcium measurements in serum and plasma-total and ionized. Crc Critical Reviews in Clinical Laboratory Sciences 11, 271–304 (1979). [DOI] [PubMed] [Google Scholar]
  53. McLean F. C. & Hastings A. B. Clinical estimation and significance of calcium-ion concentrations in the blood. Am. J. Med. Sci. 189, 601–613 (1935). [Google Scholar]
  54. Blaine J., Chonchol M. & Levi M. Renal Control of Calcium, Phosphate, and Magnesium Homeostasis. Clin. J. Am. Soc. Neph. 10, 1257–1272 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Hoenderop J. G. J., Nilius B. & Bindels R. J. M. Calcium absorption across epithelia. Physiol Rev 85, 373–422 (2005). [DOI] [PubMed] [Google Scholar]
  56. Albarede F., Telouk P. & Balter V. In Non-traditional stable isotopes Vol. 82 (eds Teng F.-Z., Dauphas N. & Watkins J.) (Mineralogical Society of America, 2017). [Google Scholar]
  57. White P. J. Calcium channels in higher plants. Biochim. Biophys. Acta-Biomembranes 1465, 171–189 (2000). [DOI] [PubMed] [Google Scholar]
  58. Wiegand B. A., Chadwick O. A., Vitousek P. M. & Wooden J. L. Ca cycling and isotopic fluxes in forested ecosystems in Hawaii. Geophys. Res. Lett. 32 (2005). [Google Scholar]
  59. Ikeda T., Boero M. & Terakura K. Hydration properties of magnesium and calcium ions from constrained first principles molecular dynamics. J. Chem. Phys. 127 (2007). [DOI] [PubMed] [Google Scholar]
  60. Tang L. et al. Structural basis for Ca2+ selectivity of a voltage-gated calcium channel. Nature 505, 56-+ (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Tang L. et al. Structural basis for inhibition of a voltage-gated Ca2+ channel by Ca2+ antagonist drugs. Nature 537, 117–121 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Cobert F. et al. Experimental identification of Ca isotopic fractionations in higher plants. Geochim. Cosmochim. Acta 75, 5467–5482 (2011). [Google Scholar]
  63. Schmitt A. D. et al. Calcium isotope fractionation during plant growth under a limited nutrient supply. Geochim. Cosmochim. Acta 110, 70–83 (2013). [Google Scholar]
  64. Holmden C. & Belanger N. Ca isotope cycling in a forested ecosystem. Geochim. Cosmochim. Acta 74, 995–1015 (2010). [Google Scholar]
  65. Mazen A. M. A., Zhang D. Z. & Franceschi V. R. Calcium oxalate formation in Lemna minor: physiological and ultrastructural aspects of high capacity calcium sequestration. New Phytologist 161, 435–448 (2004). [DOI] [PubMed] [Google Scholar]
  66. Gaussian 09, Revision B.01, Gaussian, Inc.: Wallingford CT (2009).
  67. Becke A. D. Density-functional thermochemistry. 3. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993). [Google Scholar]
  68. Lee C. T., Yang W. T. & Robert G. P. Development of the colle-salvetti correlation-energy formula into a functional of the electron-density. Physical Review B 37, 785–789 (1988). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep44255-s1.pdf (137.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES