Abstract
The use of isotopically labeled tracer substrates is an experimental approach for measuring in vivo and in vitro intracellular metabolic dynamics. Stable isotopes that alter the mass but not the chemical behavior of a molecule are commonly used in isotope tracer studies. Because stable isotopes of some atoms naturally occur at non-negligible abundances, it is important to account for the natural abundance of these isotopes when analyzing data from isotope labeling experiments. Specifically, a distinction must be made between isotopes introduced experimentally via an isotopically labeled tracer and the isotopes naturally present at the start of an experiment. In this tutorial review, we explain the underlying theory of natural abundance correction of stable isotopes, a concept not always understood by metabolic researchers. We also provide a comparison of distinct methods for performing this correction and discuss natural abundance correction in the context of steady state 13C metabolic flux, a method increasingly used to infer intracellular metabolic flux from isotope experiments.
Keywords: stable isotopes, natural abundance correction, metabolic flux analysis, reproducibility
1. Introduction
Metabolic fluxes are measurements of intracellular metabolic activity that are often more descriptive than measurements of intracellular metabolite concentrations (Nielsen, 2003; Sauer, 2006). Isotope labeling is used to quantify metabolic fluxes in vivo and in vitro (Cascante and Marin, 2008; Nielsen, 2003). In an in vitro isotope labeling experiment, an isotopically labeled tracer substrate is introduced to a live cell culture. The distribution of isotopic enrichment between cellular metabolites is then evaluated using mass spectrometry (MS) or nuclear magnetic resonance (NMR). Subsequently, metabolic fluxes are inferred by the relative distribution of isotopic enrichment through metabolic pathways (Chance et al., 1983; Dauner and Sauer, 2000; Wittmann, 2002). The estimated flux measurements can then be used to assess the biochemical connectivity and kinetics of a metabolic network.
The traditional uses of isotope labeling experiments fall under mass isotopomer distribution analysis, a term that is sometimes used interchangeably with isotopomer enrichment assays and isotopomer spectral analysis (Buescher et al., 2015; Chubukov et al., 2013; Crown et al., 2016; Hellerstein and Neese, 1999; Kelleher et al., 1994; Mehrmohamadi et al., 2014; Papageorgopoulos et al., 1999; Revelles et al., 2013; Shestov et al., 2016; Strong et al., 1985; Wittmann, 2007). These assays can measure the kinetics of condensation reactions, such as polymeric protein and fatty acid synthesis, by adding tracers labeled with stable isotopes to catabolic biochemical pathways and tracing the transfer of isotopic labels between enriched precursors and their macromolecular products. The dynamics of molecular synthesis can then be inferred by a series of theoretical or experimental calibrations that compare the macromolecular isotopic signatures of the relevant cellular compounds to pre-determined metabolic fluxes (Tserng and Kalhan, 1983).
When analyzing data from isotope labeling experiments, it is imperative to separate isotopic labelling that came from the addition of an isotopically labeled tracer and isotopic labelling that came from the natural abundance (NA) of stable isotopes (Rosenblatt et al., 1992). The mass spectra of metabolites can be significantly altered by atoms of stable isotopes that occur naturally at non-negligible abundances, such as carbon, hydrogen, nitrogen, oxygen, and sulfur (Berglund and Wieser, 2011). Accordingly, a number of methods for NA correction have been developed and widely implemented (Allen and Ratcliffe, 2009; Biemann, 1962; Brauman, 1966; Brunengraber et al., 1997; Dauner and Sauer, 2000; Dunstan, 1988; Fernandez et al., 1996; Jennings and Matthews, 2005; Lee et al., 1991; Millard et al., 2012; Moseley, 2010; Rosenblatt et al., 1992; Wahl et al., 2004; van Winden et al., 2002a; Wittmann, 2002; Yang et al., 2009) Functional enrichment assays that are only analyzed qualitatively and do not require high accuracy may not require NA correction in some circumstances. However, measurement errors (including those that arise from improper correction of NA) can yield misleading results in quantitative analyses such as mass isotopomer distribution analysis (Fernandez et al., 1996) and in the non-linear parameter estimation associated with 13C metabolic flux analysis (MFA) (Wittmann, 2002).
In two definitive papers on NA correction of stable isotopes, Rosenblatt (1992) and Fernandez et al. (1996) demonstrated the consequences of flawed NA correction on measurements of isotopomer distributions. Accordingly, they drew a clear distinction between the incorrect “classical” method and the correct “skewed” method for NA correction. Wittmann et al. (2002) also demonstrated similar consequences in a mathematical analysis of MFA. While these articles (and others) make it clear that the classical correction approach should not be used, we found evidence that inadequate correction of NA method may continue in the published literature. A search for research articles published between 2009 and 2015 that cite either Biemann (1962) or Brauman (1966) (two papers that rely on classical-type correction approaches) returned a number of peer reviewed articles. While simply citing the classical method alone does not suggest inadequate correction of NA, several of these articles either did not also cite later methods that relied on the skewed approach or made it clear within the manuscript that a form of classical correction was performed (Olstad et al., 2007; Walls et al., 2014; Zheng et al., 2015). In our experience, the underlying theory of NA correction is not always well understood by metabolic researchers. Thus, one of the primary motivations of this review is to clarify the difference between the older classical approach and the accepted optimal approach for NA correction as well as to demonstrate why understanding the distinction between these methods is important. We do so by explaining the complex mathematical concepts underlying this critical procedure in a way that is accessible to a broad audience. Moreover, given the massive amounts of data generated by the metabolomics community, scientists must be cognizant of the pitfalls of different quantitative approaches in order to guarantee the reproducibility of published research data.
In this work, we illustrate methods for NA correction, while demonstrating that inadequate correction of NA can result in erroneous estimates of isotopomer distribution and flux estimates. In particular, we review three related correction approaches: matrix-based classical correction (Biemann, 1962; Brauman, 1966), matrix-based “skewed” correction (Fernandez et al., 1996; van Winden et al., 2002a), and a least-squares implementation of the “skewed” correction method (Millard et al., 2012). We have adopted the terminology (“classical” and “skewed”) used by Rosenblatt et al. (1992) and Fernandez at al. (1996) when discussing the different approaches. We evaluate the performance of each method using synthetic datasets. We further evaluate these methods in the context of steady state 13C MFA implemented in OpenFLUX (Quek et al., 2009), which is based on the widely used elementary metabolite unit framework (Antoniewicz et al., 2007), using both liquid chromatography (LC) and gas chromatography (GC) MS based datasets.
2. Correcting mass isotopomer distributions
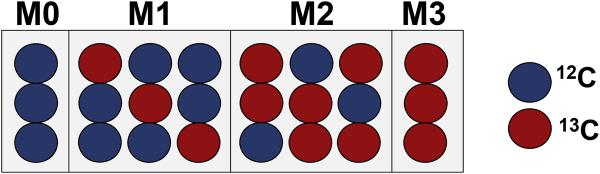
Isotope labeling experiments exploit the natural phenomenon of isotopic isomers. A metabolite can have distinct isotopic isomers (also known as isotopomers) with the same chemical formula but a different number and arrangement of isotopes of one or more elements. The collection of isotopomers of a metabolite can be further grouped into either positional or mass isotopomers. Positional isotopomers have identical global isotopic composition but differ in the position of their isotopes (e.g., [1-13C] glucose is a positional isotopomer of [6-13C] glucose). Mass isotopomers, also known as isotopologues, are isotopic isomers that differ in the number and arrangement of isotopes, resulting in different molecular weights (Brunengraber et al., 1997). A three carbon molecule will have up to 8 positional isotopomers and 4 mass isotopomers based on the isotopic composition of 12C and 13C (Figure 1). For each metabolite measured in a biomass sample, spectrometers distinguish mass isotopomers by the mass shift of spectral peaks relative to the nominal mass of the metabolite. The spectral peak of the lowest molecular weight is usually the nominal mass of the metabolite. The remaining satellite spectral peaks typically correspond to mass isotopomers containing heavier (but possibly lighter) isotopes that are identified as M0, M1, M2, etc. (where the number following the M indicates the atomic mass shift from the nominal mass of M0).
Figure 1. Mass and positional isotopomers of a three carbon molecule containing 12C and 13C isotopes.
For a three carbon molecule that contains 12C and/or 13C there are 2n positional isotopomers, where n is the number of carbons in the molecule. In this example, there are eight unique positional isotopomers. A mass isotopomer or an isotopologue is made up of one or more isotopomers of the same mass. A metabolite can have up to n + 1 mass isotopomers. Here, there are four mass isotopomers with four distinct molecular weights that sequentially differ by one atomic mass unit. The isotopomer composed of only 12C corresponds to the nominal mass of the molecule and also represents the mass isotopomer with the lowest molecular weight (M0). The higher mass isotopomers (M1, M2, and M3) represent, respectively, molecules with one, two, or three 13C atoms with a mass shift of one, two, or three atomic mass units. Blue circles indicate 12C and red circles indicate 13C.
A mass isotopomer distribution (MID), which may also be referred to as a mass distribution vector or MDV, quantitates the relative abundance of mass isotopomers of a metabolite (Hellerstein and Neese, 1999; Lee et al., 1991; Yang et al., 2009). The fractional abundance of the i-th mass isotopomer in a MID, FAMi, can be calculated by
| (1) |
where i is the incremental increase in atomic mass, Imi is the measured spectral intensity obtained at a specific mass-to-charge ratio corresponding to an M0+i mass shift, and n is the total number of possible mass isotopomers for a given metabolite. The sum of all FAMi values in a MID is 1.
MIDs enriched with heavy carbon can be used to evaluate hypotheses about physiological or cellular mechanisms. In particular, mathematical models can characterize the structure and kinetics of metabolic networks using constraints from experimental incorporation and distribution of stable isotopes of carbon across metabolites (Cobelli et al., 1987). Carbon is naturally found as two stable isotopes, 12C and 13C, which have relative abundances of 98.9% and 1.1%, respectively (Table 1). The International Union of Pure and Applied Chemistry (IUPAC) maintains the Table of Isotopic Compositions of the Elements (TICE), which was recently revised to quantify uncertainty in measurements of isotopic standards (Meija et al., 2016). Carbon is also found as a radioactive isotope, 14C, which is present in trace amounts and often used for carbon dating (Firestone et al., 1999). Nonetheless, 13C is frequently used in isotope labeling experiments because it is easily distinguished from 12C via MS or NMR and its lack of radioactivity. Because 13C naturally occurs at a non-negligible level, its NA can impact the interpretation of mass spectral data. Therefore, inadequate NA correction of stable isotopes can magnify the uncertainty in MID measurements and therefore yield misleading conclusions about cellular processes. While this work primarily addresses NA correction of stable isotopes in 13C based isotope labeling experiments, the results and conclusions can be generalized to experiments with other commonly used heavy stable isotopes such as 15N.
Table 1.
The natural abundance of stable isotopes utilized by all correction methods tested.
| Element | Stable Isotopes | natural abundance of isotopes (in order listed) | |||
|---|---|---|---|---|---|
| Hydrogen (H) | 1H, 2H | 0.999885 | 0.000115 | ||
| Carbon (C) | 12C, 13C | 0.9893 | 0.0107 | ||
| Nitrogen (N) | 14N, 15N | 0.99632 | 0.00368 | ||
| Oxygen (O) | 16O, 17O, 18O | 0.99757 | 0.00038 | 0.00205 | |
| Silicon (Si) | 28Si, 29Si, 30Si | 0.922297 | 0.046832 | 0.030872 | |
| Sulphur (S) | 32S, 33S, 34S, 36S | 0.9493 | 0.0076 | 0.0429 | 0.0002 |
In an isotope labeling experiment, all measured mass isotopomers may contain interference from naturally occurring stable isotopes along with enrichment of stable isotopes from the labeled tracer substrate. Experimentally, it is the latter quantity that is of interest. While qualitative inspection of uncorrected MIDs may be sufficient for some empirical investigations, more detailed analyses of measured MIDs will almost always require the correction of naturally occurring isotopes prior to quantitative processing (Figure 2). Visual comparison of labeled and unlabeled samples can provide information about whether observed isotopic enrichment is experimentally derived or represents contribution from NA. Nonetheless, simply subtracting an unlabeled MID from a labeled MID will not adequately correct for NA or quantify experimental enrichment (Buescher et al., 2015). Commonly used methods for the accurate correction of NA rely on metabolite-specific correction factors that can be represented in a correction matrix (CM) that separate NA from enrichment in measured MIDs (Biemann, 1962; Brauman, 1966; Dunstan, 1988; Fernandez et al., 1996; Millard et al., 2012; Moseley, 2010; Rosenblatt et al., 1992). Ideally, these correction factors are derived directly from measurements of compound-specific standards. However, such an approach requires the expensive and laborious collection of numerous standards for every metabolite measured in an experiment. An alternative approach is to calculate the expected NA distribution of these standards using elemental correction factors with a combinatorial probability function derived from the known NA of the constituent atoms in a metabolite (Table 1). Whether NA distributions are experimentally measured or theoretically computed, they can be augmented with calibration experiments to account for instrumentation noise (Fernandez et al., 1996; Jennings and Matthews, 2005). Ultimately, the choice of whether to correct or not for NA depends on several factors including the tool for detection of mass isotopmers, method for analysis of isotope labeling data, and the biological insight warranting an isotope labeling experiment.
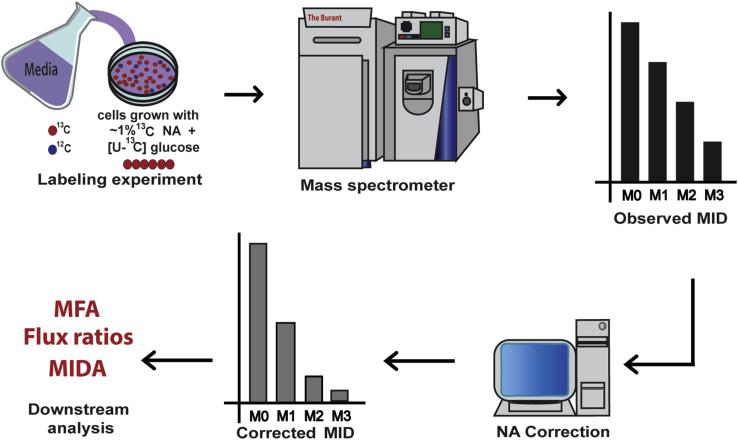
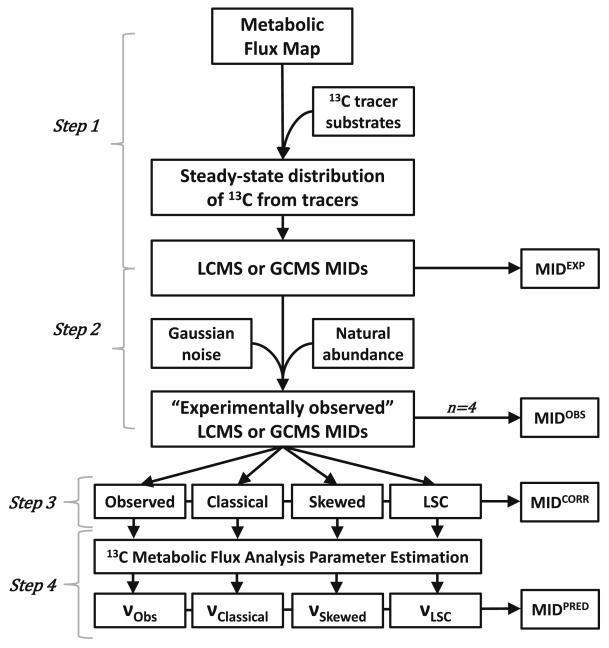
Figure 2. Workflow of a 13C labeling experiment.
A typical workflow of a 13C isotope labeling experiment is presented. Cells are first grown in media containing at least one 13C labeled substrate. After the experiment, samples are analyzed via mass spectrometry. The spectral data are processed and mass isotopomer distributions (MIDs) of metabolites of interest are produced. The observed MIDs are corrected for natural abundance (NA) of stable isotopes by a computer program to generate corrected MIDs that can be used for downstream quantitative analysis.
The choice of specrometeric detection tool can dictate the extent of interference of NA on enrichment of stable isotopes from the labeled tracer. An analytical detection tool such as GCMS that requires dervitization to enable chromotagrpahic seperation chemically introduces often Si-containing bulky moieties to measured metabolites. These additional moieties often comprise the primariy source of NA in measured MIDs and likely warrant correction for NA regardless of the method for anlaysis of the MID. In contrast, detection tools that do not require deriatiztion agents such as LCMS generate MIDs where the primary soruce of NA is the metabolite carbon backbone. In such cases, low interfernece from NA may not necessarily warrant NA correction depending on the computational method used to analyze the MID.
In addition to spectrometric tools, analytical and computational tools for the analysis of distribution of isotopes in labeling experiments also dictate the necessity for NA correction. For direct interpretation of 13C labeling patterns, also called 13C tracer analysis, necessity for correction depends on the sensitivity of the tracer analysis to measurements error in the MIDs. Realtively simpy estimates of nutrient or pathway contribution to the production of a certain metabolite may be only marginally sensitive to small errors due to NA or tracer impurity as explained in Buescher et al. Yet, Fernandez et al. demonstrated an example where a simple estimate of the contribution of gluconeogenesis to gluose in perfused rat liver is significantly sensitive to NA error. For 13C metabolic flux analysis, there are also various software packages based on differing algorithms which vary in their treatment of NA (Quek et al., 2009; Sokol et al., 2012; Srour et al., 2011; Weitzel et al., 2013; Young, 2014; Zamboni et al., 2005). Some of these applications require NA correction of input data for at least the non-carbon elements while others can simulate internally the NA of the non-carbon elements and the carbon backbone. Taking into account the numerous and varied spectrometric and computational tools available, it is imperative for researchers to investigate the sensitivtiy of their specific experimental and analytical approach to errors in MIDs due to NA and decide on whether to correct or not for NA accordingly.
2.1 Methods for the correction of natural abundance: a brief history
Biemann (1962) illustrated an early method for decomposing the spectrum of a mixture made up of two isotopomers of the same compound. This method was adapted to NA correction because an isotopically enriched compound consists of at least two isotopomers: a natural isotopomer and an enriched isotopomer. Accordingly, the Biemann approach was widely adapted for the deconvolution of NA from isotopic enrichments. In a stepwise fashion, the Biemann approach computed the contribution of naturally abundant isotopes to each mass spectral peak of a labeled compound based on the measured spectral peaks of an unlabeled standard. A few years later, Brauman (1966) formulated a complementary method that utilized matrix notation and a least-squares approach to infer the individual spectrum of isotopomers that make up a molecule. Brauman’s method demonstrated the concept of an abundance matrix, which is a metabolite specific matrix of correction factors that describe the contribution of naturally abundant isotopes to the measured spectral abundances (or intensities) of the metabolite (Jennings and Matthews, 2005). In the context of NA correction, abundance matrices are commonly termed correction matrices.
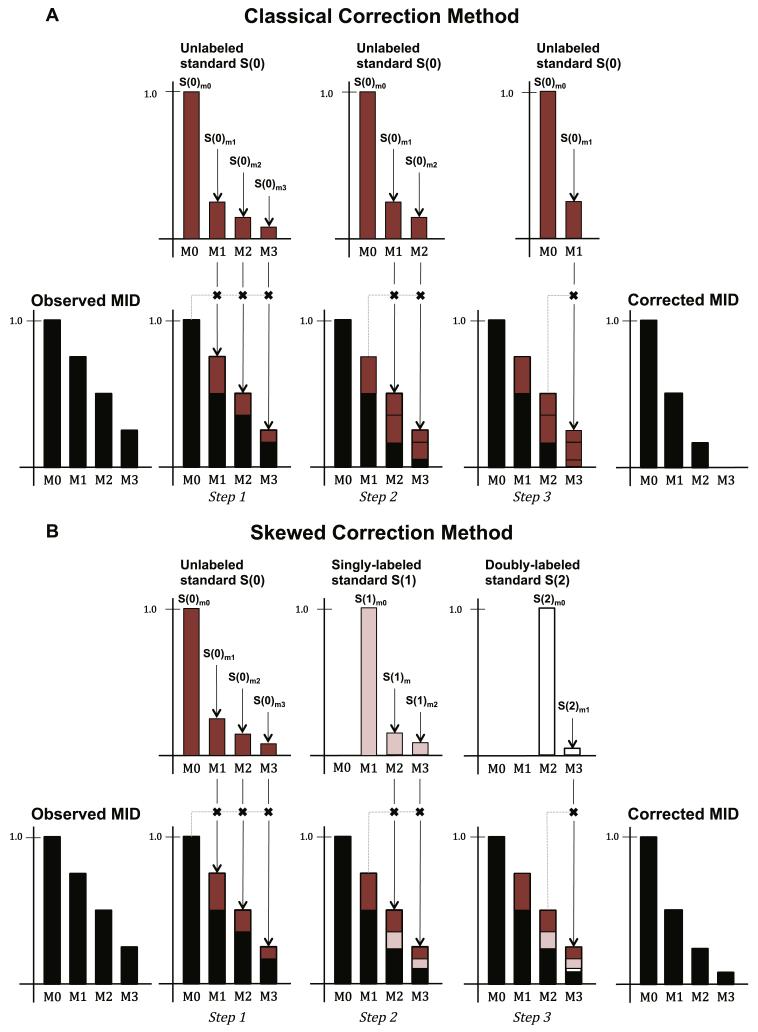
While they represent important and fundamental advances, the approaches of Biemann (1962) and Brauman (1966) made the same flawed assumption about the distribution of stable isotopes. Specifically, their methods assumed that for any metabolite, the MID of a labeled standard (with known enrichment of isotopes) is equivalent to the MID of an unlabeled standard (without any enriched isotopes) except for a mass shift corresponding to the number of enriched isotopes in the labeled standard. Therefore, they assumed that only a single measurement (or theoretical estimate) of an unlabeled standard was sufficient for NA correction (Figure 3A). Why this is incorrect is explained below. Throughout this review, we refer to correction methods that rely heavily on this assumption as classical approaches (Fernandez et al., 1996; Rosenblatt et al., 1992). A direct consequence of the classical assumption is often a systematic overestimation of the contribution of NA and underestimation of the contribution of experimental enrichment from a labeled substrate.
Figure 3. Correcting for natural abundance by the classical and skewed correction methods.
An observed (uncorrected) MID of a three-carbon metabolite with four measured mass isotopomers is used as an example. The observed MID is assumed to have enrichment from a tracer substrate as well as inherent natural abundance (NA). (A) In the classical correction method, the MID of a pure standard, S(0), is measured (or computed). S(0) consists of mass isotopomer that are 1, 2, or 3 atomic mass units heavier than the nominal mass of the pure metabolite (and are identified as S(0)m1, S(0)m2, and S(0)m3, respectively) which represent the proportion of 13C from NA. Sequentially, the observed MID is adjusted based on the MID of S(0). Step 1: The unlabeled standard is used to compute the proportions of the M1, M2, and M3 abundance that can be attributed to the pool of naturally abundant isotopomers. The observed M0 absolute value (which is also the expected M0 absolute value) is multiplied by the relative proportion of m1 to m0, m2 to m0, and m3 to m0 in the S(0) MID, and the resulting contributions are removed from the observed M1, M2, and M3 abundances, respectively. Step 2: Next, S(0) is used to compute the proportion of M2 and M3 abundances that can be attributed to the pool of naturally abundant isotopomers in a similar fashion. Step 3: Finally, a proportion of M3 due to natural abundance is computed. After subtraction of each sequentially adjusted proportion from the observed MID, the remaining fractional abundances represent the corrected MID. (B) In the skewed correction method, the S(0) MID is measured (or computed) along with the MIDs of n-labeled standards. In this example, the standards include singly-, doubly-, and triply-labeled standards, or S(1), S(2), and S(3), respectively. The MID profiles of each labeled standard are different. For example, the S(2)m1 to S(2)m0 proportion is much lower than the corresponding S(0)m1 to S(0)m0 proportion. Similar to the classical method, the contribution from isotopomers that are singly, doubly, and triply labeled with naturally abundant stable isotopes are removed from the observed mass isotopomers to yield the corrected MID. The classical correction, however, overestimates the presence of naturally abundant heavy stable isotopes in labeled metabolites. In this example, the overestimation by the classical method eliminated the M3 abundance in the corrected MID. While the fractional abundance values of a MID typically sum to 1, in these examples we scaled the M0 nominal mass abundance to 1 to better illustrate the correction process.
In reality, enrichment of stable isotopes from an isotopically labeled substrate results in a non-linear shift in the distribution of naturally abundant isotopes (Figure 3B), which the classical approach does not account for. Dunstan (1988) addressed this limitation by using a probability equation that more accurately modeled the multinomial distribution of stable isotopes in a MID. In addition, Rosenblatt et al. (1992) derived correction factors that took into account what they referred to as a “skew” in the distribution of naturally abundant isotopes due to experimental (in contrast to natural) isotopic enrichment. These correction factors were specific to the derivation of molar percent excess, a measure of the enrichment of a particular isotope above the measure of its NA. Lee et al. (1991) extended Brauman’s approach to account for the multinomial “skew” effect via a binomial probability equation for the correction of 13C NA (because carbon only occurs in one of two stable forms). Each of these approaches relied on compound-specific NA distributions that were either measured experimentally or computed using theoretical elemental abundances from a multinomial probability equation.
Ideally, for every experiment, correction factors will be derived from measurements of pure and n-labeled standards for all measured mass isotopomers. These experiment specific measurements can adjust for fluctuations in the NA of stable isotopes that may arise from variations in both instrumentation and naturally abundant isotopic content in tracer compounds (Allen and Ratcliffe, 2009; Fernandez et al., 1996; Jennings and Matthews, 2005). To do so, however, requires calibration procedures and measurements of a very large number of standards, which is an expensive and laborious process when performed routinely. To address these limitations, Fernandez et al. (1996) developed a computer program that used a theoretical correction matrix method that accounted for isotope distribution “skew” and developed an optimization function that adjusted for instrumentation error using one unlabeled standard for each metabolite. The optimization function minimized the difference between the measured and predicted mass spectra of the unlabeled standard (Fernandez et al., 1996). This approach was a considerable improvement over laboriously measuring multiple standards for each metabolite. Later, Jennings and Matthews (2005) developed a similar approach that relied on the measurement of a single unlabeled standard to derive “skew” based correction factors while also leveraging Brauman’s least squares approach to account for both instrumental and chemical noise.
2.2 The correction matrix method
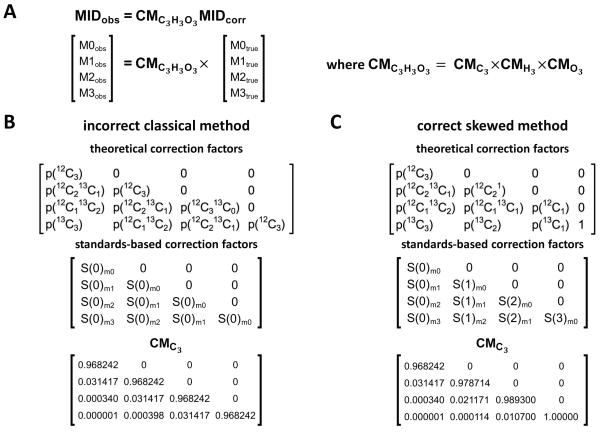
The correction matrix method is an algebraic approach for NA correction using correction factors derived either experimentally or theoretically. To illustrate this procedure, we use pyruvate (C3H3O3) as an example for a measured metabolite. The observed MID (MIDobs) of pyruvate is equal to the product of the correction matrix for pyruvate and the corrected MID (MIDcorr) (Figure 4A):
| (2) |
Thus, the corrected MID of pyruvate is calculated by multiplying the observed MID by the inverse of the CM:
| (3) |
where consists of pyruvate specific correction factors that describe how the spectral peaks of naturally abundant 13C contribute to spectral peaks that overlap (or convolve) the spectral peaks of the corrected MID of pyruvate. The corrected MID represents to the relative abundance of 13C from experimental enrichment only.
Figure 4. Correcting for natural abundance of stable isotopes in pyruvate via correction matrices.
(A) The expression for the correction of natural abundance (NA) of stable isotopes in pyruvate (C3H3O3) is written in vector form. CMC3H3O3. The correction matrix (CM) for pyruvate, is the product of the individual elemental matrices for carbon (), hydrogen (), and oxygen (). The correction factors in CMC3 can be calculated directly from theoretical probabilities or experimentally derived from measured standards. The form that CMC3 will take in both (B) the classical and (C) the skewed correction methods is summarized. The non-zero entries in the theoretical CMs represent the conditional probability of naturally finding the combination of 12C and 13C atoms indicated. For the classical approach, the columns of a CM correspond to the MIDs produced by an unlabeled standard. For the skewed approach, the columns of a CM correspond to the MIDs produced by standards of increasing isotopic content. The first column represents the MID of an unlabeled standard, while the second column represents the MID of a singly labeled standard, and so on. Each S(n)mi entry in the standards-based correction matrices represent the measured abundance for the Mi fraction of the MID of an n-labeled standard. The equivalent diagonal values characteristic of classical CMs come from the erroneous assumption that the presence of n atoms of 13C will arise from NA with the same likelihood across standards, regardless of the number of intentionally labeled carbons in the standard. More generally, the assumption can be stated as MIDS(0) = MIDS(1) = … = MIDS(n), where n is the number of atoms of the isotopically enriched element to be corrected in the metabolite, and MIDS(n) is the MID of the n-labeled standard.
There is an important and fundamental difference in the way that CMs are constructed in the classical and skewed correction approaches. As mentioned above, the classical approach makes the assumption that MIDs of singly, doubly, triply, and, more generally, n-labeled standards – S(1), S(2), S(3), and S(n) respectively – are equivalent to the MID of an unlabeled pure standard, S(0), except shifted by 1, 2, 3, or n atomic mass units, respectively (Figure 3A). In reality, a stable isotope labeling experiment will result in a non-linear shift in the distribution of naturally abundant isotopes, a phenomenon referred to as “skew” in the literature. This non-linear shift arises because the experimental introduction of 13C from a tracer substrate lowers the probability that higher mass isotopomers arise from NA in a non-linear manner. The MID of a labeled standard is not, therefore, equivalent to the MID of its unlabeled counterpart offset by the appropriate mass shift (Figure 3B). Returning to the example of pyruvate, the probability that one of the carbons in an unlabeled standard of pyruvate will be 13C due to NA is significantly higher than the probability that the sole unlabeled carbon in a doubly-labeled standard of pyruvate will be 13C due to NA. The classical approach incorrectly treats these probabilities as equivalent.
When correcting for NA of 13C in pyruvate using the skewed approach, CMC3 accounts for the non-linear shift in the distribution of 13C from NA via correction factors derived from the fractional abundance values corresponding to the MIDs of four standards (Figure 3B and Figure 4A,C): S(0), S(1), S(2), and S(3). These correction factors may either be measured experimentally or theoretically derived by simulating the fractional abundance of their corresponding mass isotopomers (Allen and Ratcliffe, 2009; Dunstan, 1988; Fernandez et al., 1996; Lee et al., 1991; van Winden et al., 2002a).
Accordingly, using the skewed approach, MIDs of unlabeled and 13C labeled standards are used to construct a CM as follows:
| (4) |
An element-wise expansion of the right-hand side of Eqn. 4 illustrates the underlying logic of this approach:
| (5) |
The M0 spectral peak of an observed MID is an isotopomer containing only 12C isotopes. The probability of this isotopomer naturally occurring is represented as S(0)m0, which corresponds to the relative abundance of the M0 base peak of an unlabeled standard, S(0). The M1 spectral peak of an observed MID is an isotopomer containing one 13C isotope because of either NA or because of experimental enrichment. The probability of this isotopomer naturally occurring corresponds to the relative abundances of the M1 peak of an unlabeled standard, S(0)m1, and the M0 peak of a singly-labeled standard, S(1)m0.. The remaining correction factors are derived in a similar fashion.
A metabolite specific CM can be constructed with the measured MIDs of unlabeled and labeled standards (Eqn 4). Alternatively, an equivalent metabolite specific CM can be computed by matrix multiplication of the elemental CM for each constituent element in the metabolite. In the case of 13C labeled pyruvate, there would be three elemental CMs, CMC3, CMH3, and CMO3, which contain correction factors for carbon, hydrogen and oxygen, respectively:
| (6) |
| (7) |
| (8) |
Elemental correction matrices can be constructed using combinatorial probability equations rather than from explicit measurements of all relevant standards. In particular, the probability of each elemental isotopomer (an isotopomer that consists only of atoms of the same element) can be computed as follows:
| (9) |
where N is the number of atoms of the element (e.g., carbon, hydrogen, or oxygen) in the fragment, n is the number of naturally occurring isotopes, I1, …, In, of the element, p(Ii) is the NA of the i-th isotope, and f(Ii) is the frequency of the i-th isotope in a fragment. For example, the probability that an elemental isotopomer consisting of 16O3 17O2 18O1 will naturally occur in a compound containing exactly 6 atoms of oxygen is computed as follows:
where 0.99757, 0.00380, and 0.00205 are the NA probabilities for 16O, 17O and 18O isotopes, respectively (Table 1).
Using the probability for each elemental isotopomer, the MID for each theoretical standard can easily be derived analytically. An expression is derived based on all possible isotopic combinations sorted by mass. As such, the MID of the O3 fragment is expressed as follows:
where N is the total number of oxygen atoms in the fragment, i is the mass shift of the standard peak, and j, and k are the number of atoms of 17O, and 18O respectively in a possible elemental fragment. Here, the multinomial coefficient represents the number of possible isotopomers of identical mass at each peak m0+i. For example, the second peak of the theoretical elemental standard for O3 is expressed as follows:
In a similar fashion, labeled standards can be analytically expressed for the carbon elemental matrices as follows:
where n indicates the number of 13C incorporated from labeling.
As previously discussed, manual measurement of the MIDs of standards needed to correct all metabolites measured in an experiment can be expensive and labor intensive. It is usually more practical to rely on theoretical CMs based on the fractional abundance values that are well approximated from multinomial probability theory (Allen and Ratcliffe, 2009; Dauner and Sauer, 2000; Dunstan, 1988; Fernandez et al., 1996; Lee et al., 1991; Rosenblatt et al., 1992; van Winden et al., 2002a). This alternate approach requires precise knowledge of the exact molecular formula of all metabolites measured as well as the NA of heavy (or light) stable isotopes of all elements present in measured metabolites. It should be noted that the methods described above are not able to simultaneously correct for the simultaneous labeling of two different elements (e.g., exposing cells simultaneously to both 2H and 13C) using unit-resolved isotopologue peaks as measured by typical LCMS and GCMS methods. Correction via a CM will result in partial correction only. However, simultaneous NA correction for the labeling by different elements can be performed for isotope-resolved isotopologue measurements by ultra-high resolution MS (Carreer et al., 2013).
2.3 Iterative correction methods
Mass spectral data from tracer experiments are often imperfect. Missing peaks and low spectral intensity can result in negative fractional abundance values when these measurements undergo correction via the correction matrix method. One approach for handling negative values is to flatten the unrealistic negative values to zero, then renormalize the MIDs using the total area under the positive mass spectral peaks of the corrected MID. To directly address the problem of missing values, Moseley (2010) suggested pre-processing the raw measurement by interpolating the missing fractional abundance using the expected isotopic profile of each metabolite. After processing for missing values, the method relies on an iterative approach that utilizes a series of algebraic equations to correct individual mass isotopomer peaks in increasing mass order.
Millard et al. (2012) later developed the IsoCor software program, which relies on an iterative implementation that explicitly addresses the problem of negative fractions after NA correction. Because not all isotopologue can be measured with unit-resolved MS, the non-linear approach of IsoCor for correcting NA has a theoretical advantage over linear matrix-based correction. This approach uses a non-linear least-squares optimization algorithm to minimize residuals due to experimental noise along with the skewed correction matrix method. The least-squares optimization is implemented via the limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm (Byrd and Segre, 2016), which is a numerical optimization algorithm with an explicit lower boundary of zero to eliminate any potential negative fractions. Thus IsoCor provides an alternative method for avoiding potential negative fractions in corrected MIDs. Nonetheless, the method employs skewed based CMs for performing the actual correction on the observed measurements and for simulating the expected measurements using inverse CMs. Therefore, IsoCor varies from the skewed matrix correction method by the inclusion of an iterative least-squares optimization function which attempts to improve model fitting and ensure the positivity of all fractional abundances via explicit lower boundary constraints.
2.4 Correction for high-resolution isotopologue data
The choice of the MS instrument generating isotopologue peaks can also dictate the appropriate method for correcting NA. So far we have only discussed NA correction in the context of unit mass (single dalton) resolved isotopologue data available from typical LCMS and GCMS instruments. Ultra-high accurate and resolved Fourier Transform MS instruments can, however, unambiguously distinguish mass-to-charge peaks accurately up to four decimal places resulting in hundreds to thousands of peaks for many compounds. High-resolution isotopic clusters can therefore resolve differences between incorporation of different elements such as 13C and 15N. Such high resolution of isotopologue data warranted computationally tractable approaches for denoising and NA correction. (Carreer et al., 2013; Moseley, 2010). These data can also be corrected for NA using the linear matrix-based approaches described in this article if CMs are constructed from molecular formulas of the ions detected. For instance, isotopically-resolved molecular ions related to carbon must be corrected with CMs constructed by molecular formulas that exclude NA from other incorporated elements such as heavy nitrogen.However, for the remainder of this article, we discuss matrix-based approaches for NA correction mainly in the context of unit-resolved isotopologue data.
2.5 Additional factors that may impact natural abundance correction
Because tracer substrates are unlikely to be labeled with 100 percent purity, correction matrices should account for purity of the enriched element. In 13C isotope labeling experiments, the elemental CM for carbon should accordingly compensate for tracer purity in each theoretical n-labeled standard. To do so, theoretical computations of n-labeled standards (columns in Eqn. 4 and 6) are simply convolved n times with a vector indicating the tracer purity. For instance, the MID for a two-carbon singly-labeled standard enriched with 13C at 95% purity would be computed as follows:
where t(12C) and t(13C) indicate the isotopic abundance of carbon isotopes in the tracer substrate. Because it is theoretically labeled with an impure 13C tracer, this singly-labeled standard would have a non-zero isotopologue peak of approximately 0.049 below its expected nominal mass.
Variation in the MID of standards can also arise from variation in elemental isotopic abundances. These variations are due to chemical and physical fractionations which are influenced by the source of a biological material (Coplen et al., 2009; Meija et al., 2016). Fernandez et al. accounted for such variations by estimating experiment-specific elemental isotopic abundances with non-linear parameter fitting using unlabeled standards from control samples. In a similar fashion, IsoCor inherently corrects for these variations by implementing non-linear least-squares optimization to minimize variation between measured MIDs and the simulated MIDs (Millard et al., 2012). These variations correspond to measurement noise including instrumentation error and variation in natural abundance of isotopes. For linear matrix-based correction for NA, elemental isotopic abundances must be measured a priori and would be best estimated with parameter fitting similar to the work of Fernandez et al.
3. Comparison of correction methods
In this tutorial review, we evaluated the performance of the classical matrix method, skewed matrix method, and the least-squares skewed-based IsoCor method, which we refer to as the classical, skewed and least-squares skewed correction (LSC) methods, respectively. The method we refer to as the skewed approach in this paper properly accounts for the non-linear shift in the distribution of naturally abundant isotopes (or “skew”) and is the accepted method for correction for NA. As previously discussed, the classical method is known to overestimate NA in a MID the consequence of which is demonstrated in Figure 3, where classical correction yields a corrected MID with no M3 abundance and skewed correction yields a small but non-negligible M3 abundance in the corrected MID. While we could have reasonably left the erroneous classical method out of this review, we chose to include it in order to evaluate its performance when systematically compared to the skewed matrix and LSC approaches under varying noise levels.
First, the three correction methods were applied to measurements of three unlabeled standards. No observable qualitative or quantitative differences were found in the corrected MIDs of unlabeled standards of aspartate, lactate, or glutamate when measured by LC-MS or GC-MS (Supplemental Figure S1), suggesting the three approaches perform equally well for MIDs containing only NA in the absence of experimental enrichment. The apparent accuracy of the sub-optimal classical method when correcting an unlabeled standard is not surprising given that classical correction factors are based on NA probabilities derived from an unlabeled standard.
We next evaluated the performance of each correction method when applied to a set of hypothetical glutamate MID measurements (Figure 5). When the fractional abundance of each mass isotopomer in the observed MID were equal, no qualitative or quantitative differences were observed in the corrected MIDs (Figure 5A). However, when at least one fractional abundance in the observed MID was very small, differences between skewed and classical correction as well as differences between skewed and LSC correction were apparent (Figure 5B-D). The observed differences between skewed and classical are not unexpected for reasons discussed previously. The observed differences between skewed and LSC correction, which raise questions about which method is most appropriate for routine usage, are likely a direct result of the explicit lower boundary set by LSC to eliminate potential negative fractions. To systematically evaluate the effects of these correction differences in realistic experimental conditions, we corrected simulated MIDs for which the expected MID was known a priori in the presence of increasing amounts of random noise. This approach also enabled us to evaluate how differences in correction impact parameter estimation as performed by 13C based MFA.
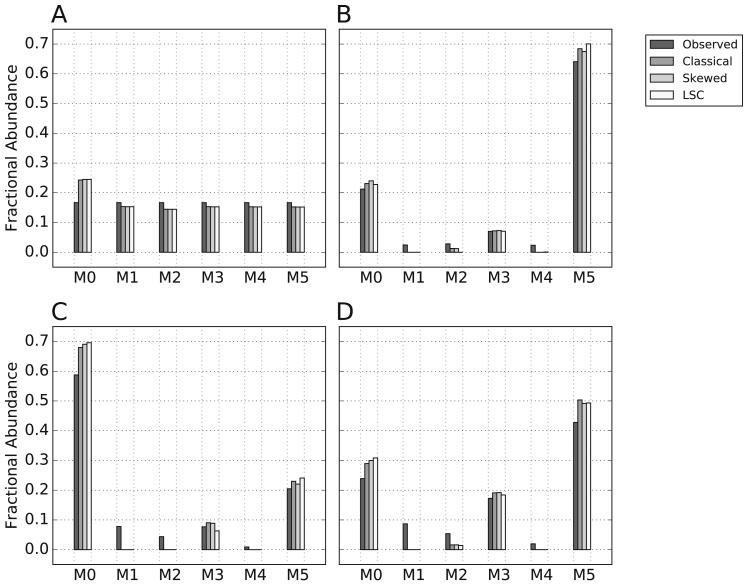
Figure 5. Correction of hypothetical mass isotopomer distributions of glutamate.
Four hypothetical measured (observed) mass isotopomer distributions (MIDs) of glutamate were corrected for natural abundance by classical, skewed, or LSC. The molecular formulas used for correction of glutamate and an assumed derivatizing agent were C5H8NO4 and C14H34Si3, respectively. In (A) all fractional abundances in the MID were assumed equivalent. In (B-D), MIDs were selected with small observed values for the M1, M2, and M4 fractions.
We developed a metabolic model of glucose metabolism for cancer breast cell lines to evaluate how well each method corrects for NA in the presence of both experimental noise and enrichment from commonly used 13C tracers. The workflow of the experimental approach is outlined in Figure 7 and the metabolic network is illustrated in Figure 6. The network includes reactions involved in glycolysis and the tricarboxylic acid (TCA) cycle in breast cancer cell lines (Wynn et al., 2016). The input fluxes are glucose and glutamine, and the output fluxes are alanine, alpha-ketoglutarate, aspartate, glutamine, lactate, and oxaloacetate. An arbitrary, yet physiologically meaningful, set of fluxes was pre-defined for this model (Supplemental Table 1). The expected enrichment at isotopic steady state after the addition of [1,2-13C] glucose and [U-13C] glutamine was calculated based on the carbon transitions and predetermined flux values listed in Supplemental Table 1 (Figure 7, Step 1). The tracers were assumed to be pure with 100% positional labeling and multiplicative Gaussian noise was added to each MID (see Methods).
Figure 7. Workflow of in silico experiment designed to evaluate the performance of three methods for the correction of natural abundance of stable isotopes.
Step 1: From the network defined in Figure 6 and Supplemental Table 1, the expected steady state isotopic distribution after the addition of two tracer substrates ([1,2-13C] glucose and [U-13C] glutamine) was calculated. Step 2: From the computed isotopic tracer distribution, expected MIDs from either LC-MS or GC-MS (the latter assumed fragmentation and derivatization by silylation reagent N-tert-butyldimethylsilyl- N-methyltrifluoroacetamide, MTBSTFA) were generated. Theoretical natural abundance (NA) of stable isotopes (Table 1) were added to the MIDs. Next, Gaussian noise was added to each MID 4 times to simulate 4 replicates of experimentally observed measurements. The simulated LC-MS and GC-MS data utilized MIDs from metabolites listed in Supplemental Table 2 and Supplemental Table 3, respectively. Step 3: For NA correction, each MID replicate (n=4) was treated under four distinct correct conditions: not corrected (Observed), corrected by the classical matrix method (Classical), corrected by the skewed matrix method (Skewed), and corrected by the least-squares skewed correction (LSC) correction method. Step 4: Each set of uncorrected or corrected MIDs (n=4 for each of the 4 cohorts) was used as input to 13C metabolic flux analysis (MFA). The MFA-estimated output fluxes for each dataset are identified as νObs, νClassical, νSkewed, and νLSC. The MFA-predicted output MIDs are computed from these optimal fluxes. At the end of Step 3 and Step 4, MID errors were calculated and the variance-weighted sum of squares residual (SSR) was calculated and used in a goodness-of-fit chi-square test to assess the adequacy of the correction methods (Step 3) and flux parameter estimation (Step 4).
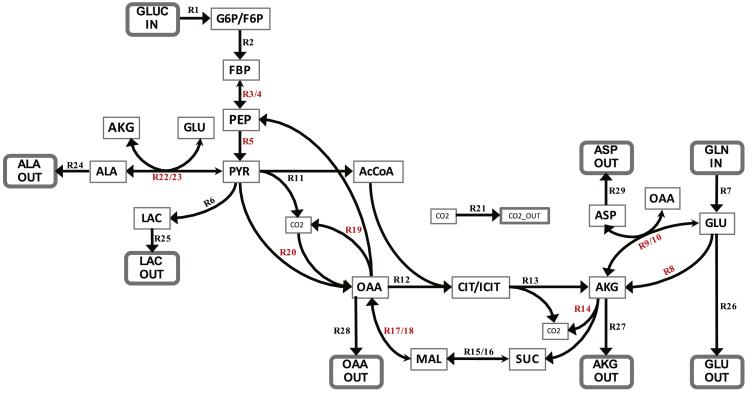
Figure 6. Network of glucose metabolism used for metabolic flux analysis.
A network based on central carbon metabolism that encompassed glycolysis, the TCA cycle, and various amino acid drains as well as anapelrotic and gluconeogenetic fluxes was constructed and used for MFA. In reversible reactions, the larger arrowhead indicates the forward direction. The carbon atom transitions associated with this network are included in Supplemental Table 1. Free (independent) fluxes are highlighted in red. Abbreviations: AcCoA - acetyl-CoA; AKG - α-ketoglutarate; ALA - alanine; ASP - aspartate; CIT/ICIT – citrate/isocitrate pool; CO2 - carbon dioxide; FBP - fructose 1,6-bisphosphate; G6P/F6P, glucose-6-phosphate/fructose-6-phosphate pool; GLN, glutamine; GLU, glutamate; GLUC, glucose; LAC, lactate; MAL, malate; OAA, oxaloacetate; PEP, phosphoenolpyruvate; PYR, pyruvate; SUC, succinate.
At the end of Step 2 in Figure 7, analogous sets of LC-MS- and GC-MS-based MIDs, each consisting of 1,000 experimental replicates, were generated after convolution first with NA and then with noise from a Gaussian distribution. These MIDs were then processed in four parallel treatment conditions (Figure 7, Step 3): (i) Observed: no NA correction, (ii) Classical: NA correction via the classical method, (iii) Skewed: NA correction via the skewed method, and (iv) LSC: NA correction via IsoCor. For each metabolite, we randomly sampled 4 replicate MIDs from the total set of 1000 simulated to mimic an actual experimental setup where only a small number of biological samples are usually available.
Under identical experimental conditions, metabolite measurements produced via LC-MS and GC-MS analyses will be different. Because of the presence of a derivatizing agent, the fractional abundance values produced by GC-MS come from heavier compounds with substantially more NA from stable isotopes. Moreover, the fragmentation of the compounds by GC-MS provides some positional labeling information that is not available from an LC-MS analysis. Therefore, we simulated experimentally observed MIDs produced by both LC-MS and GC-MS (Figure 7, Step 2) for 8 metabolites, which contained a total of 44 and 55 fractional abundance values, respectively (Supplemental Table 2 and Supplemental Table 3).
3.1 Evaluating the natural abundance correction accuracy of each method
The performance of each correction method was evaluated by computing the deviation in observed and corrected MIDs from the set of expected MIDs (). Here, the expected MIDs () correspond to fractional abundances of the true mass isotopomer distributions that were simulated by our pipeline (Figure 7, Step 1); observed MIDs (MOBS) correspond to fractional abundance of the expected MIDs that have been convolved with natural abundance and Gaussian noise (Figure 7, Step 2); while the corrected MIDs (MCORR) correspond to the fractional abundance of observed MIDs after correction with for natural abundance (Figure 7, Step 3). Accordingly, the variance-weighted sum of squared residuals (WSSR) was computed as follows:
| (10) |
where n is the number of backbone carbons for the i-th metabolite, and k is the total number metabolites measured. Thus, Mi,j is the j-th fractional abundance of the i-th metabolite. The WSSR follows a chi-square distribution if the MID residuals follow a normal distribution and estimates for the variance of the residuals are known. For each fractional abundance, each weight is inversely proportional to the variance of its residuals. The WSSR statistic was used in a chi-squared goodness of fit test (Sokal et al., 1995) at a significance level of 0.05 to evaluate how closely the corrected MIDs compared to the expected MIDs.
In general, an adequate correction model will correct a set of MIDs only for presence of NA. Therefore, we also evaluated the performance of each correction model by comparing the magnitude of correction performed to the residuals expected due to NA alone. This was accomplished by evaluating the squared magnitude of correction (SMOC), the expected SMOC (the overall error in the observed MID, including deviation from the expected MID due to NA as well as other sources, such as noise), and the expected error in the observed MIDs that came only from NA (ERRORNA). These statistics were computed as follows:
| (11) |
| (12) |
| (13) |
where indicates the convolution of the expected MID with NA.
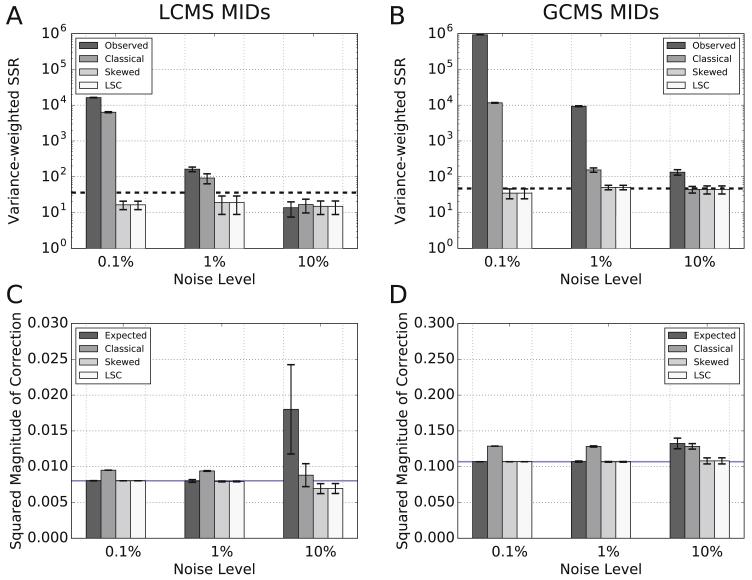
For both the LC-MS (Figure 8A) and GC-MS (Figure 8B) datasets at all noise levels, the WSSR for MIDs corrected by the skewed and LSC methods were below the goodness-of-fit cutoff (Figure 8A-B), indicating that NA corrections performed by these methods performed adequately under all conditions tested. In contrast, at noise levels below 10%, classical correction was not adequate (Figure 8A-B). In these cases, classical correction overestimated NA and, accordingly, overcorrected the MIDs (Figure 8C-D). The over-correction is demonstrated by the classical correction SMOC, which was always larger than the associated ERRORNA (blue line in Figures 8C-D).
Figure 8. Error analysis of MIDs corrected by different methods.
(A-B) The variance-weighted SSR measures the deviation of uncorrected and corrected MIDs from the expected (A) LC-MS or (B) GC-MS MIDs. In all cases, four correction treatments were tested: (i) observed (no correction), (ii) classical correction, (iii) skewed correction, and (iv) LSC correction. All tests were repeated under three distinct noise levels. The dashed line indicates the goodness of fit cut-off at a significance level of 0.05. (C-D) The squared magnitude of correction (SMOC) metric describes the deviation in the set expected or corrected MIDs from the set of observed MIDs for (C) LC-MS and (D) GC-MS data sets. This is a test of whether the corrected MIDs appropriately estimate the bias in the observed MIDs due to natural abundance. Four types of MIDs were compared (i) expected (the magnitude of correction that would correct for NA and random error), (ii) classical correction, (iii) skewed correction, and (iv) LSC correction. All tests were repeated under three distinct noise levels. The blue line indicates the expected error in the observed MIDs that came only from NA (ERRORNA).
In the extreme case where random error is much larger than error from NA (e.g., 10% noise), it is not unexpected that all correction methods meet the goodness-of-fit cutoff (Figure 8A-B). This is because WSSR measures how well each method corrects NA while controlling for variance (i.e. noise) as a weighting factor. After all, the correction methods were not designed to correct for gross random errors. As demonstrated in Figure 8C-D, the expected SMOC is a measure of the observed error from both NA (blue lines) and random Gaussian noise (expected SMOC above blue line). If the expected SMOC is mostly due to random noise, as in LC-MS MIDs with 10% noise, all correction methods as well as not correcting at all yielded WSSRs below the goodness-of-fit cutoff (Figure 8A). For analysis of compounds with GC-MS, a compound must be volatile and thermally stable, which typically requires chemical derivatization. The NA of derivatization residue must be considered in the correction for NA. This additional NA results in an expected SMOC that is mostly due to NA. Therefore, not correcting at all for NA in GC-MS MIDs (observed in Figure 8B) did not pass the goodness-of-fit cutoff at 10% noise.
3.2 Comparing the impact of each correction method on 13C metabolic flux analysis
We next evaluated how each correction method impacted the estimation of metabolic fluxes using both LC-MS- and GC-MS-based 13C steady state MFA, which we describe briefly below. The same in silico generated MIDs that were corrected and analyzed in Figure 8 were used as input for a set of MFA simulations. Briefly, after correction (Figure 7, Step 3), 4 randomly sampled replicates of LC-MS MIDS generated for each metabolite (Supplemental Table 2) were used as input to 13C MFA (Figure 7, Step 4). This process was repeated with the in silico generated GC-MS MIDs (Supplemental Table 3).
13C metabolic flux analysis (MFA) is a computational approach for estimating absolute metabolic flux in a network by solving a constrained least squares optimization problem where the difference between experimentally measured MIDs and predicted MIDs is minimized (Wiechert, 2001). While 13C MFA is well reviewed elsewhere (Quek et al., 2010; Schmidt et al., 1997; Wiechert, 2001; Zamboni et al., 2009), we provide a brief introduction.
MFA is a powerful tool for estimating intracellular metabolic fluxes (Libourel and Shachar-Hill, 2008; Wittmann, 2002; Young et al., 2008; Zamboni and Sauer, 2009). MFA relies on non-linear optimization, steady-state mass balance equations, and a set of measured extracellular fluxes. Steady-state MFA attempts to find the set of fluxes that satisfy S × v = 0, where S is the stoichiometric matrix and v is the vector of fluxes in a network. The final output of MFA is often a metabolic flux map consisting of a diagrammed biochemical network that contains an estimate of the absolute steady state flux of each reaction in the diagram. As in flux balance analysis (Orth et al., 2010), a related constraint-based stoichiometric approach, MFA does not require knowledge of the enzyme kinetics catalyzing metabolic reactions (Edwards and Palsson, 2000).
Even when extracellular flux constraints are added, the systems modeled by MFA are typically underdetermined because there are more fluxes than metabolites in a metabolic model. In 13C MFA, 13C based isotope labeling experiments add additional experimental constraints to the underdetermined metabolic model in order to reduce the degrees of freedom and improve inference of the metabolic fluxes (Bonarius et al., 1998; Wiechert, 2001). Accordingly, 13C MFA constrains the MFA approach with an isotopomer matrix that describes the distribution of isotopes from isotopically enriched substrates into the metabolic network (Antoniewicz et al., 2007; Bonarius et al., 1998; Christensen and Nielsen, 1999; Marx et al., 1996; Sokol et al., 2012; Srour et al., 2011; Weitzel et al., 2013; Wiechert et al., 1999; van Winden et al., 2002b; Zupke and Stephanopoulos, 1995). In the case of 13C isotope labeling experiments, the matrix represents the carbon atom transitions involved in all modeled metabolic reactions (Schmidt et al., 1997).
13C MFA requires knowledge of atom transitions involved in a network, measurements of MIDs after the introduction of a labeled tracer, and, typically, a system at isotopic steady state (as is necessary in steady-state 13C MFA). Importantly, if it were possible to know all metabolic fluxes at steady state a priori, a unique mathematical solution exists for calculating the isotopic distribution produced by any tracer combination added to the network. The objective of 13C MFA is to solve the underdetermined inverse problem of identifying a set of unknown intracellular fluxes from a small subset of measured MIDs (i.e. a sample of isotopic distribution) (Antoniewicz et al., 2006; Schmidt et al., 1997). In practice, the objective of 13C MFA is to identify the optimal fluxes that reproduce the measured data supplied as input to the simulation (Wiechert and de Graaf, 1997).
In our investigations, we used steady-state 13C MFA, which relies on the use of tracer substrates containing one or more carbons labeled as 13C and measurements taken at isotopic steady state. We generated mass isotopomer data in silico and used 13C MFA to test the effect of pre-correcting the MIDs for all atoms with the three correction methods. Simulations were performed on a biologically realistic network of central carbon metabolism (Figure 5). For simulations with MIDs that did not correct for the carbon backbone, observed (uncorrected), the existence of NA in the labeled substrate tracers of the network (glucose and glutamine) were assumed. We undertook our analysis using OpenFLUX, which is built upon the widely used elementary metabolite unit framework (Antoniewicz et al., 2007). While we relied on OpenFLUX because of its ease of use and open source code base, other tools for performing MFA exist (Srour et al., 2011; Weitzel et al., 2013; Young, 2014; Zamboni et al., 2005).
The metabolic network model (Figure 5) contains nine free fluxes that represent the minimal set of fluxes from which the remaining network fluxes can be computed from the system of equations defining the network (Zamboni and Sauer, 2009). Four of the nine fluxes are strictly unidirectional based on thermodynamic considerations (R5, R8, R14, and R20). The other five fluxes are the reverse reactions of bidirectional fluxes (R4, R10, R16, R18, and R23). The uptake rate of the tracers ([1,2-13C]glucose and [U-13C]glutamine) along with the secretion rates of lactate, alpha-ketoglutarate, and oxaloacetate were used as model constraints.
OpenFLUX (Quek et al., 2009) provides an optimal estimate for each network flux that is bounded by a 95% confidence interval (Antoniewicz et al., 2006). In general, it is challenging for MFA to resolve the forward and reverse fluxes of bidirectional reactions. However, it is often capable of estimating the net flux through these bidirectional reactions. Therefore, in the metabolic network (Figure 5), we evaluate the performance of MFA estimation of the reverse reactions of bidirectional fluxes by estimating the accuracy of estimates of the corresponding net fluxes of their reactions. In the subsequent analysis, the net flux R3/R4 is determined by the predefined flux of the uptake of glucose tracer substrate into the network, because the concentration of fructose 1,6-bisphosphate (FBP) must be balanced by the uptake rate of glucose tracer, R1 flux, and the net flux R3/R4 (Figure 5). Therefore, we exclude the free flux R4 (phosphoenolpyruvate to fructose bis-phosphate) from the subsequent analysis.
3.3 Evaluating the impact of natural abundance correction by each method on flux estimates
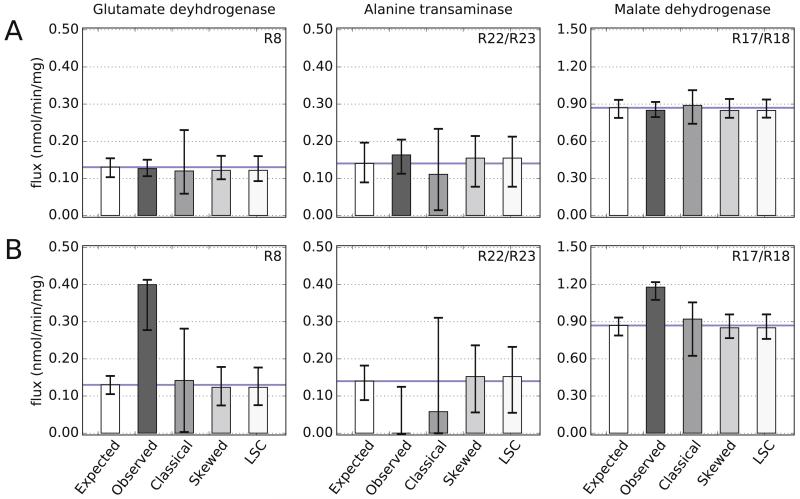
MFA with MIDs that were classically corrected performed worse than MFA with MIDs that were skewed corrected. For LC-MS-based MFA, classical correction predicted 95% confidence intervals that correctly estimate the optimal value for seven of the eight free fluxes (Figure 9 and Supplemental Figure 2). However, MFA with skewed and LSC corrected MIDs yielded better optimal estimates of fluxes. In addition, the 95% confidence intervals for MFA using classical MIDs was consistently larger than the intervals predicted by MFA with skewed or LSC corrected MIDs. For isotope labeling experiments with low NA, as in the case of LC-MS measurements, even MFA with MIDs not corrected at all (Observed), slightly outperformed classical correction (Figure 9A). However, for isotope labeling experiments with high NA, as in the case of GC-MS measurements, correction was imperative for accurate estimate of fluxes with MFA (Figure 9B). In our analysis, MFA with observed GC-MS MIDs did not correctly predict any of the free fluxes. This is likely due to derivatization, a required process for GC-MS, which results in higher NA error in MIDs.
Figure 9. Estimates of metabolic fluxes by MFA using MIDs corrected by different methods.
13C MFA using differently corrected or uncorrected input MIDs results in differing flux estimates in nmol per min per mg of utilized glucose. True flux values are indicated by a blue line. MFA using expected MIDs (i.e. no NA incorporation) estimates the true fluxes correctly. For isotope labeling experiments with low NA, as in the case of LC-MS (A), MFA with MIDs that are observed (uncorrected) or corrected using either of the classical, skewed, or LSC approaches estimates the true fluxes within the 95% confidence intervals of each model. However, MFA with skewed- and LSC-corrected MIDs estimate optimal fluxes (mean of bars) that are closet to the true value and display smaller confidence intervals than MFA with MIDs that are classically corrected. For isotope labeling experiments with high NA, as in the case of GC-MS (B), MFA with skewed- and LSC- corrected MIDs approaches vastly outperform MFA with classically-corrected or observed (uncorrected) MIDs. Top right corner of each plot indicates the reaction number. Error bars are based on four simulations for each test condition.
3.4 Evaluating the impact of natural abundance correction by each method on MID estimates
While MFA is a powerful tool for estimating intracellular flux, an important limitation of MFA is that a simulation may converge to a faulty but optimal set of flux estimates with small (but misleading) confidence intervals (Antoniewicz et al., 2006; Srour et al., 2011). In the MFA simulations, input MIDs that were not corrected converged to faulty flux estimates with tight confidence intervals (Figure 9; see, for example, flux estimates for Alanine transaminase and Malate dehydrogenase for the LC-MS and GC-MS simulations, respectively). Even with appropriately corrected MIDs, this scenario can arise because of poor assumptions about the network structure (Libourel and Shachar-Hill, 2008; Zamboni et al., 2009) or because of gross measurement errors (Antoniewicz et al., 2006). For these reasons, it is recommended that the adequacy of a network model used in MFA be also assessed via a chi-squared goodness of fit test at a significance level of 0.05 (Antoniewicz et al., 2006).
In the context of MFA, the goodness of fit test also relies on a variance-weighted SSR (WSSRMFA) as its statistic, but compares the optimal MIDs predicted by MFA (Figure 7, Step 4) to the corrected MIDs used as input to MFA (Figure 7, Step 3). Ideally, the optimal MIDs predicted by MFA (Figure 7, Step 4) are compared to the actual expected MIDs (Figure 7, Step 2), which is only possible for theoretical simulations, such as described here, for which the expected measurements are known a priori:
| (14) |
The goodness of fit statistic follows a chi-square distribution with the number of degrees of freedoms equal to the number of individual mass isotopomer fractional abundance values used as input minus the number of free fluxes in the system. For the LC-MS- (44 fractional abundances) and GC-MS-based (55 fractional abundances) MFA simulations, the weighted SSR follows a chi-square distribution of 27 and 38 degrees of freedom, respectively, because the model has eight dependent MID fractional abundances, and nine free fluxes.
The ability of a given correction method to correct a MID prior to MFA simulations (Figure 8) corresponded with its impact on MFA model adequacy (Supplemental Figure 3). As before, in the LC-MS- and GC-MS-based MFA simulations (Figure 9), the skewed and LSC methods performed comparably, and their respective WSSRMFA were not rejected by the goodness-of-fit cutoff in any test condition (Supplemental Figure 3).
In summary, for the LC-MS and GC-MS tests at all noise levels tested, the skewed and LSC methods had variance-weighted SSRs below the significance cut-off. Together, the results of our critical analysis suggest that for the correction of MIDs generated by LC-MS or GC-MS the skewed correction, as implemented in INCA (Young, 2014), or the LSC method, as implemented in IsoCor (Millard et al., 2012), is a very reliable correction method.
4. Discussion
In this tutorial review, we have discussed the theoretical basis of three methods for the correction of NA of stable isotopes. We evaluated how well each method corrects for NA and how the use of each method may impact flux estimation by steady state 13C MFA analysis. Our comparative analyses relied on MIDs that were theoretically simulated as if they were measured be either LCMS or GC-MS. The expected MIDs were convolved with NA and noise and later corrected for NA of stable isotopes by either of three corrections methods. We used four in silico generated replicate MIDs to simulate a realistic experimental setup in which the number of biological replicates is typically limited to three or four samples by time and resources. In the case of steady state 13C MFA using a realistic metabolic network (Figure 6), the four replicate MIDs used in our all comparisons were randomly selected from a set of 1000 LC-MS or GC-MS simulated MIDs that included NA of constituent atoms with varying levels of Gaussian noise. The same analyses were repeated with the full set of 1000 replicates. No differences in results or conclusions between the n=4 and n=1000 analyses were found (data not shown).
The classical correction method (Figure 3A) is based on the erroneous assumption that the MIDs of labeled standards are identical (but shifted in mass) to a corresponding unlabeled standard. The skewed correction method (Figure 3B) does not make this assumption and, instead, relies on either the direct measurements of standards for all measured mass isotopomers in an experiment (an impractical approach in most cases) or theoretically calculated equivalent measurements derived from multinomial probability theory – the later approach provides a very good approximation of the non-linear distribution on stable isotopes. Both the classical and skewed matrix methods evaluated rely on a CM (Figure 4) to transform observed MIDs into corrected MIDs (Eqn. 2 and 3). We compared these two methods to IsoCor, which is based on a skewed correction approach, but with a least-squares optimization function that ensures the positivity of all fractional abundances after correction.
Several studies (Dunstan, 1988; Fernandez et al., 1996; Rosenblatt et al., 1992; van Winden et al., 2002a) have demonstrated the inadequacy of the classical correction method for decomposition of NA in isotope labeling experiments. Nonetheless, there is reason to believe that the classical correction method is still used by some researchers (Olstad et al., 2007; Walls et al., 2014; Zheng et al., 2015). A search of the literature over the past five years for papers that cite classical methodologies revealed research papers that cite and likely use this method, suggesting either that some acceptance of the use the classical method continues or that some researchers do not fully appreciate the difference between this method and later methods. Our results reaffirm that the classical correction method should be avoided, particularly when downstream quantitative analysis will be used.
For the correction of either LC-MS or GC-MS data, the algebraically simple skewed correction method and the open-source IsoCor’s iterative least squares correction approach consistently performed well (Figures 8 and 9). Error analysis revealed that classical correction overestimates the bias due to NA (Figure 8). We also evaluated how errors with classical correction can be magnified in downstream analyses such as MFA. In an analysis of 13C MFA performed with classically-corrected MIDs, predicted flux and MID estimates failed the goodness-of-fit test in all but at an extremely high noise level of 10% -- a condition that should be rare in controlled experiments (Figure 9 and Supplemental Figure 3). Together our analyses suggest failing to correct or relying on the classical-correction for NA correction will produce highly inaccurate estimates of metabolic fluxes under most experimental conditions.
Some software implementations of 13C MFA only expect NA correction to be pre-performed on non-carbon backbone atoms because the interference from NA in the carbon backbone is simulated directly in the iterative optimization function. In contrast, our MFA-based analyses relied on the pre-correction of all atoms prior to simulation. In the case of OpenFlux, the user may choose to correct for NA prior to simulation or to allow OpenFlux to simulate NA (Quek et al., 2009). To confirm using OpenFLUX for 13C MFA simulations when all atoms were pre-corrected is a valid approach for evaluating how different correction methods impact downstream flux estimates, we performed the following test. OpenFlux MFA simulations were run using MIDs that were corrected for all atoms (including the carbon backbone) by the skewed approach or corrected for all atoms except the carbon backbone (see Methods). While the latter approach produced confidence intervals that were somewhat smaller than when all atoms were pre-corrected via the skewed approach (Supplemental Figure 4), only small differences in estimated flux values was observed between these two approaches. Moreover, the WSSRMFA for the two approaches were very similar and both were below the goodness fit cut-off.
In this work, we have provided a review of the theory of NA correction of stable isotopes using both mathematical and intuitive explanations. In addition, our critical analyses have reaffirmed the accuracy of skewed-based correction of NA. We also reaffirmed that classical correction, which evidence suggests is still used within the scientific community to some extent, is inadequate for the correction of NA and estimation of isotopic enrichment. The use of classical correction, therefore, should be avoided.
5. Methods
5.1 Computer implementation
A program that implements both the classical and skewed matrix methods was written in MATLAB. The program handles negative fractions by setting them to zero and subsequently renormalizing the MIDs. The core functions used for skewed correction are available as part of the Isotopomer Network Compartmental Analysis (INCA) suite (Young, 2014). LSC tests were performed using IsoCor (Millard et al., 2012), which was run in Python 2.7.2. The Matlab based OpenFLUX (Quek et al., 2009) package was used for all MFA simulations. All MATLAB scripts including OpenFLUX were run in MATLAB R2012a, and all computer simulations were run either on Intel i5 CPU @ 2.40 GHz running Windows 7 or Intel Nehalem/i7 Core processors running Red Hat Linux.
5.2 Generation of in silico mass isotopomer data
Arbitrary steady state fluxes (Figure 6, and Supplemental Table 1) were predefined and used to calculate the MIDs expected after exposure to 13C based tracers. We refer to these enriched MIDs as the expected MIDs. Because all network fluxes were defined a priori, the unique steady state isotopic distribution after the introduction of a tracer could be directly calculated (Antoniewicz et al., 2006; Schmidt et al., 1997). Briefly, the predefined flux map () and the input substrate tracer () were used to compute (the expected MIDs) from the following equation:
where F is a non-linear function that maps an input substrate’s known MID ( ) to a simulated MID in the network metabolite vector using the flux vector ; here we have adopted the notation used by Quek et al. (Quek et al., 2009). Two functions in OpenFLUX (Quek et al., 2009) were used to perform this task: fluxGenerator(_free) computes the network fluxes () given a selected subset of independent (free) fluxes, while mdvGenerator() computes the MIDs () using the network fluxes.
The expected MIDs were convolved with NA of stable isotopes based on multinomial probabilities. These probabilities correspond to the fractional abundance of stable isotopes of the elements (Supplemental Table 1). Eqn. 2 was used to incorporate NA into the expected MIDs to simulate experimentally measured data, which we refer to as the observed MIDs.
5.3 Addition of noise to simulated measurements
For the in silico experiments based on a metabolic model (Figure 6), MIDs were convolved with NA based on the relative abundance of stable isotopes of each element in the molecular formula of the compounds. Multiplicative Gaussian noise was added to each MID 1,000 times to generate 1,000 experimentally observed sets of uncorrected MIDs for each metabolite. In particular, for every MID of n fractional abundances, n biases were generated from a normal distribution of mean 1 and a fixed standard deviation (with base-10 logarithmically increasing standard deviation ranging from 0.001 to 0.10), then the fractional abundances were multiplied by the random biases. Three distinct noise levels were tested: 0.1%, 1.0%, and 10% noise, with 1,000 experimental replicates at each noise level. All MIDs were normalized so that the sum of all fractions equaled one. Thus, a standard deviation of 0.10 is equivalent to contamination with 10% noise (Figure 7, Step 2). For analysis in this article, we sampled four of the 1000 experimental replicates. We performed similar analyses on the full set of 1000 replicates, which yielded the same results and conclusions, and therefore are not shown.
5.4 OpenFlux simulations
In this work, all atoms in the MIDs were corrected prior to OpenFlux simulations unless otherwise indicated (e.g., all but CBB in Supplemental Figure 4). When all atoms were corrected, simulations were run assuming no NA was present in the simulated tracer. Thus, we assumed the tracer added was completely pure with 0% NA (e.g., the substrate vector describing known 13C labeling in [1,2-13C] glucose was defined as [1 1 0 0 0 0] rather than [0.99, 0.99 0.0107 0.0107 0.0107 0.0107]). The observed MIDs of metabolites selected as input to 13C MFA simulations were either left uncorrected or corrected by the classical, the skewed, or the LSC method. However, we also ran MFA simulations with all atoms except the carbon backbone corrected (Supplemental Figure 4). In this case, simulations were run assuming the existence of NA in the tracer substrate, but we corrected for the carbon in the tracer fragment from the derivatizing agent for GC-MS MIDs.
Supplementary Material
Acknowledgements
This work was partially supported by the James S. McDonnell Foundation (Grant No. 220020223) and the Michigan Regional Comprehensive Metabolomics Resource Core (NIH U24 DK097153). FSM is supported by the NIH Grant T32 GM071340 and NSF DGE 1545220. We are grateful to Drs. Charles Burant and Charles Evans for several helpful discussions. We also thank Dr. Evans for providing the standard data we corrected in Supplemental Figures 1.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allen DK, Ratcliffe RG. In: Quantification of Isotope Label. Plant Metabolic Networks; Schwender J, editor. Springer; New York: 2009. pp. 105–149. [Google Scholar]
- Antoniewicz MR, Kelleher JK, Stephanopoulos G. Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements. Metab. Eng. 2006;8:324–337. doi: 10.1016/j.ymben.2006.01.004. [DOI] [PubMed] [Google Scholar]
- Antoniewicz MR, Kelleher JK, Stephanopoulos G. Elementary metabolite units (EMU): a novel framework for modeling isotopic distributions. Metab. Eng. 2007;9:68–86. doi: 10.1016/j.ymben.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berglund M, Wieser ME. Isotopic compositions of the elements 2009 (IUPAC technical report) Pure Appl. Chem. 2011;83:397–410. [Google Scholar]
- Biemann K. Mass spectrometry: organic chemical applications. McGraw-Hill; New York: 1962. [Google Scholar]
- Bonarius HP, Timmerarends B, de Gooijer CD, Tramper J. Metabolite-balancing techniques vs. 13C tracer experiments to determine metabolic fluxes in hybridoma cells. Biotechnol. Bioeng. 1998;58:258–262. doi: 10.1002/(sici)1097-0290(19980420)58:2/3<258::aid-bit20>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- Brauman JI. Least Squares Analysis and Simplification of Multi-Isotope Mass Spectra. Anal. Chem. 1966;38:607–610. [Google Scholar]
- Brunengraber H, Kelleher JK, Des Rosiers C. Applications of mass isotopomer analysis to nutrition research. Annu. Rev. Nutr. 1997;17:559–596. doi: 10.1146/annurev.nutr.17.1.559. [DOI] [PubMed] [Google Scholar]
- Buescher JM, Antoniewicz MR, Boros LG, Burgess SC, Brunengraber H, Clish CB, DeBerardinis RJ, Feron O, Frezza C, Ghesquiere B, et al. A roadmap for interpreting 13C metabolite labeling patterns from cells. Curr. Opin. Biotechnol. 2015;34:189–201. doi: 10.1016/j.copbio.2015.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrd RH, Peihuang L, Nocedal J, Zhu C. A limited memory algorithm for bound constrained optimization. SIAM Sci. Comp. 1995;16:1190–1208. [Google Scholar]
- Carreer WJ, Flight RM, Moseley HNB. A Computational Framework for High-Throughput Isotopic Natural Abundance Correction of Omics-Level Ultra-High Resolution FT-MS Datasets. Metabolites. 2013;3:853–866. doi: 10.3390/metabo3040853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cascante M, Marin S. Metabolomics and fluxomics approaches. Essays Biochem. 2008;45:67–82. doi: 10.1042/BSE0450067. [DOI] [PubMed] [Google Scholar]
- Chance EM, Seeholzer SH, Kobayashi K, Williamson JR. Mathematical analysis of isotope labeling in the citric acid cycle with applications to 13C NMR studies in perfused rat hearts. J. Biol. Chem. 1983;258:13785–13794. [PubMed] [Google Scholar]
- Christensen B, Nielsen J. Isotopomer analysis using GC-MS. Metab. Eng. 1999;1:282–290. doi: 10.1006/mben.1999.0117. [DOI] [PubMed] [Google Scholar]
- Chubukov V, Uhr M, Le Chat L, Kleijn RJ, Jules M, Link H, Aymerich S, Stelling J, Sauer U. Transcriptional regulation is insufficient to explain substrate-induced flux changes in Bacillus subtilis. Mol. Syst. Biol. 2013;9:709. doi: 10.1038/msb.2013.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobelli C, Toffolo G, Bier DM, Nosadini R. Models to interpret kinetic data in stable isotope tracer studies. Am. J. Physiol. 1987;253:E551–564. doi: 10.1152/ajpendo.1987.253.5.E551. [DOI] [PubMed] [Google Scholar]
- Coplen TB, Böhlke JK, De Bievre BP, Ding T, Holden NE, Hopple JA, Krouse HR, Lamberty A, Peiser HS, Revesz K, et al. Isotope-abundance variations of selected elements (IUPAC Technical Report) Pure Appl. Chem. 2009;74:1987–2017. [Google Scholar]
- Crown SB, Kelleher JK, Rouf R, Muoio DM, Antoniewicz MR. Comprehensive metabolic modeling of multiple 13C-isotopomer data sets to study metabolism in perfused working hearts. Am. J. Physiol. Heart Circ. Physiol. 2016;311:H881–H891. doi: 10.1152/ajpheart.00428.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dauner M, Sauer U. GC-MS Analysis of Amino Acids Rapidly Provides Rich Information for Isotopomer Balancing. Biotechnol. Prog. 2000;16:642–649. doi: 10.1021/bp000058h. [DOI] [PubMed] [Google Scholar]
- Dunstan RH. Calculation of the relative frequencies of stable isotope labelled and unlabelled molecules in a gas chromatographic peak using gas chromatography/mass spectrometry. Biol. Mass Spectrom. 1988;15:473–478. [Google Scholar]
- Edwards JS, Palsson BO. The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. 2000;97:5528–5533. doi: 10.1073/pnas.97.10.5528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez CA, Des Rosiers C, Previs SF, David F, Brunengraber H. Correction of 13C mass isotopomer distributions for natural stable isotope abundance. J. Mass Spectrom. 1996;31:255–262. doi: 10.1002/(SICI)1096-9888(199603)31:3<255::AID-JMS290>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Firestone RB, Baglin CM, Chu SYF. Table of Isotopes: 1999 Update. 1999.
- Hellerstein MK, Neese RA. Mass isotopomer distribution analysis at eight years: theoretical, analytic, and experimental considerations. Am. J. Physiol. - Endocrinol. Metab. 1999;276:E1146–E1170. doi: 10.1152/ajpendo.1999.276.6.E1146. [DOI] [PubMed] [Google Scholar]
- Jennings ME, Matthews DE. Determination of complex isotopomer patterns in isotopically labeled compounds by mass spectrometry. Anal. Chem. 2005;77:6435–6444. doi: 10.1021/ac0509354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelleher JK, Kharroubi AT, Aldaghlas TA, Shambat IB, Kennedy KA, Holleran AL, Masterson TM. Isotopomer spectral analysis of cholesterol synthesis: applications in human hepatoma cells. Am. J. Physiol. 1994;266:E384–395. doi: 10.1152/ajpendo.1994.266.3.E384. [DOI] [PubMed] [Google Scholar]
- Lee WN, Byerley LO, Bergner EA, Edmond J. Mass isotopomer analysis: theoretical and practical considerations. Biol. Mass Spectrom. 1991;20:451–458. doi: 10.1002/bms.1200200804. [DOI] [PubMed] [Google Scholar]
- Libourel IGL, Shachar-Hill Y. Metabolic Flux Analysis in Plants: From Intelligent Design to Rational Engineering. Annu. Rev. Plant Biol. 2008;59:625–650. doi: 10.1146/annurev.arplant.58.032806.103822. [DOI] [PubMed] [Google Scholar]
- Marx A, de Graaf AA, Wiechert W, Eggeling L, Sahm H. Determination of the fluxes in the central metabolism of Corynebacterium glutamicum by nuclear magnetic resonance spectroscopy combined with metabolite balancing. Biotechnol. Bioeng. 1996;49:111–129. doi: 10.1002/(SICI)1097-0290(19960120)49:2<111::AID-BIT1>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- Mehrmohamadi M, Liu X, Shestov AA, Locasale JW. Characterization of the Usage of the Serine Metabolic Network in Human Cancer. Cell Rep. 2014;9:1507–1519. doi: 10.1016/j.celrep.2014.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meija J, Coplen TB, Berglund M, Brand WA, De Bievre BP, Gröning M, Holden NE, Irrgeher J, Loss RD, Walczyk T, et al. Isotopic compositions of the elements 2013 (IUPAC Technical Report) Pure Appl. Chem. 2016;88:293–306. [Google Scholar]
- Millard P, Letisse F, Sokol S, Portais J-C. IsoCor: correcting MS data in isotope labeling experiments. Bioinformatics. 2012;28:1294–1296. doi: 10.1093/bioinformatics/bts127. [DOI] [PubMed] [Google Scholar]
- Moseley HN. Correcting for the effects of natural abundance in stable isotope resolved metabolomics experiments involving ultra-high resolution mass spectrometry. BMC Bioinformatics. 2010;11:139. doi: 10.1186/1471-2105-11-139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen J. It Is All about Metabolic Fluxes. J. Bacteriol. 2003;185:7031–7035. doi: 10.1128/JB.185.24.7031-7035.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olstad E, Olsen GM, Qu H, Sonnewald U. Pyruvate recycling in cultured neurons from cerebellum. J. Neurosci. Res. 2007;85:3318–3325. doi: 10.1002/jnr.21208. [DOI] [PubMed] [Google Scholar]
- Orth JD, Thiele I, Palsson BØ. What is flux balance analysis? Nat. Biotechnol. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papageorgopoulos C, Caldwell K, Shackleton C, Schweingrubber H, Hellerstein MK. Measuring Protein Synthesis by Mass Isotopomer Distribution Analysis (MIDA) Anal. Biochem. 1999;267:1–16. doi: 10.1006/abio.1998.2958. [DOI] [PubMed] [Google Scholar]
- Quek L-E, Wittmann C, Nielsen LK, Krömer JO. OpenFLUX: efficient modelling software for 13C-based metabolic flux analysis. Microb. Cell Factories. 2009;8:25. doi: 10.1186/1475-2859-8-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quek L-E, Dietmair S, Krömer JO, Nielsen LK. Metabolic flux analysis in mammalian cell culture. Metab. Eng. 2010;12:161–171. doi: 10.1016/j.ymben.2009.09.002. [DOI] [PubMed] [Google Scholar]
- Revelles O, Millard P, Nougayrède J-P, Dobrindt U, Oswald E, Létisse F, Portais J-C. The Carbon Storage Regulator (Csr) System Exerts a Nutrient-Specific Control over Central Metabolism in Escherichia coli Strain Nissle 1917. PLOS ONE. 2013;8:e66386. doi: 10.1371/journal.pone.0066386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenblatt J, Chinkes D, Wolfe M, Wolfe RR. Stable isotope tracer analysis by GC-MS, including quantification of isotopomer effects. Am. J. Physiol. - Endocrinol. Metab. 1992;263:E584–E596. doi: 10.1152/ajpendo.1992.263.3.E584. [DOI] [PubMed] [Google Scholar]
- Sauer U. Metabolic networks in motion: C-based flux analysis. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100109. n/a-n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt K, Carlsen M, Nielsen J, Villadsen J. Modeling isotopomer distributions in biochemical networks using isotopomer mapping matrices. Biotechnol. Bioeng. 1997;55:831–840. doi: 10.1002/(SICI)1097-0290(19970920)55:6<831::AID-BIT2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- Shestov AA, Lee S-C, Nath K, Guo L, Nelson DS, Roman JC, Leeper DB, Wasik MA, Blair IA, Glickson JD. 13C MRS and LC–MS Flux Analysis of Tumor Intermediary Metabolism. Front Onco. 2016;6:135. doi: 10.3389/fonc.2016.00135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal RR, Rohlf FJ. Biometry: the principles and practice of statistics in biological research. WH Freeman and Company; New York: 1995. [Google Scholar]
- Sokol S, Millard P, Portais J-C. influx_s: increasing numerical stability and precision for metabolic flux analysis in isotope labelling experiments. Bioinformatics. 2012;28:687–693. doi: 10.1093/bioinformatics/btr716. [DOI] [PubMed] [Google Scholar]
- Srour O, Young JD, Eldar YC. Fluxomers: a new approach for 13C metabolic flux analysis. BMC Syst. Biol. 2011;5:129. doi: 10.1186/1752-0509-5-129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strong JM, Upton DK, Anderson LW, Monks A, Chisena CA, Cysyk RL. A novel approach to the analysis of mass spectrally assayed stable isotope-labeling experiments. J. Biol. Chem. 1985;260:4276–4281. [PubMed] [Google Scholar]
- Tserng KY, Kalhan SC. Calculation of substrate turnover rate in stable isotope tracer studies. Am. J. Physiol. - Endocrinol. Metab. 1983;245:E308–E311. doi: 10.1152/ajpendo.1983.245.3.E308. [DOI] [PubMed] [Google Scholar]
- Wahl SA, Dauner M, Wiechert W. New tools for mass isotopomer data evaluation in 13C flux analysis: Mass isotope correction, data consistency checking, and precursor relationships. Biotechnol. Bioeng. 2004;85:259–268. doi: 10.1002/bit.10909. [DOI] [PubMed] [Google Scholar]
- Walls AB, Bak LK, Sonnewald U, Schousboe A, Waagepetersen HS. Metabolic mapping of astrocytes and neurons in culture using stable isotopes and gas chromatography-mass spectrometry (GC-MS) Brain Energy Metabolism. 2014:73–105. [Google Scholar]
- Weitzel M, Nöh K, Dalman T, Niedenführ S, Stute B, Wiechert W. 13CFLUX2—high-performance software suite for 13C-metabolic flux analysis. Bioinformatics. 2013;29:143–145. doi: 10.1093/bioinformatics/bts646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiechert W. 13C Metabolic Flux Analysis. Metab. Eng. 2001;3:195–206. doi: 10.1006/mben.2001.0187. [DOI] [PubMed] [Google Scholar]
- Wiechert W, de Graaf AA. Bidirectional reaction steps in metabolic networks: I. Modeling and simulation of carbon isotope labeling experiments. Biotechnol. Bioeng. 1997;55:101–117. doi: 10.1002/(SICI)1097-0290(19970705)55:1<101::AID-BIT12>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Wiechert W, Möllney M, Isermann N, Wurzel M, de Graaf AA. Bidirectional reaction steps in metabolic networks: III. Explicit solution and analysis of isotopomer labeling systems. Biotechnol. Bioeng. 1999;66:69–85. [PubMed] [Google Scholar]
- van Winden WA, Wittmann C, Heinzle E, Heijnen JJ. Correcting mass isotopomer distributions for naturally occurring isotopes. Biotechnol. Bioeng. 2002;80:477–479. doi: 10.1002/bit.10393. [DOI] [PubMed] [Google Scholar]
- van Winden WA, Heijnen JJ, Verheijen PJT. Cumulative bondomers: A new concept in flux analysis from 2D [13C,1H] COSY NMR data. Biotechnol. Bioeng. 2002;80:731–745. doi: 10.1002/bit.10429. [DOI] [PubMed] [Google Scholar]
- Wittmann C. Metabolic Flux Analysis Using Mass Spectrometry. In: Scheper T, editor. Tools and Applications of Biochemical Engineering Science. Springer; Berlin Heidelberg: 2002. pp. 39–64. [DOI] [PubMed] [Google Scholar]
- Wittmann C. Fluxome analysis using GC-MS. Microb. Cell Factories. 2007;6:6. doi: 10.1186/1475-2859-6-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wynn ML, Yates JA, Evans CR, Wassenhove LDV, Wu ZF, Bridges S, Bao L, Fournier C, Ashrafzadeh S, Merrins MJ, et al. RhoC GTPase Is a Potent Regulator of Glutamine Metabolism and N-Acetylaspartate Production in Inflammatory Breast Cancer Cells. J. Biol. Chem. 2016;291:13715–13729. doi: 10.1074/jbc.M115.703959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang TH, Bolten CJ, Coppi MV, Sun J, Heinzle E. Numerical bias estimation for mass spectrometric mass isotopomer analysis. Anal. Biochem. 2009;388:192–203. doi: 10.1016/j.ab.2009.03.005. [DOI] [PubMed] [Google Scholar]
- Young JD. INCA: a computational platform for isotopically non-stationary metabolic flux analysis. Bioinformatics. 2014;30:1333–1335. doi: 10.1093/bioinformatics/btu015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young JD, Walther JL, Antoniewicz MR, Yoo H, Stephanopoulos G. An elementary metabolite unit (EMU) based method of isotopically nonstationary flux analysis. Biotechnol. Bioeng. 2008;99:686–699. doi: 10.1002/bit.21632. [DOI] [PubMed] [Google Scholar]
- Zamboni N, Sauer U. Novel biological insights through metabolomics and 13C-flux analysis. Curr. Opin. Microbiol. 2009;12:553–558. doi: 10.1016/j.mib.2009.08.003. [DOI] [PubMed] [Google Scholar]
- Zamboni N, Fischer E, Sauer U. FiatFlux--a software for metabolic flux analysis from 13C-glucose experiments. BMC Bioinformatics. 2005;6:209. doi: 10.1186/1471-2105-6-209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamboni N, Fendt S-M, Rühl M, Sauer U. 13C-based metabolic flux analysis. Nat. Protoc. 2009;4:878–892. doi: 10.1038/nprot.2009.58. [DOI] [PubMed] [Google Scholar]
- Zheng W, Tayyari F, Gowda GAN, Raftery D, McLamore ES, Porterfield DM, Donkin SS, Bequette B, Teegarden D. Altered glucose metabolism in Harvey-ras transformed MCF10A cells. Mol. Carcinog. 2015;54:111–120. doi: 10.1002/mc.22079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zupke C, Stephanopoulos G. Intracellular flux analysis in hybridomas using mass balances and in vitro 13C NMR. Biotechnol. Bioeng. 1995;45:292–303. doi: 10.1002/bit.260450403. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.