Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Mar 9.
Published in final edited form as: Phys Med Biol. 2009 Nov 24;54(24):7401–7415. doi: 10.1088/0031-9155/54/24/010

Method comparison of automated matching software-assisted cone-beam CT and stereoscopic kilovoltage x-ray positional verification image-guided radiation therapy for head and neck cancer: a prospective analysis

Clifton D Fuller 1,2,3,6,*, Todd J Scarbrough 3,4, Jan-Jakob Sonke 5, Coen R N Rasch 5, Mehee Choi 3, Joe Y Ting 4, Samuel J Wang 3, Niko Papanikolaou 1,2, David I Rosenthal 6
PMCID: PMC5343752  NIHMSID: NIHMS846626  PMID: 19934488

Abstract

We sought to characterize interchangeability and agreement between cone-beam computed tomography (CBCT) and digital stereoscopic kV x-ray (KVX) acquisition, two methods of isocenter positional verification currently used for IGRT of head and neck cancers (HNC). A cohort of 33 patients were near-simultaneously imaged by in-room KVX and CBCT. KVX and CBCT shifts were suggested using manufacturer software for the lateral (X), vertical (Y) and longitudinal (Z) dimensions. Intra-method repeatability, systematic and random error components were calculated for each imaging modality, as were recipe-based PTV expansion margins. Inter-method agreement in each axis was compared using limits of agreement (LOA) methodology, concordance analysis and orthogonal regression. 100 daily positional assessments were performed before daily therapy in 33 patients with head and neck cancer. Systematic error was greater for CBCT in all axes, with larger random error components in the Y- and Z-axis. Repeatability ranged from 9 to 14 mm for all axes, with CBCT showing greater repeatability in 2/3 axes. LOA showed paired shifts to agree 95% of the time within ±11.3 mm in the X-axis, ±9.4 mm in the Y-axis and ±5.5 mm in the Z-axis. Concordance ranged from ‘mediocre’ to ‘satisfactory’. Proportional bias was noted between paired X- and Z-axis measures, with a constant bias component in the Z-axis. Our data suggest non-negligible differences in software-derived CBCT and KVX image-guided directional shifts using formal method comparison statistics.

Introduction

The advent of modern conformal radiotherapy techniques places a greater premium upon positional verification, as substantial deviation from treatment planning simulations secondary to comparatively small geometric differentials may occur (Bel et al 1996, Bos et al 2005, Keall et al 1999, Lebesque et al 1995, Papiez and Langer 2006, Remeijer et al 1999, van Herk 2004, van Herk et al 1997, 2000, 2002, 2003, Kaiser et al 2006). Reduction of uncertainty, as conceptualized by PTV margin minimization, is possible though positional set-up error minimization. Consequently, a variety of image-guided radiotherapy techniques (IGRT) have been implemented clinically in order to maximize allineation to the isocenter. Among these techniques, both stereoscopic kV x-ray (KVX) (Wu et al 2007, Serago et al 2006, Verellen et al 2006, Sorensen et al 2006, Pisani et al 2000, Scarbrough et al 2006) and cone-beam CT (CBCT) (Boda-Heggemann et al 2006, Guckenberger et al 2006, Jaffray et al 2002, Letourneau et al 2005, Pouliot et al 2005, Thilmann et al 2006) have seen ready implementation into clinical practice, albeit, as with many IGRT techniques, a modicum of attempts to compare distinct measurement methods head-to-head in various anatomic sites (Godfrey et al 2007, Willoughby et al 2006a, 2006b, Wu et al 2007, Scarbrough et al 2006).

While series detailing target alignment with KVX and CBCT have been performed (Boda-Heggemann et al 2006, Wu et al 2007, Borst et al 2007), to our knowledge, none compared using the same automatching software package or with specific method comparison statistical approaches (Bland and Altman 1986, 1995a, 1995b, 1996, 1999, 2003, 2007). Method comparison remain a rarity within the imaging literature (Schramm et al 2004, Bradley et al 1999, Mahnken et al 2005, Bielak et al 2001, Bland and Altman 2003, Hilson 2004) and are minimally encountered within radiotherapy communiqués (Moseley et al 2007, Fuller et al 2006).

The specific aims of this prospective study included the following.

  1. Summarization of distributional and set-up error characteristics of near-simultaneous KVX and CBCT imaging method-derived positional using the same image coregistration/alignment software package.

  2. Examination of KVX and CBCT paired software-suggested shifts using established strategies for method comparison.

  3. Generation of hypotheses for future prospective research.

Methods

Study cohort

Patients with tumors of the salivary glands, oral cavity, pharynx or larynx treated were eligible for analysis. A total of 33 patients with head and neck cancers were enrolled in a prospective protocol, consisting of a paired, near simultaneous evaluation of spatial location using both KVX and CBCT.

Simulation and localization systems

Patients were simulated in the treatment position using in a dedicated CT scanner (2.5 mm slice thickness/68-slice; GE LightSpeed, General Electric, Chicago, IL) after administration of IV contrast (Visipaque, Amersham/GE Health, Chicago, IL). Customized headrests and mask (Civco, Kalona, IA) were used for immobilization. CBCT and stereoscopic kV x-ray were acquired near simultaneously at approximately biweekly intervals throughout a patient’s course of treatment (dependent upon the scheduling exigencies in the department). CBCT/kV x-ray analyses were performed using the attached on-board imager (Varian Medical Systems, Palo Alto, CA). CBCT (2.5 mm slice thickness, full-fan geometry, full bowtie filter, 360° rotation) was obtained after the patient was immobilized in the standard fashion. Specific mechanical and technical parameters of this manufacturer-supplied hardware/software system have been profiled in depth in extant manuscripts. CBCT acquisition methodology has likewise been detailed (Bissonnette et al 2008, Jaffray 2007, Jaffray et al 2002, Letourneau et al 2005, Djodjevic 2007) and has, in phantom verification analyses, a reported geometric accuracy of 0.8 ± 0.2 mm (Djodjevic 2007). Automatic CBCT to simulation CT (3D–3D) registration was undertaken with manufacturer-supplied software (Varian OBI 1.3/Varian Vision, Varian Medical Systems, Palo Alto, CA). A kV x-ray pair was then obtained, typically within 2–5 min. A rectangular region of interest was set by the physician in the AP and lateral views on the initial day of setup and was replicated for matching purposes throughout treatment (Djodjevic 2007, Fox et al 2006). The kV x-ray OBI/automatching hardware/software system has been presented previously (Kim et al 2008, Mechalakos et al 2007, Sorcini and Tilikidis 2006), in phantom verification tests, and is reported to have demonstrated ‘overall uncertainty in the positioning of known offsets [of] approximately 1.4 mm for most clinical cases’ (Fox et al 2006). Automatic KVX to DRR (2D–2D) registration was also accomplished using the same manufacturer-supplied software package (Varian OBI 1.3/Varian Vision, Varian Medical Systems, Palo Alto, CA). The aforementioned software version utilizes a registration framework for 2D–2D automatching wherein an initial image set (designated as the fixed image) and a subsequent dataset (moving image) are spatially mapped using transform parameters. The registration task is performed via iterative optimization problem using established algorithms (Wells et al 1996, Kim et al 2007, Balter and Kessler 2007) to evaluate image-intensity agreement after sequential matching steps. Specifically, widely implemented mutual information (Maes et al 2003, Viola and Wells III 1997) and pattern intensity (Penney et al 1998, 2001) algorithms are implemented for 2D–2D and 3D–3D optimization (as in this series). The manufacturer-supplied automatching software uses a distinct approach for 2D–3D matching (which was not evaluated in this study), which requires radio-opaque marker identification in the planning CT and implements a prior-knowledge-based approach using epipolar triangulation to generate a least-squares match between the three-dimensional marker position in planning CT and planar image sets.

Recorded shifts represent the coregistration/allineation software derived values without physician/observer modification. Analysis and matching of kV x-rays was performed in less than 1 min. The CBCT acquisition and matching process was accomplished in approximately 5–6 min total. Patients were always ultimately shifted and treated based on the software-suggested kV x-ray shifts with physician validation/confirmation, using daily ‘on-line’ correction.

Statistical analysis

For each paired-method positional acquisition, the origin was defined as the point in space identified by the initial isocenter position using immobilization-mask-based markers. Utilizing a three-dimensional Cartesian coordinate system, this spatial location was designated as a ‘zero point’ with X/Y/Z coordinates of 0, 0, 0. Software-derived shifts for each system were recorded in millimeters, specified as X-, Y- or Z-axis. The KVX software-derived shifts were characterized as lateral (left/right) XKVX, vertical (AP/PA) YKVX and longitudinal (superior/inferior) ZKVX coordinates. Similar nomenclature was utilized to label the corresponding axes (XCBCT, YCBCT, ZCBCT) for CBCT-based shifts. Statistical analysis was performed using JMP v6 (SAS Institute, Cary, NC, USA), EZ-Rose (Baas 2000) (University of Wales-Bangor, UK) and Oriana (Kovach Computing Services, Anglesey, Wales, UK) software packages.

Intra-method summary statistics

Series median, mean and standard deviation (SD) were calculated in each axis for each imaging platform. The 360° rotational distribution of each imaging modality was evaluated for uniformity using Watson’s test for uniformity (Watson 1967) of a circular distribution with a non-corrected α = 0.05. The mean vector orientation ±95% confidence interval, Batschelet’s circular standard deviation (Batschelet 1981) and distribution type were calculated using software for circular data analysis.

Error component estimation and margin calculation

Systematic and random error components for the entire cohort were assessed via the method of van Herk et al (2004), where systematic error component (Σ) was calculated as the standard deviation of the mean set-up correction for each individual patient, and the random error component (σ) was determined by calculating the root mean square of the series standard deviation of every patients’ set-up error. Systematic errors for ΣKVX and ΣCBCT were calculated. Probabilistic target volume coverage margins were assessed via methods described in previous series. As a measure of clinical usable margins (M), margins suggested by van Herk et al (2004), which provides a minimum cumulative CTV dose of at least 95% of the prescribed dose for 90% of the patient population, was calculated as M = 2.5Σ + 0.7σ.

Method comparison and concordance

The Altman–Bland analysis was implemented to determine method agreement in cases when a ‘gold-standard’ has not been established (Bland and Altman 1986, 1996, 1999). The mean difference (X̄KVX-CBCT), standard deviation of differences (SDKVX-CBCT) and 95% limit of agreement (LOA KVX-CBCT; ±1.96 times the standard deviation of the differences) were calculated. While there are no statistical thresholds (e.g. p-values) for LOA, this allows clinicians to determine whether such a differential is clinically meaningful, as the LOA indicates a range wherein measurements from each device may be expected to agree in 95% of cases. Since this dataset comprises multiple measures for each patient, the unequal replicates variant of the Altman–Bland analysis was performed (Bland and Altman 1999). This calculation involves estimation of intra-method repeatability (that is the variability between fractions on the same patient using the same measurement technique). The Altman–Bland repeatability coefficients, RKVX and RCBCT, which represent the 95% confidence interval of the within-subject standard deviations (i.e. square root of the residual mean square for each method) were calculated.

As an evaluative measure of concordance between techniques (Arbillaga et al 2002, King and Chinchilli 2001a, 2001b, Lin 1989), Lin’s concordance coefficient was calculated. Lin’s concordance coefficient (LCC), initially used to compare whether a series of observations reproduces an original series when the variance between measurement devices is unequal, is calculated as the product of the Pearson correlation coefficient (rP) and a bias correction factor (Cb). Techniques/methods are regarded as equivalent if the coefficient is greater than a specified threshold, with concordance increasing as rP approaches 1.0. Partik’s categorical grading criteria may then be implemented in order to convert the numeric value of Lin’s concordance coefficient into an ordinal scale (Partik et al 2002); Partik’s criteria designates values of LCC > 0.95 as ‘excellent’, >0.90 ‘very good’, >0.80 ‘fairly good’, >0.70 ‘middling/satisfactory’ >0.60 ‘mediocre’, >0.50 ‘poor’ and ≤0.50 as ‘unacceptable’.

Deming orthogonal regression was implemented to assess bias-corrected correlation between paired measures, using the ratio of variances between KVX and CBCT cohorts, as well as proportional and constant between method bias (Fuller et al 2006, Konings 1982, Martin 2000).

Results

A sequential series total of 100 paired positional alignments were recorded in 33 patients, with a mean of three alignment pairs per patient.

Intra-method summary statistics

Median, mean and standard deviation are summarized in table 1. A three-dimensional graphical plot of all points, with 95% isosurface, is shown for KVX and CBCT in figures 1(a) and (b), respectively. The mean directional shift in each cardinal axis was within 1 mm or less for all axes, for both modalities. Circular statistics revealed a nonuniform, Gaussian distribution for both KVX and CBCT localization, with range of rotation between −4.9° and +4.2° for KVX, and −5.3° and +5.3° for CBCT positioning. Summarization of circular statistics is presented in table 2.

Table 1.

Distributional parameters by positional imaging modality for each axis.

Axis Median (mm) Mean (mm) SD (mm)
XCBCT 1.0 0.6 4.2
YCBCT 0.02 0.03 4.7
ZCBCT 1.0 1.0 4.2
XKVX −0.5 −0.3 4.7
YKVX 0.01 −0.1 2.8
ZKVX 1.0 0.8 6.2
Open in a new tab

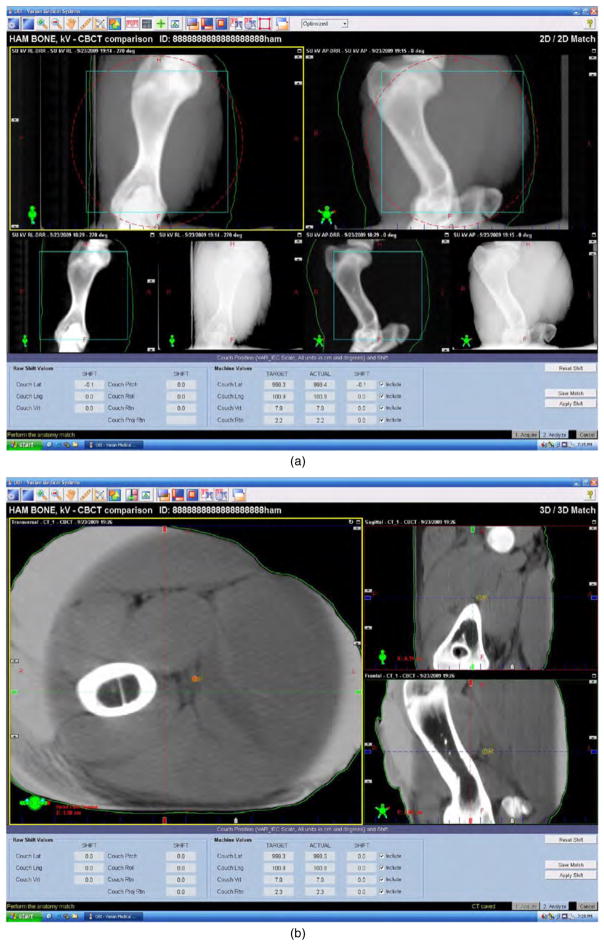
Figure 1.

Figure 1

Open in a new tab

(a), (b) Screenshot of automated shift output. Screen capture of image/numeric output of automated shift correction using KVX (2D–2D registration (a) and CBCT (3D–3D registration (b), using tissue equivalent bone-in phantom (Honeybaked Ham, Norcross, GA).

Table 2.

Rotational statistics by imaging modality.

ROTCBCT ROTkvx
M 1.06 ± 0.37 1.01 ± 0.39
SDB 1.22 1.53
Open in a new tab

All values in degrees; M = mean rotation in degrees ±95% confidence interval of mean; SDB = Batschlelet’s circular standard deviation.

Error component estimation and margin calculation

Systematic and random error calculations for each modality are summarized in table 3. Probabilistic PTV margin expansion values derived from aforementioned margin recipes are shown in table 4.

Table 3.

Systematic (Σ) and random error component (σ) values (mm).

X-axis Y-axis Z-axis
ΣCBCT 3.7 3.5 3.7
ΣKVX 3.5 3.3 2.4
σ CBCT 2.5 3.9 2.0
σ KVX 4.3 3.7 1.8
Open in a new tab

Table 4.

Recipe-suggested PTV expansion margins (M), by positional imaging modality.

Axis M (mm)
XCBCT 10.9
YCBCT 11.5
ZCBCT 10.7
XKVX 11.7
YKVX 10.9
ZKVX 7.3
Open in a new tab

Method comparison and concordance

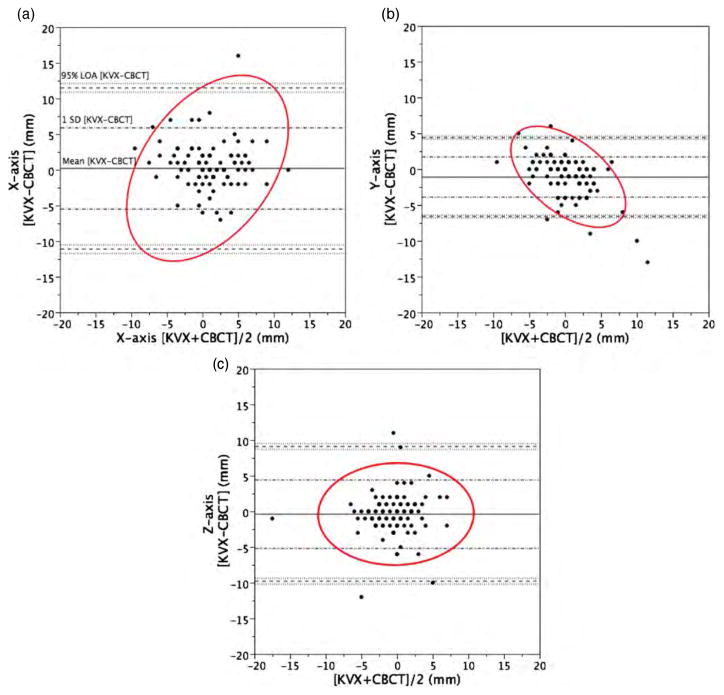
Method comparison using the Altman–Bland analysis is demonstrated in tabular format in table 5. KVX-CBCT comparison exhibited 95% limits of agreement of ±11.3 mm in the X-axis, ±9.4 mm in the Y-axis and ±5.5 mm in the Z-axis. The greatest between-method axis differential was noted in the X-dimension, suggesting that lateral shifts are notably more different between KVX and CBCT localization than Y- and Z-axes. Graphical plots of Altman–Bland analyses are shown in figures 2(a)–(c). Repeatability coefficients are listed in table 5. For every dimension except the superior–inferior axis (Z), CBCT showed a smaller repeatability coefficient (table 6).

Table 5.

Altman–Bland analysis.

X̄KVX-CBCT SDKVX-CBCT LOAKVX-CBCT
X 0.2 ±5.7 ±11.3
Y −0.4 ±4.8 ±9.4
Z −1.1 ±2.8 ±5.5
Open in a new tab

Limits of agreement analysis (X̄KVX-CBCT = mean of differences between paired measures; SDKVX-CBCT = standard deviation of differences between paired measures; LOAKVX-CBCT = 95% limits of agreement). All values in mm.

Figure 2.

Figure 2

Open in a new tab

(a)–(c) Altman–Bland plots. Altman–Bland plots of method agreement by cardinal axis between CBCT and KVX, in mm, with 95% density ellipse in red. Mean difference, SD of difference and 95% limits of agreement (1.96 × SD) are labeled on (a).

Table 6.

Intra-subject Altman–Bland repeatability coefficients, by axis/modality.

Axis RKVX (mm) RCBCT (mm)
X 20.1 11.3
Y 14.9 14.0
Z 7.2 9.0
Open in a new tab

Deming orthogonal regression is shown graphically in figures 3(a)–(c). The bias-corrected correlation was lowest in the X-axis, which exhibited a proportional bias between KVX and CBCT (p < 0.05). Proportional and constant bias was noted at the p < 0.05 level for the Z-axis. Concordance analysis is presented in table 7, with all axes showing ‘mediocre’ to ‘fairly good’ concordance.

Figure 3.

Figure 3

Open in a new tab

(a)–(c) Deming regression plots. Variance-weighted orthogonal regression fit (dark line) and line of identity (dashed line) for each axis between CBCT and KVX, in mm. The 95% distribution is shown in dashed ellipses. Deming orthogonal regression coefficients are shown as captions.

Table 7.

Concordance measures.

Pearson R Cb LCC PC
X 0.70 0.98 0.70 Satisfactory
Y 0.81 0.99 0.80 Fairly good
Z 0.74 0.88 0.64 Mediocre
Open in a new tab

Concordance coefficient calculation, showing uncorrected Pearson’s R value, bivariate bias correction (Cb), Lin’s concordance coefficient (LCC) and Partik’s criteria categorical evaluation.

Discussion

Rapid technical progress and the ready availability of novel radiotherapy equipment have meant that the vast majority of image-guided techniques are implemented in the absence of comparative series with other modalities; this has resulted in a heterogeneous use of different positional verification systems across institutions (Ling et al 2006). A host of planar and volumetric image-guidance platforms are available commercially, some with distinctive proprietary features (Zeidan et al 2007, Pouliot et al 2006, Meyer et al 2007, McBain et al 2006, Letourneau et al 2005, Jaffray et al 2002, Godfrey et al 2006, Court et al 2007). To date, the vast majority of target localization series have focused upon prostatic cancer (Fuss et al 2003, Lohr et al 2007, Scarbrough et al 2006). In an effort to determine inter-and intra-platform variation, we have sought to characterize specific indicative parameters affording comparison of image-guidance techniques for head and neck cancers. However, direct comparison of image-guidance system-derived shifts using either means comparison (i.e. t-tests) or least-squares regression is statistically inappropriate when one device has not been established as a gold standard (Bland and Altman 1995b). Consequently, in addition to standard intra-method distributional and error analysis, we sought to characterize method agreement implementing established statistical tests. By and large, rotational distributions, as assessed by CBCT and KVX, were of negligible magnitude and likely contributed little to inter-method variation (table 2).

This study includes evaluation of error components, which are potentially more practically useful than intra-method descriptive statistics for the evaluation of positional accuracy. In this series, non-negligible (i.e. >1 mm) differences were noted in between cumulative measures of systematic and random error in the X- and Z-axes, respectively. Comparison of the systematic and random error components of the difference between paired measures indicates that a nonnegligible residual set-up error would be expected using correction on KVX after CBCT, and further alluding to a distinct error profile between devices. Given margin expansion recipes (Stroom et al 1999, van Herk 2004, van Herk et al 2000) are reflective of this fact, as systematic error is weighted several fold higher than random error in mathematical accounting of set-up uncertainty.

Inter-method comparison analyses presented herein are indicative of the relative statistical agreement between devices. The Altman–Bland analysis resulted in the finding that measurement on KVX-CBCT comparison exhibited 95% limits of agreement of ±11.3 mm in the X-axis, ±9.4 mm in the Y-axis, and ±5.5 mm in the Z-axis. Whether such discrepancies are of importance must be made as a clinical judgment, as the Altman–Bland analysis presents no ‘threshold’ or p-value, leaving determination of the significance relative of between-device differentials to clinicians.

There are several potential rationales for the observed differentials between KVX and CBCT. The information sets of planar radiographic and tomographic transmission images are quite different, as KVX techniques utilize planar image-datasets, which are then aligned to two-dimensional DRRs, while CBCT affords combination of volumetric data from the kV simulation CT and the treatment CBCT. Additionally, both modalities utilize requisite operator-dependent region of interest (ROI) determination, which may differ between modalities. Consequently, when a given mutual information software system (in this case Varian OBI v 1.3) coregisters said images with the simulation CT, distinct automatching software algorithms are implemented, possibly resulting in differing distributions. However, we would then expect differences to be observed in suggested shifts using a standardized phantom. In order to ensure that observed differentials in KVX and CBCT were not attributable to calibration error on either imaging device or the software platform, a post hoc quality assurance test was performed using a tissue equivalent phantom (figure 1, Honeybaked Ham, Norcross, GA). The phantom was offset by a known value and automatched as per the methods section. After a series of repeated measures (n = 10), sequential near simultaneous phantom measures for each device were within 1 mm of the physical offset employed (i.e. less than or equal to the minimum spatial resolution of the KVX platform output), suggesting minimal calibration/quality assurance deviations. This is consistent with previous reporting by for example Djodjevic (2007), who reported mean ±SD differences between KVX and CBCT on a series of phantom alignments for lateral, vertical and longitudinal axes of 0.5 ± 0.1, 0.5 ± 0.1 and 0.7 ± 0.4 mm, respectively. Despite the best efforts to undertake near simultaneous images using both techniques, it is possible that patient motion might introduce some artifact into the positioning process. This possibility has been raised in similar series (Li et al 2008), and, if true, would place renewed focus on patient immobilization in IGRT for head and neck sites. However, the repeatability coefficient differential observed is suggestive that, presumably at the software level, processes involved in generation of shift automatching exhibit resultant CBCT shifts with greater repeatability over serial imaging of the same patient compared to KVX. This indicates some possible influence of the software package, rather than intrinsic properties of the imaging modalities.

Furthermore, growing awareness that the human neck is not a rigid, but rather a deformable structure (van Kranen et al 2009), necessarily means that the capacity for correction for head and neck positional variability through translational correction is therefore necessarily limited. Consequently, IGRT software systems that implement a region of interest as a reference for correction may be compromised due to cervical deformation, in addition to ROI delineation variability. Volumetric images could thus present an opportunity the ability to more accurately define the anatomy for alignment using more eloquent software corrections (van Herk et al 2004).

Recently, Wu et al presented data evaluating near-simultaneous kVX, CBCT and digital tomosynthesis (DTS) image-acquisition for IGRT (Wu et al 2007) and observed differentials in daily shifts similar in magnitude to this study, albeit without implementing formal method comparison statistical measures. Manual image alignment was performed in their KVX/CBCT/DTS series, whereas in the present study, software suggested shifts without operator manipulation are detailed. Additionally, Li et al have recently published a similarly sized dataset comparing single institution results comparing KVX and CBCT for head and neck (Li et al 2008). Their dataset provides an excellent complement to the independent institutional dataset presented herein. The data presented by Li et al which also examined mechanisms of immobilization resulted in substantially smaller recommended safety margins than those derived from the present dataset, which may reflect institutional variation in immobilization.

While similar to the analysis presented by Li et al (2008), this dataset was analyzed using formal method comparison analyses, avoiding potential statistical errors associated with implementation of the t-test or uncorrected regression analysis for the examination of between-method differentials (Fuller et al 2006, Bland and Altman 1986, 1999, 2003, 2007). Such comparative series are essential as they are only way mechanism to characterize the relative performance between an ever-increasing field of competitive image-guidance devices with regard to representation of physical phenomenon (e.g. patient motion), hardware or software processes. Finally, since all data were collected at a single institution and are a numerically limited sample, the obvious standard caveats apply.

Conclusions

Finally, the following may be surmised from our analysis.

  1. KVX and CBCT show non-negligible measurement differences when measuring the same patients near-simultaneously.

  2. CBCT exhibits greater repeatability in two of three measured axes compared to KVX.

  3. Error component analysis shows distinct error profiles for given axes using KVX and CBCT.

This study, which to our knowledge represents the largest reported formal method comparison analysis of these two image-guidance techniques, should serve as an impetus for future method comparison series. Our group is currently exploring novel method comparison techniques (Roy 2006, 2009), which may provide capacity for definitive recommendation of one platform over another. In the interim, based on our series, we do not recommend utilizing CBCT and KVX data interchangeably for head and neck positional verification. Patient shift derived from one imaging platform should be implemented throughout therapy, and automated shift corrections from one platform should not be substituted with one another.

Acknowledgments

CDF is supported by a grant from the National Institutes of Health/National Institute of Biomedical Imaging and Bioengineering, ‘Multidisciplinary Training Program in Human Imaging’ (5T32EB000817-04); this funder had no role in study design, in the collection, analysis and interpretation of data, in the writing of the manuscript, nor in the decision to submit the manuscript for publication. Portions of this data were presented at the ASTRO Translational Research in Radiation Oncology and Radiology, 7–8 September 2007, San Francisco, CA, USA, and the European Society for Therapeutic Radiology and Oncology (ESTRO 27) Meeting, 14–17 September 2008, Göteborg, Sweden.

Abbreviations

CBCT

cone beam computed tomography

KVX

stereoscopic kV x-ray

OBI

on-board imager

HNC

head and neck cancer(s)

CT

computed tomography

DRR

digital reconstructed radiography

SD

standard deviation

LOA

95% limit of agreement

IGRT

image-guided radiotherapy

IMRT

intensity modulated radiotherapy

References

  1. Arbillaga HO, Montgomery GP, Cabarrus LP, Watson MM, Martin L, Edworthy SM. Internet hand x-rays: a comparison of joint space narrowing and erosion scores (Sharp/Genant) of plain versus digitized x-rays in rheumatoid arthritis patients. BMC Musculoskelet Disord. 2002;3:13. doi: 10.1186/1471-2474-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baas J. EZ-ROSE: a computer program for equal-area circular histograms and statistical analysis of two-dimensional vectorial data. Comput Geosci. 2000;26:153–66. [Google Scholar]
  3. Balter JM, Kessler ML. Imaging and alignment for image-guided radiation therapy. J Clin Oncol. 2007;25:931–7. doi: 10.1200/JCO.2006.09.7998. [DOI] [PubMed] [Google Scholar]
  4. Batschelet E. Circular Statistics in Biology. New York: Academic; 1981. [Google Scholar]
  5. Bel A, van Herk M, Lebesque JV. Target margins for random geometrical treatment uncertainties in conformal radiotherapy. Med Phys. 1996;23:1537–45. doi: 10.1118/1.597745. [DOI] [PubMed] [Google Scholar]
  6. Bielak LF, Sheedy PF, 2nd, Peyser PA. Coronary artery calcification measured at electron-beam CT: agreement in dual scan runs and change over time. Radiology. 2001;218:224–9. doi: 10.1148/radiology.218.1.r01ja34224. [DOI] [PubMed] [Google Scholar]
  7. Bissonnette JP, Moseley D, White E, Sharpe M, Purdie T, Jaffray DA. Quality assurance for the geometric accuracy of cone-beam CT guidance in radiation therapy. Int J Radiat Oncol Biol Phys. 2008;71:S57–61. doi: 10.1016/j.ijrobp.2007.06.086. [DOI] [PubMed] [Google Scholar]
  8. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–10. [PubMed] [Google Scholar]
  9. Bland JM, Altman DG. Comparing methods of measurement: why plotting difference against standard method is misleading. Lancet. 1995a;346:1085–7. doi: 10.1016/s0140-6736(95)91748-9. [DOI] [PubMed] [Google Scholar]
  10. Bland JM, Altman DG. Comparing two methods of clinical measurement: a personal history. Int J Epidemiol. 1995b;24(Suppl 1):S7–14. doi: 10.1093/ije/24.supplement_1.s7. [DOI] [PubMed] [Google Scholar]
  11. Bland JM, Altman DG. Measurement error. BMJ. 1996;312:1654. doi: 10.1136/bmj.312.7047.1654. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135–60. doi: 10.1177/096228029900800204. [DOI] [PubMed] [Google Scholar]
  13. Bland JM, Altman DG. Applying the right statistics: analyses of measurement studies. Ultrasound Obstet Gynecol. 2003;22:85–93. doi: 10.1002/uog.122. [DOI] [PubMed] [Google Scholar]
  14. Bland JM, Altman DG. Agreement between methods of measurement with multiple observations per individual. J Biopharm Stat. 2007;17:571–82. doi: 10.1080/10543400701329422. [DOI] [PubMed] [Google Scholar]
  15. Boda-Heggemann J, Walter C, Rahn A, Wertz H, Loeb I, Lohr F, Wenz F. Repositioning accuracy of two different mask systems-3D revisited: comparison using true 3D/3D matching with cone-beam CT. Int J Radiat Oncol Biol Phys. 2006;66:1568–75. doi: 10.1016/j.ijrobp.2006.08.054. [DOI] [PubMed] [Google Scholar]
  16. Borst GR, Sonke JJ, Betgen A, Remeijer P, van Herk M, Lebesque JV. Kilo-voltage cone-beam computed tomography setup measurements for lung cancer patients; first clinical results and comparison with electronic portal-imaging device. Int J Radiat Oncol Biol Phys. 2007;68:555–61. doi: 10.1016/j.ijrobp.2007.01.014. [DOI] [PubMed] [Google Scholar]
  17. Bos LJ, Van Der Geer J, van Herk M, Mijnheer BJ, Lebesque JV, Damen EM. The sensitivity of dose distributions for organ motion and set-up uncertainties in prostate IMRT. Radiother Oncol. 2005;76:18–26. doi: 10.1016/j.radonc.2005.06.010. [DOI] [PubMed] [Google Scholar]
  18. Bradley AJ, Carrington BM, Lawrance JA, Ryder WD, Radford JA. Assessment and significance of mediastinal bulk in Hodgkin’s disease: comparison between computed tomography and chest radiography. J Clin Oncol. 1999;17:2493–8. doi: 10.1200/JCO.1999.17.8.2493. [DOI] [PubMed] [Google Scholar]
  19. Court LE, Allen A, Tishler R. Evaluation of the precision of portal-image-guided head-and-neck localization: an intra- and interobserver study. Med Phys. 2007;34:2704–7. doi: 10.1118/1.2747050. [DOI] [PubMed] [Google Scholar]
  20. Djodjevic M. Medicinsk Strålningsfysik. Stockholm: Stockholm University and Karolinska Institute; 2007. Evaluation of geometric accuracy and image quality of an on-board imager (OBI) p. 66. [Google Scholar]
  21. Fox T, Huntzinger C, Johnstone P, Ogunleye T, Elder E. Performance evaluation of an automated image registration algorithm using an integrated kilovoltage imaging and guidance system. J Appl Clin Med Phys./Am Coll Med Phys. 2006;7:97–104. doi: 10.1120/jacmp.v7i1.2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fuller CD, Thomas CR, Schwartz S, Golden N, Ting J, Wong A, Erdogmus D, Scarbrough TJ. Method comparison of ultrasound and kilovoltage x-ray fiducial marker imaging for prostate radiotherapy targeting. Phys Med Biol. 2006;51:4981–93. doi: 10.1088/0031-9155/51/19/016. [DOI] [PubMed] [Google Scholar]
  23. Fuss M, Cavanaugh SX, Fuss C, Cheek DA, Salter BJ. Daily stereotactic ultrasound prostate targeting: inter-user variability. Technol Cancer Res Treat. 2003;2:161–70. doi: 10.1177/153303460300200213. [DOI] [PubMed] [Google Scholar]
  24. Godfrey DJ, Ren L, Yan H, Wu Q, Yoo S, Oldham M, Yin FF. Evaluation of three types of reference image data for external beam radiotherapy target localization using digital tomosynthesis (DTS) Med Phys. 2007;34:3374–84. doi: 10.1118/1.2756941. [DOI] [PubMed] [Google Scholar]
  25. Godfrey DJ, Yin FF, Oldham M, Yoo S, Willett C. Digital tomosynthesis with an on-board kilovoltage imaging device. Int J Radiat Oncol Biol Phys. 2006;65:8–15. doi: 10.1016/j.ijrobp.2006.01.025. [DOI] [PubMed] [Google Scholar]
  26. Guckenberger M, Meyer J, Vordermark D, Baier K, Wilbert J, Flentje M. Magnitude and clinical relevance of translational and rotational patient setup errors: a cone-beam CT study. Int J Radiat Oncol Biol Phys. 2006;65:934–42. doi: 10.1016/j.ijrobp.2006.02.019. [DOI] [PubMed] [Google Scholar]
  27. Hilson A. Bland-Altman plot. Radiology. 2004;231:604. doi: 10.1148/radiol.2312031472. author reply 605. [DOI] [PubMed] [Google Scholar]
  28. Jaffray DA. Kilovoltage volumetric imaging in the treatment room. Front Radiat Ther Oncol. 2007;40:116–31. doi: 10.1159/000106031. [DOI] [PubMed] [Google Scholar]
  29. Jaffray DA, Siewerdsen JH, Wong JW, Martinez AA. Flat-panel cone-beam computed tomography for image-guided radiation therapy. Int J Radiat Oncol Biol Phys. 2002;53:1337–49. doi: 10.1016/s0360-3016(02)02884-5. [DOI] [PubMed] [Google Scholar]
  30. Kaiser A, Schultheiss TE, Wong JY, Smith DD, Han C, Vora NL, Pezner RD, Chen YJ, Radany EH. Pitch, roll, and yaw variations in patient positioning. Int J Radiat Oncol Biol Phys. 2006;66:949–55. doi: 10.1016/j.ijrobp.2006.05.055. [DOI] [PubMed] [Google Scholar]
  31. Keall PJ, Beckham WA, Booth JT, Zavgorodni SF, Oppelaar M. A method to predict the effect of organ motion and set-up variations on treatment plans. Australas Phys Eng Sci Med. 1999;22:48–52. [PubMed] [Google Scholar]
  32. Kim GY, Pawlicki T, Le QT, Luxton G. Linac-based on-board imaging feasibility and the dosimetric consequences of head roll in head-and-neck IMRT plans. Med Dosim. 2008;33:93–9. doi: 10.1016/j.meddos.2007.05.004. [DOI] [PubMed] [Google Scholar]
  33. Kim J, Li S, Pradhan D, Hammoud R, Chen Q, Yin F-F, Zhao Y, Kim JH, Movsas B. Comparison of similarity measures for rigid-body CT/Dual X-ray image registrations. Technol Cancer Res Treat. 2007;6:337–46. doi: 10.1177/153303460700600411. [DOI] [PubMed] [Google Scholar]
  34. King TS, Chinchilli VM. A generalized concordance correlation coefficient for continuous and categorical data. Stat Med. 2001a;20:2131–47. doi: 10.1002/sim.845. [DOI] [PubMed] [Google Scholar]
  35. King TS, Chinchilli VM. Robust estimators of the concordance correlation coefficient. J Biopharm Stat. 2001b;11:83–105. doi: 10.1081/BIP-100107651. [DOI] [PubMed] [Google Scholar]
  36. Konings H. Use of Deming regression in method-comparison studies. Survey Immunol Res. 1982;1:371–4. doi: 10.1007/BF02918550. [DOI] [PubMed] [Google Scholar]
  37. Lebesque JV, Bruce AM, Kroes AP, Touw A, Shouman RT, van Herk M. Variation in volumes, dose-volume histograms, and estimated normal tissue complication probabilities of rectum and bladder during conformal radiotherapy of T3 prostate cancer. Int J Radiat Oncol Biol Phys. 1995;33:1109–19. doi: 10.1016/0360-3016(95)00253-7. [DOI] [PubMed] [Google Scholar]
  38. Letourneau D, Wong JW, Oldham M, Gulam M, Watt L, Jaffray DA, Siewerdsen JH, Martinez AA. Cone-beam-CT guided radiation therapy: technical implementation. Radiother Oncol. 2005;75:279–86. doi: 10.1016/j.radonc.2005.03.001. [DOI] [PubMed] [Google Scholar]
  39. Li H, et al. Comparison of 2D radiographic images and 3D cone beam computed tomography for positioning head-and-neck radiotherapy patients. Int J Radiat Oncol Biol Phys. 2008;71:916–25. doi: 10.1016/j.ijrobp.2008.01.008. [DOI] [PubMed] [Google Scholar]
  40. Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–68. [PubMed] [Google Scholar]
  41. Ling CC, Yorke E, Fuks Z. From IMRT to IGRT: frontierland or neverland? Radiother Oncol. 2006;78:119–22. doi: 10.1016/j.radonc.2005.12.005. [DOI] [PubMed] [Google Scholar]
  42. Lohr F, Boda-Heggemann J, Wenz F, Wiegel T. Image-guided radiotherapy for prostate cancer. Aktuelle Urol. 2007;38:386–91. doi: 10.1055/s-2007-980118. discussion 5. [DOI] [PubMed] [Google Scholar]
  43. Maes F, Vandermeulen D, Suetens P. Medical image registration using mutual information. Proc IEEE. 2003;91:1699–722. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
  44. Mahnken AH, Koos R, Katoh M, Spuentrup E, Busch P, Wildberger JE, Kuhl HP, Gunther RW. Sixteen-slice spiral CT versus MR imaging for the assessment of left ventricular function in acute myocardial infarction. Eur Radiol. 2005;15:714–20. doi: 10.1007/s00330-004-2592-x. [DOI] [PubMed] [Google Scholar]
  45. Martin RF. General deming regression for estimating systematic bias and its confidence interval in method-comparison studies. Clin Chem. 2000;46:100–4. [PubMed] [Google Scholar]
  46. McBain CA, et al. X-ray volumetric imaging in image-guided radiotherapy: the new standard in on-treatment imaging. Int J Radiat Oncol Biol Phys. 2006;64:625–34. doi: 10.1016/j.ijrobp.2005.09.018. [DOI] [PubMed] [Google Scholar]
  47. Mechalakos JG, Hunt MA, Lee NY, Hong LX, Ling CC, Amols HI. Using an onboard kilovoltage imager to measure setup deviation in intensity-modulated radiation therapy for head-and-neck patients. J Appl Clin Med Phys./Am Coll Med Phys. 2007;8:2439. doi: 10.1120/jacmp.v8i4.2439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Meyer J, Wilbert J, Baier K, Guckenberger M, Richter A, Sauer O, Flentje M. Positioning accuracy of cone-beam computed tomography in combination with a HexaPOD robot treatment table. Int J Radiat Oncol Biol Phys. 2007;67:1220–8. doi: 10.1016/j.ijrobp.2006.11.010. [DOI] [PubMed] [Google Scholar]
  49. Moseley DJ, et al. Comparison of localization performance with implanted fiducial markers and cone-beam computed tomography for on-line image-guided radiotherapy of the prostate. Int J Radiat Oncol Biol Phys. 2007;67:942–53. doi: 10.1016/j.ijrobp.2006.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Papiez L, Langer M. On probabilistically defined margins in radiation therapy. Phys Med Biol. 2006;51:3921–39. doi: 10.1088/0031-9155/51/16/003. [DOI] [PubMed] [Google Scholar]
  51. Partik BL, Stadler A, Schamp S, Koller A, Voracek M, Heinz G, Helbich TH. 3D versus 2D ultrasound: accuracy of volume measurement in human cadaver kidneys. Invest Radiol. 2002;37:489–95. doi: 10.1097/01.RLI.0000023573.59066.43. [DOI] [PubMed] [Google Scholar]
  52. Penney GP, Batchelor PG, Hill DL, Hawkes DJ, Weese J. Validation of a two- to three-dimensional registration algorithm for aligning preoperative CT images and intraoperative fluoroscopy images. Med Phys. 2001;28:1024–32. doi: 10.1118/1.1373400. [DOI] [PubMed] [Google Scholar]
  53. Penney GP, Weese J, Little JA, Desmedt P, Hill DL, Hawkes DJ. A comparison of similarity measures for use in 2-D-3-D medical image registration. IEEE Trans Med Imaging. 1998;17:586–95. doi: 10.1109/42.730403. [DOI] [PubMed] [Google Scholar]
  54. Pisani L, Lockman D, Jaffray D, Yan D, Martinez A, Wong J. Setup error in radiotherapy: on-line correction using electronic kilovoltage and megavoltage radiographs. Int J Radiat Oncol Biol Phys. 2000;47:825–39. doi: 10.1016/s0360-3016(00)00476-4. [DOI] [PubMed] [Google Scholar]
  55. Pouliot J, et al. Low-dose megavoltage cone-beam CT for radiation therapy. Int J Radiat Oncol Biol Phys. 2005;61:552–60. doi: 10.1016/j.ijrobp.2004.10.011. [DOI] [PubMed] [Google Scholar]
  56. Pouliot J, Morin O, Aubin M, Aubry JF, Chen J, Speight J, Roach M., 3rd Megavoltage cone-beam CT: recent developments and clinical applications. Cancer Radiother. 2006;10:258–68. doi: 10.1016/j.canrad.2006.05.010. [DOI] [PubMed] [Google Scholar]
  57. Remeijer P, Rasch C, Lebesque JV, van Herk M. A general methodology for three-dimensional analysis of variation in target volume delineation. Med Phys. 1999;26:931–40. doi: 10.1118/1.598485. [DOI] [PubMed] [Google Scholar]
  58. Roy A. A new classification rule for incomplete doubly multivariate data using mixed effects model with performance comparisons on the imputed data. Stat Med. 2006;25:1715–28. doi: 10.1002/sim.2320. [DOI] [PubMed] [Google Scholar]
  59. Roy A. An application of linear mixed effects model to assess the agreement between two methods with replicated observations. J Biopharm Stat. 2009;19:150–73. doi: 10.1080/10543400802535141. [DOI] [PubMed] [Google Scholar]
  60. Scarbrough TJ, Golden NM, Ting JY, Fuller CD, Wong A, Kupelian PA, Thomas CR., Jr Comparison of ultrasound and implanted seed marker prostate localization methods: implications for image-guided radiotherapy. Int J Radiat Oncol Biol Phys. 2006;65:378–87. doi: 10.1016/j.ijrobp.2006.01.008. [DOI] [PubMed] [Google Scholar]
  61. Schramm P, Schellinger PD, Klotz E, Kallenberg K, Fiebach JB, Kulkens S, Heiland S, Knauth M, Sartor K. Comparison of perfusion computed tomography and computed tomography angiography source images with perfusion-weighted imaging and diffusion-weighted imaging in patients with acute stroke of less than 6 hours’ duration. Stroke. 2004;35:1652–8. doi: 10.1161/01.STR.0000131271.54098.22. [DOI] [PubMed] [Google Scholar]
  62. Serago CF, Buskirk SJ, Igel TC, Gale AA, Serago NE, Earle JD. Comparison of daily megavoltage electronic portal imaging or kilovoltage imaging with marker seeds to ultrasound imaging or skin marks for prostate localization and treatment positioning in patients with prostate cancer. Int J Radiat Oncol Biol Phys. 2006;65:1585–92. doi: 10.1016/j.ijrobp.2006.04.019. [DOI] [PubMed] [Google Scholar]
  63. Sorcini B, Tilikidis A. Clinical application of image-guided radiotherapy, IGRT (on the Varian OBI platform) Cancer Radiother. 2006;10:252–7. doi: 10.1016/j.canrad.2006.05.012. [DOI] [PubMed] [Google Scholar]
  64. Sorensen SP, Chow PE, Kriminski S, Medin PM, Solberg TD. Image-guided radiotherapy using a mobile kilovoltage x-ray device. Med Dosim. 2006;31:40–50. doi: 10.1016/j.meddos.2005.12.003. [DOI] [PubMed] [Google Scholar]
  65. Stroom JC, de Boer HC, Huizenga H, Visser AG. Inclusion of geometrical uncertainties in radiotherapy treatment planning by means of coverage probability. Int J Radiat Oncol Biol Phys. 1999;43:905–19. doi: 10.1016/s0360-3016(98)00468-4. [DOI] [PubMed] [Google Scholar]
  66. Thilmann C, et al. Correction of patient positioning errors based on in-line cone beam CTs: clinical implementation and first experiences. Radiat Oncol. 2006;1:16. doi: 10.1186/1748-717X-1-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. van Herk M. Errors and margins in radiotherapy. Semin Radiat Oncol. 2004;14:52–64. doi: 10.1053/j.semradonc.2003.10.003. [DOI] [PubMed] [Google Scholar]
  68. van Herk M, Betgen A, Jaffray D, Remeijer P, Smitsmans M, Sonke JJ, Zijp L. An integrated system for on-line cone-beam CT image guided radiotherapy—software aspects. Proceedings of the 14th International Conf. on the Use of Computers in Radiation Therapy (ICCR); Seoul: Jeong Publishing; 2004. [Google Scholar]
  69. van Herk M, Gilhuijs KG, de Munck J, Touw A. Effect of image artifacts, organ motion, and poor segmentation on the reliability and accuracy of three-dimensional chamfer matching. Comput Aided Surg. 1997;2:346–55. doi: 10.1002/(SICI)1097-0150(1997)2:6<346::AID-IGS5>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
  70. van Herk M, Remeijer P, Lebesque JV. Inclusion of geometric uncertainties in treatment plan evaluation. Int J Radiat Oncol Biol Phys. 2002;52:1407–22. doi: 10.1016/s0360-3016(01)02805-x. [DOI] [PubMed] [Google Scholar]
  71. van Herk M, Remeijer P, Rasch C, Lebesque JV. The probability of correct target dosage: dose-population histograms for deriving treatment margins in radiotherapy. Int J Radiat Oncol Biol Phys. 2000;47:1121–35. doi: 10.1016/s0360-3016(00)00518-6. [DOI] [PubMed] [Google Scholar]
  72. van Herk M, Witte M, Van Der Geer J, Schneider C, Lebesque JV. Biologic and physical fractionation effects of random geometric errors. Int J Radiat Oncol Biol Phys. 2003;57:1460–71. doi: 10.1016/j.ijrobp.2003.08.026. [DOI] [PubMed] [Google Scholar]
  73. van Kranen S, van Beek S, Rasch C, van Herk M, Sonke JJ. Setup uncertainties of anatomical sub-regions in head-and-neck cancer patients after offline CBCT guidance. Int J Radiat Oncol Biol Phys. 2009;73:1566–73. doi: 10.1016/j.ijrobp.2008.11.035. [DOI] [PubMed] [Google Scholar]
  74. Verellen D, Soete G, Linthout N, Tournel K, Storme G. Optimal control of set-up margins and internal margins for intra- and extracranial radiotherapy using stereoscopic kilovoltage imaging. Cancer Radiother. 2006;10:235–44. doi: 10.1016/j.canrad.2006.05.011. [DOI] [PubMed] [Google Scholar]
  75. Viola P, Wells WM. Alignment by maximization of mutual information. Int J Comput Vision. 1997;24:137–54. [Google Scholar]
  76. Watson GS. Another test for the uniformity of a circular distribution. Biometrika. 1967;54:675–7. [PubMed] [Google Scholar]
  77. Wells WM, Viola P, Atsumi H, Nakajima S. Multi-modal volume registration by maximization of mutual information. Med Image Anal. 1996;1:31–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
  78. Willoughby TR, Forbes AR, Buchholz D, Langen KM, Wagner TH, Zeidan OA, Kupelian PA, Meeks SL. Evaluation of an infrared camera and X-ray system using implanted fiducials in patients with lung tumors for gated radiation therapy. Int J Radiat Oncol Biol Phys. 2006a;66:568–75. doi: 10.1016/j.ijrobp.2006.05.029. [DOI] [PubMed] [Google Scholar]
  79. Willoughby TR, et al. Target localization and real-time tracking using the Calypso 4D localization system in patients with localized prostate cancer. Int J Radiat Oncol Biol Phys. 2006b;65:528–34. doi: 10.1016/j.ijrobp.2006.01.050. [DOI] [PubMed] [Google Scholar]
  80. Wu QJ, Godfrey DJ, Wang Z, Zhang J, Zhou S, Yoo S, Brizel DM, Yin FF. On-board patient positioning for head-and-neck IMRT: comparing digital tomosynthesis to kilovoltage radiography and cone-beam computed tomography. Int J Radiat Oncol Biol Phys. 2007;69:598–606. doi: 10.1016/j.ijrobp.2007.05.045. [DOI] [PubMed] [Google Scholar]
  81. Zeidan OA, Langen KM, Meeks SL, Manon RR, Wagner TH, Willoughby TR, Jenkins DW, Kupelian PA. Evaluation of image-guidance protocols in the treatment of head and neck cancers. Int J Radiat Oncol Biol Phys. 2007;67:670–7. doi: 10.1016/j.ijrobp.2006.09.040. [DOI] [PubMed] [Google Scholar]

RESOURCES