Longitudinal Multiple Sclerosis Lesion Segmentation: Resource & Challenge

Abstract

In conjunction with the ISBI 2015 conference, we organized a longitudinal lesion segmentation challenge providing training and test data to registered participants. The training data consisted of five subjects with a mean of 4.4 time-points, and test data of fourteen subjects with a mean of 4.4 time-points. All 82 data sets had the white matter lesions associated with multiple sclerosis delineated by two human expert raters. Eleven teams submitted results using state-of-the-art lesion segmentation algorithms to the challenge, with ten teams presenting their results at the conference. We present a quantitative evaluation comparing the consistency of the two raters as well as exploring the performance of the eleven submitted results in addition to three other lesion segmentation algorithms. The challenge presented three unique opportunities: 1) the sharing of a rich data set; 2) collaboration and comparison of the various avenues of research being pursued in the community; and 3) a review and refinement of the evaluation metrics currently in use. We report on the performance of the challenge participants, as well as the construction and evaluation of a consensus delineation. The image data and manual delineations will continue to be available for download, through an evaluation website¹ as a resource for future researchers in the area. This data resource provides a platform to compare existing methods in a fair and consistent manner to each other and multiple manual raters.

1. Introduction

Multiple sclerosis (MS) is a disease of the central nervous system (CNS) that is characterized by inflammation and neuroaxonal degeneration in both gray matter (GM) and white matter (WM) (Compston and Coles, 2008). MS is the most prevalent autoimmune disorder affecting the CNS, with an estimated 2.5 million cases worldwide (World Health Organization, 2008; Confavreux and Vukusic, 2008) and was responsible for approximately 20,000 deaths in 2013 (Global Burden of Disease Study 2013 Mortality and Causes of Death Collaborators, 2015). MS has a relatively young age of onset with an average age of 29.2 years and interquartile onset range of 25.3 and 31.8 years (World Health Organization, 2008). Symptoms of MS include cognitive impairment, vision loss, weakness in limbs, dizziness, and fatigue. The term multiple sclerosis originates from the scars (known as lesions) in the WM of the CNS that are formed by the demyelination process, which can be quantified through magnetic resonance imaging (MRI) of the brain and spinal cord. T₂-weighted (T₂-w) lesions within the WM (or WMLs), so called because of their hyperintense appearance on T₂-w MRI, have become a standard part of the diagnostic criteria (Polman et al., 2011). However, it is a labor intensive and somewhat subjective task to identify and manually delineate or segment WM hyperintensities from normal tissue in MR images. This objective is made more difficult when considering a longitudinal series of data, particularly when each data set at a given time-point for an individual consists of several scan modalities of varying quality (Vrenken et al., 2013). MS frequently involves lesions that may be readily apparent on a scan at one time-point, but not in subsequent time-points (He et al., 2001; Gaitán et al., 2011; Qian et al., 2011). Delineating the scans individually without reference to previous images, may lead to errors in detection of damaged tissue; such as previously lesioned areas that have contracted, undergone remyelination, are no longer inflamed, or a combination thereof. These damaged areas may correlate with disability, although it is as yet unclear precisely how they are related and through what exact mechanism they affect changes in symptoms (Meier et al., 2007; Filippi et al., 2012). Thus there is an apparent need for the automatic detection and segmentation of WMLs in longitudinal CNS scans of MS patients.

Three major subtypes or stages of WMLs can be visualized using MR imaging (Filippi and Grossman, 2002; Wu et al., 2006): 1) gadolinium-enhancing lesions, which demonstrate blood-brain barrier leakage, 2) hypointense T₁-w lesions, also called black holes that possess prolonged T₁-w relaxation times, and 3) hyperintense T₂-w lesions, which likely reflect increased water content stemming from inflammation and/or demyelination. These latter lesions are the most prevalent type (Bakshi, 2005) and are hyperintense on proton density weighted (PD-w), T₂-w, and fluid attenuated inversion recovery (FLAIR) images. Both enhancing and black hole lesions typically form a subset of T₂-w lesions. Quantification of T₂-w lesion volume and identification of new T₂-w and enhancing lesions in longitudinal data are commonly used to gauge disease severity and monitor therapies, although these metrics have largely been shown to only weakly correlate with clinical disability (Filippi et al., 2014). Pathologically, we can differentiate the different stages of an MS WML as pre-active, active, chronic active, or chronic inactive depending on the demyelination status, adaptive immune response, and microglia behavior. Lesions with normal myelin density and activated microglia are termed pre-active, while sharp bordered demyelination reflects active lesions. Chronic active lesions have a fully demyelinated center and are hypocellular, and chronic inactive lesions have complete demyelination and an absence of any microglia. Current MRI technologies are very sensitive to T₂-w WMLs, however they do not provide any insight about pathological heterogeneity (Jonkman et al., 2015).

Despite this, MRI has gained prominence as an important tool for the clinical diagnosis of MS (Polman et al., 2011), as well as understanding the progression of the disease (Buonanno et al., 1983; Paty, 1988; Filippi et al., 1995; Evans et al., 1997; Collins et al., 2001). A variety of techniques are being used for automated MS lesion segmentation (Anbeek et al., 2004; Brosch et al., 2015, 2016; Deshpande et al., 2015; Dugas-Phocion et al., 2004; Elliott et al., 2013, 2014; Ferrari et al., 2003; Geremia et al., 2010; Havaei et al., 2016; Jain et al., 2015; Jog et al., 2015; Johnston et al., 1996; Kamber et al., 1996; Khayati et al., 2008; Rey et al., 1999, 2002; Roy et al., 2010, 2014b; Schmidt et al., 2012; Shiee et al., 2010; Subbanna et al., 2015; Sudre et al., 2015; Tomas-Fernandez and Warfield, 2011, 2012; Valverde et al., 2017; Weiss et al., 2013; Welti et al., 2001; Xie and Tao, 2011) with several review articles available that describe and evaluate the utility of these methods (García-Lorenzo et al., 2013; Lladó et al., 2012), though semi-automated approaches have also been reported (Udupa et al., 1997; Wu et al., 2006; Zijdenbos et al., 1994). The early work on WML segmentation used the principle of modeling the distributions of intensities of healthy brain tissues and segmenting outliers to those distributions as lesions. An early example of this is Van Leemput et al. (2001), which augmented the outlier detection with contextual information using a Markov random field (MRF). This idea was extended by Aït-Ali et al. (2005) by using an entire time series for a subject, estimating the tissue distributions using an iterative Trimmed Likelihood Estimator (TLE), followed by a segmentation refinement step based on the Mahalanobis distance and prior information from clinical knowledge. Later improvements to the TLE based model include mean shift (García-Lorenzo et al., 2008, 2011) and Hidden Markov chains (Bricq et al., 2008). Other approaches to treating the WM lesions as an outlier class include methods based on support vector machines (SVM) (Ferrari et al., 2003), coupling of local & global intensity models in a Gaussian Mixture Model (GMM) (Tomas-Fernandez and Warfield, 2011, 2012) and using adaptive outlier detection (Ong et al., 2012).

As an alternative to the outlier detection approach other methods create models with lesions as an additional class. Examples of this include: k-nearest neighbors (k-NN) (Anbeek et al., 2004), a hierarchical Hidden Markov random field (Sajja et al., 2004, 2006); an unsupervised Bayesian lesion classifier with various regions of the brain having different intensity distributions (Harmouche et al., 2006); a Bayesian classifier based on the adaptive mixtures method and an MRF (Khayati et al., 2008); a constrained GMM based on posterior probabilities followed by a level set method for lesion boundary refinement (Freifeld et al., 2009); a fuzzy C-means model with a topology consistency constraint (Shiee et al., 2010); and adaptive dictionary learning (Deshpande et al., 2015; Roy et al., 2014a, 2015b); along with many other techniques.

The majority of these methods operate in an unsupervised manner using statistical notions about distributions to identify lesions. There has also been significant work done to develop supervised methods, which use training data to identify lesions within new subjects. One such approach included an anatomical template-based registration to help modulate a k-NN classification scheme (Warfield et al., 2000), which used features from the images as well as distances to the template following the registration. Sweeney et al. (2013b) presented a logistic regression model that assigned voxel-level probabilities of lesion presence. Roy et al. (2014b) demonstrated a patch-based lesion segmentation that used examples from an atlas to match patches in the input images using a sparse dictionary approach. Variants of this supervised machine learning solution include: generic machine learning (Xie and Tao, 2011); dictionary learning and sparse-coding (Roy et al., 2014a, 2015b; Weiss et al., 2013); and random forest (RF) work by Mitra et al. (2014), variations of the RF approach include Geremia et al. (2010, 2011) using multi-channel MR intensities, long-range spatial context, and asymmetry features to identify lesions; Jog et al. (2015) producing overlapping lesion masks from the RF that were averaged to create a probabilistic segmentation, and Maier et al. (2015) used extra tree forests (Geurts et al., 2006) which are robust to noise and uncertain training data.

There has been less work on automated methods for serial lesion segmentation (segmentation of lesions for the same subject over different time-points). The earliest reported approach (Rey et al., 1999, 2002) performed an optical flow registration between successive rigidly registered time-points, then used the Jacobian of the deformation field to identify the lesions. Published at about the same time, Kikinis et al. (1999) used 4D connected component analysis for longitudinal lesion segmentation. Prima et al. (2002) introduced voxel wise statistical testing to identify regions with significantly increased intensity over time, treating the appearance of WMLs as a change-point problem. Welti et al. (2001) created a feature vector of radial intensity-based descriptors of lesions from four contrast images at multiple time-points. The course of these descriptors is then analyzed with a principal component analysis (PCA) to build a model of spatio-temporal lesion evolution. Projection of candidate lesions into the PCA space was used to identify lesions, with the maximal temporal gradient of a FLAIR image being used to identify the onset of the lesion. Bosc et al. (2003) used a pipeline comprised of iterative affine registration, deformable registration, image resampling, and intensity normalization, followed by a temporal change point detection scheme. Their change point detection used a generalized likelihood ratio test (GLRT) (Hsu et al., 1984) that computes the probabilities of the two hypotheses (no change vs. significant change). We note that the initial steps of Bosc et al. (2003), up to change detection, are now considered standard preprocessing for time-series data and is similar to the preprocessing that was performed on the data in our challenge. As previously mentioned Aït-Ali et al. (2005) extended the outlier detection approach (Van Leemput et al., 2001) to the entire time series using TLE followed by refinement steps. Roy et al. (2015a) extended their 3D example patch-based lesion segmentation algorithm to 4D by considering a time series of patches from available training data. Other work evaluated WML changes over time (Battaglini et al., 2014; Elliott et al., 2010; Ganiler et al., 2014; Roura et al., 2015; Sweeney et al., 2013a) with the focus being on the appearance/disappearance of lesions by subtraction of the intensity images of consecutive time-points. As there clearly has been a relative dearth of work on the automated segmentation of time-series WMLs, and as there is no approach that has gained widespread acceptance, a main purpose of this paper is to provide a public database to reignite work in this area.

Public databases have played a transformative role in medical imaging, an early example of this is the now ubiquitous BrainWeb (Collins et al., 1998) computational phantom (see also Cocosco et al. (1997) and Kwan et al. (1999)). With over one hundred citations per year for the last decade, it is almost inconceivable to write an MR-based brain segmentation paper without including an evaluation on the BrainWeb phantom. These public databases have served to standardize comparisons and evaluation criteria. In recent years there has been a shift in the community to launch these data sets as a challenge associated with a workshop or conference (Styner et al., 2008; Schaap et al., 2009; Heimann et al., 2009; Menze et al., 2015; Mendrik et al., 2015; Maier et al., 2017). In particular, the 2008 MICCAI MS Lesion challenge (Styner et al., 2008) was a significant step forward in the sharing of clinically relevant data. These benchmark data sets allow for a direct comparison between competing methods without any unique data issues, and just as importantly, these benchmarks remove the barrier of data that limits the number of researchers working in a particular area. An important feature of benchmarks is the retention of the test data set labels from the public domain avoiding the “unintentional overtraining of the method being tested” and preserving “the method's segmentation performance in practice” (Menze et al., 2015).

In this paper, we present details of the Longitudinal White Matter Lesion Segmentation of Multiple Sclerosis Challenge (hereafter the Challenge) that was conducted during the 2015 International Symposium on Biomedical Imaging (ISBI). The Challenge data will serve as an ongoing resource with future submissions for evaluation possible through the Challenge Website². In Section 2, we outline the data provided to the Challenge participants, the set-up of the Challenge, and the evaluation metrics used in comparing the submitted results from each team. Section 2 also includes a description of our Consensus Delineation, which avoids the biases of depending on a single rater. Section 3 provides an overview of the methods involved in the Challenge with complete descriptions of each algorithm included in Appendix B. Section 4 includes the comparison between the manual delineations, algorithms, and the Consensus Delineation. We conclude the main body of the manuscript with a discussion of the impact of this Challenge and future directions in WML segmentation in Section 5. Appendix A includes a complete description of the protocol used for the manual delineation. Appendix C includes the results from the Challenge at ISBI.

2. Materials and Metrics

Teams registered for the Challenge, and received access to a Training Set of images in February of 2015. Followed one month later by the first evaluation data set (Test Set A), with the Teams having one month to return their results for evaluation. One week before the Challenge event at ISBI 2015, Teams were provided with a second evaluation data set (Test Set B). Teams were told that the time between downloading Test Set B and the return of their results would be timed for comparison. Participants were informed of the criteria for the Challenge prizes, which were furnished by the National MS Society. Details of the data, preprocessing, and the Challenge metrics are provided below. The results of the Challenge are provided in Appendix C.

2.1. Challenge Data

The Challenge participants were given three tranches of data: 1) Training Set; 2) Test Set A; and 3) Test Set B. The Training Set consisted of five subjects, four of which had four time-points, while the fifth subject had five time-points. Test Set A included ten subjects, eight of which had four time-points, one had five time-points, and one had six time-points. Test Set B had four subjects–three with four time-points and two with five time-points. Two consecutive time-points are separated by approximately one year for all subjects. Table 1 includes a demographic breakdown for the training and test data sets. Challenge participants did not know the MS status of the subjects of each data set.

Table 1.

Demographic details for the training data and both test data sets. The top line is the information of the entire data set, while subsequent lines within a section are specific to the patient diagnoses. The codes are RR for relapsing remitting MS, PP for primary progressive MS, and SP for secondary progressive MS. N (M/F) denotes the number of patients and the male/female ratio, respectively. Time-points is the mean (and standard deviation) of the number of time-points provided to participants. Age is the mean age (and standard deviation), in years, at baseline. Follow-up is the mean (and standard deviation), in years, of the time between follow-up scans.

Data Set	N (M/F)	Time-Points Mean (SD)	Age Mean (SD)	Follow-Up Mean (SD)
Training	5 (1/4)	4.4 (±0.55)	43.5 (±10.3)	1.0 (±0.13)
RR	4 (1/3)	4.5 (±0.50)	40.0 (±7.55)	1.0 (±0.14)
PP	1 (0/1)	4.0	57.9	1.0 (±0.04)
Test A	10 (2/8)	4.3 (±0.68)	37.8 (±9.18)	1.1 (±0.28)
RR	9 (2/7)	4.3 (±0.71)	37.4 (±9.63)	1.1 (±0.29)
SP	1 (0/1)	4.0	41.7	1.0 (±0.05)
Test B	4 (1/3)	4.5 (±0.58)	43.3 (±7.64)	1.0 (±0.05)
RR	3 (1/2)	4.7 (±0.58)	44.8 (±8.65)	1.0 (±0.05)
PP	1 (0/1)	4.0	39.0	1.0 (±0.04)

Each scan was imaged and preprocessed in the same manner, with data acquired on a 3.0 Tesla MRI scanner (Philips Medical Systems, Best, The Netherlands) using the following sequences: a T₁-weighted (T₁-w) magnetization prepared rapid gradient echo (MPRAGE) with TR = 10.3 ms, TE = 6 ms, flip angle = 8°, & 0.82 × 0.82 × 1.17 mm³ voxel size; a double spin echo (DSE) which produces the PD-w and T₂-w images with TR = 4177 ms, TE₁ = 12.31 ms, TE₂ = 80 ms, & 0.82 × 0.82 × 2.2 mm³ voxel size; and a T₂-w fluid attenuated inversion recovery (FLAIR) with TI = 835 ms, TE = 68 ms, & 0.82 × 0.82 × 2.2 mm³ voxel size. The imaging protocols were approved by the local institutional review board. Each subject underwent the following preprocessing: the baseline (first time-point) MPRAGE was inhomogeneity-corrected using N4 (Tustison et al., 2010), skull-stripped (Carass et al., 2007, 2010), dura stripped (Shiee et al., 2014), followed by a second N4 inhomogeneity correction, and rigid registration to a 1 mm isotropic MNI template. We have found that running N4 a second time after skull and dura stripping is more effective (relative to a single correction) at reducing any inhomogeneity within the images (see Fig. 1 for an example image set after preprocessing). Once the baseline MPRAGE is in MNI space, it is used as a target for the remaining images. The remaining images include the baseline T₂-w, PD-w, and FLAIR, as well as the scans from each of the follow-up time-points. These images are N4 corrected and then rigidly registered to the 1 mm isotropic baseline MPRAGE in MNI space. Our registration steps are inverse consistent and thus any registration based biases are avoided (Reuter and Fischl, 2011). The skull & dura stripped mask from the baseline MPRAGE is applied to all the subsequent images, which are then N4 corrected again. All the images in the Training Set, Test Set A, and Test Set B, had their lesions manually delineated by two raters in the MNI space. Rater #1 has four years of experience delineating lesions, while Rater #2 has 10 years experience with manual lesion segmentation and 17 years experience in structural MRI analysis. We note that the raters were blinded to the temporal ordering of the data. The protocol for the manual delineation followed by both raters is in Appendix A. The preprocessing steps were performed using JIST (Version 3.2) (Lucas et al., 2010).

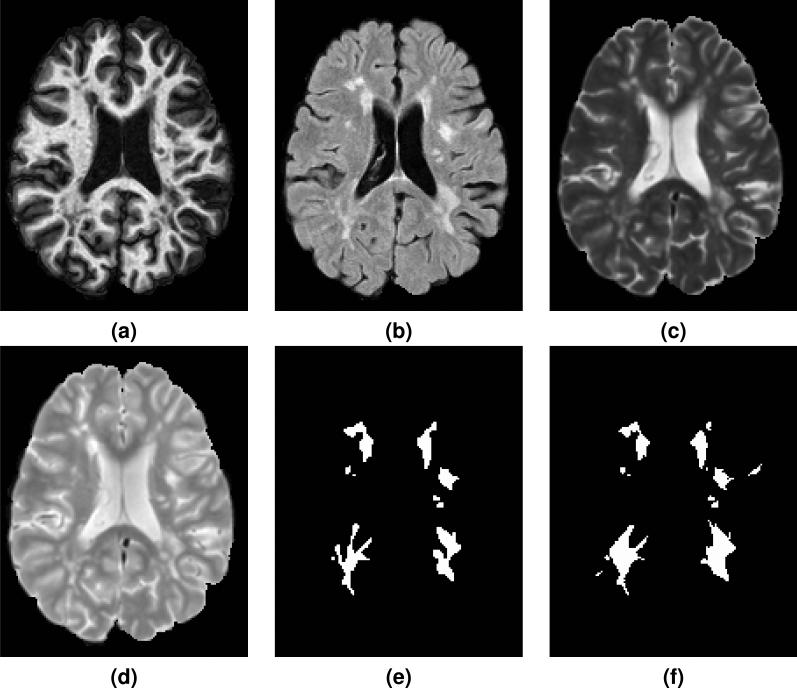
Figure 1.

Shown are the preprocessed (a) MPRAGE, (b) FLAIR, (c) T₂-w, and (d) PD-w images for a single time-point from one of the provided Training Set subjects. The corresponding manual delineations by our two raters are shown in (e) for Rater #1 and (f) for Rater #2.

For each time-point of every subject's scans in the Training Set, Test Set A, and Test Set B, the participants were provided the following data: the original scan images consisting of T₁-w MPRAGE, T₂-w, PD-w, and FLAIR, as well as the preprocessed images (in MNI space) for each of the scan modalities. The Training Set also included manual delineations by two experts identifying and segmenting WMLs on MR images: details about the delineation protocol and lesion inclusion criteria are in Appendix A.

As teams registered for the Challenge, they were provided with the Training Data. One month prior to the scheduled Challenge, Test Set A was made available to participants. The results for Test Set A could be returned to the organizers at any time prior to the Challenge event, though a preferred return date was given. The third data set, Test Set B, was provided to participants one week before the Challenge event with the caveat that teams would be timed. The times used were based on the initial download time for each team and the time at which they returned their results to the Challenge organizers. In Appendix C we include a comparison of the ten Challenge participants on both Test Set A & B, and in Appendix C.1 we report the time it took participants to process and return Test Set B.

2.2. Challenge Metrics

To compare the results from the participants with our two manual raters and Consensus Delineation, we used the following metrics: Dice overlap (Dice, 1945), positive predictive value, true positive rate, lesion true positive rate, lesion false positive rate, absolute volume difference, average symmetric surface distance, volume correlation, and longitudinal volume correlation. The Dice overlap is a commonly used volume metric for comparing the quality of two binary label masks. It is defined as the ratio of twice the number of overlapping voxels to the total number of voxels in each mask. If ${\mathcal{M}}_R$ is the mask of one of the human raters and ${\mathcal{M}}_A$ is the mask generated by a particular algorithm, then the Dice overlap is computed as

$$\mathrm{Dice}({\mathcal{M}}_R,{\mathcal{M}}_A)=2\frac{\mid {\mathcal{M}}_R\cap {\mathcal{M}}_A\mid }{\mid {\mathcal{M}}_R\mid +\mid {\mathcal{M}}_A\mid },$$

where |·| is a count of the number of voxels. This overlap measure has values in the range [0, 1], with 0 indicating no agreement between the two masks, and 1 meaning the two masks are identical.

The positive predictive value (PPV) is the voxel-wise ratio of the true positives to the sum of the true and false positives,

$$\mathrm{PPV}({\mathcal{M}}_R,{\mathcal{M}}_A)=\frac{\mid {\mathcal{M}}_R\cap {\mathcal{M}}_A\mid }{\mid {\mathcal{M}}_R\cap {\mathcal{M}}_A\mid +\mid {\mathcal{M}}_R^c\cap {\mathcal{M}}_A\mid },$$

where ${\mathcal{M}}_R^c$ is the complement of ${\mathcal{M}}_R$ which when intersected with ${\mathcal{M}}_A$, represents the set of false-positives. PPV is also known as precision. The true positive rate (TPR) is the voxel-wise ratio of the true positives to the sum of true positives and false negatives, calculated as

$$\mathrm{TPR}({\mathcal{M}}_R,{\mathcal{M}}_A)=\frac{\mid {\mathcal{M}}_R\cap {\mathcal{M}}_A\mid }{\mid {\mathcal{M}}_R\cap {\mathcal{M}}_A\mid +\mid {\mathcal{M}}_R\cap {\mathcal{M}}_A^c\mid }.$$

Lesion true positive rate (LTPR) is the lesion-wise ratio of true positives to the sum of true positives and false negatives. We define the list of lesions, ${\mathcal{L}}_R$, as the 18-connected components of ${\mathcal{M}}_R$ and define ${\mathcal{L}}_A$ in a similar manner. Then

$$\mathrm{LTPR}({\mathcal{M}}_R,{\mathcal{M}}_A)=\frac{\mid {\mathcal{L}}_R\cap {\mathcal{L}}_A\mid }{\mid {\mathcal{L}}_R\cap {\mathcal{L}}_A\mid +\mid {\mathcal{L}}_R\cap {\mathcal{L}}_A^c\mid },$$

where $\mid {\mathcal{L}}_R\cap {\mathcal{L}}_A\mid$ counts any overlap between a connected component of ${\mathcal{M}}_R$ and ${\mathcal{M}}_L$; which means that both the human rater and algorithm have identified the same lesion, though not necessarily having the same extents. Lesion false positive rate (LFPR) is the lesion-wise ratio of false positives to the sum of false positives and true negatives,

$$\mathrm{LFPR}({\mathcal{M}}_R,{\mathcal{M}}_A)=\frac{\mid {\mathcal{L}}_R^c\cap {\mathcal{L}}_A\mid }{\mid {\mathcal{L}}_R^c\cap {\mathcal{L}}_A\mid +\mid {\mathcal{L}}_R^c\cap {\mathcal{L}}_A^c\mid },$$

where ${\mathcal{L}}_R^c$ is the 18-connected components of ${\mathcal{M}}_R^c$.

Absolute volume difference (AVD) is the absolute difference in volumes divided by the true volume,

$$\mathrm{AVD}({\mathcal{M}}_R,{\mathcal{M}}_A)=\frac{\mathrm{Max}(\mid {\mathcal{M}}_R\mid ,\mid {\mathcal{M}}_A\mid )-\mathrm{Min}(\mid {\mathcal{M}}_R\mid ,\mid {\mathcal{M}}_A\mid )}{\mid {\mathcal{M}}_R\mid }.$$

Average symmetric surface distance (ASSD) is the average of the distance (in millimeters) from the lesions in ${\mathcal{M}}_R$ to the nearest lesion identified in ${\mathcal{M}}_A$ plus the distance from the lesions in ${\mathcal{M}}_A$ to the nearest lesion identified in ${\mathcal{M}}_R$.

$$\mathrm{ASSD}({\mathcal{M}}_R,{\mathcal{M}}_A)=\frac{{\sum }_{r\in {\mathcal{L}}_R}d(r,{\mathcal{L}}_A)+{\sum }_{a\in {\mathcal{L}}_A}d(a,{\mathcal{L}}_R)}{2},$$

where $d(r,{\mathcal{L}}_A)$ is the distance from the lesion r in ${\mathcal{L}}_R$ to the nearest lesion in ${\mathcal{L}}_A$. A value of 0 would correspond to ${\mathcal{M}}_R$ and ${\mathcal{M}}_A$ being identical.

Volume correlation (TotalCorr) is the Pearson's correlation coefficient (Pearson, 1895) of the volumes, whereas longitudinal volume correlation (LongCorr) is the Pearson's correlation coefficient of the volumes within a subject. Each of the various metrics is computed for both raters and then used to compute a normalized score which was used to determine the Challenge winner. For the Consensus Delineation the metrics are computed directly between each rater/method and the Consensus Delineation.

2.3. Inter-Rater Comparison

Rater #1 has four years of experience delineating lesions, while Rater #2 has 10 years experience with manual lesion segmentation and 17 years experience in structural MRI analysis. We note that the raters were blinded to the temporal ordering of the data. The protocol for the manual delineation followed by both raters is in Appendix A. Table 2 shows an inter-rater comparisons for all 82 images—21 coming from the Training data, 43 from Test Set A, and 18 from Test Set B. See Fig. 1 for an example delineation. The results highlight the subjective nature of manual delineations based on differing interpretations of the protocol (See Appendix A) and scan data, and further emphasize the need for development of fully-automated methods. Importantly, our inter-rater Dice overlap of 0.6340 is better than the Dice overlap of 0.2498 the 2008 MICCAI MS Lesion challenge (Styner et al., 2008) had between their two raters on ten scans they both delineated. However, we note that using just the Dice overlap masks some of the differences between the two raters. In particular the volume differences—as measured by AVD—are quite stark.

Table 2.

Inter-rater comparison averaged across the 82 images from the training and test data set. The first table displays the symmetric metrics: Dice, average symmetric surface distance (ASSD), & longitudinal correlation. The second table shows the asymmetric metrics: positive predictive value (PPV), true positive rate (TPR), lesion false positive rate, lesion true positive rate, and absolute volume difference (AVD). R1 refers to Rater #1, R2 to Rater #2, and “R1 vs. R2” denotes that R1 was regarded as the truth within the comparison.

Symmetric Metrics
Dice	0.6340
ASSD	3.5290
Longitudinal Correlation	−0.0053

Asymmetric Metrics	R1 vs. R2	R2 vs. R1
PPV	0.7828	0.5688
TPR	0.5029	0.8224
Lesion FPR	0.1380	0.5630
Lesion TPR	0.4370	0.8620
AVD	0.3726	0.6117

2.4. Consensus Delineation

To avoid the biases of depending on either rater, we choose to construct a Consensus Delineation for each of the 61 images included in Test Set A and B. To achieve such a delineation, we employ the simultaneous truth and performance level estimation (STAPLE) algorithm (Warfield et al., 2004). STAPLE is an expectation-maximization algorithm for the statistical fusion of binary segmentations. The algorithm considers several segmentations and computes a probabilistic estimate of the true segmentation—as well as other quantities. Given that we have only two manual delineations for each patient image, we have taken the Challenge Delineations provide by each team (see Section 3 and Appendix B for details) and included them with our two manual delineations in construction of the Consensus Delineation. In brief, STAPLE estimates the true segmentation from an optimal combination of the input segmentations, the weights for which are determined by the estimated performance level of the individual segmentations. The resultant Consensus Delineation, from the STAPLE combination of the 14 algorithms and 2 manual raters, is regarded as the “ground truth” for the comparisons within Section 4. The Consensus Delineation provides the opportunity to simultaneously compare the human raters and the Challenge participants across all of our metrics; this—to our knowledge—is something that has not been reported in any previous Challenge (Styner et al., 2008; Schaap et al., 2009; Heimann et al., 2009; Menze et al., 2015; Mendrik et al., 2015; Maier et al., 2017).

3. Methods Overview

We present a brief overview of each of the methods used in this paper, complete details of each approach are available in Appendix B. Figures 2 and 3 show results of each algorithm on a typical slice from one time-point of one of our data sets, as well as the corresponding MPRAGE, FLAIR, and T₂-w images. Ten teams originally submitted results for the Challenge data sets and were able to participate in the Challenge event (see Section 2.1 for a complete description of the data). In addition to these methods, we received results for two methods from teams that did not participate in the Challenge event. To provide some context with the 2008 MICCAI MS Lesion challenge (Styner et al., 2008), we also include the methods that finished first and third in that challenge. Where we present descriptions or results of the methods, we use a colored square to help identify methods and within that square we denote methods that are unsupervised with the letter U and those that require some training data (supervised methods) with the letter S. When considering the Consensus Delineation in Section 4, we identify Rater #1 and #2 with colored squares with the letter M to denote manual delineations.

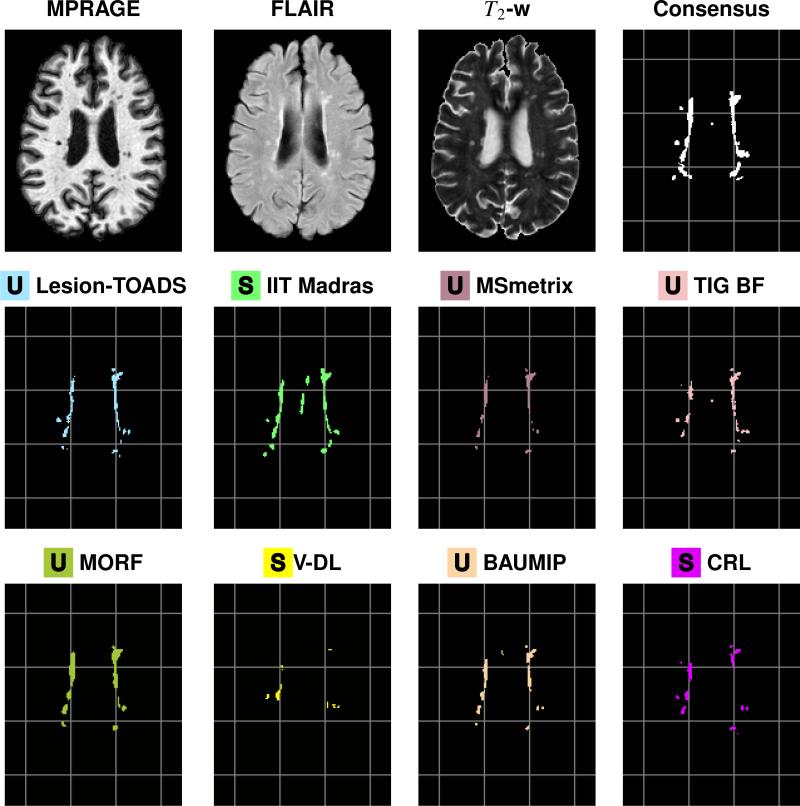
Figure 2.

Delineations are shown for a sample slice from the preprocessed MPRAGE, FLAIR, and T₂-w images for a time-point of a test data set, followed by our Consensus Delineation and the results for the top eight delineations as ranked by their Dice Score with the Consensus. For ease of reference, a grid has been added underneath the delineations. The bottom eight delineations, as ranked by their Dice Score with the Consensus, can be see in Fig. 3.

Figure 3.

Delineations are shown for a sample slice from the preprocessed MPRAGE, FLAIR, and T₂-w images for a time-point of a test data set, followed by our Consensus Delineation and the results for the bottom eight delineations as ranked by their Dice Score with the Consensus. For ease of reference, a grid has been added underneath the delineations. The top eight delineations, as ranked by their Dice Score with the Consensus, can be see in Fig. 2.

3.1. Challenge Participants

Team CMIC

Multi-Contrast PatchMatch Algorithm for Multiple Sclerosis Lesion Detection

(F. Prados, M. J. Cardoso, N. Cawley, O. Ciccarelli, C. A. M. Wheeler-Kingshott, & S. Ourselin)

Team CMIC used the PatchMatch (Barnes et al., 2010) algorithm for MS lesion detection. The main contribution of this work is the generalization of the optimized PatchMatch algorithm to the context of MS lesion detection and its extension to multimodal data.

Team VISAGES GCEM

Automatic Graph Cut Segmentation of Multiple Sclerosis Lesions

(L. Catanese, O. Commowick, & C. Barillot)

Team VISAGES GCEM used a robust Expectation-Maximization (EM) algorithm to initialize a graph, followed by a min-cut of the graph to detect lesions, and an estimate of the WM to help remove false positives. GCEM stands for Graph-cut with Expectation-Maximisation.

Team VISAGES DL

Sparse Representations and Dictionary Learning Based Longitudinal Segmentation of Multiple Sclerosis Lesions

(H. Deshpande, P. Maurel, & C. Barillot)

Team VISAGES DL used sparse representation and a dictionary learning paradigm to automatically segment MS lesions within the longitudinal MR data. Dictionaries are learned for the lesion and healthy brain tissue classes, and a reconstruction error-based classification approach for prediction.

Team CRL

Model of Population and Subject (MOPS) Segmentation

(X. Tomas-Fernandez & S. K. Warfield)

Inspired by the ability of experts to detect lesions based on their local signal intensity characteristics, Team CRL proposes an algorithm that achieves lesion and brain tissue segmentation through simultaneous estimation of a spatially global within-the-subject intensity distribution and a spatially local intensity distribution derived from a healthy reference population.

Team IIT Madras

Longitudinal Multiple Sclerosis Lesion Segmentation using 3D Convolutional Neural Networks

(S. Vaidya, A. Chunduru, R. Muthuganapathy, & G. Krishnamurthi)

Team IIT Madras modeled a voxel-wise classifier using multi-channel 3D patches of MRI volumes as input. For each ground truth, a convolutional neural network (CNN) is trained and the final segmentation is obtained by combining the probability outputs of these CNNs. Efficient training is achieved by using sub-sampling methods and sparse convolutions.

Team PVG One

Hierarchical MRF and Random Forest Segmentation of MS Lesions and Healthy Tissues in Brain MRI

(A. Jesson & T. Arbel)

Team PVG One built a hierarchical framework for the segmentation of a variety of healthy tissues and lesions. At the voxel level, lesion and tissue labels are estimated through a MRF segmentation framework that leverages spatial prior probabilities for nine healthy tissues through multi-atlas label fusion (MALF). A random forest (RF) classifier then provides region level lesion refinement.

Team IMI

MS-Lesion Segmentation in MRI with Random Forests

(O. Maier & H. Handels)

Team IMI trained a RF with supervised learning to infer the classification function underlying the training data. The classification of brain lesions in MRI is a complex task with high levels of noise, hence a total of 200 trees are trained without any growth-restriction. Contrary to reported observations, no overfitting occurred.

Team MSmetrix

Automatic Longitudinal Multiple Sclerosis Lesion Segmentation

(S. Jain, D. M. Sima, & D. Smeets)

MSmetrix (Jain et al., 2015) is presented, which performs lesion segmentation while segmenting brain tissue into CSF, GM, and WM, with lesions identified based on a spatial prior and hyperintense appearance in FLAIR.

Team DIAG

Convolution Neural Networks for MS Lesion Segmentation

(M. Ghafoorian & B. Platel)

Team DIAG utilizes a deep CNN with five layers in a sliding window fashion to create a voxel-based classifier.

Team TIG

Model Selection Propagation for Application on Longitudinal MS Lesion Segmentation

(C. H. Sudre, M. J. Cardoso, & S. Ourselin)

Based on the assumption that the structural anatomy of the brain should be temporally consistent for a given patient, Team TIG proposes a lesion segmentation method that first derives a GMM separating healthy tissues from pathological and unexpected ones on a multi-time-point intra-subject group-wise image. This average patient-specific GMM is then used as an initialization for a final time-point specific GMM from which final lesion segmentations are obtained. Team TIG submitted new results after the completion of the Challenge to address a bug in their code, the second submitted results are denoted TIG BF. Both sets of results are included in Appendix C; however, the Consensus Delineation was only compared to the bug fixed results (TIG BF).

3.2. Other Included Methods

These methods did not participate in the Challenge, however they are included to add to the richness and variety of the methods presented. MORF and Lesion-TOADS represent methods that finished first and third in the 2008 MICCAI MS Lesion challenge (Styner et al., 2008), respectively, and as such offer the opportunity to provide a reference between the two challenges. In particular, the two algorithms offer different perspectives on the problem (supervised versus unsupervised, respectively) while also testing the ongoing viability of these two methods within the field. Our third included method (MV-CNN)—based on deep-learning—is a state-of-the-art approach; the authors of MV-CNN submitted their results to the Challenge Website while this manuscript was in preparation. As a deep-learning method, MV-CNN represents a key direction in which the medical imaging community is moving. While the fourth included method, BAUMIP, submitted results for both Challenge data sets but was unable to participate at the Challenge event.

BAUMIP

Automatic White Matter Hyperintensity Segmentation using FLAIR MRI

(L. O. Iheme & D. Unay)

BAUMIP is a method based on intensity thresholding and 3D voxel connectivity analysis. A simple model is trained that is optimized by searching for the maximum obtainable Dice overlap.

MV-CNN

Multi-View Convolutional Neural Networks

(A. Birenbaum & H. Greenspan)

MV-CNN is a method based on a Longitudinal Multi-View CNN (Roth et al., 2014). The classifier is modeled as a CNN, whose input for every evaluated voxel are patches from axial, coronal, and sagittal views of the T₁-w, T₂-w, PD-w, and FLAIR images of the current and previous time-points. That is multiple contrasts, multiple views, and multiple time-points. MV-CNN consists of three phases: Preprocessing the Challenge data, Candidate Extraction, and CNN Prediction. The Challenge data is preprocessed by intensity clamping the top and bottom 1% and the intensity values are scaled to the range [0, 1].

MORF

Multi-Output Random Forests for Lesion Segmentation in Multiple Sclerosis

(A. Jog, A. Carass, D. L. Pham, & J. L. Prince)

MORF is an automated algorithm to segment WML in MR images using multi-output random forests. The work is similar to Geremia et al. (2011) in that it uses binary decision trees that are learned from intensity and context features. However, instead of predicting a single voxel, an entire neighborhood or patch is predicted for a given input feature vector. The multi-output decision trees implementation has similarities to output kernel trees (Geurts et al., 2007). Predicting entire neighborhoods gives further context information such as the presence of lesions predominantly inside WM, which has been shown to improve patch based methods (Jog et al., 2017). This approach was originally presented in Jog et al. (2015). Geremia et al. (2011) finished first at the 2008 MICCAI MS Lesion challenge (Styner et al., 2008), and thus this should represent a good proxy for that work.

Lesion-TOADS

A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions

(N. Shiee, P.-L. Bazin, A. Ozturk, D. S. Reich, P. A. Calabresi, & D. L. Pham)

Lesion-TOADS (Shiee et al., 2010) is an atlas-based segmentation technique employing topological and statistical atlases. The method builds upon previous work (Bazin and Pham, 2008) by handling lesions as topological outliers that can be addressed in a topology-preserving framework when grouped together with the underlying tissues. Lesion-TOADS finished third at the 2008 MICCAI MS Lesion challenge (Styner et al., 2008), however there have been some improvements in the method in the intervening years.

4. Consensus Comparison

We construct a Consensus Delineation for each test data set by using the simultaneous truth and performance level estimation (STAPLE) algorithm (Warfield et al., 2004). The Consensus Delineation uses the two manual delineations created by our raters as well as the output from all fourteen algorithms. The manual delineations and the fourteen algorithms are treated equally within the STAPLE framework. In the remainder of this section, we regard the Consensus Delineation as the “ground truth” and using our metrics compare the human raters and all fourteen algorithms to this ground truth. The TIG BF results from Team TIG were used in the construction of the Consensus Delineation. We refer to the collection (two manual raters and fourteen algorithms results) as the Segmentations. The construction of a Consensus Delineation provides the opportunity to simultaneously compare the human raters and the Challenge participants across all of our metrics. This may help us answer the question:

Can automated lesion segmentation now replace the human rater?

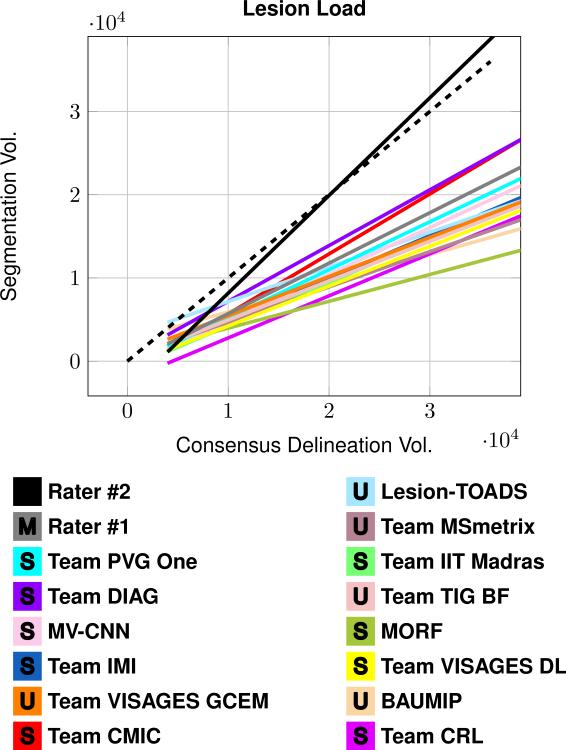
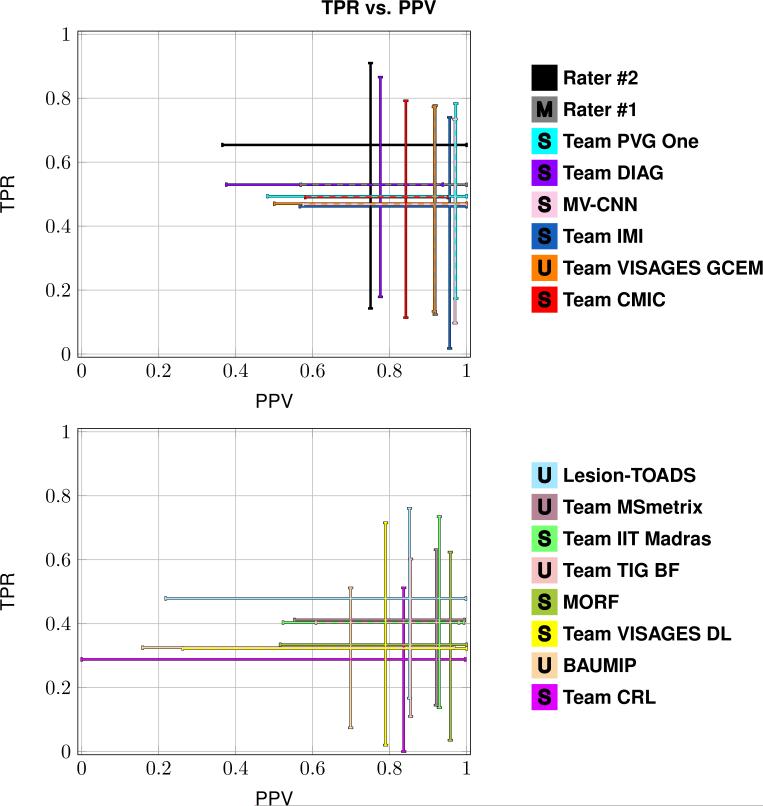
Table 3 presents the Dice overlap score between the Consensus Delineation and the Segmentations; which include the mean Dice overlap across the 61 patient images in Test Set A and B, as well as the standard deviation, and the range of reported values. Figure 4 shows a least squares linear regression between the lesion load estimated by each of the Segmentations and that given by the Consensus Delineation. Figure 5 shows two plots summarizing true positive rate (TPR) against positive predictive value (PPV) for the Segmentations. The plot was split into two plots, each containing a group of eight segmentations, for ease of viewing. Table 4 includes the mean, standard deviation, and range of the average symmetric surface distance (ASSD). Within Table 4, the Segmentations are ranked by their mean ASSD with the Consensus Delineation. Figure 6 shows two plots summarizing the lesion true positive rate (LTPR) and the lesion false positive rate (LFPR)—again this plot is split into two groups of eight for ease of viewing. Finally, we have Table 5 which has the mean, standard deviation, and range for the longitudinal correlation (LongCorr).

Table 3.

Mean, standard deviation (SD), and range of Dice overlap scores for the Segmentations against the Consensus Delineation. The Segmentations are ranked by their mean Dice overlap.

	Dice
Method	Mean (SD)	Range
	0.670 (±0.178)	[0.246, 0.843]
	0.658 (±0.149)	[0.218, 0.852]
	0.638 (±0.164)	[0.291, 0.872]
	0.614 (±0.133)	[0.282, 0.824]
	0.614 (±0.164)	[0.177, 0.830]
	0.609 (±0.160)	[0.035, 0.829]
	0.607 (±0.147)	[0.235, 0.832]
	0.598 (±0.177)	[0.200, 0.816]
	0.579 (±0.121)	[0.279, 0.773]
	0.561 (±0.131)	[0.245, 0.764]
	0.550 (±0.153)	[0.233, 0.811]
	0.540 (±0.139)	[0.190, 0.719]
	0.474 (±0.180)	[0.068, 0.747]
	0.432 (±0.196)	[0.039, 0.827]
	0.426 (±0.123)	[0.136, 0.631]
	0.415 (±0.172)	[0.000, 0.664]

Figure 4.

The plot shows a least squares linear regression fit between the lesion load estimated by each of the Segmentations and that from the Consensus Delineation. The dashed line represents a line of unit slope. All volumes are in mm³.

Figure 5.

Each subplot shows the range of values for the true positive rate (TPR) and the positive predictive value (PPV) between eight of the Segmentations and the Consensus Delineation. The top plot shows the top eight Segmentations as ranked by the Dice overlap, and the bottom plot shows the remaining eight Segmentations. The desirable point on each of the subplots is the upper right hand corner, where TPR is 1 and PPV is 1.

Table 4.

Mean, standard deviation (SD), and range of the average symmetric surface distance (ASSD) for the Segmentations against the Consensus Delineation. The Segmentations are ranked by their mean ASSD.

	ASSD
Method	Mean (SD)	Range
	2.16 (±3.83)	[0.54, 18.86]
	2.26 (±1.78)	[0.54, 7.16]
	2.29 (±1.43)	[0.84, 7.53]
	2.38 (±1.89)	[0.80, 8.15]
	2.71 (±1.33)	[1.60, 8.03]
	2.86 (±2.08)	[0.66, 9.27]
	2.99 (±3.45)	[0.58, 17.96]
	3.06 (±1.65)	[1.07, 7.37]
	3.11 (±2.80)	[0.55, 11.96]
	3.26 (±2.57)	[0.89, 11.49]
	3.31 (±2.10)	[1.03, 9.26]
	3.59 (±4.80)	[0.81, 35.83]
	3.85 (±2.68)	[0.97, 10.36]
	5.28 (±4.69)	[0.84, 26.68]
	5.68 (±4.42)	[1.67, 25.07]
	6.14 (±6.36)	[1.56, 7.53]

Figure 6.

Each subplot shows the range of values for the lesion true positive rate (LTPR) and the lesion false positive rate (LFPR) between eight of the Segmentations and the Consensus Delineation. The top plot shows the top eight Segmentations as ranked by the Dice overlap, and the bottom plot shows the remaining eight Segmentations. The desirable point on each of the subplots is the lower right hand corner, where LTPR is 1 and LFPR is 0.

Table 5.

Mean, standard deviation (SD), and range of the longitudinal correlation (LongCorr) for the Segmentations against the Consensus Delineation. The Segmentations are ranked by their mean LongCorr.

	LongCorr
Method	Mean (SD)	Range
	0.657 (±0.483)	[−0.583, 0.997]
	0.607 (±0.582)	[−0.693, 1.000]
	0.432 (±0.524)	[−0.567, 1.000]
	0.424 (±0.634)	[−0.763, 0.998]
	0.421 (±0.615)	[−0.919, 0.999]
	0.402 (±0.634)	[−0.974, 0.990]
	0.376 (±0.654)	[−0.636, 1.000]
	0.340 (±0.623)	[−0.955, 0.998]
	0.327 (±0.679)	[−0.900, 0.970]
	0.249 (±0.696)	[−0.943, 0.998]
	0.220 (±0.728)	[−0.981, 0.984]
	0.181 (±0.540)	[−0.785, 0.976]
	0.171 (±0.634)	[−0.899, 0.969]
	0.153 (±0.746)	[−0.930, 1.000]
	0.042 (±0.675)	[−0.999, 0.991]
	0.031 (±0.683)	[−0.980, 0.999]

5. Discussion and Conclusions

5.1. Inter-rater Comparison

As organizers, we felt that the overall performance of our two raters relative to each other was disappointing (see Table 2). For example, the inter-rater Dice overlap of 0.6340 was below that of other inter-rater studies of MS lesions: Zijdenbos et al. (1994) reports a mean inter-rater Dice overlap of 0.700, they refer to Dice overlap as similarity. They also note that when restricted to the same scanner their inter-rater Dice overlap rose to 0.732—as reported earlier all of our data was acquired on the same scanner. However, the 2008 MICCAI MS Lesion challenge (Styner et al., 2008) had two raters repeat ten of the scans and their inter-rater mean Dice overlap was 0.2498. We therefore believe that our inter-rater performance is acceptable, especially considering our raters worked on 82 data sets—61 in Test Set A and B, and another 21 in the Training Set.

5.2. Consensus Delineation

The Consensus Delineation afforded us the opportunity to directly compare the quality of our two manual raters with the submitted results. When performing statistical comparisons we use an α level of 0.001. If the Dice overlap (Table 3) is considered the definitive metric for rating lesion segmentation then the expert human raters are still better than algorithms. However, the level of expertise is important, we note that Rater #2 has a decade more delineation experience than Rater #1. A two-sided Wilcoxon Signed-Rank Paired Test (Wilcoxon, 1945) between the highest ranking algorithm (Team PVG One) and the highest ranking manual delineation (Rater #2) reaches significance with a a p-value of 0.0093. Whereas, the same test, between Team PVG One and Rater #1 does not reach significance (p-value of 0.1076). Of course Dice overlap is a crude metric with volumetric insensitivities. From Fig. 4, we can see that the least squares linear regression of Rater #2 is closest to the line of unit slope suggesting that it may be a proxy for the lesion load as represented by the Consensus Delineation. We do note that the Consensus Delineation, as generated by STAPLE, may be overly inclusive—which would explain the grouping together of all the other Segmentations in Fig. 4. Figure 5 shows a cross-hairs plot of the range of true positive rate (TPR) versus the positive predictive value (PPV). The desired operating point for any segmentation in this plot is the upper right hand corner (TPR = 1, PPV =1). Rater #2 is the closest to this desired operating point, with Rater #1 second, and Team PVG One third. A two-sided Wilcoxon Signed-Rank Paired Test comparing the distance from the operating points to the desired operating point between either Rater #2 or Rater #1 and Team PVG One had p-values of 0.0058 and 0.0458, respectively. Again, suggesting that the level of expertise is critical in achieving the best results. A similar analysis of Fig. 6 shows that MV-CNN operates closest to the desired optimal point (in this case the lower right hand corner), with Rater #1 second, and Lesion-TOADS third. Moreover, the two-sided Wilcoxon Signed-Rank Paired Test has a p-value of < 0.0001 between MV-CNN and Rater #1. This suggests that MV-CNN may be better than manual delineators when it comes to LFPR and LTPR. Tables 4 and 5 show other metrics that are generally not reported in the lesion segmentation literature. However, both of which suggest advantages to the use of algorithms over manual raters. For the average symmetric surface distance (ASSD); of the algorithms that rank above Rater #2, only Team PVG One is statistically significantly different with a p-value of < 0.0001. However, with respect to longitudinal correlation (see Table 5) none of the algorithms are statistically significantly better than the highest rated manual delineation, which comes from Rater #2. Based on the comparison to the Consensus Delineation, there is not clear evidence to suggest that any of the automated algorithms is better than the manual delineations of Rater #1 and #2.

5.3. Best Algorithm

We caution that we cannot truly answer the question of which algorithm is the true best for WML segmentation. We have chosen a metric collection that was felt to best represent desirable properties in a longitudinal lesion segmentation algorithm. However, as can be seen in Section 4, arguments can be made for several of the algorithms to be named the best depending on the chosen criteria. For example, if LongCorr (see Table 5) is deemed most important, then Team IIT Madras would be considered the best. By switching to consider the Dice overlap, Team IIT Madras with a mean score of 0.550 is behind eight other algorithms, and both human raters. In contrast several methods (Team PVG One, Team DIAG, MV-CNN, Team IMI, & Team VISAGES GCEM) have mean Dice overlap above 0.600 with the Consensus Delineation. With Team PVG One having 42 cases (out of 61) with a Dice overlap over 0.600. Details about the Winner of the Challenge is in Appendix C.

5.4. Future Work

As organizers, we were surprised that most of the submitted approaches did not take advantage of the longitudinal nature of the data. For example, Team MSmetrix used a temporally consistency step to correct their WML segmentations, yet had bad longitudinal correlation, LTPR, & LFPR, relative to the other Challenge participants in the comparison with the Consensus Delineation. This would seem to imply that existing ideas about temporal consistency do not represent the biological reality underlying the appearance and disappearance of WMLs. It should be noted that the longitudinal consistency of the raters was poor, as the raters were presented with each scan independently and were themselves not aiming for longitudinal consistency. Longitudinal manual delineation protocols should be augmented so as not to blind the raters to the ordering of the data. The hope would be that all the information can be used to obtain the most accurate and consistent results possible. However, it remains a challenge as to how the longitudinal information can be incorporated into the manual delineation protocol. We believe that by making this challenging data set available and providing an automated site for method comparisons, the Challenge data will foster new efforts and developments to further improve algorithms and increase detection accuracy.

The results of the Consensus Delineation suggest that there is still work to be done before we can stop depending on manual delineations to identify WMLs. This is a disappointing state, considering the amount of research that has been done in this area in the last two decades. The situation is made worse when considering the shortcomings of the manual delineations and the automated algorithms. Clearly longitudinal consistency is an area in which all the automated algorithms could improve. Our human raters were blinded to the temporal ordering of the data, unlike the algorithms, and it is not clear at this juncture how the human raters performance might have changed given this information. Of course, this only covers what we would reasonably expect WML segmentation algorithms to do today. We should expect them to be able to classify the three types of WML (enhancing, black hole, & T₂-w) and localize as periventricular or cortical lesions, eventually providing more specific location classifications such as juxtacortical, leukocortical, intracortical, and subpial. These properties may be important in distinguishing the status of patients. The next generation of MS lesion detection software needs to address these issues.

An issue which we had not intended to explore was the failure of global measures. Lesion load—as determined by lesion segmentation—is an important clinical measure; the reduction (or stabilization) of which through automated or semi-automatic image analysis methods is one of the primary outcome measures to determine the efficacy of MS therapies. Lesion load and several other global measures fail to predict the disease course; instead we need to use location specific measures—as mentioned above—to serve as outcome predictors or staging criteria for monitoring therapies (Filippi et al., 2014). Beyond this there is a desire for measures that help in identifying the pathophysiologic stages of MS lesions (pre-active, active, chronic active, or chronic inactive) (Jonkman et al., 2015).

Appendix A. Lesion Protocol

The following protocol was used in the creation of the MS lesion masks, which were created in our 1 mm isotropic MNI space.

1. Review the possibilities for presentation of MS lesions in brain scans, an excellent resource is Sahraian and Radue (Sahraian and Radue, 2007). It is also a good idea to familiarize yourself with the paint and mask functions in MIPAV (McAuliffe et al., 2001; Bazin et al., 2005) before you begin, although this protocol description can serve as a basic guide.

2. Open MIPAV. If you have not done so in the past, add the Paint toolbar to the interface (Toolbars > Paint toolbar). The Image toolbar should be present by default; if not, go to Toolbars > Image toolbar.

3. Open two copies of the FLAIR scan and one copy each of the T₁-w, T₂-w, and PD-w scans (File > Open image (A) from disk > select files > Open). These should be appropriately co-registered in the axial view with identical slice thickness and field of view values before beginning this process.

4. Click on the T₁-w scan to select it, then click on the WL button on the MIPAV toolbar to bring up the Level and Window adjuster. This should automatically result in a reasonable tissue contrast for viewing potential lesions on the T₁-w. If the contrast is inadequate, change the window and level settings. Close the tool when you are satisfied with the contrast.

5. Enlarge each image three times using the magnifying glass + button on the Image toolbar for a total magnification of 4×. Arrange the images on your display with the two FLAIR copies next to each other. Ensure that the scans are properly aligned with one another horizontally. This will enable you to quickly check the other images to identify and verify tissue abnormalities as lesions (or not) while working on the FLAIR mask.

6. Link the scans together by first clicking on the Sync slice number button on the Image toolbar (two arrows one pointing left and the other pointing right). Then click on each scan and select the Link images button (broken links next to Sync slice number button; the broken links change to an intact link when activated). This will ensure that all of the scans stay on the same slice as the FLAIR while you work. Click on one of the scans, then scroll up and down while looking from side to side over the images to verify proper registration and check for image processing errors (e.g., missing pieces of brain).

7. Select one of the FLAIR scans, then click on the Paint Grow button (looks like a paint bucket) on the Paint toolbar to open the intensity and connectivity-based paint mask generator.

8. Open the Paint Power Tools plugin. The icon (lightbulb) should be at the right end of the Paint toolbar. Look at the Threshold section. Find the maximum intensity value present in the scan by observing the number in the right-hand box (upper threshold).

9. Look at the Paint Grow tool. Find the section marked Set maximum slider values. Change the maximum slider values in the paint mask generator to reflect the maximum intensity in the scan, and click Set.

10. Choose a lesion with well-defined borders and strong hyperintensity on the FLAIR scan. Click on the most hyperintense area in the lesion.

11. Move the second slider (Delta below selected voxel intensity) to the right until it encompasses most of the lesioned tissue.

12. Scroll up and down through the image to ensure that the selection is limited to the lesioned area and does not include hyperintensities due to noise or artifact. If non-lesioned tissue is included, move the slider back to the left until this tissue is deselected.

13. Move the first slider (Delta above selected voxel intensity) to the right to ensure that all voxels of higher intensity in the lesion are selected.

14. Repeat this process until all well-defined lesions in the FLAIR scan have been selected, remembering to scroll up and down frequently to prevent masking of non-lesioned tissue. In general, this process will result in a rough draft of a lesion mask.

    Do not use this process for any area that is affected by scan artifact or for any hyperintensity that is not clearly a lesion. Investigate questionable areas during the later stages of the delineation process.

    If a decision is to be made between fully encompassing a lesion and additional non-lesioned tissue or partially covering a lesion without extraneous tissue, choose the latter option. It tends to be easier, within MIPAV, to add to a mask than subtract from it.

15. When you are satisfied with your rough mask, save it as an unsigned byte mask (VOI > Paint conversion > Paint to Unsigned byte mask). This will give you the binary mask data you have generated thus far. When the mask image appears, go to the File menu and choose Save image as. Enter the file name and desired extension, then click Save.

16. Close the binary mask and the Paint Grow tool.

17. To begin, move your pointer over the area around the edge of a lesion, hold the mouse button down, and notice the intensity difference between the interior and exterior of the lesion. Record the intensity value for the area at the edge of the lesion.

    Because many MS lesions are found in close proximity to the ventricles, it is useful to start in the middle slice in the axial view. Delineate from the middle axial slice to the superior aspect of the brain, scroll down to check your work, and then delineate from the middle to the inferior view.

18. On the Paint Power Tools interface, click the box next to Threshold. Enter the intensity value for the outside edge of the lesion in the first box; this will restrict your paint to voxels between that intensity (lower threshold) value and the value listed in the box to the right (upper threshold).

    There is no need to change the value in the right box unless you are delineating lacunes. In that case, you should set the left box to the lowest possible value, and change the upper threshold to the highest value found on the edge of the lacune.

19. Click on the paintbrush icon on the paint toolbar. Paint around the edge of the lesion to test your threshold. You may need to paint and erase (paint = left mouse button, erase = right mouse button) the first time you do it, and then the threshold should be activated. You may also need to adjust the lower threshold value (left box). If too many voxels are being excluded from the lesion mask, lower the threshold value for a more inclusive range. If too many voxels are being included, increase the threshold value.

20. If you wish, you can change the paintbrush size by clicking on the drop-down menu in the center of the Paint toolbar and selecting one of the options.

    You may also customize your paintbrush options by clicking on the Paint brush editor button (looks like a group of paintbrushes) to the right of this menu. This will open a grid size selector that allows you to specify the width and height of the grid for your paintbrush in pixels (default is 12×12). Click OK, and the grid will open. Draw the shape you want for your paintbrush, then go to the “Grid options” menu to save (Grid options > Save paint brush > input file name > Save). Your custom paintbrush will appear in the menu the next time MIPAV is opened, so restart the program if you want to use it immediately.

21. As you move to different slices, you may need to readjust the lower threshold. Not all of the lesion edges have the same intensity value, and intensities often differ between lesions at the anterior vs posterior areas of the same slice.

22. During this process, it is extremely important to scroll up and down frequently in order to get a sense of each lesion's shape and ensure mask continuity. For every hyperintensity identified, scrolling up and down can also help to rule out false positives. Be sure to look at the other scans, particularly the T₂-w, in order to verify that what you are selecting is a lesion.

    In some cases, a lesion may be much more readily visible on the T₂-w scan. If this occurs, it is possible to delineate that portion directly on the T₂-w scan and add this small mask area to your FLAIR mask. This is particularly relevant when the FLAIR image contains a great deal of artifacts. If you cannot adequately capture the lesion on the FLAIR, use the T₂-w.

23. When debating what to include in the mask, keep these things in mind.

    • (a)
      Lesions usually have rounded or smoothed edges.
    • (b)
      Lesions appear distinctly hyper- or hypo- intense when compared with surrounding tissue (usually hyperintense on FLAIR, PD-w, and T₂-w scans, and hypointense on T₁-w),
    • (c)
      Lesions will usually be found near the ventricles, in the corpus callosum, or in the deep white matter, though juxtacortical lesions are not uncommon.
    • (d)
      Lesions may appear in the cerebellum, brainstem, temporal lobes, or basal ganglia at a lower intensity relative to the majority of the lesions. It is especially important to use information from the other scans when attempting to detect and delineate lesions in these areas.
    • (e)
      Include white matter encompassed by closed, well-defined clusters of lesions. Do not include internal white matter if the cluster is open.
    • (f)
      Include all CSF inside lacunes.
    • (g)
      If a lesion is adjacent to clearly hyperintense areas near the ventricles, and you can confirm that these areas appear damaged in the T₁-w scan, include them in the mask. Lesioned tissue bordering the ventricles looks ragged and dark on T₁-w scans.
    • (h)
      Do not include diffusely abnormal white matter (DAWM) in the masks for ISBI scans. The intensity of DAWM is between normal white matter and lesioned tissue on FLAIR. DAWM looks mottled on T₁-w, may radiate outward like a halo from a focal lesion, and is usually found around the ventricles.

24. Save your work frequently or use the automatic save function in the Paint Power Tools interface. Check the box next to Auto save under Misc., then set the number in the box to reflect how often you want the mask to be automatically saved (default is 10 minutes).

25. For some lesions, you may need to turn the paint threshold off and use the standard paint option, which will not restrict your paint to any specific intensity values. To do this, simply uncheck the box next to Threshold.

26. When you have finished delineating the lower portions of the brain, go back through the entire scan and check your work against the other images, focusing specifically on any areas that may have been difficult to verify as lesions. Edit as necessary.

27. Save your final mask.

28. To load a mask that you have worked on previously, select the FLAIR scan, then click on the second button from the left on the paint toolbar (appears to be a folder opening with a four-square gradient in front of it). Choose your mask file, click Open, and your mask will be loaded over the FLAIR.

29. If you would like to edit your mask after opening it from a saved file, open the Power Paint Tools, click on Mask to Paint under the Import/Export section at the bottom of the interface, and continue working.

Appendix B. Methods

For completeness, we provide descriptions of the Challenge Participants in Appendix B.1 and in Appendix B.2 we describe other methods that were not part of the Challenge which we included in our evaluation. Where we present descriptions or results of the methods, we use a colored square to help identify methods and within that square we denote methods that are unsupervised with the letter U and those that require some training data (supervised methods) with the letter S.

Appendix B.1. Challenge Participants

Table B.1 provides a synopsis of these methods and the MR sequences used by each individual team during the Challenge.

Team CMIC

Multi-Contrast PatchMatch Algorithm for Multiple Sclerosis Lesion Detection

(F. Prados, M. J. Cardoso, N. Cawley, O. Ciccarelli, C. A. M. Wheeler-Kingshott, & S. Ourselin)

Team CMIC used the PatchMatch (Barnes et al., 2010) algorithm for MS lesion detection. The main contribution of this work is the generalization of the optimized PatchMatch algorithm to the context of MS lesion detection and its extension to multimodal data.

The original PatchMatch algorithm was designed to look for similarities between two 2D patches within the same image (Barnes et al., 2010). Later, the Optimized PAtchMatch Label (OPAL) fusion approach extended patch correspondences between a target 3D image and a reference library of 3D training templates (Ta et al., 2014). Here, the PatchMatch algorithm is used to locate pathological regions through the use of a template library comprising a series of multimodal images with manually segmented MS lesions. By matching patches between the target multimodal image and the multimodal images in the template library, PatchMatch can provide a rough estimate of the location of the lesions in the target image.

OPAL uses the sum of the squared differences (SSD) between two patches over one single modality to measure patch similarity. This is replaced with an l₂-norm over the multimodal patches, which are assumed to be in the same space. To improve computational speed, as in the original OPAL method, the computation of the patch similarity is stopped if the current sum is superior to the previous minimal multimodality SSD. As this PatchMatch algorithm has a non-binary output, an adaptive threshold value is used to binarize the probabilistic mask. A robust range (with 2% outliers on both tails) of all voxels with non-zero probabilities is calculated, and then the mean of the values inside the robust range is computed. This mean is then used as the threshold to binarize the probabilistic segmentation. Finally, if the highest probability within the robust range is below 0.1 the method assumes that no lesions have been detected, meaning that the patient is lesion-free.

Team VISAGES GCEM

Automatic Graph Cut Segmentation of Multiple Sclerosis Lesions

(L. Catanese, O. Commowick, & C. Barillot)

Team VISAGES GCEM uses a robust Expectation-Maximization (EM) algorithm to initialize a graph, followed by a min-cut of the graph to detect lesions, and an estimate of the WM to help remove false positives. GCEM stands for Graph-cut with Expectation-Maximisation.

A region of interest is defined based on the thresholded T₂-w image. Each voxel within the region of interest is represented in a graph and connected to two terminal nodes, known as the source and sink, which respectively represent the object class for MS lesions and normal appearing brain tissues (NABT). Spatially neighboring nodes are connected by n-links weighted by boundary values that reflect the similarity of the two considered voxels. The contour information contained in the n-links weights is computed using a spectral gradient (García-Lorenzo et al., 2009). The regional term represents how the voxel fits into the given models of object and background. The edges between a node of the image and the terminal source and sink nodes are called t-links. Normally these models are estimated using seeds given as manual input. Instead, the Team uses an automated version of the graph cut where the object and background seeds for the initialization are computed from the images. To do so a 3-class multivariate GMM is employed, representing CSF, GM, and WM with lesions being treated as outliers to these three classes.

The seeds are estimated using a robust EM algorithm (García-Lorenzo et al., 2011), which optimizes a trimmed likelihood in order to be robust to outliers. The algorithm then alternates between the computation of the GMM parameters and the % of outlier voxels. From the GMM NABT parameters, the Mahalanobis distance is computed of each voxel to each of the classes in the GMM NABT model. This distance is then used to compute a p-value for determining the probability of each voxel belonging to each of the three classes. For each voxel i its smallest p-value p_i is retained. As the sinks represent voxels that are close to NABT, the t-link weights W_bi are defined as W_bi = 1 – p_i. To help distinguish MS lesions from other outliers (vessels, etc.), the fact that MS lesions are hyperintense compared to WM in T₂-w sequences is used. A fuzzy logic approach is used to model this based on the previously computed model of GMM NABT, which determines fuzzy weights from which the corresponding t-link weights are computed, see García-Lorenzo et al. (2009) for complete details.

The MS lesions are assumed to appear surrounded by WM and not adjacent to the cortical mask border. Any candidate lesions that violate either of these criteria are removed. Finally, all candidate lesions smaller than 3mm³ are discarded.

Team VISAGES DL

Sparse Representations and Dictionary Learning Based Longitudinal Segmentation of Multiple Sclerosis Lesions

(H. Deshpande, P. Maurel, & C. Barillot)

Team VISAGES DL used sparse representation and a dictionary learning paradigm to automatically segment MS lesions within the longitudinal MR data. Dictionaries are learned for the lesion and healthy brain tissue classes, and a reconstruction error-based classification approach for prediction.

Modeling signals using sparse representation and a dictionary learning framework has achieved promising results in image classification (Deshpande et al., 2015; Mairal et al., 2009; Roy et al., 2014a, 2015b; Weiss et al., 2013). Sparse coding finds a sparse coefficient vector $\mathit{a}\in {\mathbb{R}}^k$ for representing a given signal $\mathit{x}\in {\mathbb{R}}^n$ using a few atoms of an over-complete dictionary $D\in {\mathbb{R}}^{k\times n}$. The sparse representation problem is represented as min_a ||a||₀ such that ${\Vert \mathit{x}-D\mathit{a}\Vert }_2^2\le ϵ$ where ϵ is the error in the representation. This l₀ problem can be more efficiently solved as the l₁ minimization problem

$$\underset{\mathit{a}}{\min }{\Vert \mathit{x}-D\mathit{a}\Vert }_2^2+\lambda {\Vert \mathit{a}\Vert }_1,$$

where λ balances the trade-off between error and sparsity. For a set of signals ${\left\{\mathit{x}\right\}}_1^m$, a dictionary D is found from the underlying data such that each signal is sparsely represented by a linear combination of atoms,

$$\underset{D,{\left\{{\mathit{a}}_i\right\}}_1^m}{\min }\sum _1^m{\Vert {\mathit{x}}_i-D{\mathit{a}}_i\Vert }_2^2+\lambda {\Vert {\mathit{a}}_i\Vert }_1.$$

The optimization is an iterative two-step process involving sparse coding with a fixed D followed by a dictionary update for fixed atoms ${\left\{a_i\right\}}_1^m$.

The following preprocessing steps are used in the approach. Artifacts in the Challenge data are removed through denoising the images using a non-local means approach (Coupé et al., 2008). The images are then linearly rescaled to the range [0, 255] followed by a longitudinal intensity normalization (Karpate et al., 2014). A leave-one-out cross-validation experiment was used to determine an optimal patch size of 5 × 5 × 5. Patches of this size were then extracted and rasterized centered on every second voxel in the input images, this was done to reduce the computational complexity inherent in using every voxel. Patches in the training data are determined to belong to either the healthy tissue class or the lesion class, based on the manual delineations. Patches are finally normalized to limit their individual norms below or equal to unity. From the training data class-specific dictionaries are learned for the two classes.

Given a test patch, the patch classification is performed in two steps: First the sparse coefficients for each class are learned. The test patch is then assigned to the class with which it has minimum representation error. As the healthy class data represents complex anatomical structures such as CSF, GM, and WM, it has more variability in comparison to the lesion class. To account for this, the healthy class is allowed to have a larger dictionary size than the lesion class. As the patches are centered on every other voxel in the image, a majority vote multi-patch scheme is used to determine the classification of each voxel. All patches that overlap a particular voxel contribute their classification to determine the winner of the majority voting. The following parameters are used in solving the l₁ minimization problem: a sparsity parameter of λ = 0.95 with a dictionary size of 5, 000 for the healthy tissue class and a size of 700 to 2, 500 for the lesion class, depending on the total lesion load.

TEAM VISAGES DL performed longitudinal intensity normalization as a preprocessing step to negate the intensity differences across the different time points for a single MS patient. However, there are large intensity differences across several patients in the provided data set. The Team believes that improved classification results could be obtained after performing intensity normalization across all patients.

Team CRL

Model of Population and Subject (MOPS) Segmentation

(X. Tomas-Fernandez & S. K. Warfield)

Inspired by the ability of experts to detect lesions based on their local signal intensity characteristics, Team CRL proposes an algorithm that achieves lesion and brain tissue segmentation through simultaneous estimation of a spatially global within-the-subject intensity distribution and a spatially local intensity distribution derived from a healthy reference population.

To address the limitations of intensity-based MS lesion classification, the imaging data used to identify lesions is augmented to include both an intensity model of the patient under consideration and a collection of intensity and segmentation templates that provide a model on normal tissue. The approach is called a Model of Population and Subject (MOPS) intensities (Tomas-Fernandez and Warfield, 2015). Unlike classical approaches in which lesions are characterized by their intensity distribution compared to all brain tissues, MOPS aims to distinguish locations in the brain with an abnormal intensity level when compared with the expected value at the same location in a healthy reference population.

A reference population of fifteen healthy volunteers was acquired including T₁-w, T₂-w FSE (Fast spin echo), FLAIR-FSE, and diffusion weighted images on a 3T clinical MR scanner from GE Medical Systems (Waukesha, WI, USA, see Tomas-Fernandez and Warfield (2015) for details about acquisition and spatial alignment). The MOPS algorithm combines a local intensity GMM derived from the reference population with a global intensity GMM estimated from the imaging data. Intuitively, the local intensity model down weights the likelihood of those voxels having an abnormal intensity given the reference population. Since MRI structural abnormalities will show an abnormal intensity level compared to similarly located brain tissues in healthy subjects, MS lesions are identified by searching for areas with low likelihood.

Team IIT Madras

Longitudinal Multiple Sclerosis Lesion Segmentation using 3D Convolutional Neural Networks

(S. Vaidya, A. Chunduru, R. Muthuganapathy, & G. Krishnamurthi)

Team IIT Madras modeled a voxel-wise classifier using multi-channel 3D patches of MRI volumes as input. Two convolutional neural networks (CNNs) were trained, each of which represented one of the trained raters. The final segmentation is obtained by combining the probability outputs of these two CNNs. Efficient training is achieved by using sub-sampling methods and sparse convolutions.

The provided data is preprocessed such that all subjects and time-points are histogram-matched to the first provided patient and time-point, then normalized using the mean CSF value, followed by a robust (1%) data truncation (Avants et al., 2011). A voxel-wise classifier is employed to perform the segmentation task with 3D patches from each of the four channels (T₁-w, T₂-w, PD-w, and FLAIR) being fed to the classifier. As MS Lesions only constitute a very small percentage of the MRI volume, the data is sampled to reduce the class imbalance between WML and NABT. Each image volume is divided into subvolumes of equal size, with patches only selected from those subvolumes that contain lesion voxels greater than a set threshold. This sampling technique speeds up the training of the CNNs for segmentation by using the sparse convolution method (Li et al., 2014).

All convolutional layers in the CNN use the softplus activation function, with training done using a logarithmic likelihood as cost function, and optimization carried out using mini-batch gradient descent with momentum. The CNN consists of four layers with the input being image patches of size 19 × 19 × 19 voxels from each of the four modalities concatenated. The second and third layers consist of 60 filters of size 4 × 4 × 4 and 3 × 3 × 3 respectively, with the third layer being a multi-layer perceptron (1 × 1 × 1 × 200) and the final output being a binary classification. Two CNNs were trained for each of the two trained raters, and the posterior probability maps of the lesion class from the CNNs generate the initial prediction of the MS lesions. As the Challenge is focused on WML, a WM mask is applied to the predictions by registering the test images with a brain template and removing any lesion predictions that are outside the template WM mask.

Team PVG One

Hierarchical MRF and Random Forest Segmentation of MS Lesions and Healthy Tissues in Brain MRI

(A. Jesson & T. Arbel)

Team PVG One built a hierarchical framework for the segmentation of a variety of healthy tissues and lesions. At the voxel level, lesion and tissue labels are estimated through a MRF segmentation framework that leverages spatial prior probabilities for nine healthy tissues through multi-atlas label fusion (MALF). A random forest (RF) classifier then provides region level lesion refinement.

Training consists of three stages: Stage one involves building a set of lesion and healthy tissue atlases, referred to as pathological atlases as they are based on MS patient data. These are to be used as spatial priors for new test data. Stage two involves performing an initial segmentation of 9 healthy tissue structures in each of the patient training cases in order to build healthy and lesion intensity distributions. Stage three involves training the RF.

Stage One included the 21 subjects from the Challenge training data with intensity values averaged over several time-points and 20 subjects from the training data provided by Styner et al. (2008): these are combined to create atlases of pathological tissues. Healthy tissue labels for each pathological atlas are generated through MALF from multiple labels from 35 subjects from the MICCAI 2012 Grand Challenge on Multi-Atlas Labeling. The 134 provided labels are concatenated into nine tissue classes: CSF, lateral ventricles, other ventricles, deep GM, cortical GM, cerebellar GM, WM, cerebellar WM, and brainstem. The NABT tissues labels are augmented by the provided manual delineations to complete the pathological atlases.

Stage Two involves performing the same procedure as Stage One on the 21 training time-points provided. This leads to a set of healthy and lesion labels and associated weights, which are used to guide voxel sampling for building intensity distributions of healthy tissues and lesions. Here intensity distributions of each class are modeled as GMMs.

Stage Three involves determining the labels at each voxel for each time-point of each training subject using the models determined in Stages One and Two. The resulting segmentations are used to group together lesion voxels into lesion candidates. A regional random forest model (RRF) is then trained using the distance minimum, mean, and variance of each candidate lesion to each healthy tissue; the size, volume, and solidity of each candidate lesion; and the principal moments and inertia matrix of the ellipse estimating the shape of each candidate lesion as features.

The MALF estimation of spatial tissue priors uses the rigid and affine components of ANTs (Avants et al., 2008) and the non-linear framework of MIND (Heinrich et al., 2012, 2013). Label fusion is performed through a regional similarity method, and lesion priors are augmented through outlier detection. In addition to the preprocessing provided by the challenge, intensity normalization was performed using a sigmoidal function, where the parameters are determined by the mean and variance of intensities over several regions of interest. To reduce within image artifacts the data was de-noised based on a non-local means method (Coupé et al., 2008).

Team IMI

MS-Lesion Segmentation in MRI with Random Forests

(O. Maier & H. Handels)

Team IMI trained a RF with supervised learning to infer the classification function underlying the training data. The classification of brain lesions in MRI is a complex task with high levels of noise, hence a total of 200 trees are trained without any growth-restriction. Contrary to reported observations, no overfitting occurred.

All data was preprocessed to harmonize each sequences intensity profile by a learning-based intensity standardization method. From each of the four MRI sequences, the following features are extracted: 1) voxel intensity; 2) voxel intensity after Gaussian smoothing (σ = 3, 5, and 7 mm); 3) three different local histogram configurations; and 4) each voxels’ distance to the image center. Features 1–3 provide information about gray-level values at different scales and mean intensity distributions in small areas around each voxel, see Maier et al. (2015) for a more complete explanation of these features. The Challenge is concerned with WML, thus a probability based tissue segmentation is obtained (Zhang et al., 2001) on the T₁-w MPRAGE sequence providing probabilities for CSF, GM, and WM. The feature vector is computed with voxel gray value and voxel gray value after Gaussian smoothing (σ = 3, 7, 15, and 31 mm).

Stratified random sampling is employed to extract a representative sub-set from the training data, reducing the amount of training samples and thus the training time. The original background-to-lesion ratio of each subject is kept intact, leading to an unequal class representation, which has been found to be advantageous (Maier et al., 2015). To obtain a binary segmentation mask, the RFs probability output is thresholded at a value of 0.4, introducing a slight bias in favor of the lesion class that compensates for the unbalanced class ratio in the training set. Finally, single unconnected lesion voxels are removed as outliers, holes in binary lesion objects are closed and a single-iteration closing operation with a 3D square-connected component is applied.

Team MSmetrix

Automatic Longitudinal Multiple Sclerosis Lesion Segmentation

(S. Jain, D. M. Sima, & D. Smeets)

MSmetrix (Jain et al., 2015) is presented, which performs lesion segmentation while segmenting brain tissue into CSF, GM, and WM, with lesions identified based on a spatial prior and hyperintense appearance in FLAIR.

The lesion segmentation has four stages: brain segmentation, outlier estimation, pruning, and lesion filling. The brain segmentation uses an EM algorithm to formulate a probabilistic model of CSF, GM, and WM, from the T₁-w image. In the outlier estimation step, an outlier class is estimated from the FLAIR image of the same patient using the three tissue class segmentations from the previous step as prior information. This is also done with an EM algorithm with the inclusion of an outlier map. The pruning stage segments the lesions in the outlier map, as not every outlier is a lesion. To differentiate lesions from NABT, some additional a priori information about the location and the appearance of the lesions is incorporated. Lesions need to be in the WM region and the underlying intensities of the outliers should be hyperintense compared to the GM intensities from the FLAIR. Finally, the lesion segmentation is used to fill in the lesions in the bias corrected T₁-w image with WM intensities. These four stages are repeated until convergence and the lesion segmentation is produced as an output.

Each time-point was initially processed independently with a subsequent temporal consistency correction, similar to Xue et al. (2006). The temporal consistency, C_it, for a voxel i at time-point t is defined based on its temporal neighborhood ${\mathcal{N}}_{it}^{\text{Temp}}\in \{t-1,t,t+1\}$ as

$$C_{it}=1-\frac{{\delta }_{N_{it}^{\text{Temp}}}}{\mid {\mathcal{N}}_{it}^{\text{Temp}}\mid -1},$$

where ${\delta }_{N_{it}^{\text{Temp}}}$ is the number of times the segmentation label changes in ${\mathcal{N}}_{it}^{\text{Temp}}$. The label at voxel i for time-point t, L_it, is defined based on the temporal consistency of its 3 × 3 × 3 spatial neighborhood, ${\mathcal{N}}_{it}^{\mathrm{Spa}}$, as follows,

$$L_{it}=\{\begin{array}{cc}{L}_{it}\hfill & \text{if}\frac{1}{T}\sum _{t=1}^T{C}_{it}\ge 0.5,\hfill \\ \mathrm{mode}\left({\left\{\underset{j\in {\mathcal{N}}_{jt}^{\mathrm{Spa}}}{\arg \max }{C}_{jt}\right\}}_{t=1}^T\right)\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Thus, if the consistency is high enough, the labels remain unchanged by the temporal consistency; otherwise, it is replaced with the modal value of the segmentation labels of its most consistent neighbors.

Team DIAG

Convolution Neural Networks for MS Lesion Segmentation

(M. Ghafoorian & B. Platel)

Team DIAG utilizes a deep CNN with five layers in a sliding window fashion to create a voxel-based classifier.

The image intensity is normalized using a 95th percentile with values at and above that set to 1; all values below that are linearly rescaled in the range [0, 1]. The CNN learns to label n × n patches indicating if the central voxel is a lesion or NABT. A leave-one-out cross validation is employed to provide training data for the CNN. While sampling from a patient, all available time-points and all possible lesion patches are used. An equal number of NABT patches are randomly chosen to ensure balance between the two classes in the training data. The approximate final sizes of the five created training data sets are 430k, 320k, 540k, 570k, and 560k respectively. No data augmentation methods have been applied to artificially increment the size of the data. Since human experts are usually better at specificity than sensitivity, the logical OR operation is used to create a better reference standard from the two provided human expert annotations.

To classify the image patches, a five layer CNN is trained that takes 32 × 32 patches from the available four channels (T₁-w, T₂-w, PD-w, & FLAIR) as its input samples. There are four convolutional layers with rectified linear non-linearities that have respectively 15 filters of size 13 × 13, 25 filters of size 9 × 9, 60 filters of size 7 × 7, and finally 130 filters of size 3 × 3. Pooling is not used since it results in a sort of translation invariance that is not desirable for a classifier that assigns the label of the whole patch to its central voxel. A final logistic regression model classifies the resulting responses to the filters in the last convolutional layer. Stochastic gradient descent is used for the optimization with a batch size of 64 and a learning rate of 0.0001. We run the optimization for 50 epochs and pick the best classifier based on the validation set misclassification rate.

Team TIG

Model Selection Propagation for Application on Longitudinal MS Lesion Segmentation

(C. H. Sudre, M. J. Cardoso, & S. Ourselin)

Based on the assumption that the structural anatomy of the brain should be temporally consistent for a given patient, Team TIG proposes a lesion segmentation method that first derives a GMM separating healthy tissues from pathological and unexpected ones on a multi-time-point intra-subject group-wise image. This average patient-specific GMM is then used as an initialization for a final time-point specific GMM from which final lesion segmentations are obtained.

The proposed model can be divided into four major steps. First, the provided T₁-w and T₂-w data are rigidly registered to the FLAIR image of each time-point. ICBM atlases are also aligned to the transformed T₁-w image and used as an initialization for a three modalities EM segmentation in a framework that not only corrects for any possible remaining bias field but also for an initial separation between inliers and outliers. This is done on log-transformed and bounded intensities. The second step creates an intra-subject multi-time-point group-wise average. This is performed through an iterative set of affine registrations refined afterwards by non-rigid deformations (Modat et al., 2014). To standardize the intensity information, histogram-matching is progressively performed between the individual time-points and the group-wise image using only the model inliers and applying a polynomial fit of degree 2. The intensity matching allows for a direct transfer of the selected group-wise model to each specific time-point. The third step involves running a GMM on the matched group-wise images (T₁-w, T₂-w, and FLAIR). The number of classes to correctly model the inlier and outlier components of the four main anatomical regions (CSF, GM, WM, and non-brain) is determined automatically, by finding a balance between model fit and complexity. Once the final model converges, one can obtain a group-wise tissue segmentation and an inlier/outlier classification. To finalize the result, the group-wise tissue segmentation is transformed back to each time-point and subsequently smoothed out using a Gaussian filter. For each time-point, this smoothed segmentation is used as a prior for a new GMM model fit improving on the inlier/outlier separation. The lesion extraction process relies simply on the choice of the relevant component from the outlier part of the model based on the location and intensity heuristics.

Team TIG submitted new results after the completion of the Challenge to address a bug in their code, the second submitted results are denoted TIG BF. Both sets of results are reported in Table C.3. However, only the originally submitted results are included in Tables C.1 and C.2.

Appendix B.2. Other Methods

Table B.2 provides an overview of these methods and the data they use.

BAUMIP

Automatic White Matter Hyperintensity Segmentation using FLAIR MRI

(L. O. Iheme & D. Unay)

BAUMIP is a method based on intensity thresholding and 3D voxel connectivity analysis. A simple model is trained that is optimized by searching for the maximum obtainable Dice overlap.

Firstly, a mapping is constructed of the intensities of every training image to those of a reference image, which in this case is the first time-point for the first subject. The histogram of the whole brain foreground voxels is computed from the FLAIR image, with the assumption that the peak is that of a normal distribution so that its 7 dB drop is more than twice its Full Width at Half Maximum (FWHM). The intensity I_{7 dB} of this point is guaranteed to be amongst the highest intensity values of the image. With this value as a minimum threshold for the WM hyperintensity, the threshold is defined as

$$T=I_{\text{Peak}}(1-w)+I_{7\mathrm{dB}},$$

where w is a to be determined weight. Voxels that exceed this threshold are segmented as WM lesions. For a more detailed description and evaluation of the method, see Iheme et al. (2013).

The 3D connectivity analysis involves examining every detected voxel for the degree of connectivity with each of its neighboring voxels. This is equivalent to analyzing the volumetric significance of every detected lesion. The training data was used to determine a minimum volume for lesions; connected components that are below this volume threshold are deemed insignificant and assumed to be false positives. To further reduce the incidence of false positives at the corpus callosum, the interhemispheric fissure is estimated using a RANSAC-based approach (Ekin, 2006). Lesions that fall within a prescribed distance of the interhemispheric fissure are also removed as false positives.

MORF

Multi-Output Random Forests for Lesion Segmentation in Multiple Sclerosis

(A. Jog, A. Carass, D. L. Pham, & J. L. Prince)

MORF is an automated algorithm to segment WML in MR images using multi-output random forests. The work is similar to Geremia et al. (2011) in that it uses binary decision trees that are learned from intensity and context features. However, instead of predicting a single voxel, an entire neighborhood or patch is predicted for a given input feature vector. The multi-output decision trees implementation has similarities to output kernel trees (Geurts et al., 2007). Predicting entire neighborhoods gives further context information such as the presence of lesions predominantly inside WM. This approach was originally presented in Jog et al. (2015).

From the co-registered T₁-w, T₂-w, FLAIR, and expert manual delineations, 3 × 3 × 3 sized patches for each voxel i are extracted. Small patches provide local context for a particular voxel with the patch for the manual segmentation being the desired output of the multi-output decision trees. The multi-modality intensity features are augmented with a global context for each voxel i consisting of the mean intensity of a large window (of size 11 × 11 × 3) calculated at a fixed radial distance from i and multiple angles within the axial plane. The final feature vector is created by concatenating the local intensity patches from the three modalities (T₁-w, T₂-w, & FLAIR) and global context features, and x_i is used to denote the feature vector of i (see Jog et al. (2015) for complete details).

Learning a multi-output random forests is similar to the random forest algorithm (Breiman, 2001). With independent vectors, x_i, and dependent vectors, y_i, which are the 3 × 3 × 3 patch of the manual delineation. Given a node q in a decision tree, with training samples Θ_q = {[x₁; y₁], . . ., [x_m; y_m]} and the mean of the dependent vectors denoted by $\overline{{\mathit{y}}_q}$, then the squared distance from the mean is computed as

$$\sum _{k=1}^m\sum _{j=1}^{27}{\left({\mathit{y}}_{kj}-\overline{{\mathit{y}}_{qj}}\right)}^2.$$

For a particular feature, f, and threshold π_f, the data in q (Θ_q) are separated into two disjoint sets Θ_qL = {[x_i; y_i]|∀i, x_if ≤ π_f} and Θ_qR = {[x_i; y_i]|∀i, x_if > π_f}. f and π_f are chosen such that the combined squared distance of the two daughter nodes q_L and q_R of q is minimized.

To predict a lesion segmentation on a new image, the local and global context features from the T₁-w, T₂-w, and FLAIR images are constructed as mentioned above. The trained multi-output tree ensemble is applied to each extracted feature vector. The input vector travels through the tree as its features are evaluated against the ones in the tree nodes, until it lands in a leaf node. Leaf nodes consist of at least 50 training samples, each a 27-dimensional label vector. These label vectors provide a percentage of lesion voxels. The output from the multi-output decision ensemble is smoothed using a Gaussian filter with σ = 1. This smoothed membership image is thresholded to create a binary lesion mask. A 3-class fuzzy k-means segmentation (Bezdek, 1980) of the T₁-w image provides an initial WM mask. Lesions inside WM are labeled as GM in this 3-class fuzzy k-means segmentation, thus forming holes in the initial WM mask. Therefore, MORF fills the initial WM mask and regards any lesions found outside the filled WM mask as false positives; these lesions are removed from the final MORF output.

Lesion-TOADS

A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions

(N. Shiee, P.-L. Bazin, A. Ozturk, D. S. Reich, P. A. Calabresi, & D. L. Pham)

Lesion-TOADS is an atlas-based segmentation technique employing topological and statistical atlases. The method builds upon previous work (Bazin and Pham, 2008) by handling lesions as topological outliers that can be addressed in a topology-preserving framework when grouped together with the underlying tissues.

A complete description of Lesion-TOADS is available in Shiee et al. (2010), as it represents a continuation of the development of TOADS (Bazin and Pham, 2008); a brief review of that work is provided here. TOADS segments the brain into several major structures (sulcal CSF, ventricular CSF, cortical GM, cerebral WM, cerebellar GM, cerebellar WM, putamen, thalamus, caudate, and brainstem) and Lesion-TOADS introduces the delineation of WML. TOADS incorporates statistical and topological atlases with a fuzzy clustering framework giving topologically consistent segmentation of healthy brain anatomy. A topologically consistent hard segmentation of the brain is initialized from a topological atlas and used to modulate the influence of similar intensity clusters that are non-contiguous. The statistical and topological atlases are rigidly registered to the MR image initiating an iterative process alternating between intensity based tissue segmentation and topology preserving fast marching. Lesion-TOADS augments TOADS by handling the union of WML and WM as a topological consistent object, with both WML and WM having the same spatial prior. Other improvements of Lesion-TOADS over TOADS include: 1) redefining the cluster distance function to account for the intensity profile of WML to help distinguish it from the partial volume mix of GM & WM, or CSF & WM, which can cause false positives; and 2) multichannel weights to take advantage of the discriminative power of FLAIR images in distinguishing WML from NABT.

MV-CNN

Multi-View Convolutional Neural Networks

(A. Birenbaum & H. Greenspan)

MV-CNN is a method based on a Longitudinal Multi-View CNN (Roth et al., 2014). The classifier is modeled as a CNN, whose input for every evaluated voxel are patches from axial, coronal, and sagittal views of the T₁-w, T₂-w, PD-w, and FLAIR images of current and previous time-points. That is multiple contrasts, multiple views, and multiple time-points. MV-CNN consists of three phases: Preprocessing the Challenge data, Candidate Extraction, and CNN Prediction. The Challenge data is preprocessed by clamping the top and bottom 1% and the intensity values are scaled to the range [0, 1].

The Candidate Extraction phase disqualifies the majority of the image voxels from being lesions, thus dramatically improving the performance of CNN prediction. MV-CNN bases its candidate extraction on two clinical rules (Mechrez et al., 2016):

1. Lesions appear as hyperintense in FLAIR images and can be roughly approximated by thresholding the FLAIR image;

2. Lesions tend to be found in WM or the boundary between WM and GM. Thus a probabilistic WM template (Mazziotta et al., 2001) is registered to the FLAIR image using a mutual information cost function. Due to misregistration errors the WM template is gray-scale dilated by a radius R.

   $$\mathrm{Mask}\left(x\right)=\{\begin{array}{cc}1\hfill & (I_{\mathrm{FLAIR}}\left(x\right)\ge T_{\mathrm{FLAIR}})\bigcap ((P_{\mathrm{WM}}\oplus {\mathcal{B}}_R)\left(x\right)\ge T_{\mathrm{WM}}),\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

   Where I_FLAIR(x) is the FLAIR intensity at x, P_WM(x) is the WM probability which is dilated by ${\mathcal{B}}_R$, a ball of radius R, and the thresholds are T_FLAIR & T_WM. The parameters T_FLAIR, T_WM, and R are determined by cross-validation.

The CNN Prediction phase assigns a lesion probability to each voxel in the image Mask(x). The input to the CNN are 24 patches of 32 × 32 pixels from all four images, three orthogonal views, and two consecutive time-points. All input patches of a single view and time-point are processed by three convolution layers with the following parameters 24 at 4 × 5 × 5, 32 at 24 × 3 × 3, and 48 at 32 × 3 × 3. The first two convolution are followed by a 2 × 2 max pooling layer. Thus for each time-point a 48 × 4 × 4 tensor representation is obtained. The tensors of two consecutive time-points from a single view are concatenated and processed by a 48 at 96 × 1 × 1 convolution layer and a fully connected layer whose output is a vector of 16 neurons, which is the full representation of a single view. Vectors from axial, coronal, and sagittal views are concatenated and processed by two fully connected layers of 16 and 2 output neurons respectively. Softmax is applied to the output of the last fully connected layer to obtain a non-lesion and lesion probability, while the rest of the convolution and fully connected layers are followed by Leaky ReLU activation (α = 0.3) and Dropout layers (p = 0.25). Voxels are assigned the lesion label if their lesion probability is higher than a threshold T_CNN.

The CNN's weights were optimized for 500 epochs by AdaDelta (Zeiler, 2012) to minimize the categorical cross-entropy. Each training batch consisted of 64 negative samples and 64 positive samples which were extracted with random rotations in the cardinal planes, drawn from a Gaussian distribution (μ = 0°, σ = 5°). Values for the thresholds and dilation radius were determine via cross-validation to maximize the mean Dice score, with T_FLAIR = 0.91, T_WM = 0.5, T_CNN = 0.99, and R = 2.

Appendix C. Challenge Results

In this section, we present a comparison of the ten Challenge participants, outlined in Section 3.1. Table C.1 shows the score achieved by each participant for a normalized version of each of Dice, PPV, TPR, and LTPR; the normalization is done relative to the inter-rater metrics by dividing by the inter-rater score, so that the relative value of the metric is boosted. For example, N-Dice is computed as,

$$\text{N-Dice}\left({\mathcal{M}}_A\right)=\frac{\underset{r\in \mathcal{R}}{\min }\left(\mathrm{Dice}({\mathcal{M}}_r,{\mathcal{M}}_A)\right)}{\mathrm{Dice}({\mathcal{M}}_{r_1},{\mathcal{M}}_{r_2})},$$

where $\mathcal{R}$ is the set of all raters, and the denominator is the inter-rater score. Also shown in Table C.1 are the 1 – LFPR, the Longitudinal Correlation (LongCorr), and the Total Correlation (TotalCorr). The results in Table C.1 and the Challenge are ranked based on a weighted score (20% 1 – LFPR, 20% N-LTPR, 20% LongCorr, 20% TotalCorr, and 20% for the average of N-Dice, N-PPV, & N-TPR). Figures 2 and 3 show the result generated by each team on the same subject, as well as showing the preprocessed data, manual delineations generated by the two raters, and our Consensus Delineation.

Appendix C.1. Efficiency Performance Comparison

The participants were told prior to downloading Test Set B, that they would be timed on how long it took them to return the results for that data set. The results for the time taken for each of the ten Challenge participants are listed in Table C.2. The various run times provide a frame of reference for each of the methods and may serve as a guide for which method is most appropriate for a given situation. For example, consider the convolutional neural network based approach proposed by Team DIAG which takes an order of magnitude less time and has similar Dice scores to Team PVG One, and thus Team DIAG might be preferred over Team PVG One. Alternatively, researchers may have a minimum acceptable score in another metric, the reported times allow them to identify the quickest method with the required performance level. The ranking for the efficiency performance was based on a combination of the return time of Test Set B and the final ranking of the teams in the Challenge (see Table C.1). The ranking of both were summed and the team with the lowest combined sum was deemed the most efficient. This allowed us to have a balance between speed and the accuracy of the method relative to both human raters.

Appendix C.2. Challenge Website

To facilitate the dissemination of the data and promote the sharing of results we have created a website³. Visitors to the site can see a list of the Top 25 submitted results. Currently only fifteen results are listed: ten from the Challenge, plus a bug fixed version of a Challenge participant, and an additional four results—which are outlined in Section 3 and described in detail in Appendix B. Groups interested in running their methods on the data need only register for an account, download the data, and upload their results. The uploader of the results will receive an e-mail within ten minutes detailing the results on a per subject and per time-point basis. The report includes the following computed metrics: Dice, Jaccard, PPV, TPR, LFPR, LTPR, AVD, SSD, algorithm and manual lesion volume. For algorithm A, the Website score is computed as follows,

$$\frac{1}{\mid \mathcal{R}\mid }\frac{1}{\mid \mathcal{S}\mid }\left(\sum _{r\in \mathcal{R}}\sum _{s\in \mathcal{S}}\frac{\mathrm{Dice}({\mathcal{M}}_r,{\mathcal{M}}_A)}{8}+\frac{\mathrm{PPV}({\mathcal{M}}_r,{\mathcal{M}}_A)}{8}+\frac{1-\mathrm{LFPR}({\mathcal{M}}_r,{\mathcal{M}}_A)}{4}+\frac{\mathrm{LTPR}({\mathcal{M}}_r,{\mathcal{M}}_A)}{4}+\frac{\mathrm{Corr}({\mathcal{M}}_r,{\mathcal{M}}_A)}{4}\right),$$

where $\mathcal{S}$ is the set of all subjects, $\mathcal{R}$ is the set of all raters, and Corr is the Pearson's correlation coefficient of the volumes. This is then linearly normalized by the inter-rater scores between each other such that the lower inter-rater score has an overall rating of 90. This was designed to mimic the scoring of the 2008 MICCAI MS Lesion challenge (Styner et al., 2008). Table C.3 shows the ranking as displayed on the Challenge Website.

Appendix C.3. Overall Performance

From the main Challenge results (see Table C.1) it is clear that there is very little separating the performance of the top three teams. An interesting characteristic of these three algorithms is that they are machine learning based. However Team DIAG, which finished far off from the winning Team IIT Madras, used at its core a convolutional neural network engine. This suggests that a more refined approach to using machine learning technologies is needed to maximize their effectiveness. This point can also be inferred from the performance of MORF on the reduced data set made available through the Challenge Website (see Table C.3). We had expected MORF to perform better than Lesion-TOADS as it should have represented an improvement on the work of Geremia et al. (2011) which ranked first at the 2008 MICCAI Grand Challenge on MS Lesion Segmentation (Styner et al., 2008), whereas Lesion-TOADS was ranked third at the same challenge. The disappointing performance of MORF could be due in part to the differences in the training data and choices about how much and which portion of the available data was used to train the method. However, it may simply reflect a basic instability in machine learning based approaches.

Table B.1.

An overview of the methods and data used by the Challenge participants. We denote methods that are unsupervised with the letter U and those that require some training data (supervised methods) with the letter S.

Name	Approach	Sequences
	Multimodal patch matching with an l2-norm	T1-w, T2-w, PD-w, & FLAIR
	Robust EM initialized graph cut	T1-w, T2-w, & FLAIR
	Class specific sparse dictionaries	T1-w, T2-w, PD-w, & FLAIR
	Mixture of global & local intensity distributions from a reference population	T1-w, T2-w, & FLAIR
	n3 Convolutional Neural Networks	T1-w, T2-w, PD-w, & FLAIR
	Hierarchical MRF & random forest refinement	T1-w, T2-w, & FLAIR
	Random forests	T1-w, T2-w, PD-w, & FLAIR
	Hierarchical EM followed by temporal consistency check	T1-w& FLAIR
	n2 Convolutional Neural Networks	T1-w, T2-w, PD-w, & FLAIR
	Hierarchical subject specific GMM	T1-w, T2-w, & FLAIR

Table B.2.

An overview of the methods and data used by the eleventh Challenge submission, and three state-of-the-art methods. We denote methods that are unsupervised with the letter U and those that require some training data (supervised methods) with the letter S.

Name	Approach	Sequences
	Threshold and 3D connectivity analysis	FLAIR
	Multi-output random forests	T1-w, T2-w, & FLAIR
	Fuzzy c-means with topology constraint	T1-w & FLAIR
	Multi-view (2.5D) Convolutional Neural Networks	T1-w, T2-w, PD-w, & FLAIR

Table C.1.

Final rankings from the Challenge participants (Appendix B.1). The metrics (Dice, PPV, TPR, & LTPR) have been normalized relative to the inter-rater metrics and denoted with the prefix “N-”. The Final Score is weighted in the following manner: 20% 1 – LFPR, 20% N-LTPR, 20% LongCorr, 20% TotalCorr, and 20% for the average of N-Dice, N-PPV, & N-TPR.

Name	N-Dice	N-PPV	N-TPR	1 – LFPR	N-LTPR	LongCorr	TotalCorr	Final Score	Ranking
	0.9448	1.2465	0.7395	0.5873	0.6656	0.5540	0.8753	0.7179	1
	1.0599	1.2664	0.8857	0.8479	0.5209	0.2503	0.8506	0.7041	2
	1.0149	1.3172	0.8404	0.7318	0.6037	0.2542	0.8611	0.6981	3
	0.9390	1.0671	0.8194	0.6104	0.4666	0.3268	0.8543	0.6518	4
	0.9417	1.2008	0.7544	0.6246	0.5340	0.3325	0.8583	0.6506	5
	1.0212	1.2238	0.8917	0.6944	0.6805	0.0576	0.7958	0.6435	6
	0.8509	0.8688	0.8779	0.4202	0.7413	0.2123	0.8027	0.6102	7
	0.7062	1.1122	0.5140	0.5863	0.3495	0.3268	0.8543	0.5642	8
	0.5970	1.1083	0.3987	0.4281	0.6184	0.1770	0.8075	0.5487	9
	0.6830	1.0082	0.5554	0.5608	0.4603	0.1716	0.6459	0.5188	10

Table C.2.

The participants were timed on how long it took them to return their results for Test Set B, which are listed in the column denoted “Total Time”. The rank sum combination of Total Time and their final place in the Challenge (see Table C.1) was used to rank the efficiency of the teams.

Name	Total Time (HH:MM:SS)	Time Rank	Challenge Rank	Efficiency Rank
	3:18:09	2	3	1
	5:59:17	6	1	2
	4:03:13	3	4	3
	3:02:30	1	7	4
	5:05:18	4	5	5
	29:08:04	8	2	6
	5:53:51	5	6	7
	24:47:55	7	8	8
	31:56:04	9	9	9
	52:38:47	10	10	10

Table C.3.

Rankings from the Challenge Website for the Challenge participants (Appendix B.1) and the other state-of-the-art methods (Appendix B.2).

Name	Challenge Rank	Website Score
	2	90.698
	3	90.283
	—	90.070
	6	89.807
	1	89.159
	5	88.744
	—	88.465
	4	88.009
	—	87.917
	—	87.376
	8	87.017
	7	86.916
	9	86.436
	10	86.068
	—	84.140

^†Team TIG submitted new results after the completion of the Challenge to address a bug in their code, the second submitted results are denoted TIG BF.