Free-breathing Volumetric Fat/Water Separation by Combining Radial Sampling, Compressed Sensing, and Parallel Imaging

Abstract

Purpose

Conventional fat/water separation techniques require that patients hold breath during abdominal acquisitions, which often fails and limits the achievable spatial resolution and anatomic coverage. This work presents a novel approach for free-breathing volumetric fat/water separation.

Theory and Methods

Multi-echo data are acquired using a motion-robust radial stack-of-stars 3D GRE sequence with bipolar readout. To obtain fat/water maps, a model-based reconstruction is employed that accounts for the off-resonant blurring of fat and integrates both compressed sensing and parallel imaging. The approach additionally enables generation of respiration-resolved fat/water maps by detecting motion from k-space data and reconstructing different respiration states. Furthermore, an extension is described for dynamic contrast-enhanced fat-water-separated measurements.

Results

Uniform and robust fat/water separation is demonstrated in several clinical applications, including free-breathing non-contrast abdominal examination of adults and a pediatric subject with both motion-averaged and motion-resolved reconstructions, as well as in a non-contrast breast exam. Furthermore, dynamic contrast-enhanced fat/water imaging with high temporal resolution is demonstrated in the abdomen and breast.

Conclusion

The described framework provides a viable approach for motion-robust fat/water separation and promises particular value for clinical applications that are currently limited by the breath-holding capacity or cooperation of patients.

INTRODUCTION

Separation of fat and water plays an important role in numerous clinical MRI applications (1), including abdominal, cardiac, and breast examinations. Often, spectral saturation techniques are applied to suppress signal contributions from fat prior to data acquisition. However, these approaches typically fail in regions with B₀ field inhomogeneities. Chemical-shift encoding methods, also referred to as “Dixon” methods, have been shown to be more robust to moderate B₀ inhomogeneities (2). In addition, they provide both a “fat-suppressed” water-only image and a “water-suppressed” fat-only image, which retrospectively can also be combined into synthetic in-phase and opposed-phase images. In order to encode the differences in resonance frequency of fat and water, Dixon techniques require acquisition of multiple images with slightly different echo times (TE). Therefore, the overall scan time is prolonged, which poses a challenge for applications in the abdomen where scans have to be performed during a breath-hold. Typically, only 15–20 seconds can be used for acquiring all data, and the available time can be even less for sick, elderly, or pediatric patients. To accelerate data acquisition, combinations of fat/water separation with parallel imaging (PI) (3), compressed sensing (CS) (4,5), or both (6,7) have been proposed. However, the achievable spatial resolution and anatomic coverage remains limited due to the requirement that, conventionally, data can only be acquired as long as the patient is suspending respiration. This requirement results from the high motion sensitivity of phase-encoded Cartesian k-space acquisitions.

Radial sampling schemes are inherently less sensitive to motion (8,9). It has been recently shown that the combination of a radial trajectory with a T₁-weighted 3D gradient echo (GRE) sequence can be used for motion-robust imaging in various clinical applications (9), including free-breathing examination of the abdomen (10). One major limitation, however, consists in blurring of off-resonant signal components such as fat, which results from the varying k-space readout direction and traditionally makes it necessary to use spectral fat suppression. However, in the presence of B₀ inhomogeneities, residual fat often remains visible. Furthermore, suppression of fat signal makes it impossible to use the data for fat-content assessment, as needed, e.g., for identifying fat-containing lesions such as renal angiomyolipomas and adrenal adenomas, or for detecting fat infiltration of organs as in liver steatosis. Despite commercial availability of radial 3D GRE sequences, clinical exam protocols therefore still require acquisition of conventional Cartesian non-fat-suppressed T₁-weighted images in in-phase/opposed-phase conditions.

Combination of fat/water separation with radial sampling has the potential to overcome these limitations. Previously described approaches perform the separation as post-processing step after image reconstruction (11–16). However, these methods do not account for the blurring of fat (17), which can severely impair image quality, especially when high field strengths or low receiver bandwidths are used.

In this work, we describe a model-based approach for radial Dixon imaging, which estimates separate fat and water maps directly from the k-space data. This enables incorporating the fat off-resonance frequency into the signal model, which results in deconvolution of the blurring. Furthermore, both compressed sensing and parallel imaging can be added to the reconstruction. The proposed reconstruction framework is entitled Dixon RAdial Volumetric Encoding (Dixon-RAVE).

Two extensions are presented. eXtra-Dimensional (XD-) Dixon-RAVE allows generating respiration-resolved fat/water images. This is achieved by detecting respiratory motion from k-space data and reconstructing different motion states, following the previously presented eXtra-Dimensional Golden-Angle Radial Sparse Parallel (XD-GRASP) technique (18). The second extension is DCE-Dixon-RAVE, which enables fat-water-separated dynamic contrast-enhanced (DCE) measurements.

Results are shown for several imaging applications at 1.5 and 3 Tesla (T), including (i) volunteer and patient free-breathing volumetric abdominal measurements, (ii) pediatric abdominal imaging, (iii) DCE-MRI of the abdomen, (iv) breast imaging, and (v) DCE-MRI of the breast.

The Dixon-RAVE source code is available for download at http://cai2r.net/resources/software/dixon-rave-matlab-code.

THEORY

Dixon-RAVE: Optimization problem and signal model

The general Dixon-RAVE optimization problem to estimate fat, water, and field map directly from k-space data can be written as follows (4):

$$\text{argmin}{\displaystyle \sum }_{c,t}\parallel \mathrm{E}{\left(W,F,\Phi \right)}_{\mathrm{c},\mathrm{t}}-y_{\mathrm{c},\mathrm{t}}{\parallel }_2^2+{\lambda }_{\mathrm{W}}\parallel \mathrm{S}{\left(W\right)\parallel }_1+{\lambda }_{\mathrm{F}}\parallel \mathrm{S}{\left(F\right)\parallel }_1$$ [1]

where y are the acquired radial k-space data, and E is the forward operator that synthesizes k-space data from the to-be-estimated water (W), fat (F), and B₀ field (Φ) maps. The data fidelity term is evaluated and summed for each coil element c and for each echo time t. Compressed sensing can be included by using spatial finite differences as sparsifying transform S for the fat and water maps, which is equivalent to total variation (TV) regularization. As the field map Φ is assumed to be smooth, edge-preserving TV regularization is omitted in this case. E is the forward operator, which transforms the desired parameters to k-space data and can be expressed as:

$$\mathrm{E}{\left(W,F,\Phi \right)}_{\mathrm{c},\mathrm{t}}=\text{FT}\left(C_{\mathrm{c}}\cdot \text{exp}\left(2\mathrm{\pi }\mathrm{i}\cdot \Phi \cdot t_{\mathrm{n}}\right)\cdot W\right)+D\left(t\right)\cdot \text{FT}\left(C_{\mathrm{c}}\cdot \text{exp}\left(2\mathrm{\pi }\mathrm{i}\cdot \Phi \cdot t_{\mathrm{n}}\right)\cdot F\right)$$ [2]

FT is an operator which performs a non-uniform fast Fourier transform (NUFFT). A Kaiser-Bessel window is used as interpolation kernel for the integrated gridding step. This is followed by a conventional FFT. t_n are the different echo times. To account for the off-resonant blurring of fat due to radial readout, D(t) models the chemical shift in k-space, taking into account the exact readout time points t = t_n + T_n,k of the samples k of each spoke:

$$D\left(t\right)={\displaystyle \sum }_{m=1}^6{\mathrm{\alpha }}_{\mathrm{m}}\cdot \text{exp}(2\mathrm{\pi }\mathrm{i}\cdot \mathrm{\Delta }{f}_{\mathrm{m}}\cdot \left(t_{\mathrm{n}}+{\tau }_{\mathrm{n},\mathrm{k}}\right))$$ [3]

Because of the multiple resonance frequencies of the fat spectrum, a 6-peak model is applied (19). To incorporate parallel imaging, multiplications with the different coil sensitivity profiles C_c are integrated into the forward operator.

XD-Dixon-RAVE: Motion-resolved reconstruction

Although the employed radial trajectory is inherently robust to motion, artifacts such as blurring or streaking can remain for deep breathing. The previously proposed XD-GRASP technique (18) mitigates this issue for fat-suppressed 3D radial GRE imaging by reconstructing an extra motion dimension. The required respiratory motion signal is directly extracted from the acquired k-space data. It has been shown that this approach has the potential to significantly enhance image quality for free-breathing abdominal examinations (20).

To further improve the motion robustness of Dixon-RAVE, both techniques can be combined. The modified optimization problem for XD-Dixon-RAVE is as follows:

$$\text{argmin}{\displaystyle \sum }_{c,t}\parallel \mathrm{E}{\left(W,F,\Phi \right)}_{\mathrm{c},\mathrm{t}}-y_{\mathrm{c},\mathrm{t}}{\parallel }_2^2+{\lambda }_{\mathrm{W}}\parallel \mathrm{S}{\left(W\right)\parallel }_1+{\lambda }_{\mathrm{F}}\parallel \mathrm{S}{\left(F\right)\parallel }_1+{\lambda }_{\mathrm{\Phi }}\parallel \mathrm{S}{\left(\Phi \right)\parallel }_1$$ [4]

where y are the k-space samples, now binned into N_bin different motion states. The resulting dimensions for y are [N_read-N_proj-N_z-N_coil-N_bin], where N_coil equals the number of receive channels, N_proj the number of projections per motion state and N_read the number of readout samples. S is the sparsifying transform. Here, finite differences along the respiratory dimension are used as transform for all three parameters water (W), fat (F), and field map (Φ). E is the forward operator. Except for the dimensions of the fitted parameters W, F, and Φ, which now reflect the additional respiratory dimensions, E remains unchanged compared to Equation 2. The dimensions of W, F, and Φ for the XD-Dixon-RAVE reconstruction are [N_x-N_y-N_z-N_bin] compared to [N_x-N_y-N_z] before.

The respiratory signal, which is used to sort the data into N_bin motion states, is extracted from the dataset using the first echo. In particular, projection profiles along the k_z-direction are computed, followed by a principal component analysis (PCA) for post-processing (18,21).

DCE-Dixon-RAVE: Dynamic contrast enhanced fat/water separation

The second extension of Dixon-RAVE enables its use for DCE imaging. Recently, the GRASP technique for radial DCE imaging (22) has been presented in several clinical applications, including liver (10) and breast (23) examinations. To allow for reconstruction of dynamic time series, this method acquires data continuously during injection of a contrast agent. Afterwards, consecutive projections are grouped into N_frames (undersampled) frames, each consisting of N_proj projections. Due to use of the golden-angle ordering scheme, approximately uniform k-space coverage is achieved for any number of projections N_proj and in particular for Fibonacci numbers (e.g. 13 or 21) (24). A combined parallel imaging and compressed sensing reconstruction is applied to generate dynamic images with high temporal and spatial resolution.

To enable fat-water-separated DCE imaging, the GRASP approach is combined with Dixon-RAVE by injecting the contrast agent during a continuous 3D multi-echo acquisition. After data sorting, the k-space data y have the dimension [N_read-N_proj-N_z-N_coil-N_frames], which equals the dimension of the respiratory-sorted data in XD-Dixon-RAVE. Therefore, Equation 4 can be applied to obtain 4-dimensional time-resolved W, F, and Φ maps of dimensions [N_x-N_y-N_z-N_frames].

Sequence design

A T₁-weighted radial 3D gradient echo (GRE) sequence with RF and gradient spoiling is used for data acquisition (9). k-Space is sampled with a stack-of-stars scheme using standard partition encoding and linear reordering for the k_z-plane in order to acquire all partitions for each projection angle in one block. For the k_x-k_y-plane, radial golden-angle ordering (24) is employed due to its favorable properties regarding approximately uniform k-space coverage for arbitrary sampling windows. All projections along the partition direction k_z are acquired sequentially for the same rotation angle before the procedure is repeated for the next rotation angle, which improves motion robustness (9) and enables binning of full radial projections into dynamic frames or respiration states, as required for XD-Dixon-RAVE and DCE-Dixon-RAVE. Within each repetition time (TR), three echoes are collected by using a bipolar readout in order to maximize scan efficiency. For improved temporal incoherence, a slightly different sampling pattern is applied for each echo (4,7). In particular, subsequent radial projections are rotated by 2°, which was empirically chosen after evaluating image quality of acquisitions with different rotation angles (shown in supporting Figure 1). The rotation is achieved by inserting small blip gradients between the readout gradients of the echo train. Additionally, the amplitudes of the readout and spoiler gradients have to be adjusted accordingly, which is similar to the implementation of the gradient-echo train of a radial GRASE sequence (25). The gradient switching pattern and the resulting k-space scheme are schematically shown in Figure 1. In the following, this acquisition scheme will be referred to as RAdial Volumetric Encoding (RAVE) sequence.

Fig. 1.

Gradient switching pattern and k-space sampling scheme of the bipolar multi-echo readout. For improved k-space coverage, subsequently acquired projections within one TR are rotated by 2°. This is achieved by inserting additional blip gradients (dark grey) and by scaling the amplitudes of the readout and spoiler gradients accordingly.

To account for system imperfections such as gradient delays, multiple projections (e.g. 160) with opposing orientations are acquired before the actual image acquisition (26). This allows estimating the k-space shift along the readout direction, which is then used to adapt the trajectory for the gridding procedure. The calibration scan is performed with the same bipolar readout that is employed for subsequent data acquisition. Because these additionally acquired projections simultaneously serve as preparation shots for reaching steady-state, scan time is not prolonged.

Reconstruction implementation

To solve the general optimization problem (Equation 1 and 4, respectively), an iteratively regularized Gauss-Newton method is employed, which consists of an outer and inner loop. For the outer loop, the problem is linearized (4) around the estimate x_n = [W_n, F_n, Φ_n] from the nth iteration step:

$$\mathrm{E}\left(x_n+dx\right)\approx \mathrm{E}\left(x_n\right)+d\mathrm{E}\left(x_n\right)dx$$ [5]

where dE(x_n) is the Jacobian of E(x) at x_n. This linearized problem is then solved in the inner loop using a non-linear conjugate gradient algorithm. The outer loop is iterated 5 times, and the inner loop is repeated 30 times.

Due to non-convexity of the problem, a gradient-based method such as the Gauss-Newton algorithm does not necessarily converge to the correct global minimum. Therefore, initialization with a reasonable field map is crucial. This is achieved by using a multi-seed safest-first region growing algorithm (27), which is applied before the actual minimization. All acquired radial projections and all readout samples for each projection are used to estimate the initial field map.

Because the optimization problem is solved iteratively and because 3D datasets with many partitions have to be processed, the presented method is computationally demanding. Different measures are applied to reduce the computational complexity. First, a PCA is used directly after loading the data to compress the acquired multi-channel dataset into 4 eigenmodes (28). Second, an inverse Fast Fourier Transform (iFFT) is applied to remove phase encoding along the slice direction. This is possible due to uniform sampling along the k_z-dimension and enables simultaneous reconstruction of different slices. Gridding steps for mapping between k-space and image-space are performed with the NUFFT-toolbox by Fessler and Sutton (29). Coil sensitivity maps are computed with the adaptive array-combination technique (30), which is applied on the entire acquired dataset.

Image reconstruction is performed in Matlab (The MathWorks, Natick, MA), using a server with two 16-core Intel Xeon CPUs and 256 GB RAM. Reconstruction time for a 3D Dixon-RAVE dataset (72 slices, 256 projections each) was ≈ 55 min. The motion-resolved XD-Dixon-RAVE reconstruction time (72 slices, 6 frames with 100 projections each) was ≈ 2:52 h. Approximately 13:09 h were needed for DCE-Dixon-RAVE (144 slices, 19 frames with 21 projections each).

METHODS

To provide an overview of all three presented techniques, Figure 2 lists the used acronyms, a short description, and figure numbers with corresponding results.

Fig. 2.

Overview of the presented techniques, including figure numbers with corresponding results.

Imaging studies

All volunteer and patient measurements for this prospective study were approved by the IRB and were HIPAA compliant. Written informed consent was obtained for all imaging studies, except for breast imaging, where it was waived. Before displaying the images, 4-fold bilinear interpolation was applied.

Free-breathing 3D abdominal imaging

A free-breathing volumetric abdominal scan was performed on one healthy volunteer (female, age = 31) and on one patient with a liver carcinoma and gallstones (female, age = 80) using a 3 T scanner (Magnetom Prisma, Siemens Healthcare, Erlangen, Germany) equipped with a 24-channel spine coil array in combination with an 18-channel body coil array. The RAVE sequence was used to acquire 72 slices in axial orientation with slice resolution of 72%. For each slice, three echoes were sampled with bipolar readout. 600 radial projections per echo were collected with the following acquisition parameters: field-of-view (FOV) = 350×350×216 mm³, flip angle = 9°, TR = 6.31 ms, TE1/TE2/TE3 = 1.41/3.01/4.61 ms, readout bandwidth = 780 Hz/px. Using a matrix size of 256×256 pixels, the resulting resolution was 1.37×1.37×3.0 mm³. Total scan time was 3:18 min.

Sequential spokes within each TR were rotated by 2°. To demonstrate the effect of the rotation, the volunteer scan was repeated without this modification.

For improved depiction of the off-resonant fat blurring, the volunteer acquisition was also performed with reduced bandwidth of 280 Hz/px. Due to the longer readout, the TR had to be increased to 13.3 ms with echo times of TE1/TE2/TE3 = 2.54/6.45/10.40 ms, yielding a scan time of 6:57 min.

For the patient scan, also a conventional Cartesian breath-hold Dixon acquisition was performed. Imaging parameters were matched to the RAVE sequence, but the scan time was reduced to one breath-hold period of 18 s by changing the following parameters: Parallel imaging acceleration factor = 3, TR = 4.58 ms, TE1/TE2 = 1.23/2.46 ms, phase resolution = 75%, slice partial Fourier = 7/8, readout bandwidth for TE1 = 980 Hz/px, readout bandwidth for TE2 = 590 Hz/px.

All RAVE datasets were processed with the Dixon-RAVE technique by solving Equation 1. To show the undersampling capabilities, only the first 256 radial projections were used for reconstruction, corresponding to an undersampling factor of (256∙π/2)/256 ≈ 1.57. This resulted in a total effective acquisition time of 1:25 min. Due to the moderate undersampling factor, no additional regularization was used (λ_W = λ_F = 0). Reconstructions were carried out twice. First, the exact readout time points t = t_n + T_n,k were used for the operator D(t) (Equation 3). Then, T_n,k was set to zero, using only the specified echo times TE1/TE2/TE3.

To demonstrate the XD-Dixon-RAVE approach, a respiratory-motion curve was extracted from the data. Using this information, the entire dataset (600 projections) was sorted into six different motion states, resulting in 100 radial projections per state (undersampling factor of (256∙π/2)/100 ≈ 4.0). Image reconstruction was performed by running the optimization procedure (Equation 4) with λ = λ_W = λ_F = λ_Φ. An empirically chosen value of λ = 0.2 provided a good tradeoff between removing undersampling artifacts and maintaining motion information (see supporting Figure 2).

Pediatric free-breathing 3D abdominal imaging

A pediatric patient (male, age = 2) was scanned at a 1.5 T scanner (Magnetom Aera, Siemens Healthcare, Erlangen, Germany) using a 24-channel spine coil array in combination with an 18-channel body coil array. The acquisition was performed without sedation, which poses a significant challenge with conventional MRI techniques in pediatric subjects of this age. RAVE was used to acquire 72 axial slices with a slice resolution of 72% using the following parameters: FOV = 250×250×144 mm³, flip angle = 12°, TR = 6.60 ms, TE1/TE2/TE3 = 1.58/3.15/4.72 ms, readout bandwidth = 810 Hz/px, matrix size = 256×256, resolution = 0.98×0.98×2.0 mm³, acquired projections = 600, total scan time = 3:27 min.

The dataset was reconstructed with Dixon-RAVE using all acquired projections. Furthermore, motion was detected from the k-space data analogously to the XD-Dixon-RAVE approach, revealing that severe bulk motion occurred during the second half of the scan. To reduce motion artifacts, data from this time interval was discarded and the Dixon-RAVE image reconstruction was repeated using only the first 300 acquired projections with consistent motion state (undersampling factor of (256∙π/2)/300 ≈ 1.3). For both reconstructions, no additional regularization (λ_W = λ_F = 0) was applied.

DCE free-breathing 3D liver imaging

Free-breathing DCE-RAVE liver examination was performed in a volunteer (male, age = 47) at a 3 T scanner (Magnetom Prisma, Siemens Healthcare, Erlangen, Germany). For signal reception, a 24-channel spine coil array in combination with an 18-channel body coil array was used. Data acquisition was started 20 seconds prior to intravenous injection of a half dose (8.2 ml) of Magnavist (Bayer Healthcare, Germany), followed by a 20 ml saline flush. Injection rate was 2 mL/s. 80 partitions in axial orientation were acquired using the following parameters: FOV = 380×380×240 mm³, flip angle = 15°, TR = 6.31 ms, TE1/TE2/TE3 = 1.41/3.01/4.61 ms, readout bandwidth = 780 Hz/px, slice resolution = 50%, matrix size = 256×256, resolution = 1.48×1.48×3.0 mm³. 1200 projections per partition were sampled, resulting in a total scan time of 5:04 min.

For image reconstruction with DCE-Dixon-RAVE, 21 spokes per frame were combined to achieve a temporal resolution of 5.3 s/volume. This corresponds to an undersampling factor of (256∙π/2)/21 ≈ 19.1. The same regularization parameter of λ = 0.8 was chosen for the fat, water, and field maps. This value was selected empirically and gave a good balance between temporal fidelity and removal of undersampling artifacts.

To visualize the uptake of contrast agent in different areas, regions of interests (ROIs) with 15–25 pixels were drawn. Afterwards, the absolute signal values in all ROIs were averaged and the time curves of the resulting values were displayed.

3D breast imaging

While motion-robustness is less problematic for breast imaging, a major problem of conventional fat-saturated techniques consists in the frequently insufficient degree of fat suppression. To show the advantage of Dixon-RAVE, breast imaging was performed in a patient (female, age = 54, extensive cancer in the left breast) using a 3 T scanner (Magnetom Trio, Siemens Healthcare, Erlangen, Germany) equipped with a 16-channel bilateral breast array. 144 slices in axial orientation with a slice resolution of 50% were acquired with RAVE using the following parameters: FOV = 320×320×173 mm³, flip angle = 10°, TR = 6.54 ms, TE1/TE2/TE3 = 1.50/3.12/4.74 ms, readout bandwidth = 870 Hz/px, matrix size = 320×320, resolution = 1.0×1.0×1.2 mm³, acquired projections = 400 (undersampling factor of (320∙π/2)/400 ≈ 1.3), total scan time = 3:10 min. Dixon-RAVE without additional regularization (λ_W = λ_F = 0) was employed to reconstruct the dataset.

For comparison, a conventional clinical T₁-weighted gradient echo acquisition with fat-saturation was performed. Imaging parameters of the Cartesian acquisition were: FOV = 320×320×211.2 mm³, flip angle = 10°, TR/TE = 4.74/1.79 ms, readout bandwidth = 350 Hz/px, matrix size = 448×291, resolution = 0.71×0.71×1.10 mm³, total scan time = 2:07 min. Additionally, a conventional Cartesian Dixon acquisition was performed. Except for the following changes, imaging parameters were matched to the RAVE sequence: TR = 5.83 ms, TE1/TE2 = 2.45/3.68 ms, slice resolution = 61%, asymmetric echo = strong, monopolar readout gradients with bandwidth = 490 Hz/px, total scan time = 2:45 min.

DCE 3D breast imaging

Similarly to conventional fat-suppressed morphologic breast imaging, DCE-MRI of the breast using techniques such as GRASP (22) relies on the quality of spectral fat saturation. In practice, the degree of fat suppression is often limited, resulting in reduced image quality. Therefore, the improvement achievable with Dixon-RAVE was demonstrated for this application.

DCE-Dixon-RAVE breast imaging was performed in one patient (female, age = 31) using a 3 T scanner (Magnetom Trio, Siemens Healthcare, Erlangen, Germany) equipped with a 16-channel bilateral breast array. Imaging parameters were identical to the conventional 3D breast scan (see above), except for the flip angle of 13°, which was chosen to increase T₁-weighting. 400 projections were acquired in each partition. Total scan time was 3:10 min. Data acquisition started 2 minutes before intravenous injection of gadobutrol (Gadavist; Bayer Healthcare LLC, Whippany, NJ) using a standard dose of 0.1 mM/kg of body weight and followed by a 20 mL saline flush, both injected at a rate of 2 mL/s. To capture the early post-contrast phase, the scan continued for another 1:10 min.

Temporal resolution of 6.1 s/volume was achieved for DCE-Dixon-RAVE by combining 13 spokes per frame, which corresponds to an undersampling factor of (320∙π/2)/13 ≈ 38.7. The regularization parameter was set to λ = 0.8. ROIs consisting of 9–36 pixels were drawn in the heart, breast carcinoma, and glandular tissue.

RESULTS

Free-breathing 3D abdominal imaging

The fat blurring caused by the radial trajectory is shown in Figure 3. For low receiver bandwidth and field strength of 3T (first row), severe blurring occurs. A higher bandwidth such as 780 Hz/px (second row) leads to reduced, but still visible blurring (arrows). When the exact readout time points are used in the operator D(t) (right-hand side), the blurring is removed.

Fig. 3.

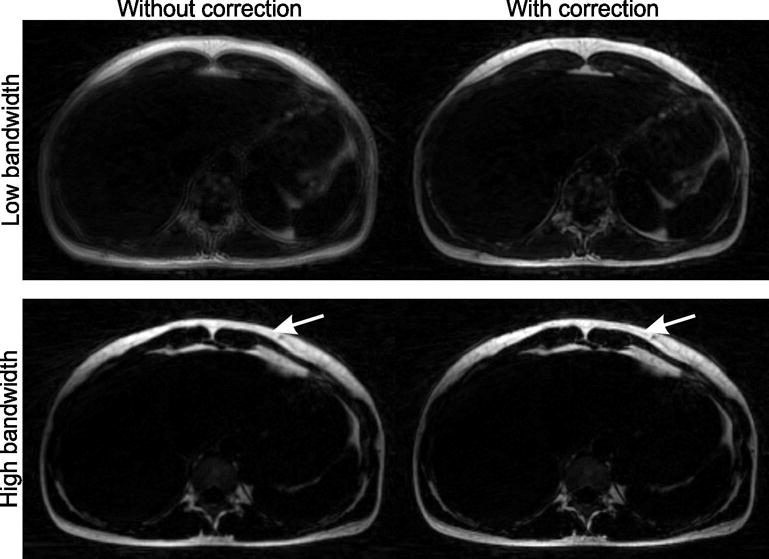
Due to the off-resonant blurring of fat, image quality can be severely degraded with radial acquisition. This is particularly problematic for low receiver bandwidths (e.g. 280 Hz/px, first row, left hand-side). Although the effect is less evident for higher bandwidths (e.g. 780 Hz/px, second row), slight blurring is still visible when no correction is applied (arrow). By properly modeling this effect in the reconstructions, sharp fat images can be obtained (right-hand side).

Figure 4 shows the effect of using a slightly different sampling pattern for each echo within one TR. Here, Dixon-RAVE reconstruction was performed on datasets consisting of 256 projections per partition. If the same sampling pattern is used for each echo (left-hand side, blip angle 0°), streaking artifacts are visible. These artifacts are reduced when the orientation for subsequent echoes is rotated by 2° (right-hand side). Corresponding results for a wider range of blip angles (0/0.1/1/2/5°) are shown in supporting Figure 1.

Fig. 4.

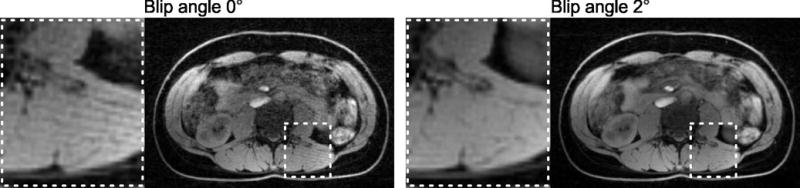
When all echoes within one TR are acquired with the same projection angle, streaking artifacts can be seen in the resulting image (blip angle 0°, left-hand side). Rotation of subsequent projections (blip angle 2°, right-hand side) reduces these artifacts.

XD-Dixon-RAVE reconstructions of the volunteer measurement are shown in Figure 5. Due to the radial sampling pattern, a respiratory signal can be extracted from k-space data (Figure 5a). Neglecting this information and using all projections independently from their motion state results in slight blurring (Dixon-RAVE, Figure 5b). Fat and water maps, which were generated with XD-Dixon-RAVE, are shown in Figure 5c. As it can be seen, breathing motion is resolved and the level of blurring is reduced in comparison to the motion-averaged images. The Dixon-RAVE reconstruction of the entire imaging volume is provided as supporting information (Dixon-RAVE_SuppInfo1).

Fig. 5.

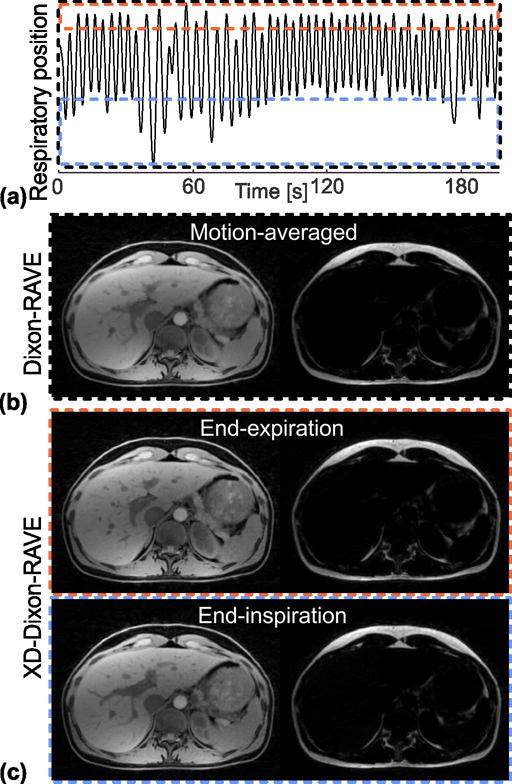
(a) RAVE data can be sorted into different respiratory states based on the extracted respiratory curve, ranging from end-expiration to end-inspiration (dashed boxes).

(b) The conventional Dixon-RAVE reconstruction uses all projections regardless of their motion state, which results in motion-averaged fat and water maps, where fine structures are slightly blurred. (c) By reconstructing the sorted data with XD-Dixon-RAVE, respiratory motion is resolved and the blurring is reduced.

Figure 6 shows results from the free-breathing patient scan, reconstructed with both Dixon-RAVE and XD-Dixon-RAVE. For comparison, images obtained with conventional Cartesian breath-hold Dixon are also shown. Although the RAVE scan and the Cartesian Dixon scan were acquired back-to-back, slices are not perfectly aligned. Compared to the volunteer scan (Figure 5), breathing motion was more severe. This can be seen in the gallstones in partition 1 (top row, dashed box), which appear blurred for Dixon-RAVE (left-hand side). This blurring is resolved with XD-Dixon-RAVE (middle column) and the gallstones can be separated from each other. The general image sharpness is comparable to the breath-hold Dixon acquisition (right-hand side). The bottom row shows a neuroendocrine carcinoma metastasis in the liver (solid arrow). In the Cartesian breath-hold Dixon scan, ghosting artifacts appear along the phase-encoding direction due to residual motion (dashed arrows). With the proposed methods, which employ radial sampling, these artifacts translate into slight streaking.

Fig. 6.

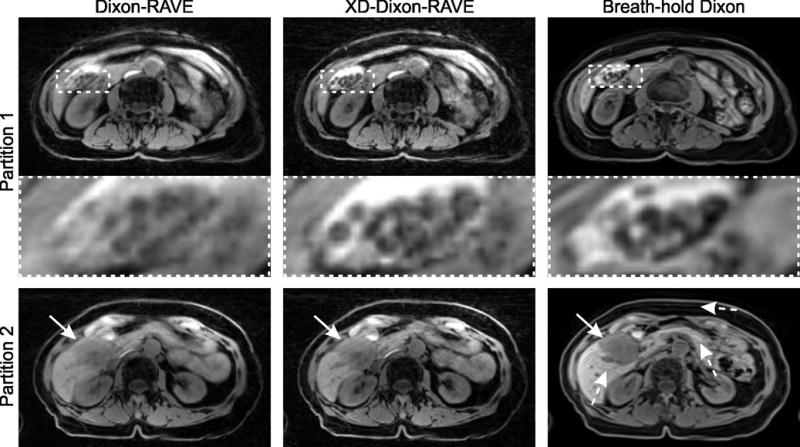
(a) Free-breathing abdominal scan of an 80-year-old patient with gallstones and liver carcinoma. Results are shown for Dixon-RAVE (left-hand side), respiratory-resolved XD-Dixon-RAVE (center column, inspiration phase), and conventional Cartesian breath-hold Dixon (right-hand side).

Due to breathing motion, gallstones are slightly blurred with Dixon-RAVE. This is resolved with both XD-Dixon-RAVE and breath-hold acquisition. In partition 2, the liver carcinoma (solid arrows) is clearly depicted. Due to residual motion in the breath-hold exam, ghosting artifacts occur in the Cartesian Dixon scan (dashed arrow), which is not the case for the radial acquisitions.

Pediatric free-breathing 3D abdominal imaging

Figure 7 shows two slices of the pediatric exam without sedation. Consistent fat/water separation was achieved despite severe bulk patient motion. When using all projections for the Dixon-RAVE reconstruction, the overall image quality is poor. However, the extracted motion curve indicates bulk motion in the second half of the scan. When these projections are discarded and only data from the first half of the scan is used for image reconstruction, diagnostic image quality is achieved and a hypo-intense lesion between the left psoas muscle and the vertebral body (partition 2, arrow) is clearly delineated.

Fig. 7.

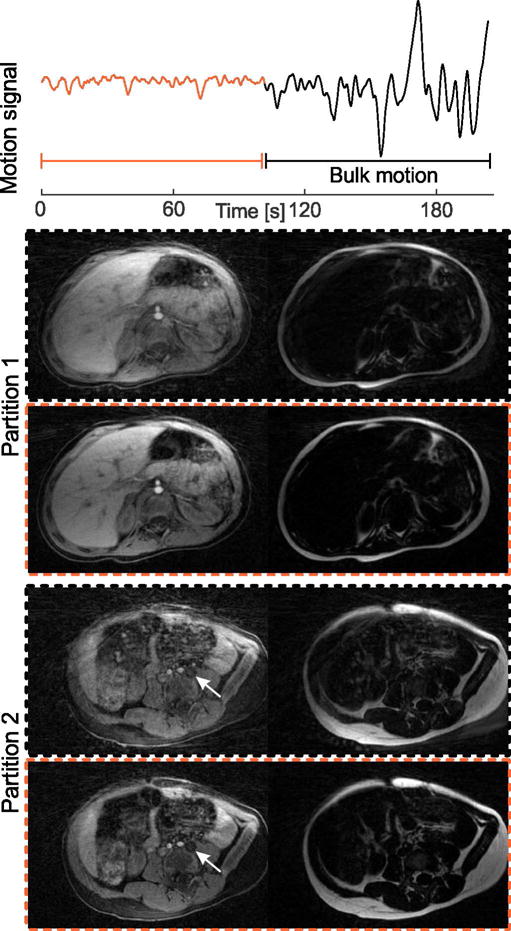
(a) Dixon-RAVE scan of a 2-year-old pediatric patient. The extracted motion curve indicates that severe bulk motion occurred during the second half of the scan. Therefore, if all data are used for the reconstruction (black dashed box), image quality is degraded. When discarding the second half of the scan and only using the first 300 out of 600 acquired projections (orange dashed box), diagnostic image quality is obtained, fine details are visible, and a hypo-intense lesion (arrow) is clearly delineated.

DCE free-breathing 3D liver imaging

Results from the volunteer DCE abdominal scan are shown in Figure 8. The three perfusion phases clearly reveal the contrast uptake in both the aorta and the portal vein. An abnormal pattern can be seen in the kidney cyst (arrow), which does not enhance after injecting contrast agent. The dynamic contrast uptake is visualized as supporting information (DCE-Dixon-RAVE_SuppInfo2).

Fig. 8.

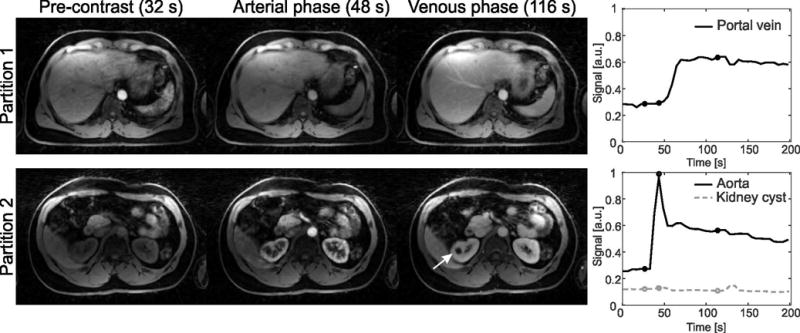
DCE abdominal scan of a volunteer, reconstructed with DCE-Dixon-RAVE. Temporal resolution was 5.3 s/volume. The different perfusion phases, marked with circles in the time-intensity curves, are clearly depicted. No uptake of contrast agent occurs in a kidney cyst (arrow), while both aorta and portal vein show the expected enhancement behavior.

3D breast imaging

Figure 9 shows an exemplary slice of the patient breast exam. While the degree of fat-suppression in the conventional fat-suppressed GRE image varies over the FOV (dashed arrow), both Dixon methods achieve robust fat/water separation over the entire volume. All methods clearly depict an extensive carcinoma in the left breast (arrow).

Fig. 9.

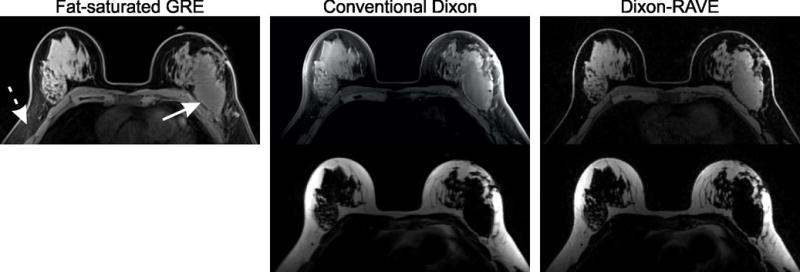
Breast scan of a patient using Cartesian fat-saturated gradient echo, conventional Cartesian Dixon, and Dixon-RAVE. While residual fat is visible in the conventional fat-suppressed image (dashed arrow), both Dixon methods achieve uniform suppression of fat. The solid arrow points to an extensive carcinoma in the left breast, which is clearly depicted on all images.

DCE 3D breast imaging

An exemplary slice of the patient DCE breast measurement, which was reconstructed with DCE-Dixon-RAVE, is shown in Figure 10. No suspicious regions can be seen on the pre-contrast image (left-hand side), but the uptake of contrast agent clearly reveals extensive cancer in the right breast. Additionally, signal enhancement in the heart and in normal glandular tissue (dotted arrow) can be seen. These findings are confirmed by the corresponding time-intensity curves.

Fig. 10.

DCE water images and extracted time-intensity curves of a patient with breast cancer, generated with DCE-Dixon-RAVE. The depicted frames are marked with circles in the time curve. Spatial resolution is 1.0 × 1.0 × 1.2 mm³, temporal resolution is 6.1 s/volume. Contrast uptake of an extensive breast carcinoma (solid arrow) and of glandular tissue (dashed arrow) can be clearly seen.

DISCUSSION

Fat/water separation is of high value for several clinical applications. Usually, Cartesian phase encoding is used, which makes the data acquisition sensitive to motion. Dixon-RAVE has been proposed to overcome this limitation and to allow motion-robust free-breathing fat/water imaging. Due to the model-based reconstruction approach, compressed sensing, parallel imaging, and removal of the off-resonant blurring of fat can be incorporated. Two extensions were presented, which allow motion-resolved free-breathing measurements (XD-Dixon-RAVE) and dynamic contrast-enhanced fat/water separation (DCE-Dixon-RAVE).

An advantage of directly fitting the parameters of interest to the acquired k-space data is that undersampling artifacts are inherently reduced (31). Therefore, additional regularization by total variation does not necessarily have to be included. This was confirmed in the presented Dixon-RAVE experiments where reasonable quality could be achieved without visible image degradation such as staircasing-artifacts, which typically appear for TV-based regularization. However, if higher undersampling factors are used, use of TV regularization might become necessary to suppress streaking artifacts. This holds true for the shown XD-Dixon-RAVE and DCE-Dixon-RAVE experiments where temporal TV was applied to obtain adequate image quality. Previous work additionally included field-map-smoothness constraints in the cost function (4,7). However, no visual difference could be seen for the data acquired in this work.

Additional reduction in scan time can be achieved by using an elliptical instead of circular field of view (32,33). This especially applies to applications with anisotropic object dimensions such as in breast imaging or abdominal imaging, where scan time reductions of approximately 33% with no increase of streaking artifacts have been reported (33). As for all fat/water separation methods, the accuracy of the field map is crucial to avoid swapping of the fat/water signal. Here, a multi-seed safest-first region growing algorithm (27) was applied, which produced no fat/water swapping in the majority of the performed measurements. If necessary in practice, a more complex approach such as whole-image optimization using graph-cuts (34,35) can be employed to further improve the stability of the field map used for initialization of the optimizer.

While dynamic fat and water maps are reconstructed with XD/DCE-Dixon-RAVE, a static field map is used for initialization, which is calculated from all acquired projections. Although this represents a simplification, the dynamic frames showed consistent fat/water separation. A possible refinement is to calculate separate low-resolution field maps for each reconstructed temporal frame, which can be done because the k-space center area is inherently oversampled by the radial trajectory. Another simplification of the current approach is that the signal model only accounts for phase accumulation during readout caused by the fat components but not for B₀-related phase drifts. Taking into account the non-instantaneous readout time and including the field map in the calculation can further improve image quality (36). However, due to the additional increase in reconstruction time this measure omitted.

The 3D stack-of-stars trajectory can be implemented in different ways. One possibility is to acquire all projections for one partition before repeating this procedure for the next partition. In this case, the motion-sensitive Cartesian sampling direction is updated only every N_proj repetition times. As a consequence, motion that occurs during this time interval (N_proj∙TR) affects data consistency, which impairs the overall motion robustness. An alternative scheme, which was used throughout this work, is to acquire all partitions for one projection angle before continuing with the next projection angle. This ensures that the Cartesian sampling direction is updated every repetition time, leading to high data consistency and reduced motion artifacts (9).

Estimation of breathing motion for the XD-Dixon-RAVE reconstructions was performed with an already existing technique (18,21) using the first echo to extract the motion signal. Due to use of the stack-of-stars sampling scheme, the same motion state is applied for sorting all subsequently acquired partitions at each angle. Because breathing can also occur within the partitions, this approach may not always deliver optimal accuracy. An improvement may be achieved by acquiring DC navigator signals within each TR (37), which would allow sorting the acquired partition data independently. However, this approach comes with two disadvantages. First, the partition-encoding gradients have to be rewound at the beginning of each TR, which results in increased TR and, consequently, overall increased scan time. Second, the reconstruction of different slices cannot be decoupled using an iFFT along the k_z-direction. Therefore, the entire 3D dataset has to be processed in entirety, which makes distributed reconstruction of slices on independent processor cores difficult. One way to overcome this is to perform the time-intensive mapping between k-space and image-space on a GPU (38).

As demonstrated for the pediatric scan, bulk patient motion can severely impact the image quality despite the generally high motion insensitivity of radial sampling. However, bulk motion can be detected from the k-space data and motion-corrupted projections can then be excluded from reconstruction. For the case shown, this allowed to recover images with diagnostic value. An analogous approach was recently also described for retrospective removal of bulk motion in lung imaging (39). In our initial implementation, the time interval where bulk motion occurred was manually selected. An automatic detection algorithm and a more thorough evaluation of the correlation between the amount of discarded data and the resulting image quality are subject of ongoing work.

One limitation of the presented Dixon-RAVE framework is the extensive computing time, which makes offline processing mandatory. For integration into the clinical workflow and to enable clinical evaluation, acquired data are automatically transferred to a dedicated reconstruction server using the Yarra software framework (https://yarra.rocks). Reconstruction times can still be quite long, which may be addressed by use of C++ implementations or GPU computing. Nevertheless, in our experience, reconstruction time is not too critical as long as the image calculation process is fully automated and does not create additional work load for the technicians. To provide feedback to the technicians regarding the success of the exam before the patient is removed from the MRI scanner, a rapid gridding reconstruction of one echo time image without fat/water separation can be performed on the MRI system (40).

Currently, a fixed number of iterations are used to solve the optimization problem for all different Dixon-RAVE implementations. However, fewer iterations may be sufficient for Dixon-RAVE reconstructions with only moderate undersampling. Thus, optimizing the number of iterations for different undersampling factors and different Dixon-RAVE variants might allow reducing the reconstruction time.

In this work, the regularization parameter λ for both XD-Dixon-RAVE and DCE-Dixon-RAVE was empirically chosen to achieve a good tradeoff between removal of streaking artifacts and temporal fidelity. However, for a clinical implementation, a more sophisticated way for determining λ might be required. One possibility would be to perform reconstructions with a set of different regularization parameters. Subsequently, radiologists would choose the most appropriate value for λ, which could then be used for exams with the same acquisition protocol (18,22). Examples for reconstructions with different regularization parameters λ are shown in supporting Figure 2 for XD-Dixon-RAVE and in supporting Figure 3 for DCE-Dixon-RAVE, respectively. Automatic estimation of optimal values for λ could be achieved using an image-quality metric (41) or using information directly derived from the k-space data (42,43). Another simplification in the current implementation is that the same regularization parameter was applied for the water, fat, and field maps. Although this provided good overall image quality for all shown cases, this constraint can be removed if necessary. In a DCE-Dixon-RAVE reconstruction, for example, contrast uptake is only seen in the water image while the fat and field maps are almost invariant. Thus, the temporal finite differences for the fat and field map are lower, justifying higher values λ_F and λ_Φ compared with λ_W.

A possible extension of the Dixon-RAVE framework is to combine the two demonstrated concepts of XD-Dixon-RAVE and DCE-Dixon-RAVE. This allows obtaining respiratory-resolved fat-water-separated DCE images, which has potential to further improve the image quality of free-breathing fat-water-separated DCE scans. As a disadvantage, the combination leads to additionally increased reconstruction times, which might make it necessary to use GPUs.

So far, Dixon-RAVE was only used for traditional fat/water separation. However, quantitative chemical shift imaging including both T₂* and accurate fat-fraction estimation is of high clinical interest (44). For this purpose, usually six or more echoes have to be acquired (2). This might be problematic for breath-hold abdominal exams, where either resolution or anatomic coverage have to be reduced to limit acquisition time. Therefore, free-breathing (XD/DCE-) Dixon-RAVE would also improve quantitative imaging. The use of Cartesian model-based approaches for quantitative fat/water imaging has already been demonstrated (7,45), and the combination with (XD/DCE-) Dixon-RAVE should be possible in a straightforward manner, which will be subject of future work.

CONCLUSION

Dixon-RAVE allows generating motion-robust free-breathing fat and water images. This is achieved by combining the concepts of model-based fat/water separation, radial sampling, compressed sensing, and parallel imaging. Residual motion-induced blurring can be reduced by using XD-Dixon-RAVE, which incorporates extra motion dimensions in the optimization. Furthermore, fat-water-separated DCE imaging with high temporal and spatial resolution is possible with DCE-Dixon-RAVE. The Dixon-RAVE framework promises high value for clinical imaging applications that require fat/water separation, in particular applications that previously have been restricted by limited breath-holding capabilities of patients.