New Insights About Time-Varying Diffusivity and Its Estimation from Diffusion MRI

Abstract

Purpose

Characterizing the relation between the applied gradient sequences and the measured diffusion MRI signal is important for estimating the time-dependent diffusivity, which provides important information about the microscopic tissue structure.

Theory and Methods

In this article, we extend the classical theory of Stepišnik for measuring time-dependent diffusivity under the Gaussian phase approximation. In particular, we derive three novel expressions which represent the diffusion MRI signal in terms of the mean-squared displacement, the instantaneous diffusivity, and the velocity autocorrelation function. We present the explicit signal expressions for the case of single diffusion encoding and oscillating gradient spin-echo sequences. Additionally, we also propose three different models to represent time-varying diffusivity and test them using Monte-Carlo simulations and in vivo human brain data.

Results

The time-varying diffusivities are able to distinguish the synthetic structures in the Monte-Carlo simulations. There is also strong statistical evidence about time-varying diffusivity from the in vivo human data set.

Conclusion

The proposed theory provides new insights into our understanding of the time-varying diffusivity using different gradient sequences. The proposed models for representing time-varying diffusivity can be utilized to study time-varying diffusivity using in vivo human brain diffusion MRI data.

INTRODUCTION

Diffusion magnetic resonance imaging (dMRI) is a noninvasive technique for probing the microscopic structure of complex media by measuring the diffusive motion of molecules within the structure. In medical science, it provides useful measures to characterize the structure of biological tissue using in vivo measurements. Consequently, it has been widely used to study brain abnormalities in various mental disorders (1–3).

Q-space imaging is a commonly used approach for understanding the diffusive motion of water molecules (4). It involves utilizing multiple single diffusion encoding (SDE) sequences that have a fixed diffusion time and pulse width. Then, the ensemble average propagator, which is the distribution of the displacement of the water molecules (or the displacement of the center of mass of their trajectories (5) for finite-pulse width), can be computed using the inverse Fourier transform of the dMRI measurements acquired using different gradient strengths (6–8). From the ensemble average propagator, several diffusion measures, such as the pore-volume and kurtosis (8,9), can be estimated to characterize the tissue structure. Some recent work has been done on estimating more specific tissue information, such as axon diameter, using the q-space imaging technique (10–13). Due to the limited gradient strength of the clinical scanner, the contribution of the intra-axonal water signal with diameter 3 μm or smaller, is extremely small compared to the overall dMRI signal, which makes it difficult to accurately estimate the axon diameter (14). Note that, an overwhelming majority of axons in the human brain are less than 3 μm in diameter (15). Further, these axons undulate in a sinusoid fashion leading to further complications in the estimation of quantities such as axon diameter (16).

An alternative approach for characterizing tissue microstructure is to measure the time-dependent diffusivity of water molecules. This structural disorder can be quantified by measuring the time-varying diffusivity, which in turn is related to the axonal packing structure of the tissue. The inhomogeneities and hinderances from tissue structures persistently alters the diffusive motion of molecules. As a result, the mean-squared displacement of molecules is not a linear function of diffusion time (as in free diffusion), leading to a nonlinear time-dependence of the apparent diffusivity. A few works have explored the relation between the microscopic axonal arrangement of brain tissue and the time-dependent diffusivity (17,18). Moreover, the time-dependent diffusivity can also be measured using any type of gradient sequences, such as oscillating gradients (19,20). Most of these latter works rely on the theoretical formulation first proposed by Stepišnik (21), which elucidates the relation between the time-dependent diffusivity and dMRI measurements. This relation was expressed in the frequency domain using the inner product between the spectrum of the velocity process and the spectrum of the cumulative gradient sequence. In this article, we extend this theory and derive three new formulations from the time-domain dynamics of the diffusion process and express the signal in terms of the time-varying mean-squared displacement (or position autocorrelation function), or the instantaneous diffusivity and show its connection to the velocity autocorrelation function. These formulations provide additional insight into our understanding of the relation between the pulse sequences and dMRI measurements, which has not been explored to-date. The derivations presented in this work can be quite useful for designing optimal gradient sequences to capture important aspects of the diffusion process.

THEORY

Gaussian Phase of the Diffusing Spins

Let g(t) denote a diffusion encoding gradient sequence along a given direction scaled by the gyromagnetic ratio. Let x_k(τ) denote the displacement of a diffusing spin k, at time τ along a particular direction. Then, the phase change of the spin in the presence of a gradient g(t) is given by: ${\varphi }_k(\tau )={\int }_0^{\tau }g(t)x_k(t)\mathit{dt}$. The diffusion MRI signal contributed by this spin is then given by exp (−iϕ_k(τ)). The ensemble diffusion MRI signal is then given by: s(g, τ) = ⟨exp (−iϕ_k(τ))⟩ where ⟨·⟩ denotes the ensemble average over all diffusing spins. If ϕ_k(τ)’s are independent samples from a zero-mean Gaussian distribution with covariance denoted by ⟨ϕ²(τ)⟩, then the signal can be approximated by:

$$s\left(g,\tau \right)=\exp \left(-\frac{1}{2}\langle {\varphi }^2(\tau )\rangle \right),$$

with,

$$\begin{array}{cc}\hfill \langle {\varphi }^2(\tau )\rangle & ={\int }_0^{\tau }{\int }_0^{\tau }g(t)\langle x(t)x(s)\rangle g(s)\mathit{dsdt}\hfill \\ \hfill =& {\int }_0^{\tau }{\int }_0^{\tau }g(t)R(t,s)g(s)\mathit{dsdt}\hfill \end{array}$$ [1]

where R(t, s) := ⟨x(t)x(s)⟩ denotes the position autocorrelation function of the diffusion process, see for example (21).

An alternative expression for ⟨ϕ²(τ)⟩ was also introduced by Stepišnik (21) in terms of the velocity autocorrelation function. Let $\mathcal{D}(t,s)≔\langle v(t)v(s)\rangle$ denote the velocity autocorrelation function of the diffusion process, where v(t) is the velocity of the diffusing spin at time t. The stationarity of the diffusion process implies: $\mathcal{D}(t,s)=\mathcal{D}(\mid t-s\mid )$, that is, it only depends on the time difference ∣t – s⟩. Using the following definition for a variable q:

$$q(t)≔{\int }_0^{t}g(s)\mathit{ds},$$ [2]

the mean-squared phase can be written as:

$$\langle {\varphi }^2(\tau )\rangle ={\int }_0^{\tau }{\int }_0^{\tau }q(t)\mathcal{D}(\mid t-s\mid )q(s)\mathit{dsdt}.$$ [3]

Let $\tilde{\mathcal{D}}(\omega )$ denote the spectrum of the velocity process, that is, $\tilde{\mathcal{D}}(\omega )$ is the Fourier transform of $\mathcal{D}(t)$. Let $\tilde{q}(\omega )$ denote the Fourier transform of q(t). Then, we can rewrite Eq. [3] as:

$$\langle {\varphi }^2(\tau )\rangle =\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\tilde{q}(\omega )\tilde{\mathcal{D}}(\omega )\tilde{q}(-\omega )d\omega .$$ [4]

The single integral in Eq. [4] makes it more convenient than the expressions in Eqs. [1] and [3] to estimate the time-varying diffusivity. Hence, it has been used to estimate short-time diffusivity using OGSE pulses (19,20,22) as well as long-time diffusivity using SDE sequences (14,23).

If the velocity spectrum $\tilde{\mathcal{D}}(\omega )$ is estimated from Eq. [4], then the velocity autocorrelation $\mathcal{D}(t)$ can be computed using inverse Fourier transform. The meansquared displacement R(τ) := ⟨x²(τ)⟩ can be computed using:

$$R(\tau )=2{\int }_0^{\tau }(\tau -t)\mathcal{D}(t)\mathit{dt},$$ [5]

and the apparent diffusion coefficient can be computed using (18):

$$D(t)=\frac{R(t)}{2t},$$ [6]

and finally, the instantaneous diffusivity is given by:

$$D_{\text{inst}}(t)=\frac{\partial R(t)}{2\partial (t)},$$ [7]

which is the half of the partial derivative of R(t).

Most works have used Eq. [4] as their main theoretical guideline for measuring the time-varying diffusivity using different types of gradient sequences (14,19,22,23). Further, proper knowledge of the time-varying diffusivity can provide specific information about the packing structure of the underlying tissue, as described in detail in (23). However, as seen in Eqs. [5–7], the velocity spectrum $\tilde{\mathcal{D}}(\omega )$ is indirectly related to the time-varying diffusivity via a sequence of transforms. In the subsequent sections, we derive novel formulations that represent the dMRI signal directly in terms of the mean-squared displacement and the instantaneous diffusivity. Thus, additional transforms become un-necessary to estimate the time-varying diffusivity. Additionally, these mathematical relations provide an alternative viewpoint for understanding the role that the applied gradients play in capturing the diffusion process. Existing work in (17) shows that the time-varying diffusivity at short time scale is quite relevant to understanding tissue structure. In the present work, we directly work in the timedomain, which allows to easily understand the diffusion process at short and long-time scales.

Mean-Squared Displacement

From the stationary condition of the velocity process, the mean-squared displacement only depends on the experimental diffusion time but not on the starting time (or position) of the spins. Thus, we can write:

$$\langle {(x(s)-x(t))}^2\rangle =\langle x{(\mid s-t\mid )}^2\rangle =R(\mid s-t\mid ).$$

By expanding the above equation in terms of R(s, t) and R(t), we have

$$R(s,t)=\frac{1}{2}[R(s)+R(t)-R(\mid s-t\mid )].$$ [8]

If g(t) satisfies the spin echo condition, that is, ${\int }_0^{\tau }g(t)\mathit{dt}=0$, then the following identities hold:

$${\int }_0^{\tau }g(t)R(s)g(s)\mathit{dt}={\int }_0^{\tau }g(t)R(t)g(s)\mathit{ds}=0.$$

Thus, we can re-write Eq. [1] as follows:

$$\langle {\varphi }^2(\tau )\rangle =-\frac{1}{2}{\int }_0^{\tau }\mathit{ds}{\int }_0^{\tau }\mathit{dt}[g(t)R(\mid s-t\mid )g(s)].$$ [9]

After several algebraic manipulations, we arrive at one of the fundamental contributions of this work, directly involving the mean-squared displacement or the position autocorrelation function, that is, Eq. [9] is equivalent to (see Appendix for a detailed derivation):

$$\langle {\varphi }^2(\tau )\rangle =-{\int }_0^{\tau }R(t)c(t)\mathit{dt},$$ [10]

where

$$c(t)≔{\int }_0^{\tau }g(s)g(t+s)\mathit{ds},$$ [11]

is the autocorrelation function of the gradient sequence g(t) for 0 ≤ t ≤ τ and it is assumed that g(t) is equal to zero for t ≥ τ. We point out several interesting properties of Eq. [11]. First, the function c(t) is invariant to any change in the sign of g(t), that is, it has the same value for g(t) and −g(t). Second, the function c(t) is also invariant to the direction of time, that is, replacing g(t) by $\widehat{g}(t)=g(\tau -t)$ will not change c(t). Moreover, the integral ${\int }_0^{\tau }c(t)\mathit{dt}=0$. The derivation for Eqs. [10 and 11] is provided in the Appendix.

To summarize, the dMRI signal acquired using any gradient sequence g(t), 0 ≤ t ≤ τ that satisfies the spinecho condition can be expressed as:

$$s(g,\tau )=\exp \left(\frac{1}{2}{\int }_0^{\tau }R(t)c(t)\mathit{dt}\right),$$ [12]

where R(t) is the mean-squared displacement function and c(t) is the autocorrelation function of the gradient sequence defined in Eq. [11]. We note that, this expression provides a new way to understand the dMRI signal, which has not been explored before in the literature. Thus, c(t) is a weighting function (or sampling function) of R(t). In particular, this expression can be used to design appropriate gradient sequences, such that either short or long-time portion of R(t) is weighed in a desired manner.

Connection to Instantaneous Diffusivity

As the mean-squared displacement and the instantaneous diffusivity are related as described earlier, we use Eq. [10] to derive a direct relation between these quantities and the dMRI signal. Let C(t) denote the cumulative gradient autocorrelation function:

$$C(t)≔{\int }_0^{t}c(s)\mathit{ds},$$ [13]

for 0 ≤ t ≤ τ. Using integration by parts, we rewrite Eq. [10] as follows:

$$\langle {\varphi }^2(\tau )\rangle =-{\int }_0^{\tau }R(t)\mathit{dC}(t),$$ [14]

$$=-R(t)C(t){\mid }_{t=0}^{\tau }+{\int }_0^{\tau }C(t)\mathit{dR}(t),$$ [15]

$$=2{\int }_0^{\tau }{D}_{\text{inst}}(t)C(t)\mathit{dt}.$$ [16]

Thus, the ensemble mean-squared phase is given by:

$$\langle {\varphi }^2(\tau )\rangle =2{\int }_0^{\tau }{D}_{\text{inst}}(t)C(t)\mathit{dt}.$$ [17]

This gives an alternative way to express the dMRI signal acquired using any gradient sequence g(t), 0 ≤ t ≤ τ, and written in terms of the instantaneous diffusivity:

$$s(g,\tau )=\exp \left(-{\int }_0^{\tau }{D}_{\text{inst}}(t)C(t)\mathit{dt}\right),$$ [18]

where D_inst(t) is the instantaneous diffusivity and C(t) is the cumulative autocorrelation function defined in Eq. [13]. Again, the design choices of the gradient sequence directly influences the weighting of the time-varying instantaneous diffusivity.

Velocity Autocorrelation Function

In this section, we introduce the time-domain version of Eq. [4] to express the dMRI signal in terms of the velocity autocorrelation function. First, we note that using Parseval’s Theorem, Eq. [4] can be equivalently written as:

$$\langle {\varphi }^2(\tau )\rangle =\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\tilde{\mathcal{D}}(\omega ){\mid \tilde{q}(\omega )\mid }^{2}d\omega ={\int }_{-\infty }^{\infty }\mathcal{D}(t)b(t)\mathit{dt},$$ [19]

where b(t) is given by:

$$b(t)={\int }_0^{\tau }q(s)q(t+s)\mathit{ds},$$ [20]

which is the autocorrelation function of the spectrum ${\mid \tilde{q}(\omega )\mid }^2$ of the q-space-trajectory, and q(t) = 0 for t ≥ τ due to the spin-echo condition. As b(t) = 0 for ∣t∣ > τ, the second integral in Eq. [19] is equal to ${\int }_{-\tau }^{\tau }\mathcal{D}(t)b(t)\mathit{dt}$. Thus, the velocity spectrum contributed by $\mathcal{D}(t)$ with ∣t∣ ≥ τ does not contribute to the first integral of Eq. [19] though the integral has two infinite bounds. Every model for $\mathcal{D}(\omega )$ used in computing the diffusion signal leads to an assumption about $\mathcal{D}(t)$ being unmeasurable at ∣t∣ ≥ τ.

We note that an alternative approach for estimating the velocity autocorrelation function is to use R(t) given by Eq. [5]. Taking the first order derivative on both sides of Eq. [5], we have

$$\frac{\partial R(\tau )}{\partial \tau }=2{\int }_0^{\tau }\mathcal{D}(t)\mathit{dt}.$$

Taking the second derivative, we obtain the velocity autocorrelation $\mathcal{D}(t)$ given by:

$$\mathcal{D}(t)=\frac{{\partial }^{2}R(t)}{2\partial t^2}.$$ [21]

At t = 0, R(t) usually leads to a singular $\mathcal{D}(t)$. For example, if R(t) = 2D₀t for a constant diffusivity D₀, the corresponding $\mathcal{D}(t)$ is given by $\mathcal{D}(t)=D_0\delta (t)$ where δ(·) denotes the Dirac delta function.

To summarize, the dMRI signal can also be expressed as:

$$s(g,\tau )=\exp \left({\int }_{-\tau }^{\tau }\mathcal{D}(t)b(t)\mathit{dt}\right)$$ [22]

where $\mathcal{D}(t)$ is the velocity autocorrelation function and b(t) is the autocorrelation function of the q-space-trajectory defined in Eq. [20].

Single Diffusion Encoding Sequence

In this subsection, we present the expressions for c(t), C(t), and b(t), respectively, for a SDE sequence with finite pulse width (see Fig. 1 for a quick figurative intuition). These expressions will provide insight into our understanding of the effects of pulse width and diffusion time in measuring time-varying diffusivity. A standard SDE sequence is given by:

$$g(t)=\{\begin{array}{cc}g\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ -g\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}$$

where g is the maximum gradient strength and τ = Δ + δ. If Δ ≥ 2δ, then c(t) and C(t) are given by:

$$\begin{array}{cc}\hfill c(t)=& \{\begin{array}{ccc}2g^2(\delta -t),\hfill & \hfill & \text{if}0\le t<\delta ,\hfill \\ 0,\hfill & \hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ g^2(\Delta -\delta -t),\hfill & \hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ g^2(t-\Delta -\delta ),\hfill & \hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \\ \hfill C(t)=& \{\begin{array}{cc}{g}^2(2\delta t-t^2)\hfill & \text{if}0\le t<\delta ,\hfill \\ g^2{\delta }^2\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ g^2{\delta }^2-\frac{1}{2}{g}^2{(t-\Delta +\delta )}^2\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ \frac{1}{2}{g}^2{(\Delta +\delta -t)}^2\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \end{array}$$ [23]

Conversely, if Δ ≤ 2δ, then c(t) and C(t) are given by:

$$\begin{array}{cc}\hfill c(t)=& \{\begin{array}{ccc}2g^2(\delta -t),\hfill & \hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ g^2(\delta +\Delta -3t),\hfill & \hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ g^2(\Delta -\delta -t),\hfill & \hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g^2(t-\Delta -\delta ),\hfill & \hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \\ \hfill C(t)=& \{\begin{array}{cc}{g}^2(2\delta t-t^2)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ g^2(-\frac{3}{2}{t}^2+(\Delta +\delta )t-\frac{1}{2}{(\Delta -\delta )}^2)\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ g^2{\delta }^2-\frac{1}{2}{g}^2{(t-\Delta +\delta )}^2\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ \frac{1}{2}{g}^2{(\Delta +\delta -t)}^2\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \end{array}$$ [24]

The q-space-trajectory defined in Eq. [2] is given by:

$$q(t)=\{\begin{array}{cc}gt\hfill & \text{if}0\le t<\delta ,\hfill \\ g\delta \hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g(\Delta +\delta -t)\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}$$ [25]

We note that the maximum value of q(t) is equal to gδ, which is usually referred to as the q-value in SDE experiments. The autocorrelation function of q(t) defined in Eq. [20] is given by:

$$b(t)=\{\begin{array}{cc}{g}^2{\delta }^2(\Delta -\frac{\delta }{3}-t)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ \frac{g^2{(\Delta +\delta -t)}^3}{12}\hfill & \text{if}\Delta -\delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}$$ [26]

and b(t) = b(−t) for t<0. We note that $b(0)=g^2{\delta }^2(\Delta -\frac{\delta }{3})$, which is usually referred to as the b-value.

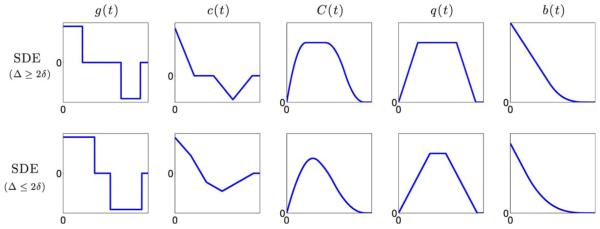
FIG. 1.

Representative plots of g(t), c(t), q(t), and b(t) for SDE gradient sequence. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 1 shows some representative plots for g(t), q(t), c(t), C(t), and b(t) for a SDE sequence. We note that the function b(t) is linear for 0 ≤ t ≤ Δ − δ.

Oscillating Gradient Spin-Echo Sequence

The formulations developed in previous sections are quite general and can be used for any gradient sequence. In this section, we derive some of the expressions for OGSE gradient pulses. The OGSE sequences are also often used for identifying tissue microstructure (19,22). Depending on the initial phase, sine-modulated (OGSES), and cosine-modulated (OGSEC) sequences can be written as follows:

$$\begin{array}{cc}\hfill g_{\sin }(t)=& \{\begin{array}{cc}g\sin (\omega t),\hfill & \text{if}0\le t<\delta ,\hfill \\ 0,\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g\sin (\omega (t-\Delta )),\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \\ \hfill g_{\cos }(t)=& \{\begin{array}{cc}g\cos (\omega t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g\cos (\omega (t-\Delta ))\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \end{array}$$ [27]

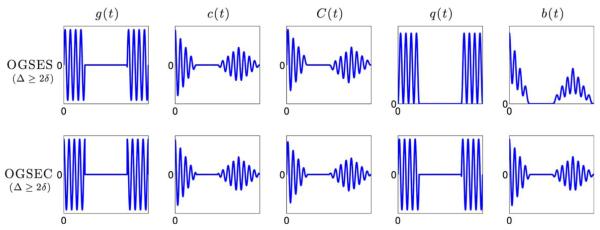
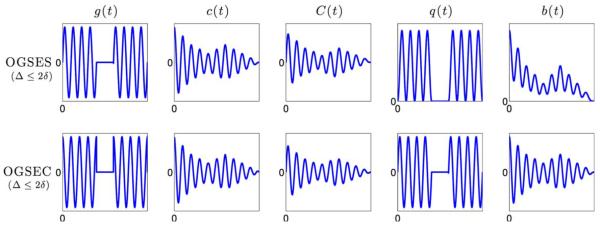
where δ = 2kπ/ω for some integer k. The expressions for c(t), C(t), q(t), and b(t) for OGSES and OGSEC sequences were derived after several algebraic manipulations and are given in the Appendix. These functions are also illustrated in the upper and lower panels of Figure 2 for the case when Δ ≥ 2δ and Δ ≤ 2δ, respectively.

FIG. 2.

Illustrations of the g(t), c(t), q(t), and b(t) of OGSES and OGSEC sequence with Δ ≥ 2δ. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The C(t) plots in Figures 1 and 2 illustrate a key difference between SDE and OGSE sequences. In the case when Δ ≥ 2δ, the maxima of C(t) for SDE is obtained in the interval t ∈ [δ, Δ − δ], while it is zero for OGSE sequences. As expected, C(t) for OGSE gradients samples the higher frequency part of the instantaneous diffusivity compared to SDE sequences. Thus, it provides more information about the short-time scale diffusivity.

Note that, when Δ ≤ 2δ, c(t) samples the mean-squared displacement during the entire time period of Δ + δ unlike for the case when Δ ≥ 2δ. This could be an important design consideration when playing OGSE gradient pulses.

Modeling the Mean-Squared Displacements

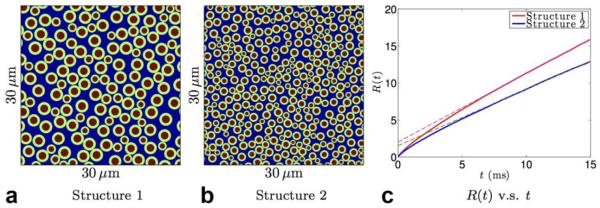
In order to estimate the mean-squared displacement of the time-varying diffusivity from a few measurements (typical of clinical acquisitions), it is important to design appropriate models for these quantities. The diffusivity in inhomogeneous environment is a monotonically decreasing function of time due to hinderances (14,17,18). As a result, the mean-squared displacement R(t) is a monotonically increasing concave function of diffusion time. As an example, the red and blue lines in Figure 4c illustrate the mean-squared displacement of diffusing particles using Monte-Carlo simulations in the extra-axonal space of the tissue structures shown in Figures 4a,b, respectively. More detailed information about the simulation is provided in the Methods. We note that, the mean-squared displacement converges to an apparently linear function of time as illustrated by the dashed lines, though according to (14), the diffusivity, that is the slope of R(t), may be slowly changing at very long time scales of t ⪢ 100 ms. These features can be utilized to develop models for the mean-squared displacements.

FIG. 4.

Illustration of the mean-squared displacement in two synthetic tissue structures: (a) and (b) are the synthetic cross-sectional planes of parallel axonal bundles with red areas being the axons, green the myelin, and blue the extra-axonal space. c: The mean-squared displacement of simulated diffusing particles in the extra-axonal space of the two tissue structures. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Different models have been used and proposed in the literature for representing time varying diffusivity. Specifically, an exponential model can be derived from the Ornstein-Uhlenbeck model (24,25), whereas a logarithmic model was used by (14), and a power-law model has been used to study anomalous diffusion in disordered media (26). Our goal in the next section is to determine if any of these models perform better or all represent the time-varying data equally well. Consequently, we incorporate these three models for representing time-varying mean-squared displacement as follows:

$$R_1(t)=2[D_{\infty }t+A_1(1-e^{-{\alpha }_{1}t})],$$ [28]

$$R_2(t)=2[D_{\infty }t+A_2\ln (1+{\alpha }_{2}t)],$$ [29]

$$R_3(t)=2[D_{\infty }t+A_3{t}^{{\alpha }_3}],$$ [30]

where A_i, α_i ≥ 0 for i = 1, 2, 3, α₃ ≤ 1, and D_∞ ≥ 0 is the long-time limit of the diffusivity. We note that the Ornstein-Uhlenbeck model (24) results in an exponential mean-squared displacement function similar to the second term of R₁(t). The exponential function also provides a good approximation to diffusion in restricted pores (25). For long-time scale, the expression R₂(t) ≈ 2[D_∞t + A₂ ln (t)] was used in (14) to study the diffusion in the extra-axonal space. The second term in R₃(t) has been studied in anomalous diffusion in disordered media (26).

From Eq. [21], the velocity autocorrelation functions corresponding to the mean-squared displacements in Eqs. [28–30] are given by:

$${\mathcal{D}}_1(t)=D_{\infty }\delta (t)-A_1{\alpha }_1^2{e}^{-{\alpha }_{1}t},$$ [31]

$${\mathcal{D}}_2(t)=D_{\infty }\delta (t)-\frac{A_2{\alpha }_2^2}{{(1+{\alpha }_{2}t)}^2},$$ [32]

$${\mathcal{D}}_3(t)=D_{\infty }\delta (t)-A_3{\alpha }_3(1-{\alpha }_3)t^{{\alpha }_3-2},$$ [33]

which all have negative values for t > 0.

Mean-Squared Phase Changes for Time-Varying Models

For the three time-varying models of mean-squared displacement R(t) given by Eqs. [28–30], we present the expressions for ⟨ϕ²(τ)⟩ with c(t) given by Eq. [23]. We denote the corresponding ensemble mean-squared phase by $\langle {\varphi }_1^2(\tau )\rangle$, $\langle {\varphi }_2^2(\tau )\rangle$, and $\langle {\varphi }_3^2(\tau )\rangle$, respectively. Then, we get:

$$\begin{array}{cc}\hfill & \langle {\varphi }_1^2(\tau )\rangle =\langle {\varphi }_{\infty }^2(\tau )\rangle \hfill \\ \hfill & +\frac{2A_1}{{\alpha }_1^2}\left(2{\alpha }_1\delta -2+2e^{-{\alpha }_1\delta }-e^{-{\alpha }_1(\Delta -\delta )}+2e^{-{\alpha }_1\Delta }-e^{-{\alpha }_1(\Delta +\delta )}\right),\hfill \end{array}$$ [34]

$$\begin{array}{cc}\hfill & \langle {\varphi }_2^2(\tau )\rangle =\langle {\varphi }_{\infty }^2(\tau )\rangle \hfill \\ \hfill +& \frac{2A_2}{{\alpha }_2^2}[\frac{\delta }{{\alpha }_2}-{({\alpha }_2\delta +1)}^2\ln (1+{\alpha }_2\delta )+\frac{{({\alpha }_2(\Delta -\delta )+1)}^2}{2}\phantom{]}\hfill \\ \hfill & \ln (1+{\alpha }_2(\Delta -\delta ))-{({\alpha }_2\Delta +1)}^2\ln (1+\alpha \Delta )+\hfill \\ \hfill & \phantom{[}\frac{{({\alpha }_2(\Delta +\delta )+1)}^2}{2}\ln (1+\alpha (\Delta +\delta ))],\hfill \end{array}$$ [35]

$$\begin{array}{cc}\hfill & \langle {\varphi }_3^2(\tau )\rangle =\langle {\varphi }_{\infty }^2(\tau )\rangle +\frac{2A_3}{(1+{\alpha }_3)(2+{\alpha }_3)}\hfill \\ \hfill & (-2{\delta }^{2+{\alpha }_3}+{(\Delta -\delta )}^{2+{\alpha }_3}-2{\Delta }^{2+{\alpha }_3}+{(\Delta +\delta )}^{2+{\alpha }_3}),\hfill \end{array}$$ [36]

where $\langle {\varphi }_{\infty }^2(\tau )\rangle =2g^2{\delta }^2(\Delta -\delta ∕3)D_{\infty }$ is the mean-squared phase due to the D_∞t term in the R_i(t)’s. These expressions will be used in all of our experiments described in the next section.

METHODS

Monte-Carlo Simulations

We studied the mean-squared displacement of diffusing particles in two synthetic cellular and axonal packings in a two-dimensional substrate. The simulated field of view of these structures was 100 × 100 μm². Figures 4a,b only illustrate a partial field of view of the two structures with size 30 × 30 μm². The green circles (regions) are the myelin sheaths that surround the axons shown in red. The g-ratio (the ratio between the inner and outer radii of each green circle) for all axons was set to 0.6. The intra-axonal volume fraction, myelin volume fraction and extra-axonal volume fraction for the two structures are {0.23, 0.41, 0.36} and {0.23, 0.40, 0.37}. The average axon radii were 1.1 and 0.7 μm, respectively.

In our Monte-Carlo simulations, a total of 10⁵ particles were randomly selected from a uniform distribution within the extra axonal space. During a time step of dt = 0.005 ms, each particle moved a distance of $2\sqrt{Ddt}\mu m$ along a randomly selected direction with D = 2 μm²/ms. The boundaries were considered impermeable, so that the particles would reflect off the myelin sheaths. The displacement of a diffusing particle can be computed by projecting its trajectory along an arbitrary direction, which was chosen as the horizontal axis in this example. Then, the mean-squared displacement R(t) was computed from all the diffusion trajectories in the extra-axonal space.

Data Acquisition

We applied the proposed approach to measure the time-varying diffusivity in an in vivo dMRI data set of a healthy subject. The data set was acquired on the MGH Connectome Scanner with the following experimental parameters: δ = {12, 8, 8, 8, 8, 4, 4, 4, 4, 4}ms; Δ = {26, 18, 23, 18, 23, 15, 18, 15, 18, 13}ms, and g = {149, 223, 194, 169, 147, 299, 261, 220, 192, 300}mT/m, respectively. The maximum and the minimum b-value of the data set were 4990s/μm² and 695s/μm², respectively. In each SDE experiment, diffusion weighting was applied along 60 gradient directions that were uniformly spread on the unit sphere. The spatial resolution was 2 × 2 × 2 mm³ and the echo time for all the experiments was set to be constant.

Signal Models

Diffusion Tensor Imaging (DTI) (27) has been a main tool for estimating the apparent molecular diffusivity using diffusion MRI, which does not distinguish signals contributed by molecules from the intra- and extra-axonal spaces. Recent studies have shown that the time-dependent diffusivity is mainly due to molecular diffusion in the extra-axonal space (14), while the intraaxonal compartment is almost time-independent. This is because, the dMRI signal decay due to diffusion in the ultrasmall axonal radii [less than 3 μm (15) is very small and is practically a constant at q-values that can be imaged on current clinical scanners. Thus, separating the intra- and extra-axonal signals into two separate compartments might provide a more accurate estimation of the time-dependent diffusivity (from extra-axonal space). To systematically test this hypothesis, we estimated the time-varying diffusivity using several models with in vivo dMRI measurements, which are explained below.

The first model we used was the standard DTI model (27) given by:

$$S_{\text{DTI}}(b,\mathit{u})=\exp (-b{\mathit{u}}^{T}D\mathit{u}),$$ [37]

where the b-value is given by b = g²δ²(Δ − δ/3) and the diffusion tensor D is assumed to be time-invariant. We also assume that the diffusion tensor D is cylindrically symmetric, that is, the two smaller eigenvalues of D are equal.

We further modify the DTI model as follows:

$$S_{\text{const}.+\text{DTI}}(b,\mathit{u})={\mathit{u}}^{T}F\mathit{u}+(1-{\mathit{u}}^{T}F\mathit{u})\exp (-b{\mathit{u}}^{T}D\mathit{u}),$$ [38]

where F is a positive semidefinite tensor with the same set of eigenvectors as D and the eigenvalue of F corresponding to the largest eigenvalue of D is set to zero, while the other two eigenvalues of F are assumed to be equal. Due to the very small axonal radii (15), the intraaxonal molecular diffusion processes contribute little to the signal decay (14). Thus, we assume that the intraaxonal signal is given by a constant u^TFu term for any u in the orthogonal direction of the orientation of the underlying fiber bundle, very similar to the intra-axonal compartment of the NODDI model (28), though without orientation dispersion. The time-dependent signal decay is completely modeled by the second term in Eq. [38], but in this model, the apparent diffusivity is still assumed to be time invariant.

To incorporate the time-varying diffusivity into Eq. [38], we propose the following set of models of the form:

$$\begin{array}{cc}\hfill & S_{i,j}(g,\delta ,\Delta ,\mathit{u})\hfill \\ \hfill & ={\mathit{u}}^{T}F\mathit{u}+(1-{\mathit{u}}^{T}F\mathit{u})\exp \left(-\frac{1}{2}{\mathit{u}}^T{\Phi }_{i,j}(g,\delta ,\Delta )\mathit{u}\right),\hfill \end{array}$$ [39]

where Φ_i,j is a cylindrical tensor whose eigenvalue along the fiber bundle is given by $\langle {\varphi }_i^2(\tau )\rangle$ with mean-squared displacement R_i(t) and the eigenvalues in the cross-sectional plane are given by $\langle {\varphi }_j^2(\tau )\rangle$ from Eq. [34]. The different combinations of i, j leads to a total number of nine models in the form S_i,j for i, j ∈ {1, 2, 3}. The model parameters for these models were estimated using the lsqnonlin.m command in Matlab (The MathWorks Inc., Natick, MA).

We note that our method for estimating the time-varying diffusivities is fundamentally different from the method used in (23), where multiple dMRI data sets were acquired using the same pulse width δ but varying diffusion time Δ. However, the apparent diffusion tensor for each data set was computed using a time-invariant DTI model. Our method, on the other hand, estimates the mean-squared displacement R_i(t) of the diffusing molecules directly by integrating all measurements. Moreover, the DTI model of (23) does not separate the intra- and extra-axonal compartments [although they are used to infer the biophysical meaning of the time-varying diffusivity in (23), which may also lead to bias in the estimated time-varying diffusivity.

Comparison Metrics

To understand the goodness of fit of the above models as well as to determine if there is any significant evidence for the time-varying nature of the diffusion coefficient, we compared the performance of all the above models using the following measures:

1. Normalized mean-squared error (NMSE). In each voxel, the total number of measurements is K = 600. Let s(k) for k = 1, …, K denote the kth measurement and $\widehat{s}(k)$ denote the corresponding estimated signal. Let $\mathcal{S}$ denote a subset of the indices of measurements. Then the NMSE of the estimated signal in the set $\mathcal{S}$ is computed as $\text{NMSE}={\sum }_{k\in \mathcal{S}}{\mid s(k)-\widehat{s}(k)\mid }^2∕{\sum }_{k\in \mathcal{S}}s{(k)}^2$. In the experiments, we computed three sets of NMSE. The first set $\mathcal{S}$ contained all the dMRI measurements at a voxel. Let v denote the principle direction of the fiber bundle, and let u_k denote the gradient direction of the kth measurement. Then, the second set ${\mathcal{S}}_{\Vert }≔\{k\in \mathcal{S}\mathrm{s}.\mathrm{t}.\mid {\mathit{u}}_{\mathrm{k}}\cdot \mathit{v}\mid \ge 0.9\}$, contained measurements that were close to the orientation of the fiber bundles. The third set ${\mathcal{S}}_{\perp }≔\{k\in \mathcal{S}\mathrm{s}.\mathrm{t}.\mid {\mathit{u}}_{\mathrm{k}}\cdot \mathit{v}\mid \le 0.1\}$ contained measurements close to the cross-sectional plane of the fibers. The NMSE’s for the three sets are denoted by NMSE_all; NMSE_∥, and NMSE_⊥, respectively.

2. AIC and BIC. In practice, it is desirable to have a parsimonious model which provides low NMSE using as few parameters as possible. The number of parameters for S_DTI and S_const.+DTI are 4 and 6, respectively, while each of the model of the form S_R∥,_R⊥ = S_i,j has 9 parameters. Thus, even if S_R∥,_R⊥ has lower NMSE, we still need to take into account the effect of the number of parameters when testing the time-varying diffusivities. To this end, we compare the models using the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The model with the lowest AIC or BIC has the best fit.

RESULTS

Simulation Results

The red and blue lines in Fig. 4c show the mean-squared displacements for the diffusing particles in the extra-axonal space of the two synthetic structures in Figures 4a,b, respectively. The magenta and green dashed lines indicate that the mean-squared displacements are approximately linear with respect to the diffusion time at the long-time scale. Since the diffusivity is time-varying, the y-intercept of the straight lines are about 2 and 1.5 μm². We note that these intercepts are much larger than the mean-squared displacement from the intra-axonal space of axons with radii of 1.1 and 0.7 μm, which is about 0.61 and 0.25 μm², respectively. Thus, estimation of these offsets (intercepts) can provide important information about the microstructure of the underlying tissue.

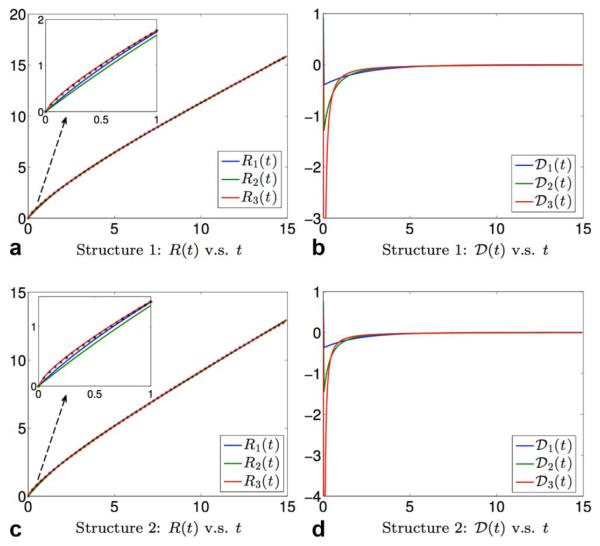
One of the aims of the Monte-Carlo study is to determine which of these models more accurately represent the observed time-varying mean-squared displacement. Consequently, we used these models in Eqs. [28–30] to fit the simulated R(t) shown in Figure 4c. The blue, green and red curves in Figures 5a,c correspond to the estimated results from R₁(t), R₂(t), and R₃(t) from Structures 1 and 2, respectively, while the true R(t) from simulation is shown in black stellar markers. For t ≤ 1 ms; R₃(t) fits the data better than the other two models, but the differences between the three models are almost indistinguishable for t ≥ 2 ms. The corresponding estimated velocity autocorrelation functions for the two structures are shown in Figures 5b,d, respectively. We note that ${\mathcal{D}}_3(t)$ has the fastest change close to zero and all the three functions ${\mathcal{D}}_i(t),i=1,2,3$, have singularities at t = 0.

FIG. 5.

Illustration of the estimated mean-squared displacement and velocity autocorrelation function for the two structures shown in Fig. 4: The blue, green, and red curves in (a) and (c) show the estimated mean-square displacements using Eqs. [28–30], respectively, while the back stars show the true values from simulation. The blue, green and red lines in (b) and (d) show the estimated velocity autocorrelation functions using Eqs. [31–33], respectively. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The c(t), C(t), and b(t) functions shown in Figure 1 and the R(t), $\mathcal{D}(t)$ plots in Figure 5 provide further insights into our understanding of the effects of changing the experimental parameters δ and Δ when measuring dMRI signals using SDE experiments. We note that if the pulse width δ is fixed, then changing Δ shifts the right triangular part of c(t) along the time axis. As the slope of R(t) is constant or varies slowly at long-time scale, changing Δ may not provide useful information about the fast time-varying diffusivity at short-time scale. A more effective approach for measuring the time-varying R(t) is to vary δ, which will change the left triangular part of c(t), thus providing more useful information about R(t) at the short-time scale. Moreover, Figure 1 implies that changing Δ will shift b(t) along the vertical axis without changing the slope of its linear part. Conversely, changing the pulse width δ also alters the slope of the linear part of b(t), providing a possibly more effective approach for measuring the time-varying velocity autocorrelation function.

In Vivo Data Results

We collected the comparison metrics for the 11 models at voxels where the FA was larger than 0.8, that is, where we expect a single predominant fiber bundle (no crossing). The comparison results are illustrated in Table 1. We note that S_const.+DTI has significantly lower NMSE, AIC, and BIC than S_DTI, indicating that a multicompartment model is a better fit that a simple DTI model. Moreover, all the nine models with time-varying diffusivities, S_1,1, S_1,2, …, S_3,3, also have consistently lower NMSE, AIC, and BIC than S_const.+DTI, indicating that the apparent diffusivity in the extra-axonal space is time-varying. Among the nine models, S_1,2 has the lowest overall NMSE and the lowest NMSE in the perpendicular direction of the fiber bundles, while S_2,1 has the lowest NMSE along the parallel direction of the fiber bundle. Moreover, S_1,1 has the lowest AIC and BIC, indicating that the model in Eq. [28] may be a better option for characterizing the mean-squared displacements in this in vivo data set, though other models can provide very similar results.

Table 1.

Comparison of the Estimation Results of 11 dMRI Signal Models at Voxels where FA > 0:8

	NMSEall	NMSE∥	NMSE⊥	AIC	BIC
S DTI	0.1013	0.1906	0.0945	−1152.5	−1134.5
S const.+DTI	0.0771	0.1765	0.0754	−1271.8	−1249.4
S 1,1	0.0746	0.1627	0.0714	−1295.8	−1256.2
S 1,2	0.0745	0.1601	0.0710	−1295.1	−1255.5
S 1,3	0.0747	0.1598	0.0712	−1294.2	−1254.7
S 2,1	0.0749	0.1595	0.0723	−1294.3	−1254.7
S 2,2	0.0748	0.1610	0.0718	−1294.5	−1254.9
S 2,3	0.0748	0.1598	0.0733	−1294.1	−1254.6
S 3,1	0.0758	0.1659	0.0735	−1293.0	−1253.4
S 3,2	0.0762	0.1663	0.0742	−1290.7	−1251.1
S 3,3	0.0756	0.1648	0.0718	−1293.7	−1254.1

DISCUSSION AND CONCLUSION

In this article, we extended the classical result by Stepišnik (21) on measuring the time-dependent diffusivity using diffusion MRI. We derived three novel formulations for representing the dMRI signal under the Gaussian phase approximation given by:

$$\begin{array}{cc}\hfill s(g,\tau )& =\exp \left(\frac{1}{2}{\int }_0^{\tau }R(t)c(t)\mathit{dt}\right),\hfill \\ \hfill & =\exp \left(-{\int }_0^{\tau }{D}_{\text{inst}}(t)C(t)\mathit{dt}\right),\hfill \\ \hfill & =\exp \left({\int }_{-\tau }^{\tau }\mathcal{D}(t)b(t)\mathit{dt}\right),\hfill \end{array}$$

where R(t), D_inst(t), and $\mathcal{D}(t)$ are the mean-squared displacement, the instantaneous diffusivity, and the velocity autocorrelation function of the diffusing spins, respectively. These quantities are intrinsic properties of the tissue structure, and can provide insight into the packing structure of the tissue (23). The above formulations are expressed in terms of c(t), which is the autocorrelation function of the gradient sequence g(t), or C(t) which is the cumulative function of c(t), while b(t) is a generalization of the b-value. These equations provide new insight to understand the importance of the different experimental parameters in measuring time varying diffusivity and the difference between gradient sequences. Significantly, the proposed theory could potentially be applied to optimize the gradient sequences to improve the performance of diffusion MRI for measuring specific tissue properties.

Moreover, we also introduced three functions for modeling the time-varying mean-squared displacement of water molecules and compared them using a simulated data set and an in vivo human brain data set, respectively. The simulation results show that accurate estimation of the time-varying diffusivity allows to distinguish two axonal packing structures with similar axonal and myelin volume fractions. The structure with large axonal radii tends to have higher apparent diffusivity. The experimental results using in vivo data also show strong evidence for the existence of time-varying diffusivity. The exponential model for the mean-squared displacement provides slightly better performance in fitting the in-vivo data than the other two models. A comprehensive study using large data sets is required to understand the time-varying diffusivity in more complex tissue structures, which will be part of our future work.

FIG. 3.

Illustrations of the g(t), c(t), q(t), and b(t) of OGSES and OGSEC sequence with Δ ≤ 2δ. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

APPENDIX A

Derivation for Eq. [10]

The double integral in Eq. [9] can be written as:

$$\begin{array}{cc}\hfill & {\int }_0^{\tau }{\int }_0^{\tau }g(t)R(\mid s-t\mid )g(s)\mathit{dsdt}\hfill \\ \hfill & ={\int }_0^{\tau }{\int }_0^{t}g(t)R(t-s)g(s)\mathit{dsdt}+{\int }_0^{\tau }{\int }_t^{\tau }g(t)R(s-t)g(s)\mathit{dsdt},\hfill \end{array}$$ [40]

$$={\int }_0^{\tau }{\int }_0^t[g(t)R(t-s)g(s)+g(\tau -t)R(t-s)g(\tau -s)]\mathit{dsdt},$$ [41]

$$={\int }_0^{\tau }R(t){\int }_0^{\tau -t}[g(s)g(t+s)+g(\tau -s)g(\tau -t-s)]\mathit{dsdt}.$$ [42]

From Eqs. [40 and 41], a change of variables was applied to change s, t to τ − s and τ − t, respectively. From Eq. [41] and [42], the integral was computed along the level set of t − s using substitution of variables. We should note that the following equality holds for a stationary process:

$${\int }_0^{\tau -t}g(\tau -s)g(\tau -t-s)\mathit{ds}={\int }_0^{\tau -t}g(s)g(t+s)\mathit{ds}.$$

Thus, Eq. [42] is equal to $2{\int }_0^{\tau }R(t)c(t)\mathit{dt}$ where c(t) is given by Eq. [11]. The reverse time-invariant property of c(t) follows directly from Eq. [42].

Derivation for Eq. [17]

To derive Eq. [17], we first show that C(τ) = 0 for C(t) defined in Eq. [13]. To this end, we substitute the definition of c(t) in Eq. [13] and obtain:

$$\begin{array}{cc}\hfill C(\tau )& ={\int }_0^{\tau }g(s){\int }_0^{\tau }g(s+t)\mathit{dtds},\hfill \\ \hfill & =-{\int }_0^{\tau }g(s)\left({\int }_0^{s}g(t)\mathit{dt}\right)\mathit{ds},\hfill \\ \hfill & =-\frac{1}{2}{\left({\int }_0^{s}g(t)\mathit{dt}\right)}^2{\mid }_{s=0}^{\tau }=0,\hfill \end{array}$$

where the second equality was obtained using ${\int }_0^{\tau }g(s+t)\mathit{dt}=-{\int }_0^{s}g(t)\mathit{dt}$.

APPENDIX B

The c(t), C(t), q(t) and b(t) functions for OGSE sequences.

After several algebraic manipulations, we obtain the following expressions for c(t), C(t), q(t), and b(t) functions for OGSES and OGSEC sequences. For notational simplicity, we first define the following functions:

$$\begin{array}{cc}\hfill & \alpha (x,y)≔{\int }_0^x\sin (\omega s)\sin (\omega (s+y))\mathit{ds},\hfill \\ \hfill & =\frac{1}{2}\cos (\omega y)x+\frac{1}{4\omega }\sin (\omega y)-\frac{1}{4\omega }\sin (\omega (2x+y)),\hfill \\ \hfill & \beta (x,y)≔{\int }_0^x\cos (\omega s)\cos (\omega (s+y))\mathit{ds},\hfill \\ \hfill & =\frac{1}{2}\cos (\omega y)x-\frac{1}{4\omega }\sin (\omega y)+\frac{1}{4\omega }\sin (\omega (2x+y)),\hfill \\ \hfill A(t)& ≔{\int }_0^t\alpha (\delta -s,s)\mathit{ds}=\frac{\delta -t}{2\omega }\sin (\omega t)+\frac{1}{{\omega }^2}(1-\cos (\omega t)),\hfill \\ \hfill & B(t)≔{\int }_0^t\beta (\delta -s,s)\mathit{ds}=\frac{\delta -t}{2\omega }\sin (\omega t).\hfill \end{array}$$

If Δ ≥ 2δ, then the c(t), C(t), q(t), and b(t) functions for OGSES are given by:

$$\begin{array}{cc}\hfill c_{\sin }(t)=& \{\begin{array}{cc}2g^2\alpha (\delta -t,t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0,\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ g^2\alpha (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ g^2\alpha (\Delta +\delta -t,t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{C}_{\sin }(t)=\{\begin{array}{cc}2g^{2}A(t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ -g^{2}A(\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ g^{2}A(t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \\ \hfill q_{\sin }(t)=& \{\begin{array}{cc}\frac{g}{\omega }(1-\cos (\omega t))\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \delta \le t<\Delta ,\hfill \\ \frac{g}{\omega }(1-\cos (\omega (t-\Delta )))\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{b}_{\sin }(t)=\{\begin{array}{cc}\frac{2g^2}{{\omega }^2}\left[\delta -t+\frac{2}{\omega }\sin (\omega t)+\beta (\delta -t,t)\right]\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ \frac{g^2}{{\omega }^2}\left[t-\Delta +\delta +\frac{2}{\omega }\sin (\omega (\Delta -t))+\beta (t-\Delta +\delta ,\Delta -t)\right]\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ \frac{g^2}{{\omega }^2}\left[\Delta +\delta -t+\frac{2}{\omega }\sin (\omega (t-\Delta ))+\beta (\Delta +\delta -t,t-\Delta )\right]\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \end{array}$$

The corresponding functions for OGSEC are given by:

$$\begin{array}{cc}\hfill c_{\cos }(t)=& \{\begin{array}{cc}2g^2\beta (\delta -t,t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ g^2\beta (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ g^2\beta (\Delta +\delta -t,t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{C}_{\cos }(t)=\{\begin{array}{cc}2g^{2}B(t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ -g^{2}B(\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ g^{2}B(t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \\ \hfill q_{\cos }(t)=& \{\begin{array}{cc}\frac{g}{\omega }\sin (\omega t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \delta \le t<\Delta ,\hfill \\ \frac{g}{\omega }\sin (\omega (t-\Delta ))\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{b}_{\cos }(t)=\{\begin{array}{cc}\frac{2g^2}{{\omega }^2}\alpha (\delta -t,t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \text{if}\delta \le t<\Delta -\delta ,\hfill \\ \frac{g^2}{{\omega }^2}\alpha (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ \frac{g^2}{{\omega }^2}\alpha (\Delta +\delta -t,t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Conversely, if Δ ≤ 2δ, then the c(t), C(t), q(t), and b(t) functions for OGSES are as follows:

$$\begin{array}{cc}\hfill c_{\sin }(t)=& \{\begin{array}{cc}2g^2\alpha (\delta -t,t)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ 2g^2\alpha (\delta -t,t)+g^2\alpha (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ g^2\alpha (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g^2\alpha (\Delta +\delta -t,t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{C}_{\sin }(t)=\{\begin{array}{cc}2g^{2}A(t)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ 2g^{2}A(t)-g^{2}A(\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ -g^{2}A(\Delta -t)\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g^{2}A(t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \\ \hfill q_{\sin }(t)=& \{\begin{array}{cc}\frac{g}{\omega }(1-\cos (\omega t))\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \delta \le t<\Delta ,\hfill \\ \frac{g}{\omega }(1-\cos (\omega (t-\Delta )))\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \\ \hfill b_{\sin }(t)=& \{\begin{array}{cc}\frac{2g^2}{{\omega }^2}\left[\delta -t+\frac{2}{\omega }\sin (\omega t)+\beta (\delta -t,t)\right]\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ \frac{2g^2}{{\omega }^2}\left[\delta -t+\frac{2}{\omega }\sin (\omega t)+\beta (\delta -t,t)\right]+\frac{g^2}{{\omega }^2}\left[t-\Delta +\delta +\frac{2}{\omega }\sin (\omega (\Delta -t))+\beta (t-\Delta +\delta ,\Delta -t)\right]\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ \frac{g^2}{{\omega }^2}\left[t-\Delta +\delta +\frac{2}{\omega }\sin (\omega (\Delta -t))+\beta (t-\Delta +\delta ,\Delta -t)\right]\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ \frac{g^2}{{\omega }^2}\left[\Delta +\delta -t+\frac{2}{\omega }\sin (\omega (t-\Delta ))+\beta (\Delta +\delta -t,t-\Delta )\right]\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \end{array}$$

The corresponding functions for OGSEC are given by:

$$\begin{array}{cc}\hfill c_{\cos }(t)=& \{\begin{array}{cc}2g^2\beta (\delta -t,t)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ 2g^2\beta (\delta -t,t)+g^2\beta (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ g^2\beta (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g^2\beta (\Delta +\delta -t,t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{C}_{\cos }(t)=\{\begin{array}{cc}2g^{2}B(t)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ 2g^{2}B(t)-g^{2}B(\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ -g^{2}B(\Delta -t)\hfill & \text{if}\delta \le t<\Delta ,\hfill \\ g^{2}B(t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}\hfill \\ \hfill q_{\cos }(t)& =\{\begin{array}{cc}\frac{g}{\omega }\sin (\omega t)\hfill & \text{if}0\le t<\delta ,\hfill \\ 0\hfill & \delta \le t<\Delta ,\hfill \\ \frac{g}{\omega }\sin (\omega (t-\Delta ))\hfill & \text{if}\Delta \le t<\Delta +\delta ,\hfill \end{array}\phantom{\}}{b}_{\cos }(t)=\{\begin{array}{cc}\frac{2g^2}{{\omega }^2}\alpha (\delta -t,t)\hfill & \text{if}0\le t<\Delta -\delta ,\hfill \\ \frac{2g^2}{{\omega }^2}\alpha (\delta -t,t)+\frac{g^2}{{\omega }^2}\alpha (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\delta ,\hfill \\ \frac{g^2}{{\omega }^2}\alpha (t-\Delta +\delta ,\Delta -t)\hfill & \text{if}\Delta -\delta \le t<\Delta ,\hfill \\ \frac{g^2}{{\omega }^2}\alpha (\Delta +\delta -t,t-\Delta )\hfill & \text{if}\Delta \le t<\Delta +\delta .\hfill \end{array}\phantom{\}}\hfill \end{array}$$