Trans-bonded pairs of E-cadherin exhibit a remarkable hierarchy of mechanical strengths

Abstract

Classical cadherins are primary mediators of calcium-dependent cell interactions in multicellular organisms. Organized in five tandemly repeated E-cadherin (EC) modules, the extracellular segments of these membrane-spanning glycoproteins interact homophilically between opposing cells to create highly regulated patterns of attachment stabilized by cytoskeletal elements inside the cells. Despite many structural and functional studies, a significant controversy exists in regard to the organization of cadherin binding in adhesion sites. Supported by considerable evidence, perhaps the most widely held view is that opposing N-terminal EC1–EC2 (EC12) domains form a “zipper” of bonds. However, immobilized on two atomically smooth surfaces and pushed to adhesive contact, opposing cadherins become fully interdigitated and unbind through three discrete jumps comparable with domain dimensions when pulled apart. So the question remains as to whether mechanical adhesion strength emanates solely from interactions between the peripheral N-terminal domains or involves multiple overlapping domains. It is also unclear whether a primary adhesion complex is formed by a single opposing pair of cadherins or whether the complex involves a more complicated network of cis-bonded multimers. To address these questions, we used a special jump/ramp mode of force spectroscopy to test isolated pairwise interactions between recombinant fragments of ECs. Besides the formation of strong trans-bonded dimers, we find a remarkable hierarchy of rupture strengths for bonds between the full five-domain fragments that suggests multiple mechanical functions for cadherins, perhaps providing distinct properties needed for transient-specific recognition as well as stable tissue formation.

Adhesive contacts between cells play a crucial role in most aspects of tissue organization, differentiation, and function. One of the major classes of cell adhesion molecules is the classical cadherins. These membrane-spanning glycoproteins are thought to be primary mediators of calcium-dependent cell interactions in multicellular organisms (1, 2). The extracellular segment is organized in five tandemly repeated E-cadherin (EC) modules, which are numbered from the outermost N-terminal domain (EC1–EC5). ECs on opposing cells interact homophilically (3) to create highly regulated patterns of attachment during development and highly clustered structures in adult tissues (e.g., junctional plaques) stabilized by cytoskeletal elements inside the cells (4). Numerous structural and functional studies have focused on the molecular mechanism of cadherin-mediated cell adhesion and the organization of cadherin domain interactions in the adhesion complex. Data from mutational and domain-exchange experiments (5, 6), electron microscopy (7), binding kinetics (8), and structural studies (9) have established that the N-terminal EC1 and EC2 domains are critically important for adhesion, supporting the model of a N-terminal “zipper” proposed many years ago (10). However, a quite different picture of cadherin interactions has come from physical tests of macroscopic adhesion between supported layers of C-cadherins using the surface force apparatus (SFA) (11, 12). When most strongly adherent, the distance between the SFA surfaces was equivalent to the full five-domain length, implying significant overlap, and then during separation, the distance increased in domain-size steps through two intervening states of weaker adhesion. From the perspective of adhesive function, the SFA tests indicated that mechanical strength involved other EC domains as well as EC1–EC2 (EC12) in trans-bonded interactions between cadherins but did not exclude the possibility of more complicated arrangements with cis-bonded multimers as postulated in several studies (13–15).

We have used an ultrasensitive instrument, called the “biomembrane force probe” (BFP) (16, 17), to form discrete attachments between antiparallel cadherins and then test rupture strengths by loading with precise force histories spanning time frames from 0.001 to >1 sec. Recombinant protein fragments of the full-length EC ectodomains (EC15) and/or just the two outer modules (EC12) were linked at very low concentrations to the BFP tip and target microbeads to produce a high percentage (≈90%) of single pairwise interactions at contact. Testing these complexes with both steady ramps of force and a special jump/ramp mode of force application, we discovered a hierarchy of rupture strengths, characterizing different subpopulations of the attachments and likely representing different substates of cadherin binding. We were able to clearly distinguish between two groups of these substates because of their different responses to pulling speed, one group revealing short apparent lifetimes from 0.1 to 1 sec and the other revealing exceptionally long apparent lifetimes from 10² to10⁵ sec, when extrapolated to zero force. The markedly different mechanical strengths of these subpopulations at different speeds suggest an intrinsic capability of cadherins to perform diverse adhesive functions, from transient-weak interaction to durable-strong cohesion, depending on the binding state.

Methods

Plasmid Constructions for the EC Fragments. The cDNA of full-length mouse EC (kindly provided by L. Larue, Institut Curie) was used for PCR amplification of DNA coding for the two cadherin fragments in this study. All of the constructs were fused with a C-terminal histidine tag. For EC12, the construct of the plasmid is described in ref. 8. For EC15 N-terminal sequence, the primer was 5′-GCG TCT GCC GGG AAG CTT ATG GGA GCC CCG GTG CCG C-3′, and for the C-terminal sequence, the primer was 5′-GAC TAT GCG GCC GCC TAG TGG TGG TGG TGG TGG TGC TTC ATG CAG TTG TTG ACC GT-3′. The resulting fragment was inserted into the HindIII/NotI site of pcDNA3 (Invitrogen). Details of the production and purification of the two-domain (EC12) and five-domain (EC15) EC proteins can be found in Supporting Text and Fig. 5, which are published as supporting information on the PNAS web site.

Coupling of EC Fragments to Glass Microspheres and the Test Environment. As described in ref. 17 and outlined in Supporting Text, small (2 μm) glass microspheres for BFP tips were functionalized with both streptavidinated polyethylene glycol (PEG) 3400-biotin and a very low concentration of a PEG 3400-linked cadherin fragment. Larger (4–5 μm) target spheres were decorated in the same way with a null PEG 3400 (no biotin) and a low concentration of the PEG 3400-linked cadherin fragment. Tests of the interactions between these EC spheres were performed in a microscope chamber that contained 75 mM NaCl, 10 mM Hepes, and 1 mM CaCl₂. Removal of Ca²⁺ eliminated attachments between the EC spheres, and tests of PEG-linked spheres against cadherin-linked spheres in Ca²⁺ yielded only a few attachments (see controls superposed in Fig. 4 d and e).

Fig. 4.

Mechanical strenghts of trans-bonded EC12 fragments measured with steady ramps of force and discrimination of short-lived substates with a jump/slow ramp and a jump/fast ramp sequence of force. (a) Histogram obtained from a steady ramp test of EC12 vs. EC12 at 100 pN/sec, yielding only a few small forces comparable with the results for nonspecific interactions. (b) Histogram obtained from a fast steady ramp test of EC12 vs. EC12 at 10,000 pN/sec. Superposed as cyan and green curves are Gaussian approximations modeling the two weakly bound substates. (c) The most frequent forces obtained from the EC12 vs. EC12 distributions are plotted vs. the logarithms of the force rates. The open symbols map the positions of the cyan and green substate distributions that best fit the force statistics in steady ramp histograms at loading rates of 1,000 and 10,000 pN/sec (b). The filled symbols are the positions of the peaks in the histograms from the jump/slow and jump/fast ramp tests (d and f). Here, the errors in the most frequent forces are comparable to the size of the symbols. (d and e) Histograms of EC12 vs. EC12 rupture forces obtained in the jump/slow ramp mode. The majority of attachments (66%) failed during the jump and appear in d; the jump survivors (33%) failed within a small range of force under the slow ramp of 30 pN/sec and appear in e. The gray bins show the expected levels of nonspecific forces as measured in tests of EC12 tips vs. PEG-linked spheres in Ca²⁺, which have been rescaled to reflect the same number of bead–bead touches. (f) Histogram of EC12 vs. EC12 rupture forces obtained by using a faster ramp phase in the jump/ramp test. Increased to 1,000 pN/sec, the faster ramp after the jump spread out the attachments surviving the jump, producing a prominent narrow peak. The distributions modeling the two weakly bound substates of EC12 vs. EC12 interactions are identified by cyan and green curves superposed in d and f. The curves plotted in b, d, and f are based on off rates defined by the following exponential dependences on force: k_rupt ≈ (10 per sec) exp(f/7 pN) for the cyan substate and k_rupt ≈ (1 per sec) exp(f/7 pN) for the green substate. [Note that the small wings of higher forces, ≈14% of all attachments in b and ≈10% in f, seem to arise from double attachments as indicated by the green dashed curves. As described in Supporting Text, these extensions to the peak regions were calculated based on the single-bond parameters and the assumption that forces were shared equally by two adjacent attachments, failing in random sequence (25).]

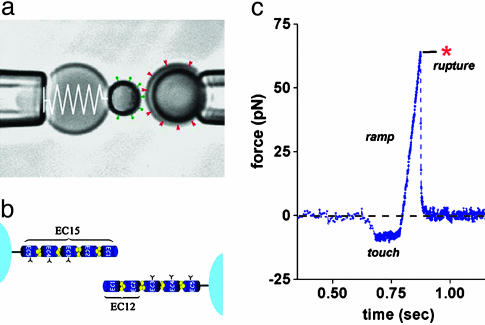
BFP. The “spring” in the ultrasensitive BFP (Fig. 1a) is a PEG-biotinylated red blood cell that is pressurized by micropipette suction into a spherical shape; the BFP “tip” is formed by attaching a streptavidinated protein-functionalized glass microsphere (17, 18). With precision control of the pipette suction, the BFP spring constant k_f is preset in the range from 0.2 to 2 pN/nm. Binning and digitizing a few video lines at a scan rate of 1,500 per sec along the symmetry axis of the probe, displacements of the BFP tip and target bead are tracked along the pulling direction at time intervals of 0.6 msec and at a resolution of approximately ±6 nm; BFP tip displacement × spring constant k_f = force. Through programmed control of the linear piezo translator connected to the target-holding pipette, the “steady ramp” mode (pulling force/time = constant) of testing is performed by retraction of the target at constant speed V_t after a 0.1-sec period of “soft” touch to the BFP tip (Fig. 1c). Because of the flexible PEG coupling between the cadherins and microsphere surfaces, the “effective” mechanical stiffness was somewhat less than the preset value of the BFP spring constant (i.e., ≈0.8–0.9 k_f), but as seen in Fig. 1c, the ramps of force applied to cadherin bonds were perfectly linear. In the special “jump/ramp” mode of testing (18), an initial “jump” in force is produced by pulling at a very fast speed (set between 1 and 2 × 10⁴ nm/sec, equivalent to a fast force ramp between 2 and 5 × 10³ pN/sec) for a preset time (e.g., ≈5 msec to reach 10–30 pN). Then, the retraction speed is abruptly lowered within 0.6 msec to create a slower “ramp” as illustrated in Fig. 3a. Varying piezo retraction speeds from 40 to 33,000 nm/sec and BFP spring constants from 0.25 to 1.54 pN/nm, nominal loading rates for force ramps are programmed from ≈30 to 50,000 pN/sec. However, when pulled at extremely fast speeds (≥20,000 nm/sec), a viscous correction due to probe damping has to be added to the BFP elastic force as quantified in ref. 17. These corrections were minimized by selecting the BFP spring constant at each loading rate according to the formula described in ref. 17 for achieving the best resolution in force. The uncertainty (±SD) in BFP force is shown as a function of loading rate in Fig. 2c.

Fig. 1.

The BFP and a test of mechanical strength between trans-bonded EC15 fragments. (a) Videomicrograph of the BFP with a pipette-pressurized red cell as a force transducer, labeled by a spring on the left. The 2-μm streptavidinated glass bead carrying cadherin proteins (shown as green pins) was attached to the previously biotinylated red cell as a probe tip; a 4-μm glass bead (on the right) also decorated with cadherin was used as a target (shown as red wedges). (b) Schematic illustration of cadherins linked to the microbeads and the labeling of modules (see Fig. 5 for gels showing the isolated fragments). The cadherin densities on both the BFP tip and target beads were kept very low so that bead–bead contact in1 mM Ca²⁺ would produce infrequent pairwise attachments. (c) A force vs. time trace obtained from pulling on a pairwise EC15 vs. EC15 attachment by retracting the target at constant speed. Formed during 0.1-sec touch, the attachment survived for ≈0.07 sec under the steady force ramp, breaking precipitously at ≈64 pN.

Fig. 3.

Long-lived substates of EC15 vs. EC15 interactions exposed by a jump/slow ramp force sequence and merging of these substates when tested with fast steady ramps of force. (a) A force vs. time trace obtained when testing a pairwise EC15 vs. EC15 attachment in the jump/slow ramp mode. The attachment survived the jump at 2,200 pN/sec loading rate to ≈20 pN, then lived for ≈1.5 sec under the subsequent slow ramp of 30 pN/sec, rupturing at ≈55 pN. (b) Histogram of EC15 vs. EC15 rupture forces obtained by using the jump/slow ramp mode demonstrated in a. Rising off scale, the two magenta bins illustrate the small percentage (≈33%) of attachments that broke during the jump, indicating a subpopulation of weak fast-failing EC15 vs. EC15 interactions. The majority (≈66%) of EC15 vs. EC15 attachments survived the jump and split into two narrowly distributed groups, one stronger and longer-lived than the other. Identified by blue and red color-coded curves, the distributions modeling the failure of the two strongly bound substates were matched to the bimodal histogram in b (from the jump/slow ramp test) and to the peak regions in histograms from all steady ramp tests. For the curves plotted here, the off rate for each substate was defined by an exponential dependence on force, k_rupt ≈ (0.01 per sec) exp(f/5 pN) for the blue substate and k_rupt ≈ (10^–6 per sec) exp(f/3 pN) for the red substate. (c) Illustration of the fit by using Gaussian approximations for the blue and red substate distributions to the data from the steady ramp test at 10,000 pN/sec in Fig. 2b. The dotted-black curve shows the sum of the two distributions, each including the force error. (See Supporting Text and Figs. 8 and 10 for additional details and fits to histograms at other loading rates.) (d) Plot of the most frequent forces in distributions vs. the logarithms of the force rates. The open symbols map the positions of the blue and red substate distributions that matched the force statistics local to the peaks in steady ramp histograms (c). The filled symbols are positions of the two peaks in the histogram from the jump/slow ramp test (b). The errors in these most frequent forces are smaller than the size of the symbols.

Fig. 2.

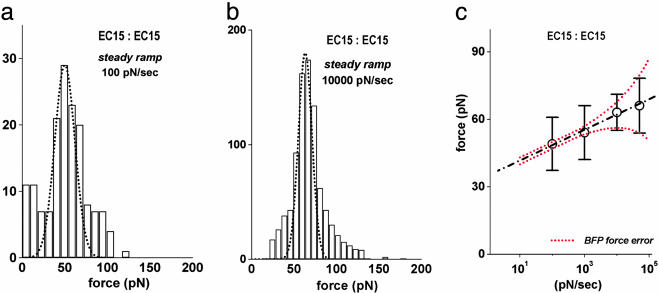
Mechanical strengths of trans-bonded EC15 fragments measured with steady ramps of force. (a) Histogram of EC15 vs. EC15 rupture forces obtained by using a slow steady ramp of 100 pN/sec. The dashed curve is a Gaussian that encompasses the force statistics local to the prominent peak. The SD (±12 pN) defining the Gaussian significantly exceeds the experimental force error of ±1.5 pN at this loading speed. (b) Histogram of EC15 vs. EC15 rupture forces obtained by using a 100-fold faster ramp of 10,000 pN/sec. Here, the Gaussian spread defining the dashed curve is comparable to the force error of ±5–6 pN. (c) The means ± SD for the Gaussian fits to the single peaks in the histograms of EC15 vs. EC15 rupture forces are plotted vs. the logarithms of the loading rates for the steady ramp tests. The linear regression (dashed black line) implies an off rate for EC15 vs. EC15 attachments rising exponentially with force as k_rupt(f) ≈ (5 × 10^–6 per sec) exp(f/3 pN). The two dotted red curves show the linear regression ± the force error at each loading rate.

Theoretical Model for Kinetically Limited Rupture of Single Bonds. The physical concept underlying the analysis of single-bond rupture is that the application of tensile force to a bond dramatically increases its “off rate” (failure rate) by lowering the free-energy barrier impeding bond dissociation. Thus, assuming that passage of the barrier contributes a fixed length x_β in the direction of force, the simplest model for the kinetic rate k_rupt of bond failure is an exponential function of force, k_rupt(f) ≈ (1/t_off) exp(f/f_β), with f_β defined by the ratio of thermal energy to the length gained in bond rupture, k_BT/x_β, and by the apparent-unstressed off rate, 1/t_off, as first postulated by Bell (19). Under the steady ramp of force (force = r_f × time) applied by constant speed separation from a probe tip, the failure rate increases exponentially with time, and the distributions p(f) of rupture forces can be described by a generic density function (20, 21), p(y) = exp[y – exp(y) + 1], using a simple relation based on the loading rate, y = f/f_β – log_e[r_f t_off/f_β]. With the positions of force peaks defined by, f* = f_β log_e[r_f t_off/f_β], we have used this model for kinetically limited failure to fit probability distributions to the peak regions in histograms for rupture of EC attachments following the simple procedure described in Supporting Text. Requiring a close fit over a large span in loading rates, we have obtained the force scales f_β and the preexponential off rates 1/t_off that characterize weakly and strongly bound substates of the EC interactions. Notably, when the experimental force error σ_exp at very fast loading rates became greater than ≈1.2 f_β characterizing the spread due to kinetics of failure, the force statistics were best approximated by Gaussian distributions using the mean force from the kinetic model, <f> ≈ f_β log_e[0.56 r_f t_off/f_β] given r_f > 10 f_β/t_off, and a SD defined by σ_f ≈ (σ_exp² + 1.42 f_β²)^1/2, as described in Supporting Text. (See also Fig. 6, which is published as supporting information on the PNAS web site.)

Results

EC15 vs. EC15. We used the steady ramp mode (Fig. 1c) to first test interactions between the full five-domain protein immobilized on beads at extremely low density. Consistent with the high probability of forming single transdimer attachments, the majority of the rupture forces from these tests formed a single prominent peak in each histogram as shown by the Gaussian functions encompassing the peak regions in Figs. 2 a and b (see also Figs. 7–10, which are published as supporting information on the PNAS web site, for histograms at other loading rates). Exploring loading rates r_f from 100 to 50,000 pN/sec, we were amazed to find little shift either in the positions of the Gaussian envelopes circumscribing these peaks or in their widths as the loading rate was increased. When plotted vs. the logarithm of loading rate as shown in Fig. 2c, the very small linear shift in the histogram force peak implies that the off rates for the EC15 vs. EC15 attachments were increasing extremely rapidly under each force ramp, essentially rising as steep exponentials with time as described in Methods (see Supporting Text for further details). From the linear fit to the data in Fig. 2c, the slope indicated a small characteristic force, f_β ≈ 3 pN, for the exponentiation of the off rate under the rising force. At the same time, extrapolation of the linear regression to zero force implied a small preexponential factor, or a very long characteristic lifetime, t_off ≈ 2 × 10⁵ sec, for the EC15 vs. EC15 interaction. Together, these parameters suggested an off rate given by k_rupt ≈ (5 × 10^–6 per sec) exp(f/3 pN). Given the steep exponential rise in failure rate with force, the spread in statistics local to the force peaks should be small, consistent with a SD predicted by the kinetics, σ_f ≈ 1.2 f_β at the loading rates <10,000 pN/sec where measurement errors σ_exp were negligible (Fig. 2c). However, the width of each histogram peak was found to be much broader than predicted by σ_f² ≈ σ_exp² + 1.4 f_β², until reaching the fast loading rates ≥10,000 pN/sec. Moreover, at the fastest loading rate of 50,000 pN/sec, the force error alone could account for the spread, leaving no evidence of the spread due to bond kinetics. So despite exhibiting a single well defined peak in force distributions at all loading rates, the spread in EC15 vs. EC15 rupture forces under slow speed loading seemed to indicate the presence of closely grouped subpopulations of interactions.

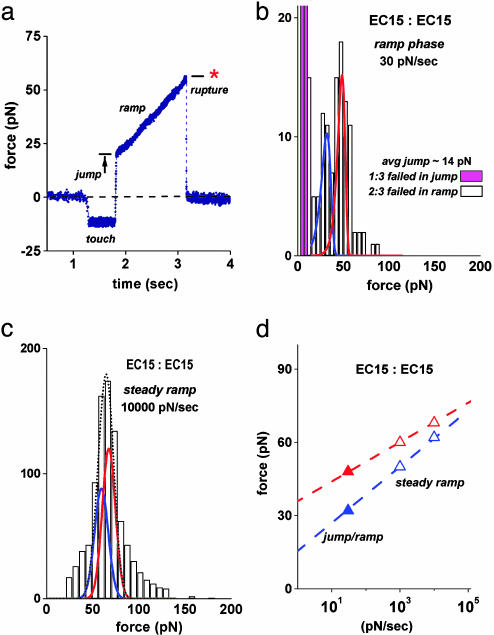
To expose the putative subpopulations of different EC15 vs. EC15 binding states, we used a recently described mode of force spectroscopy called the jump/ramp (18). As demonstrated by the force–time trace in Fig. 3a, the approach was to first jump within 0.01 sec to a small preset force of 10–30 pN with a fast loading rate of 2,200 pN/sec, then abruptly switch to a slower ramp, 30 pN/sec in this case. The objective was to eliminate the weak fast-failing complexes during the jump phase and to reveal the strongly bound complexes in the slow ramp phase. Indeed, when applied to EC15 vs. EC15 interactions, ≈33% of attachments failed rapidly during the jump phase, whereas the majority (≈66%) of attachments failed during the following slow ramp phase. Most significantly, the forces for the stronger attachments in the slow ramp phase were separated clearly into two narrow groups, one with a peak at 32 pN and the other with a peak at a higher force of 48 pN, as shown in Fig. 3b. Formed during bead–bead contacts with the same 0.1-sec period of touch and ≈15 pN impingement force, similar subpopulations of the two strongly bound EC15 vs. EC15 substates were likely present in the steady ramp tests, and because they represent the majority of all attachments, it follows that these strongly bound substates must have accounted for the majority of forces forming the prominent peaks in the steady ramp histograms (see Figs. 2 a and b and 7a).

Treating the off rates of the strongly bound substates as exponential functions of the force, we have used the theory described in Methods to model the force distributions for each strong substate. Varying the two kinetic parameters (f_β, 1/t_off) defining the off rate for each substate, we fit the model distributions to the force peak regions in histograms obtained from both the jump/slow ramp and all steady ramp tests following the procedure outlined in Supporting Text. Examples of the distributions found to characterize the strongly bound substates of EC15 vs. EC15 interactions are illustrated by the blue and red curves superposed on histograms from the jump/slow ramp and a fast steady ramp in Fig. 3 b and c. The best fit to all of the EC15 vs. EC15 histograms yielded the following force scales for exponentiation of the failure rates: f_β ≈ 3–4 pN for the “red substate” and f_β = 5 pN for the “blue substate” (Table 1). Even though differing by <2-fold in the force scale f_β, the mechanical strengths of the strong EC15 vs. EC15 subpopulations were separated by the slow 30 pN/sec ramp because of a nearly 10,000-fold difference in their preexponential factors, i.e., 1/t_off ≈ 10^–6 to 10^–5 per sec for the red substate and 1/t_off = 10^–2 per sec for the blue substate (Table 1). (Note that the lower force in a confidence range for f_β in Table 1 corresponds to the slower unstressed off rate, i.e., longer lifetime.) Summarized in what is called a “dynamic force spectrum,” the most frequent rupture forces from these distributions are plotted vs. the logarithms of the loading rates in Fig. 3d, demonstrating convergence with increase in loading rates as verified by the narrow force peak at 10,000 pN/sec (Fig. 3c).

Table 1. Parameters governing strengths of EC interactions.

Substate (color code)	toff, sec	fβ, pN	xβ, nm
EC12:EC12/15
cyan	0.12-.09	6-7	0.67-0.57
green	2-1	6-7	0.67-0.57
EC15:EC15
blue	100	5	0.8
red	106-105	3-4	1.3-1.0

EC12 vs. EC12. We also examined interactions between the two outermost domains (EC12) to determine whether the strengths of EC12 module interactions could account for the EC15 vs. EC15 rupture forces. When probed in the steady ramp mode, surprisingly, the strengths of the EC12 module attachments essentially vanished at loading rates ≤100 pN/sec as shown in Fig. 4a. The EC12 module interactions only exhibited an appreciable strength when subjected to very fast loading, yielding much broader distributions of rupture forces than found for EC15 vs. EC15 (Fig. 4b). The disappearance of strength for EC12 vs. EC12 <100 pN/sec indicated that the EC12 module interactions were characterized by fast off rates in the range of 1–10 per sec when unstressed. It also suggested that weak EC12 module interactions may have contributed to the failure of EC15 vs. EC15 attachments at small forces during the rapid jump and the onset of the slow ramp.

We were puzzled by the apparently fast dissociation of EC12 module interactions given that a slower off rate was obtained in a flow chamber assay of interactions between the same EC12 fragments (8). Hence, we speculated that the broad force distributions exhibited by EC12 interactions under steady ramps >1,000 pN/sec might reflect more than one weak complex. To test this hypothesis, we again used the jump/slow (30 pN/sec) ramp, probing both EC12 vs. EC12 interactions and EC12 vs. EC15. (Data for EC12 vs. EC15 appear in Supporting Text and Fig. 11, which is published as supporting information on the PNAS web site.) Nearly identical in both cases, the majority of attachments (≈66%) broke during the jump phase at 2,200 pN/sec with a force distribution that exhibited a prominent peak at low force (Fig. 4d). The remaining (≈33%) attachments at the end of the jump then failed within a small range of force under the slow 30 pN/sec ramp as shown in Fig. 4e. Further examining the EC12 vs. EC12 attachments that survived the jump, we performed a special jump/fast ramp test, switching the ramp phase to 1,000 pN/sec after the jump phase. As expected, the force statistics for the jump survivors were spread out by the faster ramp and exhibited a prominent peak plus a small-broad tail of high forces (Fig. 4f). Clearly demonstrated by comparison of Fig. 4 d and f, using different ramp speeds after the jump led to a separation of two subpopulations of weak attachments. The first group failed almost completely in the jump phase under a ramp of 2,200 pN/sec before reaching a jump force of ≈30 pN. The second group failed almost completely within a few piconewtons after the jump under a ramp of 30 pN/sec but could be strengthened to ≈50 pN by using a ramp of 1,000 pN/sec.

Again treating the off rates of the weakly bound EC12 substates as exponential functions of the force, we used the theory for kinetically limited rupture to model force distributions for the two weak substates. Varying the two kinetic parameters (f_β and 1/t_off) defining the off rate for each substate, we matched the model distributions to the peak regions in histograms obtained from both the jump/slow and jump/fast ramp tests as well as the steady ramp tests at 1,000 and 10,000 pN/sec. These fits are identified by the “cyan and green” distributions superposed on the histograms in Fig. 4 b, d, and f. Interestingly, distributions predicted with the kinetic parameters for the weakly bound substates of EC12 module interactions also were found to match the distinct subpopulation of low forces appearing in histograms from steady ramp tests of EC15 vs. EC15 interactions (see Figs. 9 and 10). Summarized as before in a dynamic force spectrum, the most frequent rupture forces from these distributions are plotted vs. the logarithms of the loading rates in Fig. 4c, demonstrating a similar force scale of f_β ≈ 6–7 pN for exponentiation of the failure rates. The 10-fold difference in the preexponential factors for the failure rates, 1/t_off ≈ 8–11 per sec for the cyan substate and ≈ 0.5–1 per sec for the green substate, enabled a clear identification of each subpopulation in the jump/fast ramp test (Fig. 4 d and f). The parameters describing the green substate are closely similar to those obtained from the flow chamber experiment (8).

Interpretation

Testing pairwise EC15 vs. EC15, EC12 vs. EC12, and EC12 vs. EC15 interactions, we have exposed four substates of mechanical strength, presumably formed randomly upon contact between the probe tip and target microbeads. The kinetic parameters governing the failure rates of these substates are summarized in Table 1, labeled by the color code (cyan, green, blue, and red) used for the probability distributions matched to the force histograms in Figs. 3 and 4. The most intriguing feature of the kinetic parameters listed in Table 1 is the enormous increase in the apparent lifetimes t_off from 0.09–0.12 and 1–2 sec for the weak substates to 10² and 10⁵–10⁶ sec for the strong substates and the corresponding decrease in the thermal force scales f_β from 6–7 to 5 and 3–4 pN, respectively. Most important, the ascending lifetimes among the EC15 vs. EC15 and EC12 vs. EC12 interactions imply a corresponding hierarchy in the heights of the activation energy barriers impeding their dissociation [i.e., k_BT Δlog_e(t_off) = ΔE_b]. Thus, when multiplied by thermal energy (k_BT ≈ 0.6 kcal/mol), the differences between logarithms of the substate lifetimes suggest that the activation energies for the stronger blue and red substates of EC15 vs. EC15 interactions exceed the activation energies for the weakest cyan substate of EC12 module interactions by ΔE_b ≈ 4–5 kcal/mol and ΔE_b ≈ 8–10 kcal/mol, respectively, and the activation energy for the cyan substate being ≈1 kcal/mol lower relative to the green substate. At the same time, the descending force scales f_β among the EC15 vs. EC15 and EC12 vs. EC12 interactions show that rupture of the two stronger interactions contributes at least twice the length (x_β = k_BT/f_β) in the direction of force as compared with rupture of the weaker EC12 module interactions.

Discussion and Conclusions

We find that single trans-bonded pairs of EC15 exhibit an unusual hierarchy of mechanical strengths, revealing substates of the homophilic interactions with very different kinetic off rates under tensile force. The hierarchical response suggests that pairwise contact between cadherins leads to overlapping multidomain interactions analogous to the discrete states of adhesion observed when separating hundreds of thousands of cadherin attachments in a macroscopic SFA experiment (11, 12). However, unlike the large jumps in distance between adhesive minima seen in the SFA experiments, the small distances implied by thermal force scales f_β in our experiments reflect the lengths gained from passage of kinetic barriers and thus are unrelated to the sizes of domains. Furthermore, the hierarchy of barrier energies derived from logarithms of the characteristic substate lifetimes cannot be compared quantitatively with the energy minima derived from the mechanical force instabilities in the SFA tests, yet the energy differences are intriguingly similar in ratio. Conversely, clearly relevant to our measurements are the previous tests of interactions between full-length vascular endothelial-cadherins by AFM (15). The AFM tests of vascular endothelial-cadherins yielded forces at different pulling speeds somewhat similar to our results for the weak green substate of EC12 vs. EC12 interactions; however, the force distributions were much broader than in Fig. 4b, and the force traces exhibited multistep detachment events. In addition, the widths of force distributions in the AFM experiments were found to increase with duration of touch, which the authors attributed to increase in the number of multimeric attachments (15). By comparison, we rarely observed a double step of detachment in thousands of trials between the EC beads with very low surface densities; when formed, attachments ruptured abruptly as seen in Figs. 1c and 3a. Moreover, as we show in Fig. 10 and Supporting Text, increasing the period of touch from 0.1 to 3 sec in tests of EC15 vs. EC15 enriched the stronger blue and red subpopulations and eliminated the weak fast-dissociating subpopulations.

The hierarchy of pairwise mechanical strengths for EC starts with the short-lived EC12 module interactions that possess strength only under rapid application of stress. Perhaps representing the N-terminal domain interactions imaged in x-ray crystal structure (9), the strengths of these weak substates may characterize the adhesivity of the trans-bonded cadherins conceptualized in the zipper model (10). From the perspective of function, the fast release and low strength associated with EC12 module interactions could be advantageous in the exploratory recognition process that likely occurs in the early stages of cell patterning (8). These fast-failing interactions are well documented in cadherin studies (2, 5–14, 22–24). Transitioning to deeper-bound configurations indicated by the blue and red substates of the full five-domain interactions, attachments then could provide sufficient strength to stabilize a newly formed tissue structure and thus sustain large stresses under deformation. Although the inner domains of EC15 seem much less accessible for trans-dimerization, they still seem to play an important role in adhesion as suggested by earlier studies using the conserved cysteines (24) in the EC5 domain plus blocking with inhibitory antibodies (23), as well as in more recent assays of binding and adhesion (24).