Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2016 Dec 29;230(4):524–531. doi: 10.1111/joa.12581

Zygomatic bone shape in intentional cranial deformations: a model for the study of the interactions between skull growth and facial morphology

S Ketoff 1,2,3, F Girinon 3, S Schlager 4, M Friess 5, T Schouman 1,2,3, P Rouch 3, R H Khonsari 1,2,✉
PMCID: PMC5345617  PMID: 28032345

Abstract

Intentional cranial deformations (ICD) were obtained by exerting external mechanical constraints on the skull vault during the first years of life to permanently modify head shape. The repercussions of ICD on the face are not well described in the midfacial region. Here we assessed the shape of the zygomatic bone in different types of ICDs. We considered 14 non‐deformed skulls, 19 skulls with antero‐posterior deformation, nine skulls with circumferential deformation and seven skulls with Toulouse deformation. The shape of the zygomatic bone was assessed using a statistical shape model after mesh registration. Euclidian distances between mean models and Mahalanobis distances after canonical variate analysis were computed. Classification accuracy was computed using a cross‐validation approach. Different ICDs cause specific zygomatic shape modifications corresponding to different degrees of retrusion but the shape of the zygomatic bone alone is not a sufficient parameter for classifying populations into ICD groups defined by deformation types. We illustrate the fact that external mechanical constraints on the skull vault influence midfacial growth. ICDs are a model for the study of the influence of epigenetic factors on craniofacial growth and can help to understand the facial effects of congenital skull malformations such as single or multi‐suture synostoses, or of external orthopedic devices such as helmets used to correct deformational plagiocephaly.

Keywords: artificial skull deformation, cross‐validation approach, mesh registration, statistical shape model, zygoma

Introduction

Intentional cranial deformations (ICD) were ubiquitous mutilations performed at an early age with the purpose of permanently modifying the shape of the skull (Dingwall, 1931). Using different types of external devices, the skulls of newborns were artificially deformed starting from birth and during at least the first year of life. Artificially deformed skulls are reported from all over the world, and even from Western Europe – one of the best known examples of European ICDs are artificial deformations from the region of Toulouse in South‐Western France. ICDs were especially prevalent in pre‐Columbian South‐American populations of Northern Chile and Southern Bolivia (Dingwall, 1931). ICDs are not performed anymore but Toulouse‐type deformations from Southern France are reported as late as the beginning of the 20th century (Janot et al. 1993). Collections of deformed skulls kept in anthropological collections such as in the Muséum National d'Histoire Naturelle (Musée de l'Homme) in Paris are a unique material for studies on the interactions between external mechanical constraints and craniofacial growth (Antón, 1989; Cheverud et al. 1992; Khonsari et al. 2013a).

Many classifications have been proposed for sorting the different types of artificial skull deformations; the most basic classification involves two subtypes: (i) antero‐posterior (AP) deformations, characterized by flattening at the front and back, and lateral bulging of the head and (ii) circumferential (C) deformations, resulting in a cone‐shaped skull vault (Dingwall, 1931; Antón, 1989; Cheverud et al. 1992; Kohn et al. 1993). AP deformations were obtained by applying solid compression devices (boards, flat stones) on the forehead and the occiput and C deformations were obtained by wrapping the head with compressive bandages (Dingwall, 1931; Schijman, 2005). Toulouse (T) deformations, mostly reported during the 19th century and until the World War I, resulted from a mechanism similar to C deformations: several compressives bandages, often ornate, were used to wrap the head of newborns; morphologically, T deformations resemble C deformations (Dingwall, 1931; Janot et al. 1993). AP deformations have been subdivided into: (i) oblique (APo) and (ii) erect (APe) deformations, mostly according to the angle between the compression devices applied on the forehead and the upper orbital rim, although the criteria for such a subdivision varies according to different authors (Dingwall, 1931; Dembo & Imbelloni, 1938). In the present study, we considered AP deformed skulls as a homogeneous group, assuming that the subdivision into APo and APe deformations is not always morphologically obvious.

Modifying the outline of the skull using external devices has an influence on the structure of the face (Antón, 1989; Cheverud et al. 1992; Kohn et al. 1993). This influence has been characterized in numerous previous studies and is attributed to two factors: (i) obtuse posterior skull base angles (platybasia) in deformed skulls compared with non‐deformed skulls and (ii) deformation of the frontal bone (Antón, 1989; Cheverud et al. 1992; Kohn et al. 1993). More precisely, it has recently been established that external constraints exerted on the skull vault modify the three‐dimensional morphology of the orbits and the maxillary sinuses (Khonsari et al. 2013a). I has also been shown that the thickness of skull vault bones are modified in the zones where pressure is exerted by the deformation devices (Grupe, 1984; Khonsari et al. 2013a; Boman et al. 2016).

The zygomatic bone forms part of the orbital floor and the morphology of this bone may thus be affected by ICDs. Nevertheless, the specific effects of ICDs on the shape and the antero‐posterior projection of the zygomatic bone have not been studied in detail to date. Interestingly, the projection of the zygomatic bone is important in defining facial features, as it contributes to determining the antero‐posterior projection of the midfacial soft‐tissues (Whitaker & Bartlett, 1991).

The relationships between external constraints exerted on the skull and craniofacial architecture are also particularly relevant in the context of the prevention of positional posterior plagiocephaly due to supine sleep position. In fact, since the ‘Back‐to‐Sleep’ campaign of 1994, parents are advised to put their newborn babies to sleep in a supine position to prevent sudden infant death (Willinger et al. 1998). This campaign has provided excellent results for sudden death prevention but has caused an increase in posterior skull deformations known as posterior positional plagiocephaly (Argenta et al. 1996; Turk et al. 1996), from 0.3% (O'Broin et al. 1999) before the campaign to 8.2% currently (Boere‐Boonekamp & van der Linden‐Kuiper, 2001). Posterior plagiocephaly is associated with facial asymmetry (Netherway et al. 2006). One of the methods for correcting posterior plagiocephaly is using custom‐made helmets that exert external pressure on the skull vault. By correcting the posterior flattening of the head that defines posterior plagiocephaly, helmet therapy also aims to correct facial asymmetry (Lee et al. 2015). The questions raised by the assessment of the efficiency of helmets on facial asymmetry thus have striking similarities with the study of the facial repercussion of artificial skull deformations.

In this study we intended to characterize midfacial shape in different categories of ICDs and thus better understand the interactions between the skull and the face during growth. We considered skulls with AP, C and T deformations and compared them with non‐deformed (ND) skulls from the same ethnic backgrounds (Khonsari et al. 2013a). Mean model skulls for each group were obtained using mesh registration, and the external surfaces of the mean zygomatic bones were compared using various image analysis methods.

Our findings suggest that the shape of the zygomatic bone is modified in a specific way by each deformation modality. Similar interactions and effects on facial structure could occur when helmets are used for the treatment of posterior positional plagiocephaly.

Materials and methods

We considered a study sample of 14 ND skulls, 19 skulls with AP deformations, 9 skulls with C deformations and 7 skulls with T deformations (Khonsari et al. 2013a). C and AP skulls were from Bolivia, T skulls were from South‐Western France, and ND skulls were sampled from the same two regions. We used the common morphological definitions for C and AP deformations (Dingwall, 1931; Antón, 1989; Cheverud et al. 1992; Kohn et al. 1993). All skulls were part of the collections of the Muséum National d'Histoire Naturelle (Musée de l'Homme) in Paris (Supporting Information Table S1). All individuals were adults, defined by the fusion of the spheno‐occipital synchondrosis. Information on sex was not available. We subjected each skull to paleopathological examination to rule out premature suture fusion (craniosynostosis), previous trauma and taphonomic deformations (Khonsari et al. 2013a).

Skulls were scanned using a standard medical CT‐scanner according to a previously published protocol specifically designed for dry skulls (Badawi‐Fayad et al. 2005; Khonsari et al. 2013a). Segmentation was performed using mimics 18.0 (Materialise, Leuwen, Belgium). Meshes were cleaned using geomagic studio (3DSystems, Rock Hill, SC, USA).

A topological mesh was obtained using a registration process involving all skulls. The registration process required a reference mesh, defined as a clean mesh chosen from among previously segmented skulls. After choosing a reference mesh, all 48 remaining meshes were aligned based on this reference using three manual landmarks (left porion, right porion and nasion). Iterative closest point method (Besl & McKay, 1992) was used to refine the superimposition. Non‐rigid registration was then performed to morph the reference skull onto all other skulls. The first step of non‐rigid registration involved a Gaussian matching algorithm (Moshfegui et al. 1994), which was used to find the closest target vertices on the target skull when starting from the reference skull mesh. This matching algorithm allowed the associated displacement field between this reference and the target to be computed. This displacement field was then smoothed using a Gaussian kernel. At the end of each iteration, to obtain a realistic shape, the morphed reference mesh was weighted with its projection on a Gaussian process model using Gaussian kernels (Gerig et al. 2014), as previously implemented in r (R Core Team 2016) (Rüdell & Schlager, 2013; Schlager & Rüdell, 2013; Schlager & Jefferis, 2016). By applying this process to the 49 fully segmented skulls, we obtained skulls with similar mesh topology. A global mean model was then computed as the barycenter of each vertex. To improve the regularity of the mesh, this mean skull was uniformly re‐meshed with a mean resolution of 1.7 mm per edge (corresponding to the resolution of the target meshes). A new reference mesh was thus defined before re‐applying the previous process to obtain final, clean‐registered meshes. Using this method, we defined mean models for ND skulls, AP, C and T groups (Fig. 1).

Figure 1.

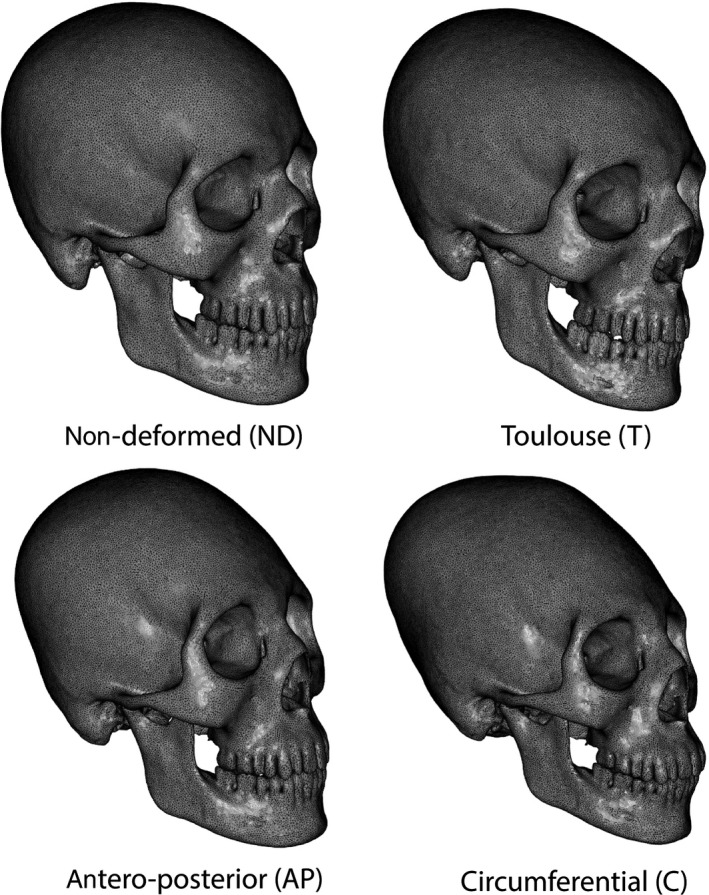
Figure 1

Open in a new tab

Mean models for control, antero‐posterior, Toulouse and circumferential populations.

The limits of the zygomatic bone where defined as: (i) the fronto‐zygomatic suture, (ii) the maxillo‐zygomatic suture and (iii) the insertion of the zygomatic arch on the temporal bone. Regions of interest corresponding to the zygomatic bone were outlined in mimics 18.0 (Materialise, Leuwen, Belgium) (Fig. 2).

Figure 2.

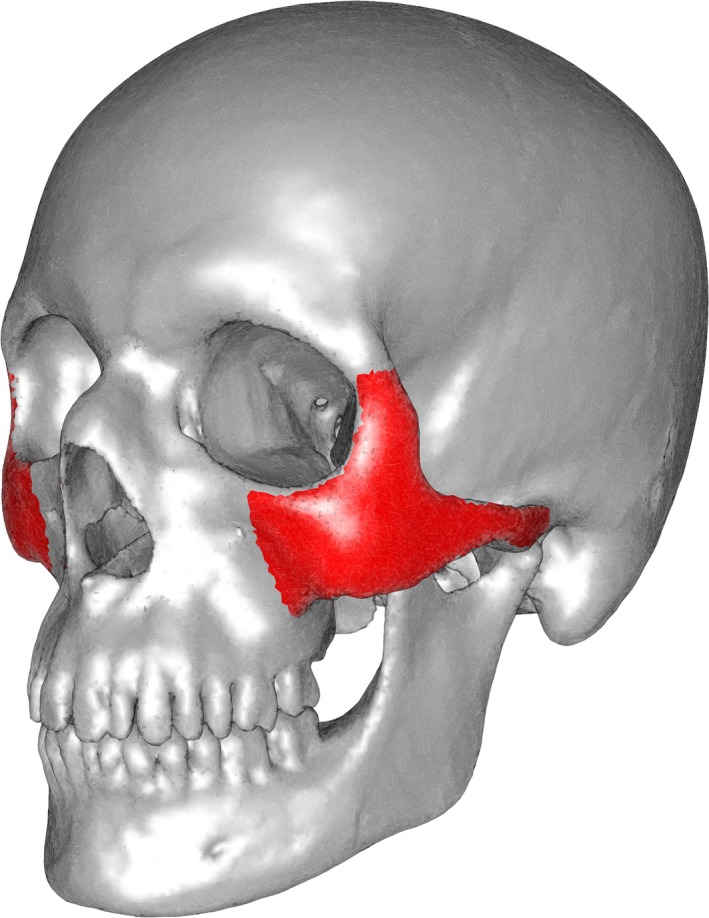
Figure 2

Open in a new tab

Reference skull (in silver) with regions of interest (ROI, in red) containing the body of the right and left zygomatic bones and the zygomatic part of the temporal bone.

We computed the distance between the mean non‐deformed skull and the means of each deformation type using the orthogonal projection of all vertices of the mean non‐deformed mesh on each mean deformed mesh vertex. Mapping these distances on the surface of the mean model using a color code (Fig. 3) allowed the relative spatial position of the mean deformed zygomatic bones to be estimated relative to the same bone in non‐deformed skulls: a positive distance (red color code) indicated that the deformed zygomatic bone was more projected than in ND skulls, and a negative distance (blue color code) meant that the deformed zygomatic bone was less projected than in ND skulls (Fig. 4).

Figure 3.

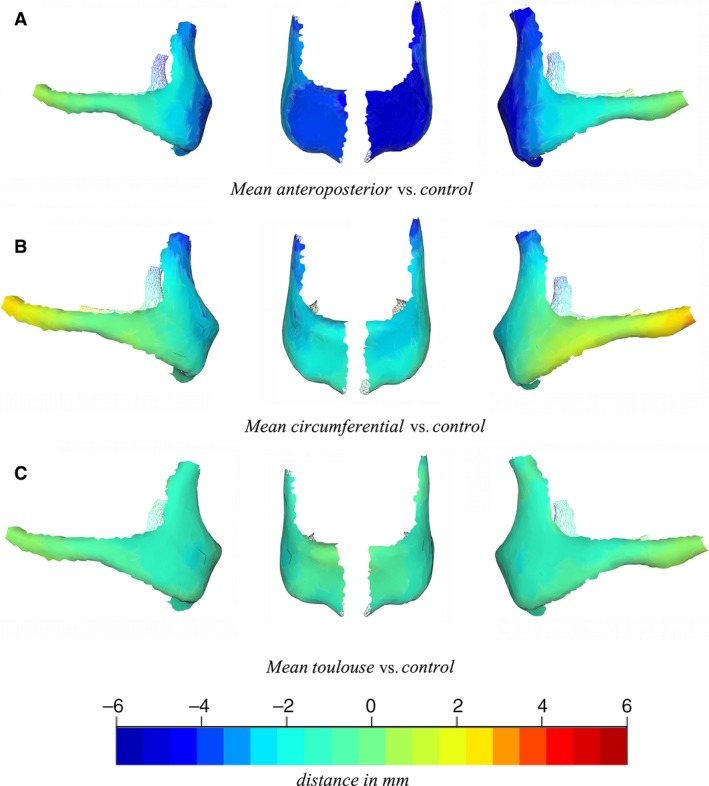
Figure 3

Open in a new tab

Distance maps between the mean non‐deformed zygoma and the mean models for the three types of deformation: antero‐posterior (A), circumferential (B) and Toulouse (C), showing different degrees of zygoma hypo‐projection. From left to right on each row: right lateral view, right frontal view, left frontal view, left lateral view.

Figure 4.

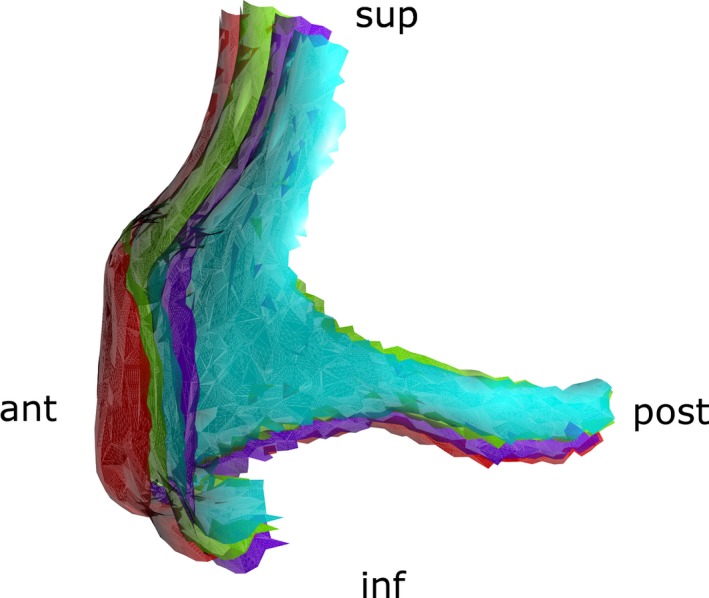
Figure 4

Open in a new tab

Position of the mean right zygomatic bones relative to control (red): antero‐posterior (purple), circumferential (blue) and Toulouse (green). ant., anterior; inf., inferior; post., posterior; sup., superior.

Principal component analysis on the vertices of the zygomatic bones showed that the first 17 components accounted for 90% of the variance in shape. Zygomatic bones had been aligned using rigid registration (Procrustes alignment). We considered only these 17 components for the rest of the study. Royston's multivariate normality test was used to spot outliers and obtain a multivariate normal subset of data using the mvn package in r (Korkmaz et al. 2014). Multivariate analysis of variance (manova) was performed on the multivariate normal subset of data after removing the outliers to screen for statistically significant shape differences within groups ND, AP, C and T. Canonical variate analysis (CVA; Campbell & Atchley, 1981) was used to define the principal axes separating the different groups. Using Euclidean distances or Mahalanobis distances (defined as the Euclidian distance weighted by the inverse of the covariance) between a subject and its group, we were able to classify the skulls. Permutation testing (1000 rounds) was performed on this Mahalanobis distance using the adonis function from the vegan package in r (Oksanen et al. 2014). To estimate the classification accuracy when considering an individual skull without knowing to which group (ND, AP, C, T) it belonged, we performed a cross‐validation study and obtained cross‐validated percentages. Finally, to illustrate the main trend in shape variation defining the differences between groups, we performed a 3D rendering of the first canonical axis distinguishing ND from AP, C and T (Fig. 5).

Figure 5.

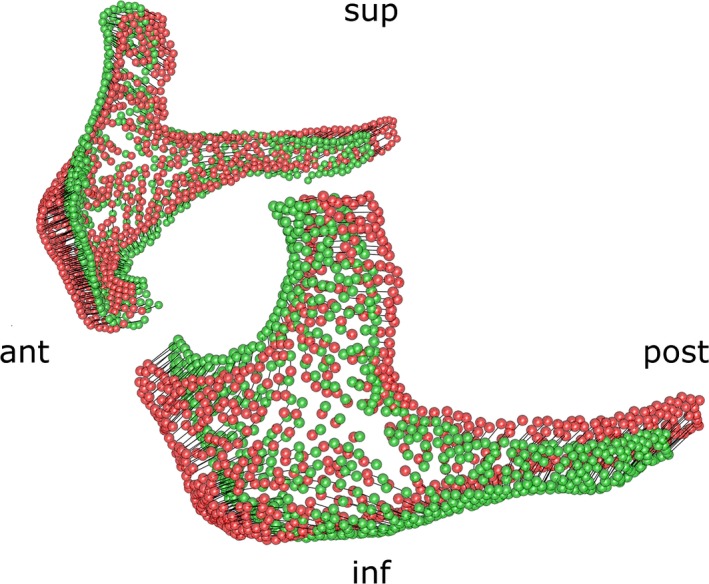
Figure 5

Open in a new tab

3D visualization of the first canonical axis characterizing differences between all groups; the axis corresponds mostly to an antero‐posterior movement of the zygomatic bone. ant., anterior; inf., inferior; post., posterior; sup., superior.

Results

Color coding of the distance between the three mean deformed zygomatic bones and the mean non‐deformed zygomatic bone showed qualitative differences between groups (Fig. 3). Royston's multivariate normality test showed that the dataset was not multivariate normal (H = 28.69, P < 0.001) and allowed five outliers (4 C skulls and 1 AP skull) to be identified. The same normality test performed on the sub‐dataset without the outliers showed that the dataset was multivariate normal (H = 6.74, P < 0.001). Statistical differences between ND, AP, C and T groups were confirmed by manova in both groups with and without outliers (Table 1).

Table 1.

Multivariate analysis of variance (manova) results showing significant differences between ND, AP, C and T groups

Degrees of freedom Pillai's trace F df df error P
With outliers 3 0.95 3.96 15 129 < 0.0001
Without outliers 3 0.82 2.87 15 114 < 0.001
Open in a new tab

Euclidian distances between mean deformed zygomatic bones and mean ND were different for AP and C but not for T: the significance of shape differences based on Euclidian distances was assessed using permutation testing (1000 rounds) (Table 2).

Table 2.

Significance of shape differences based on Euclidian distances (P < 0.01), assessed using permutation testing (1000 rounds)

Antero‐posterior Circumferential Control
Circumferential < 0.001
Control < 0.001 0.002
Toulouse 0.004 0.087 0.607
Open in a new tab

Permutation testing (1000 rounds) on Mahalanobis distances was also significant (Table 3 Supporting Information Table S2). By computing Mahalanobis distances and thus taking into account biases due to scale effects, we found that all deformed groups including T were significantly different from mean ND (Table 3). To assess whether the shape of the zygomatic bone alone was sufficient to define the type of deformation, we computed cross‐validation classification percentages (Table 4) but did not obtain satisfactory results; the overall classification accuracy was close to 50%, which is better than random but still poor.

Table 3.

Significance of shape differences based on Mahalanobis distances (P < 0.01), assessed using permutation testing (1000 rounds)

Antero‐posterior Circumferential Control
Circumferential < 0.0001
Control 0.0005 < 0.0001
Toulouse 0.0002 0.0005 0.004
Open in a new tab

Table 4.

Cross‐validated classification accuracies in percent. The overall classification accuracy was 53.06%

% Antero‐posterior Circumferential Control Toulouse
Antero‐posterior 78.95 0.00 21.05 0.00
Circumferential 11.11 33.33 22.22 33.33
Control 42.86 7.14 42.86 7.14
Toulouse 28.57 28.57 14.28 28.57
Open in a new tab

In brief, AP, C and T deformations had specific and significant repercussions on the shape of the zygomatic bone. The main trend in shape variation differentiating all deformed groups from non‐deformed skulls was the antero‐posterior projection of the zygomatic bone (Fig. 5). Deformed skulls showed different degrees of zygomatic bone hypoprojection: ND < T < C < AP (Figs 3 and 4). Nevertheless, the differences in shape between non‐deformed and deformed skulls were not sufficient to attribute a deformation type to a population when using the shape of the zygomatic bone as the only source of information.

Discussion

According to cultural anthropological data, the devices used to induce intentional deformations did not exert direct mechanical pressure on the face (Dingwall, 1931; Schijman, 2005). The changes in zygomatic bone structure due to ICDs are thus an interesting model for the study of the interactions between skull growth and facial growth: general conclusions on these interactions can be drawn from our results.

Limitations of the study

This is the first study to focus on the 3D craniofacial anatomy of Toulouse‐type intentional deformations. Nevertheless, our samples for all three AP, C and T groups were small and further studies on larger samples, especially of circumferential and Toulouse‐type deformed skulls, are required to support our results. In particular, Toulouse deformations have rarely been studied using current morphometric approaches (Janot et al. 1993) and little is known about the prevalence of this practice and its cultural background. Our study calls for further investigations on the most emblematic Western European example of artificial skull deformation.

We could not take into account population effects in this study and this constitutes a limitation, as intrinsic differences in zygomatic architecture may exist between South American and French populations and thus interfere with our results, despite the fact that our control group included both South American and French non‐deformed skulls. Furthermore, data on sex were not available and this could constitute a bias, as it is known that sexual dimorphism affects the facial bones (Walrath et al. 2004). Finally, we grouped together the two subtypes of AP deformations (AP erect and AP oblique) despite the ongoing debate on the differential effects of APe and APo forms on craniofacial architecture (Friess & Baylac, 2003).

The fact that the cross‐validated CVA failed to distinguish clearly between zygoma in different types of deformation also requires further investigation. CVA is commonly used in morphometrics for classification purposes and identifies axes which maximize the variance between groups and minimize the intra‐group variance. Nevertheless, whereas the failure of CVA to distinguish zygomas from different groups hints at a common growth response to the diverse mechanical constraints of the deformation devices, the group differences in Euclidean distances suggest otherwise. Clearly, larger datasets are required to help elucidate this aspect of cranial plasticity.

Recent advances on mechanotransduction and mechanosensation

The understanding of the interactions between craniofacial growth and mechanical forces has been the subject of recent advances. Bone formation due to the response of craniofacial sutures to repeated external constraints during mastication has been proven experimentally (Opperman, 2000; Herring, 2008). Theoretical models have reproduced the interactions between mechanical forces and sutural bone formation and contributed to the dissection of the cellular events involved in the response of craniofacial bones to external stimuli (Zollikofer & Weissmann, 2011; Khonsari et al. 2013b). More interestingly, several molecular pathways involving the primary cilia have been incriminated in mechanosensation and mechanotransduction at the level of skull bones, based on in vitro (Patel & Honoré, 2010; Xiao & Quarles, 2010) and in vivo studies (Kolpakova‐Hart et al. 2008; Hou et al. 2009; Khonsari et al. 2013c). All together, these results suggest that molecular, cellular and tissular processes could account for the response of skull bones to external mechanical forces. The shape modifications in the zygomatic bone most probably involve several of these transduction phenomena.

Intentional skull deformations from a clinical point of view

Clinical situations are described where zygomatic bone deformations seem to be secondary to skull deformations. In unicoronal synostoses, where the main anomaly is the early closure of one of the two coronal sutures, zygomatic anomalies are reported (Goodrich, 2005; Pfaff et al. 2013) but the early fusion of additional craniofacial sutures, such as the frontosphenoidal suture, may be incriminated and interact with facial growth (Showalter et al. 2012).

Helmets are one of the treatment modalities for posterior positional plagiocephaly. Helmet therapy has been shown to modify the shape of the face and zygomatic bones (Lee et al. 2015; Lim et al. 2016) and contribute to correct the facial asymmetry associated with posterior plagiocephaly. Nevertheless, most of the helmets available for clinical use directly compress the zygomatic arch and the lateral aspect of the zygomatic bones (Lee et al. 2015), and this direct compression most probably accounts for the reported changes in facial bone structure.

On the contrary, in the three ICD modalities we considered, AP, C and T, there was no direct constraint exerted on the face (Dingwall, 1931) and there is no reason to suppose the occurrence of any premature fusions of skull vault and/or craniofacial sutures. We thus illustrate a unique situation where mechanical forces exclusively exerted on the skull modify the structure of the midface. These findings are consistent with several previous reports dedicated to the facial effects of cranial deformations: in fact, some authors have reported changes in facial height and breadth as well as facial protrusion in ICDs (Oetteking, 1924; Rogers, 1975; Friess & Baylac, 2003), while others have found no effects at all (Ewing, 1950; Cocilovo, 1975). Here, the use of innovative three‐dimensional methods allowed the quantification of the facial morphological modifications secondary to constraints exerted on the vault alone. In this context, ICDs are an extreme example of the same phenomena involved in the skull shape modifications due to supine sleep position, which eventually cause the development of posterior plagiocephaly.

Conclusion

Here we provide the first three‐dimensional quantitative assessment of mid‐facial modifications in ICDs. The fact that cranial deformation demonstrably affects the shape of the zygomatic bone is an illustration of the plasticity of the face during the first years of life and of the numerous indirect factors influencing the craniofacial structure. ICDs are in fact an extreme example of effects that are also exerted to a lesser extent by more moderate factors such as sleep position during infancy.

The study of artificial deformations illustrates the fact that the structure of the adult face is the outcome of all mechanical forces exerted on the craniofacial region during growth. More generally, studying the shape of the zygoma is important when trying to characterize human craniofacial architecture: the zygoma is a major contributor to the position of facial soft‐tissues. Nevertheless, the three‐dimensional zygomatic shape is not easy to describe or quantify. The framework we provide could thus be used in further comparative anatomical studies of the human midface and, beyond that, any anatomical structure with a shape that is difficult to quantify.

Authors’ contributions

Serge Ketoff: performed the analyses, wrote the paper. François Girinon: performed the analyses, wrote the paper. Stefan Schlager: designed the analysis method, performed the analyses. Martin Friess: designed the sample composition, classified the skulls. Thomas Schouman: performed the paleopathological analysis of the skulls. Philippe Rouch: supervised the statistical analysis of the results. Roman Khonsari: performed the analyses, wrote the paper.

Conflict of interest

No conflict of interest.

Supporting information

Table S1. List of dry skulls included into the study.

Click here for additional data file. (9.5KB, xls)

Table S2. Significant permutation testing (1000 rounds) on Mahalanobis distances.

Click here for additional data file. (13KB, doc)

Acknowledgements

R.H.K. and S.K. were supported by the Union des Blessés de la Face et de la Tête, Fondation des ‘Gueules Cassées’. S.K. was supported by the Fédération Française d'Orthodontie (FFO).

References

  1. Antón SC (1989) Intentional cranial vault deformation and induced changes of the cranial base and face. Am J Phys Anthropol 79, 253–267. [DOI] [PubMed] [Google Scholar]
  2. Argenta LC, David LR, Wilson JA, et al. (1996) An increase in infant cranial deformity with supine sleeping position. J Craniofac Surg 7, 5–11. [DOI] [PubMed] [Google Scholar]
  3. Badawi‐Fayad J, Yazbeck C, Balzeau A, et al. (2005) Multi‐detector row CT‐scanning in paleoanthropology at various tube current settings and scanning mode. Surg Radiol Anat 7, 1–8. [DOI] [PubMed] [Google Scholar]
  4. Besl PJ, McKay ND (1992) A method for registration of 3D shapes. IEEE Trans Pattern Anal Mach Intell 14, 239–256. [Google Scholar]
  5. Boere‐Boonekamp MM, van der Linden‐Kuiper LL (2001) Positional preference: prevalence in infants and follow‐up after two years. Pediatrics 107, 339–343. [DOI] [PubMed] [Google Scholar]
  6. Boman F, Froment A, Charlier P (2016) Variations in the thickness of the cranial vault in a deformed skull from pre‐Hispanic Ancón (Peru). Bull Mém Soc Anthropol Paris 28, 221–225. [Google Scholar]
  7. Campbell NA, Atchley WR (1981) The geometry of canonical variate analysis. Syst Zool 30, 268–280. [Google Scholar]
  8. Cheverud JM, Kohn LAP, Konigsberg LW, et al. (1992) Effects of fronto‐occipital artificial cranial vault modification on the cranial base and face. Am J Phys Anthropol 88, 323–345. [DOI] [PubMed] [Google Scholar]
  9. Cocilovo JA (1975) Estudio de dos factores que influencian la morphologia craneana en una collección Andina: El sexo y la deformación artificial. Rev Inst Anthropol 2, 197–212. [Google Scholar]
  10. Dembo A, Imbelloni J (1938) Deformaciones Intencionales del Cuerpo Humano de Carácter Étnico. Buenos Aires: José Anesi. [Google Scholar]
  11. Dingwall EJ (1931) Artificial Cranial Deformation. A Contribution to the Study of Ethnic Mutilation. London: John Bale Sons & Davidson. [Google Scholar]
  12. Ewing FJ (1950) Hyperbrachycephaly as influenced by cultural conditioning. Peabody Mus Am Archeol EthnolHarvard University Papers 23, 1–99. [Google Scholar]
  13. Friess M, Baylac M (2003) Exploring artificial cranial deformation using elliptic Fourier analysis of Procrustes aligned outlines. Am J Phys Anthropol 122, 11–22. [DOI] [PubMed] [Google Scholar]
  14. Gerig T, Shahim K, Reyes M, et al. (2014) Spatially varying registration using Gaussian processes. Med Image Comput Comput Assist Interv 17, 413–420. [DOI] [PubMed] [Google Scholar]
  15. Goodrich JT (2005) Skull base growth in craniosynostosis. Childs Nerv Syst 21, 871–879. [DOI] [PubMed] [Google Scholar]
  16. Grupe G (1984) On diploic structures and their variability in artificially deformed skulls. J Hum Evol 13, 307–309. [Google Scholar]
  17. Herring SW (2008) Mechanical influences on suture development and patency. Front Oral Biol 12, 41–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hou B, Kolpakova‐Hart E, Fukai N, et al. (2009) The polycystin kidney disease 1 (Pkd1) gene is required for the response of osteochondroprogenitor cells to midpalatal suture expansion in mice. Bone 44, 1121–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Janot F, Strazielle C, Awazu Pereira Da Silva M, et al. (1993) Adaptation of facial architecture in the Toulouse deformity. Surg Radiol Anat 15, 75–76. [DOI] [PubMed] [Google Scholar]
  20. Khonsari RH, Friess M, Nysjö J, et al. (2013a) Shape and volume of craniofacial cavities in intentional skull deformations. Am J Phys Anthropol 151, 110–119. [DOI] [PubMed] [Google Scholar]
  21. Khonsari RH, Olivier J, Vigneaux P, et al. (2013b) A mathematical model for mechanotransduction at the early steps of suture formation. Proc R Soc B 280, 20122670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Khonsari RH, Ohazama A, Ramin R, et al. (2013c) Multiple postnatal craniofacial anomalies are characterized by conditional loss of polycystic kidney disease 2 (Pkd2). Hum Mol Genet 22, 1873–1885. [DOI] [PubMed] [Google Scholar]
  23. Kohn LAP, Leigh SR, Jacobs SC, et al. (1993) Effects of annular cranial vault modification on the cranial base and face. Am J Phys Anthropol 90, 147–168. [DOI] [PubMed] [Google Scholar]
  24. Kolpakova‐Hart E, McBratney‐Owen B, Hou B, et al. (2008) Growth of cranial synchondroses and sutures requires polycystin‐1. Dev Biol 321, 407–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Korkmaz S, Goksuluk D, Zararsiz G (2014) MVN: an R package for assessing multivariate normality. R J 6, 151–162. [Google Scholar]
  26. Lee MC, Hwang J, Kim YO, et al. (2015) Three‐dimensional analysis of cranial and facial asymmetry after helmet therapy for positional plagiocephaly. Childs Nerv Syst 31, 1113–1120. [DOI] [PubMed] [Google Scholar]
  27. Lim H, Chung J, Park DH, et al. (2016) Long‐term results of remodeling the facial bones with a soft moulding helmet in beagles: the ‘reciprocally stimulated growth’ hypothesis. Br J Oral Maxillofac Surg 54, 40–45. [DOI] [PubMed] [Google Scholar]
  28. Moshfegui M, Ranganath S, Nawyn K (1994) Three‐dimensional elastic matching of volumes. IEEE Trans Image Process 2, 128–138. [DOI] [PubMed] [Google Scholar]
  29. Netherway DJ, Abbott AH, Gulamhuseinwala N, et al. (2006) Three‐dimensional computed tomography cephalometry of plagiocephaly: asymmetry and shape analysis. Cleft Palate Craniofac J 43, 201–210. [DOI] [PubMed] [Google Scholar]
  30. O'Broin ES, Allcutt D, Early MJ (1999) Posterior plagiocephaly: proactive conservative management. Br J Plast Surg 52, 18–23. [DOI] [PubMed] [Google Scholar]
  31. Oetteking B (1924) Declination of the pars basilaris in normal and artificially deformed skulls; a study based on skulls of the Chumash of San Miguel Island, California and on those of the Chinook. Indian Notes Monogr 27, 3–25. [Google Scholar]
  32. Oksanen J, Blanchet FG, Kindt R, et al. (2014) Adonis: permutational multivariate analysis of variance using distance matrices. In: Vegan: R functions for vegetation ecologists v. 2.2‐0 URL: http://r-forge.r-project.org/projects/vegan/.
  33. Opperman LA (2000) Cranial sutures as intramembranous bone growth sites. Dev Dyn 219, 472–485. [DOI] [PubMed] [Google Scholar]
  34. Patel A, Honoré É (2010) Polycystins and renovascular mechanosensory transduction. Nat Rev Nephrol 6, 530–538. [DOI] [PubMed] [Google Scholar]
  35. Pfaff MJ, Wong K, Persing JA, et al. (2013) Zygomatic dysmorphology in unicoronal synostosis. J Plast Reconstr Aesthet Surg 66, 1096–1102. [DOI] [PubMed] [Google Scholar]
  36. R Core Team (2016) R: a language and environment for statistical computing v. 3.2.4. R Foundation for Statistical Computing. Vienna, Austria: URL: https://www.R-project.org [Google Scholar]
  37. Rogers SL (1975) Artificial deformation of the head: New World examples of ethnic mutilation and note on its consequences. San Diego Mus Pap 8, 1–34. [Google Scholar]
  38. Rüdell A, Schlager S (2013) Shape analysis of the human zygomatic bone – data evaluation. Am J Phys Anthropol 150, 238. [Google Scholar]
  39. Schijman E (2005) Artificial cranial deformation in newborns in the pre‐Columbian Andes. Childs Nerv Syst 21, 945–950. [DOI] [PubMed] [Google Scholar]
  40. Schlager S, Jefferis G (2016) Morpho: calculations and visualisations related to geometric morphometrics. V. 2.4. The Comprehensive R Archive Network. URL: https://github.com/zarquon42b/Morpho.
  41. Schlager S, Rüdell A (2013) Shape analysis of the human zygomatic bone – surface registration. Am J Phys Anthropol 150, 243. [Google Scholar]
  42. Showalter BM, David LR, Argenta LC, et al. (2012) Influence of frontosphenoidal suture synostosis on skull dysmorphology in unicoronal synostosis. J Craniofac Surg 23, 1709–1712. [DOI] [PubMed] [Google Scholar]
  43. Turk AE, McCarthy JG, Thorne CH, et al. (1996) The ‘back to sleep campaign’ and deformational plagiocephaly: is there a cause for concern? J Craniofac Surg 7, 12–18. [DOI] [PubMed] [Google Scholar]
  44. Walrath DE, Turner P, Bruzek J (2004) Reliability test of the visual assessment of cranial traits for sex determination. Am J Phys Anthropol 125, 132–137. [DOI] [PubMed] [Google Scholar]
  45. Whitaker LA, Bartlett SP (1991) Skeletal alterations as a basis for facial rejuvenation. Clin Plast Surg 18, 197–203. [PubMed] [Google Scholar]
  46. Willinger M, Hoffman HJ, Wu KT, et al. (1998) Factors associated with the transition to nonprone sleep positions of infants in the United States: the National Infant Sleep Position Study. JAMA 280, 329–335. [DOI] [PubMed] [Google Scholar]
  47. Xiao ZS, Quarles LD (2010) Role of the polycystin‐primary cilia complex in bone development and mechanosensing. Ann N Y Acad Sci 1192, 410–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zollikofer CPE, Weissmann JD (2011) A bidirectional interface growth model for cranial interosseous suture morphogenesis. J Anat 219, 100–114. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Table S1. List of dry skulls included into the study.

Click here for additional data file. (9.5KB, xls)

Table S2. Significant permutation testing (1000 rounds) on Mahalanobis distances.

Click here for additional data file. (13KB, doc)

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES