A New Framework to Explain Sensorimotor Beta Oscillations

Abstract

Oscillatory activity in the beta frequency range from sensorimotor cortices is modulated by movement; however, the functional role of this activity remains unknown. In a recent study, Tan et al. tested a novel hypothesis that beta power reflects estimates of uncertainty in parameters of motor forward models.

It is well established that oscillatory activity originating from sensorimotor cortices in the beta frequency range (~15–30 Hz) is modulated by movement. Beta power decreases when we move and is transiently increased once the movement has stopped (postmovement beta synchronization, PMBS) [1]. However, despite extensive research into these neuronal oscillations, their functional role is not known [2]. In a recent study, Tan et al. [3] tested a novel theory of the functional role of sensorimotor PMBS that provides an important link between theoretical models of motor control and neurophysiological measures of sensorimotor activity.

Every movement we make stimulates peripheral sensory receptors that provide sensory feedback of the motor act. It is thought that, when we move, we predict the sensory consequences of that movement (through forward models) and compare this prediction to the actual sensory input [4,5]. Any difference between the predicted and actual sensory input will result in a prediction error, which is used to update the forward model for more accurate future predictions. To determine the relevance of any prediction errors, the model requires estimations of both the uncertainty in the motor prediction and the uncertainty of the actual sensory input [6]. This can be likened to a two-sample t-test: a measure of the variance (uncertainty) of each sample is essential to determine whether any difference between the sample means is significant. Tan et al. [3] manipulated task uncertainty to modulate the uncertainty in parameters of the model and tested the hypothesis that PMBS was correlated with these parameters.

The authors measured cortical activity with EEG from 17 healthy participants while they performed a visuomotor adaptation task. Participants were instructed to move a joystick to direct a cursor from the centre of a circle to a target located at one of eight points on the circumference of the circle. Participants completed 80 trials of either: (i) a random prime, in which a random angular error varying from trial to trial was added between the actual movement of the joystick and the visual feedback of the cursor (–60° to 60°); or (ii) a stable prime in which the perturbation (0°) remained stable across trials. Afterwards, all participants performed 150 trials of a constant 60° perturbation, followed by another 80 trials of no perturbation, for each condition. The authors predicted that, during the random priming block, participants’ uncertainty in parameters of the forward model (estimation uncertainty) would be high due to their inability to correctly predict future movements, whereas when the perturbation was stable, this uncertainty would be low. They predicted that PMBS would correlate with this uncertainty rather than with the movement error. A Bayesian learning model, which uses the mean and variance of the movement error across trials to estimate this uncertainty, was applied to the behavioural data. The authors then correlated the magnitude of the PMBS in each condition with the estimated values of uncertainty. They reported that the amplitude of the PMBS over sensorimotor cortex was negatively correlated with this uncertainty variable. This result is consistent with a novel functional role of PMBS, which suggests that beta oscillations are related to the uncertainty of the parameters of generative models that underlie motor control.

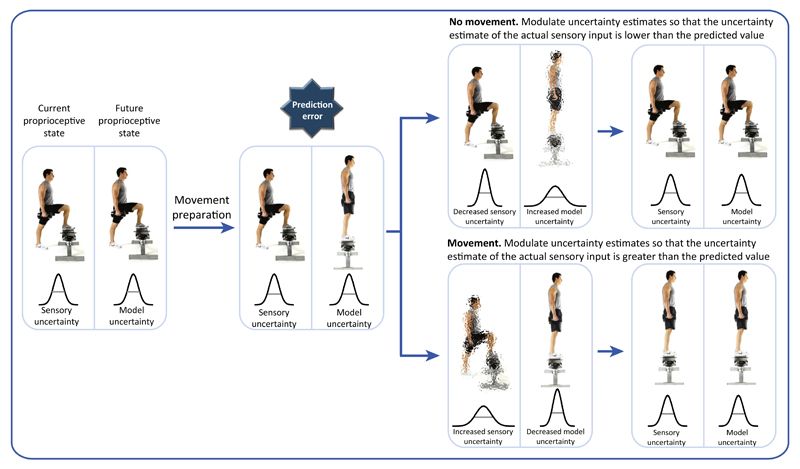
Although this paper introduces a new functional account for PMBS, this account does not generalize easily to explain all known modulations in sensorimotor beta oscillations. For example, it is known that beta power decreases during movements. If the new account is applied to this desynchronisation, then the conclusion would be that we have the highest uncertainty in our model while we move. This would seem unlikely. However, uncertainty is not only estimated for parameters of the forward model. According to motor control theory, an estimate of uncertainty in the actual sensory input is also required. The importance of the estimate of uncertainty at both of these levels was highlighted in a recent theoretical account of motor control and movement initiation: active inference [7]. Within this framework, it has been proposed that an increase in the estimate of the uncertainty of the actual sensory input is an essential step for being able to move (Figure 1). However, the neurophysiological correlates of this change in uncertainty are unknown. The study by Tan et al. [3] makes it possible to hypothesise that sensorimotor beta oscillatory power might be either the neurophysiological correlate of the estimate of uncertainty or causally modulating the uncertainty. Indeed, prima facie there is compelling evidence to predict that sensorimotor beta power and estimates of sensory uncertainty might be negatively correlated. For example, sensorimotor beta oscillations are known to be attenuated during motor preparation and execution [8], when active inference would predict an increase in sensory uncertainty. Similarly, increases in sensorimotor beta power are associated with the inhibition of executed actions [9], when active inference would require a decrease in somatosensory uncertainty to inhibit an action. Finally, sensorimotor beta power is augmented in patients with Parkinson's disease compared with healthy controls [10], when active inference would predict a lower level of sensory uncertainty in patients with Parkinson's disease compared with healthy controls.

Figure 1. Schematic Illustrating Movement Initiation within the Active Inference Framework.

In the schematic, each panel depicts both the actual and the predicted sensory inputs. The character shows the action that is currently being performed (left) alongside the predicted action (right). The width of the distributions below and the clarity of the figure illustrate the uncertainty in these values. Before we start to plan a new movement, our prediction of our sensory input and the actual sensory input are equivalent (left panel). According to the active inference framework, when we start to prepare a movement, we generate a prediction of what the sensory input of this movement will be and this creates a prediction error between the current and the predicted sensory states (second panel). To minimize this error, an individual can: (i) stay still and update their prior beliefs (within the forward model) so that the predicted sensory input matches the actual sensory input (top row); or (ii) move, so that the actual sensory input matches the predicted sensory input (bottom row). Modulating the relative uncertainty in these sensory states will determine which option is selected. For example, to initiate movement [option (ii)], the uncertainty in the current sensory state is increased such that the individual will shift to the predicted sensory state with the lowest uncertainty.

Tan et al. [3] have provided the first demonstration of a link between a key parameter in theoretical models of motor control, uncertainty, and modulations in sensorimotor beta power. Future work will be required to investigate whether the modulations in beta power are best accounted for by modulations in the uncertainty of the actual sensory input, the uncertainty of the model space, or the relative uncertainties of the two.