Closed Loop Control of a Tethered Magnetic Capsule Endoscope

Abstract

Magnetic field gradients have repeatedly been shown to be the most feasible mechanism for gastrointestinal capsule endoscope actuation. An inverse quartic magnetic force variation with distance results in large force gradients induced by small movements of a driving magnet; this necessitates robotic actuation of magnets to implement stable control of the device. A typical system consists of a serial robot with a permanent magnet at its end effector that actuates a capsule with an embedded permanent magnet. We present a tethered capsule system where a capsule with an embedded magnet is closed loop controlled in 2 degree-of-freedom in position and 2 degree-of-freedom in orientation. Capitalizing on the magnetic field of the external driving permanent magnet, the capsule is localized in 6-D allowing for both position and orientation feedback to be used in a control scheme. We developed a relationship between the serial robot's joint parameters and the magnetic force and torque that is exerted onto the capsule. Our methodology was validated both in a dynamic simulation environment where a custom plug-in for magnetic interaction was written, as well as on an experimental platform. The tethered capsule was demonstrated to follow desired trajectories in both position and orientation with accuracy that is acceptable for colonoscopy.

I. Introduction

Since their clinical introduction in 2000, capsule endoscopes have served as a passive means for inspecting the gastrointestinal tract. Although the entire bowel can be visualized, the capsules in current clinical use are restricted to passive movement from peristalsis. Active capsule endoscopy has been a field of study for more than 10 years now. Methodologies for active actuation through the bowel have included hand-held, legged, inch-worm type, wheeled, gastric submarine, electromagnetic, and via permanent magnet mounted at a serial robot's end effector [20]. Complexity and fragility of the miniaturized designs has stymied the development of mechanical means of actuation through the lumen. Ability to induce clinically relevant forces and torques while maintaining a compact form factor has resulted in permanent magnet driving to be the preferred capsule actuation means [15]. Simple hand-held permanent magnet actuation has been investigated and has been shown to enable quick movement of a capsule through a straight lumen; however, hand motions are too imprecise to approach a target (e.g. lesion) or to maneuver the camera field of view (e.g. pan and tilt). To enable such fine movements, mounting the external permanent magnet (EPM) on a robot's end effector has been investigated. Robotic driving has been shown to facilitate more precise control and is imperative for diagnostics and therapeutics [6]. Magnetic capsule driving has been investigated in the esophagus, stomach, and colon.

Standard colonoscopes have been shown to induce tissue stress which is the primary cause of discomfort during the procedure and often leads to the need for sedation. The use of a front driven device, instead of one pushed from the rear, has been hypothesized to diminish tissue stress, and as a result, patient discomfort [24]. Operation of a colonoscopy device requires fine movements and the ability to accurately position the device to both inspect and conduct therapeutic intervention at a point of interest (e.g. lesion). Although actuating a permanent magnet-embedded colonoscope has been shown to enable necessary fine movements, procedure times in phantom trials were shown to be over twice as long as traditional procedures [2]. Contributing factors to the long procedure time include an indirect mapping of the user interface to capsule motion (user actuates robot directly), user difficulty in choosing a specific degree-of-freedom (DoF) to actuate for a particular resultant motion. Any disturbances in the device's path, such as the colon's haustral folds, may hinder motion, resulting in the need for the user to backtrack the actuating magnet and regain magnetic coupling with the capsule. To make magnetic colonoscopy a feasible replacement for the traditional procedure, closed loop control is necessary where desired capsule motions can be specified by the user for the capsule directly, as opposed to the actuating magnet. The resultant effect can be perceived as driving a vehicle through the lumen, with position and orientation being achieved by commanding appropriate manipulator motions, and thus induced magnetic forces and torques, via software.

Knowledge of the global pose (position and orientation) of the endoscopic capsule is necessary for implementing closed loop control. Though numerous localization methodologies have been investigated in recent years, only a few are feasible for in vivo procedures and can be used in the presence of strong magnetic fields. The following five methods are compatible with magnetic fields: (1) fluoroscopic imaging, which unnecessarily exposes the patient to X-Rays [4], (2) triangulation of gamma ray emissions from positron markers on a capsule [22], (3) simultaneous video processing and radio-frequency sensing [3], (4) internal magnetic field sensing and mapping to a magnetic field model [16, 7]. Method (4) directly utilizes the actuation method for localization and is thus the most practical for permanent driving applications and [7] is the only method applicable for real-time control.

Although several groups have implemented open loop magnetic capsule control [4, 6, 9, 12], only a few have worked towards a control scheme that utilizes capsule position feedback. The first work towards closed loop capsule control was done in 2013 by Salerno et al.. In this study, a constrained magnetic dragging set up was made with 2-DoF localization that enabled planar position feedback. The focus of this work was force model validation rather than the study of capsule mobility [18]. In 2015, Mahoney et al. demonstrated 3-DoF closed loop position and 2-DoF open loop orientation control of an untethered magnetic capsule for gastric exploration. Using a serial robot with a magnet at the end effector, they were able to move a submerged tetherless capsule through desired trajectories in a tank of liquid as proof of concept for a distended stomach. Visual real-time localization was used in this work that relies on external cameras and thus lacks in clinical relevance. Assumptions made during this study include: the capsule's magnetic moment (heading) aligns with the EPM's field, motions occur in low speeds and with low accelerations, and no disturbances impede capsule motion [15]. In this paper, we expand this approach and develop full closed loop control of both position (2-DoF) and orientation (2-DoF), integrate it with a clinically implementable real-time localization algorithm, and apply a control scheme for position and orientation trajectory following.

Traveling within the lumen of the colon to perform a screening examination necessitates motion through an approximately 180 cm long tortuous pathway whose diameter ranges from 34.5mm (sigmoid colon) to 75 mm (cecum) and has a minimum of 3 major anatomic turns (splenic flexure, hepatic flexure, and sigmoid colon) that commonly have bends greater than 90° with a radius of curvature of 2-5cm [1, 10, 11, 21]. Despite the lack of error metric reporting for traditional endoscopes in the literature, we can conclude that positional accuracy is on the order of centimeters by inferring from the scale that spans the body of the endoscope and due to colonoscopy being a manual procedure. The use of wide-angle cameras gives leeway to endoscope orientation accuracy requirements; although accuracies of approximately 1° are desired for tissue sampling (biopsies and polyp removal). To achieve motion and diagnostic capability equivalent to or better than the traditional endoscope, which is necessary for colon examination, we have developed a soft-tethered magnetically driven capsule platform inspired by the magnetic-air-capsule system introduced in [23]. Traditional endoscopes necessitate high stiffness and rigidity to enable pushing the tip forward from the bodily entry point; however, this rigidity induces significant tissue stress and is a major cause for patient discomfort. The tethered capsule takes on a front-actuated approach in that the propulsion force is applied by the EPM at the tip of the device thus alleviating the normally present tissue stress. This is the first study on a closed loop control of a tethered magnetic device suitable for therapeutic endoscopy. We have built upon the theoretical formulations of [15] and expanded their approach to closing the control loop in orientation as well as position, and applied the methodology to a tethered capsule system that is not submerged. Having lost the damped behavior of motion in a liquid, the tethered capsule remains pressed against a barrier while being attracted by the EPM. Although the capsule cannot be levitated, it can be tilted away from the barrier and, in the case of a loss of magnetic coupling, can be recaptured. Magnetic coupling force can be computed using magnetic models, knowledge of which can be used to monitor and prevent high contact forces that, in colonoscopy, may result in pain-inducing tissue stress. This is the first closed loop control approach to tethered device driving that utilizes clinically relevant real-time localization where environmental disturbances are present, specifically from the tether and interaction with a constraining barrier (e.g. colonic tissue wall).

II. System Design

Our tethered capsule platform consists of a 6-DoF serial manipulator (RV-6SDL, Mitsubishi Corp, Japan) with a 1.48 Tesla residual flux density cylindrical EPM (N52 grade, 4″ diameter and length, axial magnetization, ND N-10195, Magnet World Inc., USA) mounted at its end effector. The capsule (20 mm diameter, 22 mm length) contains a cylindrical permanent magnet (D77-N52, axial magnetization, K&J Magnetics Inc, USA) with a residual flux density of 1.48 Tesla. The capsule preserves all the functionalities of a traditional endoscope by employing a soft tether that enables the use of traditional endoscopic tools. Routed through the tether are a camera wire (Micro ScoutCam ™1.2, Medigus Ltd., Israel), a tool channel extracted from a traditional endoscope, an irrigation/insufflation channel, and highly compliant electrical wires. Circuitry in the capsule includes 6 Hall-effect sensors and an inertial measurement unit that are used for real-time localization.

A. Magnetic Localization

In this study, we use a localization scheme that is similar to the one described in [7]. The 6-DoF localization strategy utilizes the external magnetic field that is used for actuation of the capsule. Two Hall-effect sensor triplets are placed strategically around the internal magnet such that the field sensed is negligible and, owing to superposition of magnetic fields, measurement of an externally applied field is possible. Accelerometer and gyroscope readings allow for rotation of the measured external magnetic field at the capsule (b^c) into world, and then the EPM's frame (b^m). Thus:

$${\mathit{b}}^m=R_w^m{R}_c^w{\mathit{b}}^c$$ (1)

An a priori generated magnetic field map is searched and the capsule position is computed. The magnetic field map is generated offline using a finite element analysis software such as COMSOL (COMSOL Multiphysics, Sweden) by numerically solving for the magnetic field of the EPM on a uniform grid of points according to the magnetic current model [7] of an axially magnetized cylindrical magnet:

$$\mathit{b}(\mathit{p})=\frac{{\mu }_0}{4\pi }\underset{s^{″}}{\oint }{\mathit{j}}_{\mathit{m}}({\mathit{p}}^{″})\times \frac{(\mathit{p}-{\mathit{p}}^{″})}{{|\mathit{p}-{\mathit{p}}^{″}|}^3}{\mathit{\text{ds}}}^{″}$$ (2)

where p is a point on the uniform grid, p″ is a point on the surface of the permanent magnet and j_m is the equivalent surface current density. The magnetic field map, as shown in Fig. 2a, is symmetric about the magnet's longitudinal axis. This symmetry is exploited to dramatically improve the efficiency of the search algorithm where instead of searching the entire 3D map, only one quadrant of a plane is searched, thereby allowing real-time localization.

Fig. 2.

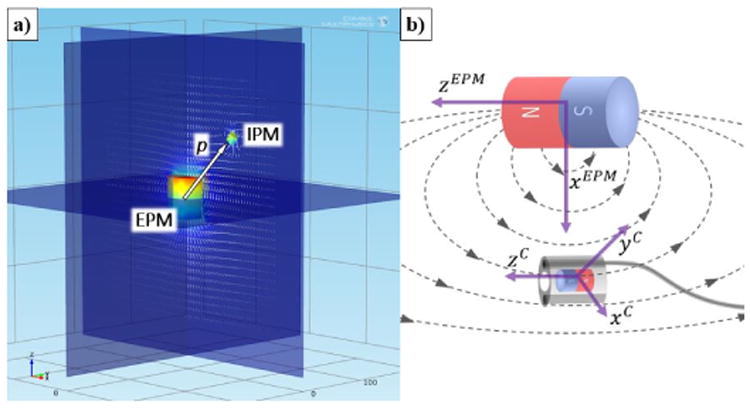
(a) Rendering generated in COMSOL showing the sum of the magnetic fields of the external and internal permanent magnets (EPM and IPM). Sensor readings from the capsule are used to search the field map of the EPM to localize the capsule. (b) At the indicated capsule position, the magnetic field of the EPM is along z^EPM.

The orientation of the capsule is obtained through the quaternion based explicit complementary filter (ECF) described in [8] that fuses acceleration (denoted as a) and angular velocity (denoted as Ω) from the six axis inertial measurement unit (IMU) on board the capsule. The acceleration measurement is used to estimate the true direction of gravity ḡ in the frame of the capsule ( ${\overline{\mathit{g}}}^c=\frac{\mathit{a}}{\Vert \mathit{a}\Vert }$) while the current estimate of the capsule's orientation, q̂, is used to predict the direction of gravity ĝ^c.

$$\begin{array}{c}{\widehat{\mathit{g}}}^c={\widehat{\mathit{q}}}^{\ast }\otimes \mathit{r}(\widehat{\mathit{z}})\otimes \widehat{\mathit{q}}\\ \widehat{\mathit{z}}={[\begin{array}{ccc}0& 0& -1\end{array}]}^{\top }\end{array}$$ (3)

where r(·) is an operator that forms a pure quaternion out of a vector. The relative rotational error of the two direction vectors, e, is used in a proportional-integral (PI) control loop, the dynamics of which are expressed as:

$$\dot{\mathit{q}}=\frac{1}{2}\widehat{\mathit{q}}\otimes \mathit{r}(\mathbf{\Omega }+\mathit{\delta })$$ (4)

$$\mathit{\delta }=k_P\mathit{e}+k_I\int \mathit{e}$$ (5)

$$\mathit{e}={\overline{\mathit{g}}}^c\times {\widehat{\mathit{g}}}^c$$ (6)

where δ is the output of the PI block and represents the correction factor on the angular velocity, k_P and k_I are gains of the PI block.

As a consequence of integrating angular velocity, the filter implementation, in its original form, requires knowledge of the capsule's initial orientation. Furthermore, even though the integral term in the PI control loop is used to compensate for gyroscope bias, the fact remains that without an absolute heading reference, errors continue to accumulate. In this work, the ECF is extended to exploit the magnetic field of the actuator magnet as an absolute heading reference.

The magnetic field of the actuator magnet is measured in the capsule frame. Thus, without knowing the correct orientation of the capsule, it cannot be expressed in world frame. However, as Madgwick et al. [14] have shown in their magnetic distortion compensation formulation, the measured magnetic field can be normalized to have components only in the worlds x and z axes.

As shown in Fig. 2b, for a cylindrical magnet, the positions along (x, y, 0) contain magnetic fields with components only in the direction of magnetization, in this case, z. When the magnet frame is in close alignment with the world frame, the magnetic field measurements near the (x, y, 0) plane are characterized by small values in the radial direction of the magnet. When this condition occurs, the magnetic field in the axial direction can be used as an absolute reference. Hence, the normalized magnetic field in capsule frame b̂^c is rotated into the EPM frame b̂^m, which is then projected into a vector with only x and z components where they designate the radial and axial directions, respectively.

$${\widehat{\mathit{b}}}^c=\frac{\mathit{b}}{\Vert \mathit{b}\Vert }$$ (7)

$${\widehat{\mathit{b}}}^m={\widehat{\mathit{q}}}_c^m\otimes \mathit{r}({\widehat{\mathit{b}}}^c)\otimes {\widehat{\mathit{q}}}_c^{m\ast }$$ (8)

$${\overline{\mathit{b}}}^m=\left[\begin{array}{ccc}{b}_x^m& 0& \sqrt{b_y^{m^2}+b_z^{m^2}}\end{array}\right]$$ (9)

This new vector, b̄^m, is converted back to the capsule frame and the relative rotational error between the original measurement b̂^c and the new projected vector b̄^m is used to compute an error term e′ that is fed back into the PI control loop.

$${\overline{\mathit{b}}}^c={\mathit{q}}_m^c\otimes \mathit{r}({\overline{\mathit{b}}}^m)\otimes {\mathit{q}}_m^{c\ast }$$ (10)

$${\mathit{e}}^{\prime }={\widehat{\mathit{b}}}^c\times {\overline{\mathit{b}}}^c$$ (11)

Thus, the overall error term from Eq. (6) becomes:

$$\mathit{e}={\overline{\mathit{g}}}^c\times \widehat{\mathit{g}}+{\widehat{\mathit{b}}}^c\times {\overline{\mathit{b}}}^c$$ (12)

The addition of e′ to the filter allows for gyroscope bias to be corrected whenever the capsule is located near the (x, y, 0) plane. The proximity to this plane can be used to weight e′ such it is only applied when the condition is satisfied, which conveniently, occurs frequently during closed loop control.

III. Closed Loop Control

Our system can be characterized as a permanent magnet with a tether that applies a disturbance force on its motion by adding weight and friction, as well as impeding angular rotation. The following theoretical formulation is applicable for controlling a permanent magnet mounted at the end effector of a 6-DoF serial manipulator. These derivations utilize and build on the formulations of Mahoney and Abbott [15] and, to the extent that it is allowable, we maintain terminology and structure of formulation to avoid ambiguity. The general formulations before derivation are reported here from [15] for completeness. Our aim was the generalization of the methodology for applications where disturbances are present that prevent the capsule from aligning with the EPM's field. We also do not assume the capsule to be submerged. Applying force on the capsule, and thus against the constraining barrier, translates to friction that impedes capsule motion. We relate system inputs—robot joint commands—directly to resulting capsule motions. To do so, we linearize the small changes of force and torque applied on the capsule that result from small motions of the EPM. Nomenclature used in the derivation is described in Table 1.

Table I. Nomenclature.

Symbol	Description
υ	Vector (lowercase, bold)
M	Matrix (uppercase)
I	Identity matrix ∈ ℝ3
υ̇	Rate of change of parameter with respect to time
υ̂	Unit vector
pa	Position of robot end-effector
pc	Capsule position
p = pc − pa	Relative capsule position vector
mc	Magnetic moment of capsule's magnet
ma	Magnetic moment of EPM
fm	Force induced by EPM on capsule
τm	Torque induced by EPM on capsule

The force, f_m, and torque, τ_m, induced on the capsule's magnet are described by the dipole-dipole model as:

$${\mathit{f}}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})=\frac{3{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^4}({\widehat{\mathit{m}}}_{\mathit{a}},{{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }+{\widehat{\mathit{m}}}_{\mathit{c}}{{\widehat{\mathit{m}}}_{\mathit{a}}}^{\top }+({{\widehat{\mathit{m}}}_{\mathit{c}}}^{\mathrm{T}}Z{\widehat{\mathit{m}}}_{\mathit{a}})I)\widehat{\mathit{p}}$$ (13)

$${\mathit{\tau }}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})=\frac{{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^3}{\widehat{\mathit{m}}}_{\mathit{c}}\times D(\widehat{\mathit{p}}){\widehat{\mathit{m}}}_{\mathit{a}}$$ (14)

where D = 3p̂p̂^⊤ − I and Z = I − 5p̂p̂^⊤

A. Derivation of the actuating-force-torque Jacobian

The robot's geometric Jacobian J_ℛ(q) ∈ ℝⁿ is used to linearize the relationship between joint velocities and the end effector twist as follows:

$$\left[\begin{array}{c}{\dot{\mathit{p}}}_a\\ {\mathit{\omega }}_a\end{array}\right]=J_{\mathcal{R}}(q)\dot{\mathit{q}}$$ (15)

Owing to the axial symmetry of the EPM, rotation about the EPM's longitudinal axis will not result in a change in the heading of m̂_a. Mahoney et al. specified an actuator Jacobian matrix J_𝒜(q) that maps manipulator joint velocities q̇ to the resultant ${\dot{\widehat{\mathit{m}}}}_{\mathit{a}}$ where any rotation ω_a parallel to m̂_a makes no contribution to ω_a. The resulting relation may be written with a skew matrix form of the cross product and results in a rank five, and thus singular, Jacobian.

$$\left[\begin{array}{c}{\dot{\mathit{p}}}_a\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{a}}\end{array}\right]=\left[\begin{array}{cc}I& 0\\ 0& S{({\widehat{\mathit{m}}}_{\mathit{a}})}^{\top }\end{array}\right]J_R\dot{\mathit{q}}=J_A\dot{\mathit{q}}$$ (16)

Where S(a) ∈ SO(3) denotes the skew-symmetric form of the cross-product operation:

$$S\left(\right[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\left]\right)=\left[\begin{array}{ccc}0& -a_z& a_y\\ a_z& 0& -a_x\\ -a_y& a_x& 0\end{array}\right]$$ (17)

The nonlinear force and torque expressions above can be linearized with the use of a Jacobian matrix J_ℱ(p, m̂_a, m̂_c) ∈ ℝ^6×9 that is developed by differentiating the expressions for force and torque with respect to p, m̂_a, and m̂_c. The Jacobian thus yields:

$$\left[\begin{array}{c}\dot{\mathit{f}}\\ \dot{\mathit{\tau }}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial {\mathit{f}}_{\mathit{m}}}{\partial \mathit{p}}& \frac{\partial {\mathit{f}}_{\mathit{m}}}{\partial {\widehat{\mathit{m}}}_{\mathit{a}}}& \frac{\partial {\mathit{f}}_{\mathit{m}}}{\partial {\widehat{\mathit{m}}}_{\mathit{c}}}\\ \frac{\partial {\mathit{\tau }}_{\mathit{m}}}{\partial \mathit{p}}& \frac{\partial {\mathit{\tau }}_{\mathit{m}}}{\partial {\widehat{\mathit{m}}}_{\mathit{a}}}& \frac{\partial {\mathit{\tau }}_{\mathit{m}}}{\partial {\widehat{\mathit{m}}}_{\mathit{c}}}\end{array}\right]\left[\begin{array}{c}\dot{\mathit{p}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{a}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}\right]=J_{\mathcal{F}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})\left[\begin{array}{c}\dot{\mathit{p}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{a}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}\right]$$ (18)

Each component of the Jacobian is derived in the Appendix.

We wish to impart small changes in force and torque induced by motion of the end effector of the manipulator (EPM) which is done by setting these to be outputs of a controller.

$$\left[\begin{array}{c}\dot{\mathit{f}}\\ \dot{\mathit{\tau }}\end{array}\right]=\left[\begin{array}{c}{K}_{pe}{\mathit{e}}_p\\ K_{po}{\mathit{e}}_o\end{array}\right]$$ (19)

The position error is simply e_p = p_c − p_cdes with z-component set to zero. The orientation error is obtained by computing the angle between the heading axis of the capsule and the desired heading: e_o = ĥ_c × ĥ_des where ĥ_c and ĥ_des are the capsule's and desired headings, respectively. Note that the other two axes of the capsule's orthonormal triplet are oriented arbitrarily since the DoF to orient these is lost.

The Jacobian expression can be rearranged to allow for term decoupling as follows:

$$\left[\begin{array}{c}\dot{\mathit{f}}\\ \dot{\mathit{\tau }}\end{array}\right]=J_{\mathcal{F}}\left[\begin{array}{c}\dot{\mathit{p}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{a}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}\right]=J_{\mathcal{F}}\left(\right[\begin{array}{c}{\dot{\mathit{p}}}_c\\ 0\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}]+[\begin{array}{ccc}-I& 0& 0\\ 0& I& 0\\ 0& 0& 0\end{array}\left]\right[\begin{array}{c}{\dot{\mathit{p}}}_{\mathit{a}}\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{a}}\\ 0\end{array}\left]\right)=J_{\mathcal{F}}\left(\right[\begin{array}{c}{\dot{\mathit{p}}}_{\mathit{c}}\\ 0\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}]+[\begin{array}{ccc}-I& 0& 0\\ 0& I& 0\\ 0& 0& 0\end{array}\left]\right[\begin{array}{c}{J}_{\mathcal{A}}\\ 0\end{array}\left]\dot{\mathit{q}}\right)$$ (20)

We now define the actuating-force-torque Jacobian J_ℱ𝒜 as follows:

$${\mathcal{J}}_{\mathcal{F}\mathcal{A}}=J_{\mathcal{F}}\left[\begin{array}{ccc}-I& 0& 0\\ 0& I& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{J}_{\mathcal{A}}\\ 0\end{array}\right]$$ (21)

resulting in:

$$\left[\begin{array}{c}\dot{\mathit{f}}\\ \dot{\mathit{\tau }}\end{array}\right]-J_{\mathcal{F}}\left[\begin{array}{c}{\dot{\mathit{p}}}_{\mathit{c}}\\ 0\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}\right]=J_{\mathcal{F}\mathcal{A}}\dot{\mathit{q}}$$ (22)

As aforementioned, the actuator Jacobian J_𝒜 is singular owing to the existence of infinite configurations that result in an identical m̂_a and thus a singular Jacobian matrix J_ℱ𝒜. To solve for a desired q̇, we utilize weighted damped-least-squares as well as capitalize on a redundant DoF.

B. Redundancy resolution

With a redundant DoF in J_ℱ𝒜, there exist infinite manipulator motions that complete a desired task of inducing specific forces and torques on the capsule's magnet. This redundancy can be utilized to satisfy secondary desired tasks of the manipulator. Local optimization is desirable as the eventual implementation of this presented control scheme is to be used during real-time teleoperation, as opposed to implementing global optimization where knowledge of the entire trajectory is required a priori.

To solve (22), the inverse of the singular Jacobian J_ℱ𝒜 must be computed. The weighted-least squares redundancy resolution approach of [25] allows for dynamically specifying a weight matrix W_q ∈ ℝ^n×n (n is the number of DoF of the manipulator) to penalize large speeds of each joint while minimizing the manipulator's joint speeds. An objective function h is chosen to be the joint limiting function described by [5] that assigns higher weights (inhibit motion), that approach infinity as a joint approaches its limit.

$$\mathit{h}(\mathit{q})=\sum _{i=1}^n\frac{1}{4}\frac{{(q_{i,\mathit{\text{max}}}-q_{i,\mathit{\text{min}}})}^2}{(q_{i,\mathit{\text{max}}}-q_i)(q_i-q_{i,\mathit{\text{min}}})}$$ (23)

Whose gradient is defined as follows [5]:

$$\nabla {\mathit{h}}_{\mathit{i}}=\frac{1}{4}\frac{{(q_{i,\mathit{\text{max}}}-q_{i,\mathit{\text{min}}})}^2(2q_i-q_{i,\mathit{\text{max}}}-q_{i,\mathit{\text{min}}})}{{(q_{i,\mathit{\text{max}}}-q_i)}^2{(q_i-q_{i,\mathit{\text{min}}})}^2}$$ (24)

Where Δh_i form the diagonals of the weight matrix W_q. A second weight matrix W_x ∈ ℝ^6×6 can be used to limit motion in task (force and torque) space [19]. Owing to the capsule being tangentially aligned with its tether at the point of contact, motion along this direction results in the least interference from the tether. If the capsule were to travel in a direction that is not aligned with its heading, the tether would induce a higher disturbance. To avoid this, we wish to prioritize capsule heading over position control resulting in heading being generally aligned with the capsule's direction of motion. This prioritization is implemented by increasing weights (favoring motion) in W_x that correspond to the torque components of the task space.

In implementing weighted-least squares, we wish to minimize the following function [19]:

$$\underset{\dot{\mathit{q}}}{min}({\Vert W_x(\dot{\mathit{x}}-J_{\mathcal{F}\mathcal{A}}\dot{\mathit{q}})\Vert }^2+{\alpha }^2{\Vert W_{\mathit{q}}^{-1}\dot{\mathit{q}}\Vert }^2)$$ (25)

where α is a user-defined constant.

The solution to the manipulator's joint velocities given a desired end effector velocity is described by q̇ = J⁺ẋ where J⁺ is denoted as the weighted least-squares inverse of the Jacobian and is defined as $J^{+}=J_W^{\top }{(J_W{J}_W^{\top }+\alpha I)}^{-1}$ where J_W = W_xJ_ℱ𝒜W_q.

When a redundant DoF is available in the manipulator, the null space of the Jacobian, which contains the set of joint velocities that result in no motion of the end effector, can be utilized to pursue secondary tasks. The null space projection matrix is defined by (I − J⁺ J). The joint solution for a typical redundant manipulator can then be written as:

$$\dot{\mathit{q}}=J^{+}\dot{\mathit{x}}+\beta (I-J^{+}J)\mathit{o}$$ (26)

where o is an arbitrary vector and β is a user-defined constant [5].

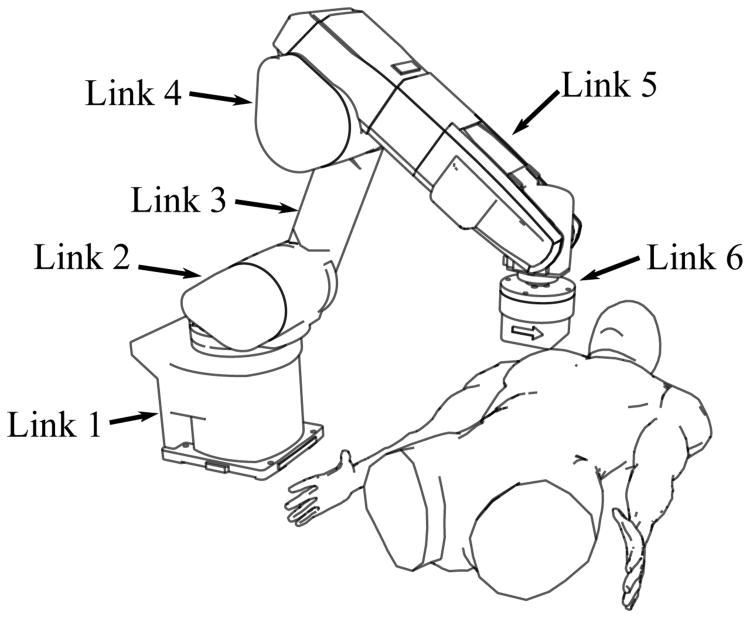
During colonoscopy, an elbow-up configuration of the 5th and 6th links of the serial manipulator is desired, as shown in Fig. 3. Although weighted least-squares penalizes unwanted motions, it does not facilitate desired joint positions. Gradient projection, a local optimization scheme first introduced by Liegeois [13], automatically corrects joint angles to be in the middle of their limits. These limits can be set to thus maintain a desired manipulator orientation that is both well suited for the colonoscopy procedure and avoids a singular manipulator configuration. The joint solution using our actuating-force-torque Jacobian can be written such that g is an objective function to be locally minimized or maximized, ∇g indicates the gradient of that function.

Fig. 3.

Intended robot-patient positioning for tethered capsule colonoscopy. Links 5 and 6 are desired to maintain elbow-up configuration.

$$\dot{\mathit{q}}=J_{\mathcal{F}\mathcal{A}}^{+}\left(\right[\begin{array}{c}\dot{\mathit{f}}\\ \dot{\mathit{\tau }}\end{array}]-J_{\mathcal{F}}[\begin{array}{c}{\dot{\mathit{p}}}_c\\ 0\\ {\dot{\widehat{\mathit{m}}}}_{\mathit{c}}\end{array}\left]\right)+(I-J^{+}J)\beta \nabla \mathit{g}$$ (27)

The objective function g is chosen to be the joint norm function given by:

$$\mathit{g}(\mathit{q})=\frac{1}{2}{({\mathit{q}}_{\mathit{\text{des}}}-\mathit{q})}^{\top }{W}_J({\mathit{q}}_{\mathit{\text{des}}}-\mathit{q})$$ (28)

whose gradient is defined as ∇g = −W_J (q_des − q) where ∇g is an n× 1 vector and W_J ∈ ℝ^n×n is a weight matrix used to prioritize which joints must satisfy the objective function.

IV. Validation

A. Validation via Dynamic Simulation Environment

We have used the open-source Robotic Operating System (ROS) [17] for developing the tethered capsule platform's software. Using ROS has allowed for developing stand-alone pieces of code that readily enable software simulation as well as hardware testing of the device. For proof-of-concept algorithm validation, we have utilized a dynamic simulation environment. This simulation is made in Gazebo; an open-source simulation environment with a physics engine. As seen in Fig. 4, the simulation includes the robot, capsule with tether, a floor, and a horizontal barrier. Gazebo's native simulation environment includes parameters such as gravity, robot kinematics, capsule inertia and friction, friction of the horizontal barrier, and tether properties. The tether's continuum configuration is modeled with the use of a finite number of rigid cylindrical links, each with a specified inertia and friction, connected by universal joints with a specified stiffness. Universal joints have been chosen because they allow for multi-axis bending and transmit torsion along the tether. Joint stiffness has been experimentally chosen such that simulation behavior resembles that of the physical system when bending is induced magnetically, however, further work to characterize the stiffness is anticipated. We have developed a custom Gazebo plug-in for computing magnetic forces and torques via the dipole-dipole model that are used in Gazebo's ODE solver to compute resultant capsule motion. The distributed-charges and current magnetic model have been shown to be accurate, even at small distances between magnets, and will be investigated in the near future [18]. The dynamic simulator has allowed for control and trajectory following before experimentation on the physical platform. Each trajectory that was used in the physical experiment was first tested in simulation.

Fig. 4.

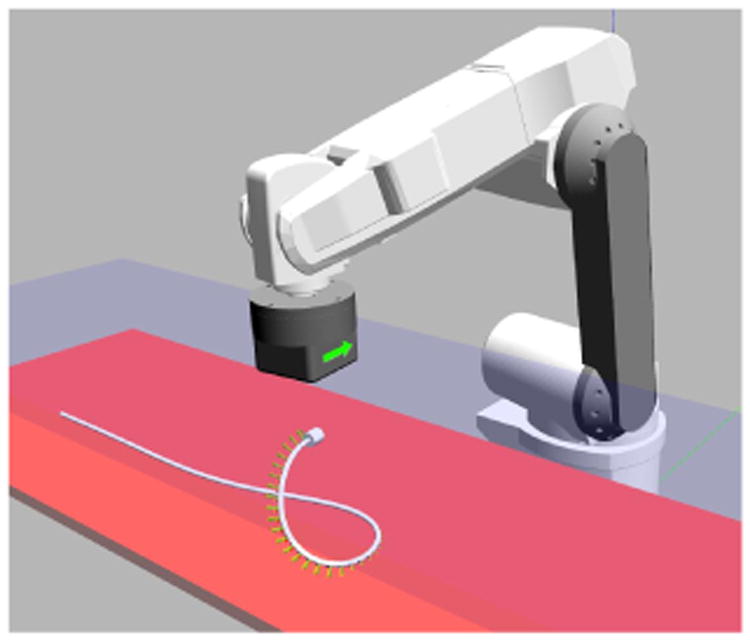
Gazebo simulation environment with built-in physics engine. A custom plug-in allows for simulation of magnetic interaction between the EPM and capsule.

B. Experimental Validation

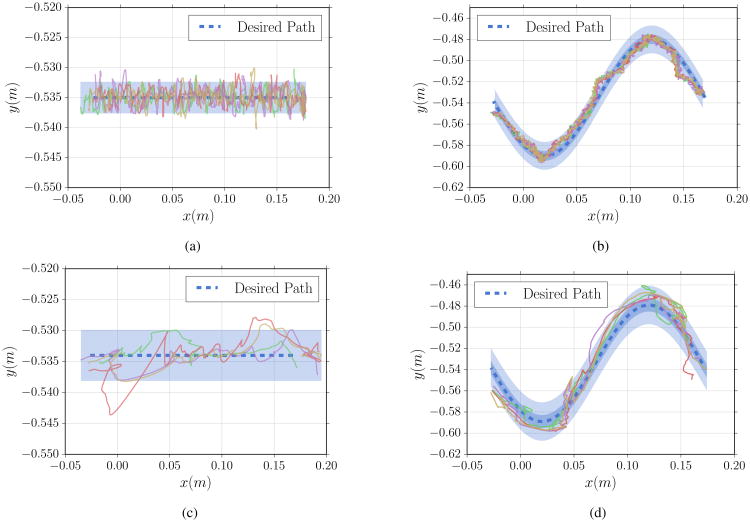
To assess the viability of our approach, the controller was tasked with maneuvering the capsule along desired trajectories. The tethered capsule was inserted between two horizontal layers acting as vertical barriers for the capsule as shown in Fig. 5. The tether passed through a constraint device with a circular hole that served to prevent lateral motion near the beginning of the planned trajectories. Two sets of trials were conducted on respective trajectory paths. During each trial, the tethered capsule was commanded to approach a desired position and maintain a commanded heading. A linear proof-of-concept trajectory was used as an initial indicator of desired capsule motion, as was seen in simulation. A sinusoidal trajectory (amplitude = 5.5 cm, wavelength = 20 cm) was implemented to demonstrate the capability of both position and heading control in the presence of tether-induced disturbance. During both sets of trials, the capsule's heading was commanded to align tangentially with the trajectory path and maintain a horizontal orientation so that the capsule is in contact with the barrier along its length. This was implemented with a clinical consideration that necessitates clear visualization of the lumen. As seen in Figs. 6, 7, the tethered capsule followed along the generated paths with acceptable accuracy. Four trials were conducted for each trajectory both in simulation and experiment with closed control and localization running at 100 Hz. In the simulation environment, Gaussian noise with a standard deviation of 6 mm was added to simulate the localization errors reported in [7]. The same low pass filter was used in both the simulation and physical environment. For all trajectories, deviations were measured in the lateral (y) direction. Lower deviations were observed in the simulation environment owing to idealized mechanical and frictional properties that could not accurately model the tether's interaction with the environment.

Fig. 5.

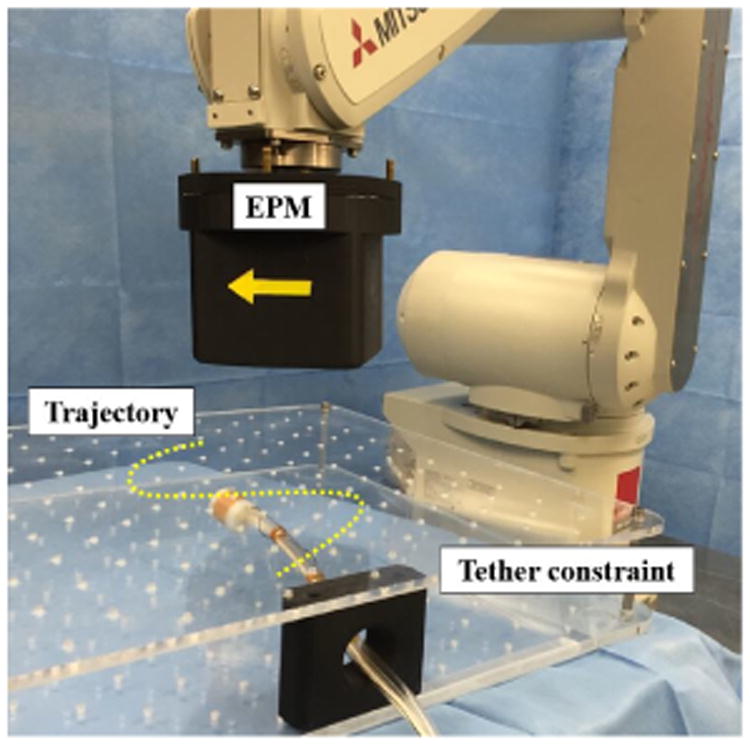
Experimental setup for trajectory following of the tethered capsule. The tether is constrained near the beginning of the trajectory. The sinusoidal trajectory is shown for visualization purposes only.

Fig. 6.

Results of four trials of the capsule being maneuvered through the two types of desired trajectories while maintaining an orientation that is parallel to the vertical barrier surface. The shaded region shows one (only for b, d) and three standard deviations from the mean. Simulation results are shown in (a) and (b) while experimental results are shown in (c) and (d).

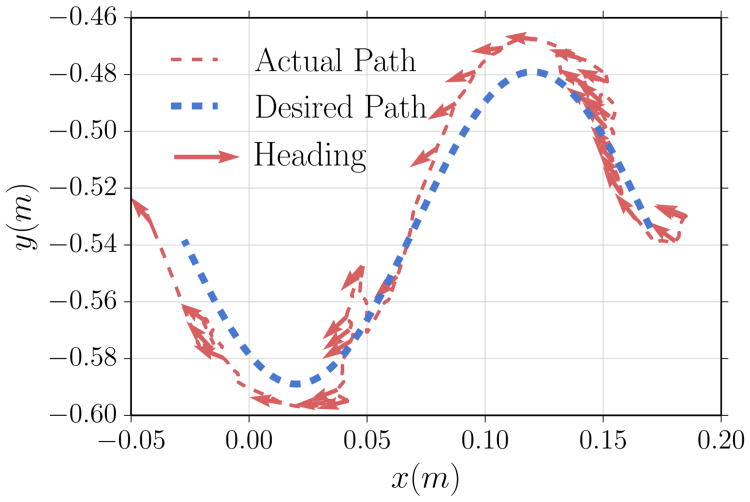
Fig. 7.

The tethered capsule was commanded to follow this sinusoidal trajectory starting near x = 0.2 m and maintain a heading that was tangential to the sine curve. This heading is parallel to the vertical barrier.

In the straight line trajectory trials, the mean deviation in simulation was 1.1 ± 0.9 mm with a maximum error of 5.2 mm, while the mean deviation in the experiment was 1.2 ± 1.4 mm with a maximum error of 9.6 mm. For the sine wave trajectories, the mean deviation in simulation was 5.0 ± 4.3 mm with a maximum error of 21.9 mm. The mean error in the heading angle was 0.11 ± 0.11 radians with a maximum error of 0.48 radians. For the experimental data, the mean deviation was 10.3 ± 6.7 mm with a maximum error of 35.7 mm. The mean error in the heading angle was 0.26 ± 0.18 radians with a maximum error of 0.71 radians.

Our tethered capsule can achieve accurate motions within a ± 10 mm boundary. This meets our requirement considering that (a) this error spans the thickness of our capsule (20 mm diameter), (b) the approximate colon diameter ranges from 34.5 mm to 75 mm and (c) the error is greater than our margin of positioning error [24, 10]. Although orientation errors of 0.26 radians (15°) were recorded in our experiments, these errors were computed along the trajectory and, therefore, do not fully characterize the static orientation accuracy that could be achieved with the system. Accurate angular motion is required for tissue sampling (biopsy or polyp removal) commonly performed with the endoscope held in one stable position, making important to consider static orientation accuracy as a goal to characterize in future work. Larger errors at the start of each path (near +x) are due to the start points of each trajectory being set manually and letting the controller command the capsule to the desired path. Additionally, these errors in the sinusoidal trajectory trials can be attributed to the capsule being near the tether constraint where bending is difficult. As this trial is a preliminary step in implementing closed loop control, which is key for real-time computer assisted teleoperation, time of response was not optimized as we plan to focus on this in future work.

V. Conclusion

In this study we built upon and expanded a closed loop control scheme for actuating a tethered magnet-embedded capsule. We developed a complimentary plug-in for an open source dynamic simulation environment to test our control methodology. Once having successfully tested trajectory following in simulation, we implemented the control on our physical platform. To obtain both position and orientation feedback, we implemented a clinically applicable real-time localization scheme that utilizes the driving magnet's magnetic field map. Orientation was obtained by fusing accelerometer and gyroscope data through an extended complimentary filter. Magnetic field data was used to further improve the performance of this filter and alleviate adverse gyroscope drift effects. This pose feedback was then used with the control scheme and the tethered capsule successfully followed commanded position and orientation trajectories. The observed position errors were within the geometry of the capsule itself and well within the bounds of an average colon diameter and thus acceptable for the screening procedure. Previous studies have demonstrated trajectory following of untethered capsules with limitations such as mechanically constraining a capsule's motion [18] or submerging the capsule and controlling its orientation in open loop [15]. The novelty in our results is the demonstration of closed loop control of a tethered magnetic capsule in 4 DoF: motion in the horizontal plane, panning, and tilting, as well as the integration of magnetic localization and the demonstration of a customized dynamic simulation environment for algorithm development. Although outcomes were promising, further work is necessary; specifically in mechanical tether characterization. Currently, all effects of the tether and capsule friction act as disturbances in capsule motion. The tether's frictional and bending stiffness should be accounted for to assist in control. We hypothesize that estimation and incorporation of these disturbing forces and torques in the control scheme will assist in maneuvering inside the space-constrained colon.

Fig. 1.

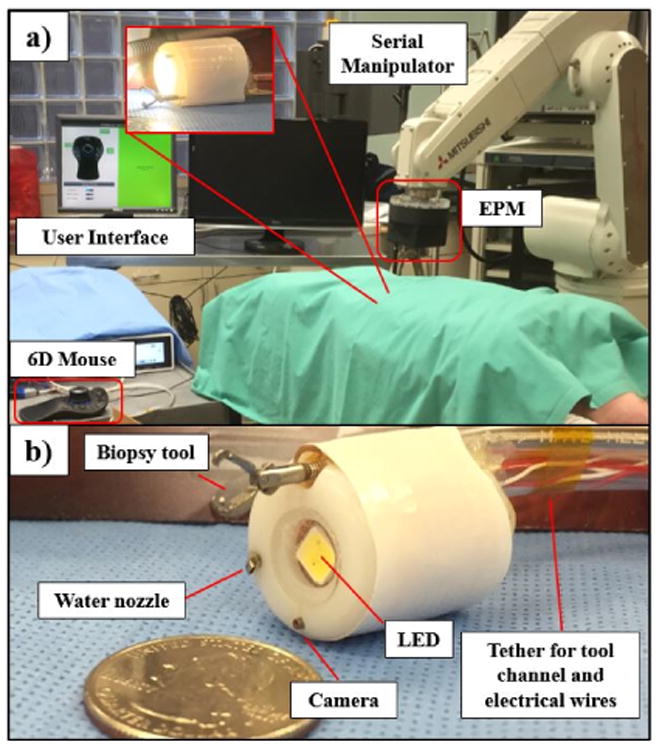
(a) Tethered capsule system during in vivo colonoscopy trial (b) The capsule maintains all functionality of a standard colonoscope.

VII. Appendix

The following is a derivation of the terms of the Jacobian J_ℱ(p, m̂_a, m̂_c). Each term of J_ℱ represents a partial derivation of the force and torque equations of the dipole-dipole model.

$$J_{\mathcal{F}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})=\left[\begin{array}{ccc}{F}_p& F_{ma}& F_{mc}\\ T_p& T_{ma}& T_{mc}\end{array}\right]$$ (29)

where G = I − p̂p̂^⊤, Z = I − 5p̂p̂^⊤, and D = 3p̂p̂^⊤ − I. The terms of the Jacobian are defined as follows:

$$F_p=\frac{\partial {\mathit{f}}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})}{\partial \mathit{p}}=\frac{3{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^5}({\widehat{\mathit{m}}}_{\mathit{a}}{{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }Z+{\widehat{\mathit{m}}}_{\mathit{c}}{{\widehat{\mathit{m}}}_{\mathit{a}}}^{\top }Z+{{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }{\widehat{\mathit{m}}}_{\mathit{a}}Z-5\widehat{\mathit{p}}{\widehat{\mathit{p}}}^{\top }{\widehat{\mathit{m}}}_{\mathit{a}}{{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }G-5\widehat{\mathit{p}}{\widehat{\mathit{p}}}^{\top }{\widehat{\mathit{m}}}_{\mathit{c}}{{\widehat{\mathit{m}}}_{\mathit{a}}}^{\top }G-5{{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }\widehat{\mathit{p}}{\widehat{\mathit{p}}}^{\top }{\widehat{\mathit{m}}}_{\mathit{a}}Z)$$ (30)

$$F_{ma}=\frac{\partial {\mathit{f}}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})}{\partial {\widehat{\mathit{m}}}_{\mathit{a}}}=\frac{3{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^4}({{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }\widehat{\mathit{p}}I+{\widehat{\mathit{m}}}_{\mathit{c}}{\widehat{\mathit{p}}}^{\top }+\widehat{\mathit{p}}{{\widehat{\mathit{m}}}_{\mathit{c}}}^{\top }Z)$$ (31)

$$F_{mc}=\frac{\partial {\mathit{f}}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})}{\partial {\widehat{\mathit{m}}}_{\mathit{c}}}=\frac{3{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^4}({\widehat{\mathit{m}}}_{\mathit{a}}{\widehat{\mathit{p}}}^{\top }+{{\widehat{\mathit{m}}}_{\mathit{a}}}^{\top }\widehat{\mathit{p}}I+\widehat{\mathit{p}}{{\widehat{\mathit{m}}}_{\mathit{a}}}^{\top }Z)$$ (32)

$$T_p=\frac{\partial {\mathit{\tau }}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})}{{\partial }_{\mathit{p}}}=\frac{3{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi }\left(S\right(\frac{{\widehat{\mathit{m}}}_{\mathit{c}}}{{\Vert \mathit{p}\Vert }^3}\left)\right(\widehat{\mathit{p}}{{\widehat{\mathit{m}}}_{\mathit{a}}}^{\top }\left(\frac{G}{\Vert \mathit{p}\Vert }\right)+\left(\frac{G}{\Vert \mathit{p}\Vert }\right){\widehat{\mathit{p}}}^{\top }{\widehat{\mathit{m}}}_{\mathit{a}})+S(D{\widehat{\mathit{m}}}_{\mathit{a}})(\frac{{\widehat{\mathit{m}}}_{\mathit{c}}{\widehat{\mathit{p}}}^{\top }}{\Vert \mathit{p}\Vert }\left)\right)$$ (33)

$$T_{ma}=\frac{\partial {\mathit{\tau }}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})}{\partial {\widehat{\mathit{m}}}_{\mathit{a}}}=\frac{{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^3}S({\widehat{\mathit{m}}}_{\mathit{c}})D$$ (34)

$$T_{mc}=\frac{\partial {\mathit{\tau }}_{\mathit{m}}(\mathit{p},{\widehat{\mathit{m}}}_{\mathit{a}},{\widehat{\mathit{m}}}_{\mathit{c}})}{\partial {\widehat{\mathit{m}}}_{\mathit{c}}}=-\frac{{\mu }_0\Vert {\mathit{m}}_{\mathit{a}}\Vert \Vert {\mathit{m}}_{\mathit{c}}\Vert }{4\pi {\Vert \mathit{p}\Vert }^3}S(D{\widehat{\mathit{m}}}_{\mathit{a}})$$ (35)