Abstract
An extensive analysis of structural databases is carried out to investigate the relative flexibility of B-DNA and A-RNA duplexes in crystal form. Our results show that the general anisotropic concept of flexibility is not very useful to compare the deformability of B-DNA and A-RNA duplexes, since the flexibility patterns of B-DNA and A-RNA are quite different. In other words, ‘flexibility’ is a dangerous word for describing macromolecules, unless it is clearly defined. A few soft essential movements explain most of the natural flexibility of A-RNA, whereas many are necessary for B-DNA. Essential movements occurring in naked B-DNAs are identical to those necessary to deform DNA in DNA–protein complexes, which suggest that evolution has designed DNA–protein complexes so that B-DNA is deformed according to its natural tendency. DNA is generally more flexible, but for some distortions A-RNA is easier to deform. Local stiffness constants obtained for naked B-DNAs and DNA complexes are very close, demonstrating that global distortions in DNA necessary for binding to proteins are the result of the addition of small concerted deformations at the base-pair level. Finally, it is worth noting that in general the picture of the relative deformability of A-RNA and DNA derived from database analysis agrees very well with that derived from state of the art molecular dynamics (MD) simulations.
INTRODUCTION
Nucleic acids are long, flexible polymers able to adapt their structure to changes in sequence, presence of drugs or proteins, mechanical stress, or changes in the solvent environment (1–3). The deformability of nucleic acids is of special importance in their ability to be recognized by specific proteins, which in some cases can dramatically distort their canonical structure (4–12). In fact, the sequence-dependent deformability of DNA duplexes is believed to be a kind of ‘secondary genetic code’ that can enhance or reduce the ability of a given DNA segment to be packed in nucleosomes, or to be recognized by proteins (6,8,12,13).
Most theoretical and experimental studies of nucleic acids deformability have been focused on the B-DNA duplex [for reviews see references (11,14)]. These studies have suggested that the deformability of B-DNA can be mostly understood by considering changes in helical parameters at the dinucleotide level. For example, Dickerson found that subtle changes in roll can explain the bending of DNA in many protein–DNA complexes (7). Local bending and twisting was also used to predict nucleosome stability in different DNA sequences (10). Lavery et al. (5) suggested that simple local distortions can explain large structural changes in DNA upon binding to proteins. Similar conclusions were reached by Beveridge's group (12). Furthermore, Olson and coworkers (9) found that subtle changes in local twist can explain most heterogeneity in 38 B-DNA structures collected from NDB. Finally, Okonogi et al. have recently presented direct experimental evidence (15,16) that local distortions are propagated to the entire duplex. In summary, several indirect evidences suggest that the flexibility of B-DNA can be understood as a combination of small geometrical distortions at the constituting steps.
The characterization of the flexibility pattern of A-RNA has received less attention, despite the fact that deformability of short and medium pieces of A-RNA can modulate its interaction with other macromolecules. Electron micrography, gel electrophoresis, hydrodynamic measurements or fiber diffraction (17–19) suggest that A-RNA is generally more rigid than DNA. The same generic conclusion was reached from different NMR experiments (20,21). Furthermore, the larger polymorphism in the B-family compared with the A-family found in crystal structures has been traditionally used as an additional evidence of the greater flexibility of B-DNA compared with A-RNA (1–3).
Molecular dynamics (MD) simulations by Cheatham and Kollman (22) showed that the backbone in A-RNA was more rigid than in B-DNA, which was taken as a probe of the greater flexibility of B-DNA compared with A-RNA. Similar conclusions were reached by Westhof's group from MD simulations of B-DNA and A-RNA homopolymers (23,24).These conclusions have been recently challenged by MD simulations from MacKerell's group (25), who concluded, from a 5 ns CHARMM-MD simulation, that A-RNA fluctuates more than B-DNA at the base-pair level. Recent extended MD simulations performed in our group (26) on B-DNA and A-RNA dodecamers revealed that the deformability pattern is more complex than expected. Thus, B-DNA has on average greater entropy than A-RNA, confirming that it is less globally rigid. However, depending on the type of perturbation considered, B-DNA is more or less flexible than A-RNA. Our analysis pointed out that DNA is more flexible than A-RNA in terms of medium and high frequency movements related to local backbone transitions with little impact on the global helical properties of the duplex. However, when only the first essential movements (i.e. those with the lowest frequency) are considered, A-RNA is surprisingly more flexible than B-DNA. Stiffness analysis using helical coordinates allowed us to quantify the helical deformability of B-DNA and A-RNA, showing that B-DNA is more or less flexible than A-RNA depending on the helical coordinate considered. In other words, the B-DNA backbone is clearly more flexible than the A-RNA one, but backbone movements sampled by B-DNA do not imply changes in the global helical conformation in many cases. The flexibility of B-DNA and A-RNA, thus, appears to be more complex and subtle than initially thought, and its analysis requires more attention than usually given.
In this paper we will continue our investigation of the relative flexibility of B-DNA and A-RNA duplexes. Here we will analyze crystal databases to determine: (i) the relative flexibility of B-DNA and A-RNA in the ‘conformational space’ sampled by structures of duplexes deposited in NDB, (ii) the nature of the distortions from the ideal helical conformation induced by sequence and crystal lattice on A-RNA and B-DNA duplexes, and (iii) whether or not the movements sampled during a MD trajectory are equivalent to those sampled by different chemical structures present in NDB.
METHODS
Database definition
A crucial step in the analysis was the selection of a significant set of structures to define the normal conformational space sampled by B-DNA and A-RNA duplex structures deposited in NDB. Since the number of structures in the database is small and all the methods used to characterize the flexibility in nucleic acids are directly or indirectly based on the harmonic oscillator model, elimination of anomalous structures is necessary to guarantee the reliability of the results.
First all B-DNA and A-RNA duplexes solved by X-ray crystallography and deposited in the 2003 version of the NDB server (http://ndbserver.rutgers.edu) were filtered to eliminate structures containing proteins, drugs, mismatchings, overhanging bases or more than three unusual bases (other than A, T, G, C or U) in canonical Watson–Crick pairings. Second, to reduce severe lattice artefacts (27) all B-DNA and A-RNA duplexes shorter than 8 bp were also removed. Third, helical analysis (28) of the remaining structures is performed at the canonical base-pair level removing those base pairs showing one or more unusual helical parameter (more than three times out of the standard deviation from the average for this step type) since the presence of these base pairs in database can bias the harmonic analysis. For backbone analysis (see Essential dynamics), those structures where the backbone RMSD of the central 6mer portion of the duplex deviates by >3 Å from the mode were eliminated from the set of structures defined after the second step. This procedure reduces the database to 367 B-DNA and 209 A-RNA steps for analysis. All (33 A-RNA and 66 DNA) structures selected were solved by X-ray techniques with a resolution better than 3 Å (a list of the database of structures is shown in Table S1 of Supplementary Material).
The preceding selection procedure eliminates a sizeable amount of experimental data and reduces the population of certain steps (e.g. there are only nine TA steps for B-DNA and eight AU steps for A-RNA), limiting then our ability to characterize flexibility at the sequence level as done by other authors (7–9,29). However, it guarantees that: (i) perturbations are within the harmonic limit, that is, conformations considered can be reached under typical thermal energy (10,30) by unperturbed naked nucleic acids, (ii) harmonic models fitted to represent flexibility of naked B-DNA and A-RNA are not dependent on the spurious presence of outliers in the database, (iii) results for B-DNA and A-RNA can be directly compared without concerns derived from the different nature of the perturbation induced by proteins, mutations or drugs in both types of nucleic acids.
Energetic analysis
The step interaction energy (stacking + hydrogen bond) for all steps in the database was determined after addition of hydrogens with AMBER6.0 (31), and capping of the nucleobase at the C1′ with a methyl group (i.e. the sugar was substituted by an united-atom CH3 group keeping the atomic definition of the nucleobases in neutral subsystems). PARM-99 (31,32) was used to describe the nucleobase–nucleobase interactions.
Helical parameters
All the structures collected were analyzed to derive helical parameters using the 3DNA (28). Bending angles (distortion, θ, and directionality, φ) were computed as described by Sherer et al. (33) from tilt (τ) and roll (ρ) angles as shown in Equations 1 and 2. Unless otherwise noted, we always refer to local helical parameters. Additional geometrical parameters were derived with analysis modules in AMBER and with in house software.
![]()
![]()
where δ = 1 if ρ < 0 and 0 otherwise, defining then positive bending towards the major groove.
Essential dynamics
The set of structures of B-DNA and A-RNA in the database were used to create a ‘pseudo-trajectory’ in the NDB conformational space. For this purpose, all the backbone heavy atoms of the central (six-steps) portion of the duplexes were superposed (oriented with respect to a common reference system), thus leading to two separate files for B-DNA and A-RNA, respectively. Once these pseudo-trajectory files were created we computed the essential motions in the NDB conformational space: i.e. the geometrical changes that explain more conformational variability in B-DNA and A-RNA induced by the sequence and crystallization conditions. To this end, covariance matrices for common atoms of DNA and A-RNA (i.e. by excluding 2′-OH/H) were built and diagonalized. The eigenvectors define the type of essential motions in NDB conformational space, and the associated eigenvalues determine how much of variance in the trajectory is explained by each eigenvector.
The similarity between the type of movements in NDB conformational space between B-DNA and A-RNA can be determined by using absolute (γ) and relative (κ) similarity indexes (34–37), as shown in Equations 3 and 4.

where νiA stands for the unitary eigenvector i of nucleic acid A (B-DNA or A-RNA), and n is the minimum number of essential motions that account for a given variance in the trajectory (we found that eight modes explained at least 80% of variance of any trajectory or pseudo-trajectory).

where the self-similarity indexes γAAT are obtained by comparing eigenvectors obtained with the first and second parts of the same pseudo-trajectory.
Interestingly, Equations 3 and 4 can be used to compare pseudo-trajectories in NDB conformational space with trajectories in geometrical space collected from extended MD simulations of B-DNA and A-RNA duplexes. For this purpose we built and diagonalized covariance matrices containing the fluctuations of the central six-steps backbone heavy atoms obtained after 10 ns MD simulations in water of 12mer B-DNA and A-RNA duplexes (26). This analysis allowed us to quantify to what extent the small harmonic movements induced in B-DNA and A-RNA by changes in structure or crystal environment are the same than those explored spontaneously by a typical B-DNA duplex in aqueous solution. Finally, we also explored whether or not the type of severe distortions needed to bind DNA to proteins can be explained based on the essential movements sampled by naked DNA in either NDB or Cartesian space. For this purpose, similarity indexes were computed between MD-trajectories or pseudo-trajectories derived from naked B-DNAs in NDB and an extended database of B-DNAs containing naked B-DNA and A-RNA bound to proteins.
Entropy calculation
Samplings in NDB database are too limited to provide converged entropies using pseudo-harmonic models (38,39). However, we can obtain a rough estimate of entropy in the helical space by assuming that helical entropy only depends on base-pair rotations (roll, twist and tilt). Dividing the conformational space in a discrete three-dimensional grid (5° spacing), the entropy can be computed from the probability of existence of a given microstate Pμ as shown in Equation 5 (40). To make the results comparable entropies were in general calculated using datasets of equal size for B-DNA and A-RNA (see below).
![]()
Stiffness analysis
If the deformation of B-DNA and A-RNA is assumed to be harmonic, i.e. if conformational sampling is Gaussian (see above), the stiffness of these molecules can be characterized by the force constants associated with each deformation. Such force constants can be derived from the Gaussian fluctuations at constant temperature detected in either MD trajectories or structural databases (8,13,26,35,36,41,42). A first set of reasonable deformation variables are the essential movements determined as described above (26,36). Since these movements are orthogonal, no coupling terms exist, and pure force constants can be derived as shown in Equation 6.
![]()
where λi is the eigenvalue (in Å2) associated with the essential movement νi determined by diagonalization of the covariance matrix, T is the temperature (in Kelvin), k is the Boltzmann's constant and Ki is a force constant associated with the essential motion.
Alternatively, the deformation can be measured by using helical parameters (tilt, roll, twist, shift, slide and rise). These variables are closer to chemical intuition than essential movements, but are not orthogonal, complicating the concept of stiffness matrix (F = F(Kij)), where the non-diagonal elements correspond to coupling terms. As shown by others (8,13,41,42), the stiffness matrix can be easily determined by inversion of the covariance matrix C = C(〈<xixj>〉) computed in the helical space as shown in Equation 7.
![]()
Furthermore, the determinant of the covariance matrix in helical space (8,43) provides a measure of the generalized conformational volume sampled by B-DNA and A-RNA structures in NDB. With some caution, due to the unit-dependence of this parameter (when it is computed combining rotational and translational parameters), this value can be used to roughly characterize the general deformability of both nucleic acids in the NDB conformational space.
![]()
Finally, it is worth noting that the methods outlined here to compute stiffness rely on the assumption that the deformations detected in the ensemble of structures arise from the intrinsic flexibility of the structure, that is, no external forces (like the presence of bound proteins or drugs) bias the ensemble of selected structures. In order to guarantee this point, the analysis was performed using the reduced database of naked B-DNA and A-RNA (n databases). We also generated an extended database (n+p database) containing naked B-DNAs as well as heavily distorted fragments of DNA taken from the W. Olson database (8). Since DNA-bound complexes are not distorted equally in all portions of the structure we incorporated only the 6mer fragment to this database where the protein induces the largest distortions in the DNA. This extended data-base contains then both relaxed and heavily distorted DNAs. Analysis of this database will provide information on the large structural deformations needed to fit the duplex geometry to that in DNA–protein complexes.
RESULTS AND DISCUSSION
General crystal properties
There is a general thought that the greater flexibility of B-DNA should be reflected in the comparison of the structural characteristics of the available X-ray crystallographic structures of B-DNA and A-RNA. Thus, a common thought in the field is that a greater flexibility of a structure should be reflected in its crystallization in a more diverse range of crystallographic space groups and in a generally worse resolution and higher temperature factors in the solved structures. Inspection of the database of naked B-DNA and A-RNA (see Table 1) indicates that they have been solved with similar resolution, the number of crystallographic forms of A-RNA is higher than that of B-DNA, and the temperature factor is on average higher for A-RNA than for B-DNA. Therefore, these simple properties do not support the general idea that B-DNA is more flexible than A-RNA. In fact the real significance of these parameters as descriptors of flexibility seems very questionable.
Table 1. Average temperature factor, number of crystallographic space groups and resolution in NDB-crystal structures of B-DNA and A-RNA duplexes showing no chemical alterations nor bound ligands (drugs or proteins).
| B-DNA | A-RNA | |
|---|---|---|
| Average temperature factor (degrees) | 20 | 29 |
| Number of crystallographic space groups | 14 | 20 |
| Resolution (Å) | 1.9 | 1.9 |
Short duplexes and hairpins were eliminated from the study. The total number of structures considered was 74 (B-DNA) and 67 (A-RNA).
Equilibrium helical parameters
The base-pair translations (shift, slide and rise) and rotations (tilt, roll and twist) were computed for all the steps in the database of naked B-DNA and A-RNA. Fitting against different continuous functions (http://www.xycoon.com/continuousdistributions.htm) show that in most cases the distribution of values for each type of base step was nearly Gaussian, which allowed us to roughly characterize the distributions of values from the mean and its associated standard deviation (see Table S2 in Supplementary Material). Values for steps where sampling is poor must however be taken with caution. The overall distributions (mixing all the base steps) have in all the cases reasonable Gaussian shapes (data available upon request). Average values are close to the expected values for canonical B and A forms (3), the major differences between B-DNA and A-RNA being found for roll (close to 0 in B-DNA and around 8° for A-RNA), twist (4° smaller in A-RNA) and slide (0.3 Å for B-DNA and around −1.6 Å for A-RNA). Standard deviations associated with the average shift, rise and tilt are similar for B-DNA and A-RNA, whereas large values are found for B-DNA in roll, twist and slide (see Table S2 in Supplementary Material). Analysis of the results demonstrates that the largest dispersion of roll, twist and slide in B-DNA is due to a greater sequence-induced variability (see Table S2 in Supplementary Material).
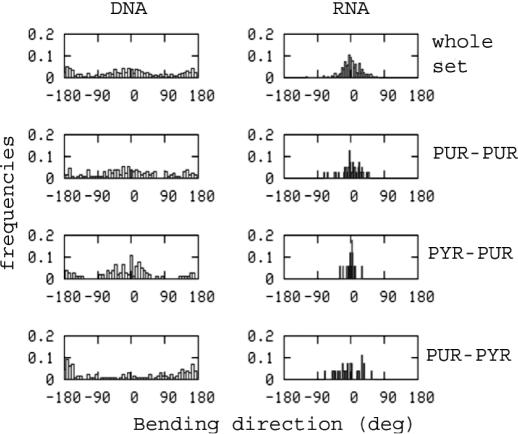
Tilt and roll can be combined to obtain information on the intrinsic bending of B-DNA and A-RNA (see Methods), which depends on the bending angle and the bending directionality (θ and φ) in Equations 1 and 2. The former indicates the magnitude of the bending, and the latter the direction (towards major or minor groove) of the bending. Histogram plots (see Figure 1) show that there are no major differences in terms of the bending angle between B-DNA and A-RNA, and in fact, the distribution of θ values is slightly smoother for A-RNA than for B-DNA. There are, however, major differences in the bending direction, since A-RNA bends only towards the major groove (φ distribution centered around 0°), while B-DNA bends towards both major and minor grooves (bimodal φ distribution centered around 0 and 180°). Moreover, there are little sequence-induced changes in the bending of A-RNA (both in terms of θ and φ), whereas larger differences are detected for B-DNA, since Pur-Pyr steps have a greater tendency to bend to the major groove, while Pyr-Pur show the opposite trend (see Figure 1).
Figure 1.
Histogram representation of the bending angle in crystal structures of B-DNA and A-RNA.
Nucleobase interaction energies
The different arrangement of nucleobases in B-DNA and A-RNA might lead to different nucleobase–nucleobase interaction energies. Hydrogen-bonding is very good for both B-DNA and A-RNA, close to the limit of perfect interactions in the gas phase (44). Overall, the hydrogen bond is slightly better for B-DNA [AT (−10.4 ± 3.8); GC (−25.5 ± 5.4)] than for A-RNA [AU (−9.4 ± 4.2); GC (−23.9 ± 6.9)], but the difference is rather small to be significant. The stacking is on average better (>2 kcal/mol) for B-DNA than for A-RNA (see Table 2), suggesting that the greater compactness of A-RNA does not lead to better stacking between nucleobases. The change from B-DNA to A-RNA parameters does not have the same effect for all the steps, which implies that the ordering of stacking stability for the different steps in B-DNA and A-RNA is different. The largest difference is found for GC, which has the best stacking for A-RNA, but one of the worst for B-DNA (see Table 2). Finally, it is worth noting that the range of variability of stacking energies in B-DNA and A-RNA is similar.
Table 2. Stacking energies (in kcal/mol) for the different steps in B-DNA and A-RNA (standard deviations in parenthesis).
| Step | B-DNA | A-RNA |
|---|---|---|
| AA | −17.5(1.7) | −13.7(0.8) |
| AC | −18.1(1.5) | −13.8(1.1) |
| AG | −15.8(1.5) | −14.0(1.5) |
| AT/AU | −16.7(1.0) | −15.4(1.0) |
| CA | −19.5(1.5) | −14.4(1.2) |
| CC | −14.9(1.8) | −11.1(2.3) |
| CG | −19.2(2.4) | −15.6(1.7) |
| GA | −14.7(1.6) | −14.2(1.4) |
| GC | −14.7(2.4) | −16.9(1.3) |
| TA/UA | −17.0(0.9) | −16.0(1.4) |
| Averagea | −16.8(1.7) | −14.5(1.5) |
| Averageb | −16.7(2.7) | −14.3(2.4) |
The ‘average’ values correspond to the stacking × base step in a segment of B-DNA with the same amount of each base stepa or with the same composition of base steps found in the databaseb.
Global flexibility
The global flexibility of A-RNA and B-DNA was examined from the amount of conformational space occupied by the structures included in the database. To this end, both Shanon's entropy and Go's conformational volume (see Methods) in helical space were determined. Due to the limited size of the sampling set, both parameters were determined for the entire set of nucleic acids, and not for the different base pairs. Results in Table 3 strongly suggest that the B-DNA is more flexible than the A-RNA. Thus, the B-DNA has a conformational volume >5 Å3 deg3 larger than that of A-RNA. Furthermore, Shanon's entropy associated with helical rotations is ∼2 cal/K mol larger for B-DNA than for A-RNA. Therefore, B-DNA is able to sample more different conformations than A-RNA in order to adapt its structure to changes in sequence or crystal environment. It is worth noting that the same conclusion was recently obtained when flexibility in the Cartesian space was studied by MD simulations (26).
Table 3. Parameters describing global flexibility of B-DNA and A-RNA.
| Parameter | B-DNA | A-RNA |
|---|---|---|
| Entropy | 11.3 | 9.5 |
| 11.0 | ||
| Conformational volume | 7.1 | 1.7 |
| 7.0 |
Entropies are in cal/K mol and conformational volumes are in Å3 deg3. Values in italics correspond to the average values obtained by selecting seven random subsets of B-DNAs of the same size than the total A-RNA set.
Essential dynamics
As noted above, we can generate pseudo-trajectories by linking all the common elements of B-DNA or A-RNA structures accessible in NDB. Principal component analysis can then be used to determine the essential movements that explain most of the structural deformations induced by changes in sequence or crystal environment. The eigenvalues provide direct information on the deformability of structures along their essential movements, and the eigenvectors describe the nature of these movements.
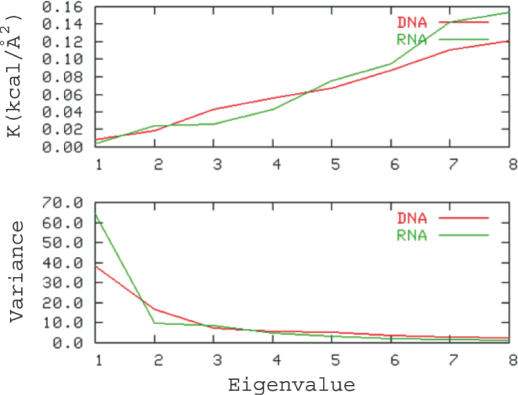
A-RNA has a simpler deformability pattern than B-DNA, since only three principal components explain 80% of variance in the A-RNA pseudo-trajectory. The deformation pattern of B-DNA is more complex and eight components are necessary to explain the same level of variance. The first essential movements always correspond to twisting and untwisting transitions, which are related to changes (sometimes correlated) of roll and twist. Interestingly, the force constants associated with the first essential movements are higher for B-DNA than for A-RNA, whereas the situation reverses for higher modes (see Figure 2, top). This suggests that the distortion in A-RNA is dominated by only a few movements, which explains a large percentage of variance, and have very low force constants as shown in Equation 6 and Figure 2. The opposite situation occurs for B-DNA, which has a more complex deformation pattern and where a large number of distortions having low force constants make significant contributions to the total deformability of the molecule. It is worth noting that a similar result has been recently inferred from the analysis of the deformability in Cartesian space in MD simulations of B-DNA and A-RNA (26; note that for a typo error force constants (in cal/mol Å2) displayed in figure 4 of reference 26 must be multiplied by 10).
Figure 2.
Associated force constants (top) and variance (bottom) explained by the first eigenvectors obtained by PCA of the database of crystal structures of B-DNA and A-RNA.
The set of eigenvectors obtained by principal component analysis (PCA) can be used to measure the similarity between the deformability patterns determined in the two (pseudo-) trajectories as shown in Equations 3 and 4. Though the values in Table 4 must be viewed with caution due to possible errors arising from the limited size of the crystallographic databases, they clearly point out a reasonable similarity between the different trajectories. A very high similarity index (κ = 0.96) is found between the essential movements detected in the pseudo-trajectory built up by mixing naked B-DNAs and the most deformed 6mer DNAs in the DNA–protein database [DNA(n) and DNA(n+p) databases]. This result is very surprising considering that DNA exhibits a much wider range of distortion in the DNA(n+p) database than in the DNA(n). Clearly, this excellent agreement demonstrates that binding to proteins implies conformation changes in the nucleic acid, which are similar to those spontaneously happening in DNA, to adapt its structures to changes in sequence or environment.
Table 4. Relative similarity indexes (κ, Equation 4) between different trajectories and pseudo-trajectories.
| DNA(n+p) | DNA(MD) | A-RNA(n) | A-RNA(MD) | |
|---|---|---|---|---|
| DNA(n) | 0.96 | 0.61 | 0.70 | 0.50 |
| DNA(n+p) | 1.00 | 0.61 | 0.71 | 0.63 |
| DNA(MD) | 1.00 | 0.62 | 0.61 | |
| A-RNA(n) | 1.00 | 0.69 |
The index n refers to naked B-DNA or A-RNA, and n+p refers to an extended set containing naked B-DNA and those distorted in protein–DNA complexes. MD eigenvectors were derived from trajectories of B-DNA and A-RNA26. Calculations were always performed considering 6mer duplexes. In the case of the DNA–protein complexes, only the 6mer DNA showing the largest distortion for each DNA–protein complex was introduced in the study.
Even though B-DNA and A-RNA have different patterns of essential movements, there is a reasonably good conservation in the nature of these movements (see Table 4). When the B-DNA and A-RNA structures collected from MD trajectories are compared, the similarity index is ∼0.6, which is remarkably high considering that similarity indexes between MD trajectories of two different B-DNAs are typically ∼0.7(35). Interestingly, the same level of similarity is found (see Table 4) when pseudo-trajectories of crystallographic B-DNA and A-RNA structures are compared. Such an agreement in the NDB conformational space agrees with MD studies on the similarity between the essential dynamics of B-DNA and A-RNA in the Cartesian space (26). Finally, essential movements obtained from database analysis and from MD simulations are quite similar (κ in the range 0.6–0.7), which demonstrates that the conformational space sampled in NDB is equivalent to the Cartesian space sampled spontaneously by nucleic acids. Furthermore, this agreement suggests that the distortion required to adapt the DNA to the conformation found in protein–DNA complexes is similar to those happening spontaneously in naked B-DNA This exciting finding points out the existence of a ‘parallel genetic code’, probably conserved along evolution, which favours DNA structures whose essential movements favour the transitions needed to accommodate proteins necessary to control DNA function.
Stiffness analysis
Essential dynamics provides important information on the deformability of B-DNA and A-RNA along their easiest deformation modes. Unfortunately, this information is often difficult to manipulate, since essential movements are a complex combination of Cartesian movements. For this reason, we perform an alternative stiffness analysis that exploits the covariance matrix in helical space (see Methods). The force constants obtained in this way represent the energetic response of B-DNA or A-RNA to deformation along helical coordinates (shift, slide, rise, tilt, roll and twist) and provides a complementary view of the relative flexibility of B-DNA and A-RNA.
The easiest deformations in B-DNA and A-RNA are related to local rotations, especially those related to roll and twist. Changes in translation parameters are strongly penalized, especially those involving changes in rise, which would lead to the loss of stacking (see Table 5). Diagonal force constants derived from the analysis of the DNA(n+p) databases are only 25% smaller than those obtained from naked B-DNAs (see Table 5). This is a surprisingly small difference (see Methods), which demonstrates that deformation in DNA upon binding of proteins is achieved by combining small, easy to achieve, local changes at the base-pair level (5), not the result of large distortions in singular base steps. Finally, we should note that results in Table 5 give strong support to previous work by Olson et al. (8), who used a database of DNA structures in protein–DNA complexes (taking both distorted and undistorted fragments) to derive sequence-dependent force constants for naked B-DNAs. Indirectly, the agreement between force constant derived from the n+p and n databases support the validity of simple harmonic models to describe quite important distortions, which a priori might escape the limit of validity of this simple model.
Table 5. Stiffness matrices associated with helical perturbations for naked B-DNA and A-RNA (top and bottom) and for an extended DNA database containing naked B-DNA and the most deformed DNA fragments in DNA–protein complexes (Olson's database of protein–DNA complexes).
| Shift | Slide | Rise | Tilt | Roll | Twist | |
|---|---|---|---|---|---|---|
| DNA(n) | ||||||
| Shift | 2.31082 | 0.09175 | −0.09175 | −0.11564 | −0.05113 | −0.00285 |
| Slide | 1.17627 | 0.98557 | 0.01765 | −0.02734 | −0.07371 | |
| Rise | 18.05446 | −0.14935 | 0.05237 | −0.27328 | ||
| Tilt | 0.06253 | −0.00445 | −0.00184 | |||
| Roll | 0.02708 | 0.01387 | ||||
| Twist | 0.02669 | |||||
| DNA(n+p) | ||||||
| Shift | 1.66491 | 0.05778 | 0.06154 | −0.06276 | 0.00065 | 0.00168 |
| Slide | 1.08977 | 0.67920 | −0.00373 | −0.02581 | 0.05305 | |
| Rise | 10.47476 | −0.00321 | −0.00362 | −0.13664 | ||
| Tilt | 0.04689 | −0.00065 | 0.00024 | |||
| Roll | 0.02078 | 0.01022 | ||||
| Twist | 0.02146 | |||||
| A-RNA(n) | ||||||
| Shift | 2.54995 | 0.05198 | 0.03773 | −0.09609 | −0.00506 | −0.01015 |
| Slide | 5.73142 | 1.88597 | 0.05159 | −0.04125 | −0.17395 | |
| Rise | 13.05905 | 0.01095 | −0.10001 | −0.15162 | ||
| Tilt | 0.05947 | −0.00299 | −0.00543 | |||
| Roll | 0.03665 | 0.01135 | ||||
| Twist | 0.04713 | |||||
Force constants associated with translations are in kcal/mol Å2, those corresponding to rotations are in kcal/mol deg2 and hybrid terms in kcal/mol deg Å.
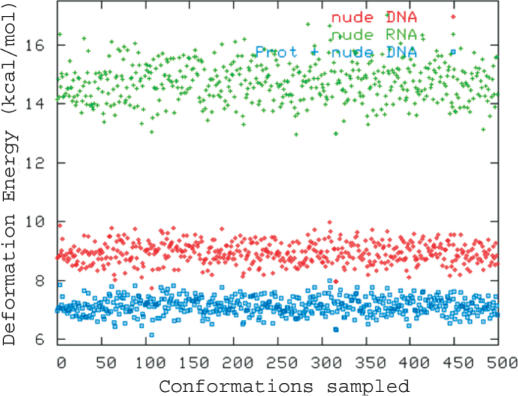
Distortion energies (in Figure 3) suggest that the whole B-DNA is more flexible in the NDB conformational space than A-RNA (see Figure 3), but the analysis of stiffness matrices (Table 5) demonstrates the existence of subtle differences in the deformability of B-DNA and A-RNA (see Table 5). Thus, despite the fact that in general B-DNA is more flexible than A-RNA, deformations of rise or tilt are more difficult for B-DNA than for A-RNA, and in fact the largest general rigidity of A-RNA is mainly related to slide and twist deformations, which are much less penalized in B-DNA compared with A-RNA. It is worth noting that these subtle effects are also found in the analysis of structures sampled in MD simulations of canonical B-DNA and A-RNA duplexes [see Table 5, (26)]. In summary, both database analysis and MD simulations strongly suggest that the concepts ‘flexibility’ or ‘rigidity’ can be meaningless if they are not associated with a type of distortion, and that more accurate definition of these concepts need to be used to characterize nucleic acids.
Figure 3.
Elastic deformation energy (in kcal/mol) determined for a common perturbation level for B-DNA and A-RNA. Calculations for B-DNA are repeated considering force constants obtained from the analysis of naked B-DNA and from the analysis of the extended database containing both naked and protein-bound DNAs.
A-DNA
This paper has been focussed on the two major conformations of DNA and A-RNA duplexes under physiological conditions. However, some interest exists in determining the flexibility properties of A-type conformation of DNA. The flexibility analysis of A-DNA structure is handicapped by the bias in the composition of the database derived (using the same cleaning protocol) from NDB. Thus, there are four times more GC than AT pairs, several steps like d(AA), d(AT) and d(AG) have none or very few examples in the database, whereas d(GC) and d(CG) steps are massively over-represented. In summary, the database of A-DNA is very biased, and results derived from its analysis might have very large errors. However, and despite the caution needed, the similarity in the pattern of flexibility of A-DNA and A-RNA becomes clear. For example, we found relative similarity indexes (κ in Equation 4) ∼0.95 between A-DNA and A-RNA essential movements and 0.7 between B- and A-DNAs, indicating that the nature of the easiest deformations of A-DNA is very close of those of A-RNA and not so close from those of B-DNA. Similarly, diagonal stiffness matrices obtained from helical analysis are (translations in kcal/mol Å2 rotations in kcal/mol deg2): 2.499 (shift), 6.524 (slide), 15.889 (rise), 0.122 (tilt), 0.034 (roll) and 0.0422 (twist). These values are very close to those of naked A-RNA in Table 5 and quite different to those of B-DNA shown in the same Table. In summary, quantitative analysis of A-DNA structure is not advisable with current database composition, but qualitative results derived here (extended results are available upon request) strongly suggest that, A-DNA is similar to A-RNA not only in structural terms, but also in flexibility terms.
CONCLUSIONS
There is a lot of evidence that chemical and Cartesian spaces reasonably agree, and that the ability of a given nucleic acid to adapt its structure to changes in its sequence or environment is a direct consequence of its flexibility in the Cartesian space. This finding supports the validity of database analysis in the description of B-DNA or A-RNA flexibility.
The type of movements necessary to adapt B-DNA to the very distorted geometries needed for protein binding are similar to those spontaneously happening in B-DNA, and can be understood as an addition of small local changes. The energy introduced by the protein is used to move farther than usual in distortion patterns, which were implicitly coded in the DNA in a sort of ‘secondary genetic code’.
Measures of global flexibility, like the conformational volume, Shanon's entropy or deformation energies suggest that, as generally accepted, B-DNA is more flexible than A-RNA. However, essential dynamics and helical stiffness analysis shows the limitations of the scalar concept of flexibility, since the pattern of deformability of B-DNA and A-RNA is very different. A-RNA shows a simple flexibility pattern, which can be described by a very small number of very soft essential movements, whereas that of B-DNA is much more complex and involves many relatively soft essential movements. In the helical space depending on the type of distortion, B-DNA can be more flexible or more rigid than A-RNA.
Overall, the excellent agreement between database analysis reported here and recent molecular dynamics simulations strongly support the synergy between both types of studies for a complex description of the flexibility of nucleic acids.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENTS
This work has been supported by the Spanish Ministry of Science and Technology (BIO2003-06848 and SAF2002-04282), the Fundación BBVA and the VI Framework Program of the European Union (UE project QLG1-CT-1999-00008).
REFERENCES
- 1.Bloomfield V.A., Tinoco,I., Hearst,J.E. and Crothers,D.M. (2000) Nucleic Acids: Structures, Properties, and Functions. University Science Books, Sausalito, CA. [Google Scholar]
- 2.Gait M.J. and Blackburn,G.M. (1990) Nucleic Acids in Chemistry and Biology. IRL Press, Oxford University Press, Oxford. [Google Scholar]
- 3.Saenger W. (1984) Principles of Nucleic Acid Structure. Springer, NY. [Google Scholar]
- 4.Cluzel P., Lebrun,A., Heller,C., Lavery,R., Viovy,J.L., Chatenay,D. and Caron,F. (1996) DNA: an extensible molecule. Science, 271, 792–794. [DOI] [PubMed] [Google Scholar]
- 5.Lebrun A., Shakked,Z. and Lavery,R. (1997) Local DNA stretching mimics the distortion caused by the TATA box-binding protein. Proc. Natl Acad. Sci. USA, 94, 2993–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lebrun A. and Lavery,R. (1996) Modelling extreme stretching of DNA. Nucleic Acids Res., 24, 2260–2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dickerson R.E. (1998) DNA bending: the prevalence of kinkiness and the virtues of normality. Nucleic Acids Res., 26, 1906–1926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Olson W.K., Gorin,A.A., Lu,X.J., Hock,L.M. and Zhurkin,V.B. (1998) DNA sequence-dependent deformability deduced from protein–DNA crystal complexes. Proc. Natl Acad. Sci. USA, 95, 11163–11168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gorin A.A., Zhurkin,V.B. and Olson,W.K. (1995) B-DNA twisting correlates with base-pair morphology. J. Mol. Biol., 247, 34–48. [DOI] [PubMed] [Google Scholar]
- 10.Anselmi C., Bocchinfuso,G., De Santis,P., Savino,M. and Scipioni,A. (2000) A theoretical model for the prediction of sequence-dependent nucleosome thermodynamic stability. Biophys. J., 79, 601–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Olson W.K. and Zhurkin,V.B. (2000) Modeling DNA deformations. Curr. Opin. Struct. Biol., 10, 286–297. [DOI] [PubMed] [Google Scholar]
- 12.Thayer K.M. and Beveridge,D.L. (2002) Hidden Markov models from molecular dynamics simulations on DNA. Proc. Natl Acad. Sci. USA, 99, 8642–8647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lankas F., Sponer,J., Langowski,J. and Cheatham,T.E.,III (2003) DNA basepair step deformability inferred from molecular dynamics simulations. Biophys. J., 85, 2872–2883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Olson W.K. (1996) Simulating DNA at low resolution. Curr. Opin. Struct. Biol., 6, 242–256. [DOI] [PubMed] [Google Scholar]
- 15.Okonogi T.M., Alley,S.C., Reese,A.W., Hopkins,P.B. and Robinson,B.H. (2000) Sequence-dependent dynamics in duplex DNA. Biophys. J., 78, 2560–2571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Okonogi T.M., Alley,S.C., Reese,A.W., Hopkins,P.B. and Robinson,B.H. (2002) Sequence-dependent dynamics of duplex DNA: the applicability of a dinucleotide model. Biophys. J., 83, 3446–3459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thomas J.C., Allison,S.A., Appellof,C.J. and Schurr,J.M. (1980) Torison dynamics and depolarization of fluorescence of linear macromolecules. II. Fluorescence polarization anisotropy measurements on a clean viral phi 29 DNA. Biophys. Chem., 12, 177–188. [DOI] [PubMed] [Google Scholar]
- 18.Hagerman P.J. (1988) Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem., 17, 265–286. [DOI] [PubMed] [Google Scholar]
- 19.Hagerman P.J. (1997) Flexibility of A-RNA. Annu. Rev. Biophys. Biomol. Struct., 26, 139–156. [DOI] [PubMed] [Google Scholar]
- 20.Fujiwara T. and Shindo,H. (1985) Phosphorus-31 nuclear magnetic resonance of highly oriented DNA fibers. 2. Molecular motions in hydrated DNA. Biochemistry, 24, 896–902. [DOI] [PubMed] [Google Scholar]
- 21.Shindo H., Fujiwara,T., Akutsu,H., Matsumoto,U. and Kyogoku,Y. (1985) Phosphorus-31 nuclear magnetic resonance of highly oriented DNA fibers. 1. Static geometry of DNA double helices. Biochemistry, 24, 887–895. [DOI] [PubMed] [Google Scholar]
- 22.Cheatham T.E. III and Kollman,P.A. (1997) Molecular dynamics simulations highlight the structural differences among DNA:DNA, A-RNA:A-RNA, and DNA:A-RNA hybrid duplexes. J. Am. Chem. Soc., 119, 4805–4825. [Google Scholar]
- 23.Auffinger P. and Westhof,E. (2000) Water and ion binding around A-RNA and DNA (C,G) oligomers. J. Mol. Biol., 300, 1113–1131. [DOI] [PubMed] [Google Scholar]
- 24.Auffinger P. and Westhof,E. (2001) Water and ion binding around r(UpA)12 and d(TpA)12 oligomers—comparison with A-RNA and DNA (CpG)12 duplexes. J. Mol. Biol., 305, 1057–1072. [DOI] [PubMed] [Google Scholar]
- 25.Pan Y. and MacKerell,A.D.,Jr (2003) Altered structural fluctuations in duplex A-RNA versus DNA: a conformational switch involving base pair opening. Nucleic Acids Res., 31, 7131–7140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Noy A., Perez,A., Lankas,F., Luque,F.J. and Orozco,M. (2004) J. Mol. Biol., 343, 627–638. [DOI] [PubMed] [Google Scholar]
- 27.Dickerson R.E., Goodsell,D.S. and Neidle,S. (1994) ‘…the tyranny of the lattice…’. Proc. Natl Acad. Sci. USA, 91, 3579–3583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lu X.J., Shakked,Z. and Olson,W.K. (2000) A-form conformational motifs in ligand-bound DNA structures. J. Mol. Biol., 300, 819–840. [DOI] [PubMed] [Google Scholar]
- 29.Olson W.K. (1980) Conformational statistics of polynucleotide chains. an updated virtual bond model to treat effects of base stacking. Macromolecules, 13, 721–728. [Google Scholar]
- 30.Kosikov K.M., Gorin,A.A., Zhurkin,V.B. and Olson,W.K. (1999) DNA stretching and compression: large-scale simulations of double helical structures. J. Mol. Biol., 289, 1301–1326. [DOI] [PubMed] [Google Scholar]
- 31.Case D.A., Pearlman,D.A., Caldwell,J.W., Cheatham,T.E.,III, Ross,W.S., Simmerling,C.L., Darden,T.L., Marz,K.M., Stanton,R.V., Cheng,A.L. et al. (1999) AMBER 6.0. University of California, San Francisco, CA. [Google Scholar]
- 32.Cornell W.D., Cieplak,P., Bayly,C.I., Gould,I.R., Merz,K.M.,Jr, Ferguson,D.M., Spellmeyer,D.C., Fox,T., Caldwell,J.W. and Kollman,P.A. (1995) A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc., 117, 5179–5197. [Google Scholar]
- 33.Sherer E.C., Harris,S.A., Soliva,R., Orozco,M. and Laughton,C.A. (1999) Molecular dynamics studies of DNA A-Tract structure and flexibility. J. Am. Chem. Soc., 121, 5981–5991. [Google Scholar]
- 34.Cubero E., Abrescia,N.G., Subirana,J.A., Luque,F.J. and Orozco,M. (2003) Theoretical study of a new DNA structure: the antiparallel Hoogsteen duplex. J. Am. Chem. Soc., 125, 14603–14612. [DOI] [PubMed] [Google Scholar]
- 35.Orozco M., Rueda,M., Blas,J.R., Cubero,E., Luque,F.J. and Laughton,C.A. (2004) Nucleic Acids: Molecular Dynamics Simulations. Encyclopedia of Computational Chemistry. Published online April 15, 2004. doi:10.1002/0470845015.cn0080. [Google Scholar]
- 36.Orozco M., Perez,A., Noy,A. and Luque,F.J. (2003) Theoretical methods for the simulation of nucleic acids. Chem. Soc. Rev., 32, 350–364. [DOI] [PubMed] [Google Scholar]
- 37.Rueda M., Kalko,S.G., Luque,F.J. and Orozco,M. (2003) The structure and dynamics of DNA in the gas phase. J. Am. Chem. Soc., 125, 8007–8014. [DOI] [PubMed] [Google Scholar]
- 38.Schlitter J. (1993) Estimation of absolute and relative entropies of macromolecules using the covariance matrix. Chem. Phys. Lett., 215, 617–621. [Google Scholar]
- 39.Andricioaei I. and Karplus,M. (2001) On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys., 115, 6289–6292. [Google Scholar]
- 40.Shannon C.E. (1948) A mathematical theory of communication. Bell System Tech. J., 27, 379–423. [Google Scholar]
- 41.Matsumoto A. and Olson,W.K. (2002) Sequence-dependent motions of DNA: a normal mode analysis at the base-pair level. Biophys. J., 83, 22–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lankas F., Sponer,J., Hobza,P. and Langowski,J. (2000) Sequence-dependent elastic properties of DNA. J. Mol. Biol., 299, 695–709. [DOI] [PubMed] [Google Scholar]
- 43.Go M. and Go,N. (1976) Fluctuations of an alpha-helix. Biopolymers, 15, 1119–1127. [DOI] [PubMed] [Google Scholar]
- 44.Jurecka P. and Hobza,P. (2003) True stabilization energies for the optimal planar hydrogen-bonded and stacked structures of guanine…cytosine, adenine…thymine, and their 9- and 1-methyl derivatives: complete basis set calculations at the MP2 and CCSD(T) levels and comparison with experiment. J. Am. Chem. Soc., 125, 15608–15613. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.