Valid Statistical Approaches for Analyzing Sholl Data: Mixed Effects versus Simple Linear Models

Abstract

Background

The Sholl technique is widely used to quantify dendritic morphology. Data from such studies, which typically sample multiple neurons per animal, are often analyzed using simple linear models. However, simple linear models fail to account for intra-class correlation that occurs with clustered data, which can lead to faulty inferences.

New Method

Mixed effects models account for intra-class correlation that occurs with clustered data; thus, these models more accurately estimate the standard deviation of the parameter estimate, which produces more accurate p-values. While mixed models are not new, their use in neuroscience has lagged behind their use in other disciplines.

Results

A review of the published literature illustrates common mistakes in analyses of Sholl data. Analysis of Sholl data collected from Golgi-stained pyramidal neurons in the hippocampus of male and female mice using both simple linear and mixed effects models demonstrates that the p-values and standard deviations obtained using the simple linear models are biased downwards and lead to erroneous rejection of the null hypothesis in some analyses.

Comparison with Existing Methods

The mixed effects approach more accurately models the true variability in the data set, which leads to correct inference.

Conclusions

Mixed effects models avoid faulty inference in Sholl analysis of data sampled from multiple neurons per animal by accounting for intra-class correlation. Given the widespread practice in neuroscience of obtaining multiple measurements per subject, there is a critical need to apply mixed effects models more widely.

1.1 Introduction

The central nervous system’s ability to process and distribute information relies on neural connectivity, and a key determinant of neural connectivity is the morphology of the dendrite (Libersat and Duch 2004; Menon and Gupton 2016; Scott and Luo 2001). Altered dendritic morphology, including increased or decreased dendritic arborization are a shared feature of many neurodevelopmental disorders (NDDs) (Bourgeron 2009; Fukuda et al. 2005; Garey 2010; Keown et al. 2013; Supekar et al. 2013) and neurodegenerative diseases (Cochran et al., 2014, Kweon et al., 2016). Therefore the analysis of dendritic morphology is a critical tool in neuroscience studies.

1.1.1 Analysis of dendritic morphology in brain tissue sections

A common problem encountered in neuroscience research is how to analyze complex dendritic structures. Sholl analysis is a method that has been widely used for decades to describe the complexity of neurons both from brain tissue sections and in vitro systems (Sholl, 1953), and it remains a key tool in neuroscience research for this application. In this method, concentric circles at specified radii (usually in 10 micrometer (μm) increments) are centered on the neuronal soma and the number of dendritic intersections at each circle is counted. Commonly reported endpoints from this analysis include the sum of all intersections within the Sholl radii, the number of intersections at individual radii, and the area under the curve for the whole or regions of the neuron (Ferreira et al., 2013, Sholl, 1953). However, the statistical analysis of data generated using the Sholl technique is not consistent in the literature.

1.1.2 Methods commonly used to analyze Sholl data and associated problems

A common experimental design in studies of dendritic morphology, as well as many other studies in neuroscience, is that of multiple observations per subject, for example analyzing multiple neurons from one experimental animal. Simple linear models are commonly used to analyze these data; however, these models do not account for the clustered data structure of this experimental design, despite multiple reports over that last several years describing the issues associated with these approaches (Aarts et al., 2014; Boisgontier and Cheval, 2016; Ioannis, 2005). While simple statistical methods such as t tests, Wilcoxon rank sum test, ANOVA, and regression are in widespread use, there are many situations in scientific research where the data structure violates the assumptions of these simple models. The effects of intra-subject correlation have been understood for several decades (Walsh, 1947). In the case where more than one observation is made on the same subject animal, for example, measurements on multiple neurons per animal, intra-subject correlation violates the assumption of complete independence of the observations. While in the last several years, the use of mixed effects models has increased in a variety of scientific and medical disciplines, neuroscience has lagged behind (Boisgontier and Cheval, 2016), despite publications warning of the sharp increase in faulty experimental designs, false positives, and spurious inferences that result (Aarts et al., 2014; Boisgontier and Cheval, 2016; Ioannis, 2005).

As Aarts et. al., 2014 point out, an increase in the number of neurons per animal gives the appearance of a large increase in power if a simple linear model is used. However, the true increase in power with increasing numbers of neurons per animal is relatively small, and this is only accounted for when the correct mixed effects model is used. Resources should be geared towards more animals rather than more neurons per animal. The reason for this is that data observed on neurons from the same animal are likely to have more in common with each other than with neurons from a different animal. Hence, an additional neuron from the same animal does not provide the same amount of additional information as another neuron from a different animal. When a simple linear model is fit to test for differences between treatments or other characteristics on two or more groups of animals, the variance is calculated under the assumption that each observation is independent of every other. The lower variability caused by similarity (dependence) between neurons from the same animal will result in an under-estimation of the within condition variance, which in turn results in an under-estimation of the p-value for the test of differences between conditions.

Many (Aarts et al., 2014, Galbraith et al., 2010, Senn, 1998) have shown through simulation and theoretical proofs that studies using simple linear models to analyze data with multiple measurements per subject have very high false positive rates. That is, if there is in fact no difference between the conditions, studies that do not adequately account for the clustered nature of the data will falsely yield a statistically significant result a large percentage of the time. Mixed effects models correctly model the clustering that results from measurements made on multiple neurons per animal and, hence, produce accurate p-values upon which inference is based. In the case of Sholl profile analysis where the number of intersections is measured at each radius, there is multi-level nesting (radii within neuron as well as neuron within animal) and an autoregressive covariance structure because measurements made at radii close to each other are likely to be more highly correlated than those far from each other. The commonly performed t test cannot accommodate either the multi-level nesting or the autoregressive covariance; in contrast, mixed effects models can accommodate both. One solution is a repeated measures analysis across radii, but this approach does not control for clustering due to multiple neurons per animal. Some authors (Wallin-Miller et al., 2016; Pawluski et al., 2012; Beauquis et al., 2013) have approached this problem by averaging the measurements across neurons to obtain one observation per animal at each radius, and then using a repeated measures analysis across radii. While this approach does not violate any model assumptions it does result in the loss of information about variability across neuron.

An additional complication in Sholl profile analysis is the multiple testing at multiple radii. Type one error inflation can be severe when multiple tests are performed. For example, when 10 radii are used, the probability of at least one type I error is about 40%. It is not uncommon for researchers performing Sholl profile analysis to fail to correct for global type I error inflation, and those who do often use methods that are either too severe, leading to an unnecessary loss of power, or too lenient, leading to a less than adequate control of error inflation. For example, using Bonferroni’s is too severe, while the Least Significant Difference correction for post-hoc comparisons is too lenient; more appropriate would be Scheffe’s (Neter et. al. 1996; Zar, 1984). Here, we illustrate how to implement a method for controlling the false discovery rate in Sholl profile analysis, which addresses the issue of experiment-wise type I error inflation but is both powerful and accurate (Benjamini and Hochberg, 1995).

In this study, we review some of the issues involved in the analysis of clustered data, examine the misuse of the t test and the Wilcoxon rank sum test. We also compare the results of using mixed effects models versus simple linear models on real data from Sholl analyses of dendritic arborization of Golgi stained male and female wild type mouse hippocampal neurons to show how results of statistical analyses differ between the correct method (mixed effects models) and the incorrect method (simple linear models). Finally, we provide SAS® software code and annotated output for use of the mixed model in analyzing neuron architecture to simplify the analysis for non-statisticians.

2.1 Methods

2.1.1 Animals

All procedures and protocols were approved by the University of California, Davis Animal Care and Use Committee and were conducted in accordance with the NIH Guide for the Care and Use of Laboratory Animals. C57Bl/6J wild type mice were purchased from Jackson Labs (Bar Harbor, ME) and housed in clear plastic cages containing corn cob bedding. Mice were maintained on a 12 h light and dark cycle at 22 ± 2 °C. Feed (Diet 5058, LabDiet, St. Louis, MO) and water were available ad libitum.

2.1.2 Golgi Staining and Sholl Analysis

For this study we used an existing data set consisting of 10 (5 male; 5 female) wild type C57Bl/6J juvenile mice with the number of neurons analyzed per mouse ranging from 1 to 8. Postnatal day (P) 28 mice were euthanized via CO₂ inhalation. Brains were removed, bisected and immediately processed for Golgi staining using the FD Rapid GolgiStain kit (FD NeuroTechnologies Inc., Columbia, MD) according to the manufacturer’s instructions. Brightfield image stacks of CA1 hippocampal pyramidal neurons were captured using an IX-81 inverted microscope (Olympus, Shinjuku, Japan) and MetaMorph Image Analysis Software (version 7.1, Molecular Devices, Sunnyvale, CA) by an individual blinded to sex. Criteria for selection of neurons for Golgi analyses have been described previously (Lein et al., 2007). Basilar dendritic arbors of selected neurons were traced using NeuroLucida (version 11, MBF Bioscience, Williston, VT) and arbor complexity was quantified by Sholl analysis using NeuroLucida Explorer (version 11, MBF Bioscience). The outcome measures were mean dendritic length, number of basilar dendritic tips divided by the total number of dendrites, the sum of dendritic intersections within Sholl radii, total area under the Sholl curve (0–150 microns analyzed at 10 micron increments) and area under the Sholl curve corresponding to the proximal (0–70 microns) and distal (70–150 microns) portions of the dendritic arbor.

2.1.3 Statistical Analyses

We used independent sample t tests, Wilcoxon rank sum tests and mixed effects ANOVA to compare the differences in standard errors and p-values obtained using simple linear models (t tests and Wilcoxon rank sum tests) versus mixed effects models. The normal and equal variance assumptions were tested using histograms, summary statistics, and residual plots. If an outcome variable did not appear to be normal or if unequal variances were observed, the appropriate transformation was used to achieve approximate normality and the appropriate model was specified to account for unequal variance. For the Wilcoxon test, we used untransformed data because this is a common practice in the field that we wanted to compare to the mixed models. We discuss a method for controlling the false discovery rate to account for multiple testing at multiple radii, a common practice in Sholl profile analysis. For the simple linear model analyses we used the SAS® procedures TTEST and NPAR1WAY. We used the SAS® software procedure MIXED for all mixed effects models. We used the variance components options to specify the covariance structure for all models except for the Sholl profile with multi-level nesting where we used an autoregressive (AM(1)) covariance structure. The SAS® procedure MULTTEST was used to obtain corrected p-values (q-values) for controlling the false discovery rate (FDR) with interpretation at FDR=.05, .10, and .20. All analyses were conducted in SAS® software version 9.4 of the SAS System for Windows® (SAS Institute Inc, Cary, NC). Code is shown in the Appendix. SAS output is shown in both the body of the article for illustration and annotated in the appendix for completeness.

2.1.4 Literature Search

A literature search was conducted via PubMed search using the search terms “Sholl analysis” and “neuron” to identify studies which examined dendritic morphology using Sholl analysis in brain tissue sections. Articles going back to 2005 were included. In vitro or computer modeling studies were excluded to keep the focus of this manuscript on data structure generated from animal studies. A summary of this search is presented in Table 1 and specific references can be found in Supplemental Table 1.

Table 1.

Summary of studies using Sholl analysis on brain tissue sections

Statistical Test	~ Percentage of Studies (79 Total Studies Examined)
T test	27
ANOVA (not using mixed effects models)	48
Mixed effects or repeated measures models	23
Not specified	3
Sampling Structure of Neurons	~ Percentage of Studies (79 Total Studies Examined)
Used multiple neurons per animal	72
Averaged multiple neurons per animal	8
No specified N value used in statistical test	33
No specified number of animals	16
No specified number of neurons/animal	37

Summary of 79 studies of dendritic morphology of neurons in brain tissue sections identified via PubMed search using the search terms “Sholl analysis” and “neuron”. Specific references can be found in Supplemental Table 1.

3.1 Results and Discussion

Without the proper statistical method that accounts for the experimental design and data structure, the results of scientific research are questionable and non-reproducible. Without the ability to accurately quantify uncertainty and reproduce experimental results, scientists are not, in fact, meeting the demands of the scientific method for testing hypotheses. These issues have been recognized by the National Institutes of Health (Collins and Tabak 2014, Landis et al., 2012, Pusztai et al., 2013) and in an effort to enhance rigor and transparency in scientific research, new reviewer guidelines assess the scientific premise, experimental design for robust and unbiased results, and consideration of relevant biological variables such as sex in grant applications.

In neuroscience, it is common for multiple neurons to be analyzed per animal and treated as independent observations, which is a violation of the model assumptions and can lead to faulty inference. Table 1 summarizes studies using Sholl analysis of Golgi-stained neurons in brain tissue sections to measure dendritic arborization, and includes the number of animals and neurons used as well as the statistical tests applied. From a total of 79 published papers examined, only ~23% reported using a mixed model approach to analyze Sholl data despite the fact that 72% of these studies use multiple neurons per animal (Table 1). Further, of the papers we reviewed, ~37% were unclear as to the number of neurons taken from each animal (Table 1). Details regarding the papers included in our review, including the experimental design and n values reported, can be found in Supplemental Table 1. Together, these results indicate the need for wider acceptance and use of standardized, correct statistical approaches to consistently quantify neuron morphology for multiple observations per animal.

3.1.1 Using mixed effects model to analyze Sholl data

Mixed effects models correctly model the clustering that results from measurements made on multiple neurons per animal, and thus produce accurate p-values upon which inference in based. The simplest mixed model is the random intercepts model. In this model, the clustering within animal is modeled by allowing each animal to have its own (random) intercept. Where n is the number of animals and k is the number of observations per animal, the model can be written:

$$y_{ij}={\beta }_0+u_i+{\beta }_1{x}_j+{\epsilon }_{ij}$$

where i = 1,…n and j = 1,…k and where ε_ij u_i are independent and where ε_ij ~N(0, σ²) and $u_i~N(0,{\sigma }_u^2)$. Here, we simplify by assuming that k is the same for every animal, but SAS® software does not require this restriction. In our example data, y_ij represents the dendritic morphological outcome from the Sholl analysis for the i^th mouse and the j^th neuron; β₀ represents the common intercept; u_i represents the individual random component of the intercept for each mouse; β₁ is the group or condition difference, in our example between male and female mice, in the dendritic morphological outcome; x_j = 0 if the mouse is female and x_j = 1 if the mouse is male. Finally, ε_ij represents the random error for the i^th mouse and the j^th neuron.

Mixed models also have a degree of flexibility in that they are robust to failures in distributional assumptions (i.e., they work well even when the errors are not normally distributed) and that they can correctly model heterogeneity of variance if the correct variance structure is specified. For example, if the variance of the outcome for the male mice appears to be larger than for the female, it can be specified in the code to estimate the variances separately and to use Satterthwaite’s approximation for the degrees of freedom. This model is written exactly as above except that to account for different variances for each sex the equation is

$${\epsilon }_{ij}~N(0,{\sigma }_m^2\ast M+{\sigma }_f^2\ast F)$$

where M = 1 if the mouse is male and 0 if female; and F = 1 if the mouse is female and 0 if male. Additionally, there are other covariance structures that can be modeled, specifically the unstructured covariance, which has the most flexibility but also requires the most parameters. For this reason, specifying the unstructured covariance model tends to work well for small models but may not converge for larger models (Kincaid, 2005).

Additionally, for data where sequential measurements are correlated with each other, such as in Sholl profile analysis with measurements taken at successive radii, an autoregressive variance structure can be specified. In the case of Sholl profile analysis, the measurements of the number of intersections at radii close to each other are likely to be more highly correlated with each other than those taken at radii far from each other. Hence, a more specialized variance structure is required. For complicated variance structures or large models with several conditions or covariates, or models where a distribution other than normal, such as binary or Poisson is required, we recommend seeking consultation and collaboration from a statistician.

When using the MIXED procedure in SAS the data should be formatted in the data file with the repeated measures per animal and neuron in long form (multiple rows per animal and neuron across radii), not wide form (multiple columns). See Appendix for an example of a properly formatted data set.

3.1.2 The normality and equal variance assumptions

The Student’s t test and its multi-group extension, ANOVA, assume complete independence of the observations and approximate normality of the response variable. When these assumptions are violated the p-value is not accurate. Mixed effects models can accommodate multiple observations per animal and heterogeneity of variance, but do assume approximate normality. However, they are robust to failures in the normality assumption, which means that they produce accurate estimates and reasonably accurate p-values, even with somewhat skewed distributions.

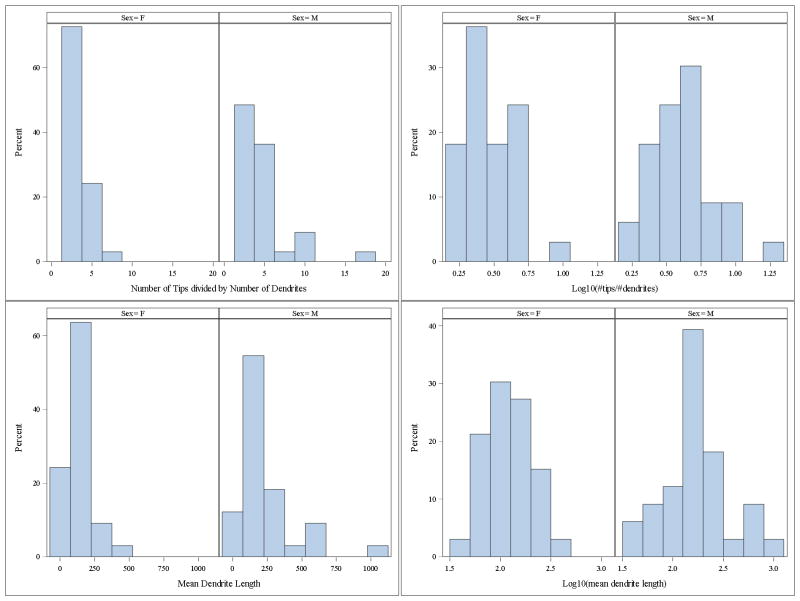
In our data set, two of the outcome variables showed both non-normality and heterogeneity of variance: the number of tips divided by the number of dendrites and mean dendrite length. Figure 1 shows the histograms of the raw and transformed data and Table 2 shows the mean and standard deviations. The transformation corected both the extreme skew and the gross inequality of variance (Fig. 1). Note that the effectiveness of the transformation needs to be verified by examining the residual panel from the mixed model.

Figure 1.

Log transformation corrects skew and inequality of variance in outcome variables. Variables, number of tips divided by number of dendrites (top) and mean dendritic length (bottom).

Table 2.

Summary statistics for raw and transformed outcome variables for females versus males.

Outcome (N=33 for both sexes)	Female Mean	Male Mean	Female Std dev	Male Std dev	Ratio of Std dev (M/F)
Number of tips / number of dendrites	3.2	4.7	1.44	3.18	2.2
Log10(no. tips / no. dendrites)	0.47	0.61	0.17	0.22	1.3
Mean dendrite length	138	229	80.9	212.1	2.6
Log10(mean dendrite length)	2.1	2.2	0.24	0.33	1.4
Total Area Under the Curve	493	630	185	328	1.8
Area Under the Curve, Distal	83	194	84	195	2.3
Area Under the Curve, Proximal	410	435	121	153	1.3

3.2 Simple linear models versus mixed effects ANOVA

We next compare side by side, the outcome when using a linear model t test versus a mixed effects ANOVA model to analyze dendritic morphology. Analytical results are shown in Table 3 to illustrate the deflation of the standard error and p-values that occurs when the intra-animal correlation is not accounted for by the statistical model such as is the case when using the t test.

Table 3.

Mean difference (Female – Male), standard errors, and p-values from t test and mixed effects ANOVA.

Outcome variable	Mean difference (F – M)	T test		Mixed effects ANOVA
		Std. error	p-value	Std. error	p-value
Log10(#tips divided by #dendrites)	−0.14	0.05	<.001	0.07	0.04
Sum Intersections	−13.9	6.56	0.04	10.1	0.15
Log10(mean dendrite length)	−0.16	0.07	0.03	0.11	0.16
Total Area Under the Curve*	−136	66	0.04	104	0.21
Area Under the Curve, Distal*	−112	37	0.004	57	0.09
Area Under the Curve, Proximal*	−25	34	0.47	50	0.55

^*Analyzed using Satterthwaite degrees of freedom to account for unequal variance.

Note that proper identification of the variance structure can affect the validity of the inference. When the heterogeneity of variance is not accounted for the p-values can change. For example, incorrectly assuming equal variance in the distal (70–150 microns from the soma) area under the curve analysis produced a p-value of p=0.042 (not shown), compared to the p=0.09 using Satterthwaite shown in Table 3. In terms of biological relevance, it is clear that the conclusions drawn from these experiments are affected by the structure of the data as well as the models used. When using t tests, nearly all variables are significantly different between the sexes; however, when accounting for the structure of the data, and the heterogeneity of variance, only one variable remains significantly different: the log-transformed number of dendritic tips divided by total dendrites, which is a measure of dendritic complexity, is significantly greater in male compared to female hippocampal neurons (Table 2, 3).

The SAS® software output for log10 mean dendrite length is shown in Table 4. The data are the estimate for the difference between males and females, with males set as the reference level, the standard error of the estimate, the degrees of freedom, the t statistic, the p-value (Pr > |t|), the set alpha level, and the lower and upper confidence limits for the 1-alpha=0.95 confidence limits. Because this is a log transformed model, we must back transform to interpret the parameter in the original units. We have 10^(−0.16) = 0.69. This means that we expect the median of mean dendritic length to be a factor of 69% less for females than for males, or equivalently, 31% less, though this difference is not statistically significant. More extensive SAS output is shown in the Appendix.

Table 4.

Table of parameter estimates for the fixed effects (SEX) from the SAS output for log10 mean dendrite length from the mixed effects ANOVA model.

Solution for Fixed Effects
Effect	Sex	Estimate	Standard Error	DF	t Value	Pr > |t|	Alpha	Lower	Upper
Intercept		2.2416	0.07577	8	29.58	<.0001	0.05	2.0668	2.4163
Sex	F	−0.1622	0.1072	56	−1.51	0.1357	0.05	−0.3769	0.05243
Sex	M	0	.	.	.	.	.	.	.

Often in these analyses, the outcome variable shows strong deviations from normality, so non-parametric techniques, such as the Wilcoxon rank sum test, are used. However, the common version of these tests also assumes independence of the observations, and that the group variances are equal. Hence, these tests cannot accommodate clustered data or heterogeneity of variances. While rank-sum tests for clustered data have been developed (Datta and Satten, 2005), these tend to be advanced techniques that a non-statistician may find difficult to implement. Comparatively, mixed model techniques are easier to explain and are available in most statistical software packages such as SAS, Matlab, R, and SPSS (Brown, 2015, Littell, et. al., 2006, Aarts, et. al., 2014). Therefore, a better solution is often to transform the data to approximate normality and use a mixed effects model that can accommodate both clustered data and any inequality of variance remaining after the transformation by specifying the correct covariance structure.

As shown in Figure 1, two parameters in our data set showed both non-normality and heterogeneity of variance: the number of tips divided by the number of dendrites and mean dendrite length. Using these examples, we next illustrate a typical occurrence when a non-parametric technique is used in response to a skewed distribution, while not taking into account the clustering or inequality of variance (Table 5).

Table 5.

The effect of sex on dendritic morphology assessed via the Wilcoxon Rank Sum Test versus Mixed Effects ANOVA.

Outcome Variable	Untransformed, Wilcoxon p-value	Log10 Transformed, Mixed Effects p-value
#tips / # dendrites	0.008	0.04
Mean dendrite length	0.046	0.162

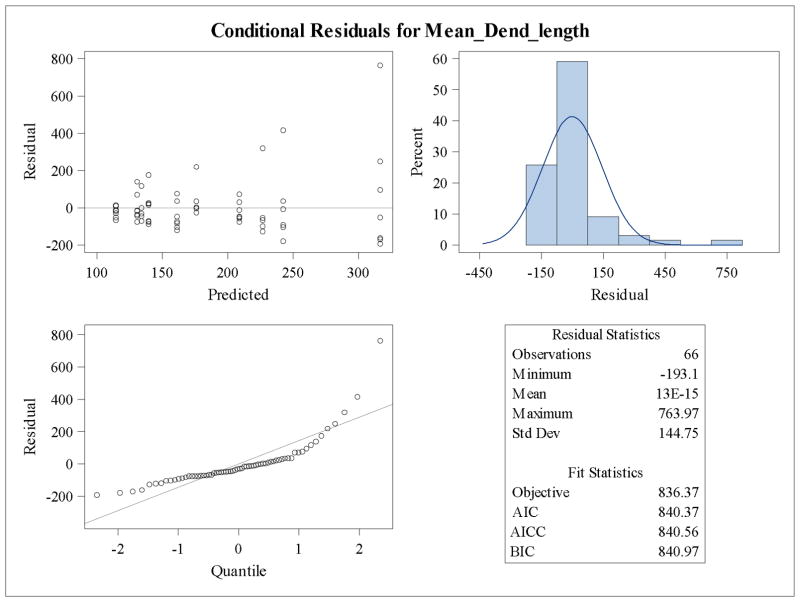
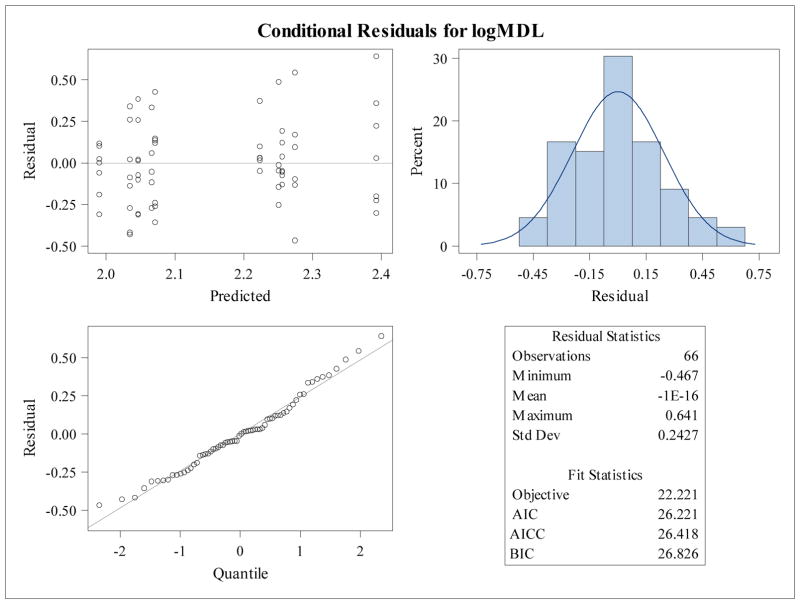
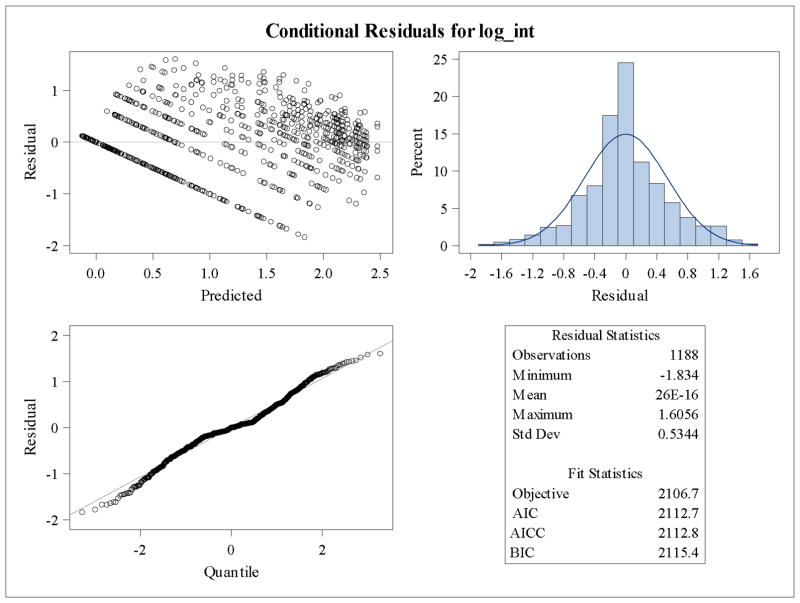
The residual panels for the mixed model for the log base 10 transformation of mean dendrite length is shown in Figure 2. The residuals have an even spread centered at zero between −0.5 and 0.5 across the range of predicted values, the histogram of the residuals is approximately symmetric and unimodal, and the residual quantile plot shows residuals lying closely on the normal quantile line (Fig. 2). If the residual panel showed problems with large deviations from normality, other transformations should be attempted to normalize the data. However, mixed models are robust to failures in normality, hence, so long as the deviations are not striking, the model will produce reasonably accurate p-values as well as accurate parameter estimates. If there appeared to be heterogeneity in the variance, Satterthwaite’s degrees of freedom could be specified during model fitting (See Appendix). Figure 2 shows the residual panel for the untransformed mean dendrite length, where it is clear that there are problems with model assumptions. Figure 3 shows the residual panel for the log10 transformation.

Figure 2.

Residual plots of untransformed mean dendritic length were produced to show lack of conformation with model distributional assumptions.

Figure 3.

Residual panel for log10 transformed mean dendritic length shows symmetry and homoscedasticity. Residual plots of transformed mean dendritic length were produced to show improvement in conformation with model distributional assumptions.

3.1.3 Sholl profile analysis: t tests vs mixed effects models at each radius

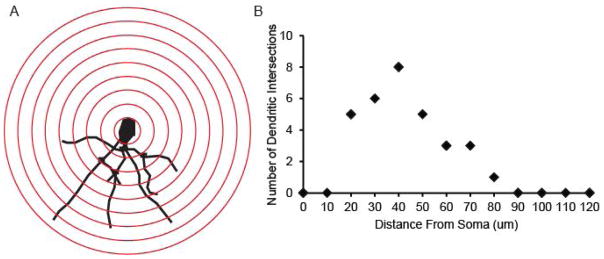
As illustrated in Table 1 and Supplemental Table 1, aside from accounting for multiple measures per neuron and per animal, there is variability in how statistically significant differences are determined using Sholl analysis. Figure 4A shows a representative tracing of the basal dendrites of a Golgi-stained pyramidal neuron in a female mouse hippocampus. The number of dendritic intersections at each radius is plotted, as represented in Figure 4B.

Figure 4.

Example Sholl profile and graph. A) Representative tracing of basal dendrites of a Golgi stained pyramidal neuron in a female mouse hippocampus. Red rings indicate radii spaced at 10μm increments from the cell body. B) Representative Sholl profile indicating the number of dendritic intersections at each radius.

When this analysis is used to compare dendritic complexity between multiple treatment groups it can become challenging to determine what is statistically and biologically significant. For example, one method of analysis is to conduct t tests (or ANOVA depending on how many treatment groups are being compared) at each individual distance from the soma. Ultimately, each radii is treated as an individual point. This procedure does not take into account neurons within animal and creates the additional problem of family-wise type I error inflation due to a large number of tests (Abdi, 2007). Multiple mixed effects models can be fit, one for each radius, and then a procedure to control the false discovery rate can be implemented, which is more powerful than classical methods for controlling the family-wise error rate (Benjamini and Hochberg, 1995).

We applied this method to our data set comparing male and female basal dendrites from Golgi stained hippocampal neurons, and compared the raw p-values for the t tests alone, the mixed models at each radius and the corrected p-values (q-values) used for inference when controlling the false discovery rate (Table 6). The q-value obtained when controlling the false discovery rate is an estimate of the false positive rate; and the q-values, while usually considered to be adjusted p-values, are not equivalent in meaning or interpretation to p-values. Hence, researchers may have more flexibility when choosing an FDR than when choosing α in traditional analyses. If a large number of radii are being tested, there is a substantial loss of power when using an FDR of 5%. The investigator should consider what is a tolerable false discovery rate given the number of radii being tested, what it implies in the context of the problem for some radii to be significant but not others, and the real-world implications of false positives. Ideally, this acceptable FDR should be decided before any analysis of the data has taken place.

Table 6.

Raw p-values from the t tests and the mixed models and the False Discovery Rate Corrected p-values for the test of differences between the sexes in the number of intersections at each radius.

Radius (microns)	Raw p-values from t tests	Raw p-values from Mixed Models	FDR Corrected LME q-values
radius 10	0.11	0.19	0.24
radius 20	0.24	0.52	0.55
radius 30	0.09	0.31	0.37
radius 40	0.55	0.86	0.86
radius 50	0.42	0.46	0.52
radius 60	0.12	0.18	0.24
radius 70	0.15	0.13	0.24
radius 80	0.12	0.08	0.21
radius 90	0.01	0.03	0.17
radius 100	0.10	0.07	0.21
radius 110	0.004	0.05	0.19
radius 120	0.016	0.04	0.17
radius 130	0.04	0.03	0.17
radius 140	0.004	0.01	0.10
radius 150	0.09	0.10	0.22
radius 160	0.17	0.18	0.24
radius 170	0.17	0.18	0.24
radius 180	0.16	0.16	0.24

Readers should also note that different approaches to controlling the false discovery rate are both currently available and in development. Some are more lenient and more powerful than the one chosen here. The simple FDR was chosen in the example as a middle-ground in the balance between too high an FDR and too low power. We recommend seeking the advice of a statistician if more advice is needed.

For our example data set, using t tests, five radii showed significant differences between male and female (radii 90, 110,120,130 and 140) at the 5% level. Using a mixed effects model, 4 of these were significantly different, with all p-values higher compared to the t tests. Using FDR q-values none of the radii were significantly different at the 5% or 10% rate, but 5 radii (the same as for the t test) were significant at the 20% rate. In this case, the investigator would consider whether a 1 in 5 likely false positive was acceptable.

These data demonstrate that based on the question being addressed, and the structure of the data, the type of analysis run can lead to different conclusions. In this case, significant differences observed using t tests at all radii may be an artifact of multiple tests being run. On the other hand if one radius is of particular interest, then using a mixed model approach on the specific radius will account for the sampling structure of the data.

3.1.4 Overall test for differences using t test versus mixed effects model

In the case of Sholl profile analysis there is multi-level nesting (radii within neuron as well as neuron within animal) and an autoregressive covariance structure because measurements made at radii close to each other are likely to be more highly correlated that those far from each other. In an overall test for differences in the number of intersections, if a t test is used, both the nesting of radii within neuron and neuron within animal is unaccounted for. This leads to a drastic false increase in power. Additionally, the autoregressive covariance structure cannot be adequately addressed. Table 7 displays the results of the t test.

Table 7a and 7b.

SAS® output using the t test to test for differences between the sexes of the ln(number of intersections + 1) at each radius for each neuron for each animal.

Sex	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
F		0.8119	0.7330	0.8908	0.9786	0.9259	1.0377
M		1.0051	0.9235	1.0866	1.0120	0.9575	1.0730
Diff (1–2)	Pooled	−0.1932	−0.3065	−0.0799	0.9954	0.9569	1.0372
Diff (1–2)	Satterthwaite	−0.1932	−0.3065	−0.0799

Method	Variances	DF	t Value	Pr > |t|
Pooled	Equal	1186	−3.34	0.0009
Satterthwaite	Unequal	1184.7	−3.34	0.0009

The SAS output shows the means for both sexes, the difference between them and the confidence intervals for the means and the standard deviations. This output also shows the results for the equal variance and Satterthwaite tests (Table 7).

The commonly performed t test cannot accommodate either the multi-level nesting or the autoregressive covariance. Mixed models can accommodate both. Table 8 shows the results for the nested mixed model that accounts for both the multi-level nesting of radii within neuron and neuron within animal, and the autoregressive covariance structure of measurements taken sequentially across space. Table 8 shows the estimated difference between the natural log(number of intersections + 1), the standard error, the degrees of freedom, the p-value (Pr > |t|) and the alpha =0.05 confidence interval. It also shows the test for an intercept of zero which is not of particular interest in this example. Figure 5 shows the residual panel for the mixed model that illustrates good conformity with distributional assumptions. Compared to independent t tests at each radii with false discovery rate correction (Table 6), using the nested mixed model there is a significant difference between male and female neurons (male more complex than female neurons) (Table 8), which accounts for both the structure of the data in terms of neurons per animal and the autoregressive covariance structure of the Sholl data. Overall, these data demonstrate the power of statistical models in both accurately representing the structure of the data and what this means in terms of drawing scientifically sound conclusions.

Table 8.

Mixed Model output for the test of differences between males and females in the ln(number of intersections + 1).

Solution for Fixed Effects
Effect	Sex	Estimate	Standard Error	DF	t Value	Pr > |t|	Alpha	Lower	Upper
Intercept		0.6496	0.2543	17	2.55	0.0205	0.05	0.1130	1.1862
Sex	F	−0.1932	0.03198	1043	−6.04	<.0001	0.05	−0.2559	−0.1304
Sex	M	0	.	.	.	.	.	.	.

Figure 5.

Residual Panel for the nested Mixed Effects ANOVA.

4.1 Conclusions

Here, we show an example data set that requires mixed effects model analysis and compare the results to common approaches that do not account for the clustered nature of the data. We show how both the standard error of the model parameters and the p-values are under-estimated, leading to faulty inference. We show an example of a common transformation that works well with these data to help normalize the distribution. We also show a method for analyzing Sholl profiles to account for both the number of neurons per animal as well as multi-level nesting and autoregressive covariance. Using this model, we identify differences between male and female basal hippocampal dendrite complexity with males showing greater complexity compared to female neurons. While we only used one example data set and only a few outcome variables, many others have shown using simulation and probability theory, the type I error inflation that occurs when using simple linear models that do not account for intra-class correlation in clustered data. Our aim here is to provide neuroscientists with a manageable method for understanding and correctly analyzing clustered data, as well as the SAS code and output to run these analyses. We strongly recommend seeking the collaboration of a statistician for those with larger or more complicated models where fitting the model may require more in-depth expertise.

Highlights.

• In vivo studies of dendritic morphology in which multiple neurons are sampled per animal often use a simple linear model to detect significant differences which can lead to faulty inference.

• Mixed models account for intra-class correlation that occurs with clustered data often generated in dendrite analysis to accurately estimate the standard deviation of the parameter estimate and, hence, produce accurate p-values.

• A mixed effects approach accurately models the true variability in data sets sampling multiple neurons per animal, such as Sholl analysis.

Appendix: SAS Data file, Code, and Output

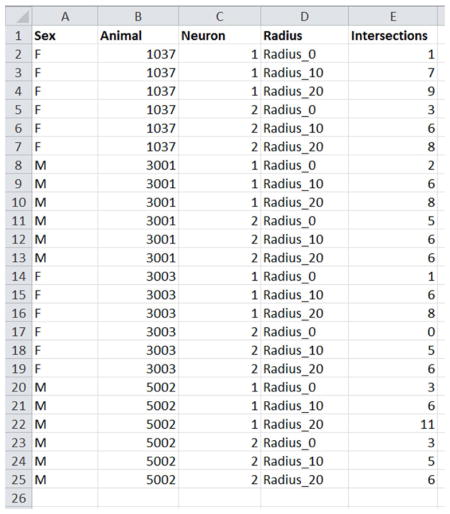
Example Data Set showing 4 animals, with 2 neurons per animal, and 3 radii per neuron

Mixed Model with Simple Covariance Structure (Variance Components)

PROC SORT

 DATA=GOLGI_HIPPO;
BY ANIMAL NEURON; /* SORTING BY SUBJECT THEN BY NEURON*/

RUN

;

PROC MIXED

 DATA=GOLGI_HIPPO PLOTS=RESIDUALPANEL;
CLASS SEX; /* SPECIFYING SEX AS A CATEGORICAL/CLASS VARIABLE */
MODEL LOGMDL = SEX/CL; /* LOGMDL AS RESPONSE, SEX AS CONDITION */
RANDOM INT / TYPE=VC SUB=ANIMAL; /* RANDOM INTERCEPT, VARIANCE COMPONENTS,
SUBJECT LEVEL IS THE ANIMAL. */

RUN

;

QUIT

;

Annotated Output for Mixed Model with Simple Covariance Structure (Variance Components)

The Mixed Procedure

Model Information
Data Set	WORK.GOLGI_HIPPO
Dependent Variable	logMDL
Covariance Structure	Variance Components
Subject Effect	Animal
Estimation Method	REML
Residual Variance Method	Profile
Fixed Effects SE Method	Model-Based
Degrees of Freedom Method	Containment

The Model Information table shows the data set, the dependent variable, the covariance structure specified, the subject level (animal), the estimation method, and other default settings for model fitting.

Class Level Information
Class	Levels	Values
Sex	2	F M

The Class Level Information table specifies the number of levels of any class variables declared in the model.

Dimensions
Covariance Parameters	2
Columns in X	3
Columns in Z per Subject	1
Subjects	10
Max Obs per Subject	8

The Dimensions table shows the number of subjects and the maximum number of observations per subject as well as covariance structure parameters.

Number of Observations
Number of Observations Read	66
Number of Observations Used	66
Number of Observations Not Used	0

The Number of Observations table identifies the number of observations and notes any that were not used due to missing values.

Iteration History
Iteration	Evaluations	−2 Res Log Like	Criterion
0	1	28.01839126
1	3	22.23198728	0.00021177
2	1	22.22128805	0.00000195
3	1	22.22119468	0.00000000

Convergence criteria met.

The previous two tables verify convergence of the procedure.

Covariance Parameter Estimates
Cov Parm	Subject	Estimate
Intercept	Animal	0.01868
Residual		0.06510

This table shows the estimates for the residual variance (ε_ij) and the random intercept variance (μ_ij).

Fit Statistics
−2 Res Log Likelihood	22.2
AIC (Smaller is Better)	26.2
AICC (Smaller is Better)	26.4
BIC (Smaller is Better)	26.8

Fit statistics are used in model selection and not usually applicable for most studies.

Solution for Fixed Effects
Effect	Sex	Estimate	Standard Error	DF	t Value	Pr > |t|	Alpha	Lower	Upper
Intercept		2.2416	0.07577	8	29.58	<.0001	0.05	2.0668	2.4163
Sex	F	−0.1622	0.1072	56	−1.51	0.1357	0.05	−0.3769	0.05243
Sex	M	0	.	.	.	.	.	.	.

The Solution for Fixed Effects table shows the estimate for Sex, which represents the difference between males and females in log10(mean dendrite length), the standard error of the estimate, the degrees of freedom, the t statistic, the p-value, the alpha level used for the confidence interval, and the upper and lower confidence limits for the 1-alpha confidence interval.

Type 3 Tests of Fixed Effects
Effect	Num DF	Den DF	F Value	Pr > F
Sex	1	56	2.29	0.1357

This table shows the Type 3 p-value for the fixed effects. This will be the same as for the parameter estimate in models with only one condition/independent variable.

The residual panel (see Figure 3) is used to verify goodness-of-fit to model assumptions. This panel of graphs shows reasonably good conformance to the normal assumption.

Code for Mixed Effects Model with Heterogeneous Covariance Structure

PROC MIXED

 DATA=GOLGI_HIPPO PLOTS =RESIDUALPANEL;
CLASS SEX;
MODEL LOGMDL = SEX/CL DDFM=SATTERTHWAITE;
RANDOM INT / TYPE=VC SUB=ANIMAL GROUP=SEX;

RUN

;

QUIT

;

The above code shows how we specify to SAS to allow estimation of different variances for each condition ( GROUP=SEX) and to use the Satterthwaite approximation for the degrees of freedom ( DDFM=SATTERTHWAITE). The output from this code will be the same as shown for the variance component model.

Code for Mixed Effects Model with multi-level nesting and Autoregressive Covariance Structure

title “Mixed Model for Total Intersections Using Autoregressive Variance
Structure”;

proc mixed

 data=sholl_zero plots=residualpanel;
class sex neuronID radius;
model log_int = sex /cl;
random radius radius(neuronID) / type=ar(

1

);

run

;

quit

;

The nested structure of the data is specified in the ‘ random’ statement with ‘ radius’ and radius within neuron (‘ radius(neuronID)’) listed as random effects. The autoregressive covariance structure is specified using the ‘ type=ar(1)’ option in the random statement. The output for this model will be very similar to the others.