Systematic analysis of bicistronic reporter assay data

Abstract

Bicistronic reporter assay systems have become a mainstay of molecular biology. While the assays themselves encompass a broad range of diverse and unrelated experimental protocols, the numerical data garnered from these experiments often have similar statistical properties. In general, a primary dataset measures the paired expression of two internally controlled reporter genes. The expression ratio of these two genes is then normalized to an external control reporter. The end result is a ‘ratio of ratios’ that is inherently sensitive to propagation of the error contributed by each of the respective numerical components. The statistical analysis of this data therefore requires careful handling in order to control for the propagation of error and its potentially misleading effects. A careful survey of the literature found no consistent method for the statistical analysis of data generated from these important and informative assay systems. In this report, we present a detailed statistical framework for the systematic analysis of data obtained from bicistronic reporter assay systems. Specifically, a dual luciferase reporter assay was employed to measure the efficiency of four programmed −1 frameshift signals. These frameshift signals originate from the L-A virus, the SARS-associated Coronavirus and computationally identified frameshift signals from two Saccharomyces cerevisiae genes. Furthermore, these statistical methods were applied to prove that the effects of anisomycin on programmed −1 frameshifting are statistically significant. A set of Microsoft Excel spreadsheets, which can be used as templates for data generated by dual reporter assay systems, and an online tutorial are available at our website (http://dinmanlab.umd.edu/statistics). These spreadsheets could be easily adapted to any bicistronic reporter assay system.

INTRODUCTION

In the last decade, polycistronic reporter assays have generally become a mainstay in molecular biology. In particular, various bicistronic systems have been widely adopted as standard experimental techniques in the fields of translation initiation (1–3), elongation (4,5), recoding (6–9) and termination (10). The ratiometric nature of the data produced from these experiments requires careful statistical treatment that is often lacking in the literature. The goal of this technical report is to propose a standardized statistical analysis pipeline for polycistronic reporter data and to provide researchers with a solid foundation on which to build their analyses.

For the purposes of this report, we have applied rigorous statistical methods to datasets originating from several sets of dual luciferase assays (DLAs) designed to measure the efficiency of various programmed −1 ribosomal frameshift (−1 PRF) signals in Saccharomyces cerevisiae. A −1 PRF signal is a cis-acting mRNA element that redirects translating ribosomes into a new reading frame after encountering a so-called ‘slippery site’ [for reviews see (11,12)]. The efficiency of frameshifting depends on the PRF signal in question (typically between 1 and 10%) and can be measured in vivo using a dual luciferase reporter (DLR) assay system (7).

Briefly, the DLA simultaneously measures the luminescence (e.g. expression) of both the Renilla and firefly luciferase enzymes synthesized from a single bicistronic mRNA. In an experimental frameshift reporter construct, the two genes are separated by a functional −1 PRF signal and the downstream firefly gene is placed into the −1 frame relative to the upstream Renilla gene. The relative expression of firefly to Renilla is normalized by a zero-frame control plasmid that lacks frameshift signal and has firefly in the zero frame. The resulting ratiometric data from our DLA is inherently sensitive to the propagation of error and therefore requires a careful statistical workup. The data are similar to the ratiometric data produced by other bicistronic assay systems despite the dissimilarity between the actual protocols producing it. This allows the methods presented in this report to be applied and extended to any polycistronic system that produces ratiometric data. Our analysis pipeline is designed to (i) systematically identify and eliminate erroneous outliers, (ii) confirm that the data are normally distributed, (iii) establish the minimum number of replicates for each dataset, (iv) minimize the propagation of error when calculating ratiometric statistics, and (v) provide a solid statistical foundation for comparing datasets from different experiments. We have supplemented this publication with a set of Microsoft Excel spreadsheets that automate the analysis and an online tutorial to help guide the reader through the analysis pipeline (http://dinmanlab.umd.edu/statistics). The robust, quantitative methods and online materials presented in this report represent an important new resource for researchers who utilize bicistronic reporters.

MATERIALS AND METHODS

Genetic methods and plasmid construction

Escherichia coli strain DH5α was used to amplify plasmids, and E.coli transformations were performed using the high efficiency method of Inoue et al. (13). YPAD and synthetic complete medium (H-) were used as described previously (14). Yeast strain JD932 (MATa ade2-1 trp1-1 ura3-1 leu2-3,112 his3-11,15 can1-100) (15) was used for in vivo measurement of programmed −1 ribosomal frameshifting. Yeast cells were transformed using the alkali cation method (16). Dual luciferase plasmids pJD375 (C₁, no frameshift signal) and pJD376 (F₁, L-A virus gag-pol frameshift signal) have been described previously (7). Putative frameshift signals from S.cerevisiae genes YOR026W/BUB3 (F₂, plasmid pJD519) and YPL128C/TBF1 (F₃, plasmid pJD478) were constructed as follows: (i) oligonucleotides from Integrated DNA Technology (Coralville, IA) were annealed and gel purified, and (ii) annealing the oligonucleotides 5′-TCGACAAAAAATCATCTTTCAGGGTGGATTGGAACGGCCCCAGTGATCCTGAGAACCCACAAAACTGGCCCG-3′ to 5′-GATCCGGGCCAGTTTTGTGGGTTCTCAGGATCACTGGGGCCGTTCCAATCCACCCTGAAAGATGATTTTTTG-3′ (F₂), and 5′-CGACAAATTTATCTCAAGCATCCTTCATCAGCTGCATCTGCTACTGAAGAGGG-3′ to 5′-GATCCTCTTCTGTAGCAGATGCAGCTGAAGAAGGATGCTGAGATAAATTTG-3′ (F₃) left overhanging single-stranded DNA complementary to SalI and BamHI restriction sites. The annealed oligonucleotides were ligated into p2mci (6). The frameshift signal was sub-cloned as a SalI–EcoRI fragment into similarly digested pJD375. The open reading frame (ORF) 1a-1b frameshift signal from the SARS-associated Coronavirus (SARS-CoV) was cloned; sense 5′-GATCCTTTTTAAACGGGTTTGCGGTGTAAGTGCAGCCCGTCTTACACCGTGCGGCACAGGCACTAGTACTGATGTCGTCTACAGGGCTTTTGAGCT-3′ and antisense 5′-CAAAAGCCCTGTAGACGACATCAGTACTAGTGCCTGTGCCGCACGGTGTAAGACGGGCTGCACTTACACCGCAAACCCGTTTAAAAAG-3′ oligonucleotides were annealed, gel purified and cloned into BamHI and SacI restricted p2mc (6). This was further sub-cloned into a pJD375-based plasmid where the reading frame was corrected using site-directed mutagenesis to add a cytosine downstream of the BamHI restriction site (F₄). A zero-frame control (C₂) plasmid was made by inserting two cytosine residues upstream of the BamHI restriction site and cells were grown in the absence or presence of 20 μg/ml of anisomycin (Sigma–Aldrich, St. Louis, MO). The annealed oligonucleotides were ligated into p2mci (6). The SARS-CoV frameshift signal (F₄) was sub-cloned as a SalI–EcoRI fragment into similarly restricted pJD375. In vivo DLAs for programmed −1 ribosomal frameshifting were performed in yeast strain JD1158 as described previously (7). Luminescence readings were obtained using a Turner Designs TD20/20 luminometer (Sunnyvale, CA). Reactions were carried out using the Dual-Luciferase® Reporter Assay System from Promega Corporation (Madison, WI).

Calculation of luminescence ratios

For each data point, the relative expression ratio of firefly luminescence (F_RLU) to Renilla luminescence (R_RLU) is given by:

where each x_i is the ratio obtained from an individual luminometer reading. For each of the frameshift reporters studied in this report (C₁, C₂, F₁, F₂, F₃ and F₄), the values of x₁−x_n comprise pooled datasets of size n (see Discussion). The statistics of this report are based on sets of ratiometric luminescence values (x₁−x_n) taken from multiple experiments and cell lysates.

Identification and exclusion of outliers

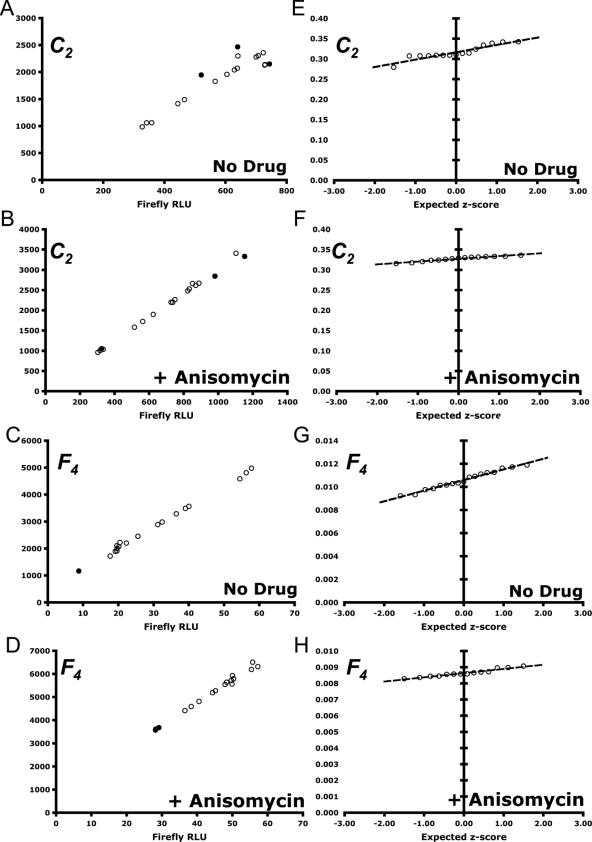
For outlier exclusion, we first determine the boundaries of each of the four quartiles within each DLA dataset: the maximum (Q_max), the 75th percentile (Q₇₅), the median (), the 25th percentile (Q₂₅) and the minimum values (Q_min) for each dataset of x₁−x_n (see Table 1). The fourth spread (fs) is calculated by

Table 1. Summary of the DLR assay datasets.

C₁ and C₂, zero-frame control reporters; F₁–F₄, frameshift reporters; Q_max, maximum ratio; Q₇₅, 75th percentile; Q₂₅, 25th percentile; Q_min, minimum ratio; , median; fs, fourth spread; O_U, standard upper outlier boundary; O_L, standard lower outlier boundary; PPCC, normal probability plot correlation coefficient; , sample mean; s_N−1², sample variance; s_N−1, sample SD; s_e, standard error of the sample mean; Ñ, minimum uncorrected sample size; N^*, minimum corrected sample size; N, actual sample size; , estimate of sample mean for the ratio of the of experimental frameshift reporter to of control reporter (i.e. frameshift efficiency); s_R², sample variance for ; s_R, sample SD of ; , standard error of the sample mean ; n/c, not calculated.

The standard upper and lower outlier boundaries are then calculated by

Data points that lie above or below the boundaries are considered outliers (e.g. Figure 1, solid data points) and are excluded from further analysis (17).

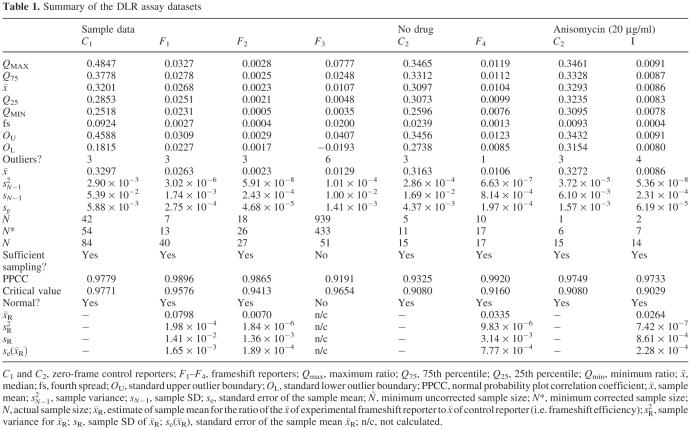
Figure 1.

Visualization of data from control reporter C₁ and experimental frameshift reporters F₁, F₂ and F₃. The raw luminescence values for C₁, F₁ and F₂ are linear and the ratio values of firefly/Renilla are normally distributed. The data for F₃, however, are neither linear nor normally distributed. (A–D) RLUs of firefly and Renilla expressed from control reporter C₁ and experimental frameshift reporters F₁, F₂ and F₃, respectively. Outliers are shown by solid data points. (E–H) Normal probability plots for data from C₁, F₁, F₂ and F₃, respectively. The x-axis corresponds to the expected z-score of each data point. The y-axis is the ratio of firefly to Renilla RLU values. The trend line shown is based on the linear regression of the data and represents the expected firefly/Renilla RLU ratio for a given z-score. Normal PPCCs for these (E–H) are shown in Table 1.

Descriptive statistics

We use standardized statistical expressions for the calculation of sample mean (), sample median (), sample variance (s_N−1²), sample SD (s_N−1) and the standard error of the sample mean (s_e) from each dataset of size n (17):

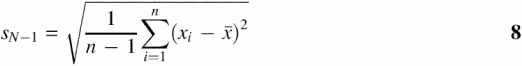
Probability plots

Probability plots were constructed and the corresponding normal probability plot correlation coefficients (PPCCs) were determined for each set of DLA data (18,19) (e.g. Figure 1A–D, 2A and B, Table 1). Briefly, the ratiometric values of firefly to Renilla luminescence (x₁−x_n, Equation 1) are rank-ordered within each dataset and each ratio is assigned a standard normal z-score (i.e. observed z-score, z_Obs) according to the following expression:

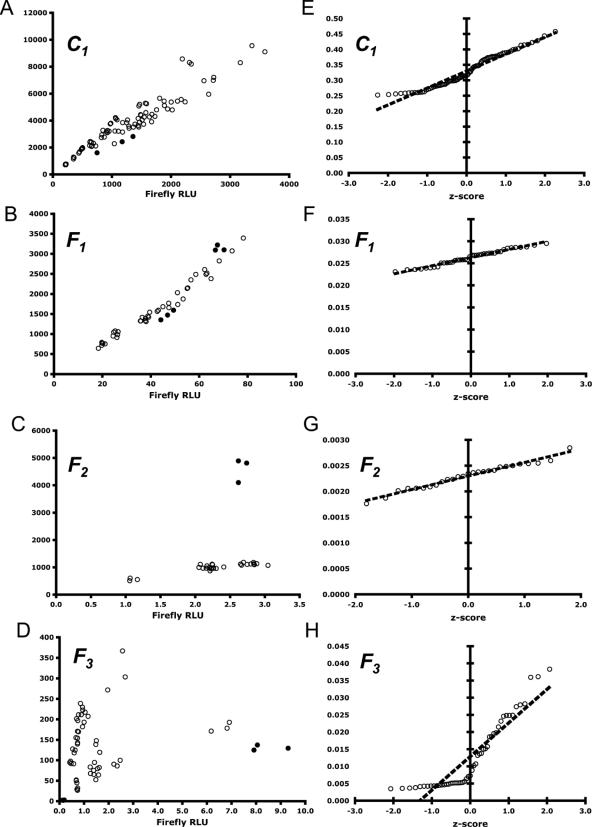
Figure 2.

Visualization of data from control reporter C₂ and experimental frameshift reporter F₄ under the effects of 20 μg/ml of anisomycin, an inhibitor of −1 PRF (26). The raw luminescence values are linear and the ratio values of firefly/Renilla are normally distributed. (A–D) RLUs of firefly and Renilla expressed from each reporter. Outliers are shown by solid data points. (E–H) Normal probability plots for each reporter. (A and E) C₂, no drug. (B and F) C₂ with anisomycin. (C and G) F₄, no drug. (D and H) F₄, with anisomycin. See Table 1 for details.

In addition, the expected z-score (z_Exp) for each value of x_i is calculated from the inverse standard normal distribution function for a given percentile rank (i.e. probability) of x_i. The paired data (x_i, z_Exp) is then plotted on a graph. Linear least squares regression is used to plot a linear trend line fitted onto the data (17). The trend line's derived formula provides an expected ratio value (y_i) for each observed value (x_i) for a given value of z_Exp. The correlation between the observed and expected values is given by the PPCC:

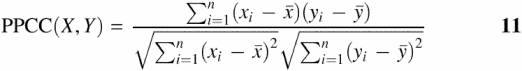
Where X and Y are the paired sets of expected and observed luciferase ratios, and are sample means, and a PPCC = 1.0 would indicate a perfect correlation between X and Y, i.e. a perfect normally distributed dataset. Another method for calculating the same PPCC value uses the correlation of paired values of z_Obs and z_Exp directly without the need for constructing a probability plot (http://dinmanlab.umd.edu/statistics). The PPCC is compared with a lookup table of critical values for a specified significance level (e.g. α = 0.05%) and sample size (n) in order to accept or reject the hypothesis that the data are normally distributed [see (19) and (http://dinmanlab.umd.edu/statistics)]. The PPCC and critical values for rejection at the 95% confidence level for each dataset are reported in Table 1.

Minimum sample size

For a given confidence level (e.g. α = 0.05) and predetermined limit on the numerical error, we calculate the minimum uncorrected sample size (17):

where Ñ is the minimum uncorrected sample size, z_α/2 is the standard normal coefficient for a given value of α/2 (e.g. α/2 = 0.025, z_α/2 = 1.96), s_N−1 is the sample SD and E is the amount of acceptable error in estimating the mean (e.g. 10% of ). It was previously shown that the use of Equation 12 for minimum sample size estimation substantially underestimates the number of trials needed for a given confidence interval (20). However, once Ñ is calculated, the minimum corrected sample size (N^*) can be found by consulting a lookup table [see (http://dinmanlab.umd.edu/statistics) and (20)]. Each dataset must have no fewer than N^* replicates for further analysis to be well substantiated.

Ratiometric statistics

The relative expression () of each experimental reporter and its corresponding control is:

where (in the case of DLAs) and are the sample mean firefly to Renilla luminescence ratios for experimental (i.e. frameshift) and control (i.e. zero-frame) reporters, respectively. The estimated sample variance (s_R²) for is given by (21):

where and are the sample means from Equation 5, and the sample variances s_E² and s_C² are from Equation 7. Equation 14 makes the assumption that and the sample variances (s_E² and s_C²) do not overlap zero (21). Researchers should take care to make sure these are valid for each dataset. From Equation 14, it follows that the sample SD (s_R) of is (22):

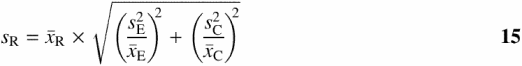
Finally, the standard error of is calculated using the following expression, which correctly accounts for the propagation of error for independent samples of different sizes:

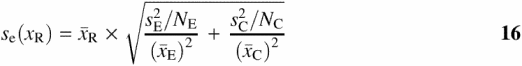
The number of replicates from each DLA dataset is specified by N_E and N_C.

Comparing datasets

We are often interested in finding the statistical significance of two differing experimental conditions (a and b) for the same experimental reporter. We use an unpaired two-sample t-test since it is appropriate for small, continuous datasets (17). For example, when comparing data from experiments a and b, we find

where v_a,b is the degrees of freedom for the t-test, and

where t_a,b is the t-statistic for conditions a, b. The values of s_Ra² and s_Rb² are the estimated sample variances (see Equation 14) for each ratio and (see Equation 13). The sample sizes n_a and n_b correspond to the sample sizes of each dataset for the experimental frameshift reporters under each experimental condition (a and b). Once the t-statistic is computed, it can then be compared to a table of critical values (available at http://dinmanlab.umd.edu/statistics) to either accept or reject each hypothesis. Finally, an estimate of the corresponding P-value of each result can also be obtained (17).

RESULTS

Data visualization

The first step for data post-processing is to visualize the raw data. At the very minimum, good visualization techniques provide a qualitative understanding of the data's robustness before any descriptive or inferential statistics have been calculated. Here, the quality and linearity of the data can be ascertained immediately by plotting the relative luminescence units (Renilla RLU versus firefly RLU) from each trial for a set of identical experiments (see Figure 1A–D and 2A–D). The linear relationship between Renilla and firefly expression in the context of the DLA system has been well characterized and can be used as a first-hand measure of data quality (7,23). For example, the linearity of the assay can be clearly seen in the control C₁ and frameshift reporter F₁ datasets (see Figure 1A–C), despite the large differences in scale. Furthermore, in frameshift reporter F₂ (see Figure 1C), three outliers are immediately identifiable, while frameshift reporter F₃ (see Figure 1D) demonstrates an unexpected scattering of the data. The linearity of the assay can also be seen even in the presence or absence of anisomycin, a translational inhibitor (see Figure 2A and C).

Identification and exclusion of outliers

While some outliers occasionally can be identified at the visualization step, it is usually preferred to use a statistical based method to quantitatively rule them out. This is useful because standardized methods eliminate human bias across datasets, and they make no assumptions about the underlying distribution of the data. In our analysis, we use Equations 2–4, and exclude data beyond the bounds of the standard outlier boundaries O_U and O_L. Outliers identified using this method can be seen as solid data points in Figure 1A–D and 2A–D. The resulting data are hereafter considered ‘trimmed’ from a statistical point of view. This provides a simple and consistent method to identify outliers and, when applied uniformly, some data points can be identified as outliers that may have not been previously obvious from simple visual inspection (e.g. so-called ‘hidden outliers’, see Figure 1A and B and 2A–D).

Descriptive statistics

We employ standardized expressions for the usual descriptive statistics on each dataset. This includes determining the sample mean (), sample median (), sample variance (s_N−1²), sample SD (s_N−1) and the standard error of the sample mean (s_e) for samples of size n (17). Each of these statistics is presented in Table 1 (see Equations 5–9).

Probability plots

After outliers have been excluded, the next step is to determine whether the data are normally distributed. This is an essential step because all of the subsequent statistical measures depend on the assumption that the data comes from a normal distribution. A χ² goodness-of-fit test for normality to either reject or accept this hypothesis is often used for this calculation (24). However, this is not an appropriate test for bicistronic data because (i) there are typically too few data points for the χ² to be valid, and (ii) whereas a χ² test is generally only appropriate for discrete data, bicistronic data are continuous. A simple solution is to construct a histogram of the ratiometric data and visually inspect each set's distribution. While histograms provide a qualitative view of the data and a visual estimate for the goodness-of-fit of the data to a normal distribution, they do not provide a quantitative means for excluding (i.e. rejecting) any particular dataset (http://dinmanlab.umd.edu/statistics).

For a more rigorous approach, we create a normal probability plot for each dataset and calculate its normal PPCC (18,19). This coefficient allows for the formal rejection or acceptance of the hypothesis that a potentially small, continuous dataset is normally distributed by comparing the value of the PPCC to a table of critical values. A sufficiently high coefficient indicates that the data are normally distributed. Using this approach, the data from C₁, C₂, F₁, F₂ and F₄ (see Figure 1E–G and 2E–H) are accepted, whereas the data from F₃ (see Figure 1H) is rejected. Rejection can occur for many reasons, including poor-data collection, corrupted experimental conditions or insufficient sample size. The PPCC and corresponding critical values for each dataset are summarized in Table 1.

Minimum sample size

Experiments in molecular biology are often limited to three replicate trials due to limitations in time, financial resources or experimental complexity. Nonetheless, triplicate experiments do not typically satisfy the requirements of proper statistical analysis. Thus, the question remains as to how many replicate experiments should be carried out. Equation 12 is commonly used to answer this question (17), but Kupper and Hafner (20) previously showed that the use of this expression for sample size estimation greatly underestimates the number of trials needed for a desired confidence interval. The corrected minimum sample size (N^*) can be found by consulting a lookup table assuming (i) the data are normally distributed, (ii) a desired confidence level (e.g. α = 0.05), and (iii) the amount of experimental error was decided a priori [see (20) and (http://dinmanlab.umd.edu/statistics)]. Generally, the acceptable amount of error for the estimate of the mean is 5–10% of its true value.

For example, the F₁ dataset has a sample mean () and sample SD (s_N−1) of 0.0263 and 0.0017, respectively. Our goal is to do enough trials to be at least 95% confident that the sample mean is at least within 10% of the true value of the mean. Using Equation 12, we find that the minimum uncorrected number of trials is Ñ. However, using Kupper and Hafner's method for sample size correction, the minimum corrected sample size is N^* = 13. With 40 samples, the F₁ dataset is of sufficient size. The values of Ñ, N^*, and the actual sample size N for each dataset are listed in Table 1.

Ratiometric statistics

Once each ratiometric dataset has been trimmed of outliers, passed a test for normalcy and found to be of sufficient size, it is then possible to begin calculating the ratiometric efficiency () of an experimental reporter relative to that of its corresponding control reporter (see Equation 13). The reporters we use in our laboratory typically measure translational frameshifting: thus, in this case, is a measure of the frameshift efficiency of the −1 PRF signal present in the experimental DLA reporter constructs F₁–F₄. However, in other translational contexts, could be, for example, the frequency of IRES-promoted initiation, or read-through suppression. A serious pitfall associated with is the potential for the propagation of error in its estimation since it is derived from a ratio of two estimates, and . The correct reporting of the error on this measurement and its estimated variance should therefore be treated carefully. Equations 14–16 take the propagation of error into account and determine best estimates for the sample variance s_R², sample SD s_R and the standard error of the sample mean . Each expression of Equations 14–16 assumes two, independent and normally distributed datasets that are related by the ratio and each component dataset has potentially unequal sample sizes (N). The importance of the estimation of s_R² in Equation 14 cannot be overstated. This value is of particular importance when determining the statistical difference between two experiments (e.g. it is used in the t-test below).

Comparing datasets

The final stage is to determine whether the two experiments, each with their own respective values of and s_R², are statistically different. The published record of studies utilizing various bicistronic reporters shows a wide variety of methods including fold change, z-tests or χ²-tests. For comparisons between datasets, a z-test is appropriate only for larger datasets with at least 40 samples each. Datasets for bicistronic reporter systems are usually not this large. Furthermore, a χ²-test is inappropriate as it requires both large sample sizes and that the data be separated of into discrete categorical values. We instead use the unpaired two-sample t-test (see Equations 17 and 18) since it is more appropriate for smaller continuous datasets (17). The requirements of this test are that the data must be normally distributed and independent, which are satisfied by the bicistronic assay datasets presented here. The hypothesis tested against states that two datasets (X and Y) come from the same population. A rejected hypothesis therefore affirms that the two datasets are indeed statistically different at some predefined confidence level (e.g. 95%, α = 0.05). The P-value obtained from this test is an estimation of the probability of an incorrect conclusion (see Table 2).

Table 2. Summary of unpaired two-sample t-test for the effects of anisomycin on ribosomal frameshifting.

Comparing drug versus no drug
Fold change	−21.17%
Degrees of freedom (v)	18
t-statistic	8.92
α	0.001
Critical value	3.92
Significant?	Yes
P-value	5.04 × 10−8

The results indicate that anisomycin effectively inhibits programmed −1 frameshifting (see text for details).

Two working examples

Our first set of frameshift reporters comprises F₁, F₂ and F₃, which are each compared to a zero-frame control reporter C₁ to measure the efficiency of frameshifting. Each of these experimental reporters contains a −1 PRF signal that was either previously characterized or that has been recently computationally identified (J. L. J. and J. D. D., manuscript in preparation). Our results show that the −1 PRF signals in reporters F₁ and F₂ are ‘well behaved’ in that they pass several tests for statistical reliability. Though the L-A virus −1 PRF signal (F₁) promoted high levels of frameshifting (Table 1, , 7.98% ± 0.165%), the PRF signal in reporter F₂ (a putative PRF signal from BUB3) is shown to be less efficient (Table 1, 0.70% ± 0.019%) but very reliable. Furthermore, the efficiency of frameshifting for F₃ (a putative PRF signal from TBF1) was not calculated (Table 1, n/c) because the dataset itself failed two important statistical reliability tests. Without the techniques presented in this report, the recoding efficiency of F₃ may have be erroneously calculated and subsequently incorrectly reported as being ∼1.86%. Thus, by utilizing these ‘quality control’ procedures, we are able to firmly reject the possibility of F₃ as being a ‘real’ −1 PRF signal, whereas the putative signal from BUB3 is indeed functional. This important, and often overlooked, aspect of reliability testing of experimental measurements demonstrates the importance of quantitatively determining the linearity, minimum sample size and normalcy of each dataset studied.

In our second example, we begin with two DLRs: a zero-frame control, C₂, and a frameshift reporter, F₄, representing the functional SARS-CoV ORF 1a-1b frameshift signal (E. P. Plant and J. D. D, manuscript in preparation). This experiment is designed to study the efficiency of ribosomal frameshifting in the presence or absence of the drug anisomycin. This well-characterized translational inhibitor is known to suppress programmed −1 ribosomal frameshifting in vivo (25). The initial dataset of raw luminescence values for each construct (with and without drug) are plotted in Figure 2A–D. The raw data are found to be linear and outliers are identified and excluded as described previously. Furthermore, each dataset passes the PPCC test for being normally distributed (see Figure 2E–H and Table 1). The values of (i.e. −1 PRF efficiency) are 2.62% ± 0.16% in the presence of 20 μg/ml anisomycin and 3.33% ± 0.50% in its absence. Using the unpaired two-sample t-test in Equations 17 and 18, we find t = 8.92 with 18 degrees of freedom (v = 18) for the effects of anisomycin on −1 PRF. A significance level of α = 0.001 indicates a critical value of t = 3.92. Numerical computation of the P-value of this finding yields P = 5.04 × 10⁻⁸; an extremely significant result. In contrast, had we applied the statistical methods utilized in previously published studies that employed bicistronic reporters (6,26,27), the variances of the two −1 PRF efficiencies would have been incorrectly calculated (data not shown). Specifically, although these alternative methods would also have indicated an ∼20% reduction in −1 PRF efficiency due to anisomycin, they would have generated incorrect P-values (P = 0.804), leading researchers conclude that anisomycin does not significantly affect −1 PRF. In contrast, application of our more rigorous statistical analytical method soundly demonstrates that anisomycin does affect programmed −1 ribosomal frameshifting in a very reproducible and statistically significant way.

DISCUSSION

In this technical report, we have outlined a statistical analysis pipeline for ratiometric data potentially derived from a wide variety of polycistronic reporter assay systems. As an example, we have successfully applied the methods outlined above to data obtained from eight datasets originating from a series of DLAs designed to measure programmed −1 ribosomal frameshifting. The reporter plasmids vary only in the nature of recoding element positioned between the Renilla and firefly ORFs. Our statistical analysis pipeline can be applied to other dual reporter systems and easily be extended to any polycistronic assay system that relies on ratiometric data. The importance of the proper statistical analysis of any dataset cannot be overstated. At a minimum, this report brings to light the statistical issues surrounding bi- or polycistronic reporter data and opens the door to more rigorous treatment of this particular data type. It is our hope that the synthesis of methodologies presented here will serve as a white paper for researchers who utilize polycistronic reporter systems. To simplify the application of the methods presented in this report, we have developed an online tutorial and several Excel spreadsheets that can be used as templates by the general research community.

We address several key features for analysis of bicistronic data in particular and summarize our findings here. First, the nature of most bicistronic reporter assays present researchers with two components of information for each experiment that are further combined into a ratio. The data are most often reported as a ratio of gene X to gene Y expression. The goal is usually to measure the expression ratio of genes X/Y in an experimental construct and observe any differences in ratio of genes X/Y expression compared with a known control. Since the data are both ratiometric and continuous in nature, propagation of error in the datasets is a primary issue that must be addressed carefully. We address this issue with Equations 14–16 for estimates of the sample variance, sample SDs and the standard error of the sample mean for a ratio of two normally distributed sample means. Once an appropriate measure of the combined variance and corresponding error is found, only then it is possible to determine whether two independent datasets are statistically different.

Second, methods designed to rule out certain data points as outliers have largely gone unreported in the literature. Outliers can, however, severely impact the quality and subsequent analysis of any dataset. Thus, their systematic exclusion should be an important first step in any analysis pipeline. We present a simple, standardized method for outlier exclusion that makes no assumptions about the underlying distribution of the data using Equations 2–4. By exploiting the property of fs, we are able to systematically exclude data points that are above or below the median. This method does not necessarily always result in the exclusion of data; frequently the maximum or minimum values for any dataset are well within the outlier boundaries. The net result is a robust, trimmed dataset that is less affected by the presence of a few outliers.

Third, a common assumption is that data are normally distributed. This is necessary because common statistical analyses rely on this assumption in order to remain valid. However, biological data are often not normally distributed due to the tendency of living cells to either maximize or minimize the efficiency of any given process. Surprisingly, there has not been a single publication utilizing a bicistronic reporter assay system that has reported attempts to check the validity of this assumption. In this report, we outline the procedure for constructing probability plots of each dataset, and present a statistically sound method for determining the normality of the data using PPCCs (see Equation 11). No subsequent statistical analysis that is fundamentally based on the properties of a normal distribution would be valid without first confirming the normalcy of the data. Failure to do this quantitatively could lead researchers to make false conclusions from their results.

Fourth, as a rule-of-thumb molecular biology experiments are typically carried out in triplicate. This is often a reality that is expected and unavoidable because many experiments are time consuming, expensive or both (e.g. blots, gel shift assays, etc.). We suggest that the ‘Three's a Charm’ rule-of-thumb should be reconsidered when experiments are relatively simple and rapid. Most bicistronic reporter assays fit these criteria because they usually take advantage of the specific activity of a pair of easily assayable enzymes. In Equation 12, we present a straightforward method to calculate the minimum corrected sample size (N^*) needed to achieve a specific level of confidence in the results. The researcher needs only to decide a priori what the acceptable level of error is for each dataset.

Using a metric to determine minimum sample size, however statistically sound, may seem unreasonable or simply cost prohibitive to some, particularly for smaller labs with limited resources. However, consider the following example. Typically, with respect to the DLA system in E.coli (6) or S.cerevisiae (7), it is not unusual for cell lysates to be collected over a course of 3 days and for three luminescence readings (firefly and Renilla) to be averaged together on each day. This produces only a single luminescence ratio each day for each reporter. Not only does this approach inadvertently cause another layer of error propagation (average of averages at the experiments end), but it is both cost and time prohibitive if the goal is to gather enough data points to satisfy Kupper and Hafner's test for minimum corrected sample size. A suitable compromise is to pool individual reads from each lysate into a larger dataset before excluding outliers and calculating any statistics. In this case, the scenario outlined above would produce nine data points each for Renilla and firefly luciferase; three for each cell lysate for each of 3 days. If the cell types, reporters used and experimental conditions are identical, pooling the data in this way builds a rigorous dataset that is more resistant to experimental bias. Furthermore, if three separate cell cultures were grown in parallel on each day, then 27 data points would then be collected for each experimental condition in same amount of time. By pooling the raw data together, it becomes possible to build a larger dataset in less time.

With regard to the effects of anisomycin on −1 PRF, the application of this analytical process is significant in two respects. First, as noted above, reliance on common calculations of mean and standard errors would have led to the incorrect conclusion that anisomycin does not affect −1 PRF. This could potentially result in the unfortunate consequence of disqualifying anisomycin and other pyrrolidines (28) for consideration as antiviral agents. Thus, the analysis presented here serves as a demonstration that the application of proper quantitative methods is critical for more than simply academic reasons. Second, the confirmation that anisomycin inhibits −1 PRF is important in helping to define the mechanism of this process. We previously proposed a model based on structural and biochemical data in which the −1 frameshift occurs after accommodation of the aminoacyl-tRNA (aa-tRNA) into the ribosomal A-site (the A/A hybrid state), and prior to peptidyltransfer (12). Recently, another group suggested that the shift occurs prior to accommodation when the aa-tRNA occupies the A/T hybrid state, i.e. while the anticodon of the aa-tRNA is in the decoding center A-site, but the 3′ acceptor end has not yet been positioned into the peptidyltransferase center (29). Anisomycin binds in the A-site of the peptidyltransferase center (30) inhibiting binding of the acceptor end of the aa-tRNA into the peptidyltransferase center (31,32). The observation that −1 PRF is inhibited by anisomycin is consistent with our model in that inhibiting the formation of the proposed substrate for the shift (i.e. inhibiting formation of the aa-tRNA in the A/A hybrid state) decreased the frequency of the reaction. In contrast, anisomycin does not affect the interaction of the aa-tRNA anticodon with the decoding center, i.e. does not impact on the formation of the aa-tRNA in the A/T hybrid state, and would not be predicted to affect −1 PRF if this were the substrate for the shift. In sum, the application of the rigorous statistical analyses to genetic data reinforces prior structural and biochemical analyses, strengthening the argument that programmed −1 ribosomal frameshifting occurs after accommodation of the aa-tRNA into the A/A hybrid state.

SUPPLEMENTARY MATERIAL

Excel spreadsheets are available at NAR Online, and a web-based tutorial from http://www.dinmanlab.umd.edu/statistics.